Selecting global climate models for regional climate change studies

Abstract

Regional or local climate change modeling studies currently require starting with a global climate model, then downscaling to the region of interest. How should global models be chosen for such studies, and what effect do such choices have? This question is addressed in the context of a regional climate detection and attribution (D&A) study of January-February-March (JFM) temperature over the western U.S. Models are often selected for a regional D&A analysis based on the quality of the simulated regional climate. Accordingly, 42 performance metrics based on seasonal temperature and precipitation, the El Nino/Southern Oscillation (ENSO), and the Pacific Decadal Oscillation are constructed and applied to 21 global models. However, no strong relationship is found between the score of the models on the metrics and results of the D&A analysis. Instead, the importance of having ensembles of runs with enough realizations to reduce the effects of natural internal climate variability is emphasized. Also, the superiority of the multimodel ensemble average (MM) to any 1 individual model, already found in global studies examining the mean climate, is true in this regional study that includes measures of variability as well. Evidence is shown that this superiority is largely caused by the cancellation of offsetting errors in the individual global models. Results with both the MM and models picked randomly confirm the original D&A results of anthropogenically forced JFM temperature changes in the western U.S. Future projections of temperature do not depend on model performance until the 2080s, after which the better performing models show warmer temperatures.

Work for the Intergovernmental Panel on Climate Change (IPCC) fourth assessment report (AR4) has produced global climate model data from groups around the world. These data have been collected in the CMIP3 dataset (1), which is archived at the Program for Climate Model Diagnosis and Intercomparison at Lawrence Livermore National Laboratory (LLNL). The CMIP3 data are increasingly being downscaled and used to address regional and local issues in water management, agriculture, wildfire mitigation, and ecosystem change. A problem such studies face is how to select the global models to use in the regional studies (2–4). What effect does picking different global models have on the regional climate study results? If different global models give different downscaled results, what strategy should be used for selecting the global models? Are there overall strategies that can be used to guide the choice of models? As more researchers begin using climate models for regional applications, these questions become ever more important.

The present paper and accompanying work investigate these questions. Here we address the regional problem, using as a demonstration case a recent detection and attribution (D&A) study of changes in the hydrological cycle of the western United States (B08 hereafter) (5–8). The insights we have obtained should relate not only to B08, but more generally to regional climate change studies that rely on information from multiple models.

A common approach in such studies is simply to average over all models with available data (9). This approach is justified by global scale results, generally examining only the mean climate, that show the “average model” is often the best (10–14). This procedure weights models that do a poor job simulating the region of interest equally with those that do a good job. It is natural to wonder whether there is a better strategy and whether this result holds for model variability as well.

An increasingly popular approach is to generate metrics of model skill, then prequalify models based on their ability to simulate climate in the region or variable of interest (2–5, 15). However, it is worth examining the underlying assumptions of this strategy. Do the models selected in this fashion provide an estimate of climate change over the historical record that is closer to observations than models rejected on this basis?

Models.

We use global model January-February-March (JFM) minimum near-surface temperature (“tasmin”) over the western U.S. as a surrogate for the multivariate analysis of B08. This variable was used directly by B08 in addition to snow water equivalent and runoff, which are more influenced by small-scale topography. We also reuse the internal climate variability (noise) estimates from B08, obtained from 1,600 years of simulation with 2 different models. B08 and its companion works found that these models provided a realistic noise estimate for use in D&A studies. Our focus here is on the climate change “signal,” not the internal variability “noise.” The reasoning is that a model with an unrealistic noise level can be identified by comparing with the observations. However, for a D&A study, it is not permissible to qualify a model for use based on how well its climate change signal agrees with observed trends. This is because retaining only models whose climate change signal agreed with observations would make it impossible to find that the observed and model-estimated signals disagree, in essence predetermining the study's conclusions.

Data from 21 global models, many with multiple realizations (see supporting information (SI) Text and Table S1), forced by 20th century changes in anthropogenic and natural factors were obtained from the LLNL CMIP3 archive (http://www-pcmdi.llnl.gov/ipcc/about_ipcc.php). We adopt the CMIP3 terminology: near-surface air temperature is “tas,” daily minimum tas is “tasmin,” surface temperature is “ts,” and precipitation is “pr”. The atmospheric resolution for the models varies (12). Many models in the archive have less tasmin than ts and pr data; only 13 have more than 1 realization with tasmin. The period analyzed is 1960–1999, because most models have no more than 40 years of tasmin data in the archive. To facilitate comparison, all model fields and the observations were put onto a common 1°×1° grid over the western U.S. using bicubic interpolation (Fig. S1).

We compare model temperatures and precipitation with a daily observed dataset gridded at 1/8° longitude by latitude resolution across the western U.S. (16). This dataset is based on the National Weather Service co-operative (co-op) network of stations, adjusted for changes in instrumentation, location, or the surrounding environment.

For sea surface temperature, we combined observed data over the period 1945–1982 (17) with National Centers for Environmental Prediction (NCEP) optimally interpolated data over the period 1983–2007 (ftp://ftp.emc.ncep.noaa.gov/cmb/sst/oisst_v2) (18).

Statistical Methods.

We evaluate the models with a broad spectrum of metrics based on temperature and precipitation, which are key to climate impacts over most of the world. More details of the metrics are given in SI Text, with a brief summary here.

All of our metrics are based on the spatial mean squared error (MSE), which can be decomposed as (19, 20):

where m(x) is the model variable of interest, o(x) are the observations, overbars indicate spatial averages, r_m,o is the product moment spatial correlation coefficient between the model and observations, and s_m and s_o are the sample spatial standard deviation of the model and observations, respectively. When comparing variables with different units, we transform the MSE to a (dimensionless) spatial skill score (SS):

A model field identical to observations has a skill score of 1, whereas a model that predicts the correct mean in a limited region, but only as a completely featureless, uniform pattern, yields a skill score of 0.

Let e_m = (m̄ − Н) be the “mean error,” and e_p = (s_m² + s_o² − 2s_ms_oγ_m,o)^1/2 be the “pattern error”; then the root mean squared error (RMSE) = (e_m² + e_p²)^1/2. This quantity lends itself to a geometric interpretation, where the mean and pattern errors can be plotted on orthogonal axes and the RMSE is the distance to the origin (cf. 20). Similarly, SS can be decomposed into the mean error, the pattern correlation (squared) between the model and observations, and the “conditional bias,” which describes a model tendency to over- or under-predict excursions (19). These decompositions are used in the next section.

Temporal variability is evaluated by using spatial patterns of temporal behavior. For example, computing the standard deviation at each point yields a spatial pattern of standard deviations; we then compare this with the same field estimated from observations. When ensemble averaging, either for one or across multiple models, we average the variability measures from each realization. We do not first ensemble average the variable, then compute its variability, which would underestimate the true variability.

We use 42 metrics to characterize each model. We begin with 4 seasonal December-January-February (DJF), March-April-May (MAM), June-July-August (JJA), and September-October- November (SON) averages of 2 variables (tas and pr) in 4 aspects: The seasonal mean and the temporal standard deviation of the seasonal data averaged into 1-, 5-, and 10-year blocks. This process gives 32 metrics. We also include the amplitude and phase of the annual harmonic for each variable, adding another 4 metrics.

The El Nino/Southern Oscillation (ENSO) and North Pacific Decadal Oscillation (NPO or PDO) (21) have a strong effect on the climate of our region. For each mode, we construct one metric describing the climate mode's sea surface temperature pattern in the region where it is defined and additional metrics describing the teleconnected effects of the climate mode in western U.S. tas and pr. This process yields another 6 metrics, for a total of 42. A method for dealing with redundant information in the metrics is given in SI Text, section 3.

All of the models have trouble simulating the amplitude of the seasonal cycle of precipitation in the western U.S. (Figs. S2–S5), a problem also noted in the previous generation of models (2). The CMIP3 models do not capture the sharp rain shadow of the Olympic and Cascade mountains, instead smearing the peak precipitation values out over a much wider region than observed. This error is likely related to horizontal resolution and is reduced as model resolution increases (22).

Another poorly simulated field is low-frequency temperature variability in spring (MAM). The models more systematically underestimate the strength of the temperature variability as the averaging period increases from 1 to 5 to 10 years. We also find that precipitation tends to have better skill scores than temperature. In this region at least, the common perception that the global models do a better job simulating temperature than precipitation does not seem to be borne out, with the exception of the amplitude of the annual harmonic of precipitation. However, this finding may be influenced by our choice of normalization in forming the skill scores, and uncertainties in observed pr are likely higher than in tas and are not accounted for in the metrics.

In evaluating the model temperature trends, we use most of the formal, fingerprint-based D&A methodology used in B08 and described more fully in ref. 7. However, no downscaling is done because of the resources that would be required to downscale all 21 models. Instead, observations and model fields are interpolated onto a common 1 °×1 ° grid. Also, we reuse the 2 control runs from B08 (the PCM and CCSM3-FV models) to estimate natural internal climate variability, because we are focusing on the climate change signal rather than the natural internal variability noise. These control runs were shown to be in reasonable accord with observations in their amplitude of ENSO and the PDO, the annual and pentadal variability of regional snow cover, and variability in large-scale precipitation minus evaporation as inferred from downscaled runoff (6, 7).

Briefly, a single spatial fingerprint of warming was defined as the leading empirical orthogonal function of the model-averaged-temperature time series over 9 mountainous regions in the western U.S. (Fig. S1). Year by year, the dot product of the regional temperatures from each model (and the observations) and the fingerprint was computed, yielding a time series of dot products. Our evaluation is based on the least-squares best fit linear trend of the dot product time series, which is simply referred to as the “trend” below. This approach differs from a simple regional averaged temperature trend by assigning weights to each region depending on how much it participates in the model-estimated warming signal.

Results

The models produce temperature trends in the western U.S. ranging from −0.05 to +0.21 °C/decade. The observed trend is +0.10 °C/decade. All 5 models with a negative trend have only 1 realization, whereas none of the 13 models with more than 1 realization has a negative ensemble-averaged trend. Because of the importance of natural variability in a limited domain, it is not uncommon for models with a strongly positive ensemble-averaged trend to have individual realizations with a negative trend. A single model realization does not provide a reliable estimate of the warming signal.

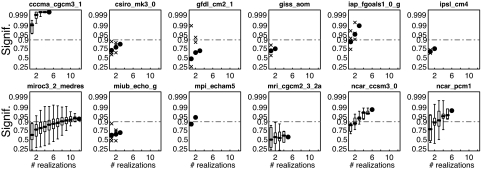
The relationship between N (the number of realizations from a single model included in the ensemble average) and the significance of the model's ensemble-averaged trend is shown in Fig. 1. Significance is assessed by comparing the ensemble-averaged trend with the distribution of trends found in the control runs, which do not include anthropogenic forcing. The significance is computed with all possible combinations of realizations for any given N. [For example, if a model has 4 realizations, 3 estimates of significance for n = 3 were computed: the average of runs (1, 2, 3), (1, 2, 4), and (2, 3, 4)]. All but 1 model show an upward trend in significance as the number of realizations increases because of the averaging away of natural internal variability. The results from some models suggest their trends would be significant if more realizations were available to reduce the noise (for example, csiro-mk3.0). At least 1 model, mri-cgcm2.3.2a, shows no detectable trend and scant evidence one would be detectable even if more realizations were available.

Fig. 1.

Statistical significance of the model JFM Tmin trend in the western U.S. (projected onto the anthropogenic fingerprint) as a function of the number of ensemble members included in the ensemble averaging. If the number of combinations of ensemble members for the indicated number of ensembles is 4 or more, whisker plots display the minimum value, 25th, 50th, and 75th percentiles, and the maximum value; otherwise, x's indicate the individual values and dots indicate the mean value.

To explore this result further, we calculate what the D&A results of B08 might have been if the 14 realizations used there had been chosen randomly from all of the models available (63 realizations total), rather than the 10 miroc-3.2 (medres) and 4 ncar-pcm1 realizations actually used. Using 10,000 random selections of 14 realizations, we found 96% of the random trials resulted in a trend significant at the 90% level, and 90% of the trials gave a trend significant at the 95% level. Therefore, the finding of B08 and ref. 8 that the JFM tasmin trend over the western U.S. is both detectable (against the background of natural internal climate variability) and attributable to combined anthropogenic and natural effects is robust to the range of temperature trends found in the CMIP3 models.

The Role of Model Quality.

Although choosing models randomly verifies the results in B08, it seems we should be able to do better. It is more appealing to use models that do a good job simulating climate in the region of interest. Does doing this make any difference to the results of our D&A study?

We order the models in terms of quality by considering each model's skill scores to be a point in n_metrics dimensional space, where n_metrics = 42. In the results shown here, the ordering is given by Δ_SS, the Euclidian distance from the model's point to perfect skill at point (1, 1, 1, …, 1). Lower values of Δ_SS indicate better matches to observations. A similar distance-based quality measure has been used before (4), although other workers have determined overall model quality by ranking the models in each metric, then averaging the ranks across the different metrics (12). We emphasize Δ_SS because it allows metrics with a wide spread of skill to have a larger impact on relative model quality than metrics with a small spread. Models can change their position in the ordering by up to 5 places depending on which method is used. However, we also tried the averaged-rank method and found it did not affect our conclusions.

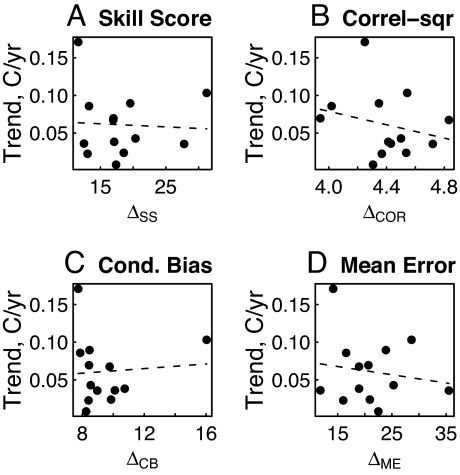
Fig. 2A shows how the magnitude of the JFM tasmin trend relates to Δ_SS. This value has been calculated using only the 13 models that have more than 1 realization with tasmin, to reduce the effects of natural internal variability. There is no statistically significant relationship between this measure of model quality and the regional tasmin trend. Fig. 2 B–D show similar results calculated with the Δs from the individual skill score components (the pattern correlation squared, conditional bias, and mean error). Again, there are no significant relationships. We repeated the analysis including models with only 1 ensemble member and again found no statistically significant relationships.

Fig. 2.

Scatterplots between various measures of model quality (x axis) and JFM tasmin trend (C/yr; y axis). (A) Using Δ calculated from the skill score (Fig. S2) as the measure of model quality. (B–D) Using Δ from the correlation-squared (Fig. S3), conditional bias (Fig. S4), and unconditional bias (Fig. S5), respectively. (A–D) Lower Δ means better agreement with observations.

These results are with individual models, but perhaps averaging across models is required for any relationships to be discerned. Accordingly, we separated the models into groups of the top 10 and bottom 11 based on Δ_SS and computed the mean JFM tasmin trend for each group. The difference in trend between the groups was compared with Monte Carlo estimates of the difference using models partitioned randomly, rather than on the basis of model quality. We found no statistically significant difference in the distribution of trends obtained when partitioning by model quality compared with random partitioning.

In summary, models can be selected for use in regional climate change studies based on the quality of their climate simulation in the region of interest. However, in our demonstration application this selection makes no systematic difference to the D&A results.

The Multimodel Ensemble.

The multimodel ensemble average (MM) is the first, second, first, and third best model in the overall skill score, correlation-squared, conditional bias, and mean error terms, respectively. The superiority of MM has been found in previous climate and numerical weather prediction studies (10–14), which have generally examined the mean climate rather than variability. These works attribute the majority of this effect to the averaging removing “random” errors between the models, but typically have shown little evidence supporting this. We now examine whether our results support this mechanism.

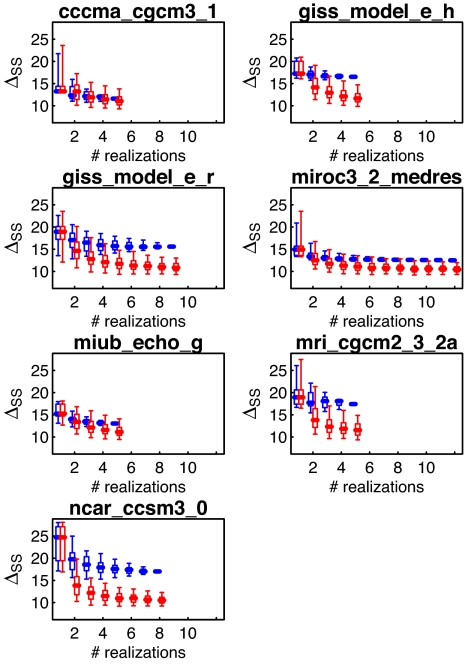
Given the important role ensemble size plays in D&A studies (Fig. 1), is MM better simply because it includes information from far more realizations than any individual model? Fig. 3 shows Δ_SS as progressively more realizations from the same model (blue) or randomly selected different models (red) are added to the ensemble average. (For both symbols, the case for n = 1 includes only realizations from the model indicated in the title; other details are given in SI Text.) For most models, skill increases (Δ_SS decreases) more quickly when different models are added to the mix than when more realizations of the same model are included. (The exception is cccma-cgcm3.1, the model with smallest Δ_SS.) This holds true even when the number of ensemble members is the same in the same-model vs. multiple-model case. Therefore, the improved performance of MM in simulating western U.S. climate does not arise simply because of a larger number of realizations in the multimodel average. Rather, incorporating information from different models contributes to the increase in skill. A similar conclusion was reached when examining global medium-range weather forecasts (19).

Fig. 3.

Model distance from perfect skill (Δ_SS) as a function of the number of realizations included in the ensemble average. Lower values indicate better agreement with observations. Blue symbols show the change in Δ_SS as progressively more ensemble members from the same model are added. Red symbols show the change as ensemble members from different models are added. Whiskers show 5th, 25th, 50th, 75th, and 95th percentiles. Symbols are horizontally offset by a small amount to avoid overlap.

Fig. 3 also shows that Δ_SS values tend to approach an asymptote after approximately 5 different models have been averaged together. This behavior suggests that stable results in D&A studies could be reached with far fewer than the 21 models used here.

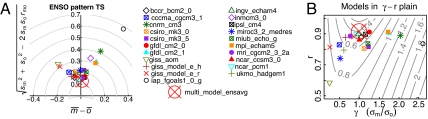
More insight into how MM reduces overall errors is gained by considering the RMSE plots. Fig. 4Adisplays an example for the ENSO pattern in sea surface temperatures. Two features stand out: (i) on the mean error (m̄ − ō) axis, errors tend to be distributed around 0; and (ii) on the pattern error y axis, MM tends to have less error than any individual model.

Fig. 4.

Errors in the individual models and the multimodel ensemble average for one particular metric. (A) Shown is RMSE plot for the ENSO pattern in surface temperature (ts). (B) Shown is pattern error in ENSO ts (y axis of A) decomposed into γ (the ratio of the standard deviation of the model to the observed) and r (the pattern correlation between the model and observed fields). Contours of the y axis value (the pattern error) from A are also shown on B; there is a minimum value of 0 located at (1, 1), and all values increase away from this minimum.

For the mean error, these results show that averaging across models increases skill because the errors across different models tend to be offsetting, which supports the line of argument in ref. 11.

The situation is less clear for the pattern error because MM tends to fall below (have less error than) the other model results, rather than falling in the center of the model cloud of points. We can write the pattern error as e_p = s_o(1 + γ² − 2 γr_m,o)^1/2, where γ ≡ s_m/s_o (cf. 20). For any particular metric, s_o (the standard deviation of the observations) is fixed, so e_p depends only on γ (the ratio of model to observed standard deviation) and r_m,o (the pattern correlation). The model values in γ - r space are shown in Fig. 4B. MM falls in the middle of the distribution of individual model points on the γ axis; i.e., the errors in the ratio of model standard deviation to observed standard deviation tend to be distributed around 1, similar to the distribution of the mean error around zero. Along the r axis, MM is again better than any individual model. Because this now is simply the pattern correlation between the model and observed fields, we suggest this behavior is caused by effectively random spatial errors in the model patterns, which again tend to average to 0. Examination of various fields, such as the ENSO pattern of surface temperatures, bears this out.

In summary, the MM tends to perform better than any individual model, but not because of the greater number of realizations in MM. Rather, it can be understood by decomposing the model errors into components arising from the mean error, an error in the ratio of the model's variance to observed, and the pattern correlation between the model and observed. Mean errors tend to be distributed around 0, and the variance ratio tends to be distributed around 1. Averaging across models reduces the error in both these aspects, both in the mean climate and when variability is considered. For the pattern correlation, averaging across models tends to give better correlation with observations than any individual model, which is consistent with the argument that effectively random spatial errors are being reduced by averaging. An analysis of cloud data concluded that the spatial smoothing effect of multimodel averaging also had some beneficial effect, although less than the averaging away of model errors (14).

The MM is formed with all models weighted equally. As an experiment, we repeatedly used a minimization procedure (with perturbed initial guesses) to find different sets of model weights that resulted in improved MM skill. Although we found many sets of weights with better skill, even when using cross-validation approaches to minimize “curve fitting,” individual model weights were not consistent between different sets of weights. We conclude that optimizing MM skill in this way is not robust.

Is MM always the best choice, even for small subsets of metrics? Using randomly selected subsets of 2 to 41 metrics, we find that MM is most likely to be the best choice for 3 or more metrics (Fig. S6). For 8 or more metrics, MM has >45% chance of being the best choice, far exceeding the likelihood of any individual model.

Our results show the best way we currently have to use information from multiple global model runs in a regional detection and attribution study is simply to form the MM. Neither selecting the models based on the quality of their climate simulations in the region of interest nor forming an optimized ensemble average based on maximizing skill resulted in a superior result over the historical period. Accordingly, we repeated our demonstration test case of JFM tasmin D&A by using MM instead of just the 2 global models used in B08. We find both detection and attribution of an anthropogenic climate change signal in western U.S. temperatures are achieved and statistically significant at the 99% level, even with only 40 years of data used here (vs. 50 years in B08).

Future Projections Based On Model Quality.

We have focused on the historical period because D&A studies require observations. A related question is whether future climate projections in our region of interest are a function of model quality. It has been found that precipitation projections over the western U.S. have no relationship to model quality, but that models with less error over the historical period predict warmer future temperatures than models with more error (2). Examination of a more limited domain, California alone, has found little relationship between the mean or spread of temperature projections and model quality metrics (3, 4).

We computed the multimodel mean annual tas over the western U.S. for all of the models, as well as for the 10 best (least Δ_SS) and 11 worst (greatest Δ_SS) models using our 42 metrics and the Special Report on Emissions Scenarios (SRES) A1B emissions scenario. The best and worst model means are statistically indistinguishable before the 2080s, but after that the better models predict ≈1 °C more warming (2.5 °C for the worst models vs. 3.5 °C for the best models).

A Monte Carlo test shows that ordering the models by quality also has the effect of ordering them by climate sensitivity more than would be expected by chance (P < 0.05), with the better models having higher climate sensitivity. Correlations between model quality and climate sensitivity are between 0.53 and 0.58 (P < 0.05), depending on which model quality (distance- or rank-based) and climate sensitivity (transient or equilibrium) measures are used.

Discussion

The availability of global climate model data generated for the IPCC AR4 report has led to an increasing number of studies that downscale global model results to examine regional impacts. This work has examined how to pick the global models to be used in a regional climate change D&A study by using as a test case JFM Tmin warming over the western U.S. (5).

It may be appealing to select global models based on the quality of their simulation in the region of interest. However, our results show this does not result in systematically different conclusions than obtained by picking models randomly. This finding suggests there is little relationship between (i) the quality of the model-simulated physics that determines regional temperature and precipitation, and (ii) the quality of the physics that determines the anthropogenic climate change signal. The lack of a direct connection between the physics might not be surprising, but the lack of connection between the model quality of the two is disconcerting.

What guidance, then, can be given for selecting which global model runs to use for a regional climate study? First, enough realizations must be chosen to account for the (strong) effects of the models' natural internal climate variability. In our test case, 14 realizations were found to be sufficient in the sense that randomly selected sets of 14 realizations from the pool of all realizations available was quite likely to have given the same results as originally obtained.

Second, we consistently found the MM to be superior to any individual model, even on estimates of variability, and for as few as 3 metrics. Although MM's superiority has been found in previous studies focusing on the mean climate, the reasons for this have not generally been elucidated. We have shown this is not simply caused by the larger number of realizations included in MM. Rather, it is caused by a tendency for the models to be distributed about a mean error of 0 and a mean ratio of model standard deviation to observed standard deviation of 1. We also find a tendency for the pattern correlation between MM and the observations to be higher than for most individual models. Averaging across models therefore tends to reduce all these errors. In our test case, model skill tended to asymptote after including approximately 5 different models, which suggests that stable hindcasts (and forecasts) can be obtained by including a manageably small group of models.

Our test case showed D&A results significant at the 99% level using MM. This result is as strong as found in the original work (5), yet using only 40 years of data instead of 50. Using an error-minimization procedure to weight the models that go into making MM can enhance overall skill, but is not robust. Also, the future climate projections of the top 10 models show ≈1 ^°C more warming over the western U.S. during this century than the bottom 11 models, although the differences are not distinguishable until after 2080. This result agrees with results using an earlier generation of models (2), although analysis over a smaller domain found that model quality had little effect on the models' projections (3, 4).

Finally, a D&A study involves comparing the climate change signal with the estimate of natural internal variability noise. This work has not assessed the impact of a poor noise estimate on the results. Instead we have focused on the signal, reusing an existing noise estimate that was shown to be realistic (5). Choosing a realistic noise estimate is relatively straightforward because it can be done by directly comparing the model results with observations. In contrast, a model's signal cannot be verified against the observations before using that model in a D&A study because that would be circular reasoning. There is no doubt, though, that a poor noise estimate can give misleading D&A results, and selection of a proper noise estimate is an integral part of any D&A study.

Supporting Information.

Further information, including Figs. S7 and S8, is available in SI.