Abstract
During the last decades, research on binary decision making elucidated some of the basic neural mechanisms underlying the decision-making process. Recently, the focus of experimental as well as modeling studies began to shift from simple binary choices to decision making with multiple alternatives. In this article, we address the question how different numbers of choice alternatives might be handled and encoded in the brain. We present a minimal, biophysically realistic spiking neuron model for decision making with multiple alternatives. Our model accounts for the relevant aspects of recent experimental data of a random-dot motion-discrimination task on both the cellular and behavioral level. Notably, all network parameters and inputs in our network are independent of the number of possible alternatives used in the tested experimental paradigms (2 and 4 alternatives and 2 alternatives with an angular separation of 90°). This avoids the use of extra top-down regulation mechanisms to adapt the network to the number of choices. Furthermore, we show that increasing the number of neurons encoding each choice alternative is positively related to the network's capacity of choice-number-independent decision making. Consequently, our results suggest a physiological advantage of a pooled, multineuron representation of choice alternatives.
Keywords: attractor networks, parietal cortex, random-dot motion, computational model
Already decades ago, decision making between multiple alternatives was the subject of psychophysical reaction-time studies, which revealed an increase in reaction times with the number of choices (1). With the objective of shedding light on the neural mechanisms underlying decision making, experimental and theoretical studies mainly focused on the simplest case of binary choice (2–4). Thereby, the lateral intraparietal area (LIP) was identified as a candidate for bounded integration in the decision process. Its neural activity correlates with the choices and reaction times of monkeys performing the random-dot motion (RDM) task (Fig. 1A), a well-established paradigm to test for accumulation and integration of evidence during decision making (5–7).
Fig. 1.
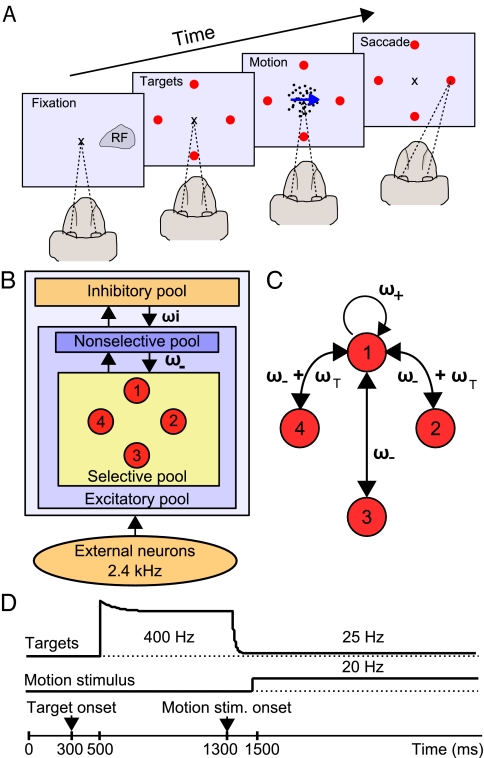
Experimental design, network architecture, and stimulation protocol. (A) The multiple-choice RDM task. While the monkey is fixating on a central point, the possible alternatives are indicated by 2 or 4 target signals. One of the targets is located in the response field (RF) of the LIP neuron recorded. After a delay, a patch of dynamic random dots appears with a proportion of dots moving coherently toward one of the targets, although the remaining dots keep moving randomly. The amount of coherence controls the task difficulty. The monkey has to decide on the net direction of motion and report its choice by a saccadic eye movement to the corresponding target. (B) Diagram of the spiking neuron network model. The network consists of a population of excitatory pyramidal neurons, structured into 4 selective pools (red) and a nonselective population, that inhibit each other through shared feedback from an inhibitory pool of interneurons. All neurons receive an external background input in the form of a Poisson spike train with a firing rate of 2.4 kHz, simulating spontaneous activity in the cerebral cortex. Unlabeled arrows denote a connectivity of 1. (C) Connectivity between selective pools shown representatively for 1 pool. The recurrent connection is denoted as ω+ and the interpool connection as ω-. Connection weights to and from neighboring pools are additionally enhanced by a value ωT. (D) Time course of input to selective pools. Depending on the number of alternatives a target input was applied to either 2 or 4 pools (see Methods and SI Methods for details). All selective pools receive an input representing the motion stimulus. Both inputs start with a latency of 200 ms after target or motion onset.
One biophysically realistic spiking neuron model of LIP that successfully simulated behavioral and physiological data from the binary RDM task was proposed by Wang (8). It is based on attractor dynamics and winner-take-all competition of 2 discrete selective populations of neurons (pools), each representing 1 alternative. Choice behavior, regardless of the number of alternatives, was captured successfully by some firing-rate models of neural networks (9–12). However, it is difficult to relate these rate models to possible physiological realizations of multiple-choice decision making.
Last year, experimental studies extended the RDM paradigm to more than 2 alternatives (11, 13). Churchland et al. (13) compared behavioral data and recordings from single LIP neurons of a 4-choice RDM task with the original 2-alternative task. Reaction times and error rates for 4 alternatives were found to be longer and higher, respectively, consistent with earlier studies (1). In an additional control condition with 2 targets separated by 90° (90° case), monkeys needed longer to decide than in the standard (180°) 2-alternative case but performed with the same accuracy. Notably, the experiments of Churchland et al. (13) provided the first electrophysiological data on a 4-alternative decision task.
Two theoretical studies (14, 15) just recently proposed continuous models of multiple-choice decision making. Both models can account for important findings of Churchland et al. (13). One, by Beck et al. (14), focused on the implementation of probability distributions and optimality, whereas the model of Furman and Wang (15), like our model, features high biophysical detail. It combines Wang's discrete 2-alternative model (8) with a model of analog sensory input (16), where a ring of neurons represents continuous directions of motion. However, it cannot account for the condition with 2 targets 90° apart. What is more, their model requires regulatory mechanisms depending on the number of alternatives, like an adaptation of the target input and an external top-down control signal during the decision-making period.
Here, we propose a different approach to extend the biophysically based binary decision model (8). Instead of a continuous representation, we increased the number of discrete neural populations that encode the possible alternatives (Fig. 1 B and C). Previously, networks with discrete populations have been adjusted to exhibit winner-take-all competition for one particular set of choice alternatives (8) or memory states (17). In our study, we analyzed how the network's competition regimes could be brought into accord for different numbers of alternatives. With a common parameter set for the 2, 4, and 90° case, we successfully simulated all experimental paradigms tested by Churchland et al. (13), without the need of any number-of-choice-dependent mechanism. Besides, we found that encoding decision alternatives by populations of neurons with a big relative pool size, a high “coding level,” favors a common decision regime for 2 and 4 choices. Taken together, our results indicate a physiological advantage of a pooled, multineuron representation of choice alternatives.
Results
In this study, we intended to design a minimal, biophysically realistic spiking neuron model of decision making for more than 2 alternatives to replicate and explain recent behavioral and electrophysiological data (13). We further aimed to extend Wang's analysis (8, 18) by exploring the effects of the size of the neural populations that encode the possible choices.
Neurons of 1 population (pool) share common inputs and connectivity. Our network contains 1 homogenous inhibitory pool of neurons, connected to all excitatory neurons. These are subdivided into 4 selective pools (red), encoding the 4 possible choices, and 1 nonselective pool, emulating the activity in the surrounding brain areas (Fig. 1B). Each selective pool contains f·NE neurons, where f is the coding level of the selective pools. The stochastic nature of the network due to finite-size effects allows decision formation even for unbiased inputs (19). This network feature and the shared feedback inhibition enable winner-take-all competition in a certain range of external inputs, referred to as “range of decision making.” The recurrent connectivity ω+ of neurons within a selective pool is higher than the connectivity ω− between selective pools (Fig. 1C). To model the circular spatial distribution of the targets in the experiment (Fig. 1A and ref. 13), we increased the connectivity between pools representing neighboring targets by the weight ωT (Fig. 1C). For a detailed description of the network connectivity, dynamics, and parameters please refer to Methods and supporting information (SI) Methods.
The proposed model can be viewed as a representation of a local microcircuit in area LIP. Consistent with LIP neurons during working memory tasks (6, 13, 20) our model exhibits persistent activity due to the strength of its recurrent connections (Fig. S1).
Spiking-Neuron Simulations in Comparison with Experimental Data.
Churchland et al. (13) tested monkeys on the RDM task (Fig. 1A), comparing 3 experimental paradigms. Either 2 opposing targets, 4 targets (90° apart) or 2 targets with an angular distance of 90° (90° case) were presented to the monkey, before the motion signal started. The targets indicated the possible directions of motion coherence to the monkey and continued to be present throughout the full trial.
In our model, the 4 selective pools are thought to represent the populations of neurons in LIP where the spatial information about 1 respective target signal and the motion directed toward this target are combined. Accordingly, we modeled the target and motion stimuli presented to the monkey as shown in Fig. 1D following the approach of Wong et al. (21). The motion input resembles the output of middle temporal area (MT) neurons projecting to LIP. MT activity represents a momentary estimate of motion direction and coherence (22). Importantly, the motion stimulus input is received by all selective neurons in the network, whereas the target input is applied just to the particular pools corresponding to the possible choices. The coherence of the random-dot motion, which controls the task difficulty, is modeled by a bias to the motion signal (see Methods). Our network is generally capable of decision making even without the target signal (Fig. S2). If the external input lies within the range of decision making, the shape of the target input affects reaction times, but not the network's capacity of decision making.
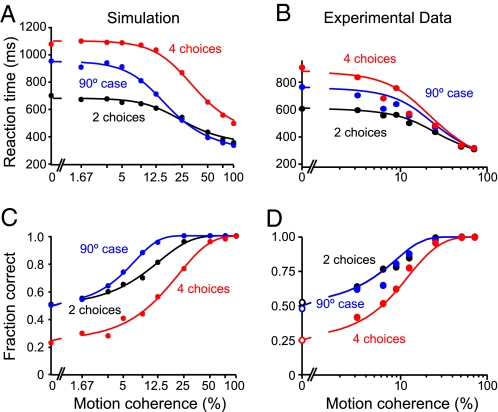
Churchland et al. (13) measured the accuracy and speed of the monkey's choices for several motion coherences (Fig. 2 B and D). Fig. 2 A and C shows the reaction times and performance, i.e., the fraction of correct choices, obtained by our simulations.
Fig. 2.
Speed and accuracy of simulated decisions and comparison to experimental data (13). (A) Simulated mean reaction times of correct trials as a function of motion coherence, fitted by a hyperbolic tangent function (see SI Methods). Decisions among 4 possible choices take longer than between 2 alternatives, whereas reaction times in the case of 2 choices 90° apart are intermediate between 2 and 4 choices for low coherence values. (B) Mean reaction times of 2 monkeys performing the RDM task (see ref. 13 for details). (C) Simulated psychometric functions, fitted by Weibull functions (see SI Methods). Performance in the 4-choice task is lower than for 2 choices. In the 90° case, accuracy is similar to the standard 2-choice case, with even higher performance at intermediate motion coherence. One thousand trials were simulated for each data point. At low motion coherence, some trials had to be excluded in the 4-alternative condition (at most 2%) and in the 90° case (at most 5%), because they failed to reach a decision within the simulation time of 4,000 ms (see SI Methods). (D) Experimentally observed performance of monkeys in the RDM task. B and D are adapted with permission from Churchland et al. (13). Please note that the scales of the simulated and experimental data are identical. For better assignment in A and C, the simulated motion coherence values are used as labels.
In the experiments as well as in our simulations, the reaction times were longer for 4 possible alternatives than for the 2-alternative case. For the 90° case, they were intermediate, with larger differences at lower motion strengths. Starting at chance level, the accuracy increased until it reached 100% for high motion strengths (Fig. 2 C and D). Except for very high coherences, choices among 4 alternatives were less accurate than binary decisions, also in comparison with the 90° case. There, the monkeys performed as well as in the standard 2-choice case. In our simulations, the accuracy in the 90° case resembles the standard binary case (Fig. 2C), with somewhat higher values at intermediate motion coherence. In summary, although we did not attempt a perfect quantitative fit to the experimental data, the psychometric functions obtained by our model simulations match the experimental observations (13) very well in all relevant aspects.
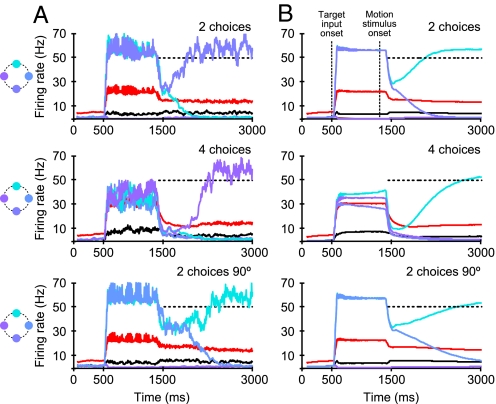
Behavioral differences between the 2, 4, and 90° case must be based on differences in the temporal evolution of the firing rates during the decision process. In Fig. 3 the simulated temporal evolution of firing rates is displayed for single trials and trial averages for each paradigm at zero motion coherence. Notably, even for zero motion strength, the network exhibits competition because of its stochastic dynamics (Fig. S3).
Fig. 3.
Simulated temporal evolution of population-averaged firing rates at zero motion coherence for single trials (A) and trial average over 1,000 network simulations (B). Red and black lines denote inhibitory and nonselective pools. Selective pools for single trials are colored according to the target illustrations (Right). For the trial average (B), the “winning” neural pools were averaged (cyan). The “losing” pools were averaged according to their inputs and relative target location to the winning population. During the target phase, the activity of the neurons representing the target-selective populations are increased to, on average (800- to 1,300-ms interval), 57 Hz in the 2-choice and 90° case compared with 36 Hz in the 4-choice case. This difference persists during the dip after the onset of the motion stimulus. Therefore, in the case of 4 targets the decision process starts at lower firing activity. The slope of the ramping activity is on average smaller in the 90° case (Bottom) than in the standard 2- (Top) and 4-choice (Middle) conditions, whereas its starting point is similar to the 2-choice case.
The general temporal structure is in good agreement with the experimental observations of LIP neurons (13, 20, 23): Throughout the target period, between target input and motion stimulus onset, the selective pools representing the targets exhibit elevated firing rates, followed by a “dip” to lower activity after motion onset and subsequent ramping activity. In the model, the dip in the firing rate is caused by a reduction of the target input with an assumed latency of only 80 ms before the motion signal is supposed to arrive in LIP with a latency of 200 ms (see SI Methods). Possible physiological origins are divided attention or upstream inhibition of the target signal caused by the onset of random-dot motion (15, 21). With the arrival of the motion signal, the integration process starts, and a decision is finally made, characterized by the ramping-up of activity of the winning pool.
A major discovery of Churchland et al. (13) was that, regardless of the number of targets and motion coherence, the decision process is terminated at 1 single activity threshold. Differences between the 2- and 4-choice cases were instead observed during the target phase and in the early motion epoch. For 4 choices, the target response was, on average, 16.1 ± 1.6 Hz lower than for 2 choices (13). Our model matches these findings well, even quantitatively. The average firing rates during the target phase for 4 alternatives are approximately 20 Hz lower than for 2 possible choices (Fig. 3 A and B). The population activity of the inhibitory neurons is ≈32 Hz (average over 800- to 1,300-ms interval) for 4 targets compared with 22 Hz for the 2-choice and 90° cases. Because there are no parameter differences between the task conditions, the differences in firing rate are caused solely by the shared feedback inhibition. The interneurons reduce the activity of the pyramidal neurons more for 4 alternatives. As in the experiments (13), the differences in firing rates of the selective target neurons persist during the dip after motion onset. Hence, the accumulation of evidence starts at lower values for 4 alternatives. In the trial average (Fig. 3B) the slope of data accumulation for correct trials is similar for the 2 conditions. In our simulations, in accordance with the experimental findings (13), a decision is reached when the population activity of 1 selective pool crosses a threshold of 50 Hz. The longer reaction times in the 4-choice task are therefore explained by the longer excursion of the neural activity to a common threshold in the experiments as well as in our simulations. The 90° condition is displayed in Fig. 3 A and B Bottom. Firing rates during the target phase are similar to the standard 2-choice case and slightly higher during the dip after motion onset. In our model, the longer average reaction times in the 90° case compared with the standard 2-choice task emerge through a prolonged symmetric state with high firing rates in both selective target pools (Fig. 3A Bottom). This leads to a smaller slope of average ramping activity toward the threshold (Fig. 3B Bottom) and thus to longer reaction times. The latter is also observed experimentally (13). The prolonged symmetric state, however, would hardly be measurable because the effect is lost in the trial average.
With increasing motion coherence and hence decreasing task difficulty, the build-up rates increase for all 3 tested paradigms (Fig. S4), explaining the faster reaction times (Fig. 2A).
Mean-Field Approximation and Range of Decision Making.
As already stressed, other than the respective number of pools receiving the target input, neither network parameters nor inputs in our model depend on the number of alternatives. The network thus exhibits categorical decision making for 2 and 4 choices for the same range of external input ν.
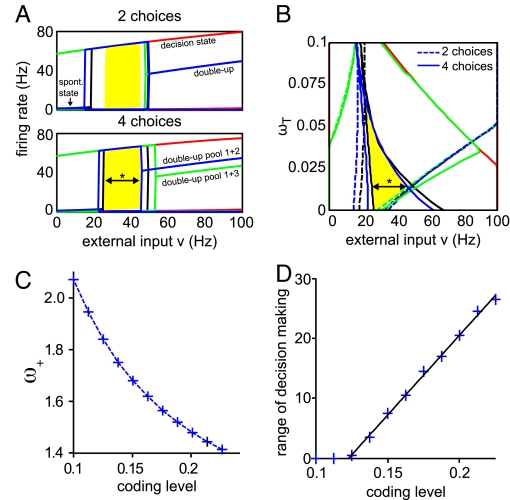
To investigate how this overlap of decision regimes for 2 and 4 choices depends on different network parameters, we used a mean-field approximation of the network model (see ref. 17 and SI Methods). With this approximation, the computational cost of scanning the parameter space can be drastically decreased, as the number of dynamical variables is reduced to 1 for each neural population. By solving the mean-field equation one obtains the approximated average firing rate of each neural population when the system has settled into a stationary state. Consequently, starting from different initial firing rates, the fixed points of the firing rates can be calculated for the selective network populations. There are 3 qualitatively different network states, whose existence and stability depend on the parameter configuration (18): The spontaneous state, with all pools firing at low rates; the decision state, where exactly 1 pool shows considerably higher activity than the others; and mixed states, with 2 or more pools firing at high rates. The 4 different initial conditions we used cover the possible firing rates at different temporal stages of the spiking simulation (see Fig. 4 and SI Methods). The range of external inputs where, for all initial conditions and both experimental paradigms, a decision is reached, i.e., 1 pool lapses into an up-state of high firing rate, was termed “range of decision-making.” It defines a region of multistable decision states.
Fig. 4.
Common range of decision making for 2 and 4 alternatives in a mean-field approximation of the network. (A and B) For the parameters used in the spiking model simulations (except ωI = 1.1 instead of 1.125), the stable fixed points were calculated with the mean-field approximation over a range of external input ν from 0 to 100 Hz in steps of 0.5 Hz for the 2- and 4-choice condition and for 4 different initial conditions. Red, 1 pool starting at 120 Hz, the rest at 0 Hz; green, 2 opposite pools 30 Hz, the rest 0 Hz; blue, all 4 pools 30 Hz; black, all 4 pools 0 Hz. (A) Stable fixed points of firing rates of the selective pools (ωT = 0.015). In the decision state, exactly 1 pool is firing at a high rate, in the double-up state 2 pools. The traces of all other pools firing at low rates (≈2 Hz) overlap. For 4 alternatives, because all pools receive the input ν, there are 2 double-up states: one with neighboring pools (e.g., 1 + 2) firing at high rates, the other with opposing pools (e.g., 1 + 3) firing at high rates. In the 2-choice case, the input ν is applied only to 2 opposing selective pools (1 + 3), and thus only these pools will fire at high rates. The yellow region labels the range of decision making (see text) where the network is in the decision state for all initial conditions. (B) Starting and end points of decision states for the different initial conditions depend on the enhanced connectivity ωT between neighboring selective pools. Keeping the other parameters fixed, the value of the neighboring connectivity ωT with the optimal, i.e., broadest, range of decision making was determined by performing the fixed-point analysis explained above for ωT = 0 to 0.1 with steps of 0.0025. There is an optimal value of ωT for one parameter set, resulting in the broadest range of decision making (* black arrow); here, ωT = 0.015 (the value used in the spiking simulation and in A). (C) Dependence of the connectivity ω+ on the coding level f for constant fixed-point firing rates. To explore the relation between f and the range of decision making, the optimal value of ωT was determined for 11 different values of f from 0.1 to 0.225. When changing the coding level, the network connectivity has to be adapted to keep the up-state fixed-point firing rates at the same values. Thus, the connectivity value ω+ was adjusted in steps of 0.0025 until the up-state fixed points matched the values for the parameters of the spiking simulation (f = 0.2 and ω+ = 1.48, see A). For the ω+ values shown, the up-states deviated by less than 2 Hz in the 20- to 60-Hz range of external inputs, for the respective coding levels. Note that by changing ω+, the connections between the selective pools ω− change accordingly because of the normalization condition. (D) Optimal range of decision making increases linearly with the coding level. For each coding level, the optimal ωT was determined as shown in B, and the broadness of the yellow region, the range of decision making, was plotted against the coding level with a precision of 0.5 Hz. The black line is a linear fit to the data.
To explore the effect of the relative size of the selective pools on the range of decision making, we performed the mean-field analysis for different coding levels. The coding level is defined as the fraction of excitatory neurons in the network selective for 1 target direction, and thus determines the relative size of the neural populations representing a specific choice (selective populations). Fig. 4A shows an example of the stable fixed points, the attractors, of the firing rates for the parameters used in the spiking simulations (coding level of 0.2, ω+ = 1.48 and ωT = 0.015). The different colors denote different initial conditions. At lower external inputs, for some initial conditions, all pools stay in their spontaneous state, whereas for higher external inputs (from ν ≈ 50 Hz) a mixed double-up state emerges. Increasing the external inputs even more will result in mixed states with 3 and 4 pools firing at high rates, as observed for example during the target phase. The yellow regions in Fig. 4 A and B depict the overlap of decision states for the 2- and 4-choice case, where for all initial conditions 1 pool wins the competition, and a categorical decision is made (the range of decision making). Fig. 4B shows the dependence of the range of decision making (width of yellow region, coding level = 0.2) on ωT, the enhancement of connectivity between neurons from neighboring selective pools. As one can see in Fig. 4B, there is an optimal value of ωT for a given parameter set (* black arrow). Fig. 4A is a horizontal cut through Fig. 4B at ωT = 0.015, the optimal value for a coding level of 0.2.
When changing the coding level, the connectivity ω+ has to be adapted as shown in Fig. 4C to keep the firing rates of the up-state at the values obtained for the spiking simulation parameters (≈ 60–80 Hz, Fig. 4A), which match the experimental observations (13). The range of decision making was then measured at its optimal ωT value and plotted against the coding level (Fig. 4D). Interestingly, we found the range of decision making to increase linearly with the coding level. For a coding level smaller than 0.125, no common decision state can be found for the 2- and the 4-choice task, regardless of the neighboring connectivity ωT. The linear relation of the coding level to the optimal range of decision making was also found for a smaller AMPA/NMDA ratio than that used in the simulations, for the same and higher connectivity ω+, confirming the generality of the outcome (Fig. S5).
Discussion
In this article, we present a biophysically realistic spiking neuron model for decision making with 2 and 4 alternatives. Notably, all network parameters and inputs in our network are independent of the number of possible alternatives we tested. Differences in firing rates and psychometric functions are solely based on the number of possible targets presented, which in the network corresponds to the number of pools receiving the target input. Moreover, we not only extended Wang's model (8) to more than 2 choice alternatives, but also analyzed how the size of the neural populations that encode the choice alternatives affects the network's capacity for multiple-choice decision making. In a mean-field approximation of the network, we found a linearly increasing relation between the relative size of the selective pools (the coding level) and the range of decision making. This implies that pooling over many neurons favors decision making independent of the number of choices.
Network Properties and Parameters.
Our network is an extension of Wang's model for binary decision making (8) to 4 alternatives. Like the original models (8, 17), our model is capable of storing information by exhibiting persistent activity, because of slow recurrent excitation, which also enables the accumulation of sensory information. Categorical decision formation in the network is based on attractor state dynamics and feedback inhibition, which mediates competition. Besides modifying the number of selective pools representing the possible choices from 2 to 4, we introduced an additional enhancing connectivity ωT between neighboring pools to model the circular location of the targets in the experiment, assuming a slightly higher correlation between pools 90° apart than between anticorrelated pools 180° apart. Quantitatively, the connectivity between neighbors is only increased by 1.7% in our simulations, but ωT proved essential to regulate the range of decision making (Fig. 4B). It is generally advantageous to optimize the overlap between the competition regimes for different numbers of alternatives, because this minimizes the need for additional regulation mechanisms like top-down signals from other brain areas. An adaptation of the network connectivity during the learning phase to optimize the range of decision making is therefore a plausible process.
Discrete or Continuous Representation.
Extending decision making to more than 2 alternatives finally amounts to the question about continuous alternatives. At present, there are no experimental results on a RDM task with more than 4 discrete or continuous alternatives. Thus, it is still not clear when subjects reach their limit to distinguish possible motion directions or how accurately they can determine motion direction in a continuous task. Infinite precision may not be needed to obtain the final resolution of the cognitive and motor systems (13). A discrete network model with a finite number of selective neural populations might thus be sufficient to account even for continuous choices.
In the following, we will discuss our results in comparison with the recently proposed continuous models (14, 15) of multiple decision making. Furman and Wang's (15) model, like ours, is a biophysically detailed attractor model. Their network consists of directionally tuned neurons whose preferred directions cover a full circle. Excitatory neurons are connected according to a Gaussian curve depending on their difference in preferred directions. This continuous approach allows for testing 8 targets spaced 45° apart. However, in 49% of the trials no categorical decisions could be made, because activity around adjacent targets tended to merge. In addition, their continuous model could not account for the differences in reaction time observed between the standard 2-choice case and the 90° case (13). The 2 conditions resulted in identical outcomes in their simulations (15).
Our discrete model with spatially tuned connections between the selective pools could account very well for all tested paradigms, including the 90° case. Additionally, we were able to explain the intermediate reaction times of the 90° case, based on a prolonged symmetric state of the 2 selective populations. Thus, pooling over many neurons and introducing a graded connectivity between the pools might represent the physiological conditions of neurons in LIP more accurately than a ring structure where each neuron encodes 1 special direction.
Beck et al. (14) took a distinct, parallel approach with respect to the biophysically realistic attractor models. Their model is focused on possible probabilistic properties of neurons. It fits Churchland's data (13) well. However, in contrast to the experimental findings, different activity thresholds were used in the 2 and 4 alternative case to terminate the decision. The probabilistic approach so far accounts well for single-cell data. Yet, to verify whether populations of LIP neurons really encode probability distributions as predicted, future multiunit recording experiments are required (14).
Importance of Pool Size.
Apart from successfully accounting for all experimental paradigms, the pool structure of our model entails an important advantage regarding the network's dynamics: Our network operates in a range of categorical decision making, independent of the tested paradigms. In Furman and Wang's model (15), the simulations needed to be controlled by inputs dependent on the number of possible targets, which were supposed to originate from unknown higher level brain areas or normalization processes. They introduced an adaptation of the target input and an external control signal during the decision-making period as mechanisms to regulate the dynamical range of decision making for the respective numbers of alternatives.
In contrast, in our model there is no need to adapt either parameters or inputs to the number of choice alternatives. Using a mean-field approximation of the model, we found that the overlap of decision regions for 2 and 4 choices increases linearly with the relative size of the selective populations that encode the choice alternatives (the coding level). A possible explanation of this effect might be given based on the recurrent connectivity. To keep the fixed-point firing rates of the model constant while increasing the coding level, the recurrent connectivity of the network has to be adapted nonlinearly, as shown in Fig. 4C. In turn, the more neurons encoding a choice alternative, the higher the recurrent activity each neuron in that pool receives. In fact, we observed that the recurrent activity a single neuron receives increases linearly with the coding level. We believe that this increase of recurrent activity stabilizes the decision state.
Furman and Wang (15) suggested that their top-down signal could also serve to control the speed–accuracy tradeoff. In our network, an input-based control of speed–accuracy tradeoff could be implemented with the advantage of being independent of the number of possible choices, following the study of Roxin and Ledberg (24), where increasing the inputs was found to decrease reaction times and performance monotonically.
Although the network structure of Furman and Wang's (15) model generally offers the possibility to simulate any number of alternatives and angular locations, a biophysically realistic model accounting for all experimental paradigms and more than 4 choice alternatives is still an objective for future research. Taken together, our results indicate the benefit of a pooled, multineuron representation of choice alternatives. We suggest that a bigger pool size, apart from the obvious advantage of redundancy in case of neural loss, or of averaging out noise by pooling across inputs, enables the network to exhibit relatively stronger recurrent inputs useful for stabilizing decision states.
Methods
Network.
Our model is based on the network introduced by Brunel and Wang (17). It was originally intended to model object working memory and persistent activity, but has already been successfully applied to model neural activity of LIP neurons in the RDM task with 2 alternatives (8). Single neurons are modeled as integrate-and-fire neurons with conductance-based synaptic responses. They are connected by 3 types of receptors that mediate the synaptic currents flowing into them: AMPA, NMDA glutamate, and GABAA receptors, which are described by realistic synaptic kinetics (see SI Methods).
Connectivity Weights.
The synaptic efficacies are assumed to be already formed and, therefore, are kept fixed during the simulation. Consistent with a Hebbian rule, cells within 1 selective pool have stronger weights for recurrent connections (ω+ > 1) because their activity is thought to be correlated, whereas anticorrelated cells between selective pools and from the nonselective to selective pools have weaker connection weights (ω− < 1). Each selective pool in our model has 2 “neighboring” selective pools, corresponding to its 2 perpendicular targets, and 1 “opposing” pool, representing the target at 180° angular distance. The connections to and from the neighboring pools are enhanced by a value ωT, assuming a slightly higher correlation between the neighboring pools than between the anticorrelated opposing pools (Fig. 1C). The connections in the network are normalized so that the overall excitatory recurrent synaptic drive remains constant with only baseline input applied to the network (spontaneous state) (17). This is accomplished by adapting ω− according to ω = 1 − f (2ωT + ω+ − 1)/(1 − f), where f is the coding level. Inhibitory-to-excitatory connections are denoted by a weight ωI. All other connections have a baseline weight of 1 (Fig. 1 B and C).
Simulation of Sensory Inputs.
Mimicking the sensory stimuli of the experimental protocol (13), an external target and motion input are applied to the network during the spiking simulation. Depending on the number and location of the targets in the different experimental conditions, the neurons of either all 4 selective pools, the 2 opposing pools or, in the 90° case, 2 neighboring pools receive the same target input during the model simulation. We assume that the target input is passed on to the respective pools as a Poisson spike train with a time-dependent firing rate of
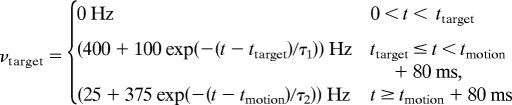 |
where ttarget = 500 ms and tmotion = 1,300 ms are the onset times for the target and the motion stimulus, respectively. The time course of the target signal follows the approach of Wong et al. (21) and is in accordance with experimental findings (13, 23). The initial exponential decay, τ1 = 100 ms can be explained by short-term adaptation. The dip in the firing rate is modeled by an exponential decrease of the target input with τ2 = 15 ms, starting with a latency of 80 ms after motion stimulus onset.
Based on electrophysiological recordings from MT neurons (22), the motion stimulus at zero coherence was simulated as a Poisson spike train with a time invariant rate of νmotion = 20 Hz to all selective pools starting at 1,500 ms. Coherent motion was modeled as a positive bias to 1 selective pool, balanced by a reduction of the motion input in the other 3 selective pools, so as to keep the total motion input to the network constant. A motion coherence of 100% corresponds to a bias of 60 Hz to 1 selective pool, resulting in a motion input of 80 Hz to this particular pool and 0 Hz to the other selective pools. We simulated 10 motion coherences: 0%, 1.67%, 3.33%, 5%, 8.33%, 12.5%, 25%, 50%, 75%, and 100%.
Spiking Network Simulations.
Each trial in the network was run for a total of 4,000 ms. A decision was reached when 1 selective pool crossed a threshold of 50 Hz and surpassed the other selective pools by at least 5 Hz. The reaction time RT was calculated as the difference between the motion onset tmotion and the time the threshold was reached tthres, plus an additional time tsaccade = 80 ms to account for saccade initiation and execution.
Mean-Field Approximation.
We followed the mean-field approximation derived in Brunel and Wang (17) to scan the parameter space to find a parameter set matching the experimental findings. This approximation provides fixed points of the population firing rates, the stationary states of the populations after the period of transients. The firing rates would be exact if the number of neurons was infinitely large and the unitary postsynaptic potentials elicited by presynaptic spikes were infinitesimally small. See Fig. 4 and SI Methods for the calculation of the range of decision making.
A more detailed description of the simulation procedure, including Table S1 with the default values as well as mathematical details of the network and the mean-field approach, can be found in SI Methods.
Supplementary Material
Acknowledgments.
We thank Anders Ledberg, Laura Dempere-Marco, and Johan Larrson for helpful discussions and comments on the manuscript. This work was supported by European Union Grant EC005-024 and by the Spanish Research Project BFU2007-61710/BFI and CONSOLIDER INGENIO 2010.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0901621106/DCSupplemental.
References
- 1.Hick WE. On the rate of gain of information. Q J Exp Psychol A. 1952;4:11–26. [Google Scholar]
- 2.Wang XJ. Decision making in recurrent neuronal circuits. Neuron. 2008;60:215–234. doi: 10.1016/j.neuron.2008.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–537. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- 4.Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends Neurosci. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- 5.Shadlen MN, Newsome WT. Motion perception: Seeing and deciding. Proc Natl Acad Sci USA. 1996;93:628–633. doi: 10.1073/pnas.93.2.628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- 7.Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36:955–968. doi: 10.1016/s0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
- 9.Usher M, McClelland JL. On the time course of perceptual choice: The leaky competing accumulator model. Psychol Rev. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- 10.Bogacz R, Usher M, Zhang J, McClelland JL. Extending a biological model of choice: multi-alternatives, nonlinearity and value-based multidimensional choice. Philos Trans R Soc Ser B. 2007;362:1655–1670. doi: 10.1098/rstb.2007.2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Niwa M, Ditterich J. Perceptual decisions between multiple directions of visual motion. J Neurosci. 2008;28:4435. doi: 10.1523/JNEUROSCI.5564-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McMillen T, Holmes P. The dynamics of choice among multiple alternatives. J Math Psychol. 2006;50:30–57. [Google Scholar]
- 13.Churchland AK, Kiani R, Shadlen MN. Decision-making with multiple alternatives. Nat Neurosci. 2008;11:693–702. doi: 10.1038/nn.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beck JM, et al. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60:1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Furman M, Wang XJ. Similarity effect and optimal control of multiple-choice decision making. Neuron. 2008;60:1153–1168. doi: 10.1016/j.neuron.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ben-Yishai R, Bar-Or RL, Sompolinsky H. Theory of orientation tuning in visual cortex. Proc Natl Acad Sci USA. 1995;92:3844–3848. doi: 10.1073/pnas.92.9.3844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brunel N, Wang XJ. Effects of neuromodulation in a cortical network model of object working memory dominated by recurrent inhibition. J Comput Neurosci. 2001;11:63–85. doi: 10.1023/a:1011204814320. [DOI] [PubMed] [Google Scholar]
- 18.Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. 2006;26:1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Deco G, Romo R. The role of fluctuations in perception. Trends Neurosci. 2008;31:591–598. doi: 10.1016/j.tins.2008.08.007. [DOI] [PubMed] [Google Scholar]
- 20.Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci. 2008;28:3017–3029. doi: 10.1523/JNEUROSCI.4761-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wong KF, Huk AC, Shadlen MN, Wang XJ. Neural circuit dynamics underlying accumulation of time-varying evidence during perceptual decision making. Front Comput Neurosci. 2007;1:6. doi: 10.3389/neuro.10.006.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Britten KH, Shadlen MN, Newsome WT, Movshon JA. Responses of neurons in macaque MT to stochastic motion signals. Vis Neurosci. 1993;10:1157–1169. doi: 10.1017/s0952523800010269. [DOI] [PubMed] [Google Scholar]
- 23.Huk AC, Shadlen MN. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J Neurosci. 2005;25:10420–10436. doi: 10.1523/JNEUROSCI.4684-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roxin A, Ledberg A. Neurobiological models of two-choice decision making can be reduced to a one-dimensional nonlinear diffusion equation. PLoS Comput Biol. 2008;4:e1000046. doi: 10.1371/journal.pcbi.1000046. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.