Inhibitory Stabilization of the Cortical Network Underlies Visual Surround Suppression

SUMMARY

In what regime does the cortical circuit operate? Our intracellular studies of surround suppression in cat primary visual cortex (V1) provide strong evidence on this question. Although suppression has been thought to arise from an increase in lateral inhibition, we find that the inhibition that cells receive is reduced, not increased, by a surround stimulus. Instead, suppression is mediated by a withdrawal of excitation. Thalamic recordings and previous work show that these effects cannot be explained by a withdrawal of thalamic input. We find in theoretical work that this behavior can only arise if V1 operates as an inhibition-stabilized network (ISN), in which excitatory recurrence alone is strong enough to destabilize visual responses but feedback inhibition maintains stability. We confirm two strong tests of this scenario experimentally, and show through simulation that observed cell-to-cell variability in surround effects, from facilitation to suppression, can arise naturally from variability in the ISN.

INTRODUCTION

Considerable evidence suggests that stimulus selectivity in primary sensory cortex emerges largely from the organization of feed-forward thalamic connections (Bruno and Sakmann, 2006; Ferster and Miller, 2000; Priebe and Ferster, 2008; Wilent and Contreras, 2005). And yet, anatomically, primary sensory cortex appears to be dominated by recurrent connections (Binzegger et al., 2004; Stepanyants et al., 2008). Here, we demonstrate that the circuitry of primary visual cortex (V1) may operate in a regime that reconciles these two views.

Theorists have proposed several functions for recurrent cortical connections. In attractor models of orientation selectivity in V1 (Ben-Yishai et al., 1995; Somers et al., 1995), strong excitatory recurrence constrains the set of stable cortical activity patterns (the network’s “attractors”) to a small (low-dimensional) subset of the large (high-dimensional) set of all possible patterns. Which one appears in response to a stimulus is determined by a correspondingly low-dimensional subset of stimulus features, such as orientation or spatial frequency, while all other stimulus features are ignored. The degree to which V1 responses closely reflect feed-forward input, however, argues against this idea (Ferster and Miller, 2000; Priebe and Ferster, 2008).

In a second proposal, recurrent connections strongly amplify feed-forward inputs so that most of the stimulus-evoked depolarization in layer 4 neurons originates intracortically (Douglas et al., 1995). Anatomically, thalamic inputs may constitute only a fraction of the total synapses in layer 4 of sensory cortex (Peters and Payne, 1993). Physiological experiments suggest, however, that recurrence only modestly amplifies (Ferster et al., 1996; Chung and Ferster, 1998) or even damps (Bruno and Sakmann, 2006; Pinto et al., 2003) the thalamic drive.

In a third proposal, strong recurrent excitation and inhibition tightly balance one another so that the net input to each neuron is only a fraction of either input alone (van Vreeswijk and Sompolinsky, 1998). This balance can explain the large variability of cortical spiking (Shadlen and Newsome, 1994) and is consistent with the balanced changes in excitation and inhibition that may occur as activity states change (Haider et al., 2006; Higley and Contreras, 2006; but see Waters and Helmchen, 2006).

Here, we provide evidence that during visual stimulation, cat visual cortex operates as an inhibition-stabilized network (Tsodyks et al., 1997) or ISN. In this regime, which includes the balanced models, excitatory recurrence is so strong as to be unstable if inhibition is fixed, but is stabilized by inhibitory feedback. Experimental evidence for the ISN arises from our study of surround suppression. Although surround suppression is nominally a form of lateral inhibition, intracellular recordings failed to reveal the expected pattern of synaptic inputs. Only the ISN model can resolve this apparent paradox.

In many cortical cells, stimuli surrounding the classical receptive field, or center, suppress spike responses to simultaneously-presented center stimuli. The orientation tuning of this suppression (Cavanaugh et al., 2002; DeAngelis et al., 1994; Jones et al., 2002; Li and Li, 1994; Ozeki et al., 2004), its timing (Knierim and Van Essen, 1992; Smith et al., 2006), susceptibility to adaptation (Durand et al., 2007; Webb et al., 2005), and spatial extent (Angelucci et al., 2002; Bair et al., 2003) all suggest that suppression originates intracortically, through local horizontal connections or feedback from higher areas. Since these connections are largely excitatory, however, they are typically assumed to act through local inhibitory interneurons to increase inhibition in surround-suppressed cells.

We have found instead that surround stimuli decrease both the inhibition and excitation received by suppressed cells. We show that these decreases cannot be accounted for by suppression of input from the lateral geniculate nucleus (LGN), and therefore must arise from intracortical input. How can an increase of intracortical input to the local circuit decrease both excitation and inhibition? Previous work has established that an ISN can lead to such a decrease (Tsodyks et al., 1997), and we show theoretically that an ISN is the only solution to this apparent paradox. In addition, we test and confirm two predictions of the ISN model regarding the time-course of surround inhibition and the source of synaptic input to surround-suppressed cells.

The ISN provides a framework within which strong recurrence may be reconciled with feed-forward models of cortical selectivity. The ISN’s strong recurrence can support complex computations (Latham and Nirenberg, 2004), yet allow neuronal responses to change smoothly with changing feed-forward input, and thus reflect the full, high-dimensional space of possible input patterns. Feed-forward inputs may determine neuronal tuning to a center stimulus, whereas the local recurrent circuitry helps set the gain through the balance between strong excitation and stabilizing inhibition. This balance may in turn be modulated by stimulus context, cortical state changes, or top-down influences.

RESULTS

Excitatory and Inhibitory Inputs Underlying Surround Suppression in V1 Cells

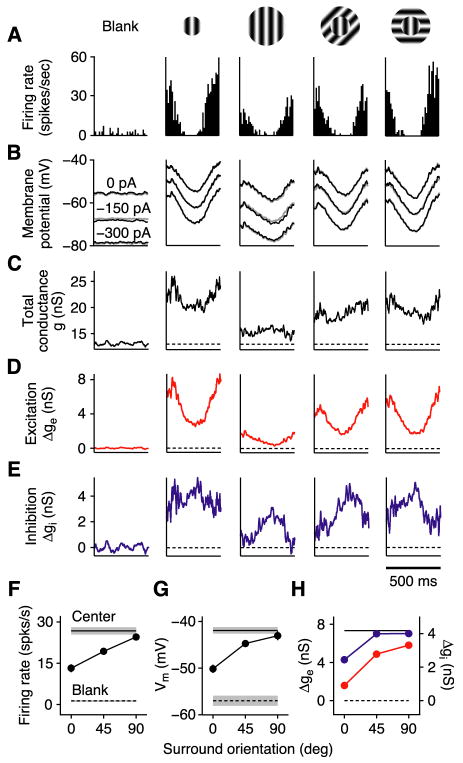
Cortical cells were classified as surround suppressed if an increase in stimulus size beyond the classical receptive field caused a statistically significant reduction in firing rate. In the simple cell in Figure 1, a 10-fold increase in stimulus size reduced the spike response by >80% (F1 component; Figures 1A and 1B). The underlying reduction in membrane potential responses was much smaller (DC component, 40%; F1 component, 30%), and like the spike responses, was selective for the orientation of the surround stimulus. A surround stimulus oriented 90° from the optimal evoked little suppression (Figure 1C).

Figure 1. Membrane potential responses of a surround-suppressed simple cell to drifting grating stimuli.

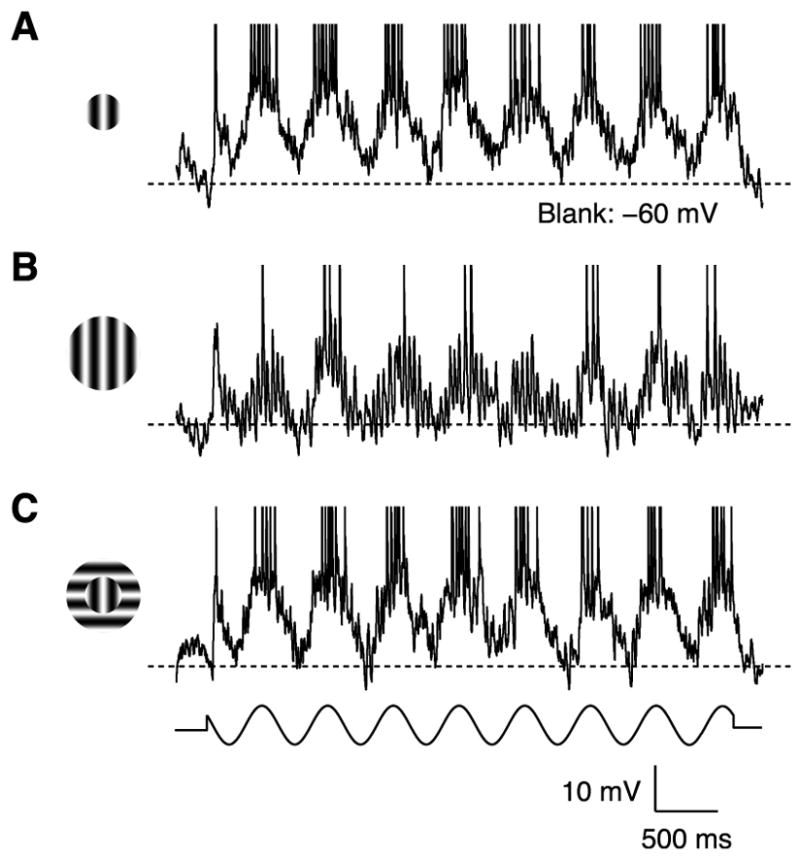
(A) A grating optimal in size, orientation and spatial frequency covered the classical receptive field (2°s diameter, 2 Hz temporal frequency, 64% contrast). K⁺-gluconate solution in the recording pipette. Dashed line: mean response to a blank stimulus.

(B) The grating diameter was increased to cover the receptive field surround (20°s diameter).

(C) The portion of the grating covering the receptive field surround was rotated orthogonal to the cell’s preferred orientation.

To investigate the mechanisms underlying this suppression (Figure 2), we measured stimulus-evoked changes in membrane conductance by injecting different levels of steady current into the cell (Figure 2B). Total membrane conductance (Figure 2C) was derived from the slope of the I–V relationship constructed at each point in time, and changes in excitatory and inhibitory conductance (Figures 2D and 2E) were derived from estimates of synaptic reversal potentials applied to the membrane equation (Anderson et al., 2000). Surprisingly, the surround stimulus reduced total conductance – and both the excitatory and inhibitory conductance – in an orientation-selective manner (Figure 2H).

Figure 2. Steady-state measurements of surround suppression in V1.

(A) Cycle-averaged spike responses of a simple cell to a blank stimulus, a center-only stimulus, and center-plus-surround stimuli with 3 different surround orientations. K⁺-gluconate solution in the recording pipette.

(B) Cycle-averaged membrane potential responses (spikes removed) with 3 different levels of injected current. Gray traces (barely visible): membrane potential reconstructed from conductance measurements.

(C–E) Stimulus-evoked changes in total membrane conductance and excitatory and inhibitory conductances derived from responses in (B). Dashed lines: mean of the blank responses.

(F–H) Firing rate (F1 component), peak membrane potential (DC+F1), and peak excitatory (red) and inhibitory (blue) conductances (DC+F1) vs. surround orientation (relative to center). Error bars (s.e.m.) are barely visible. Horizontal lines: Blank and center-only responses (shading = s.e.m.).

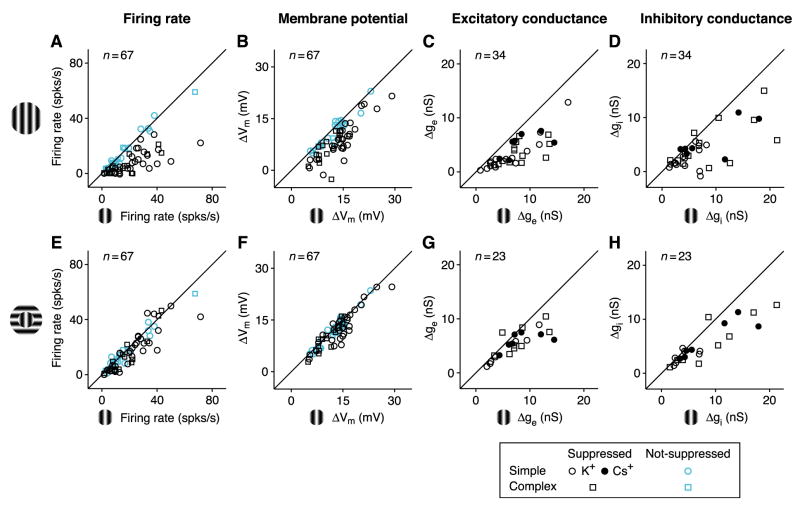
Membrane potential measurements were made from 67 cortical cells; conductance measurements were made in the 34 cells that showed surround suppression in their spike responses. For each of the 4 measures – firing rate, membrane potential, and excitatory and inhibitory conductance – we plotted response amplitude for center-plus-surround stimulation against that for center-only stimulation (Figures 3). In each plot, the amount of surround suppression for a given cell is indicated by how far each point lies below the diagonal. Several trends can be observed.

Figure 3. Surround suppression across the V1 population.

(A–D). Center-plus-surround response amplitude (surround at preferred orientation) plotted against center-only response amplitude for (A) firing rate (F1 component for 47 simple cells; DC component for 20 complex cells), (B) change in peak membrane potential, (C) change in peak excitatory conductance (21 simple; 13 complex), and (D) change in peak inhibitory conductance. For each graph, responses are measured relative to blank responses. Round and square symbols: simple and complex cells; open and closed symbols: K⁺–based or Cs⁺-based/QX-314 solution in recording pipette. In (A) and (B), cyan symbols indicate cells that showed no statistically significant suppression (17 simple, 6 complex).

(E–H) Same as (A)-(D), but with surround at the orthogonal orientation. (E) and (F), same population as (A) and (B); (G) and (H), 14 simple and 9 complex cells.

First, as expected from previous studies (Cavanaugh et al., 2002; DeAngelis et al., 1994; Li and Li, 1994; Ozeki et al., 2004), suppression in firing rate and membrane potential is much greater for the iso-oriented surround (Figures 3A and 3B) than for the cross-oriented surround (Figures 3E and 3F).

Second, as it does for many other response properties (Priebe and Ferster, 2008), including length tuning (Anderson et al., 2001), spike threshold generally amplifies surround suppression and its sensitivity to orientation, size, and contrast in spike responses relative to membrane potential responses (Figures 3A, 3B, S1, and S2). This effect is quantified and fit to a power-law threshold nonlinearity in Figure S3.

Third, in surround-suppressed cells, iso-oriented surround stimulation on average caused a reduction in both excitation and inhibition (51% and 38%; Figures 3C and 3D), rather than the increase in inhibition expected from standard models of lateral inhibition. Excitation was reduced by >25% in 85% of surround-suppressed cells; inhibition was reduced by >25% in 65% of such cells. These conductance measurements were not likely distorted by action potentials, since similar results were obtained when voltage-gated Na⁺ and K⁺ channels (and GABA_B-mediated inhibition) were blocked with intracellular QX-314 and Cs⁺ (Figures 3C and 3D, closed symbols; Figure S4).

Fourth, both excitation and inhibition are tuned for surround orientation (Figure S5), but the tuning was stronger for excitation than for inhibition. Changing the surround from iso- to cross-orientation reduced excitatory suppression in 21 of 23 cells (one-sided binomial test, p < 0.0001); over all cells, average suppression fell from 54% (Figure 3C) to 24% (Figure 3G) (one-sided paired t-test, p < 0.0001). Changing the surround orientation reduced inhibitory suppression in 16 of 23 cells (p < 0.05); average suppression fell from 42% (Figure 3D) to 27% (Figure 3H) (p < 0.06).

The standard lateral inhibition models make a critical prediction regarding the synaptic inputs underlying surround suppression, that suppression in membrane potential is driven by, and therefore should be strongly correlated with, an increase in inhibition. To test this prediction, we plotted suppression in membrane potential against suppression in excitation and inhibition (Figures 4A and 4B), quantifying suppression using a suppression index: the percentage by which the surround stimulus decreases the response to the center stimulus (SI=1−R_{center+surround}/R_center). SI=0 represents no suppression; SI=1 represents complete suppression; SI>1 represents suppression below the spontaneous level; and SI<0 represents facilitation. Using this measure, the standard lateral inhibition models would predict that the points in Figure 4B fall along a line of negative slope and intercept 0. In contrast to this prediction, suppression in membrane potential was not at all correlated with an increase in inhibition (Figure 4B, r = 0.08, p > 0.54). Instead, suppression in membrane potential was strongly correlated with – and thus appears to be driven by – a decrease in excitation (Figure 4A, r = 0.80, p < 0.00001). The lack of negative correlation between SI of membrane potential and SI of inhibition seems surprising. This expected correlation may be counteracted, however, by a positive correlation in suppressed cells between suppression in excitation and suppression in inhibition (Figure 7, below) that arises because a more strongly suppressive stimulus more strongly reduces all synaptic inputs.

Figure 4. The relationship between surround suppression in membrane potential and synaptic conductance.

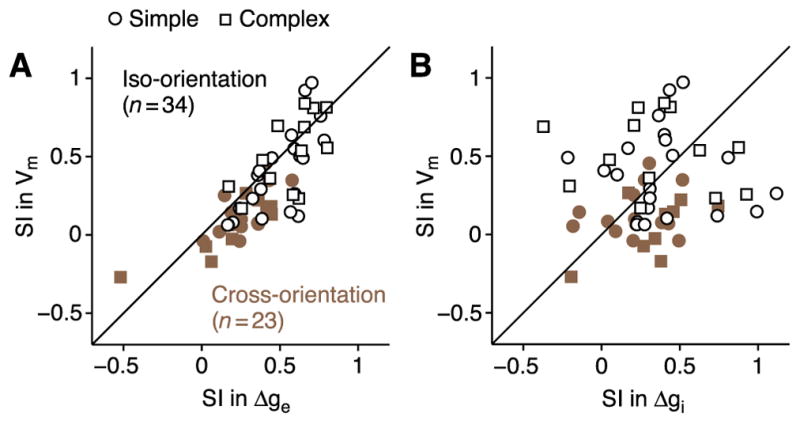
(A) Suppression index (SI = 1 − R_{center+surround}/R_center) for membrane potential plotted against SI for excitatory conductance. Open symbols: surround at preferred orientation (21 simple; 13 complex); closed symbols: surround at the orthogonal orientation (17 simple; 6 complex). (B) Same as (A) for inhibitory conductance.

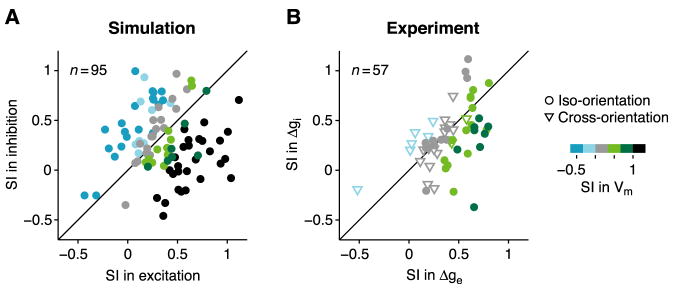
Figure 7. Surround effects in a multi-neuron ISN model.

(A) Suppression indices (SI; iso-oriented surround) of excitation and inhibition plotted against one another for 100 randomly-chosen neurons from a multi-neuron ISN model. Five cells fall outside the plot. Colors code SI of membrane potential. (B) Experimentally measured SI’s of excitatory and inhibitory conductance plotted against one another (data from Figure 4). Circles and triangles: surround effects at iso- and cross-orientation.

In the model, cells have SI > 1 for membrane potential (A, black points, meaning surround suppresses response below baseline) whenever total inhibition evoked by center-plus-surround stimulus exceeds total excitation. In real neurons, reversal-potential nonlinearities can suppress effects of inhibition on membrane potential so that SI remains <1.

Comparison of Surround Suppression in LGN and Cortex

If a decrease in excitation – rather than an increase in inhibition – drives surround suppression, what drives the decrease in excitation? One possibility is a withdrawal of feed-forward input from LGN cells, which themselves show surround suppression (Bonin et al., 2005; Jones et al., 2000; Naito et al., 2007; Solomon et al., 2002; Sun et al. 2004). To test this possibility, we asked whether the strength, orientation selectivity, and size tuning of surround suppression in LGN cells matches those of cortical simple cells, which receive a substantial portion of their input from the LGN.

To study how LGN responses change during cortical surround suppression, it is important to use the same stimuli in LGN and cortex. The center stimuli we used for measuring suppression in cortical cells were, by definition, optimal in size for these cells, and were therefore 2–3 times larger than the centers of geniculate receptive fields at comparable retinal eccentricities (<5°). These stimuli by themselves generate significant surround suppression in LGN cells (Jones et al., 2000). As a result, the surround suppression that we observed in LGN cells using center stimuli optimized for cortex was much weaker and less orientation selective than in a previous study using center stimuli optimized for the LGN (Naito et al., 2007). Nevertheless, these stimuli are most appropriate for understanding the changes in thalamic input generated during cortical surround suppression.

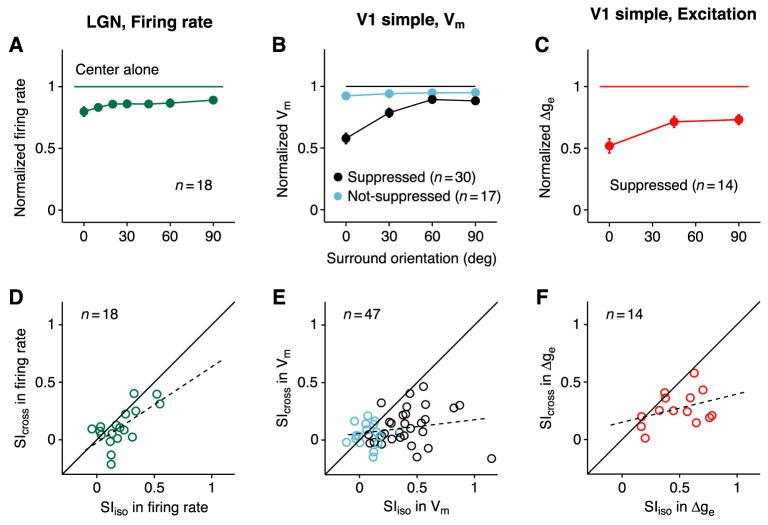
Spike responses were recorded from 18 LGN cells (13 X and 5 Y) using center stimuli at two orthogonal orientations and surround stimuli at 7 orientations relative to the center. From these responses, we calculated normalized and average responses across cells as a function of surround orientation (Figures 5A and S6) and plotted suppression indices (SI) for iso- and cross-oriented surround stimuli against one another (Figure 5D). For comparison, similar plots were constructed for the membrane potential and excitatory synaptic input to simple cells (Figures 5B and 5E, 5C and 5F).

Figure 5. Comparison of surround suppression in LGN and V1.

(A) Orientation-tuning of firing rate for 7 surround orientations (relative to center orientation), normalized to the center-only response and averaged across 18 LGN cells. The size of the center stimulus was optimal for cortical cells, and not for LGN cells (see text). Normalized responses to iso-oriented and cross-oriented surround (mean ± s.e.m.): 0.80 ± 0.04 and 0.89 ± 0.03.

(B) Orientation-tuning curve of membrane potential, normalized and averaged across V1 simple cells. Black and cyan indicate surround suppressed and non-suppressed cells. Center-normalized responses to iso-oriented and cross-oriented surround: suppressed, 0.58 ± 0.04 and 0.88 ± 0.03; non-suppressed, 0.92 ± 0.03 and 0.95 ± 0.02.

(C) Excitatory conductance in surround-suppressed simple cells. Center-normalized responses: iso-oriented surround, 0.52 ± 0.06; cross-oriented surround, 0.73 ± 0.04.

(D–F) Suppression indices (SI) for iso- and cross-oriented surround plotted against one another.

(D) Firing rate in LGN cells.

(E) Membrane potential in surround-suppressed (black, n=30) and non-suppressed (cyan, n=17) simple cells.

(F) Excitatory conductance in surround-suppressed simple cells. Dashed lines: linear regressions.

None of the properties of surround suppression in the LGN matched those of suppression in the cortex. First, the amplitude of suppression generated by an iso-oriented surround is far smaller for LGN cells (20%) than it is for the membrane potential (42%; Wilcoxon, p < 0.001) or excitatory conductance (48%; p < 0.001) of surround-suppressed simple cells, as can be seen by comparing the 0° points in Figures 5A, 5B (black), and 5C. The surround-induced reduction in LGN responses is more similar to the 8% reduction in membrane potential responses of non-suppressed cortical cells (Figure 5B, cyan), though significantly different (p < 0.05).

Second, the orientation tuning of surround suppression is much weaker in LGN cells than it is in cortical cells (Figures 5A–C). Orientation selectivity for individual cells can be seen in plots of suppression index for cross-orientation (SI_cross) against the index for iso-orientation (SI_iso). In the LGN, these two measures are strongly correlated; that is, SI is similar at iso- and cross-orientation (Figure 5D, r = 0.66, p < 0.004). In the cortex, the correlation is weak; that is, SI is much stronger at the iso-orientation than at the cross-orientation (Figure 5E, r = 0.22, p > 0.14; Figure 5F, r = 0.36, p > 0.20).

Third, size tuning is much narrower in LGN cells than it is in cortical cells (Jones et al., 2000). Starting with optimal center stimuli for LGN cells (0.4–2° in diameter), half-maximal suppression occurred with annuli of 1–2° in thickness (not shown). By contrast, for simple cells, optimal center stimuli were 2–4° in diameter and half-maximal suppression occurred for annuli of 2–5° in thickness (Figure S1). In other words, for the center stimuli used in the cortex, geniculate neurons are already almost maximally surround suppressed. Note that when stimuli with optimal sizes for LGN cells were presented, surround suppression was stronger but less tuned to surround orientation (iso-orientation: 49%; cross-orientation: 47%), in accordance with previous studies.

Together, these observations – that geniculate surround suppression is substantially weaker, less orientation tuned, and peaks at smaller stimulus diameters than cortical suppression – make it unlikely that the LGN is the source of the strong, orientation-selective surround suppression in the cortex.

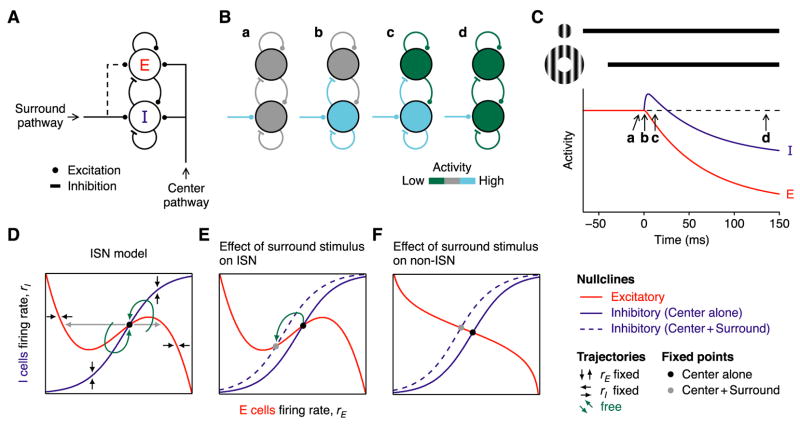
An ISN Model of Surround Suppression

To understand the possible mechanisms underlying these experimental results, we explored the behavior of simple mathematical models of the cortical circuit and found that only one cortical architecture can explain the surround-induced reduction in excitation and inhibition: An inhibition-stabilized network, or ISN (Tsodyks et al., 1997). We first modeled a cortical orientation column with two populations of cells (Figure 6A), one excitatory (E) and one inhibitory (I), each making recurrent connections onto themselves and reciprocal connections onto each other (Tsodyks et al., 1997; Wilson and Cowan, 1972). The column also receives external input from two sources: Center stimuli activate the E and I cells through feed-forward inputs from the LGN and/or other cortical cells; surround stimuli preferentially activate the I cells through lateral excitatory connections. These lateral connections could have several possible sources: layer 6 cells, which preferentially target inhibitory cells in layer 4 (McGuire et al., 1984; West et al., 2006) and have been implicated in length tuning (Bolz and Gilbert, 1986); laterally-projecting neurons within area 17 (Angelucci et al., 2002), which target both inhibitory and excitatory cells (McGuire et al., 1991); or neurons in higher cortical areas (Angelucci et al., 2002; Bair et al., 2003).

Figure 6. An inhibition-stabilized network model of surround suppression.

(A) Two populations of cells, excitatory (E) and inhibitory (I), make recurrent and reciprocal connections. Each receives excitatory feed-forward input driven by the receptive field center and lateral excitatory input driven by the receptive field surround.

(B) The sequence of events that follow when a surround stimulus (cyan; assumed for simplicity to stimulate only I cells) is added to a pre-existing center stimulus (not shown). After a transient increase in the activity of the I cells (b, c), activity in both the E and I cells decreases (d) relative to the initial level evoked by center stimulus alone (a).

(C) The temporal sequence of changes in E and I cell activities (red and blue).

(D and E) Phase-plane diagram of the network activity (D) in the presence of the center stimulus and (E) when the surround stimulus is added (dotted line). (F) Same as (E) for a non-ISN.

This overall structure closely resembles previously-described models of surround suppression (Dragoi and Sur, 2000; Schwabe et al., 2006; Somers et al., 1998). Our model, however, operates as an ISN, which makes it distinct in its balance of excitatory and inhibitory connections and in its dynamics. To be an ISN (Tsodyks et al., 1997), a network must satisfy two properties (Supplemental Text, Section 1.2). First, recurrent excitatory connections must be so strong as to be unstable during visual stimulation. That is, if the activities of inhibitory interneurons were fixed at their mean responses to the stimulus and could not vary in response to fluctuations of excitatory cells’ firing, recurrent excitation would drive the excitatory cells either to saturation or to very low firing rates. Second, when the activity of inhibitory interneurons is allowed to vary normally, inhibition stabilizes the network and allows it to respond to graded stimuli with graded levels of activity. When these two constraints are met, an increase in external, excitatory input to the inhibitory cells paradoxically causes a decrease in their firing rates in the new steady state (Tsodyks et al., 1997), which leads model cells to behave like the cells recorded in our experiments. We will later show that the ISN is the only architecture that can explain our experimental results.

To probe the model, we first apply an optimally-oriented center stimulus, which excites the E cells more strongly than the I cells (Figures 6B and 6C). The stimulus is turned on well prior to time t = −100 ms, so that at t = −50 ms the network has reached its steady state response to the center stimulus. At t = −40 ms, an iso-oriented surround stimulus is introduced, which activates excitatory cells outside the column. For simplicity, we first assume that these excitatory cells connect exclusively to the I cells. The following sequence of events occurs. (1) External excitation to the I cells from the surround pathway increases (Figures 6Ba and 6Ca). (2) Activity in the I cells increases (Figures 6Bb and 6Cb). (3) Inhibition to the E cells increases. (4) Activity in the E cells decreases (Figures 6Bc and 6Cc). (5) This decrease withdraws excitation to the I cells as well as to the E cells. The sequence to this point will occur in almost any recurrent network. Most importantly, however, if and only if the network is an ISN, the reduction in recurrent excitation to the I cells will be larger than the initial (sustained) increase in external excitation from the surround pathway that started the process (Supplemental Text, Section 2). As a result, (6) in the new steady state, the activity of both the E and I cells is reduced (Figures 6Bd and 6Cd), capturing the experimental results in Figures 2–4.

To model the network behavior in more detail, we let r_E and r_I represent the average firing rates of the E and I cells, and let i_E and i_I represent their external inputs (each being the sum of center and surround inputs). At any moment in time, the firing rates move toward the values f_E(r_E, r_I, i_E) and f_I(r_E, r_I, i_I), which are characterized by two properties: They are increasing functions of excitatory inputs (r_E and i_E or i_I) and decreasing functions of inhibitory input (r_I). A common choice is f_E(r_E,r_I,i_E) = g_E(w_EEr_E − w_EIr_I+i_E) (and similarly for f_I), where g_E( ) is a sigmoid function, and w_EE and w_EI are positive numbers representing the strength of E-to-E and I-to-E connections. The dynamics are obtained by assuming that each population’s activity moves toward the steady state (as defined by the instantaneous inputs) with the time constants τ_E and τ_I:

$${\tau }_E\frac{d}{dt}{r}_E=-r_E+f_E(r_E,r_I,i_E),$$ (1)

$${\tau }_I\frac{d}{dt}{r}_I=-r_I+f_I(r_E,r_I,i_I).$$ (2)

These equations can be derived from, and reasonably replicate the behavior of, spiking models (e.g. Ermentrout 1998).

We characterize the behavior of the model in the phase plane, i.e., the plot of r_I vs. r_E in Figure 6D (Tsodyks et al., 1997; Wilson and Cowan, 1972). We first draw the nullclines. The inhibitory (I) nullcline (Figure 6D, blue) is the set of points for which dr_I/dt = 0, and represents the values of r_I that result when r_E is clamped at different values. From Equation 2 and the properties of f_I, we can see that to maintain dr_I/dt = 0, any increase in r_E must be compensated by an increase in r_I. The I nullcline must therefore have positive slope; it approaches zero slope at upper and lower limits where the sigmoid-shaped f_I changes little with r_E. The inhibitory subnetwork by itself is stable: With r_E held fixed at any value, after a brief, vertical perturbation away from the nullcline, the network state moves vertically back to the nullcline (Figure 6D, vertical arrows). This stability arises because dr_I/dt decreases with r_I, so that dr_I/dt<0 everywhere above the I nullcline and dr_I/dt>0 everywhere below it.

Similarly, the excitatory (E) nullcline (Figure 6D, red) is the set of points for which dr_E/dt = 0, and represents the values r_E that result when r_I is clamped at different values. The shape of the E nullcline is more complex than that of the I nullcline. From Equation 1, when ∂f_E/∂r_E>1, dr_E/dt increases with r_E, so r_I must increase with r_E to maintain dr_E/dt = 0, and the nullcline must have a positive slope; whereas when ∂f_E/∂r_E<1, dr_E/dt decreases with r_E, and the nullcline must have a negative slope. Because dr_E/dt decreases with r_I, dr_E/dt<0 everywhere above the E nullcline and dr_E/dt>0 everywhere below it. Thus, where the nullcline has negative slope, if r_I is held fixed, r_E moves horizontally back to the nullcline after a small horizontal perturbation, (Figure 6D, horizontal black arrows); whereas in positive-sloping regions of the nullcline, r_E moves still further away toward stable regions of negative slope (gray arrows). Unlike the inhibitory subnetwork, then, the excitatory subnetwork is intrinsically unstable in some regions (those with positive slope), from which activity would be driven to either low or high saturated firing rates if r_I were fixed.

Under physiological conditions, inhibition and excitation are both free to vary, and the network’s steady state, or fixed point, lies at the intersection of the two nullclines, where both dr_E/dt = 0 and dr_I/dt = 0 (Figure 6D, black point). We can now restate the first requirement for being an ISN: The excitatory subnetwork is unstable at the fixed point, i.e., the two nullclines intersect on the positive-sloping portion of the E nullcline. The second requirement – that inhibition stabilize the network – requires that the nullclines intersect at a point where the slope of the I nullcline is more positive than that of the E nullcline (Supplemental Text, Section 1.2). With both requirements fulfilled, the network is stable: After a small perturbation in any direction away from the fixed point, the network ultimately settles back to the fixed point along a trajectory (Figure 6D, green arrows) determined by local network trends indicated by the black and gray arrows.

We can now understand how a surround stimulus can generate the experimentally-observed decrease in both excitation and inhibition. We assume that the predominant effect of activating the surround pathway is to increase external excitation to I cells. The result is a rise in the I nullcline (Figure 6E, dashed line), which follows directly from Equation 2: With r_E fixed, if the external excitation to the I cells increases, r_I must increase to keep dr_I/dt = 0. Because the slope of the E nullcline is positive and the slope of the I nullcline is yet more positive at their point of intersection, an upward movement of the I nullcline shifts the center-only fixed point (Figure 6E, black point) down and to the left (gray point). Just as we have observed experimentally, in the new steady state evoked by the surround stimulus, activity in both the E and I cells declines relative to the original steady state evoked by the center stimulus alone.

Most importantly, if the network were not an ISN, then the E nullcline would have negative slope at the center-only fixed point (Figure 6F), and the surround stimulus would shift the fixed point up and to the left, increasing activity in the I cells while lowering activity in the E cells. Thus, a decrease in the activity of both the E and I cells will occur if and only if the center-only fixed point is located on the positive-sloping portion of the E nullcline, that is, if and only if the network is an ISN (Tsodyks et al., 1997).

Note that these results also hold if in addition to driving the I cells, the surround stimulus weakly excites the E cells (Figure 6A, dashed line). In this case (which seems likely), the surround stimulus will move both the inhibitory and E nullclines upwards. In an ISN, however, as long as the upward motion of the I nullcline predominates, the fixed point will still move down and to the left, decreasing both E and I activity (Figure 6E).

In the ISN, immediately after the I nullcline moves upwards, the network state still sits momentarily at the old, center-only fixed point. Because this point now lies below the nullcline, dr_I/dt becomes positive. The inhibitory firing rate, r_I, will therefore initially increase before it ultimately decreases toward the new center-plus-surround fixed point (Figure 6E, green arrow), thereby generating the transient increase in inhibition seen in Figure 6C. This prediction is addressed experimentally below.

Although we have not explicitly modeled the orientation selectivity of surround suppression, we have assumed that the E and I cells, and the surround inputs, all have similar orientation preference (Dragoi and Sur, 2000; Schwabe et al., 2006; Somers et al., 1998). Thus, as the orientation of the surround stimulus is varied away from the preferred, the surround input, and therefore surround suppression, decreases.

Cell-to-Cell Variability of Surround Suppression in an ISN

The model in Figure 6 represents the average firing rates of the E and I cell populations with only one parameter each (r_E and r_I), and so cannot capture the diversity of neuronal behavior observed experimentally. We therefore constructed a multi-neuron model in which the extrernal inputs and intracortical connections varied from cell to cell (Experimental Procedures; Supplemental Text, Section 3). Suppression in excitation and inhibition varies from cell to cell in the model (Figure 7A), as it does in the data (Figure 7B). One significant difference between the two plots, however, is that cells above the diagonal are common in the model and less so in the data. These are surround-facilitated cells (Li and Li, 1994; Walker et al., 2000), which we observed, but for which we did not measure conductance. They therefore do not appear in the data. The diversity of behavior in the multi-neuron model and data suggests that suppression and facilitation may represent different segments of a continuum of surround effects. This continuum may not be randomly organized: Surround-facilitated cells tend to cluster spatially (Yao and Li, 2002) and to be a specific anatomical subtype (Song and Li, 2008).

Experimental Tests of the ISN Model’s Predictions

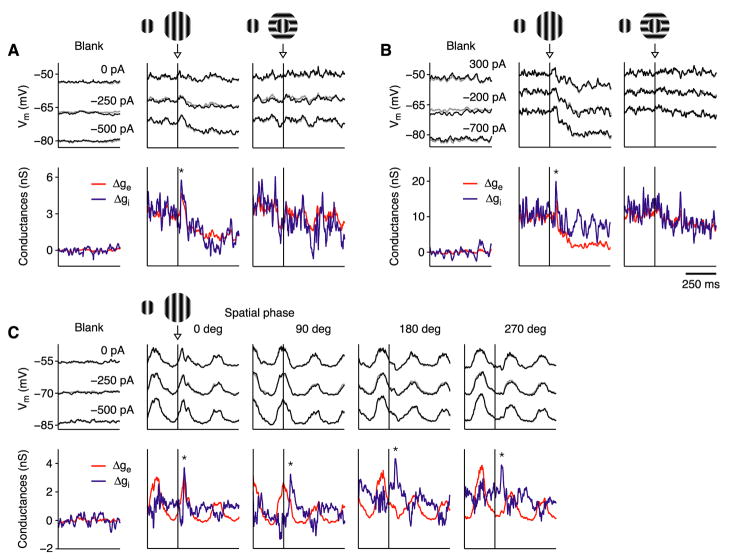
In addition to a steady-state reduction in excitation and inhibition (Figure 2), the ISN model makes two testable predictions. First, prior to reaching its steady state, ISNs (and not non-ISNs) should show a transient increase in inhibition (Figure 6C). To test this prediction, we recorded from 35 surround-suppressed cortical cells while presenting a stimulus that abruptly increased in size, from initially covering the receptive field center to covering its center and surround. In 6 of these cells (1 simple, 5 complex), the recordings were sufficiently stable to measure membrane conductance at the temporal frequencies of 10–20 Hz required to detect a transient change. Each cell showed a transient increase in inhibition of 30–50 ms duration (Figure 8). Where tested (5 complex cells), the transient was only evoked by a surround stimulus of the preferred orientation (Figures 8A and 8B). In two cells (Figures 8A and 8B), the surround stimulus transiently increased excitation as well as inhibition, which will occur in the ISN model when the surround input excites both the E and I cells. For the simple cell in Figure 8C, we varied the starting spatial phase of the grating so that the increase in stimulus size occurred during different phases of the response. No matter whether the surround stimulus was switched on during the depolarizing (2nd and 3rd columns) or the hyperpolarizing (4th and 5th columns) phase of the response, the inhibitory conductance increased transiently before both conductances decreased to their new steady-state levels. This transient increase in inhibition suggests that the surround stimulus evokes a brief response in the I cells, followed by a sustained decline. There need be no concomitant transient response in the E cells (Bair et al., 2003), however, since any transient increase in excitation may be balanced by the transient increase in inhibition.

Figure 8. Transient increase in inhibitory conductance.

Responses of cells to sudden addition of a surround stimulus (arrows) to a center stimulus that began 500 ms earlier (250 ms before traces start). The iso-oriented surround is presented at the same phase as the center. Gratings drifted at 4Hz. Black, membrane potential recorded with different currents injected; red and blue, changes in excitatory and inhibitory conductance; gray, reconstruction of membrane potential from derived conductances. K⁺-gluconate solution in recording pipette.

(A and B) Responses of 2 complex cells. A transient increase in conductance (asterisks) occurred in response to iso-oriented but not cross-oriented surround.

(C) Simple cell tested with iso-oriented surround added at 4 different response phases (starting center phase shifted by 90° for each successive stimulus). All evoked transient increase in conductance.

A second prediction of the ISN model comes from its property that surround suppression arises from a withdrawal of intracortical excitation: Cells can be strongly surround suppressed only if they receive a significant portion of their excitatory input from other cortical cells. Conversely, cells that receive most of their excitation from the LGN can show little suppression. By comparison, if surround suppression arose from an increase in synaptic inhibition, any V1 cell could be suppressed regardless of the source of its excitation. Additionally, the ISN model predicts that for cells in which LGN input predominates, what little surround suppression is observed should, like the suppression in the LGN (Figure 5), be largely untuned for the surround orientation.

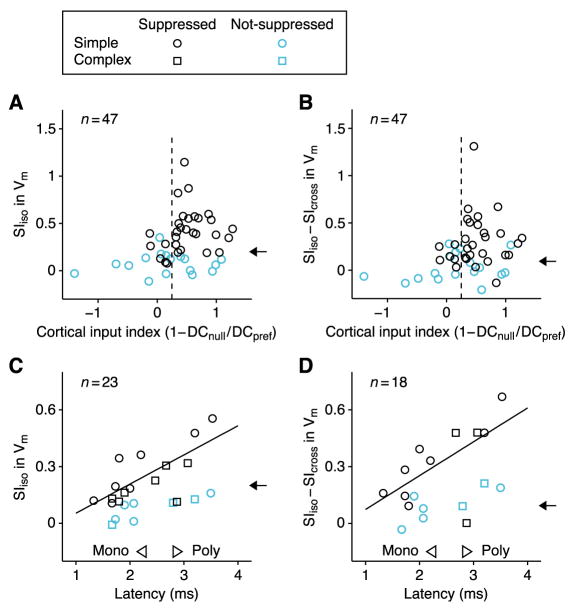
We tested these predictions in the 47 simple cells. Our proxy for the proportion of excitatory input each cell received from the cortex is a closely correlated measure, 1–DC_null/DC_pref, where DC_null/DC_pref is the ratio of the mean depolarization evoked by center gratings of the orthogonal (null) and preferred (pref) orientations (Finn et al., 2007). Consistent with the ISN model, only cells with significant cortical input (Figure 9A, 1–DC_null/DC_pref >0.25) showed strong surround suppression (SI_iso >0.4), or strongly orientation-selective suppression (Figure 9B, SI_iso–SI_cross > 0.4). Note that about half of the cells that receive significant cortical input did not show strong or strongly orientation-selective suppression. Such cell-to-cell variability can be explained by the variability of weights and inputs in the multi-neuron ISN model (Figure 7A).

Figure 9. Comparison of population data with predictions of the ISN model.

(A) Suppression indices of membrane potential for the iso-oriented surround (SI_iso) in 47 simple cells (30 surround-suppressed; 17 non-suppressed) plotted against cortical input index (CII), which correlates well with percent of excitatory input received from cortex (vs. LGN), see text. Only cells with CII>0.2 (vertical dashed line), suggesting >20% cortical input, show strong suppression. Arrow shows mean SI_iso for 18 LGN cells, which is comparable to mean values for cortical cells with little cortical input and for non-suppressed cortical cells. (B) Same as (A) for orientation selectivity of suppression (SI_iso–SI_cross), the difference between suppression induced by iso- and cross-oriented surrounds. Arrow shows mean value of SI_iso–SI_cross for 18 LGN cells. (C and D) SI_iso and SI_iso–SI_cross for membrane potential plotted against latency of response to electrical stimulation of the LGN (C, 13 simple, 10 complex; D, 13 simple, 5 complex). Cells with short latencies (<2.3 ms) receive some excitation directly from LGN; cells with long latencies (>2.8 ms) receive no monosynaptic input from LGN. Regression lines are derived from surround-suppressed cells only. Arrows as in (A) and (B). In (A)-(D): circle and square symbols, simple and complex cells; black and cyan symbols, surround-suppressed and non-suppressed cells.

Another indication of the sources of a cell’s excitation is the latency of the membrane potential response to electrical stimulation of the LGN: Cells with latencies above 2.8 ms receive input only from other cortical cells; cells with latencies below 2.3 ms receive some proportion of their input directly from the LGN (Chung and Ferster, 1998). In a subset of experiments, we measured this latency and, as predicted by the model, both the strength and orientation selectivity of suppression increased with latency (Figures 9C and 9D; SI_iso: r=0.73, p<0.01; SI_iso–SI_cross: r=0.64, p<0.04). In agreement with these results, cells located in thalamo-recipient cortical layers are less likely than cells in upper layers to show strong suppression (Akasaki et al., 2002; Jones et al., 2000; Walker et al., 2000).

A third prediction of the ISN model is that surround suppression should be little affected by local blockade of synaptic inhibition. Blocking inhibition in a small number of cells should have little effect on the overall balance of excitation and inhibition in the cortical column, and so the remaining part of the ISN should operate as before. Thus, even for the cells in which inhibition has been removed, the surround stimulus will reduce net excitation, and evoke surround suppression. Previous experiments with iontophoretic application of bicuculline (Ozeki et al., 2004) support this prediction. Unlike local blockade of inhibition, global blockade cannot easily be used to test the model. Because of the ISN’s strong excitatory recurrence, even small global attenuations of inhibition can yield a sudden instability (Chagnac-Amitai and Connors, 1989). Similar behavior, however, could emerge in a non-ISN: e.g., if the E nullcline were as in Figure 6D, but the fixed point were in the leftmost negative-sloping region, inhibitory blockade could cause a sudden jump across the positive-sloping region to the rightmost negative-sloping region.

Finally, the model and data make a strong prediction that the local inhibitory interneurons mediating surround suppression should themselves be surround suppressed, which has been observed directly (Song and Li, 2008). In contrast, the standard models of lateral inhibition (non-ISNs) predict that the surround stimulus would increase activity of inhibitory interneurons.

Alternative Models

So far, we have assumed for simplicity that the only direct effect of the surround stimulus is to increase external excitation to the local circuit. In this case, we showed that an ISN – and not a non-ISN – can replicate the observed surround-evoked decrease in inhibition, due to the paradoxical response of the I cells to external excitation (Tsodyks et al., 1997). We now generalize this result. We consider all combinations of surround-driven input, including increases or decreases in external excitation or inhibition, and show that no plausible non-ISN scenario can account for the data.

We assume a model in which the firing rate of the E cells moves toward the value: f_E(r_E,r_I,i_E) = g_E(w_EEr_E − w_EIr_I + E_E − I_E) (Equation 1). Here, E_E and I_E are the external, excitatory and inhibitory input to the E cells, with i_E = E_E − I_E. Surround-evoked changes in parameters are denoted by the prefix Δ. We denote the argument of g_E by D_E, the drive to the E cells.

We consider an arbitrary, surround-driven change in external inputs, requiring only that their net effect be suppressive: Δr_E<0. Then both nullclines may move in response to the surround (unlike in Figure 6, where only the I nullcline moved). The surround-evoked change in inhibition to the E cells is ΔI^TOT = w_EIΔr_I+ΔI_E, which we re-express by decomposing Δr_I into two components. The first component, Δr_I1, is the vertical movement from the old (center-only) fixed point to the new E nullcline with fixed r_E. Since on the nullcline r_E = g_E(D_E) and r_E is fixed, D_E must be unchanged, and therefore Δr_I1 = (ΔE_E − ΔI_E)/w_EI. The second component, Δr_I2, corresponds to the leftward movement along the new E nullcline to the new fixed point. Δr_I2 = κΔr_E, where κ is the average slope of the E nullcline between the r_E’s of the old and the new fixed-point. κ is positive for an ISN and negative for a non-ISN. In Supplemental Text (Section 2), this analysis is extended to compute changes in all firing rates and synaptic inputs.

From ΔI^TOT = w_EI(Δr_I1+Δr_I2)+ΔI_E, we find ΔE_E− ΔI^TOT = −w_EIκΔr_E. This equation expresses a simple intuition. The total change in drive that produces the suppression in firing rate, Δr_E, is ΔD_E = w_EEΔr_E+ΔE_E−ΔI^TOT, or ΔD_E = w_EEΔr_E−w_EIκΔr_E. If the decrease in feedback excitation, w_EEΔr_E, were exactly equal to ΔD_E, it would entirely account for the change Δr_E, so all other changes in input to E cells would have to sum to zero. If w_EIκΔr_E>0, the reduction in feedback excitation is too weak to account for Δr_E and must be supplemented by decrease in other input. This is the non-ISN case: The excitatory subnetwork alone is stable, meaning that if r_E were artificially decreased without allowing other changes, sufficient feedback excitation would remain to drive r_E back to its original fixed point. If w_EIκΔr_E<0, the reduction in feedback excitation is too strong and must be supplemented by increase in other input. This is the ISN case: The excitatory subnetwork alone is unstable, meaning that in response to the same decrease in r_E, so much feedback excitation would be withdrawn that r_E would fall still further. The equation says that all other changes in input to the E cells must exactly cancel this excess or deficit of feedback excitation: ΔE_E− ΔI^TOT = −w_EIκΔr_E.

We conclude that ΔI^TOT>ΔE_E in a non-ISN, but ΔI^TOT<ΔE_E in an ISN. In an ISN, one surprising consequence is another paradoxical behavior: Just as addition of external excitation to I cells leads to a reduction in the total excitation they receive, addition of external inhibition to E cells causes a reduction in the total inhibition they receive, because of the induced decrease in r_I. In a non-ISN, the total inhibition received is increased. More generally, the only way that a suppressive surround stimulus can decrease inhibition in a non-ISN is if it causes an even greater decrease in external excitation to E cells.

Thus, there are only two possible scenarios in which the surround-evoked reduction in inhibition could arise from a non-ISN. First, surround suppression might be driven entirely by withdrawal of external excitation from LGN and/or cortex. As we have shown, however, surround suppression in the LGN is too weak and too weakly orientation tuned to account for cortical surround suppression (Figure 5). Surround-evoked reduction in external cortical input seems unlikely because cortical cells whose receptive field centers lie within the surround stimulus should be excited, not suppressed, by the surround stimulus. Finally, a withdrawal of external excitation would not generate the observed transient increase in inhibition (Figure 8) nor explain the lack of strong suppression in cells receiving dominant LGN input (Figure 9).

Second, as seems likely, the surround stimulus might evoke a combination of two changes in the external input to the network: an orientation-independent withdrawal of LGN excitation to E and I cells, which accounts for a weak, orientation-untuned component of suppression, and an orientation-tuned increase in external intracortical input, which accounts for the strong, orientation-tuned component of suppression. The intracortical input presumably includes external excitation to the local circuit, predominantly to I cells but perhaps also to E cells. This combination of inputs could generate a net withdrawal of external excitation to E cells, allowing a decrease in their total inhibition in a non-ISN. Such a decrease, however, would have the wrong orientation tuning, being strongest at orientations that evoked the least suppression, unlike in the data (Figure S5).

This mismatch in orientation tuning in a non-ISN can be seen from the equation, ΔI^TOT = ΔE_E+w_EIκΔr_E. Because κ<0 in a non-ISN, the second term is positive and is largest where suppression is strongest. The first term is negative, and is either untuned for orientation or least negative where suppression is strongest (if external, intracortical input includes excitation to E cells). Thus, the overall decrease in total inhibition is strongest (ΔI^TOT is most negative) where suppression is weakest. This scenario also predicts incorrectly that the orientation tuning of excitatory and inhibitory suppression should be anticorrelated – strong suppression is evoked by stronger intracortical input, which increases the bias of inhibitory suppression toward the cross-orientation and of excitation toward the iso-orientation; instead, they are correlated (Figure S7; r=0.46, p<0.03). Finally, whereas this scenario could allow a transient increase in inhibition, it could not account for the observed transient increase in excitation (Figure 8), unless the increase in external, intracortical excitation preceded the withdrawal of external LGN excitation, which seems implausible.

Unlike any of the non-ISN scenarios, the ISN readily produces a suppression of total inhibition to E cells with the correct orientation tuning. The real circuit, of course, will be more complex, with distinct inhibitory and excitatory subpopulations. The above arguments, however, suggest that any model of surround suppression must operate in the ISN regime to account for the data.

DISCUSSION

We have found that orientation-dependent surround suppression in V1 is accompanied by a decrease in both excitatory and inhibitory input to V1 cells (Figures 1–4). This result cannot be explained by surround-induced withdrawal of feed-forward input from the LGN: Using similar stimuli in LGN as we used in cortex, we found that surround suppression in the LGN is neither strong enough nor well enough tuned for orientation to account for V1 suppression (Figure 5). On the assumption that this V1 suppression is not driven by withdrawal of external intracortical excitation to the local circuit, the results imply that V1 must be operating as an inhibition-stabilized network, or ISN (Tsodyks et al., 1997), in which recurrent excitation is strong enough to be unstable by itself, but is stabilized by feedback inhibition (Figure 6). When this ISN model includes multiple neurons with random variations in connectivity and input, it reproduces the full range of surround-induced behavior seen in V1 (Figure 7).

We have conducted two strong tests of the ISN model’s predictions. First, the steady-state decrease in excitation and inhibition caused by surround stimuli is preceded by a transient increase in inhibition (Figure 8). Second, surround suppression is weak in amplitude and weakly orientation tuned in cells that do not receive significant recurrent excitatory input (Figure 9). Together, these results provide strong evidence that V1 operates as an ISN.

In their studies of length tuning, Anderson et al. (2001) observed concomitant reductions in excitation and inhibition when a bar stimulus was lengthened along the axis of preferred orientation (their Figure 6C, compare 2 to 4, and 2 to 12°). They also observed an increase in inhibition at an intermediate length (8°), which was not tested in the current experiment. In theoretical work, we have found that such a bimodal tuning of inhibition, if not directly built in to LGN input or horizontal connectivity, will arise only in the ISN regime (D. Rubin and K.D. Miller, unpublished observations). It is not clear whether the length tuning of LGN cells (Cleland et al., 1983; Jones and Sillito, 1991) could account for cortical length tuning.

Consistent with a cortical origin for surround suppression, V1 surround suppression is delayed at least 10 ms after the onset of the center response (Knierim and Van Essen, 1992; Smith et al., 2006). By comparison, cross-orientation suppression from within the receptive field center, which is likely subcortical in origin (Li et al., 2006; Priebe and Ferster, 2006), is not delayed (Smith et al., 2006). In addition, cortical surround suppression more closely resembles responses of cortical cells than geniculate cells in its dependence on spatial and temporal frequency, adaptation, and interocular transfer (DeAngelis et al., 1994; Durand et al., 2007; Webb et al., 2005).

Previous work on ISNs and on the operating regime of cortex

Wilson and Cowan (1972) were the first to propose that a stable fixed point can exist on the unstable branch of the E nullcline. Tsodyks et al. (1997) described the paradoxical ISN behavior that increasing excitation to inhibitory cells decreases their firing rates, which is just one facet of the intriguing dynamics of ISNs (Murphy and Miller, 2009). Other models of sensory cortex have operated in the ISN regime (Adini et al., 1997; Chelaru and Dragoi, 2008; Pinto et al., 2003), but did not address the question of whether this regime was required for the results. Latham et al. (2000, Appendix B) argued that virtually all cortical fixed points should lie on a positive-sloping portion of the E nullcline, based on parameters from anatomy and slice recordings. An alternative calculation based on in vivo parameters is less conclusive, however (Supplemental Text, Section 4).

In balanced network models, strong excitation and inhibition are tightly balanced, leaving only a much smaller net input (Lerchner et al., 2006; van Vreeswijk and Sompolinsky, 1998). While the balanced networks generally operate as ISNs, ISNs need not be tightly balanced: inhibition need only cancel enough excitation to yield stability. Furthermore, many factors could offset input imbalances, e.g. intrinsic hyperpolarizing conductances could offset excitation, while temporal offsets between excitation and inhibition could mitigate excess inhibition (Gabernet et al., 2005; Troyer et al., 1998; Wilent and Contreras, 2005). In addition, a nonlinear network may move in and out of the ISN regime depending on mean firing rate, operating, for example, as a non-ISN during spontaneous activity and an ISN when responding to a stimulus (Latham et al., 2000; Pinto et al., 2003; Supplemental Text, Section 4). In contrast, the balanced network models posit that all activity regimes are in the tightly-balanced state.

Large variability in cortical responses, which motivated the balanced network models, does not by itself establish that cortex operates either as a balanced network or an ISN. Given uncorrelated inputs, the key requirement for large variability is that the mean input be subthreshold, so that spikes are triggered by fluctuations around the mean (Amit and Brunel, 1997; Troyer and Miller, 1997). Alternatively, cortical variability could arise from correlation among inputs (DeWeese and Zador, 2006).

Experimentally, the cortex appears “balanced” in that the excitation and inhibition received by cells rise and fall together in response to sensory stimuli (Anderson et al., 2000; Ferster, 1986) and during spontaneous changes in cortical state (Haider et al., 2006; Higley and Contreras, 2006; but see Waters and Helmchen, 2006). Excitation and inhibition will vary together in both ISNs and non-ISNs if the sensory input, or change in state, primarily modulates the excitatory drive to excitatory cells. If, however, the input predominantly changes the drive to inhibitory cells (or the inhibitory drive to excitatory cells), correlated movement of excitation and inhibition should occur only in ISNs (Supplemental Text, Section 2).

Conclusion

Cortical circuits are characterized by anatomically-massive recurrent connections (Binzegger et al., 2004; Stepanyants et al., 2008), which must surely be critical to the computations they perform. Inhibitory stabilization may be a general strategy allowing the cortex to maintain excitation that is strong enough to carry out complex computations, and yet maintain stability and operate with relatively low firing rates (Latham and Nirenberg, 2004).

Despite these arguments, there has been little direct evidence regarding the operating regime of cortex or other neuronal circuits. We have provided evidence that at least one area of the neocortex, V1, operates as an ISN when responding to a stimulus. Our data do not address whether the network operates as an ISN at rest.

Recent work has suggested that in visual cortex (Finn et al., 2007; Palmer and Miller, 2007; Priebe and Ferster, 2008) and somatosensory cortex (Bruno and Sakmann, 2006), tuning properties of the classical receptive field, at least in layer 4, are synthesized largely from feed-forward mechanisms. Recurrent cortical connections may then set the gain of responses. Our results argue that, during surround suppression, horizontal connections and/or feedback connections from higher areas modulate this gain by modulating the balance of excitation and inhibition in the local recurrent network. Like attractor models (Ben-Yishai et al., 1995; Somers et al., 1995), the ISN requires strong recurrence; unlike attractor models, however, the ISN does not strongly restrict the set of possible cortical responses, and enables any change in stimulus to evoke a change in response. The organization of the local circuit in an ISN may therefore allow neurons to provide a faithful, feed-forward-driven representation of local stimulus patterns, and still be modulated by global stimulus properties or behavioral context. We speculate that such an ISN regime is likely to be the domain at least of sensory and particularly primary sensory cortex, where a faithful representation of inputs is needed.

EXPERIMENTAL PROCEDURES

Physiological Experiments

Intracellular current-clamp recordings were made from primary visual cortex of anesthetized adult cats (Boudreau and Ferster 2005). Anesthesia was induced with ketamine and maintained with sodium thiopental. Eye movements were minimized with vecuronium bromide, and animals artificially ventilated. All procedures were approved by the Northwestern University Animal Care and Use Committee. Stimulus-evoked changes in membrane conductance and its excitatory and inhibitory components were measured by injecting steady currents of different amplitudes during repeated visual stimulation (Anderson et al., 2000; Boudreau and Ferster, 2005). For conductance measurements, Cs⁺ and QX-314 were introduced into the electrode to block active currents. For detailed methods, and a test of whether active currents or spiking distorted conductance measurements, see Figure S4.

Drifting sinusoidal grating stimuli (4-sec duration) were presented monocularly on a CRT monitor (Finn et al., 2007), centered on each neuron’s minimum response field. The receptive field center size was taken to be the largest stimulus that evoked a strong spike response, but for which an annulus of the same inner diameter evoked no spikes. Cells were classified as surround suppressed if mean+s.e.m. of the center-plus-surround firing rate response was smaller than mean−s.e.m. of the center-only response.

Spike responses were measured as the modulation (F1) component for simple cells and as the mean (DC) component for complex cells. Cells were classified as simple (F1/DC>1) or complex (F1/DC<1) as per Skottun et al. (1991). Membrane potential and conductance responses were measured as the peak amplitude relative to rest (DC+F1) after removing spikes from the records by a median-filter.

Steady-state surround suppression was measured using a center grating of optimal size and orientation combined with annular gratings (20° outer diameter, varying orientation) extending from the edge of the center grating (Figures 1 and 2). Transient responses to the onset of surround stimuli (Figure 8) were measured by turning on the surround stimulus 500 ms after the center.

LGN recordings (Figures 5 and S6) were made with tungsten electrodes (A layers, eccentricity <5°). Center stimuli were optimal in size for the average simple cell in the cortical population: 2° (or 4°) diameter for LGN cells with receptive field centers smaller (or larger) than 1°. Electrical stimuli to the LGN (200 μs, 0.5 mA, electrode negative) were delivered through tungsten electrodes placed at the retinotopic location matching the cortical recording electrode (Boudreau and Ferster, 2005; Chung and Ferster, 1998).

Model simulations

Simulations were based on linear dynamical equations (Supplemental Text, Section 1). The equations of the two-population model in Figure 6C were:

$$\begin{array}{l}{\tau }_E\frac{d}{dt}{r}_E=-r_E+w_{EE}{r}_E-w_{EI}{r}_I+i_E,\\ {\tau }_I\frac{d}{dt}{r}_I=-r_I+w_{IE}{r}_E-w_{II}{r}_I+i_I,\end{array}$$

where variables were defined above equations 1–2 and synaptic weights (w_EE, w_EI, w_IE, w_II) are all positive. Parameters used were: i_E=0; i_I=1; τ_E = 60 ms; τ_I = 12 ms; w_EE = 2; w_EI = 4; w_IE = 5; w_II = 7. The multi-neuron simulation (Figure 7) used N excitatory and N inhibitory neurons (N=1000). Equations were as above, except that the rates and inputs were each N-dimensional vectors and the weights each N×N matrices. We began with a two-population model that gave mean suppression as in the data (w_EE = 1.8, w_EI = 1.3, w_IE = 2.4, w_II = 1.8; i_E = 4.0, i_I = 1.6 for center stimulus; i_E = 4.4, i_I = 3.8 for center-plus-surround stimulus). Mean inputs or weights of a given type were set equal to the two-population inputs or 1/N times the two-population weights. With no variability, each cell would behave exactly as the corresponding population in the two-population model. To create variability, weights were set to zero with probability 0.95 and means of nonzero weights correspondingly multiplied by 20. Then nonzero weights and all inputs were chosen from log-normal distributions with standard deviations 2.75 times their means. To ensure network stability, for each cell, recurrent excitatory weights received were scaled to set their sum to the value it would have with no variability, and similarly for inhibitory weights received. Cells with center responses negative or less than ¼ the center response in the two-population model had all center and surround inputs and excitatory weights multiplied by 1.1 and inhibitory weights divided by 1.1; responses were reevaluated and the process repeated until there were no such cells. See Supplemental Text, Section 3.