Abstract
It was discovered 12 years ago that type IIA topoisomerases can simplify DNA topology—the steady-state fractions of knots and links created by the enzymes are many times lower than the corresponding equilibrium fractions. Though this property of the enzymes made clear biological sense, it was not clear how small enzymes could selectively change the topology of very large DNA molecules, since topology is a global property and cannot be determined by a local DNA–protein interaction. A few models, suggested to explain the phenomenon, are analyzed in this review. We also consider experimental data that both support and contravene these models.
INTRODUCTION
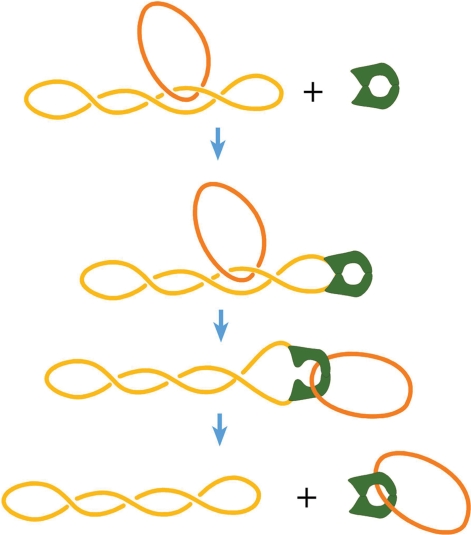
Type II DNA topoisomerases are essential enzymes that catalyze the passing of one segment of the double helix through another (1,2). They bind a DNA segment (gate or G segment) and introduce a transient double-stranded break in this segment, then capture another segment of the same or another DNA molecule (T segment) and transport it through the break. The break is resealed after the passing of the T segment. Thus, these enzymes can change the topology of circular DNA molecules, create knots and catenanes from DNA circles as well as unknot and unlink them, and also change DNA supercoiling.
In 1997, Rybenkov et al. reported an unexpected discovery related to a major subclass of type II topoisomerases. They found that type IIA DNA topoisomerases can dramatically reduce fractions of knotted and linked circular DNA molecules compared to the corresponding fractions at the thermodynamic equilibrium (3). This property of the enzymes has clear biological sense, since removing links between DNA molecules is one of their major functions. It also explains why the strand-passing reaction catalyzed by the enzymes requires energy that comes from the ATP hydrolysis incorporated into the reaction cycle (3). Indeed, the chemical reactions of breaking and rejoining DNA strands can be performed without consumption of external energy—type I topoisomerases do this catalyzing the strand-passing reaction through single-stranded DNA segments. So, evolution could develop enzymes that catalyze strand-passing through double-stranded segments without energy consumption as well. The energy is required, however, to shift a system away from the thermodynamic equilibrium, and type IIA topoisomerases do exactly this. Still, the discovery posed a puzzle that has attracted much attention in the biophysical community in the last 12 years. The problem is that topology is a global property of circular DNA molecules, and thus cannot be recognized by enzymes that only interact with DNA locally. This means that any local conformation of two DNA segments that interact with the enzyme during the reaction is compatible with any particular topology of the DNA molecule. Therefore, there is no way for the enzymes to uniquely determine topological consequences of a particular strand-passing event. However, the probability of a particular local conformation of two juxtaposed segments can depend on topology, and the enzymes can use this dependence. If some local conformation appears more often in knotted/linked molecules than in unknotted/unlinked and the enzyme use it as a substrate, it would simlify DNA topology. Of cause, in this case the enzymes will never be able to remove all knots or links in the sample of circular DNA molecules, and the experiment shows exactly this: the steady-state fractions of knots and links are greatly reduced by the enzyme action, but they are not equal to zero (3). There are always non-zero probabilities that the enzyme unlinks two linked DNA molecules and that it links two unlinked molecules. The phenomenon of topology simplification only means that the enzymes have a way to change the ratio of these probabilities. We want to understand in detail how they solve this problem.
Over the years, a few models were suggested in attempts to explain the phenomenon (3–7). These models are analyzed in this review. First, we describe the phenomenon of topology simplification in detail, starting from the concept of equilibrium distribution of topological states. Then, we present a theoretical analysis based on a general consideration of the phenomena. This analysis, complemented by computer simulations, is applied to each individual model. We also consider experimental data that both supports and contravenes these models.
EXPERIMENTAL FINDING OF TOPOLOGY SIMPLIFICATION BY TYPE IIA TOPOISOMERASES
Rybenkov et al. (3) found that the steady state fractions of knots and catenanes created by the type IIA topoisomerases in solution are many times lower than the corresponding equilibrium fractions. To describe this phenomenon properly we first have to consider what the term ‘equilibrium fraction’ means in this particular case.
Equilibrium distribution of topological states
If we have molecules in solution which adopt more than one state and an exchange between these states is possible, after some time the fractions of the molecules at different states, fi, will adopt their equilibrium values, fieq, regardless of the initial values of fi. These equilibrium fractions are specified by the free energies of the corresponding states, Gi:
where R is the gas constant and T is the absolute temperature. We could use the same equation to specify the thermodynamic equilibrium between topological states of circular DNA molecules, although there is an essential distinction in this case. An exchange between different topological states of the circular molecules is impossible, so the initial distribution of the topological states is preserved as long as the molecule backbones remain intact. We can say that in this case the equilibrium distribution corresponds to an imaginary situation where segments of the circular molecules can freely pass through one another during thermal motion. Of course, the values of fieq depend on the length of DNA molecules and solution conditions that affect the physical properties of the molecules. Thus, the first question here is: how can we measure the values of fieq if there are no exchanges between the states? Fortunately, we can do this by placing the linear DNA molecules with long sticky ends under conditions where the ends join with one another. This cyclization is a very slow process (8,9) in the timescale of the conformational rearrangements of linear DNA molecules, and therefore creates the equilibrium distribution of topological states. When the cyclization is complete, the molecules with different topologies can be separated by gel electrophoresis and we can measure their relative fractions to determine fieq.
We can also obtain the values of fieq in the computer simulation of the equilibrium conformational ensemble for circular DNA molecules. It is known that this kind of simulation is capable of predicting large-scale DNA properties very accurately (10). The DNA model describing conformations of nicked circular DNA represents a closed chain of straight impenetrable cylindrical segments with a certain bending rigidity between them (10). Such a discrete wormlike chain model has only two parameters, DNA bending rigidity (or its persistence length) and the effective diameter of the model chain, d. The value of d accounts for the electrostatic repulsion between DNA segments and usually exceeds the geometric diameter of the double helix (11). The latter parameter strongly depends on ionic conditions because the counterions screen the negatively charged DNA segments and thus reduce the electrostatic repulsion between them. Increasing the salt concentration effectively makes DNA thinner. Both parameters of the model are well known from numerous experimental and theoretical studies [see ref. (10) for review].
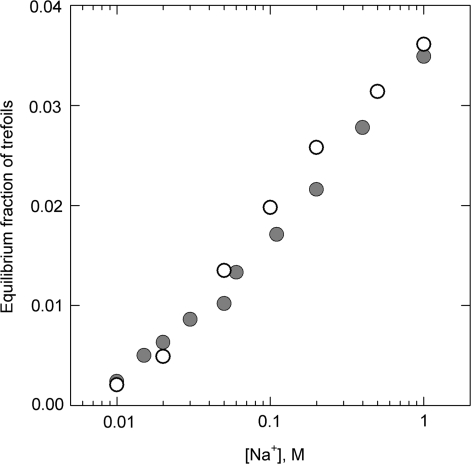
Of course, both experimental and theoretical approaches of determining the values of fieq must produce the same results, and, as shown, they do (Figure 1). Remarkably, the measured and calculated fractions of the trefoil knots are in agreement over a wide range of ionic conditions in which they change by more than the order of the value (due to the change of the electrostatic repulsion between the DNA segments). If we take into account that the theoretical calculation has no adjustable parameters, the results presented in the figure should be considered solid proof that we know how to obtain the values of fieq for different topological states.
Figure 1.
Measured and simulated equilibrium fractions of trefoil knots for different concentrations of sodium ions [based on the data from ref. (9)]. The experiments were performed with 10-kb DNA which was cyclized in solution of different NaCl concentrations via joining the cohesive ends. Each point on the graph (gray circles) is the average of 6–20 determinations. The results of computer simulation, shown by open circles, account for the salt concentration over the effective diameter of the double helix which strongly depends on NaCl concentration (11). Only traces of more complex knots were observed in the experiment.
Topology simplification by topo IIA
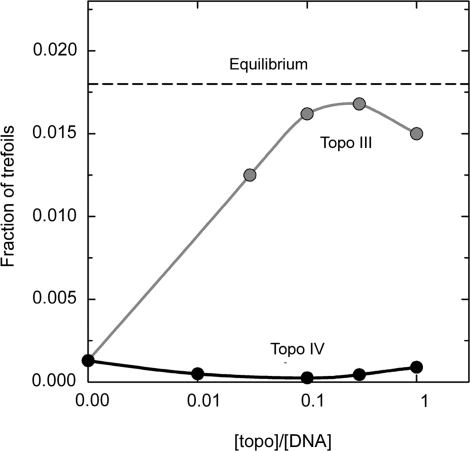
Thus, it was found that type IIA DNA topoisomerases dramatically reduce the fractions of more complex topological states, knots and links, formed by nicked circular DNAs, relative to the corresponding equilibrium fractions (Figure 2). Under the substochiometric concentrations of the enzymes in solution the fractions of knots and links reach their steady-state values, fiSS, which do not depend on the initial values of fi. In the experiment presented in Figure 2 the initial fraction of trefoil knots was 10 times lower than the equilibrium value for the salt concentration used in the experiment. However, E. coli type II topoisomerase, Topo IV, further reduced it by nearly a factor of 10. This steady state fraction of trefoils, f3SS, remained practically the same when the molar ratio of the enzyme to DNA was between 0.1 and 1. Similar, but smaller reduction of f3SS was observed for other type IIA topoisomerases (3). All tested enzymes also reduced the equilibrium fractions of linked circular DNA molecules by a factor of 3–15. Rybenkov et al. also found that the enzymes reduce the width of the topoisomer distribution in closed circular DNAs up to two times, relative to the equilibrium value. The latter effect was also studied by Trigueros et al. (7) and recently by Stuchinskaya et al. (12), who obtained similar results.
Figure 2.
Type IIA topoisomerase, topo IV from E. coli, removes topological links from DNA to level below equilibrium (3). The reaction reached its steady state at substoichiometric values of the enzyme/DNA ratio. The equilibrium value of the knot fraction for the given conditions and DNA length, 7 kb, is shown as a reference level by the dashed line. Also shown, as a control, the fraction of knots found for topo III, type I topoisomerase from E. coli, which does not consume the energy during the catalysis and thus must shift the fraction of trefoils to the equilibrium level.
Although the enzymes’ ability to simplify DNA topology below the thermodynamic equilibrium was unexpected, it explained why type IIA topoisomerases need the energy of ATP hydrolysis to catalyze the strand-passing reaction: Shifting a system away from the thermodynamic equilibrium requires energy. It was difficult to understand, however, how the enzymes accomplish this task.
GENERAL THEORETICAL ANALYSIS
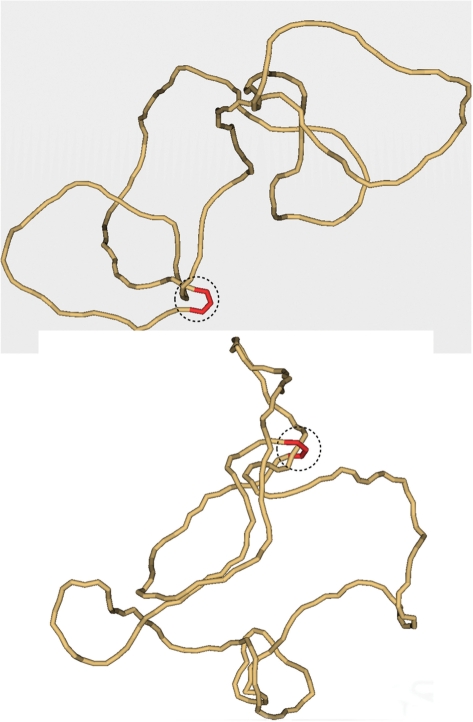
In solution, large DNA molecules form very irregular random conformations. The average size of these conformations is around 500 nm for DNA molecules of 7–10 kb in length, so they are many times larger than the enzymes. These conformations continually change due to thermal motion, and there is no way for the enzymes determining topology of such DNA molecules to change it in a desired direction. This is illustrated by Figure 3, which shows typical simulated conformations DNA molecules with different topologies. It does not mean, however, that the enzymes cannot address the problem. They have to use the local statistical properties of the molecule random conformations that may be different for the molecules with different topology. Nearly all models suggested to explain the phenomenon tried to use these properties (4–7).
Figure 3.
Typical simulated conformation of knotted (top) and unknotted (bottom) 7-kb DNA molecules. Each of the shown conformations has a segment located inside the hairpin-like G segment (red). For both conformations the potential T segment and G segment, which could interact with the enzyme, are circled by the dashed line. It seems clear from the figure that the mutual path of the segments inside the circle cannot specify topology of the entire chains. Indeed, the topology of both conformations can be easily changed outside the dashed circles. The conformations were selected from the equilibrium ensemble generated by a Metropolis Monte Carlo procedure (5).
Let us first consider knotting-unknotting process by the enzymes in general terms (we restrict our analysis by this intramolecular process for simplicity). We account for the fact that only trefoil knots appear in a notable amount in DNA molecules a few kb in length (3). Thus, the steady-state fraction of trefoils, f3SS, is specified by the rate constants k03 and k30, which correspond to the conversion of unknotted molecules to trefoils and vice versa. By definition, at the steady state the concentrations of all topological forms remain constant, so we can write:
or
where c0 and c3 are the steady-state concentrations of unknotted DNA molecules and trefoils, correspondingly. Equation (3) can be used to analyze any model of the phenomenon. The constants k03 and k30 can be estimated as:
where p0 and p3 are the probabilities of the juxtaposition of two DNA segments, for unknotted conformations and trefoils, which can result in the strand-passing reaction, r03 and r30 are the probabilities of the corresponding topology changes in the case of strand-passing, and A is a coefficient which depends on the enzyme properties and concentration. Thus,
The values on the right-hand side of Equation (5) are features of the equilibrium ensembles of DNA conformations. They can be estimated by the computer simulation of the equilibrium conformational sets for unknotted molecules and trefoils. The condition of the segment juxtaposition may include a specific geometry requirement for the G and T segments.
In the absence of any additional geometrical requirements for the juxtaposition, Equation (5) allows estimating f3eq, since, in this case:
Now we will use these equations to analyze different models of the topology simplification by type IIA topoisomerases.
THEORETICAL ANALYSIS AND EXPERIMENTAL SUPPORT OF THE MODELS
The model of knot trapping
The first model of the enzyme action was suggested by Rybenkov et al. (3). The model assumes that the enzymes first form a sliding crossover on the circular DNA by binding two of its segments. A third segment, which does not participate in the crossover, later serves as a T segment. The crossover slides along DNA changing the size of the two separated DNA domains. The model assumes that the enzyme is capable of trapping a knot in a small domain before the strand-passing reaction. Of course, in the small domain the topological equilibrium is strongly shifted to the unknotting. Although the model predicts a large reduction of f3SS, it is hardly possible to design a realistic physical mechanism of the trapping that would not consume enormous energy. Recently Stuchinskaya et al. (12) experimentally tested this model by placing obstacles for the enzyme sliding on a plasmid DNA. They found that the obstacles do not affect the ability of the enzyme to simplify DNA topology. This result strongly suggests that the knot trapping cannot be a mechanism of the topology simplification.
The model of the hairpin-like G segment
In an attempt to explain the phenomena, we suggested that the enzymes create a sharp bend in the G segment (5). If the enzymes create such a bend, they have to have a specific orientation relative to the bend. Thus, the complex with the bent G segment can provide a unidirectional passage of the T segment from inside to outside the hairpin formed by the G segment (Figure 4). Indeed, it had been known that the enzymes catalyze the passage of a T segment in one direction relative to themselves (13). A unidirectional transport requires energy that is supplied by ATP hydrolysis coupled with the strand-passing. Thus, the model suggests a reason for this unidirectional strand-passing which was difficult to understand. The directionality of strand passage is only local, since the hairpin can have any orientation relative to the DNA chain. Surprisingly though, the quantitative analysis of the model showed that it predicts a large decrease of the steady state fractions of knots and catenanes relative to the equilibrium fractions (5).
Figure 4.
The model of type IIA topoisomerase action. The enzyme (red) bends the G segment of DNA into a hairpin-like conformation. The entrance gate for the T segment of DNA is inside the hairpin. Thus, the T segment can pass through the G segment only from inside to outside the hairpin. Although it is not clear that the suggested mechanism has to provide simplification of DNA topology, the computational analysis shows that it really does (5).
To estimate the values of p0, r03, p3 and r30, required by Equation (5), we simulated equilibrium sets of DNA molecules with a bent G segment (assuming that it is bound with the protein). The simulation used the discrete wormlike chain model of DNA which was described above. The protein-bound G segment was modeled by four straight segments of the chain, and its hairpin-like conformation was kept during the simulation while joints between other segments had their normal flexibility. The length of 1 straight segment of the model chain was equal to 10 nm. Typical simulated DNA conformations with different topologies are shown in Figure 3. Conformations that had another segment inside the hairpin were selected from very large equilibrium sets of simulated conformations with a particular topology. The selected conformations were considered as suitable for the strand-passing reaction, and allowed calculation of p0 and p3. Then reaction products were calculated for each of the selected conformations to estimate r03 and r30.
The simulation showed that for a DNA molecule 7 kb in length with a hairpin-like G segment f3SS has to be reduced by a factor of 14 relative to the equilibrium value (5). This is a surprisingly large effect because the hairpin occupies such a small portion of the DNA chain (see Figure 3). The chain conformation shown at the top of Figure 3 helps to understand this result. One can see that on the projection the juxtaposed T and G segments make two of three crossings that define the trefoil. This is nearly always true if the G segment is sharply bent. As a result, the trefoil is nearly localized in the small area of the juxtaposition. It had been shown that localization of a knot in a small part of a large closed chain increases the chain entropy because the rest of the chain receives more conformational freedom (14). The hairpin-like G segment simplifies such localization and therefore increases the probability of juxtaposition of T and G segments in knotted molecules.
If type IIA topoisomerases work as it is suggested by this model, they have to bend the G segment upon the binding, and the movement of the T segment during the strand-passing reaction should occur from inside to outside the hairpin formed by the G segment. Although it had been proven that the strand-passing goes only in one direction relative to the enzyme (13,15), there were conflicting data on the G segment bending (16). Two sets of data supporting a bent conformation of the G segment were presented (5). First, the electron microscopy (EM) study showed that segments of linear or nicked circular DNA bound with the enzymes are strongly bent. It was also found that the enzymes bound with supercoiled DNA tend to be located at the superhelix apices, where the double helix has to be bent in any case. Although these data look very convincing, it is worth noting that EM studies of DNA brought many artifacts [see ref. (17), for a good example]. Second, it was shown that binding of Topo IV with short DNA fragments, about 200 bp in length, greatly facilitates fragment cyclization efficiency. Later, however, Roca and co-workers repeated the cyclization experiments with yeast topo II and did not observe any increase of cyclization efficiency (7). We tried recently to rectify the cyclization experiments with Topo IV and found that the enzyme's affinity for DNA ends is higher than for internal DNA segments. Clearly, this inhibits DNA cyclization and prevents quantitative analysis of the experiments.
A very important result, supporting the model, was obtained at the end of 2007 by Dong and Berger who published the X-ray structure of a complex between the DNA binding and cleavage core of yeast Topo II and a gate DNA segment (18). The DNA segment was sharply bent at about 150° (Figure 5). Complemented by the earlier biochemical studies, the structure showed that the directionality of a T segment passage relative to the bent G segment corresponds to one required by the model.
Figure 5.
Cartoon representation of the structure of the Topo II DNA-binding and cleavage core bound with DNA fragment [reproduced from ref. (18)]. DNA fragment, shown by orange, is bent by 150° in the complex.
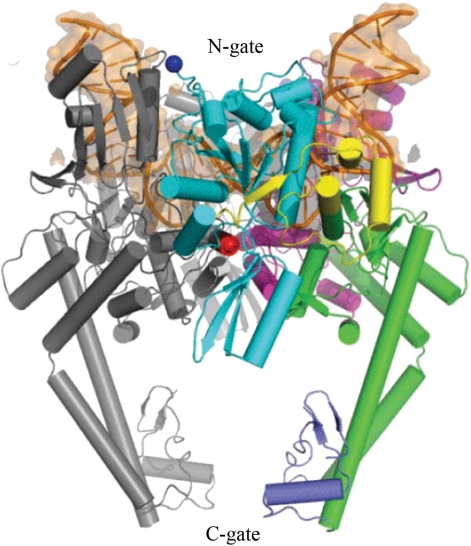
The directionality of the strand-passage relative to the enzyme was established earlier by Wang and co-workers in their very elegant biochemical experiments (13). X-ray structure of a part of yeast topo II was known at that moment and it had been suggested that the strand-passing reaction is proceeded by a two-gate mechanism (15). Roca et al. designed a mutant enzyme whereby the C-gate could be reversibly locked by disulfide links (Figure 5). Using this mutant and specially designed substrate consisting of linked supercoiled and relaxed circular DNAs, they reliably established the directionality of the T segment passage (Figure 6). It was shown that the T segment enters through N-gate and exits from C-gate of the enzyme, so it moves from inside the DNA hairpin to outside, in full agreement with the model.
Figure 6.
The two-gate mechanism of the strand-passing reaction. The diagram illustrates the experiment with mutant yeast Topo II enzyme, which the C-gate was locked by disulfide links (13). The reaction substrate consisted of the large supercoiled molecule linked with small nicked circular DNA. Unlinking of circular DNA molecules accompanied by the AMPPNP driven closure of the N-gate, left the small circular molecule topologically linked with mutant Topo II. Such an outcome is possible only if a T segment enters through the N-gate of the enzyme and exits through the C-gate.
It should be noted that the simulation shows a smaller extent of topology simplification than that found in the experiments. For example, the 14-fold reduction of the knot concentration was predicted in the simulation for 7-kb DNA, while the 90-fold reduction was observed experimentally (3). This discrepancy will not look so dramatic, however, if we take into account a limited accuracy of the theoretical analysis which is based on a very simple modeling of the actual reaction complex.
The kinetic proofreading model
The model suggested by Yan et al. (4) assumes that successive formation of two complexes of the protein-bound G segment with other segments is required for the strand-passing reaction to occur. The first complex only activates the protein but does not proceed to the strand-passing. The activating segment dissociates from the complex and only the formation of the second complex of a potential T segment with the activated protein results in the strand-passing reaction. The model is based on the assumption that the segment collisions occur more often in knotted or linked DNA molecules than in unknotted/unlinked, and the requirement of the second collision should enhance the effect of this difference. The equation for f3SS, corresponding to this model, has an additional multiplier p0/p3 [compare with Equation (5)]:
The authors’ analysis of the model, however, ignored the fact that not all strand-passing reactions change DNA topology, that is they implicitly assumed that r03 = r30 = 1. So, they obtained a simpler equation for f3SS
Under the same assumption that all strand-passages change the topology of the circular molecules one can conclude that, in the absence of any specific conformational requirements for the juxtaposition, f3eq = p0 /p3. Using the latter equation and Equation (8) the authors concluded that in their model
The value of f3eq is small for the DNA molecules used in the experiments (see Figure 1), so according to Equation (9) the model has to provide a large reduction of f3SS. However, the term r03/r30, missed in the authors’ analysis, is very important. Although r30 is close to 1, the value of r03 is very small for the considered DNA molecules (5). This means that great majority of the strand-passing events in the unknotted state do not change the topology. This term, r03/r30, rather than relatively small difference in the probabilities of juxtapositions p0 and p3, is responsible for the small value of f3eq [see Equation (6)]. In the absence of specific geometrical requirements for the juxtaposition of the G and T segments the term p0/p3 is close to 1/3 for the considered DNA molecules (5). Thus, the requirement of the second juxtaposition per se cannot substantially reduce the value of f3SS relative to f3eq.
The kinetic proofreading model can, however, provide a larger effect of topology simplification if it is combined with other models. For example, the simulation shows that the probability of the juxtaposition of a T segment with the hairpin-like G segment is 13 times higher for trefoils rather than for unknotted DNA molecules 7 kb in length (5). Thus, the proofreading model could further reduce the value of f3SS for such molecules by factor of 13, in addition to the reduction provided by the model of the hairpin-like G segment. Still, there is not any experimental indication that two collisions between the G segment-protein complex and other segments are needed for a single-strand-passing event.
The model of hooked juxtapositions
Buck and Zechiedrich suggested that the enzyme binds ‘hooked’ G and T segments (Figure 7), and such juxtapositions more often appear in knotted and linked DNA molecules (6). As a result, unknotting and unlinking should occur more efficiently, if the enzymes only catalyze strand-passing for such juxtapositions. It remains unclear if the authors assumed that both segments are bound with the enzyme simultaneously or successively. If the protein binds the G segment first and keeps/creates the bent conformation of the segment until it binds a T segment, the model becomes nearly identical to the hairpin-like G segment model. Therefore, we consider here that in the hooked juxtaposition model both segments have to be bound simultaneously. Also, the simultaneous binding corresponds to the Monte Carlo simulations, which were performed to analyze the model (19,20). Both of these simulation studies concluded that the model has to provide a large decrease of f3SS. Both simulations have essential drawbacks, however. The first study used a lattice model of DNA (19), which is absolutely inadequate for the analysis of DNA conformational properties due to a very large thickness of the chain segments [see refs (20,21), for example]. Thus, the results of the analysis are not directly relevant to knotting in circular DNA molecules. The second study used a more realistic DNA model, the freely jointed chain with proper thickness of the segments (20). This polymer model is capable of giving a good quantitative description of many global DNA properties. In particular, it predicts the correct equilibrium fraction of knots for DNA molecules longer than a few thousands base pairs (21). The analysis showed that if the enzyme binds only strongly hooked juxtapositions, it can greatly reduce the value of f3SS (20). This result is in a qualitative agreement with the analysis of the hairpin-like G segment model (21). The study, however, provides a weak support for the model of the enzyme action, since the freely jointed chain used in the simulation does not describe local DNA conformations properly. Indeed, a polymer model of straight segments cannot describe conformational properties in a scale smaller than the length of one segment. In the case of the freely jointed chain the length of one segment of the model chain corresponds to 100 nm, while the size of the DNA–protein complex is around 10–15 nm. The analysis based on the freely jointed chain model misses the fact that strongly hooked juxtapositions have an extremely low probability of appearance in circular DNA molecules a few kb in length.
Figure 7.
Diagram of a hooked juxtaposition of two DNA segments. It was suggested that such juxtapositions are typical among segment juxtaposition in linked and knotted molecules and represent a binding substrate for type IIA topoisomerases (6).
We performed an analysis of the segment juxtaposition for circular DNA of different topologies by Monte Carlo simulation, using the discrete wormlike chain model (see Supplementary Data). The simulation showed that hooked juxtapositions constitute a tiny fraction of all juxtapositions in circular DNA molecules a few kb in length, regardless of their topology. Still, if the enzymes are patient enough to catch only strongly hooked juxtapositions, the model would work because the fraction of the strongly hooked juxtaposition has to be essentially larger for knotted than for unknotted molecules. In this case the enzymes would exploit the same principle of knot localization that is the base for the hairpin-like G segment model. Indeed, it is not important for the effect of knot localization if the bent segment is bound with the enzyme or the bend appeared in this segment spontaneously. Thus, the topoisomerases could simplify DNA topology by binding hooked juxtapositions (6). However, the hooked juxtapositions are extremely rare in circular DNA of any topology. Therefore, if the topoisomerases bind only strongly hooked juxtapositions to reduce the fractions of DNA knots and links, they would act incredibly slowly.
The model of hooked juxtapositions is supported by an earlier electron microscopy study of DNA–topo II complexes (22). The authors observed that many topo II molecules are located at DNA crossovers when they are deposited on the EM grid. However, they obtained nearly the same result for topo I molecules which interact with only one double-stranded DNA segment during their catalytic act [see (23) for review]. There are no other data that support the idea of the simultaneous binding of two DNA segments by topo IIA enzymes.
A key point of the model is that the enzymes bind two juxtaposed DNA segments simultaneously rather than successively. This is rather unusual assumption in general. All well-studied cases of enzymes which catalytic acts involve two DNA segments show that they bind the segments successively (24). The mode of successive binding has a very clear advantage: formation of the full complex occurs much faster in this mode than in the mode of simultaneous binding. Of course, this kinetic argument does not mean that an enzyme cannot work in the mode of simultaneous binding. However, this mode can be essential only if the faster mode of successive binding is excluded. In the structure of the DNA–topo II complex, resolved by Dong and Berger, the enzyme is bound with one segment only, so the mode of successive binding is not excluded in this case. Thus, the existence of the structure does not support a model that assumes simultaneous binding of two DNA segments by the enzymes. Thus, the electron microscopy data remain the only experimental results supporting the idea of simultaneous binding of two DNA segments by topo IIA enzymes.
The model of three protein-bound segments
Roca and co-workers suggested that binding a third DNA segment by the enzyme should reduce the value of f3SS, partially because the probability of knotting is smaller in smaller DNA loops (7). The model resembles the knot-trapping model although it does not assume the trapping. The authors did not perform any quantitative analysis of the model and the model was not specified in sufficient details for such analysis. The authors’ analysis of the model mainly addresses the width of the topoisomer distribution, leaving open the mechanism of knot and link reduction (7). If we assume, following the analysis of various models by Bates and Maxwell (25), that topology simplification in this model results from dividing circular DNA into two loops and establishing the topological equilibrium in each of them, this would reduce the value of f3SS for 10 kb DNA molecules to approximately one half of f3eq. Thus the formation of two smaller loops per se is insufficient to obtain significant reduction in the value of f3SS. There are only very indirect data supporting the idea that topo IIA interacts with three DNA segments during the catalytic act (7).
CONCLUSIONS
The quantitative analysis and available experimental data show that the model of the hairpin-like G-segment has substantial advantages over the other suggested models. Only two simple assumptions have to be satisfied to validate the model: (i) Sharp bending of the G segment by the protein and (ii) unidirectional transport of a T segment from inside the bent G segment to outside. The experimental data provided strong support for these assumptions. Of course, it is possible that more than one mechanism contributes to the phenomenon. It is also possible that there is another mechanism of topology simplification that has not been suggested yet.
Some important questions about the phenomenon have not been solved yet. It was found by Rybenkov et al. that different topo IIA enzymes simplify DNA topology to different extents, so the steady state fractions of knots and links differ for various topo IIA (3). This observation is naturally accommodated into the model of the hairpin-like G segment, if we assume that the bend angle in the G segment is different for different enzymes (26). It would be important to study the correlation between the bend angle and the extent of topology simplification experimentally.
Clearly, the majority of the topo II enzymes are needed to simplify DNA topology to make segregation of newly replicated DNA molecules into dividing cells possible. There may be an exception, however. It is possible that maintaining the giant networks of linked DNA circles in kinetoplasts [see (27), for example] requires topoisomerases that promote linking between individual circular DNA molecules. If such enzymes exist, they have to increase the steady state fraction of knots and links relative to the equilibrium levels. Topo II enzymes responsible for assembling the network are known (28–31), and it would be very interesting to test how they change the distributions of topological states.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health grant GM54215 (to A.V.). Funding for open access charge: National Institutes of Health (GM54215).
Conflict of interest statement. None declared.
Supplementary Material
REFERENCES
- 1.Wang JC. Moving one DNA double helix through another by a type II DNA topoisomerase: the story of a simple molecular machine. Q. Rev. Biophys. 1998;31:107–144. doi: 10.1017/s0033583598003424. [DOI] [PubMed] [Google Scholar]
- 2.Schoeffler AJ, Berger JM. Recent advances in understanding structure-function relationships in the type II topoisomerase mechanism. Biochem. Soc. Trans. 2005;33:1465–1470. doi: 10.1042/BST0331465. [DOI] [PubMed] [Google Scholar]
- 3.Rybenkov VV, Ullsperger C, Vologodskii AV, Cozzarelli NR. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science. 1997;277:690–693. doi: 10.1126/science.277.5326.690. [DOI] [PubMed] [Google Scholar]
- 4.Yan J, Magnasco MO, Marko JF. A kinetic proofreading mechanism for disentanglement of DNA by topoisomerases. Nature. 1999;401:932–935. doi: 10.1038/44872. [DOI] [PubMed] [Google Scholar]
- 5.Vologodskii AV, Zhang W, Rybenkov VV, Podtelezhnikov AA, Subramanian D, Griffith JD, Cozzarelli NR. Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl Acad. Sci. USA. 2001;98:3045–3049. doi: 10.1073/pnas.061029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Buck GR, Zechiedrich EL. DNA disentangling by type-2 topoisomerases. J. Mol. Biol. 2004;340:933–939. doi: 10.1016/j.jmb.2004.05.034. [DOI] [PubMed] [Google Scholar]
- 7.Trigueros S, Salceda J, Bermudez I, Fernandez X, Roca J. Asymmetric removal of supercoils suggests how topoisomerase II simplifies DNA topology. J. Mol. Biol. 2004;335:723–731. doi: 10.1016/j.jmb.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 8.Wang JC, Davidson N. Cyclization of phage DNAs. Cold Spring Harbor Symp. Quant. Biol. 1968;33:409–415. doi: 10.1101/sqb.1968.033.01.047. [DOI] [PubMed] [Google Scholar]
- 9.Rybenkov VV, Cozzarelli NR, Vologodskii AV. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl Acad. Sci. USA. 1993;90:5307–5311. doi: 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vologodskii A. In: Computational Studies of DNA and RNA. Lankas F, Sponer J, editors. Dordrecht: Springer; 2006. pp. 579–604. [Google Scholar]
- 11.Stigter D. Interactions of highly charged colloidal cylinders with applications to double-stranded DNA. Biopolymers. 1977;16:1435–1448. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- 12.Stuchinskaya T, Mitchenall LA, Schoeffler AJ, Corbett KD, Berger JM, Bates AD, Maxwell A. How do type II topoisomerases use ATP hydrolysis to simplify DNA topology beyond equilibrium? Investigating the relaxation reaction of nonsupercoiling type II topoisomerases. J. Mol. Biol. 2009;385:1397–1408. doi: 10.1016/j.jmb.2008.11.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roca J, Berger JM, Harrison SC, Wang JC. DNA transport by a type II topoisomerase – direct evidence for a two-gate mechanism. Proc. Natl Acad. Sci. USA. 1996;93:4057–4062. doi: 10.1073/pnas.93.9.4057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Katritch V, Olson WK, Vologodskii A, Dubochet J, Stasiak A. Tightness of random knotting. Phys. Rev. E. 2000;61:5545–5549. doi: 10.1103/physreve.61.5545. [DOI] [PubMed] [Google Scholar]
- 15.Roca J, Wang J. DNA transport by a type II DNA topoisomerase – evidence in favor of a two-gate mechanism. Cell. 1994;77:609–616. doi: 10.1016/0092-8674(94)90222-4. [DOI] [PubMed] [Google Scholar]
- 16.Wang JC. DNA topoisomerases. Ann. Rev. Biochem. 1996;65:635–695. doi: 10.1146/annurev.bi.65.070196.003223. [DOI] [PubMed] [Google Scholar]
- 17.Peter BJ, Ullsperger C, Hiasa H, Marians KJ, Cozzarelli NR. The structure of supercoiled intermediates in DNA replication. Cell. 1998;94:819–827. doi: 10.1016/s0092-8674(00)81740-7. [DOI] [PubMed] [Google Scholar]
- 18.Dong KC, Berger JM. Structural basis for gate-DNA recognition and bending by type IIA topoisomerases. Nature. 2007;450:1201–1205. doi: 10.1038/nature06396. [DOI] [PubMed] [Google Scholar]
- 19.Liu Z, Mann JK, Zechiedrich EL, Chan HS. Topological Information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases. J. Mol. Biol. 2006;361:268–285. doi: 10.1016/j.jmb.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 20.Burnier Y, Weber C, Flammini A, Stasiak A. Local selection rules that can determine specific pathways of DNA unknotting by type II DNA topoisomerases. Nucleic Acids Res. 2007;35:5223–5231. doi: 10.1093/nar/gkm532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vologodskii A. Monte Carlo Simulation of DNA Topological Properties. In: Monastryrsky M, editor. Topology in Molecular Biology. Berlin-Heidelberg-New York: Springer; 2007. pp. 23–41. [Google Scholar]
- 22.Zechiedrich EL, Osheroff N. Eukaryotic topoisomerases recognize nucleic acid topology by preferentially interacting with DNA crossovers. EMBO J. 1990;9:4555–4562. doi: 10.1002/j.1460-2075.1990.tb07908.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Champoux JJ. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001;70:369–413. doi: 10.1146/annurev.biochem.70.1.369. [DOI] [PubMed] [Google Scholar]
- 24.Halford SE, Welsh AJ, Szczelkun MD. Enzyme-mediated DNA looping. Annu. Rev. Biophys. Biomol. Struct. 2004;33:1–24. doi: 10.1146/annurev.biophys.33.110502.132711. [DOI] [PubMed] [Google Scholar]
- 25.Bates AD, Maxwell A. Energy coupling in type II topoisomerases: why do they hydrolyze ATP? Biochemistry. 2007;46:7929–7941. doi: 10.1021/bi700789g. [DOI] [PubMed] [Google Scholar]
- 26.Klenin K, Langowski J, Vologodskii A. Computational analysis of the chiral action of type II DNA topoisomerases. J. Mol. Biol. 2002;320:359–367. doi: 10.1016/S0022-2836(02)00447-3. [DOI] [PubMed] [Google Scholar]
- 27.Morris JC, Drew ME, Klingbeil MM, Motyka SA, Saxowsky TT, Wang Z, Englund PT. Replication of kinetoplast DNA: an update for the new millennium. Int. J. Parasitol. 2001;31:453–458. doi: 10.1016/s0020-7519(01)00156-4. [DOI] [PubMed] [Google Scholar]
- 28.Hines JC, Ray DS. Periodic synthesis of kinetoplast DNA topoisomerase II during the cell cycle. Mol. Biochem. Parasitol. 1997;88:249–252. doi: 10.1016/s0166-6851(97)00076-5. [DOI] [PubMed] [Google Scholar]
- 29.Shapiro TA. Mitochondrial topoisomerase II activity is essential for kinetoplast DNA minicircle segregation. Mol. Cell Biol. 1994;14:3660–3667. doi: 10.1128/mcb.14.6.3660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pasion SG, Hines JC, Aebersold R, Ray DS. Molecular cloning and expression of the gene encoding the kinetoplast-associated type II DNA topoisomerase of Crithidia fasciculata. Mol. Biochem. Parasitol. 1992;50:57–67. doi: 10.1016/0166-6851(92)90244-e. [DOI] [PubMed] [Google Scholar]
- 31.Hanke T, Ramiro MJ, Trigueros S, Roca J, Larraga V. Cloning, functional analysis and post-transcriptional regulation of a type II DNA topoisomerase from Leishmania infantum. A new potential target for anti-parasite drugs. Nucleic Acids Res. 2003;31:4917–4928. doi: 10.1093/nar/gkg671. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.