Changes in brain cell shape create residual extracellular space volume and explain tortuosity behavior during osmotic challenge

Abstract

Diffusion of molecules in brain extracellular space is constrained by two macroscopic parameters, tortuosity factor λ and volume fraction α. Recent studies in brain slices show that when osmolarity is reduced, λ increases while α decreases. In contrast, with increased osmolarity, α increases, but λ attains a plateau. Using homogenization theory and a variety of lattice models, we found that the plateau behavior of λ can be explained if the shape of brain cells changes nonuniformly during the shrinking or swelling induced by osmotic challenge. The nonuniform cellular shrinkage creates residual extracellular space that temporarily traps diffusing molecules, thus impeding the macroscopic diffusion. The paper also discusses the definition of tortuosity and its independence of the measurement frame of reference.

Many biological processes involve diffusion of substances through a disordered heterogeneous medium. Diverse examples are intracellular signaling (1), intercellular signaling (2), volume transmission (3, 4), and drug delivery (5, 6). The rapid increase in the use of diffusion-weighted MRI has raised further issues about diffusion in tissues (7). In approaching such problems, two essential parameters are the extracellular space (ECS) volume fraction α, the volume ratio of the ECS compared to the whole tissue, and the tortuosity λ, a measure of how diffusing molecules are hindered by cellular obstructions. Recent studies by using osmotic challenge in brain tissue (8, 9) have shown a complex relation between these two parameters. In this paper, we apply the mathematical technique of homogenization to show that changes in cell shape provide an explanation for osmotic data and are likely to be applicable in a much wider context.

To quantify diffusion in a complex biological medium, it is necessary to apply the diffusion equation through the use of some macroscopically effective properties, such as the local average concentration, 〈C〉, and the apparent (or effective) diffusion coefficient, D*. Such macroscopic formulations have been applied successfully in the ECS of brain tissues (8–15). When discussing the ECS, λ² is frequently defined as the ratio between the diffusion coefficient, D, of a given molecule in a bulk liquid and the apparent diffusion coefficient D* of the same molecule in the ECS,

1

although other definitions have been used. Furthermore, some authors (16–18) include terms for viscosity of the ECS and hydrodynamic interaction of the diffusing molecule in their definition of λ; we exclude such factors here, to focus on the relationship between geometry and tortuosity, but briefly discuss them later in the paper and in the Appendix, which also comments on the independence of tortuosity from its measurement frame of reference.

The question of whether λ and α are related has been explored in many contexts, but because it depends on the structure of the heterogeneous medium, no universal relationship is known. It is expected that λ will decrease monotonically as α increases. This conjecture has been explored in recent experiments that varied the osmotic pressure of media bathing isolated brain tissues while measuring λ and α (8, 9, 15). These experiments changed the size of the ECS by causing cells to shrink or swell. Studies on rat cortex (9) revealed that, whereas α decreased with hypoosmolarity and increased with hyperosmolarity, λ behaved differently. In hypotonic media, λ increased monotonically as α fell, but with hypertonic media, λ reached a plateau while α continued to increase. This constant λ with increasing α cannot be accounted for easily by the influence of either the viscosity of the interstitial matrix or the size of diffusing molecules relative to the interstitial channels. Here we show that these data can be explained on a geometric basis, provided the cells change their shape during osmotic challenge.

Methods

Our analysis takes place in two dimensions. Later, we will discuss why this is sufficient to reveal all the essential features of the three-dimensional problem. Although aimed at brain tissue, the lattice models explored in this work can also be applied to other situations, e.g., a cross section of striated muscle (19) or the lateral intercellular space between epithelial cells (20).

Lattice Arrangements and Governing Equation.

Our approach was based on homogenization theory (21, 22) applied to planar diffusion through the ECS, regarded as a porous medium composed of repeating obstacles in the form of cellular elements. Cellular elements were defined as sections of cell bodies, dendrites, axons, or glial processes. These were idealized into the unit two-dimensional arrays shown in Fig. 1. Because values of α in typical brain regions are small (∼0.2) (13), and brain interstitial clefts are highly connected, the models shown in Fig. 1 capture the essential properties of the ECS. The diameter of the diffusing molecules was taken to be vanishingly small. The dimensionless center-to-center distance between neighboring cells was set to a nominal value of 2, and the center of each cellular element was assumed to be immobile during swelling/shrinkage. To allow cellular elements to alter their shape, the corners were rounded with an arc of a radius a. The parameter a, together with the intercleft distance 2h and the fixed center-to-center distance, determined the void area fraction, which we continued to denote by α. A crucial aspect of the analysis was the identification of a repeating unit, enclosed by the outer dashed lines, for each arrangement depicted in Fig. 1. Because the repeating units depicted in Fig. 1 must capture the symmetry aspects of a given problem, they apply only when the macroscopic diffusion direction ê is aligned in the Cartesian axes (x or y).

Figure 1.

Schematic diagrams of the two-dimensional lattice arrangements in different situations. Impermeable cell obstacles are represented by the depicted gray-colored cells arranged in a lattice structure. The distance 2h represents the intercleft width, and the radius a represents the small curvature of the cell membrane in deformed regions. The ECS domains were highlighted in light gray, with the rectangular dimension Γ_x × Γ_y defined as: Γ_x = Γ_y = 1 for lattice (a); Γ_x = Γ_y = for lattice (b); Γ_x = 2, Γ_y = 1 for lattice (c); Γ_x = 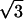, Γ_y = 1 for lattice (d); and Γ_x = , Γ_y = 3 for lattice (e).

Assuming the cell membranes are impermeable to the diffusing molecules, we can define a function ω that represents the small periodic component of the macroscopic concentration field. Then the differential equation for this periodic function in the void space of the repeating unit, Ω, is given by (16, 23),

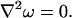2

The repeating scale has the same order as the ratio of the individual size of the cellular elements to the whole tissue, which is therefore small, and ω is regarded as a perturbation term in the macroscopic concentration profile. It is implicitly assumed that D* is time independent so long as the lattice structure remains unchanged, so that the D* derived under steady-state conditions should apply also in transient diffusion. Derivations of Eq. 2 and its boundary conditions have been given by Blum et al. (23), who considered the statistical properties of long-range random walks, and by El-Kareh et al. (16), who directly applied homogenization theory.

In most cases, because of symmetry in the arrangements of the lattice elements, only one-half or one-quarter of the entire repeating unit needs to be solved. The boundary conditions for ω depend on the direction of ê, the macroscopic diffusion direction, and on whether the boundary is an interface separating successive units in the void space or the impermeable cell walls. Let the rectangular unit be bounded between x ∈ [0, Γ_x] and y ∈ [0, Γ_y], where Γ_x and Γ_y are defined in Fig. 1 and its legend. Assuming that ê aligns with the x axis, at the interface we have

3

because of periodicity of the repeating unit, and

4

because of symmetry. Across the impermeable boundaries, the gradient for ω is specified by (16, 22)

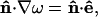5

where n̂ designates the outward normal at the solid boundaries. If ê aligns with the y axis, Eqs. 3 and 4 must be interchanged accordingly. An examination of Eq. 5 reveals that if a = 0, a singularity in ∇ω occurs at the corner shared by two adjacent straight edges of the cell. Inclusion of a smooth arc between such edges thus not only removes the singularity but also provides the transition between polyhedral and circular cells.

The apparent diffusion coefficient D* in the direction of ê is estimated from (16)

6

where A is the area of the void space in Ω. The λ calculated from Eq. 6 will be a purely geometric tortuosity factor, because hydrodynamic/viscous effects are not included in the present development. Eq. 2 was solved in a similar lattice arrangement by Bell and Crank (24), but with a different interpretation of ω. Hence their boundary conditions and the definition of D*/D also differ from ours. In the work of Blum et al. (23), a line integral along the appropriate cell boundary was adopted to define D*/D. By applying Green's theorem, the equivalence between both integral expressions can be shown. Here, however, the use of the area integral (Eq. 6) reduces the influence of numerical errors from possible singularities on the cell boundaries.

Numerical Solutions.

Eq. 2 with the corresponding boundary conditions was solved by using the numerical package pltmg 8.0 [Piecewise Linear Triangular Multi-Grid (25) finite element method]. pltmg features adaptive local mesh refinement, multigrid iteration, and a pseudoarclength continuation option for parameter dependencies. A curved boundary edge, if present, was approximated by a circular arc passing through the endpoints of the edge. pltmg uses a posteriori error estimates based on the computed solution to create refined meshes. The local error in each mesh element is defined as e_h = ω − ω_h, where ω_h is the piecewise polynomial approximation to ω. The value of e_h is found by solving a local Neumann problem in each element (26). All of the final solutions were obtained after four levels of mesh refinement with a total of 3,000 triangular vertices. Our results showed that the fourth digit after the decimal point of the D*/D value could be changed only when the number of the vertices was increased to 9,000.

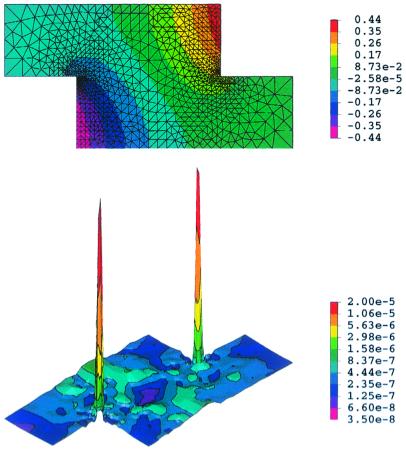
Fig. 2 shows numerical solutions output from pltmg for the x-staggered arrangement (Fig. 1c) to demonstrate the adaptive feature of mesh refinement. Fig. 2 Upper illustrates both the colored contours and the refined mesh. Note that the mesh is denser in the regions that require it, i.e., where the solution gradient is large or a singularity is likely to occur. Fig. 2 Lower shows the corresponding a posteriori error estimate, the ℋ₁ norm ∥e_h∥_ℋ1 (26). The largest numerical errors occur at the corners of the cells and result from the singularity because of a = 0. Nevertheless, the local error is only on the order of 10⁻⁵ at the corners and 10⁻⁷ elsewhere, both of which are acceptably small. If a small arc of radius a = 0.1 was added to modify the corner, the largest local errors were further reduced by three orders of magnitude.

Figure 2.

Numerical solutions (Upper) of Eq. 2 by pltmg (25) and the ℋ₁ error estimates (Lower) for the staggered lattice arrangement (c) with a = 0, h = 0.5, and ê aligned with the x axis. The ℋ₁ norm, defined as ∥e_h∥_ℋ1 ≡ [∫_Ωe_h²dΩ + ∫_Ω(∇e_h)²dΩ]^1/2 (25), estimates the sum of the magnitudes of the error itself and the gradient of the error. For visual clarity, only 1,000 vertices were shown.

Results and Discussion

Definition of Tortuosity.

An appropriate definition of tortuosity is crucial to both the interpretation of the present results and meaningful comparison with other studies. Several definitions occur in the literature. All seek to measure the hindrance a diffusing particle encounters in a porous medium in comparison to a free medium, usually equated with water. “Hindrance” is an intuitive but vague term, which may include both constitutive and geometric factors. One such factor is the viscosity of the medium, most likely arising from the extracellular matrix. Another factor stems from the finite size and specific nature of the diffusing molecules and embodies hydrodynamic interactions with the boundaries that define the pore structure. Both these factors are largely empirical, though attempts have been made to calculate them (17). These are potentially important components of tortuosity, but we omit them here to focus on the geometric factors.

Broadly, there are two approaches to the calculation of geometric tortuosity in the literature. The first is to construct a detailed model representing a small region of the local structure and then to attempt to calculate how this model would increase the local path length of a diffusing particle when compared to a free medium (17, 18, 24, 28). This approach can yield useful insight, but it has the drawback that it is hard to adequately “weight” the different paths involved to arrive at the appropriate mean value. In attempting such a weighting, some authors (27, 28) have concluded that the local geometric factor itself can be decomposed into additional components that roughly correspond to a “wiggle” factor (how much the local pore geometry deviates from straight line), a constriction factor (how local pore size varies), and a topological factor (connectivity of porous medium). Assessing the relative contributions of these factors is often problematic.

An approach that alleviates the problems of detailed analysis of path length in representative models is to derive the tortuosity from an averaging process that mimics the diffusion process itself. This involves defining the tortuosity as the solution to a diffusion problem based on an ensemble description of the porous medium. When done properly, this solution incorporates all the geometric factors mentioned above with their correct weighting. This was the approach taken in refs. 16, 23, and 24, which is adopted here. Tortuosity is then expressed as a function involving an integral (Eq. 6) over the resulting concentration distribution. The diffusion problem is usually solved in the steady state, where it reduces to Laplace's equation with appropriate boundary conditions. An advantage of this approach is that it agrees explicitly with the practical definition of tortuosity used in laboratory experiments. In such experiments, the diffusion coefficient measured in a free medium is experimentally compared to that in a porous medium; this is mimicked by the mathematical experiment.

Lattice Model Solutions.

Each lattice configuration shown in Fig. 1 was solved with a variety of combinations of a and h, and the value of λ was then plotted against a and h in Fig. 3. First, we verified that our numerical results for the configuration depicted in Fig. 1a agreed with those of Blum et al. (23) for square (a = 0) and circular cell elements (a = 1 − h). We note that along the line a = 0, the tortuosity approaches 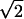as h approaches zero. According to Blum et al. (23), when arrays of square cells approach each other so that the interstices between them become vanishingly small, the random walks within each intercleft channel become effectively one dimensional. In this limit, λ depends only on the topology of the connecting channels. Interestingly, for hexagonal and triangular cells the same limit, lim_{(a = 0, h ↘ 0)} λ² = 2, occurs (Fig. 3). This is because at a = 0 and h ↘ 0, the lattice structure becomes a perfect pore network. According to pore-network theory (27, 29–32), λ² = N for N-dimensional isotropic pore networks, regardless of the number of connecting pores at each node. Our lattice simulation results obtained with a = 0 and h ↘ 0 support this conclusion for N = 2. This result was also noted by Adrian et al. in their study of impedance in muscle fibers (33).

Figure 3.

Distributions of λ vs. a and h for each lattice arrangement depicted in Fig. 1, except the diamond formation (b) displayed in the form of the difference λ^(a) − λ^(b). Superscripts in λ denote the lattice arrangement, and subscripts (x or y) denote the direction of the macroscopic diffusion ê. If λ_x = λ_y, the subscripts x, y are omitted. Judging from the smallness of λ^(a) − λ^(b), we concluded that the difference between λ^(a) and λ^(b) arose purely from numerical errors, not because of intrinsic differences in lattice structure or orientations of ê.

In regions of small h, λ decreases slightly at first, but then increases as a increases. This is because the circular cellular elements, in the limit h ↘ 0, always retain residual space between the elements. Within this space, molecules executing a random walk are likely to be trapped locally. Obviously this entrapment cannot occur if h is too large, which explains why the rising λ occurs only when h is small. In other words, under the same small intercleft distance h, the ECS gained from cellular shrinkage in the form of residual space does not help molecules diffuse through the ECS but, on the contrary, reduces macroscopic diffusion. Similar rising trends for λ along a for small h occurred for hexagonal and triangular cells. For the same h, the rising phase of λ in arrangements (d) and (e) was weaker and stronger, respectively, than for the square cells. This is to be expected, because the shape closest to that of a circular cell (a polygon with infinite number of edges) is the hexagonal cell (six edges) followed by the square cell (four edges), whereas the triangular cell (three edges) least resembles a circle.

Staggered arrangements of cells are of interest because it has been presumed that this configuration forces the diffusing molecules to meander through longer pathways than they would have taken if the cells were aligned (16). There is, however, a subtle issue of how to define a truly aligned or staggered array, and we demonstrated this point using the arrangements shown in Fig. 1 b and c. From a local viewpoint, the diamond formation in Fig. 1b is indeed staggered in the orthogonal x and y axes, even though, from a macroscopic perspective, Fig. 1b is the diagonal rotation of the aligned square formation in Fig. 1a. However, we found that the λ_x and λ_y for the same a and h in the diamond formation (b) were indistinguishable from those of the square arrangement (a). The insignificance of the differences λ^(a) − λ^(b) in Fig. 3 implies that λ in an isotropic porous medium is independent of the orientation of ê, consistent with our argument in the Appendix. Such a conclusion can be arrived at easily from homogenization theory. Even from a microscopic perspective, a random walker executes independent random walks regardless of the orientation of ê. On the other hand, the staggered arrangement depicted in Fig. 1c relocated the cell positions and thus had a different lattice structure from those in (a) or (b). An objective determination of the extent to which elements are staggered therefore should be arrived at from changes in the connectivity of the ECS channels (four for Fig. 1b and three for Fig. 1c). Because the cellular elements shown in Fig. 1c were staggered only in the x direction, arrangement (c) was anisotropic, and we did find that λ_x > λ_y for most combinations of a and h. In addition, the rising trend of λ_y along a at small h quickly vanished.

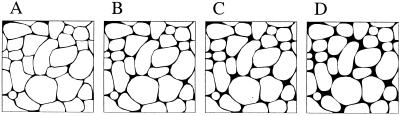
To summarize the results in Fig. 3 obtained with the lattices shown in Fig. 1: we have demonstrated that, when the intercleft h is small, the geometric λ increases with the formation of residual interstitial space between cells. This counterintuitive result offers a possible explanation of the plateau behavior of λ during osmotic challenge observed in refs. 9 and 15. In reality, however, the brain ECS does not conform to a periodic structure with a single repeating unit of identical shape. To test whether the increase in λ with increasing residual space between cells was a peculiarity of a regular lattice structure, we designed in Fig. 4 a more complex and realistic ECS unit domain comprised of many cellular elements in random shapes and arrangements, representative of a typical section of ECS ultrastructure. The value of α was incrementally increased from 0.13 to 0.22 by shrinking the area of the cellular elements in the figure. To alter the residual space between cellular elements, we assumed that, as an element diminished in size, it tended toward a round shape by selectively retracting the regions with small radii of curvature first (see the evolution of the Fig. 4 A–D). In this way, some intercleft distances between two opposing cell walls were kept approximately constant, whereas in other regions a residual space enclosed by the portions of distorted cellular elements was gradually formed. The domain for the case a = 0.22 was shown in Fig. 5, with the pltmg-generated mesh triangulation on the left and the corresponding numerical solution for ω in Inset. Because, for the realistic case it was impossible to ensure exact isotropy, both λ_x and λ_y were evaluated and the results summarized in Table 1. Over the range of α values tested here, we found that λ_y increased monotonically with α, whereas a slight decrease preceded the subsequent increase in λ_x. Both trends of λ_x and λ_y with α were seen in Fig. 3, suggesting that the increasing behavior of λ is independent of the cell shape and does not require a lattice structure. A dead-end pore (34) is a more effective trap for random walkers and, if present, would be expected to raise λ to even higher values but should not affect the conclusion about the rising λ with the residual space. Depending on how the ECS plane is sectioned relative to the cell orientation, the profiles of some cellular elements (e.g., dendritic shafts or somata) in the plane of section will not shrink in the preferred directions, as ideally depicted in Fig. 4. But this does not alter our conclusion about the formation of the residual space in three dimensions as cell volume shrinks.

Figure 4.

Configurations of the more realistic brain extracellular space, computer generated to mimic the two-dimensional section of neuropil ultrastructure commonly seen in electron microscopy. The fractions of the void area, α, were calculated to be 0.13 in A, 0.16 in B, 0.18 in C, and 0.22 in D.

Figure 5.

Triangulation of the ECS domain (12 × 12) by pltmg for case D (α = 0.22) in Fig. 4 with 1,000 vertices. Subset shows the corresponding numerical solution for ê aligned in the x axis.

Table 1.

Simulation results of λ_x and λ_y in the ECS of Fig. 4

	A	B	C	D
α	0.13	0.16	0.18	0.22
λx	1.556	1.543	1.554	1.601
λy	1.587	1.591	1.612	1.664

Relationship Between Two and Three Dimensions.

Because all our calculations were made in two dimensions, it is important to ask whether the conclusions will apply in the three-dimensional world. Dealing first with α, the volume fraction, we note that according to the Delisse Principle (35), random sections in one and two dimensions through a heterogeneous three-dimensional medium will accurately estimate the value of α in the medium. Although the depictions in Fig. 1 are not strictly random sections (for some configurations, one could find a plane or line that would lie entirely in void space), they do represent the most common random section. These simple considerations do not apply directly to tortuosity. We note that the range of values of λ, obtained with different arrangements, vary (Fig. 3 and Table 1) depending on the shape of the cellular element in the lattice unit. Because some of these values are the same as those obtained experimentally in brain, one might assume that the values computed in two dimensions mimicked the three-dimensional case. But the discussion above of the limiting values for ideal pore networks, which can be regarded as a basic test of the relationship between dimensionality and tortuosity, indicates that here λ scales as the square root of the dimension, and one may conjecture that this scaling would hold for lattice models. Although the complexity of finite element analysis in three dimensions has prevented us from testing this conjecture, we do not think that the basic conclusions of this paper are altered by this issue.

A Hypothesis Concerning Cell Shape.

From our simulations, we conclude that the rising λ with increasing α is independent of cell type and arrangement; rather, it is a consequence of the enlargement of the residual space trapped between surrounding cells. For this increasing phase of λ to appear, h must be small, and the cellular elements must shrink nonuniformly, in the sense that cells shrink faster in some regions than in others. Because such residual space will always occur when cells shrink differentially, it seems clear that the effect is independent of spatial dimensionality, so this behavior, revealed by two-dimensional simulations, is expected to appear also in three-dimensional situations. Indeed, examples of “lakes” appearing between cells in the brain have been shown in appropriately prepared electron micrographs (36–38). Thus the existence of localized residual space can provide a physical explanation for the unchanging λ seen experimentally as α increases. This hypothesis seems plausible. In the absence of mechanical strains, an isolated cell tends to maintain a spherical shape. But brain cells (which include neurons and glial cells) and their processes in vivo usually are densely packed, which means a small intercleft distance (∼200 Å wide) and that the cell membrane is unavoidably deformed. When the cellular elements of the brain shrink, it is possible that their distorted regions, where additional local strains are loaded because of the small radii of the curvature of the membrane (assumed to be an elastic lipid bilayer), will shrink first to unload the strains. An equally plausible conjecture is that constraints imposed by the cytoskeleton may distort cell shape as volume changes. Data on shape changes in ensembles of brain cells are not available; however, the present results indicate that it would be useful to try to obtain them.

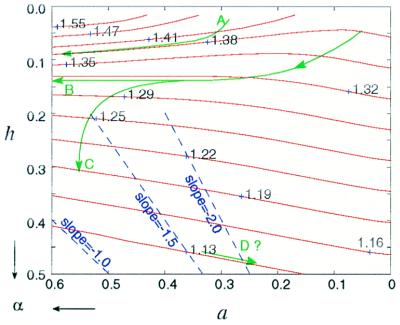
The distribution of λ for the arrangement in Fig. 3a was analyzed further in Fig. 6 to demonstrate how nonuniform cell shrinkage can account for the experimental plateau in λ. To maintain a constant λ while the cellular elements change shape, the path made by a and h must follow the contour lines. Trace A shows one possible path that will maintain a constant λ during cellular shrinkage by increasing a faster than h. It is also possible to have h fixed while a increases (trace B). One would not expect the plateau λ to be maintained indefinitely. When α becomes sufficiently large, λ must start to decline (trace C). The blue lines indicate the paths required for the perspective ratio of the cell shape to be preserved, (1 − h)/a = constant ≥ 1. Trace D (increasing h while reducing a) is physically impossible, because its slope is smaller than 1. Thus, all possible traces reside in small h regions.

Figure 6.

Contour distribution of the λ in lattice arrangement (a). Along each contour line (red), the value of λ, labeled by the nearby numbers, remains constant. Arrows at the lower-left corner indicate the directions of increasing α, which coincide with the directions of increasing a and h. Thick green curves denote possible paths of cell-shape changes during osmotic challenge. Dashed blue lines indicate the paths that preserve the shape perspective during shrinking with a constant slope defined as (1 − h)/a.

To clarify the meaning of this discussion, the theoretical values of λ vs. α, following trace B in Fig. 6, were plotted together with recent experimental data in Fig. 7. Similar trends in the curves indicate that the nonuniform changes in cell volume can well explain the asymmetric behavior of λ in the hyper- and hypotonic solutions. Nevertheless, we do not mean to imply that trace B is the actual path followed during osmotic challenge, because in the real ECS the shape of the cellular elements and arrangement probably cannot be completely characterized by so few as two parameters (a and h). We also should not expect any quantitative agreement between the theoretical and experimental values, because the theoretical λ in Fig. 7 is derived from two-dimensional simulations by using square arrays and represents only the pure geometric tortuosity of a specific lattice arrangement, whereas the experimental λ is an overall tortuosity factor in an ECS of three dimensions that may involve the issues discussed above. What our results do show, however, is that a change in cell shape resulting in the formation of residual space may be sufficient to explain present observations.

Figure 7.

Comparison of theoretical and experimental λ vs. α. The theoretical line represents trace B in Fig. 6 derived from calculations by using arrangement a in Fig. 1. Experimental data are taken from ref. 9 and J. Kume-Kick, T. Mazel, I. Vor̆ís̆ek, L. Tao, S. Hrabĕtová, & C. N. (unpublished work). Arrows on curves indicate appropriate ordinates and abscissa.

Physiological Significance.

Brain cells swell when exposed to hypotonic media and shrink when exposed to hypertonic media, with reciprocal changes in the ECS (8, 9). It is also true that brain cells swell, with reduction in volume of the ECS under normal conditions of neuronal activity, and many pathophysiological conditions, including ischemia and anoxia (39). ECS can also enlarge under some normal physiological conditions (40, 41). Indeed, changes in ECS volume may be more common than supposed, because most experiments are not instrumented to record such variations. Our results also offer an explanation for the asymmetric tissue impedance seen under varying bathing osmolarities in the hippocampus of rats (42, 43). The decrease of the apparent tissue resistance under hypertonia was far less than expected from the measured relative increase of the interstitial volume. Huang and Somjen (43) attributed this discrepancy to: (i) a substantial proportion of the current applied to measure impedance passing through the cells, and (ii) reduction of the cellular membrane conductance during hypertonic exposure. This explanation cannot completely resolve the discrepancy, because an increased cellular membrane resistance only shunts more currents through the low-resistance interstitial pathways, thus revealing more of the true impedance of the enlarging ECS. Our hypothesis of differential cellular shrinkage, on the other hand, provides a plausible alternate explanation for these experiments.

Another example of where a shape change might provide an explanation of puzzling data is during brain development. The volume fraction of the ECS is 40% immediately after birth in the cerebral cortex of the rat but diminishes to 20% by postnatal day 21 (11); however, the tortuosity does not change significantly. On the basis of this paper, one explanation for this paradox is that the brain cells undergo a change in shape during development.

Our work implies that changes in the ECS are confined not only to the volume fraction α but also to the structure of the ECS (represented by a and h in our model). As we show, the latter can affect diffusion properties, and this may be especially critical in the intersynaptic diffusion of neurotransmitters (18, 44). Our results are also relevant to nonneuronal tissue; for example, in describing diffusion in skeletal muscle (19), the lateral intercellular space of epithelial cells (20), and morphological studies of endothelial/epithelial cells under altered osmolarities (45, 46).

Hitherto, changes in cell shape have not been recognized in attempts to describe the relation between volume fraction and tortuosity in the ECS, but this mechanism introduces a new factor that may be of widespread relevance in a variety of problems that involve diffusion.

Abbreviation

ECS

extracellular space

Geometric Tortuosity and Coordinate Systems.

A fundamental implicit assumption in the concept of tortuosity is that, in a globally uniform but locally heterogeneous isotropic medium, one would obtain the same value regardless of the way the diffusion measurements were performed. In particular, the older methods of using radiotracers (10) used diffusion from a planar surface so that the flux was normal to that surface, whereas more recent work has used a point source (11–15) so that flux was radial. A recent theoretical paper (17) implied that the two types of experiment would lead to different values of geometric tortuosity. This would obviously have serious implications for the whole field of porous media research. From a fundamental perspective, however, λ must have a unique value that depends only on the properties of the medium, not on the coordinate system implicit in the measurement.

Macroscopic concentrations are defined as averages of the corresponding microscopic quantities. Such averages are taken over volumes that are small compared to the volume of the system but large enough for the transport equation to hold when applied to the volume (12, 16, 44). Consequently, the apparent diffusion coefficient of an isotropic porous medium is, in a macroscopic sense, also isotropic. The effect of different coordinate systems will be reflected in the different forms of the diffusion equation, not in the value of the apparent diffusion coefficient. Rusakov and Kullmann (17), however, derived a geometric tortuosity factor that was different in the geometry of planar and spherically symmetric diffusion, which naturally assumes the adoption of the rectangular Cartesian and spherical coordinate systems, respectively. Because the coordinate system is usually determined on the basis of geometry of diffusion symmetry that can be utilized, their theory implied a coordinate dependency in the geometric tortuosity factor. To relate such a coordinate-dependent geometric tortuosity (hereafter denoted as λ_RK) to the coordinate-independent D*, one must have, following the definitions in ref. 17 for consistency and introducing the viscosity of the extracellular matrix, which plays a role in that analysis,

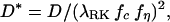7

in which the function f_η represents the influence of viscosity, and f_c is a coordinate-dependent geometric factor used to compensate the coordinate dependence in λ_RK. The product λ_RKf_c is the conventional coordinate-independent geometric tortuosity. The applicability of λ_RK alone will be limited, because all the experimental data in the literature are based on either Eq. 1 or other similarly macroscopic definitions. Indeed, one can define λ_RK, but such a tortuosity factor cannot be immediately related to D* without specifying f_c first. Unless f_c can be defined and shown to be a parameter with physical significance, there seems to be no need to introduce λ_RK. A further analysis of the methods in ref. 17 suggests that the differences obtained in planar and spherical geometry might be traced to subtleties in analyzing the detailed models used. As noted in the text, this issue has been a frequent problem with such approaches.