The impact of seasonal variability in wildlife populations on the predicted spread of foot and mouth disease

Abstract

Modeling potential disease spread in wildlife populations is important for predicting, responding to and recovering from a foreign animal disease incursion such as foot and mouth disease (FMD). We conducted a series of simulation experiments to determine how seasonal estimates of the spatial distribution of white-tailed deer impact the predicted magnitude and distribution of potential FMD outbreaks. Outbreaks were simulated in a study area comprising two distinct ecoregions in South Texas, USA, using a susceptible-latent-infectious-resistant geographic automata model (Sirca). Seasonal deer distributions were estimated by spatial autoregressive lag models and the normalized difference vegetation index. Significant (P < 0.0001) differences in both the median predicted number of deer infected and number of herds infected were found both between seasons and between ecoregions. Larger outbreaks occurred in winter within the higher deer-density ecoregion, whereas larger outbreaks occurred in summer and fall within the lower deer-density ecoregion. Results of this simulation study suggest that the outcome of an FMD incursion in a population of wildlife would depend on the density of the population infected and when during the year the incursion occurs. It is likely that such effects would be seen for FMD incursions in other regions and countries, and for other diseases, in cases in which a potential wildlife reservoir exists. Study findings indicate that the design of a mitigation strategy needs to take into account population and seasonal characteristics.

1. INTRODUCTION

Foot and mouth disease (FMD) is a highly contagious, transboundary disease of cloven-hoof animals and one of the most dangerous foreign animal diseases that might be accidentally brought into the USA [8]. Its threat to domestic livestock has been well studied. However, the potential role of wildlife species, which may serve as disease reservoirs, has been largely overlooked. The presence of non-domesticated reservoir species has been a serious obstacle to effective control of FMD outbreaks in other countries [28, 31]. In a series of outbreaks in Britain in 1946, FMD infected deer and European hedgehogs were found near infected livestock premises [28]. In the former Soviet Union, FMD has on numerous occasions been reported to have spread from cattle to Saiga antelope and vice versa. The antelope were reported to have transferred the disease to other species in places far from the original outbreak [28].

Deer are among the most commonly FMD-infected wildlife species under field conditions, and are believed to play an important role in the epizootology of FMD [28]. The USA has maintained FMD free status since 1929. A 1924 California outbreak involved deer which were exposed via contact from infected cattle1 [17]. It required two years to stamp out FMD from the deer population, and over 22 000 were slaughtered in the process [17]1. Approximately 10% of those deer slaughtered during the outbreak displayed signs of FMD infection1.

FMD infection in wildlife has also been a concern in more recent FMD outbreaks. During the 2001 FMD outbreak in the United Kingdom and the Netherlands, it was feared that deer might become infected and potentially act as a reservoir [5, 10, 31]. Evidence of FMD in wild deer was not observed in either of these outbreaks, although there were reports of wildlife displaying signs of infection [10]. Extensive serosurveillance was conducted after the outbreak, but deer were not tested [10]. Due to the nature of the cattle industry in Europe, a lack of contact between deer and livestock in these countries may have averted a disastrous situation from occurring [10].

Since FMD has not been present in the USA for such a lengthy period of time, the entire population of cloven-hoofed animals is susceptible to infection. This includes both livestock and wildlife species. Epidemic models represent an important tool to aid decision making and epidemic response to foreign animal disease incursions such as FMD. Following detection of an incursion of FMD virus in a country previously free of disease, the application of appropriate control measures is a decision that needs to be made rapidly yet with little data. In addition, political, economic and property rights issues may also guide policy decisions regardless of what is deemed to be the most effective strategy to reduce the spread of FMD. Information from model outputs that provide guidance to the probable extent of an outbreak and its time span are invaluable for decision-makers implementing disease control measures in the face of external pressures. Nonetheless, such models need to be developed, validated and tested prior to emergency situations. Strong links between disease modelers, policy and decision-makers also need to exist a priori. Models can serve not only as response and decision-making tools but also as avenues to increase awareness and collaboration with stakeholders.

In this research, a simulation model was used to investigate seasonal population impacts on the spread of FMD in wildlife. The development of this model has been previously described [7]. Briefly, it uses a state-transition (susceptible-latent-infectious-resistant, SLIR) framework to simulate the spatial spread of disease within an artificial life model (geographic automata, a generalization of cellular automata). Artificial life models can explicitly incorporate spatial relationships by allowing the interaction between units (for example, individuals or herds) within a population and a predefined neighborhood, based on a set of rules and disease states at earlier time steps. The repetitive application of transmission rules within this local neighborhood replicates the complex spatial behavior that occurs during disease outbreaks. In the Sirca model, the interaction between susceptible herds and infected herds gives rise to newly infected herds. The probability of infection is a function of the distance between herds and the relative size (or density, if a herd occupies a constant land area) of each herd. Thus, spatial arrangements and population density are incorporated into simulated disease spread. The Sirca model has been used to investigate the potential spread of FMD in feral pig populations in Queensland, Australia [7] and in feral pig and wild deer populations in Texas, USA [13, 32].

The need to use spatially-explicit simulation models for FMD has been documented [12, 16] and spatial heterogeneity has been identified as perhaps the greatest challenge to representing FMD spread across the landscape [8]. Wildlife species are particularly affected by variations in climate and natural resources [13, 32]. To capture spatial heterogeneity across the landscape, wildlife distributions should therefore be seasonally-dynamic [13, 32]. Such temporal dependency may play an important role in the spread of disease within wildlife populations, and further, into domesticated animal populations [7].

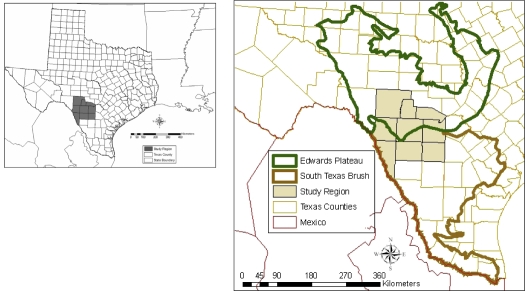
The study area chosen to investigate how seasonal-dependent variability in wildlife populations might affect the potential spread of FMD is located in South Texas (Fig. 1), and the target species was white-tailed deer (Odocoileus virginianus). Texas is the largest cattle production State in the USA and offers the unique opportunity to develop, validate and model the potential impact of foreign animal diseases, such as FMD, in the USA agricultural industry. In general, models developed in Texas to predict areas at-risk of FMD from wildlife reservoirs should be applicable to other ecologically similar areas both in the USA and abroad where potential wildlife reservoirs are present.

Figure 1.

A study area in south Texas selected to evaluate how seasonal variability in the distribution of white-tailed deer might affect the potential spread of foot and mouth disease. Two ecoregions (the Edwards Plateau and South Texas brush) represented in this study area are shown. The location of the 9 counties forming the study area, bordering Mexico, is shown in the insert. (A color version of this figure is available at www.vetres.org.)

White-tailed deer represent an important financial resource to a substantial number of ranchers in South Texas [4], and the deer population is actively managed for hunting and recreational purposes [4]2. Population management for optimum carrying capacity is important for maintaining nutritional status and population size [33]. Deer in the study area are primarily browsers (consuming leaves and twigs from shrubs and trees) during the autumn3. Grasses and forbs have been found to be important dietary components during the spring [11, 24]4. Deer will only consume grass when it is tender and green (young), as deer cannot digest mature grass3. Forb production in the study area is highly dependent on season (and particularly rainfall); forbs tend to be unpalatable to deer during late summer and late winter3. Given this shift in dietary availability, deer distributions are expected to vary by season, specifically based on rainfall and forage availability.

The aim of this research was to develop seasonal spatial distributions of wildlife (using the normalized difference vegetation index – NDVI – as a measure of forage availability) and to evaluate how seasonal variability might affect the potential spread of FMD virus. Knowledge of seasonal distributions of wildlife and the impact on the predicted spread of transboundary diseases, such as FMD, can be used to design more effective disease response and mitigation strategies. The specific objectives of this study were to: (1) incorporate seasonal variability into the predicted distribution of white-tailed deer in the study area by using bi-weekly composite NDVI values as a measure of forage availability in a regression model and (2) describe and compare the predicted FMD outbreak distribution that might be observed, given the seasonal variation in the white-tailed deer population distribution.

2. MATERIALS AND METHODS

2.1. Study site

The study area selected consists of 9 counties located in south Texas, bordering Mexico (Fig. 1). This area contains an estimated population of approximately 427 000 white-tailed deer and consists of two ecoregions − the Edwards Plateau (EP) in the north and the South Texas brush (ST) in the south − which divide the study region approximately in half (Fig. 1). Seasonal climatic variation in the study area is characterized by hot, dry summers and mild, moist winters, with average annual rainfall ranging between 750 and 1200 mm. Drought is common and periodically affects habitat resources and the wildlife population. The Edwards Plateau ecoregion contains the largest white-tailed deer population (estimated one deer per 4 ha) in Texas5. The South Texas brush ecoregion is actively managed to support hunting for white-tailed deer and the population density of deer (estimated one deer per 14 ha) is considered moderate5.

2.2. Data source

Bi-weekly composite NDVI images (1 km resolution) for 2006 (n = 26) were obtained for the study area from the United States Geological Survey (USGS) National Mapping Division’s Earth Resources Observation and Science (EROS) Data Center. The NDVI is one of a number of vegetation indices derived from remotely sensed imagery. It is associated with photosynthetically active radiation, and is the index most commonly used to estimate vegetation growth [20]. NDVI data are collected by the National Oceanic and Atmospheric Administration’s (NOAA) Advanced Very High Resolution Radiometer (AVHRR) satellite. The index is calculated from measured brightness values based on the absorption, transmittance and reflectance of energy by vegetation in the red and near-infrared portions of the electromagnetic spectrum [6, 15, 22]. To reduce cloud contamination, bi-weekly maximum NDVI composites are created using the maximum observed value for each composite period [9]. NDVI images are registered to the Lambert Equal Area Azimuthal map projection to ensure spatial accuracy to within 1 pixel, where each square pixel is 1 km² in area [29].

A baseline predicted distribution of white-tailed deer in the study region was derived by Dasymetric mapping [13]. Dasymetric mapping (also known as surface based demographic data representation) redistributes the population from a set of areal units into either a vector or raster map using ancillary data, such as land use or remotely sensed images [26]. The number of deer per county in the study area was obtained [9] and the distribution of deer was estimated using geostatistical methods, as previously described [13]. Briefly, county-level deer populations were disaggregated, based on suitable land use classes (forest, shrub and grassland) and their estimated class-specific deer carrying capacity. The number of deer per county was then proportionally distributed within land use class and the resulting fractional counts of deer at 30 m resolution were aggregated to a 1 km² integer grid matching the NDVI images. Each pixel of this grid was assumed to represent a group (herd) of deer. Thus, the grid consisted of location information (the center of each pixel, represented by x and y coordinates) and herd size. Since all square pixels were of a constant area (1 km²), deer herd size is also equivalent to deer herd density in this study. The term ‘herd’ is used subsequently to denote a group of deer, of varying number, occupying a land area of 1 km².

2.3. Seasonal deer distributions

A seasonal average NDVI coverage was derived and used to represent each of four seasons (winter, spring, summer and autumn) for white-tailed deer distributions. The 26 bi-weekly composite NDVI images were converted to raster data sets and projected using the study area polygon coverage (ArcGIS 9.1. ESRI Inc., Redlands, CA, USA). These 26 data sets were subsequently categorized into four seasons (December to February: winter, March to May: spring, June to August: summer, and September to November: autumn). An average NDVI value at the pixel level for each of the seasons was calculated and pixels located within areas of suitable land use classes (forest, shrub and grassland) were extracted (ArcGIS 9.1. ESRI Inc.) by overlaying seasonal average NDVI coverages and the 1992 National Land Cover Dataset6 land use coverage.

Regression models were used to describe the seasonal shift in the distribution of deer. The seasonal NDVI was used as an independent variable to predict the number of deer per herd (represented by pixels) as the dependent variable. These data were evaluated for a linear relationship using a correlation coefficient (Stata 10. Stata Corporation, College Station, TX, USA). Ordinary least squares (OLS) regression models were then fit [1] to the data for each season. The residuals of each of these seasonal models were evaluated for the presence of significant (P < 0.05) spatial autocorrelation, using a global Moran’s I statistic [1]. Significant spatial autocorrelation violates the assumption of independent observations and can bias standard errors, increasing the likelihood of Type I errors. In the case of significant autocorrelation of OLS model residuals, additional spatial diagnostic tests (Lagrange multipliers, LM) were used to determine whether a spatial autoregressive lag or error model should be fit. In cases where the LM tests for both the spatial lag and spatial error models were significant (P < 0.05), both types of models were evaluated and the model with the lowest log likelihood and highest pseudo-R² statistics was selected. The selection of a lag distance for spatial autoregressive models can often be subjective. For this study, an assumed home range (2 km) for deer [3] was used to generate the weights matrix for the autoregressive lag models. Within a spatial autoregressive model, the coefficient of the spatial lag term (ρ) shows the spatial dependence inherent in the data by measuring the average influence on each observation by their neighboring observations. The selected spatial autoregressive models for each season were evaluated for goodness of fit using a pseudo-R² statistic prior to simulating FMD spread within the Sirca model. The residuals of the spatial autoregressive models were also graphically evaluated for normality. The seasonal-specific spatial distributions of predicted number of deer per herd (pixel) were subsequently used as the input data sets within the Sirca simulation model.

2.4. Simulation model

The potential spread of FMD, by season and within ecoregion, was simulated using the Sirca model [7, 13, 32]. A conceptualization of disease transmission using the Sirca model is shown in Figure 2. In this model, deer herds (represented in this research as pixels) can pass through four disease states: susceptible, latent, infectious and immune. In this study, herd interactions evaluated were restricted to within a 2 km neighborhood distance and to within 8 neighboring herds [13, 32]. When calculating transmission probabilities, herds with more deer than a pre-specified maximum threshold value (30 deer per herd in this study) were assigned a probability of 1.0. The densities of the remaining herds were linearly scaled within the interval 0 to 1 by dividing each herd’s size by the maximum threshold value [13, 32]. The probability of FMD virus transmission from one herd to another was calculated as the product of the scaled deer densities of each pair of herds (susceptible and infected) evaluated, modified by the distance (2 km) by which the herds are separated.

Figure 2.

Conceptualization of modeling disease transmission in Sirca (A through D).

To incorporate chance into the model, an interaction between an infected herd and a susceptible neighboring herd (both represented as pixels) resulted in disease transmission when a value from a pseudo-random number generator was below their joint probability threshold [13, 32]. Once a herd was infected the second, third, and fourth transitions in the model depended on the specified length of the latent, infectious and immune periods. Estimates used for these parameters (3 to 5, 3 to 14, and 90 to 180 days, respectively) were derived from previous studies [13, 32]. The specific values for each herd were assigned randomly within the corresponding parameter ranges from a uniform distribution. As in previous studies, homogenous mixing was assumed to take place within (but not between) herds, and the herd was the unit of analysis [13, 32].

The same baseline modeling scenario was used for all model comparisons: to initiate the simulations within each of the 4 seasons, 5 herds (represented as pixels) in each of the two ecoregions were randomly selected (SPSS 14.0, SPSS Inc., Chicago, IL, USA) and their status designated as infected. As in previous studies, we randomly selected 5 index herd locations to allow us to simulate the spread of an “average sized oubreak” [32] which included a range of deer-density (low, medium and high) areas and ecoregions. This allowed us to assess the average effect of seasonal variation on predicted FMD spread, without the need to consider the impact of individual site selection issues. For every simulation of the Sirca model, each herd was allowed to interact with other herds within a 2 km neighborhood, representing the home range of deer within the study area. The model was simulated for a time period representing 90 days (to avoid overlap between seasons) and 100 model runs were simulated for each dataset, yielding a total of 800 model runs (4 × 2 × 100) and 72 000 model iterations (800 × 90).

2.5. Data analysis

The seasonal predicted deer distributions (represented by pixels) were described and compared by calculating the minimum, maximum, range, standard deviation, skewness, and kurtosis of the herd size frequency distributions (SPSS). From the Sirca model output, the median number of deer infected and the median number of herds (pixels; equivalently, km²) were used to characterize each set of simulations (n = 100) at the 90th model day for each season (n = 4) and ecoregion (n = 2). These 8 distributions were evaluated for normality (SAS, Cary Institute, NC, USA). A non-parametric Kruskal-Wallis one-way analysis test was used to compare the differences in predicted epidemic spread (measured both by number of deer infected and number of herds infected) between the 8 treatment groups (ecoregion and season). Because the Kruskal-Wallis test only measures significant differences between the highest and lowest groups, a post hoc Miller’s multiple comparison test (SAS) was used to evaluate differences between groups.

3. RESULTS

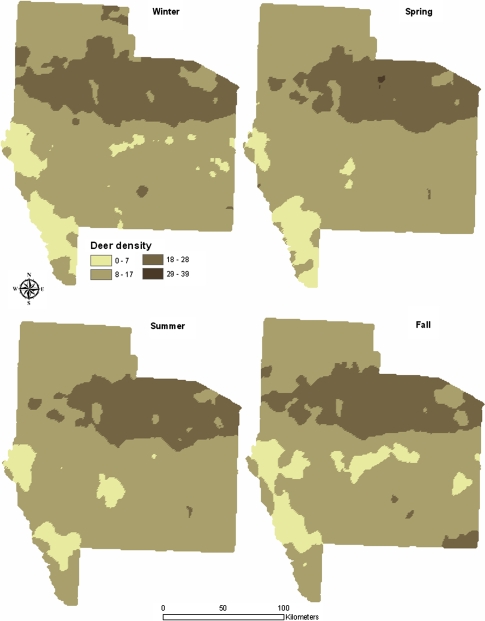
Descriptive statistics for each seasonal deer distribution are shown in Table I. Although the baseline and seasonal-specific mean number of deer (13.96) predicted per herd (pixel) in the study area was constant, compared to the baseline (non-seasonal) deer distribution, seasonal distributions were less variable (as measured by each seasonal-specific distribution’s standard deviation and range) but tended to be more positively skewed and kurtotic. Significant (P < 0.001) linear relationships between the NDVI and herd size pixels were observed for winter, spring, summer and autumn (respective correlation coefficients 0.67, 0.60, 0.55 and 0.59). Residuals of each of the four seasonal ordinary linear regression models showed significant (P < 0.001) positive spatial autocorrelation (Moran’s I 0.66, 0.71, 0.72 and 0.72, respectively). In all cases, a spatial autoregressive lag model was preferred over a spatial autoregressive error model, based on log likelihood statistics. The characteristics of these fitted seasonal-specific spatial autoregressive lag models are summarized in Table II. The spatial lag (ρ) terms were > 0.9 for all seasonal models, indicating that herd size was strongly influenced by neighboring herd sizes. Residuals of all seasonal spatial autoregressive lag models visually appeared normally distributed. The spatial distributions predicted using the autoregressive lag models for each season are shown in Figure 3. Areas of high density deer distribution were predicted in the north-eastern parts of the study area in all seasons, and were most extensive in the autumn and winter seasons.

Table I.

Descriptive statistics for white-tailed deer distributions (represented by 1 km² pixels) predicted in an area of south Texas, using information from the normalized difference vegetation index and an estimated baseline (non-seasonal) deer distribution (427 292 deer in 30 592 herds, spatially represented as pixels). Seasonal-specific mean number of deer (13.96) predicted per herd (pixel) in the study area was constant.

Distribution	SD	Minimum	Maximum	Range	Skewness	Kurtosis
Baseline	8	0	36	36	0.35	1.94
Winter	6	1	28	27	0.61	2.28
Spring	5	3	29	26	0.75	2.94
Summer	4	5	27	22	0.54	2.92
Autumn	5	0	27	27	0.39	2.67

Table II.

Characteristics of spatial autoregressive lag models fitted to seasonal white-tailed deer distributions (represented spatially by 30 592, 1 km² pixels) in an area of south Texas, derived using the normalized difference vegetation index.

Model	Parameters	Constant	NDVI	Spatial lag, ρ
Winter	Coefficient	–1.41	6.06	0.918
	Std. error	0.028	0.096	0.003
	z-value	–14.67	21.08	284.7
	Probability	< 0.001	< 0.001	< 0.001
				Pseudo-R2 = 0.837
Spring	Coefficient	–1.2	5.2	0.932
	Std. error	0.105	0.305	0.003
	z-value	–11.36	17.04	313.3
	Probability	< 0.001	< 0.001	< 0.001
				Pseudo-R2 = 0.838
Summer	Coefficient	–0.88	4.17	0.938
	Std. error	–1.02	0.28	0.003
	z-value	–8.64	14.7	331.7
	Probability	< 0.001	< 0.001	< 0.001
				Pseudo-R2 = 0.838
Autumn	Coefficient	–1.33	4.91	0.932
	Std. error	0.11	0.29	0.003
	z-value	–11.76	17.0	313.6
	Probability	< 0.001	< 0.001	< 0.001
				Pseudo-R2 = 0.838

Figure 3.

Seasonal-specific white-tailed deer distributions in a study area in south Texas selected to evaluate the effect of seasonal variability on potential spread of foot and mouth disease. Distributions were predicted using the normalized difference vegetation index and spatial autoregressive lag models (Tab. II). (A color version of this figure is available at www.vetres.org.)

The predicted spread of FMD for each season and ecoregion is summarized in Table III (number of deer) and Table IV (number of herds), and boxplots of the predicted spread of FMD for each season and ecoregion are shown in Figure 4. There were significant differences in epidemic spread by both season and ecoregion (Kruskal-Wallis χ² = 726.139, df = 7, P-value < 0.0001). In all cases a significantly higher median number of infected deer and infected herds were predicted in the Edwards Plateau ecoregion (87 792−101 385 deer and 6 050−6 416 herds) than in the South Texas brush ecoregion (40 211−54 385 deer and 4 336−4 969 herds). Miller’s multiple comparison test indicated that within the Edwards Plateau ecoregion, the highest median number of infected deer (101 385) occurred in winter, with the lowest median number in summer (87 792). The highest median number of infected herds (6 416) occurred in winter, with the lowest median number (tied by Miller’s test) in spring (6 050) and summer (6 058). Within the South Texas brush ecoregion, the highest (tied by Miller’s test) median number of infected deer and herds occurred in autumn (53 389 and 4 969, respectively) and summer (54 385 and 4 922, respectively), with the lowest median number of deer and herds in winter (40 211 and 4 336, respectively). The distributions of predicted infection for outbreaks initiated in winter in the Edwards Plateau and the South Texas brush ecoregions are shown in Figure 5.

Table III.

Predicted size (number of deer infected) of an outbreak of foot and mouth disease in a population of white-tailed deer in an area of South Texas for each season by ecoregion (Edwards Plateau and South Texas brush). Results shown are from 100 simulations of a susceptible-latent-infectious-resistant geographic automata model (Sirca) for each seasonal deer distribution.

Ecoregion	Season	Deer
		Median	Interquartile range	25%, 75% percentile	Skewness	Kurtosis
Edwards Plateau	Winter	101 385	2 868	100 305, 103 239	–0.19	–0.20
Edwards Plateau	Spring	90 913	2 885	89 233, 92 139	–2.28	10.5
Edwards Plateau	Summer	87 792	2 082	86 612, 88 707	–1.14	4.6
Edwards Plateau	Autumn	92 323	2 314	91 126, 93 445	–92	2.07
South Texas brush	Winter	40 211	1 819	39 205, 41 086	–2.9	13.9
South Texas brush	Spring	50 372	1 330	49 502, 50 866	–2.9	10.1
South Texas brush	Summer	54 385	1 753	53 462, 55 233	–4.7	29.8
South Texas brush	Autumn	53 389	1 546	52 515, 54 074	–3.01	11.7

Table IV.

Predicted size (number of deer herds infected) of an outbreak of foot and mouth disease in a population of white-tailed deer in an area of South Texas for each season by ecoregion (Edwards Plateau and South Texas brush). Results shown are from 100 simulations of a susceptible-latent-infectious-resistant geographic automata model (Sirca) for each seasonal deer distribution.

Ecoregion	Season	Deer herds
		Median	Interquartile range	25%, 75% percentile	Skewness	Kurtosis
Edwards Plateau	Winter	6 416	154	6 340, 6 496	–1.9	9.3
Edwards Plateau	Spring	6 050	139	5 972, 6 112	–3.3	16.3
Edwards Plateau	Summer	6 058	131	5 983, 6 115	–3.4	22.5
Edwards Plateau	Autumn	6 198	142	6 138, 6 281	–3.1	12.9
South Texas brush	Winter	4 336	186	4 247, 4 436	–2.9	13.6
South Texas brush	Spring	4 766	117	4 696, 4 815	–2.8	7.9
South Texas brush	Summer	4 922	161	4 842, 5 004	–4.2	23.6
South Texas brush	Autumn	4 969	132	4 891, 5 023	–2.2	7.5

Figure 4.

Foot and mouth disease infection of white-tailed deer (upper) and deer herds (lower) in an area in south Texas, predicted by 100 simulations of a susceptible-latent-infectious-resistant geographic automata model (Sirca).

Figure 5.

Probability of foot and mouth disease infection of winter-distributed white-tailed deer in an area in south Texas, predicted by 100 simulations of the Sirca model. Each simulation was initiated at the same 5 index herds (•, represented as 1 km² pixels) in either the Edwards Plateau (upper) or South Texas Brush (lower) ecoregions as infected. Probability of infection (per pixel) is shown. (A color version of this figure is available at www.vetres.org.)

4. DISCUSSION

Substantial differences were observed in the median predicted magnitude of FMD spread, both by season and ecoregion: the number of deer and herds predicted to be infected ranged from 40 211 deer and 4 336 herds in the South Texas brush ecoregion in winter to 101 385 deer and 6 416 herds in the Edwards Plateau ecoregion in winter. These differences can be explained by changes in modeled deer distribution within the study area, since all other parameters were held constant within this simulation study. Results suggest that the outcome of a transboundary disease incursion (such as FMD) in a wildlife population (such as white-tailed deer in South Texas) might depend on both where and during which time of year the incursion occurs.

Spatial autoregressive lag models using the NDVI to predict seasonal-specific deer distributions fit the data well (pseudo-R ² > 0.8 for all seasons). Although there were not substantial differences in the overall estimated number of deer in the study area based on the distributions predicted by the spatial autoregressive lag model, the predicted spatial arrangement of the population varied substantially by season (Tab. I and Fig. 4), as measured by skewness and kurtosis statistics. Thus, the difference in predicted FMD spread within these populations can be attributed to the spatial distribution patterns of the population – not to differences in the overall size of the population.

A significantly (P < 0.05) higher number of predicted FMD infected deer and herds were observed in the Edwards Plateau (northern) versus South Texas brush (southern) ecoregion, regardless of season. Within ecoregion, significant (P < 0.05) differences in the seasonal number of predicted FMD infected deer and herds was also observed. In the Edwards Plateau ecoregion both the highest number of infected deer and herds were predicted in winter, whereas in the South Texas brush ecoregion the highest numbers were predicted in summer and autumn. These results further support previous work [13] which suggested that the spatial continuity of a population might play an important role in the predicted outbreak size. This result is not surprising, since the Sirca model is a local neighborhood based spatial disease spread model [13]. The more continuity in the spatial distribution, the greater is the opportunity for interactions to occur between herds, consistent with epidemic theory and the importance of spatial heterogeneity [16, 18].

The model used in this study has been used previously to investigate wildlife-domestic species interactions (feral pigs and cattle [7, 32] and wild deer and cattle [32]) and to evaluate the impact of spatial estimation methodologies on model predicted spread of FMD in deer [13]. In the current study, our focus was on extending previous work to incorporate seasonal variability in white-tailed deer populations and subsequently to predict how the spread of FMD might vary by season. As in previous studies, we modeled only local spread [7, 13, 32]. Given that this is an actively managed and hunted population, there are likely times of the year (hunting season) where potential longer-distance FMD spread may be present.

This study focused on the initial stages of disease spread (≤ 90 days) so that the effect of between-season variability in population distributions could be assessed [13]. We also assumed that the home range of deer (2 km) was adequate for creating spatial weights for the spatial autoregressive lag models. Given that deer show high fidelity to their home range, this assumption is likely to be valid [19]. However, the spatial scale of influence of the surrounding population on seasonal deer distribution is unknown. Future work should incorporate a range of spatial weights and assess how this variation might impact model predictions of deer distribution.

The behavior of wildlife species is also seasonally-variable and should be included in future work focusing on the spread of FMD in wildlife populations. For example, the rut (breeding season) in white-tailed deer in the study area typically occurs in the Edwards Plateau ecoregion between October and December, and in the South Texas brush ecoregion in December7. During this time of the year, bucks are more likely to move around and cover larger distances than normal7. This could contribute substantially to increased spread of FMD because of greater numbers of interactions with other potentially susceptible deer. Juvenile males will also disperse from their female groups and an increase in the number of single males in the population may need to be modeled [25]. In addition, a stable population (no births or deaths) was assumed in this study because of the relatively short (≤ 90 days) time periods simulated. Future studies should incorporate such changes in the population structure, especially given that this area is intensively managed for hunting and recreation.

An assumption was made in this study that the same spatial relationship for predicting deer distributions (in the autoregressive lag models) was valid over the entire study area (both ecoregions). Ecoregions comprise similar soils, topography, land use and vegetation (habitat). Given the substantial differences in the modeled spatial distribution of deer in the two ecoregions in the study area, it is likely that some variation in the spatial relationship may exist. Future work should examine the application of regression models specific to ecoregions to determine if substantial variation does exist and whether this might impact predicted disease spread. If there are substantial differences in the spatial distributions of deer by ecoregion there is utility in developing separate ecoregion-specific regression models. However, the usefulness of ecoregion as a predictor for estimating deer distributions might be limited because some of the habitat variability is captured at a finer resolution with land use data. Using ecoregions as a marker for modeling deer behavior might also be limited because regions are a very broad scale measurement of the environment and have no associated attribute data. While it might be useful to model deer behavior with a larger number of finer resolution ecoregions, it becomes exceedingly complex: as data requirements increase, a greater number of variables have to be estimated and information on behavior within a particular ecoregion has to be derived from expert opinion. This greatly adds to uncertainty in the resulting estimates.

The NDVI has been used in numerous studies on the classification of land use and temporal vegetation variability (onset, peak, senescence) [21, 29]8^,9^,10, as well as the examination of the relationship between NDVI and livestock stocking rates in the USA [14, 27]. The NDVI was highly correlated (R² > 0.7) with dietary measurements of white-tailed deer during winter and spring in north central Texas [30], and the NDVI was significantly (P < 0.05) associated with mule deer distributions in the southwest desert in spring, summer and autumn [23]. In the present study, a single year of NDVI data was used and bi-weekly measurements were grouped into a seasonal average to predict deer distributions. As documented in previous studies [23, 30], a traditional seasonal (winter, spring, summer, autumn) breakdown was assumed to be appropriate. More detailed analysis of methods of grouping NDVI data for predicting deer distribution is warranted, as the traditional seasonal approach may not adequately capture seasonal variability in the relationship between vegetation greenness and forage availability. It was further assumed that one year of NDVI data was adequate to model seasonal variability. This assumption is valid if the interest in modeling deer distribution focuses on the most recent year; however, longer term trends may also be of interest to modelers and policy decision-makers. Future work on a short time series might provide a better understanding of the broad patterns of NDVI over time in the study area.

There are numerous areas of the USA where livestock are extensively grazed and the potential for interaction with susceptible wildlife species, such as white-tailed deer, is high. Deer move through and forage in fields between farms and enter premises with animal feed and slurry [31]. In addition, supplemental feeding of white-tailed deer for hunting purposes is a common practice in many areas of the USA [2]. Deer densities in parts of Texas are very high, and most deer inhabit private land11. As the result of extensive land use change, deer populations in Texas have formed metapopulations with high deer densities, increased contact between deer populations and potentially the risk of disease transmission to domestic livestock11. Based on a review of the literature, the current study is probably only one of two [7] to incorporate seasonal variability in wildlife distributions and to define the potential magnitude of an FMD outbreak by season. Substantial seasonal variability in the model predicted spread of FMD was found. Future work focusing on improved methods of analysis of NDVI data, spatial regression models and incorporating behavioral traits are needed to yield additional insights into the potential spread of transboundary diseases, such as FMD, in wildlife populations.

In this simulation study, the outcome of an FMD incursion was found to depend on both when and where the incursion occurred. These results are important to consider when designing disease mitigation strategies. It is likely that such effects would be seen for FMD incursions in other regions and countries, and for other diseases, in cases in which a potential wildlife reservoir exists.