Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2009 Jun 15;20(12):2943–2953. doi: 10.1091/mbc.E08-09-0909

Anterograde Microtubule Transport Drives Microtubule Bending in LLC-PK1 Epithelial Cells

Andrew D Bicek *,†, Erkan Tüzel ‡,†, Aleksey Demtchouk *, Maruti Uppalapati §, William O Hancock §, Daniel M Kroll ‖, David J Odde *,✉
Editor: Erika Holzbaur
PMCID: PMC2695801  PMID: 19403700

Abstract

Microtubules (MTs) have been proposed to act mechanically as compressive struts that resist both actomyosin contractile forces and their own polymerization forces to mechanically stabilize cell shape. To identify the origin of MT bending, we directly observed MT bending and F-actin transport dynamics in the periphery of LLC-PK1 epithelial cells. We found that F-actin is nearly stationary in these cells even as MTs are deformed, demonstrating that MT bending is not driven by actomyosin contractility. Furthermore, the inhibition of myosin II activity through the use of blebbistatin results in microtubules that are still dynamically bending. In addition, as determined by fluorescent speckle microscopy, MT polymerization rarely results, if ever, in bending. We suppressed dynamic instability using nocodazole, and we observed no qualitative change in the MT bending dynamics. Bending most often results from anterograde transport of proximal portions of the MT toward a nearly stationary distal tip. Interestingly, we found that in an in vitro kinesin-MT gliding assay, MTs buckle in a similar manner. To make quantitative comparisons, we measured curvature distributions of observed MTs and found that the in vivo and in vitro curvature distributions agree quantitatively. In addition, the measured MT curvature distribution is not Gaussian, as expected for a thermally driven semiflexible polymer, indicating that thermal forces play a minor role in MT bending. We conclude that many of the known mechanisms of MT deformation, such as polymerization and acto-myosin contractility, play an inconsequential role in mediating MT bending in LLC-PK1 cells and that MT-based molecular motors likely generate most of the strain energy stored in the MT lattice. The results argue against models in which MTs play a major mechanical role in LLC-PK1 cells and instead favor a model in which mechanical forces control the spatial distribution of the MT array.

INTRODUCTION

Microtubules (MTs) are self-assembling linear polymers that serve a range of functions within the cell, including transport and positioning of intracellular cargo via coupling to molecular motors. The mechanical stiffness of MTs has been proposed to play an important role in the mechanics of the cell (Wang et al., 1993, 2001; Ingber et al., 2000; Howard, 2001; Stamenovic et al., 2001; Ingber, 2003; Brangwynne et al., 2006). This hypothesis derives in part from the observation that in interphase animal tissue cells, MTs are commonly observed to form a radial array, which qualitatively resembles the spokes of a bicycle wheel. MTs are therefore ideally positioned to act as rigid struts that mechanically bear compressive loads in the cell to oppose and balance the tensional forces (Buxbaum and Heidemann, 1988; Ingber, 1993; Wang et al., 1993, 2001; Stamenovic et al., 2001; Ingber, 2003). The ability of MTs to resist compressive loading has recently been proposed to be enhanced by lateral reinforcement from the actin cytoskeleton, which could make MTs even more effective in their putative role as compressive struts (Brangwynne et al., 2006). MTs are indeed mechanically stiff structures, with a “flexural rigidity” (EI)—a measure of bending resistance—of ∼21 pN-m2, ∼300 times larger than that of an actin filament (Gittes et al., 1993; Howard, 2001; VanBuren et al., 2005). Note, however, that this value has only been measured in vitro; it remains a formal possibility that MTs are softer in living cells due to the presence of MT binding proteins or lattice defects.

Despite their mechanical stiffness, MTs in living cells are often highly buckled, consistent with the model prediction that MTs bear compressive loads (Wang et al., 1993, 2001; Ingber et al., 2000; Stamenovic et al., 2001; Ingber, 2003; Brangwynne et al., 2006). There have been several mechanisms suggested to cause the deformation of MTs. These include MT polymerization against a stationary distal tip (Dogterom and Yurke, 1997), acto-myosin contractility (Forscher and Smith, 1988; Waterman-Storer and Salmon, 1997; Zhou et al., 2002) and transport (Schaefer et al., 2002), and buckling of MTs due to direct interactions with molecular motors such as dynein or kinesin (Koonce et al., 1999; Burakov et al., 2003; Dujardin et al., 2003; Malikov et al., 2004; Baas et al., 2005, 2006; Brito et al., 2005; Ferenz and Wadsworth, 2007), all of which may act alone or together in the presence of thermal fluctuations.

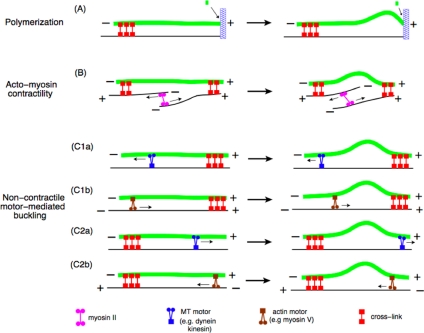
It is well known that MTs can exert pushing forces during polymerization. During mitosis, for example, it is believed that assembling MTs can exert pushing forces on chromosomes (Dogterom and Yurke, 1997). It also has been observed in vitro that MTs buckle as they assemble against microfabricated barriers (Dogterom and Yurke, 1997). In living cells, MTs are known to polymerize against the edge of the cell (Waterman-Storer and Salmon, 1997), and forces exerted by plus-end MT polymerization have been shown to play a role in positioning of the nucleus in fission yeast (Tran et al., 2001). Figure 1A is a schematic representation of a microtubule assembling against a stationary obstacle and buckling.

Figure 1.

Figure 1.

Open in a new tab

Different force mechanisms that result in MT buckling. (A) A MT can polymerize against a stationary distal tip and buckle as the MT grows. The rate of polymerization slows down as the MT buckles. (B) Acto-myosin contractility can cause a cross-linked MT to buckle. An actin-based motor, such as myosin II, can cross-link antiparallel actin filaments and contract them as it moves. As a result, a MT that is passively attached to the actin will buckle as shown in the figure. (C1a) An MT-based motor such as dynein can walk toward the minus end of a MT, which is cross-linked at the plus end, and cause it to bend. (C1b) The plus-end–directed motion of an actin based motor, such as myosin V, can cause a MT that is cross-linked to the actin to buckle. (C2a) A plus-end–directed MT-based motor, such as kinesin, can buckle a MT that is cross-linked at its minus end to the actin. (C2b) The plus-end–directed motion of an actin based motor also can buckle a MT that is oriented antiparallel to the actin filament and cross-linked at its minus end.

Another mechanism known to exert forces on MTs and buckle them is acto-myosin contractility (see Figure 1B). It has been shown that acto-myosin contractility can cause MTs to buckle and promote breaking in motile cells (Waterman-Storer and Salmon, 1997; Gupton et al., 2002). In particular MTs are observed to deform and break in central cell regions where actin retrograde and anterograde flow powered by myosin motors forms a convergence zone (Gupton et al., 2002). It also has been argued that during cell migration this mechanism plays a major role in spatially modulating MT turnover by regulating MT breakage (Gupton et al., 2002). For this mechanism to work, MTs have to interact with the F-actin bundles, and it has been suggested that MTs and F-actin bind to one another in migrating newt lung epithelial cells (Salmon et al., 2002).

Molecular motors linked to the actin cytoskeleton or MTs also can directly exert forces that are resisted by passive cross-links to the actin cytoskeleton. MT-based molecular motors, such as kinesin and dynein can bind to MTs and cause them to buckle upon movement (as shown in Figure 1C1a and 1C2a). Recent evidence also suggests that cytoplasmic dynein is localized to sites of cell–cell contact and that microtubules can become tethered to these dynein patches at the cell cortex, allowing dynein to also act as a passive cross-linker (Gundersen et al., 2004; Ligon and Holzbaur, 2007). In addition, it has been argued that cytoplasmic dynein, possibly acting together with motors such as kinesin, plays a crucial role in the maintenance of the centrosome position (Brito et al., 2005), as well as the organization of MTs into radial arrays in interphase cells (Burakov et al., 2003; Malikov et al., 2004). In migrating adherent cells such as fibroblasts, inhibition of dynein stimulates microtubule organizing center reorientation, suggesting that dynein at the cell cortex can exert a pulling force on MTs (Palazzo et al., 2001). In contrast, experiments in Dictyostelium show that overexpression of dynein induces the formation of loose bundles and results in movement of the entire MT array (Koonce et al., 1999; Brito et al., 2005). These results also suggest that the actin-rich cortical mesh serves as a relatively stiff mechanical substrate upon which MT-based motors or linker proteins bind (Brito et al., 2005). Alternatively, motors such as myosin V can cross-link actin filaments and MTs, and plus- or minus-end–directed motion against a passive cross-link can induce buckling of MTs, as shown in Figure 1C1b and 1C2b.

Interestingly, similar behavior has been observed in gliding assays in vitro in which molecular motors are attached to a rigid glass substrate (Amos and Amos, 1991; Weiss et al., 1991). In the gliding assay, a fraction of nonfunctional “dead” motors would serve as passive cross-linkers against which the “active” motors work. Similar to the in vivo observations, MTs are occasionally seen to buckle and rapidly relax when the passive cross-links fail. Despite this resemblance, there has been no quantitative comparison between the bending of MTs in gliding assays and in living cells. Moreover, to the best of our knowledge, a quantitative assessment of the various mechanisms that lead to MT deformation in a given cell type has not been reported in the literature.

Here, we report a systematic analysis of MT deformation in the periphery of living LLC-PK1 cells, and assess the contribution of the different mechanisms discussed above. We also characterize local deformations of MTs in both LLC-PK1 cells and kinesin gliding assays in vitro by using curvature distributions (Bicek et al., 2007). Our results argue against models in which MTs play a passive structural role and instead favor a model in which active motor forces and cell shape control the spatial distribution of MTs.

MATERIALS AND METHODS

Cell Culture and Transfection

LLC-PK1α (pig kidney epithelial) cells, stably transfected with green fluorescent protein (GFP)-α-tubulin (Rusan et al., 2001) were plated at low density (∼200 cells/mm2) on 35-mm glass-bottomed dishes (MatTek, Ashland, MA) and allowed to spread overnight at 37°C and 5% CO2 in Opti-MEM I (Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum. For F-actin studies, LLC-PK1 cells (American Type Culture Collection, Manassas, VA) were transiently transfected with an enhanced green fluorescent protein (EGFP)-actin plasmid (Clontech, Mountain View, CA) by using FuGENE 6 transfection reagent (Roche, Indianapolis, IN) or a Genepulser II electroporator (set at 0.25 kV, 975 mF; Bio-Rad, Laboratories, Hercules, CA) and incubated for 24–48 h. In addition, a subgroup of stably transfected LLC-PK1α cells was transiently transfected with mCherry-actin (Shaner et al., 2004) for dual expression of fluorescent MTs and F-actin.

Digital Fluorescence Microscopy

Cells were observed on a TE200 inverted microscope (Nikon, Tokyo, Japan) by using a 60×, 1.49 numerical aperture (NA) Plan Apo objective outfitted with a 2.5× projection lens for a total magnification to the camera of 150×. Fluorescent images were collected on a CoolSNAP HQ2 cooled charge-coupled device (CCD) camera (Photometrics, Tucson, AZ), with a resulting image pixel size of ∼42 nm in the combined camera/microscope system. The camera/microscope system was running under the control of MetaMorph software, version 7.2 (Molecular Devices, Sunnyvale, CA), and the cells were kept at 37°C during imaging. Time sequences were collected with the camera in streaming acquisition mode using an exposure time of 200–400 ms, with a 100-W mercury arc lamp. Images were taken in the periphery of the cell, often within cell protrusions, to ensure that individual MTs could be observed in a single focal plane. This also ensured that bending occurred almost exclusively in the two dimensions that define the focal plane.

Drug Studies

To inhibit myosin II motor activity, and hence F-actin retrograde flow, the cells were treated with 75 μM blebbistatin dissolved in dimethyl sulfoxide (DMSO) (EI-315; BIOMOL Research Laboratories, Plymouth Meeting, PA) (Murthy and Wadsworth, 2005). We collected images of a cell before the treatment and 15 min after the application of the drug.

To study the effect of polymerization on microtubule deformations, we treated the cells with nocodazole (T-101; BIOMOL Research Laboratories) and used concentrations varying between 10 nM and 50 μM to determine the optimum range to inhibit dynamic instability. The images of a given cell were taken before the treatment and after 15 min of exposure to the drug. Time-lapse images also were recorded at 2-s intervals after the treatment after 15 min.

Fluorescent Speckle Microscopy Kymographic Analysis

Kymographs of MT and F-actin motion were made using the kymograph tool of MetaMorph software, version 7.2 (Molecular Devices). Briefly, a region of interest was selected from a time series that encompassed the area to be analyzed. For F-actin motion, the region (rectangle) was typically 20 pixels (1 pixel = 42 nm in the field) wide by the length of the feature. This was to ensure that intense fluorescent speckles would remain in the region during the time series. The kymograph tool recorded the maximum pixel intensity across every row in the region for each time point in the stack. For kymographs of MT motion, an isolated MT or portion of a MT was selected that developed a bend during the time series. A region of interest was selected around the MT so that the selected MT remained inside the region during the entire time series. Again, the kymograph tool recorded the maximum pixel intensity across every row in the region for each time point in the stack. By using a large region that encompassed an isolated bending MT, the fluorescent speckle pattern recorded in the kymograph resulted in identification of the direction of the applied force. The direction of the applied force provides useful information in screening force models (shown in Figure 1) that cause MT bending.

Kinesins and In Vitro Microtubules

Drosophila melanogaster conventional kinesin heavy chain was bacterially expressed and purified by nickel column chromatography as described previously (Hancock and Howard, 1998). Two batches of kinesin motors were prepared and used in this study. Bovine brain tubulin (Williams and Lee, 1982) was purified and rhodamine labeled as described previously (Hyman et al., 1991) MTs were polymerized by mixing 32 μM rhodamine-labeled tubulin, 4 mM MgCl2, 1 mM guanosine triphosphate, and 5% DMSO in BRB80 buffer [80 mM piperazine-N,N′-bis(2-ethanesulfonic acid), 1 mM EGTA, and 1 mM MgCl2, pH 6.9 with KOH] and incubating at 37°C for 20 min. Polymerized MTs were stabilized with 10 μM paclitaxel.

Kinesin–Microtubule Gliding Assay

Flow cells were constructed by attaching a coverslip to a glass slide with double-stick tape and were incubated with casein solution (0.5 mg/ml casein in BRB80 buffer for 5 min). The flow cell was incubated with 3 μg/ml kinesin. The motors were diluted from stock to the final concentration in solutions containing 1 mM ATP and 0.2 mg/ml casein in BRB80. After 5-min incubation, motility solution containing ∼32 nM MTs, 1 mM ATP, 10 μM paclitaxel, 0.2 mg/ml casein, 20 mM d-glucose, 0.02 mg/ml glucose oxidase, 0.008 mg/ml catalase, and 0.5% β-mercaptoethanol in BRB80 buffer was introduced into the flow cell. MT movements were observed by fluorescence microscopy using a TE2000 inverted microscope (Nikon) with a 100× 1.3 NA objective. Experiments were conducted at room temperature. Images were captured by a Cascade 512B CCD camera at a frame rate of 0.5 s−1 and saved to a computer.

Semiautomated Tracking Algorithm for Identifying Microtubule Contours

A semiautomated microtubule tracking algorithm was written in MATLAB (The MathWorks, Natick, MA). The algorithm is designed to extract coordinates of a MT within user-defined rectangular regions. MTs often have complex trajectories making it difficult to fit an entire filament by using a single rectangle. We therefore split a given MT into a subset of rectangular regions before estimating the coordinates. A single MT region is specified by two points located at the two opposite corners of a rectangle. Once a region is chosen, the center of mass of the microtubule is calculated by assigning brighter pixels more weight, i.e., Rcm = Σi miri/Σi mi, where mi and ri correspond to pixel's brightness and position, respectively. The MT is then rotated about its center of mass by integer multiples of 90° to find the closest alignment with the x-axis and so that accurate vertical line-scans can be performed. We use 90° rotations to avoid loss of information due to pixellation upon rotation.

The actual coordinate estimation is done by fitting a Gaussian curve to each vertical line-scan of the region using

graphic file with name zmk01209-9084-m01.jpg

where I is the intensity value, and y denotes the vertical coordinates along the line scan. Before each fit, the lowest intensity level along a line scan is set to one by subtracting the background intensity and adding one. The initial guesses for Ioffset, I0, ym, and ς are determined from the first box corner, and as one progresses through the MT, previous fit values for the line scans are used as initial guesses. The width of the Gaussian fit is constrained to avoid extensive fitting to noise. To do this, the point spread function of the actual microscope setup, i.e., a numerical aperture value of 1.49, wavelength of 513- and 42-nm pixel size, is fitted to a Gaussian, and the SD ςPSF is determined. We then restrict ς to be in the interval [ςPSF, 3ςPSF]. The algorithm works on a per-MT region basis, and after all the regions have been analyzed, the program assembles them into a single data file. The regions are connected using linear interpolation to fill in every pixel value, and Gaussian noise of one pixel SD (Bicek et al., 2007) is added to linear line segments in between regions to match the noise level to the remaining parts of the MT.

Quantitative Analysis of Microtubule Deformation

We used local estimates of the curvatures along the MT contours to characterize the deformation. The estimation of local curvature and the construction of the curvature distribution were performed as previously described (Bicek et al., 2007). To reduce the contribution of errors from digitization and data collection procedure (Bicek et al., 2007), we coarse-grained the MT coordinates obtained using the semiautomated algorithm to an average spacing of 16 pixels. This spacing reduced the contribution of noise to a negligible level, while maintaining the features of the curvature distribution. Adjacent points along the coarse-grained coordinates were used to calculate the curvature using (Figure 2B) the following equation:

graphic file with name zmk01209-9084-m02.jpg

where κ is the local curvature and θ(s) is the tangent angle as a function of the contour length s. For a discrete chain, Δθ is the angle change between two adjacent points along the chain and Δs1 and Δs2 are the segment lengths, respectively. This relation provides an approximation of the local curvature for small angle changes and small bond lengths; using equation 2 to calculate the curvature of a circular shaped polymer will underestimate curvature by 1% at moderate curvatures (κ = 1(μm)−1) and by 17% at large curvatures (κ = 3(μm)−1) at the suggested average spacing of 16 pixels. This error is relatively small compared with the errors due to poor sampling of the distribution at such large curvatures. Regardless of the error introduced by this approximation, comparisons between different experiments can still be made by using this operational definition of curvature. The curvature distribution has been calculated by creating a histogram of the discrete curvature values obtained from equation 2. For the case of a thermally driven semiflexible polymer, the local energy should be distributed exponentially according to Boltzmann's law. Because energy is proportional to the curvature squared, the curvature distribution is Gaussian. The mean of the Gaussian is zero for polymers with zero mean curvature and the variance is inversely proportional to the persistence length (Bicek et al., 2007). In our previous work (Bicek et al., 2007), we have shown that the curvature distribution of a discretized thermally driven semiflexible polymer chain is Gaussian as long as the segment length is much smaller than the persistence length of the chain.

Figure 2.

Figure 2.

Open in a new tab

Direct observation of MT bending in LLC-PK1 cells. (A) A typical digital image of a GFP-tubulin labeled LLC-PK1 epithelial cell showing a broad distribution of MT bending in the periphery of a lamellar extension. To remain in focus, the z-coordinates must remain within ∼0.5 μm of each other, and so the microtubules that are in focus all along their length can be approximated as deforming in the x-y plane only. (B) A closer view of the MT outlined by the box in A. The x-y coordinates determined using the semiautomated algorithm are shown (in red) over the microtubule. The curvature of a MT is estimated locally by collecting a discrete set of x-y coordinates spaced 16 pixels apart along the contour (blue dots) and calculating the angle change with respect to the average arc length of three adjacent points (see equation 2). Often, highly bent MTs (MT 1) are observed directly adjacent to straight MTs (MT 2). Microtubules were not selected for analysis based on their curvature. (C) A noncentrosomal MT increases its bending during depolymerization, indicating that polymerization-based forces are unlikely to drive bending in all cases. (D) A highly bent MT rapidly relaxes after the tip depolymerizes past a putative attachment point, providing evidence that MTs are both stiff and cross-linked to other structures in the cell. Bar in all images, 3 μm.

RESULTS

Direct Observation of Microtubule Bending in Living LLC-PK1 Cells

To test the various models for MT bending in living cells, we directly observed MT bending dynamics in the periphery of LLC-PK1 cells (n = 6 cells, 125 individual MTs). Figure 2A shows a representative peripheral region of an LLC-PK1α cell stably transfected with GFP-α-tubulin (Rusan et al., 2001). Consistent with a recent report by Brangwynne et al. (2006), we found that some MTs exhibited short wavelength bending (Figure 2B), suggesting that the MTs were compressively loaded and laterally reinforced. However, we often observed that highly buckled MTs were directly adjacent to relatively straight MTs (Figure 2B), indicating that only a subset of MTs undergo short wavelength buckling at any one time.

Because the MTs in LLC-PK1 cells exhibit dynamic instability in the periphery, we considered whether MT polymerization generates endwise compressive loading on the MT as the growing plus end impinges on the cell margin. Growing MTs could transiently support compressive loads until the plus end undergoes catastrophe and the MT relaxes. However, we noted on occasion that a buckled MT increased its bending during depolymerization (Figure 2C and Supplemental Movie 2C). This observation indicates that an additional force independent of polymerization can act on the MTs.

We also observed that highly bent, depolymerizing MTs rapidly relax once the plus end depolymerized past a specific point in the cell (Figure 2D and Supplemental Movie 2D). These events suggest that the MT is cross-linked to some other static structure, possibly the cortical F-actin network, at specific points along its length. On depolymerizing past these cross-linking points, the attachment is lost and the MT tip region is free to relax and it rapidly straightens out. During relaxation, the velocity of the tip reaches velocities greater than 5 μm/s, suggesting that the MT is indeed stiff (relaxation time of the bend shown in Figure 2D is <0.2 s). This observation also suggests the idea that MT cross-links are important in sustaining MT bending.

Actomyosin Contractility

Because actomyosin contractility has been reported to buckle and break MTs (Waterman-Storer and Salmon, 1997; Gupton et al., 2002; Brangwynne et al., 2006), we directly imaged actin dynamics to determine its contribution to MT bending in LLC-PK1 cells. As shown in Figure 3A (and Supplemental Movies 3A1 and 3A2), we found that F-actin is nearly stationary, whereas MTs are simultaneously observed to deform. This time series indicates that microtubules are bending and buckling without attendant actin-based motion. In addition, we performed a kymographic analysis of mCherry-actin transfected LLC-PK1 cells. Figure 3C shows a kymograph from the cell shown in Figure 3B (and Supplemental Movie 3B) with an actin retrograde flow velocity of 6.9 ± 0.6 nm/s (n = 4 cells) to be on the time scales of seconds which compares well with the values reported by Gupton et al. (2002). To further test the role of actomyosin contractility, we inhibited myosin II ATPase activity with blebbistatin. Figure 4 shows a cell before and after treatment (t ∼15 min) with blebbistatin. MTs are highly bent in both cases, providing further evidence that actomyosin contractility does not play a major role in forming these deformations. We conclude that, at least for LLC-PK1 cells adhered to a glass substrate, F-actin–based retrograde flow is too slow to drive the fast MT bending and unbending dynamics observed experimentally.

Figure 3.

Figure 3.

Open in a new tab

F-actin and microtubule dynamics in LLC-PK1 cells. (A) The top two images from the montage show the first frame in a time series of actin (left) and tubulin (right) channels in a typical cell dually labeled with mCherry-actin and EGFP-tubulin. The middle frames show both actin and microtubule dynamics, respectively, at frame 50. The bottom frames show 50 consecutive frames of actin and microtubule dynamics, respectively, compressed into one image via a max projection (1 min 38 s elapsed time). Note that specific features (shown with red arrows) in the actin channel seem very similar in the before and after images, suggesting that actin does not move significantly over the time of the movie. In addition, the max projection image shows virtually no blurring of the actin channel due to F-actin movement. This stands in contrast to the tubulin channel before and after images where significant redistribution of the MT array results in completely different images. In addition, the max projection in the tubulin channel shows marked blurring of individual microtubules arising from movement of individual MTs during the course of the movie. (B) Typical image from an mCherry-actin–labeled LLC-PK1 cell. Time-lapse images were taken every 400 ms, and a kymograph (C) of F-actin motion was made. The white rectangle in B shows the region from which the kymograph in C was created. The F-actin kymograph shows that the actin retrograde flow is very small (∼7 nm/s), which is too slow to drive MT bending. Horizontal bar, 5 μm (A) and 3 μm (B and C). Vertical bar, 10 s (C).

Figure 4.

Figure 4.

Open in a new tab

Microtubule deformation in the absence of myosin II activity. (A) The image from a GFP-tubulin–labeled LLC-PK1 epithelial cell showing the distribution and the bending of microtubules near the cell periphery before the drug treatment. (B) The image of the same cell 15 min after the addition of blebbistatin. Time (minutes) is in relation to the addition of blebbistatin at a concentration of 75 μM. Horizontal bar, 5 μm.

Kymographics Analysis of Microtubule Buckling

The addition of αβ-tubulin heterodimeric subunits to the tip of a growing MT generates enough force to buckle MTs in vitro (Dogterom and Yurke, 1997; Janson et al., 2003; Janson and Dogterom, 2004). To determine whether polymerization forces result in large scale MT bending in vivo, we observed individual buckling events and used fluorescent speckle microscopy to record motion and deformation of the MT. The motion of MTs provides evidence for the direction of the net applied force; for the case of polymerization-based loading, the force is applied at the plus end and acts to push the MT retrogradely toward the center of the cell (Figure 1A). For a MT to buckle, there must exist nearly stationary cross-links that resist the polymerization force. Specifically, for polymerization forces to yield significant buckling, the distal portion of the MT, i.e., the plus end, must move backward at some velocity and be resisted by a slower moving (or even stationary) proximal portion of the MT (Figure 1A). We measured the velocity gradient of individual buckling events via a kymographic analysis of speckled MTs (Figure 5 and Supplemental Movie 5A) and found that polymerization-based forces rarely buckle MTs. Instead, we found that most of the large-scale buckling events originate when the proximal portion of the MT is transported anterogradely against a nearly stationary distal tip (Figure 5B). The anterograde transport of MTs is the opposite of the expected behavior for both MT polymerization-based buckling (Figure 1A) and acto-myosin contractility (Figure 1B). It is also not consistent with the scenarios depicted in Figure 1C2a and 1C2b, where the MT is transported retrogradely by molecular motors. The observed motion shows that MT bending is driven by anterograde transport of MTs distally against a stationary tip (as shown in Figure 1C1a and 1C1b). It is important to note that since the minus ends of the microtubules are difficult to identify, it is plausible that the microtubules that are transported anterogradely are fragments that are released from the centrosome.

Figure 5.

Figure 5.

Open in a new tab

MT bending dynamics in LLC-PK1 Cells. (A) Montage of a speckled MT bending and unbending. The white box represents the region from which the kymograph is created. Note that the white box is sufficiently wide so that it encompasses the entire bending microtubule for the duration of the movie. Bar, 3 μm. (B) Kymograph of the speckled microtubule in A showing that anterograde transport of the proximal microtubule coupled with a stationary distal plus end drives MT bending. Magenta arrow indicates t = 18 s from A.

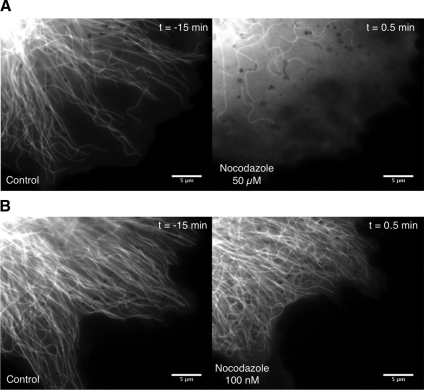
To further clarify the role of polymerization in causing the observed MT bends, we treated the cells with nocodazole to suppress dynamic instability. Figure 6A shows cells before and after (t ∼ 15 min) treatment in 50 μM nocodazole. At such a high concentration of the drug, aside from a few MTs near the cell center, most of the MTs depolymerized. The remaining MTs near the center still exhibited dynamic bending events. In the cells that are treated with 100 nM nocodazole (Figure 6B), MTs were observed to have nondynamic tips or they occasionally went through rapid depolymerization. As shown in Figure 6B, the MT deformations that are observed are qualitatively similar before and after the drug treatment. Once again, we observed dynamic bending events after the drug treatment that resulted in anterograde transport. A montage from a nondynamic buckled microtubule being transported anterogradely after nocodazole treatment is shown in Figure 7A (see also Supplemental Movie 7). As the kymograph in Figure 7B shows, the speckles along the microtubule move anterogradely toward a stationary distal tip (t = 12 s and t = 60 s).

Figure 6.

Figure 6.

Open in a new tab

Microtubule deformation in the absence of polymerization. Distribution of microtubules in the periphery of GFP-tubulin–labeled LLC-PK1 epithelial cells is shown before and after exposure to different concentrations of the drug nocodazole. (A) Nocodazole is used at 50 μM. (B) Nocodazole is used at 100 nM. Time (minutes) is in relation to the addition of nocodazole. Horizontal bar, 5 μm.

Figure 7.

Figure 7.

Open in a new tab

Bending dynamics of nonpolymerizing MTs in LLC-PK1 cells. Nocodazole at a concentration of 100 nM is used to suppress dynamic instability. (A) Montage of a speckled MT being transported anterogradely. The white box represents the region from which the kymograph is created. The blue and red boxes denote frames that correspond to t = 12 and t = 60 s, respectively. Bar, 3 μm. (B) Kymograph of the microtubule in A showing the anterograde transport of the proximal microtubule at two different times, t = 12 s (shown by the blue arrow) and t = 60 s (shown by the red arrow), against a stationary distal plus end (yellow line).

Figure 8A shows a histogram of the observed buckling mechanisms in microtubules (obtained using n = 33 MTs). The majority of the buckles observed (n = 21) are consistent with a mechanism in which the proximal portion of the microtubule is transported anterogradely against a stationary distal tip. We have also assessed the different MT transport mechanisms using the whole ensemble of buckled and unbuckled MTs. As shown in Figure 8B (obtained using n = 77 MTs), most of MT transport is anterograde (n = 33), whereas some MT transport is retrograde (n = 12) or bidirectional (n = 14). In the set of MTs used in the kymographic analysis, n = 18 were static. Although we cannot conclusively rule out a possible role of an actin-based motor such as myosin V (Figure 1C1b), we favor the idea that a MT-based motor such as dynein (Figure 1C1a) generates the dominant MT buckling forces in the periphery of LLC-PK1 cells. Assuming microtubule based motors play an important role, our results suggest that upon inhibition of the activity of a motor like dynein, the distribution will shift toward more retrograde transport, and similarly, the down-regulation of a motor like kinesin will result in more microtubules being transported anterogradely.

Figure 8.

Figure 8.

Open in a new tab

Microtubule bending mechanisms and transport direction. (A) Histogram of microtubule bending mechanisms from kymographic analysis of deforming microtubules (n = 33 MTs). Blue shows the number of MTs in which the proximal portion of the microtubule is being transported anterogradely against a stationary distal tip, whereas red shows the number of MTs in which the distal portion is being transported retrogradely against a stationary proximal portion, and magenta shows the number of both mechanisms working together to drive microtubule bending. (B) Histogram showing microtubule transport regardless of bend formation (n = 77 MTs). Green shows the number of microtubules that do not move over the observation period; blue and red show the number of microtubules that move in an anterograde and retrograde direction, respectively; and maroon shows the number of microtubules that move bidirectionally.

Molecular Motor-based Microtubule Gliding Assays In Vitro

The observations described in the previous section were consistent with a model in which MT-based motors generate the bending of MTs observed in vivo. If this model is correct, the bending dynamics observed in vivo should be reproduced in an in vitro motor gliding assay, provided that some of the purified motors can bind MTs but not retain motor function. Using a kinesin (Drosophila melanogaster kinesin heavy chain [dmKHC] dimers with hexa-his tag) gliding assay (Figure 9A), we observed the generation and dissipation of MT bending in a manner that qualitatively resembled that observed in vivo. The leading tip of gliding microtubules occasionally became stuck, while the rest of the MT continued to glide along the surface, resulting in the buildup of curvature qualitatively similar to that observed in vivo. An example of this type of bending is shown in Figure 9B (also see Supplemental Movie 9B). We also observed that highly curved MTs rapidly relax after their trailing end glided over a putative attachment site. An example of this type of relaxation is shown in Figure 9C (also see Supplemental Movie 9C); it is qualitatively similar to the relaxation behavior seen in living cells, as shown in Figure 2D.

Figure 9.

Figure 9.

Open in a new tab

MTs in gliding assays in vitro. (A) Typical digital image of a MT-kinesin gliding assay. Some MTs are highly bent, whereas other MTs are relatively straight, and MTs qualitatively seem to be deformed in a manner similar to that shown in vivo (see Figure 2A). (B) MT gliding in the direction of the arrow is cross-linked, presumably by a dead motor, at its leading tip for the first three frames while curvature develops in the MT. In the fourth and subsequent frames, the cross-link is lost, and the MT springs forward. Arrowheads denote the position of the putative cross-link. (C) A bent MT gliding in the direction of the arrow, glides past a cross-link site (arrowhead), and rapidly relaxes similar to the relaxing MT in Figure 2D. Bar, 3 μm.

Microtubule Curvature Distributions

To investigate the observed bends in MTs quantitatively, we measured the MT curvature distribution. We identified a collection of MTs from digital fluorescence images that clearly showed individual MTs in the periphery of living LLC-PK1 epithelial cells and then used our semiautomated algorithm to determine coordinates and construct the curvature distributions. Figure 2B shows a typical contour along a MT used to construct the curvature distribution. Individual MTs were selected and tracked from their tips back to a point where their shapes became ambiguous due to cross-over with other MTs.

If MT bending is driven by thermal forces (or by forces that are effectively thermal), then the distribution of curvatures should be Gaussian (Bicek et al., 2007). We found, as shown in Figure 10, that the in vivo curvature distribution has the characteristics of an exponential (and can be approximated with a biexponential function; data not shown), rather than the Gaussian distribution expected of a thermally driven polymer (shown with dashed line in Figure 10). The observed distribution is not an artifact of the image collection and analysis method, since we have validated our approach against a computational model of thermally fluctuating semiflexible polymers (Bicek et al., 2007). In our previous work (Bicek et al., 2007), we applied the model-convolution technique (Sprague et al., 2003, 2004; Bicek et al., 2007; Gardner et al., 2007) to the simulated MTs, thereby reproducing the effects of the point-spread function of the microscope and noise from the digital image acquisition process inherent in our microscope/camera system. We then showed that the observation of a thermally driven polymer via our experimental apparatus (accounting for the observed blur, digitization, and noise levels) and image analysis method will indeed result in the observation of a Gaussian curvature distribution if the data are collected at the proper spacing between coordinates (Bicek et al., 2007).

Figure 10.

Figure 10.

Open in a new tab

MT curvature distribution in living cells and gliding assays. MT bending in LLC-PK1 cells was quantified and the curvature distribution was constructed using n = 125 individual MTs from n = 6 cells. A spacing of 16 pixels corresponding to 0.67 μm was used. The curvature distributions in vivo and in vitro are shown in black and red, respectively. The experimental curvature distribution was compared with a thermal model (Gaussian) of MT bending using the flexural rigidity of Taxol-stabilized MTs (EI ∼2 pN-m2) and showed poor agreement (shown in dashed lines), especially in the tail of the distribution.

We observed more high curvatures (deformed MTs) in vivo, than expected from thermal fluctuations alone, as demonstrated by the Gaussian curve in Figure 10. While plotting the Gaussian curve in Figure 10, we used the flexural rigidity for Taxol-stabilized MTs in vitro. Note that, not only is the observed functional form different, but also that MTs in vivo would have to be much softer than in vitro MTs to have similar magnitudes in the curvature distribution. This result clearly shows that thermal forces cannot be a dominant source of bending and argues that MT softening alone cannot account for the observed high curvatures in living cells. Although MT-associated proteins can potentially bind and soften MTs, this possibility seems unlikely because it requires a large change in the material properties of MTs, whose composition and lattice structure in vivo is thought to be very similar to its composition and lattice structure in vitro. In addition, the rapid relaxation behavior of some depolymerizing MT tips further supports the view that the flexural rigidity in vivo is similar to that measured in vitro (shown in Figure 2D and Supplemental Movie 2D).

We also considered the effects of a length-dependent flexural rigidity, as recently suggested from in vitro studies (Pampaloni et al., 2006; Taute et al., 2008). If the MTs in our data set were composed of two populations, each with a different flexural rigidity, and driven only by thermal forces, the resulting curvature distribution would be the sum of two Gaussians. Such a distribution has a concave downward form in the tail, and will not able to explain the exponential tail shown in Figure 10. We therefore conclude that length-dependent changes in EI do not play a significant role in LLC-PK1 cells.

To compare with a much simpler model system, we measured the curvature distribution of the MTs in gliding assays in vitro, and we found essentially quantitative agreement between the in vitro and in vivo MT curvature distributions, as shown in Figure 10. Such agreement further supports a model where MT-based motor forces are the major driver of bending in LLC-PK1 epithelial cells.

DISCUSSION

In this study, we systematically investigated the origin of the forces that drive MT bending in living epithelial cells. This is important, because it gives insight into how the cell regulates the MT cytoskeleton, and potentially how the cell reacts to mechanical forces. We considered known force generation mechanisms, namely, acto-myosin contractility, polymerization forces, and MT- and actin-based motor forces. Our results show that anterograde MT transport, presumably mediated by MT-based motors, plays a dominant role in MT bending, whereas the other mechanisms are largely inconsequential in LLC-PK1 cells. Further experiments are necessary to determine the applicability of our results to different cell lines.

Analysis of Microtubule and F-Actin Motion

Previous work has demonstrated close correlation between the retrograde flow of F-actin and the buckling of MTs (Waterman-Storer and Salmon, 1997; Gupton et al., 2002). In addition, MTs are clearly observed to bend as they polymerize against the edge of the cell or a microfabricated barrier (Dogterom and Yurke, 1997; Waterman-Storer and Salmon, 1997). In the present study, the kymographic analysis of speckled F-actin features and MTs (Figures 3C and 5B) provides a direct method to determine the site of application and direction of active intracellular forces. Both F-actin retrograde flow and MT polymerization forces result in compressive loading of the MT. These forces act by pushing the distal segment of the MT retrogradely against a stationary, or at least a slower moving, proximal segment of the MT. In either case, the distal MT tip and its associated fluorescent speckles move retrogradely. This feature is diagnostic when screening for the origin of forces that produce MT motion, such that any force that originates within the cell interior and pushes the proximal portion of the MT outward anterogradely cannot be the result of either MT polymerization at the distal plus end or F-actin retrograde flow. Anterograde MT motion originating from within the cell body that pushes the proximal MT segments forward, while the distal segments remain stationary contradicts both the F-actin retrograde flow and MT polymerization models for MT bending in LLC-PK1 cells. Instead, our findings rather imply that the anterograde speckle movement of the proximal MT segment against a stationary distal MT segment is motor based and that the MTs are transported anterogradely against passive cross-links that hold the distal segment stationary. Our results are also consistent with earlier studies of neuronal growth cones (Schaefer et al., 2002) in which microtubules were observed to buckle during anterograde transport.

Evidence for Microtubule-based Motor-driven Buckling

The quantitative similarity between curvature distributions in the in vitro MT gliding assays and the in vivo data are remarkable. This is interesting because in this simple in vitro system, in which only thermally fluctuating, nongrowing MTs and MT-based motors are present, the curvature distribution observed in a living cell is recapitulated. The non-Gaussian nature of the resulting curvature distribution indicates the presence of active forces of nonthermal origin, such as those caused by molecular motors. These results suggest that the cell is regulating the MT array via active force generators, consistent with previous observations (Koonce et al., 1999; Burakov et al., 2003; Malikov et al., 2004; Brito et al., 2005).

For active forces to deform MTs in the gliding assay, we speculate that some dead motors act as passive cross-linkers and resist the forces generated by functional motors, resulting in MT bending. Alternatively, the motors attached to the MT could act at slightly different rates, resulting in instabilities that are “grabbed” by other nearby motors, which may further amplify the curvature. Because in vitro motor preparations invariably have some fraction of dead motors in them, we favor the former explanation, but further work will be required to distinguish between these two possibilities.

Interestingly, because both living cells and gliding assays show evidence of highly curved MTs rapidly relaxing upon loss of attachment sites, similar mechanisms may be involved. This suggests that in living cells, the MT-based motors can act as both passive cross-links that resist transport and active force generators, an emerging theme in the molecular motor field (Tao et al., 2006; Saunders et al., 2007). Alternatively, there may be a second set of molecules that passively cross-link, most likely to the stationary F-actin cytoskeleton, such as ACF7 (Chishti et al., 1998; Kodama et al., 2003). The anterograde movement of the MTs suggests that the motor that drives bending is either dynein or a minus-end–directed kinesin.

Microtubule-based Mechanotransduction

The results presented here argue against a major cell-level passive structural function for interphase MTs in LLC-PK1 epithelial cells in which MTs act as compressive struts that resist actomyosin contractility. Instead, our results lead us to favor a role where mechanical forces act to control the spatial distribution of MTs in living cells. In this model, MTs are pushed and pulled around the cell mainly by MT-based motor forces (Figure 11), although other forces discussed above are also likely to contribute to varying degrees, perhaps more dominantly in other cells types or phases of the cell cycle. Our results also argue that forces are not only generated near the tips of the MTs but also in the middle regions of the cell, suggesting that the MT based motors, such as dynein, anchored at the actin rich cortex may act on MTs and deform them, as shown in Figure 11. Some of these forces can be accommodated by the repositioning or the deformation of the centrosome. Alternatively, the forces may exceed a threshold for detachment from the centrosome and lead to MT release (Keating et al., 1997; Piehl et al., 2004). If a MT becomes highly curved due to motor or other forces acting upon it, it is more likely to break or depolymerize (Waterman-Storer and Salmon, 1997), which, over time, would reorganize the MT array in a force-dependent manner (Odde et al., 1999). However, MT breaking may not be a widespread phenomenon, because we have rarely observed MT breaking in LLC-PK1 cells, even though the magnitude of the observed curvatures was similar to that in cells where breaking has been observed (Odde et al., 1999). Mechanically based regulation of the MT array raises the possibility that the MT array could act as a mechanosensory apparatus. Similar to motor-based forces, externally applied mechanical loads could result in changes to the MT distribution. Because MTs act as “railroad tracks” for the transport of intracellular cargo, and because they are also capable of providing signals at their tips via plus-end tracking proteins, a mechanical reorganization of the MT array could cause cellular cargo or plus-end–associated signaling molecules to be redirected to another cellular location. This process could lead to a mechanotransduction event and cause a mechanical force to result in a cellular response via the MT cytoskeleton.

Figure 11.

Figure 11.

Open in a new tab

Cartoon representation of microtubule bending and transport in an LLC-PK1 cell. The motor shown in (blue) is a minus-end–directed motor, such as dynein. A typical MT cross-linked at the distal tip, buckles as a result of the motor force. The MT based motors anchored at the actin rich cortex cause the deformation of the MTs in the middle regions of the cell. The force on the given MT is presumably balanced by cross-links on MTs on the other side of the cell. Some of these forces can also presumably be accommodated by the centrosome or linkages to it.

Supplementary Material

[Supplemental Materials]
E08-09-0909_index.html (1.3KB, html)

ACKNOWLEDGMENTS

We thank Dr. Patricia Wadsworth (University of Massachusetts, Amherst, MA) for kindly supplying the LLC-PK1α cell line and Dr. Roger Y. Tsien (University of California, San Diego, La Jolla, CA) for the mCherry-actin. E. T. acknowledges support from the Institute for Mathematics and Its Applications post-doctoral fellowship, D.M.K. acknowledges support from the National Science Foundation (grant DMR-0513393) and D.J.O. acknowledges support from the National Science Foundation (grant MCB-0615568).

Abbreviations used:

MT

microtubule.

Footnotes

This article was published online ahead of print in MBC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E08-09-0909) on April 29, 2009.

REFERENCES

  1. Amos L. A., Amos W. B. The bending of sliding microtubules imaged by confocal light microscopy and negative stain electron microscopy. J. Cell Sci. Suppl. 1991;14:95–101. doi: 10.1242/jcs.1991.supplement_14.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baas P. W., Karabay A., Qiang L. Microtubules cut and run. Trends Cell Biol. 2005;15:518–524. doi: 10.1016/j.tcb.2005.08.004. [DOI] [PubMed] [Google Scholar]
  3. Baas P. W., Nadar, Vidya C., Myers K. A. Axonal transport of microtubules: the long and short of it. Traffic. 2006;7:490–498. doi: 10.1111/j.1600-0854.2006.00392.x. [DOI] [PubMed] [Google Scholar]
  4. Bicek A. D., Tüzel E., Kroll D. M., Odde D. J. Analysis of microtubule curvature. Methods Cell Biol. 2007;83:237–268. doi: 10.1016/S0091-679X(07)83010-X. [DOI] [PubMed] [Google Scholar]
  5. Brangwynne C. P., MacKintosh F. C., Kumar S., Giesse N. A., Talbot J., Mahadevan L., Parker K. P., Ingber D. E., Weitz D. A. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell. Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brito D. A., Strauss J., Magidson V., Tikhonenko I., Khodjakov A., Koonce M. P. Pushing forces drive the comet-like motility of microtubule arrays in Dictyostelium. Mol. Biol. Cell. 2005;16:3334–3340. doi: 10.1091/mbc.E05-01-0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Burakov A., Nadezhdina E., Slepchenko B., Rodionov V. Centrosome positioning in interphase cells. J. Cell. Biol. 2003;162:963–969. doi: 10.1083/jcb.200305082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Buxbaum R. E., Heidemann S. R. A thermodynamic model for force integration and microtubule assembly during axonal elongation. J. Theor. Biol. 1988;134:379–390. doi: 10.1016/s0022-5193(88)80068-7. [DOI] [PubMed] [Google Scholar]
  9. Chishti A. H., et al. The FERM domain: a unique module involved in the linkage of cytoplasmic proteins to the membrane. Trends Biochem. Sci. 1998;23:281–282. doi: 10.1016/s0968-0004(98)01237-7. [DOI] [PubMed] [Google Scholar]
  10. Dogterom M., Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
  11. Dujardin D. L., Barnhart L. E., Stehman S. A., Gomes E. R., Gundersen G. G., Vallee R. B. A role for cytoplasmic dynein and LIS1 in directed cell movement. J. Cell. Biol. 2003;163:1205–1211. doi: 10.1083/jcb.200310097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ferenz N. P., Wadsworth P. Prophase microtubule arrays undergo Flux-like behavior in mammalian cells. Mol. Biol. Cell. 2007;18:3993–4002. doi: 10.1091/mbc.E07-05-0420. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Forscher P., Smith S. J. Actions of cytochalasins on the organization of actin filaments and microtubules in a neuronal growth cone. J. Cell Biol. 1988;107:1505–1516. doi: 10.1083/jcb.107.4.1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gardner M. K., Odde D. J., Bloom K. Hypothesis testing via integrated computer modeling and digital fluorescence microscopy. Methods. 2007;41:232–237. doi: 10.1016/j.ymeth.2006.08.002. [DOI] [PubMed] [Google Scholar]
  15. Gittes F., Mickey B., Nettleton J., Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell. Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gundersen G. G., Gomes E. R., Wen Y. Cortical control of microtubule stability and polarization. Curr. Opin. Cell Biol. 2004;16:106–112. doi: 10.1016/j.ceb.2003.11.010. [DOI] [PubMed] [Google Scholar]
  17. Gupton S. L., Salmon W. C., Waterman-Storer C. M. Converging populations of F-actin promote breakage of associated microtubules to spatially regulate microtubule turnover in migrating cells. Curr. Biol. 2002;12:1891–1899. doi: 10.1016/s0960-9822(02)01276-9. [DOI] [PubMed] [Google Scholar]
  18. Hancock W. O., Howard J. Processivity of the motor protein kinesin requires two heads. J. Cell. Biol. 1998;140:1395–1405. doi: 10.1083/jcb.140.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sunderland, MA: Sinauer Associates; 2001. [Google Scholar]
  20. Hyman A., Drechsel D., Kellogg D., Salser S., Sawin K., Steffen P., Wordeman L., Mitchison T. Preparation of modified tubulins. Methods Enzymol. 1991;196:478–485. doi: 10.1016/0076-6879(91)96041-o. [DOI] [PubMed] [Google Scholar]
  21. Ingber D. E. Cellular tensegrity: defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 1993;104:613–627. doi: 10.1242/jcs.104.3.613. [DOI] [PubMed] [Google Scholar]
  22. Ingber D. E. Tensegrity I. Cell structure and hierarchical systems biology. J. Cell Sci. 2003;116:1157–1173. doi: 10.1242/jcs.00359. [DOI] [PubMed] [Google Scholar]
  23. Ingber D. E., Heidemann S. R., Lamoureux P., Buxbaum R. E. Opposing views on tensegrity as a structural framework for understanding cell mechanics. J. Appl. Physiol. 2000;89:1663–1678. doi: 10.1152/jappl.2000.89.4.1663. [DOI] [PubMed] [Google Scholar]
  24. Janson M. E., Dogterom M. A bending mode analysis for growing microtubules: evidence for a velocity-dependent rigidity. Biophys. J. 2004;87:2723–2736. doi: 10.1529/biophysj.103.038877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Janson M. E., Dood, De M. E., Dogterom M. Dynamic instability of microtubules is regulated by force. J. Cell. Biol. 2003;161:1029–1034. doi: 10.1083/jcb.200301147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Keating T. J., Peloquin J. G., Rodionov V. I., Momcilovic D., Borisy G. G. Microtubule release from the centrosome. Proc. Natl. Acad. Sci. USA. 1997;94:5078–5083. doi: 10.1073/pnas.94.10.5078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kodama A., Karakesisoglou I., Wong E., Vaezi A., Fuchs E. ACF7 An essential integrator of microtubule dynamics. Cell. 2003;115:343–354. doi: 10.1016/s0092-8674(03)00813-4. [DOI] [PubMed] [Google Scholar]
  28. Koonce M. P., Köhler J., Neujahr R., Schwartz J.-M., Tikhonenko I., Gerisch G. Dynein motor regulation stabilizes interphase microtubule arrays and determines centrosome position. EMBO J. 1999;18:6786–6792. doi: 10.1093/emboj/18.23.6786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ligon L. A., Holzbaur E.L.F. Centrosome fragments and microtubules are transported asymmetrically away from division plane in anaphase. Traffic. 2007;8:808–819. [Google Scholar]
  30. Malikov V., Kashina A., Rodionov V. Cytoplasmic dynein nucleates microtubules to organize them into radial arrays in vivo. Mol. Biol. Cell. 2004;15:2742–2749. doi: 10.1091/mbc.E03-10-0770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Murthy K., Wadsworth P. Myosin-II-dependent localization and dynamics of F-Actin during cytokinesis. Curr. Biol. 2005;15:724–731. doi: 10.1016/j.cub.2005.02.055. [DOI] [PubMed] [Google Scholar]
  32. Odde D. J., Ma L., Briggs H., DeMarco A., Kirschner M. W. Microtubule bending and breaking in living fibroblast cells. J. Cell Sci. 1999;112:3283–3288. doi: 10.1242/jcs.112.19.3283. [DOI] [PubMed] [Google Scholar]
  33. Palazzo A. F., Joseph H. L., Chen Y.-J., Dujardin D. L., Alberts A. S., Pfister K. K., Vallee R. B., Gundersen G. G. Cdc42, dynein, and dynactin regulate MTOC reorientation independent of Rho-regulated microtubule stabilization. Curr. Biol. 2001;11:1536–1541. doi: 10.1016/s0960-9822(01)00475-4. [DOI] [PubMed] [Google Scholar]
  34. Pampaloni F., Lattanzi G., Jonas A., Surrey T., Frey E., Florin E.-L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA. 2006;103:10248–10253. doi: 10.1073/pnas.0603931103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Piehl M., Tulu U. S., Wadsworth P., Cassimeris L. Centrosome maturation: measurement of microtubule nucleation throughout the cell cycle by using GFP-tagged EB1. Proc. Natl. Acad. Sci. USA. 2004;101:1584–1588. doi: 10.1073/pnas.0308205100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rusan N. M., Fagerstrom C. J., Yvon A. M., Wadsworth P. Cell cycle dependent changes in microtubule dynamics in living cells expressing green fluorescent protein-alpha tubulin. Mol. Biol. Cell. 2001;12:971–980. doi: 10.1091/mbc.12.4.971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Salmon W. C., Adams M. C., Waterman-Storer C. M. Dual-wavelength fluorescent speckle microscopy reveals coupling of microtubule and actin movements in migrating cells. J. Cell. Biol. 2002;158:31–37. doi: 10.1083/jcb.200203022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Saunders A. M., Powers J., Strome S., Saxton W. M. Kinesin-5 acts as a brake in anaphase spindle elongation. Curr. Biol. 2007;17:R453–R454. doi: 10.1016/j.cub.2007.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Schaefer A. W., Kabir N., Forscher P. Filopodia and actin arcs guide the assembly and transport of two populations of microtubules with unique dynamic parameters in neuronal growth cones. J. Cell. Biol. 2002;158:139–152. doi: 10.1083/jcb.200203038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Shaner N. C., Campbell R. E., Steinbach P. A., Giepmans B.N.G., Palmer A. E., Tsien R. Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004;22:1567–1572. doi: 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
  41. Sprague B. L., Pearson C. G., Maddox P. S., Bloom K. S., Salmon E. D., Odde D. J. Mechanisms of microtubule-based kinetochore positioning in the yeast metaphase spindle. Biophys. J. 2003;84:3529–3546. doi: 10.1016/S0006-3495(03)75087-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Sprague B. L., Gardner M. K., Pearson C. G., Maddox P. S., Bloom K., Salmon E. D., Odde D. J. Model-convolution approach to modeling fluorescent protein dynamics. signals, systems and computers. Conference Record of the Thirty-Eighth Asilomar Conference; 2004. pp. 1821–1825. [Google Scholar]
  43. Stamenovic D., Mijailovich S. M., Tolic-Norrelykke I. M., Chen J., Wang N. Cell prestress. II. Contribution of microtubules. Am. J. Physiol. Cell Physiol. 2001;282:C617–C624. doi: 10.1152/ajpcell.00271.2001. [DOI] [PubMed] [Google Scholar]
  44. Tao L., Mogilner A., Civelekoglu-Scholey G., Wollman R., Evans J., Stahlberg H., Scholey J. M. A homotetrameric Kinesin-5, KLP61F, bundles microtubules and antagonizes Ncd in motility assays. Curr. Biol. 2006;16:2293–2302. doi: 10.1016/j.cub.2006.09.064. [DOI] [PubMed] [Google Scholar]
  45. Taute K. M., Pampaloni F., Frey E., Florin E.-L. Microtubule dynamics depart from the wormlike chain model. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.028102. 028102. [DOI] [PubMed] [Google Scholar]
  46. Tran P. T., Marsh L., Doye V., Inoue S., Chang F. A mechanism for nuclear positioning in fission yeast based on microtubule pushing. J. Cell. Biol. 2001;153:397–411. doi: 10.1083/jcb.153.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. VanBuren V., Cassimeris L., Odde D. J. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys. J. 2005;89:2911–2926. doi: 10.1529/biophysj.105.060913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wang N., Butler J. P., Ingber D. E. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 1993;260:1124–1127. doi: 10.1126/science.7684161. [DOI] [PubMed] [Google Scholar]
  49. Wang N., Naruse K., Stamenovic D., Fredberg J. J., Mijailovich S. M., Tolic-Norrelykke I. M., Polte T., Mannix R., Ingber D. E. Mechanical behavior in living cells consistent with the tensegrity model. Proc. Natl. Acad. Sci. USA. 2001;98:7765–7770. doi: 10.1073/pnas.141199598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Waterman-Storer C. M., Salmon E. D. Actomyosin-based retrograde flow of microtubules in the lamella of migrating epithelial cells influences microtubule dynamic instability and turnover and is associated with microtubule breakage and treadmilling. J. Cell. Biol. 1997;139:417–434. doi: 10.1083/jcb.139.2.417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Weiss D. G., Langford G. M., Seitz-Tutter D., Maile W. Analysis of the gliding, fishtailing and circling motions of native microtubules. Acta Histochem. Suppl. 1991;41:81–105. [PubMed] [Google Scholar]
  52. Williams R. C., Jr., Lee J. C. Preparation of tubulin from brain. Methods Enzymol. 1982;85:376–385. doi: 10.1016/0076-6879(82)85038-6. [DOI] [PubMed] [Google Scholar]
  53. Zhou F. Q., Waterman-Storer C. M., Cohan C. S. Focal loss of actin bundles causes microtubule redistribution and growth cone turning. J. Cell. Biol. 2002;157:839–849. doi: 10.1083/jcb.200112014. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental Materials]
E08-09-0909_index.html (1.3KB, html)
Download video file (308.5KB, mov)
Download video file (423KB, mov)
Download video file (2.7MB, mov)
Download video file (1.7MB, mov)
Download video file (8.1MB, mov)
Download video file (2MB, mov)
Download video file (1.3MB, mov)
Download video file (1.4MB, mov)
Download video file (3.8MB, mov)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES