Phase I to II Cross-Induction of Xenobiotic Metabolizing Enzymes: a Feedforward Control Mechanism for Potential Hormetic Responses

Abstract

Hormetic responses to xenobiotic exposure likely occur as a result of overcompensation by the homeostatic control systems operating in biological organisms. However, the mechanisms underlying overcompensation that leads to hormesis are still unclear. A well-known homeostatic circuit in the cell is the gene induction network comprising phase I, II and III metabolizing enzymes, which are responsible for xenobiotic detoxification, and in many cases, bioactivation. By formulating a differential equation-based computational model, we investigated in this study whether hormesis can arise from the operation of this gene/enzyme network. The model consists of two feedback and one feedforward controls. With the phase I negative feedback control, xenobiotic X activates nuclear receptors to induce cytochrome P450 enzyme, which bioactivates X into a reactive metabolite X′. With the phase II negative feedback control, X′ activates transcription factor Nrf2 to induce phase II enzymes such as glutathione S-transferase and glutamate cysteine ligase, etc., which participate in a set of reactions that lead to the metabolism of X′ into a less toxic conjugate X″. The feedforward control involves phase I to II cross-induction, in which the parent chemical X can also induce phase II enzymes directly through the nuclear receptor and indirectly through transcriptionally upregulating Nrf2. As a result of the active feedforward control, a steady-state hormetic relationship readily arises between the concentrations of the reactive metabolite X′ and the extracellular parent chemical X to which the cell is exposed. The shape of dose response evolves over time from initially monotonically increasing to J-shaped at the final steady state - a temporal sequence consistent with adaptation-mediated hormesis. The magnitude of the hormetic response is enhanced by increases in the feedforward gain, but attenuated by increases in the bioactivation or phase II feedback loop gains. Our study suggests a possibly common mechanism for the hormetic responses observed with many mutagens/carcinogens whose activities require bioactivation by phase I enzymes. Feedforward control, often operating in combination with negative feedback regulation in a homeostatic system, may be a general control theme responsible for steady-state hormesis.

Introduction

Hormesis is defined as a biological dose-response that exhibits nonmonotonic behavior. At low doses, the endpoint response either increases or decreases from the baseline level; at high doses, the response changes its direction, forming a U- or inverted U-shaped curve (Calabrese et al., 2007). While nonmonotonic biological response may have diverse mechanistic bases (Conolly and Lutz, 2004), hormesis is believed to occur as a result of adaptation of a biological system to stressor-imposed perturbations (Stebbing, 2003; Calabrese, 2008). To ensure robust biological functions at various levels of their organization, living organisms are equipped with a variety of homeostatic defense mechanisms that are activated under stressful conditions to compensate for the undesirable perturbations (Kitano, 2004). At low stressor doses, the compensatory mechanism may overreact to some extent, resulting in a net response that is opposite to the change initially brought about by the stressor; at higher doses, the compensatory mechanism is overwhelmed, leading to a reversal of the response (Calabrese, 2001). Despite the straightforwardness of this overcompensation hypothesis, control systems underlying homeostasis and adaptive response that can result in overcompensation at low doses remain poorly understood. The lack of detailed mechanistic understanding contributes, at least in part, to the current reluctance in adopting hormesis as an alternative risk assessment model, despite that the number of reports on hormesis has grown considerably. Use of mathematical models should help to uncover the operating principles employed by homeostatic control networks and to gain insight into the structural and parametric conditions that can give rise to hormetic responses.

Hormetic responses occur primarily under two exposure scenarios (Calabrese et al., 2007). In the first scenario, the biological system is continuously exposed to a relatively constant dose of a chemical or stressor of other types. The exposure is long enough that by the time the endpoint response is recorded the system is believed to have reached a steady state. This steady-state hormesis can be found in examples of mutagenesis and carcinogenesis induced by long-term exposure to a variety of chemicals (Camurri et al., 1983; Kitano et al., 1998; Masuda et al., 2001; Sukata et al., 2002; Kinoshita et al., 2003; Kushida et al., 2005; Puatanachokchai et al., 2006). Another frequently adopted exposure scenario involves two sequential dosing events – a priming or conditioning dose is followed by a fixed second dose, with the final overall response evaluated against the conditioning dose (Murry et al., 1986; Ikonomidis et al., 1997; de Mendonca et al., 2000; Koti et al., 2003; Fan et al., 2005; Tang et al., 2005). Hormetic effects arising from this scenario are referred to as conditioning hormesis. Given that homeostatic control networks, including those defending against cellular stresses, are primarily negative feedback mediated (Houk, 1988; Zhang and Andersen, 2007), it is tempting to ask whether activation of this type of network can result in hormesis. In theory negative feedback control alone may explain conditioning hormesis, as the compensatory mechanism can be activated by the conditioning dose to help moderate perturbations caused by subsequent exposures. However, negative feedback control, be it proportional or integral, is not expected to produce steady-state hormesis, because overcompensation is impossible to occur in theory when such a control system settles to a steady state. Steady-state hormesis is believed to have more bearings to human exposure to environmental toxicants, a situation usually characterized by chronic contact with a toxicant, often at low doses. Therefore it is imperative to study homeostatic control networks that are responsible for steady-state hormesis.

An important and common homeostatic system inside the cell is the phase I, II, and III families of xenobiotic metabolizing enzymes (XMEs) that control the intracellular levels of xenobiotics and their metabolites. This system consists of an array of enzymes that metabolize xenobiotics via various reactions and eventually export these metabolites from the cell (Xu et al., 2005; Nakata et al., 2006). With phase I negative feedback control, an xenobiotic may activate xenosensor molecules such as aryl hydrocarbon receptor (AhR), constitutive androstane receptor (CAR), or pregnane X receptor (PXR) to induce phase I enzymes including cytochrome P450 enzymes (CYP), which metabolize the parent chemical into an intermediate metabolite. With phase II negative feedback control, the metabolite may activate transcription factor Nrf2 to induce so-called phase II enzymes such as glutathione S-transferase (GST), glutamate cysteine ligase (GCL), and UDP-glucuronosyltransferase (UGT), etc. These enzymes participate in a set of reactions that add hydrophilic conjugates to the metabolite. Phase III enzymes, most of which are membrane-residing transporters and regulated at least in part by Nrf2, export the conjugated metabolite from the cell. Together, the phase I, II, and III XME detoxification system controls the amounts of xenobiotics and their metabolites that can accumulate in the cell, restricting their downstream toxicity.

Although the primary function of the phase I, II, and III XMEs is to detoxify and eliminate xenobiotics, some xenobiotics are activated in these processes, mainly via metabolism by phase I enzymes. It is estimated that about ¾ carcinogens are actually XME-bioactivated products from parent procarcinogens (Nebert and Dalton, 2006). Bioactivation by phase I enzymes often converts the xenobiotics into reactive metabolites, many of which are electrophilic and can undergo redox cycling to produce free radicals. These metabolites can react with DNA, protein, and lipids. DNA modification and damage may lead to mutation and carcinogenesis. However, electrophiles and reactive oxygen species are also produced during normal cell metabolism, and in some cases, from background exposure to environmental chemicals, thus establishing a baseline of reactive chemicals in the cell. Since the pool of reactive metabolites, derived both endogenously and exogenously, could be potentially harmful to cellular health, their concentrations need to be tightly controlled.

Homeostatic regulation of reactive metabolites is controlled primarily through negative feedback mediated by phase II enzymes that are induced by electrophilic compounds (Zhang and Andersen, 2007). Crosstalk is also present from phase I to phase II and even phase III enzyme activation (Kohle and Bock, 2006; Kohle and Bock, 2007). Specifically, many phase II enzymes including GST, UGT, sulfotransferases (SULT), NADPH-Quinone Oxidoreductase 1 (NQO1), and some phase III multidrug resistance-associated protein transporters (MRP) can be directly upregulated by parent xenobiotics through nuclear receptors such as AhR, CAR, and PXR (Paulson et al., 1990; Favreau and Pickett, 1991; Emi et al., 1996; Yueh et al., 2003; Ma et al., 2004; Maher et al., 2005; Sugatani et al., 2005; Jigorel et al., 2006; Chen et al., 2007). Recently Miao et al. has found that AhR, which is activated by chemicals from the polycyclic aromatic hydrocarbon family, can directly induce Nrf2 by increasing its transcription (Miao et al., 2005). This route of phase II enzyme and Nrf2 activation by parent xenobiotics, independent of the status of their reactive metabolites, constitutes an inhibitory feedforward control for the reactive metabolites coming out of bioactivation by phase I enzymes. The emerging scheme is thus that the reactive metabolites are controlled by both feedback and feedforward processes (Fig. 1). While the feedforward control may provide an evolutionary advantage for improved xenobiotic detoxification, we believe it may also generate hormetic dose response patterns in the intracellular level of the reactive metabolite pool. In turn such changes could result in hormesis in downstream toxicity including DNA damage and mutagenesis. Damage to macromolecules may also alter the proliferation rate through affecting the cell cycle engine and the cell death rate through affecting the apoptotic signaling pathway. Together, changes in mutagenesis, cell proliferation, and apoptosis may lead ultimately to nonlinear cellular responses, such as hormesis in carcinogenesis (Kinoshita et al., 2003). In the present study, we formulated a mathematical model of the generic phase I, II, and III control system with phase I to II enzyme cross-induction. We analyzed the conditions under which this system can produce hormetic dose response behaviors and evaluated the effects of the feedforward and phase I and II feedback control on the J-shaped dose response curves.

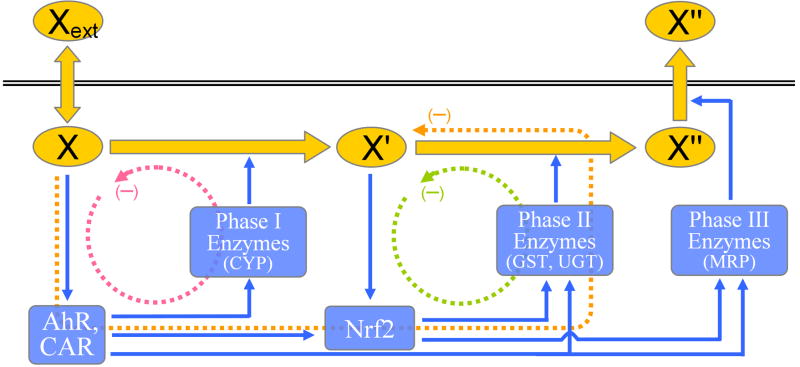
Figure 1.

Schematic representation of the phase I, II, and III xenobiotic control system. Phase I negative feedback (red dashed line) consists of xenobiotic X, nuclear receptors such as AhR, CAR, or PXR, and phase I enzymes such as cytochrome P450 (CYP). The feedback loop functions to increase the metabolism of X and thus reduce its intracellular accumulation. Operation of the feedback loop also results in increased production of metabolite X′ or bioactivation of X if X′ is reactive. Phase II negative feedback (green dashed line) consists of X′, Nrf2, and phase II enzymes such as GST and UGT, etc. The feedback loop functions to increase the metabolism of X′ and thus reduce its undesirable accumulation. Feedforward control via phase I to II cross-induction of phase II enzymes (orange dashed line) consists of X, nuclear receptors, Nrf2 and phase II enzymes. The feedforward control, driven directly by parent chemical X, functions to reduce undesirable accumulation of X′ that could be potentially reactive. X_ext: extracellular xenobiotic X; X: intracellular xenobiotic X; X′: reactive metabolite of X; X″: GSH conjugate of X′.

Methods

To test our hypothesis, we formulated an ordinary differential equation (ODE)-based generic model for the phase I, II and III xenobiotic homeostatic control system, by extending an existing model we developed previously that simulates the electrophilic stress response (Zhang and Andersen, 2007). The structure of the current model (Fig. 2) has both phase I and II feedback control and feedforward control.

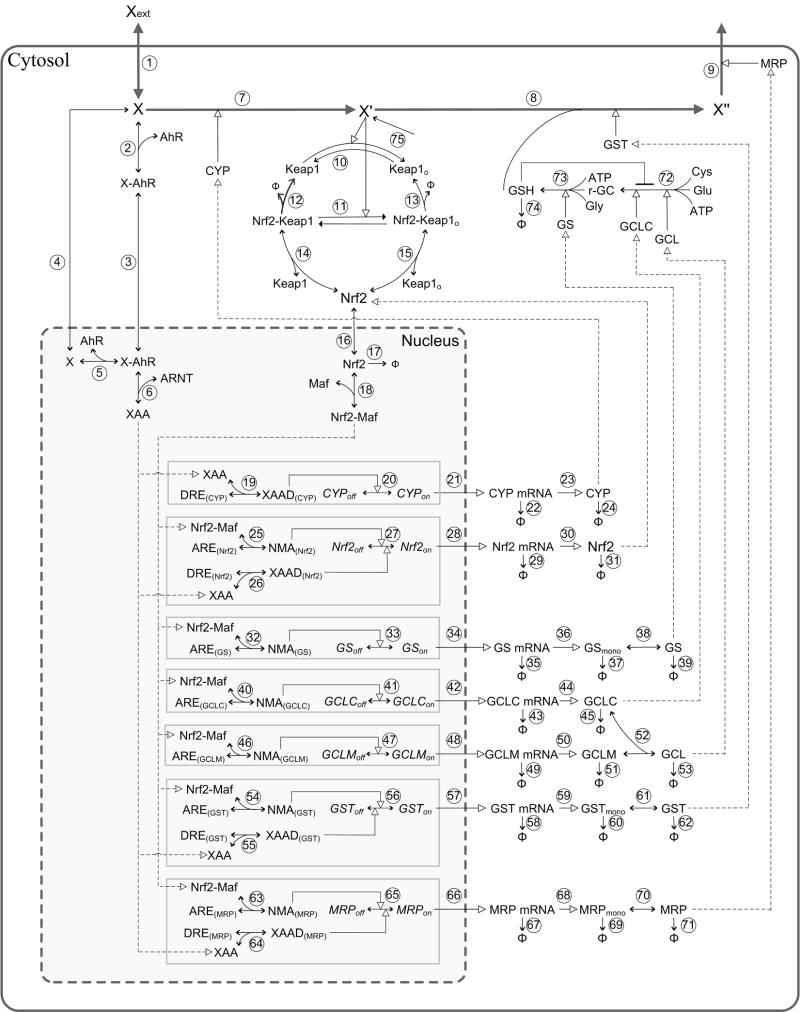
Figure 2.

Schematic diagram of the phase I, II, and III xenobiotic control model. Refer to Methods for general description of the control network, and Supplementary Materials (table S1 and S2) for synonyms and implementation details of the model. Dashed lines with empty arrow head indicate the flow of the controls within the network. The diagram was generated in PathwayLab (InNetics Inc., Linköping, Sweden).

Phase I feedback control

Lipophilic xenobiotic compound X such as those belonging to the polycyclic aromatic hydrocarbon family, diffuses freely through the cell membrane to enter the intracellular compartment (it is labeled as X_ext for its presence in the extracellular compartment). Inside the cell, X is metabolized by the existing basal phase I cytochrome P450 enzyme CYP into an intermediate metabolite X′. The parent chemical X also binds to nuclear receptor AhR (Although AhR system is used here as an example, the receptor can be CAR or PXR, etc., depending on the structure of the chemical. And it is not expected that parameter conditions associated with other type of receptors would change the results qualitatively.) in the cytosol and causes it to translocate to the nucleus. Inside the nucleus, AhR partners with aryl hydrocarbon receptor nuclear translocator (ARNT) to become a transcriptionally active heterodimer XAA (Reyes et al., 1992). The heterodimer then interacts with the dioxin response elements (DREs) in the promoter of CYP, inducing its gene transcription. The newly induced CYP enzyme joins the existing CYP pool to accelerate the metabolism of X into X′. This completes the phase I feedback control loop. By inducing CYP, the control loop functions to reduce intracellular accumulation of the parent chemical X, but it also enhances the production of the metabolite X′.

Phase II feedback control

In the model, X′ effectively represents a composite pool of reactive species that are derived both from bioactivation of xenobiotic X by CYP and from other electrophiles coming from basal cell metabolism and potential background exposure to chemicals. The latter two sources establish a baseline level of X′ in the model system. Because X′ is chemically reactive, its intracellular concentration needs to be tightly controlled and is the primary response endpoint in the present study. In the model, X′ is detoxified by covalently binding with glutathione (GSH) to form conjugated product X″, a reaction catalyzed by GST. The conjugate X″, presumably less reactive and more hydrophilic, is expelled out of the cell by the phase III transporter MRP. The reactive metabolite X′, owing to its electrophilic nature, can be detected by the molecular sensor Kelch-like ECH associating protein 1 (Keap1), which is a cytosolic cysteine-rich protein that promotes ubiquitination and eventual degradation of transcription factor Nrf2 (McMahon et al., 2003; Zhang and Hannink, 2003). A rise in the concentration of X′ leads to an increase in the degree of conjugation/oxidization of certain key cysteine residues in Keap1, rendering Keap1 less capable of targeting Nrf2 for ubiquitination and subsequent degradation (Hong et al., 2005; Kobayashi et al., 2006). The ensuing stabilization of Nrf2 results in its accumulation in the cytosol and translocation into the nucleus. In the nucleus, it is thought that Nrf2 partners with small Maf proteins to form a heterodimer Nrf2-Maf (Katsuoka et al., 2005). The latter is able to bind to the antioxidant response elements (AREs) in the promoter regions of multiple phase II and III genes, including glutamate cysteine ligase catalytic subunit (GCLC), glutamate cysteine ligase modifier subunit (GCLM), glutathione synthetase (GS), GST, as well as MRP, to upregulate their transcription (Hayashi et al., 2003; Dickinson et al., 2004; Lee et al., 2005; Maher et al., 2005; Zhu et al., 2005). The enhanced expression of GCLC and GCLM results in increased formation of the holoenzyme GCL, which, together with GS, participates in two sequential reactions to synthesize GSH de novo. GST functions to detoxify the reactive metabolite X′ into a conjugate X″, using GSH as a co-substrate. This completes the phase II feedback control loop, which operates to reduce the intracellular concentration of the reactive metabolite X′.

Feedforward control

While the nuclear receptor AhR, as activated by the parent chemical X, induces phase I enzyme CYP, it can also upregulate genes that are components of the phase II xenobiotic metabolizing system (Kohle and Bock, 2006; Kohle and Bock, 2007). In our model, we implemented this phase I to II cross-induction in two ways, in accordance to the literature. First, there are DREs in the promoter of GST gene, so that X can directly upregulate its expression via AhR (Paulson et al., 1990; Miao et al., 2003). Second, DREs are also present in the promoter of Nrf2 gene, thus X can directly regulate Nrf2 transcription via an AhR-mediated mechanism (Miao et al., 2005). The latter pathway allows the parent chemical X to induce gene expression of phase II enzyme GCLC, GCLM, GS, and GST indirectly through Nrf2. Through the direct and indirect phase I to II cross-induction, the parent chemical X can regulate the detoxification of its own metabolite X′, constituting a feedforward control for the intracellular concentration of X′. An AhR-mediated induction of phase III transporter MRP is also included in the model.

We did not consider diffusion of X′ out of the cell, given that phase I and II enzymes are usually closely situated on the membrane of the endoplasmic reticulum. Thus as soon as the intermediate metabolites are produced by phase I enzymes, conceivably they are taken up by phase II enzymes immediately for conjugation. Details of the reactions, parameter values, and ODEs for the model are provided in the supplementary Table S1 and S2, which also contain rationales and references for the choices of parameter values. Whenever possible, parameter values were obtained or derived from studies in the literature covering various chemicals and cell types, based on the general assumption that biochemical reactions proceed in similar fashions regardless of the nature of chemicals that initiate the responses. Some parameter values were estimated by constraining the model with relevant experimental data from the literature. For parameters that cannot be obtained, derived, or estimated, their values were set based on our best scientific judgment. To visually evaluate their effects on the response curve, sensitivity analyses were performed by increasing and decreasing the values of these parameters by 2-fold (Fig. S1). It is clear that in spite of some obvious variations in the steady-state X′ vs. X_ext dose response curve, as caused by the most sensitive parameters, in all cases the J-shaped profile of the curve, which is the focus of the present study, was retained. The model was first constructed and parameterized in PathwayLab (InNetics Inc., Linköping, Sweden) and then exported into MatLab (The MathWorks, Inc., Natick, MA, USA) for final simulation and analysis. Models in the format of MatLab and SBML are available for downloading as supplementary materials.

Results

Dynamics of the control system and hormetic response

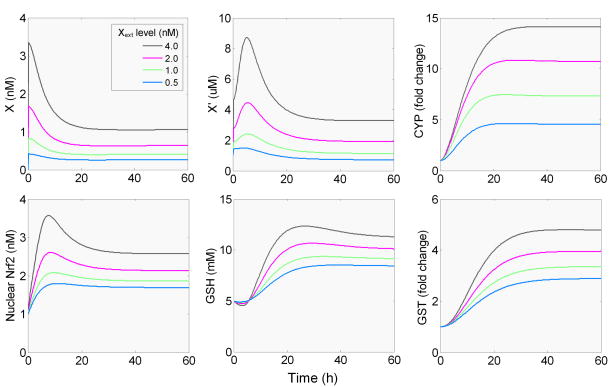
Numerical simulation of the phase I, II, and III control network (conceptualized in Fig. 1 and detailed in Fig. 2) generates a dynamic response that is typical of an adaptive system (Fig. 3). Upon continuous exposure to the xenobiotic X_ext at a constant dose, the concentration of the intracellular X rises almost instantaneously as a result of its diffusion through the cell membrane. This is followed by a steady decline as the receptor-mediated induction of CYP is initiated, which, in a feedback manner, reduces the accumulation of X by catalyzing its metabolism. X eventually settles at a new steady-state concentration that positively correlates to the dose of X_ext. X′, the reactive metabolite, also rises sharply from its baseline level as the preexisting, constitutively expressed CYP quickly metabolizes X into X′. In this case, the baseline level of X′ is generated by basal cell metabolism. With the induction of CYP, more X′ is produced, thus X′ continues to accumulate albeit at a slower rate. After reaching a peak, X′ begins to decline as a result of induction of phase II enzymes including GST, GCL, and GS here. The reactive metabolite X′ finally settles to a new steady state. Although at high X_ext doses, the steady-state concentration of X′ is above the baseline (1 μM), at low X_ext doses, X′ tends to settle at below-baseline levels, indicating a hormetic change. Intracellular GSH initially decreases as it is consumed by X′ through GST-catalyzed conjugation. But the decline is soon reversed as GCL and GS, the two GSH-synthesizing enzymes, increases significantly (data not shown). GSH eventually surpasses its basal level, reaches a peak, and then settles at an elevated steady-state concentration.

Figure 3.

Simulated time-course changes in levels of intracellular xenobiotic X, reactive metabolite X′, CYP, Nrf2, GSH and GST, in response to continued presence of various concentrations of extracellular xenobiotic (X_ext).

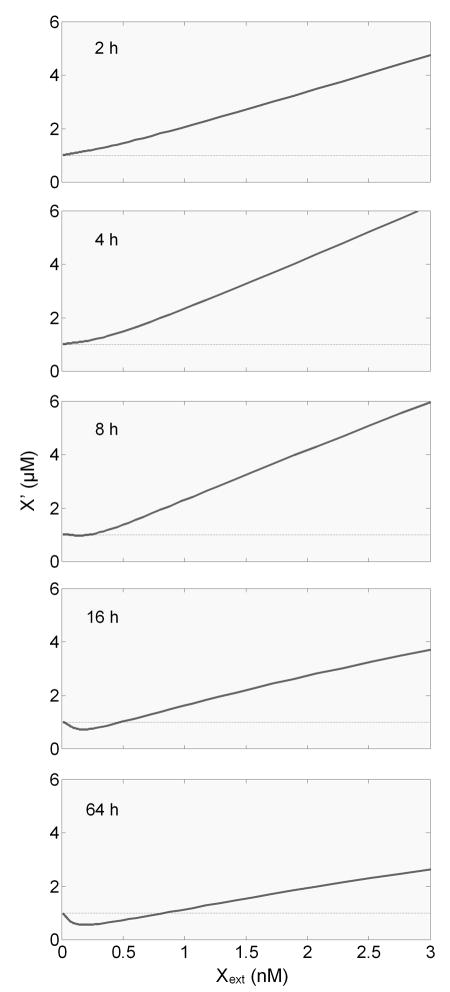
An important feature of hormesis is its time-dependent emergence following the onset of the stress – at an early time, the dose response is monotonic, and only at later times when the compensatory mechanism is considerably activated does hormesis appear (Calabrese and Baldwin, 2001b). Our simulations recapitulate such a temporal sequence with respect to the dose response curve for the reactive metabolite X′ (Fig. 4). At 2 h of exposure, X′ rises monotonically with an increase in the dose of X_ext, the parent chemical in the extracellular compartment. By 4 h the dose response curve remains monotonic but more elevated as a result of increased bioactivation by newly induced CYP. By 8 h however, X′ begins to decrease as a result of phase II enzyme induction. More importantly, for some low X_ext doses, X′ begins to dip below the baseline, albeit marginally, giving the first sign of hormesis. By 16 h the hormetic appearance is much more appreciable, and by 64 h the nadir of the J-shaped response reaches about 40% below the baseline and remains so afterwards, indicating steady-state hormesis.

Figure 4.

Simulated temporal sequence of the dose response curve between the intracellular concentration of reactive metabolite X′ and the extracellular concentration of parent xenobiotic X (X_ext). Note that the J-shaped hormesis does not become evident until 16 hours when the phase II enzymes are significantly induced (refer to Fig. 3).

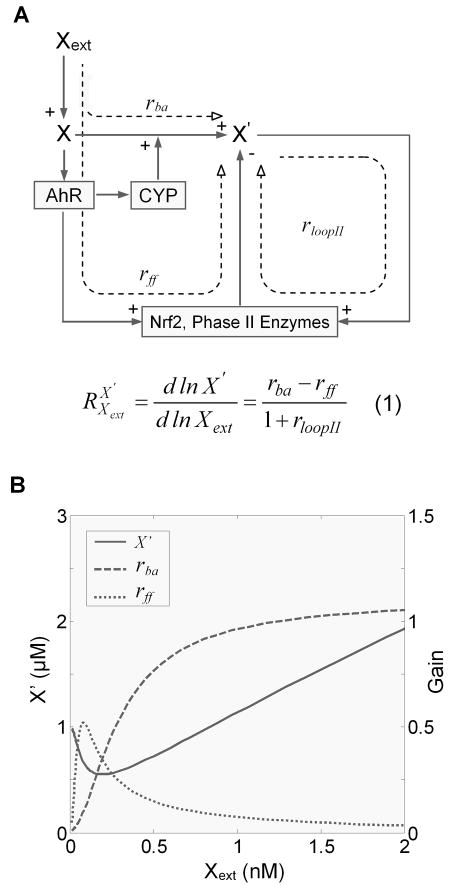
Roles of bioactivation, feedforward, and phase II feedback control in hormetic response

In the context of controlling the level of the reactive metabolite X′, the detoxification/bioactivation pathways detailed in Fig. 2 can be viewed as a homeostatic system with feedforward and feedback controls (Fig. 5A). The steady-state concentration of X′ in response to X_ext can be quantitatively captured using Signal Transfer Analysis, a theoretical framework developed from Metabolic Control Analysis and Biochemical System Theory (Savageau, 1976; Fell, 1997; Kholodenko et al., 1997). With this theory, the steady-state level of a dependent variable in response to changes in an independent variable within the interconnected biochemical network can be quantified by the response coefficients or logarithmic gains of the individual branches and loops in the network (Kholodenko et al., 1997). Specifically in our case, $R_{X_{\mathit{ext}}}^{X^{\prime }}$, the systems-level gain of X′ in response to X_ext, is expressed by Equation (1) in Fig. 5A. The bioactivation gain r_ba quantitatively defines the changes in the concentration of X′ in response to X_ext due solely to the bioactivation by receptor-mediated induction of phase I enzyme CYP. The feedforward gain r_ff quantitatively defines the changes in the concentration of X′ due solely to the detoxification by receptor-mediated cross-induction of phase II enzymes. Finally r_loopII defines the phase II loop gain controlling X′ in a Keap1-Nrf2-mediated feedback manner. By definition, the value of $R_{X_{\mathit{ext}}}^{X^{\prime }}$, relative to zero, determines the direction of changes in the concentration of X′ in response to X_ext. Equation (1) indicates that the sign of $R_{X_{\mathit{ext}}}^{X^{\prime }}$ is solely dependent on the sign of the difference between r_ba and r_ff, independent of the phase II feedback loop gain r_loopII. When the feedforward gain r_ff is greater than the bioactivation gain r_ba, $R_{X_{\mathit{ext}}}^{X^{\prime }}$ becomes negative, and as a result X′ decreases in response to an increase in X_ext; conversely, when r_ba is greater than r_ff, $R_{X_{\mathit{ext}}}^{X^{\prime }}$ becomes positive, and X′ increases in response to an increase in X_ext. Simulations indicated this is indeed the case (Fig. 5B). At low X_ext doses, the feedforward gain r_ff (dotted line) is greater than the bioactivation gain r_ba (dashed line), resulting in overcompensation by the system, thus X′ initially decreases from its baseline level, forming the descending phase of the J-shaped hormetic response. As the dose of X_ext increases, activation of the feedforward mechanism, involving Nrf2 and phase II enzyme induction, begins to approach its maximum level, causing a reversal of the feedforward gain r_ff. As it intersects with the still-rising bioactivation gain r_ba, $R_{X_{\mathit{ext}}}^{X^{\prime }}$ becomes zero, signifying the nadir of the J-shaped response (the corresponding dose of X_ext is called nadir dose). With further increases in the dose of X_ext, r_ff begins to drop below r_ba, giving rise to a positive $R_{X_{\mathit{ext}}}^{X^{\prime }}$. Accordingly, X′ reverses its course and begins to rise, forming the ascending phase of the J-shaped response.

Figure 5.

The level of reactive metabolite X′ is regulated by three processes: (1) nuclear receptor such as AhR and CYP mediated bioactivation, (2) AhR, Nrf2, and phase II enzymes mediated feedforward control, and (3) Nrf2 and phase II enzymes mediated phase II feedback control. (A) systems-level response coefficient for X′ vs. X_ext is determined by the bioactivation gain r_ba, feedforward gain r_ff, and phase II loop gain r_loopII in Equation (1). The equation indicates that the sign of the response coefficient depends solely on r_ba and r_ff. (B) Hormetic steady-state dose response for X′ vs. X_ext in relation to changes in the bioactivation gain r_ba and feedforward gain r_ff. Note when r_ba is less than r_ff for low doses of X_ext, the dose response curve trends downward; when r_ba and r_ff are equal, it corresponds to the nadir of the hormetic response; and when r_ba is greater than r_ff for high doses of X_ext, the dose response curve trends upward.

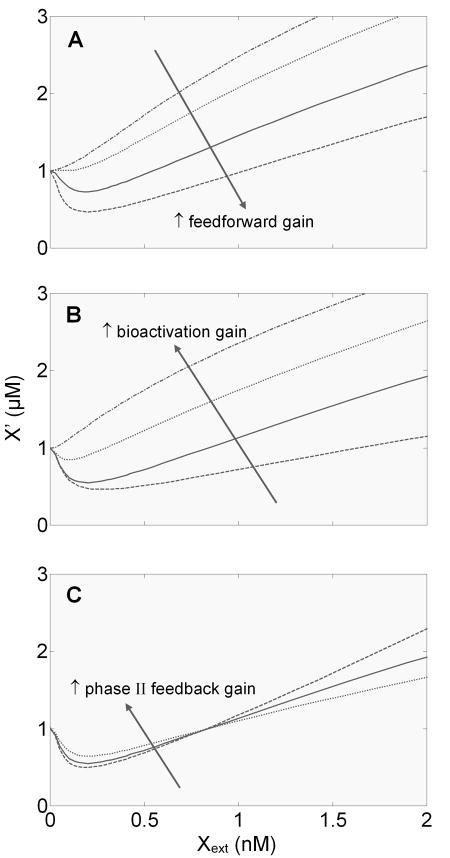
According to Equation (1) in Fig. 5, the feedforward gain, bioactivation gain, and phase II feedback gain each play a role in determining the value of $R_{X_{\mathit{ext}}}^{X^{\prime }}$, hence the shape of the hormetic response. So we next investigated how changes in these individual gains affect the shape of the hormetic response curve. As expected, when the feedforward gain is enhanced, the J-shaped response becomes more prominent with the hormetic zone (i.e., the below-baseline portion of the J-shaped curve) deepened; conversely, when the feedforward gain is dampened, the response tends to have a shallower hormetic zone (Fig. 6A). If the feedforward gain approximates the bioactivation gain within a dose range, a threshold-like response appears (dotted line in Fig. 6A). If the feedforward control is completely disabled, only a monotonically increasing response is observed (dash-dotted line in Fig. 6A). Changes in the bioactivation gain, which is regulated by the phase I feedback loop, is expected to have an opposite effect on the J-shaped curve. The more CYP is induced, the more X′ will be generated, thus the higher the bioactivation gain. As expected, an increase in the bioactivation gain reduces the depth of the hormetic zone, and when the gain is high enough only a monotonic response is observed. Conversely, a decrease in the bioactivation gain deepens the hormetic zone (Fig. 6B). According to Equation (1), although the phase II feedback loop gain does not affect the sign of $R_{X_{\mathit{ext}}}^{X^{\prime }}$, as a term in the denominator, it does affect the absolute value of $R_{X_{\mathit{ext}}}^{X^{\prime }}$. We can expect that by reducing the absolute value of $R_{X_{\mathit{ext}}}^{X^{\prime }}$, an independent increase in the phase II loop gain will reduce the depth of the hormetic zone, and conversely a decrease in the phase II loop gain will increase the depth. This was indeed demonstrated by direct simulation (Fig. 6C). But in contrast to the effect of altering the feedforward and bioactivation gains, the change in the depth of the hormetic zone is accompanied by an opposite change in the above-baseline portion of the curve. This divergent response below and above the baseline, though counterintuitive, reflects the nature of negative feedback regulation, i.e., to mitigate perturbations in both directions.

Figure 6.

Effects of varying feedforward gain, bioactivation gain, and phase II feedback loop gain on the shape of the steady-state dose response curve for reactive metabolite X′ vs. extracellular xenobiotic X (X_ext). (A) Changes in feedforward gain were implemented by simultaneously varying k_27f2 and k_56f2, which respectively control AhR-mediated Nrf2 and GST gene induction. The pair of parameter values used here are (0, 0), (0.33, 0.0066), (2, 0.04), and (8, 0.16) nM⁻¹s⁻¹. (B) Changes in bioactivation gain were implemented by varying k_20f, which controls AhR-mediated CYP gene induction. The parameter values used here are 0.003, 0.03, 0.75, and 10 nM⁻¹s⁻¹. (C) Changes in phase II feedback loop gain alone were implemented by varying the relative contribution of reactive metabolite X′ to Keap1 oxidation. This was achieved by setting k_10i (s⁻¹), k_10f (nM⁻¹s⁻¹), k_11i (s⁻¹), and k_11f (nM⁻¹s⁻¹) to the following sets of values: (1.18, 0, 1.18, 0), (0.93, 0.26×10⁻³, 0.93, 0.26×10⁻³), and (0.43, 0.76×10⁻³, 0.43, 0.76×10⁻³).

Effect of physical/chemical properties of parent chemical X on hormetic response

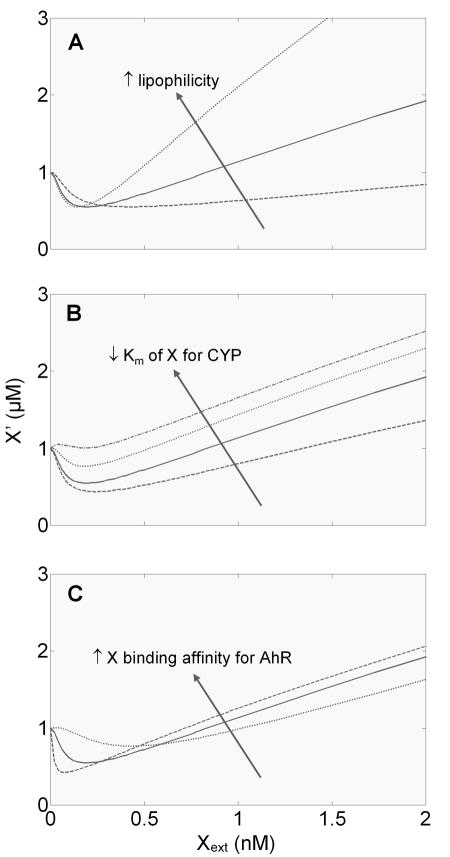
In our model system, the xenobiotic X diffuses into the cell, wherein it activates AhR and is metabolized by the CYP enzyme. Importantly, xenobiotic chemicals that follow the same mode of action are likely to differ in their lipophilicity, Michaelis-Menten constant for CYP, and binding affinity for nuclear receptors such as AhR, CAR, or PXR. In this section we set out to investigate how the differences in these physical/chemical properties affect the shape of hormetic response.

Changes in lipophilicity presumably affect the ability of a xenobiotic compound to diffuse across the lipid cell membrane, i.e., the diffusion rate in our model. Our simulation indicated that as lipophilicity increases, the width of the hormetic zone (i.e., the dose range defining the below-baseline portion of the J-shaped curve) narrows, and the nadir dose decreases; conversely as lipophilicity decreases, the hormetic zone broadens and the nadir dose increases (Fig. 7A). Interestingly, regardless of these changes, the depth of the hormetic zone remains unchanged.

Figure 7.

Effects of physical/chemical properties of xenobiotic X on the shape of the steady-state dose response curve for reactive metabolite X′ vs. extracellular xenobiotic X (X_ext). (A) An increase in the lipophilicity of X tends to reduce the width of the hormetic zone and nadir dose, without affecting the depth of the hormetic zone. Changes in lipophilicity were implemented by varying the diffusion rate constants (k_1f, k_1b, k_4f, and k_4b, which all assume equal values) for crossing the cell and nuclear membrane to the following values: 20, 100 and 500 s⁻¹. (B) A decrease in the Michaelis-Menten constant (K_7m) of X for phase I enzyme CYP tends to reduce the width and depth of the hormetic zone. The parameter values used here are 400, 100, 25, and 10 nM. (C) An increase in the binding affinity of X for its receptor tends to increase the depth and reduce the width of the hormetic zone, as well as reduce the nadir dose. Changes in the binding affinity were implemented by simultaneously varying the association rate constants (k_2f and k_5f, which assume equal values) to the following values: 0.001, 0.004, and 0.02 nM⁻¹s⁻¹. These values give dissociation constant of 10, 5, and 1 nM, respectively.

Xenobiotic compounds that can be metabolized by the same phase I enzyme are likely to have different Michaelis-Menten constant (K_m) for the enzyme. Since the reactive metabolite X′ is produced through bioactivation of the parent chemical X, an increase in the production flux, achieved through lowering K_m value, should increase the bioactivation gain, and therefore reduce the depth of the hormetic zone. Our simulation indicated that as K_m decreases, the depth of the J-shaped curve indeed decreases, consistent with this line of reasoning (Fig. 7B). The width of the hormetic zone also narrows in response to decreasing K_m, with little, if any, changes in the nadir dose. Changes in the catalytic rate constant of the phase I reaction (k_7c) have similar effects on the shape of the hormetic response (Fig. S1).

Xenobiotic compounds capable of activating nuclear receptors such as AhR can differ in their binding affinity for the receptor. An increase in the binding affinity results in more AhR activation. Since AhR can drive both phase I CYP and phase II enzyme gene expression, an increase in the binding affinity should enhance both the bioactivation and feedforward gain. But at low X_ext doses, apparently because the feedforward branch is more sensitive to changes in AhR activation than the bioactivation branch, an increase in the binding affinity results in deepening of the hormetic zone (Fig. 7C). This is accompanied by a somehow narrowing of the width of the hormetic zone and a decrease in the nadir dose.

Conditioning hormesis and negative feedback control

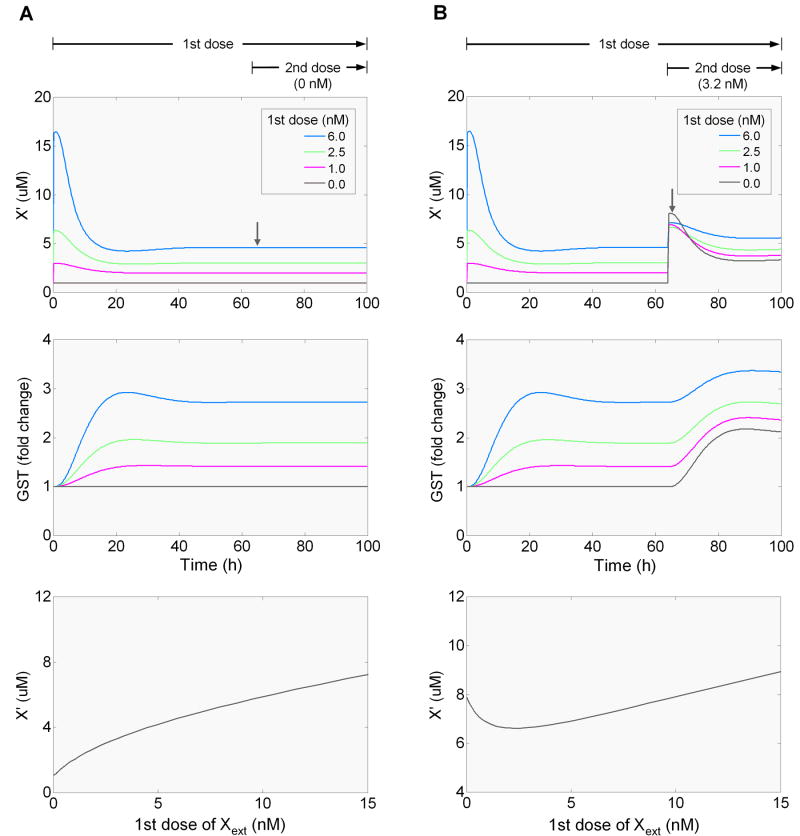
Hormesis is believed to occur as a result of the compensatory response launched by homeostatic control systems (Calabrese, 2001). Many of these control systems are known to operate with negative feedback as the underlying homeostatic mechanism (Houk, 1988; Zhang and Andersen, 2007). It is important to understand whether such a feedback control alone can generate steady-state hormesis. In this section we use the phase I, II, and III model system to investigate this issue. To examine the effect of feedback alone, we disabled the feedforward control by removing the binding of AhR heterodimer to the promoters of Nrf2, GST and MRP genes. In theory, this essentially sets the feedforward gain r_ff to zero in Equation (1) in Fig. 5, and it is obvious then that $R_{X_{\mathit{ext}}}^{X^{\prime }}$ always has a non-negative value. With $R_{X_{\mathit{ext}}}^{X^{\prime }}>=0$, the steady-state concentration of X′ will always change in the same direction as the dose of X_ext. Our simulation confirmed the analytical prediction, showing that at steady state X′ rises monotonically with X_ext (Fig. 8A).

Figure 8.

Simulations demonstrating that homeostatic control mediated by negative feedback alone cannot generate steady-state hormesis (A), but may generate conditioning hormesis involving two sequential dosing events (B). The dose response curves for X′ vs X_ext were obtained at 66 h, 2 h after the onset of the second dose (downward arrow). The results were obtained from simulations with the phase II negative feedback enabled, and the phase I negative feedback and phase I to II feedforward disabled. Disabling phase I negative feedback and phase I to II feedforward was implemented by setting CYP at a fixed concentration at 1.5 μM, and setting the initial concentrations of DRE_(Nrf2), DRE_(GST), DRE_(MRP), and DRE_(CYP) all to zero.

The next question we sought to understand is whether negative feedback control alone can generate conditioning hormesis which involves a two-dosing scenario (Calabrese et al., 2007). With the feedforward control disabled in the model, we simulated the scenario by applying a first (conditioning) dose of X_ext and then, after the system reaches steady state, superimposing a fixed second dose. Our simulation revealed that the concentration of X′, evaluated 2 h after the onset of the second dose, has a J-shaped relationship to the first dose of X_ext (Fig. 8B), indicating that smaller conditioning doses actually reduce the transient increase in the concentration of X′ in response to a second dose. This occurs because the phase II enzymes newly induced by the small conditioning dose are present, at the time the second dose is applied, to mitigate any further increase in the concentration of X′ elicited by the second dose. However, at higher conditioning doses, the phase II enzymes, albeit induced to higher expression levels, are not sufficient to keep up with the increase in the production of X′ after the second dose is superimposed, resulting in a reversal of the response. This conditioning hormesis also occurs when the feedforward control is in place (data not shown).

Discussion

A salient feature of biological systems is homeostasis, the capability to maintain a relatively stable internal milieu under a variety of stresses from the external environment. Environmental stressors, physical or chemical, at first perturb the internal milieu largely unchecked. Shortly after, the innate homeostatic control mechanism, designed to compensate for the perturbation, is mobilized into action. As a result, the perturbation is mitigated over time until a new adaptive state is reached. Because of homeostatic compensation, the extent of the final impact to the biological system is unlikely to be linearly correlated with the dose of the stressing agent, especially in the low dose region where the control mechanism actively operates (Hart and Frame, 1996; Zhang and Andersen, 2007). As a special case of nonlinear response, hormesis is emerging as a frequent biological phenomenon that is closely associated with the consequence of the homeostatic operation of biological systems (Calabrese and Baldwin, 2001a; Calabrese and Baldwin, 2003). Homeostasis in biological systems is almost invariably mediated by negative feedback and/or feedforward controls (Houk, 1988; Burg et al., 1996; Pirkkala et al., 2001; Motohashi and Yamamoto, 2004; Papandreou et al., 2005). In the present study, using the phase I, II, and III xenobiotic metabolism system as an example, we showed that feedforward control is required to engender steady-state hormetic behaviors. For conditioning hormesis which requires two sequential dosing events, negative feedback control alone is usually sufficient.

Negative feedback is the dominant form of network structure for biological homeostatic systems (Kitano, 2004). At the whole-body level, the concentrations of many hormones, ions, and nutrients in the blood are maintained within their respective physiological ranges in this manner. Examples include the blood glucose feedback control by insulin and glucagon from the pancreas, and the testosterone feedback control involving gonadotropin-releasing hormone from the hypothalamus and gonadotrophins from the anterior pituitary. At the cellular level, there are an array of homeostatic gene regulatory networks each responsible for coping with a specific type of stresses. These anti-stress gene regulatory networks, designed to counteract perturbations induced by various stresses including radiation, heat shock, oxidative stress, and hypoxia, etc, are clearly organized in a negative feedback manner, through interactions between multiple transcription factors, genes, and enzymes (Burg et al., 1996; Pirkkala et al., 2001; Motohashi and Yamamoto, 2004; Papandreou et al., 2005).

While the steady-state dose response behavior of a negative feedback-mediated circuit is most likely to be nonlinear (Zhang and Andersen, 2007), such a control scheme is theoretically unlikely to underpin nonmonotonic steady-state responses. Negative feedback regulation is designed to function by using the error signal (i.e., the amount of deviation of the controlled endpoint from its basal operating level) as the input to activate the compensatory mechanism in order to correct the deviation itself. For most of the biological negative feedback controls, which are proportional, the compensation cannot bring the controlled endpoint completely back to the basal operating level when the perturbing stressor persists. This imperfect adaption is expected because the activation of the compensatory mechanism relies on the continued presence of the error signal. If indeed perfect adaption occurred and the controlled endpoint returned to its initial state, the error signal would go to zero. Without the error signal, the system would be unable to sustain the activation of the compensatory mechanism that led to perfect adaption in the first place. Furthermore, if hormesis somehow occurred as a result of overcompensation, the error signal would become negative, which would in turn deactivate, rather than activated, the compensatory mechanism, negating the hormetic response. Even with integral feedback control in which the cumulative history of the error signal is used as the input, only perfect adaptation, but not hormesis, can be achieved (Yi et al., 2000). Thus steady-state hormesis from overcompensation is theoretically impossible for a homeostatic system relying solely on negative feedback regulation. Our simulation, with the phase II feedback control only, confirms this conclusion – although the steady-state concentration of the reactive metabolite X′ rises nonlinearly as the dose of the extracellular parent chemical X_ext increases, no hormetic type of response is observed (Fig. 8A). This monotonic relationship can also be concluded from Equation (1) in Fig. 5, which indicates that with feedback regulation only, devoid of feedforward control, the systems-level gain for X′ in response to X_ext can only take a non-negative value, ruling out nonmonotonic responses.

Even though that negative feedback regulation alone can only produce monotonic steady-state response, it does generate hormesis in some non-steady state conditions. For one, it is likely that during the adaptation to establish a new steady state, activation of the compensatory mechanism may temporarily overshoot, leading to transient hormesis. For this overcompensation to occur, it requires a relatively high feedback loop gain and a time delay from the initial perturbation to activation of the compensatory mechanism. Secondly, feedback regulation also seems adequate to explain conditioning hormesis, a phenomenon often observed with two sequential dosing events (Calabrese et al., 2007). In this case, a small conditioning dose may activate the compensatory mechanism without appreciably affecting the controlled endpoint. The activated compensatory mechanism will then work to subdue the additional disruption elicited by the application of the second dose. Within some dose limit, the higher the conditioning dose, the more activated the compensatory mechanism, and the more dampened the disruption elicited by the second dose. However, as the conditioning dose increases further, the compensatory mechanism reaches its maximal capacity eventually. As a result, the overall disruption after the second dose will begin to rise instead, delineating a hormetic response for the entire dose range. Our simulation, with only the phase II feedback control enabled, confirms the possibility of conditioning hormesis (Fig. 8B).

While negative feedback regulation is the predominant form of homeostatic control in biological systems, strong homeostatic performance requires a high feedback loop gain (Zhang and Andersen, 2007). However, too high a loop gain would significantly increase the instability of the homeostatic system, frequently leading to oscillation (Maurer et al., 2004). In many homeostatic systems, feedback regulation is complemented with feedforward control (Houk, 1988). In contrast to the responsive nature of feedback control, which becomes activated only after the controlled endpoint deviates from its basal operating level, feedforward control is preemptive in that the compensatory mechanism is activated directly by the external perturbing event or stressor, independent of the status of the internal controlled endpoint. A well-known feedforward example of cellular homeostasis is the bacterial heat shock response (El-Samad et al., 2005). In bacteria, expression of heat shock proteins can be induced by elevated levels of mis-folded proteins in a classical feedback manner, as a result of heat stress. Additionally, heat-sensing molecules in the cell, which detect the rise in temperature, can directly induce heat shock proteins in a feedforward manner, independent of the status of mis-folded proteins (Morita et al., 1999).

Compared with feedback control, feedforward control has several advantages. By driving the compensatory mechanism directly, feedforward control reduces the response time for the system to adapt to the perturbation (El-Samad et al., 2005). Feedforward control can also achieve a nearly perfect adaptation if the strength of its activation is fine-tuned to closely match the degree of disturbance. Despite these merits and unlike feedback control, feedforward control can only work against the type of stress it is designed for and will fail if a novel stressor is encountered. For instance, the heat-sensing feedforward control in bacteria can only respond to temperature changes to rescue heat-induced mis-folded proteins, yet it becomes useless if protein mis-folding is induced chemically. With feedforward control alone, homeostasis would also be compromised when the system experiences internal parametric fluctuations of its components. Therefore feedback and feedforward control are frequently coupled to achieve reliable and robust homeostatic performance.

With respect to cellular detoxification of xenobiotics, both feedback and feedforward controls appear to operate in the cell. The phase I to II cross-induction, as we described here, is a feedforward mechanism that operates to curb the accumulation of the reactive metabolites coming from phase I bioactivation. The emergence of such a feedforward mechanism, as mediated by xenosensors such as AhR, CAR, and PXR, makes great evolutionary sense as far as enhancing the fitness of biological organisms is concerned. If a biological organism frequently encounters a chemical or a family of chemicals whose metabolites, after phase I conversion, are reactive and thus harmful to the cellular well-beings, it would be selectively advantageous to engage a feedforward mechanism that can respond to the presence of the parent xenobiotics directly to curb the undesirable rise of their toxic metabolites. Then, the relative strength between the feedforward control and phase I bioactivation, as quantified by their respective gains (Fig. 5), determines the direction of changes in the steady-state concentrations of the reactive metabolites. If the bioactivation gain is always greater than the feedforward gain, the reactive metabolites would increase monotonically. If the two opposing gains are balanced within a range of low doses, a response with threshold is likely to result. Lastly if in the low-dose region the feedforward gain is greater than the bioactivation gain, denoting overcompensation in mathematical term, an initial decrease in the concentrations of the reactive metabolites would occur, which is likely to be followed by an increase at higher doses, forming a hormetic response (Fig. 5B).

Within the framework of cellular xenobiotic metabolism, whether a particular chemical generates hormetic changes in the pool of reactive species, and if it does, the actual degree and dose range of the hormetic response, depends on molecular properties that affect both the bioactivation and phase I to II cross-induction processes. These properties, including lipophilicity, binding affinity for cognate nuclear receptors, and Michaelis-Menten constant for phase I enzymes, have various effects on the appearance of the steady-state dose response curve (Fig. 7). All of them influence the width of the hormetic zone, and the latter two modulate the depth, as well. With the parameter values in the model, a decrease in the binding affinity for the nuclear receptor and an increase in the affinity for the phase I enzyme tend to reduce the depth of the J-shaped response. When these changes are large enough, only monotonic response occurs. Some chemicals may induce matched bioactivation and feedforward control within a low-dose range before the feedforward control is overwhelmed at higher doses, resulting in a response with threshold.

The pattern of induction of phase I, II, and III xenobiotic metabolizing system is a general characteristics of many xenobiotics with phase I metabolism enhancing toxicity of the parent compounds. The phase I to II feedforward control, quantified in our modeling, is likely to provide a common mechanism for generating hormetic dose response behaviors for reactive metabolites. The concentrations of these metabolites would in turn be responsible for specific downstream cellular toxicity, inducing U- or inverted U-shaped endpoint responses in processes such as protein and DNA binding, survival, mutation, and carcinogenesis (Kitchin and Brown, 1994; Kinoshita et al., 2003). It needs to be noted, however, that the proposed feedforward control in the xenobiotic metabolizing system is likely to be responsible for only a small subset of observed hormetic phenomena. Other homeostatic systems, such as DNA repair, ion and nutrient concentration control, energy regulation, heat shock response, and hypoxic response, etc., may underlie a wider spectrum of hormetic responses. The present study does imply that one important aspect of hormesis research should be identifying, in these homeostatic control systems, feedforward control pathways that can be over-activated by small perturbations to produce steady-state hormesis.

Although our study attempts to use control theory to make sense of the operation of homeostatic networks and their dose response behaviors for a system with coordinated pathway activation, phase I, II, and III xenobiotic metabolizing systems in vitro and in vivo are more complex than captured in our model here. For a given xenobiotic chemical, a number of nuclear receptors, transcription factors, genes, and enzymes may be involved in its metabolism and detoxification. A single xenobiotic molecule may be modified by multiple enzymes on multiple moiety groups, producing multiple metabolites. Nevertheless, it is clear that feedforward control is required to generate steady-state hormetic response, and this conclusion would be equally valid for other complex homeostatic systems. Indeed, feedforward control in the context of homeostatic operation can be regarded as the inhibitory branch of an incoherent feedforward loop, a network structure that is able to produce nonmonotonic responses (Kaplan et al., 2008; Kim et al., 2008).