Mapping correlations between ventricular expansion and CSF amyloid and tau biomarkers in 240 subjects with Alzheimer’s disease, mild cognitive impairment and elderly controls

Abstract

Automated ventricular mapping with multi-atlas fluid image alignment reveals genetic effects in Alzheimer’s disease, NeuroImage 40(2): 615–630); with this method, we calculated minimal numbers of subjects needed to detect correlations between clinical scores and ventricular maps. We also assessed correlations between emerging CSF biomarkers of Alzheimer’s disease pathology and localizable deficits in the brain, in 80 AD, 80 mild cognitive impairment (MCI), and 80 healthy controls from the Alzheimer’s Disease Neuroimaging Initiative. Six expertly segmented images and their embedded parametric mesh surfaces were fluidly registered to each brain; segmentations were averaged within subjects to reduce errors. Surface-based statistical maps revealed powerful correlations between surface morphology and 4 variables: (1) diagnosis, (2) depression severity, (3) cognitive function at baseline, and (4) future cognitive decline over the following year. Cognitive function was assessed using the mini-mental state exam (MMSE), global and sum-of-boxes clinical dementia rating (CDR) scores, at baseline and 1-year follow-up. Lower CSF Aβ_1–42 protein levels, a biomarker of AD pathology assessed in 138 of the 240 subjects, were correlated with lateral ventricular expansion. Using false discovery rate (FDR) methods, 40 and 120 subjects, respectively, were needed to discriminate AD and MCI from normal groups. 120 subjects were required to detect correlations between ventricular enlargement and MMSE, global CDR, sum-of-boxes CDR and clinical depression scores. Ventricular expansion maps correlate with pathological and cognitive measures in AD, and may be useful in future imaging-based clinical trials.

Introduction

Alzheimer’s disease (AD) is the commonest type of dementia (Kukull and Bowen, 2002). It is characterized by progressive neuronal degeneration and cognitive decline, and affects ~5–10% of those over age 65 and 30–40% of those over 90. Around 4.5 million people in the United States have AD, with an estimated cost to society of $100 billion per year, and up to 14 million people and their families may be affected by AD by the middle of this century if no new treatments are developed.

Diagnosis of possible or probable AD is based on clinical criteria and by exclusion of other possible causes of dementia. With current diagnostic criteria, AD-associated neuropathology is typically well-advanced by the time AD is diagnosed. Much AD research focuses on mild cognitive impairment (MCI), a transitional state between normal aging and early AD (Flicker et al., 1991), in which 6–25% of subjects per year transition to AD (Petersen et al., 2001). As drug candidates that might slow the progression of Alzheimer’s pathology began to be developed, the National Institute of Aging and pharmaceutical industry funded the Alzheimer’s Disease Neuroimaging Initiative, with the goal of developing improved methods to track AD based on imaging and other biomarkers, and to optimize methods for AD treatment trials.

MRI-based volume measurements are potential surrogates of disease progression in AD, even in the pre-clinical stages (Kantarci and Jack, 2004). Several methods can quantify structural brain changes in MRI including: region-of-interest measurements, such as hippocampal volumes and maps (Morra et al., 2008a,b), the “boundary shift integral” — a technique that quantifies differences between two successive co-registered 3D MRIs (Fox et al., 2001), and mapping methods that localize atrophy, such as voxel-based morphometry (Good et al., 2001; Whitwell et al., 2004), and tensor-based morphometry (Studholme et al., 2004, 2006; Hua et al., 2008a,b; Leow et al., in press). Even so, ventricular volume measures provide excellent sensitivity to disease effects and pre-clinical brain changes (Schott et al., 2005). In 79 healthy elderly subjects examined annually for up to 15 consecutive years, ventricular volume expansion accelerated on average 2.3 years prior to the clinical diagnosis of MCI (Carlson et al., 2008).

Despite renewed interest in its value as a predictor of clinical decline (Weiner, 2008), ventricular segmentation fell somewhat out of favor as it is time-consuming and tedious to compute, often requiring expert manual labeling of scans. Differences in inter-observer delineation or drift over time make it hard to analyze large numbers of subjects over longer time-spans. For the vast 3D MR datasets now being collected (over 3000 scans in the ADNI), manual segmentations would be impractical.

MRI-based volumetric studies of MCI and Alzheimer’s disease are now common, with much of the work focusing on medial temporal structures such as the entorhinal cortex and hippocampus that degenerate earliest (Stoub et al., 2005; Morra et al., 2008a,b). Recently, cortical thickness analyses (Thompson et al., 2003; Lerch and Evans, 2005; Braskie et al., 2008) and tensor-based morphometry (TBM; Hua et al., 2008a,b; Leow et al., in press; Raji et al., submitted for publication) have given a more complete picture of pathological structural changes.

Focusing on the ventricles specifically, Ferrarini et al. (2007) used an unsupervised clustering algorithm, generating a control average surface and a cloud of corresponding nodes across a dataset, and applied it to study ventricular shape variations in healthy elderly and AD subjects (Ferrarini et al. 2006; 2008a). As in our study, they correlated local ventricular enlargement with MMSE scores in 28 subjects with normal cognition, 26 individuals with MCI and 58 patients with severe AD (Ferrarini et al. 2008b), and with a machine learning approach, they classified previously unseen AD subjects with an accuracy of 76%. Carmichael et al. (2007a) suggested that at baseline, normal subjects who subsequently developed dementia over the course of 4 years had ventricular measures that differed from those of other normal subjects. Also, they found associations between ventricular volume and clinical conditions that are prevalent in the elderly, such as hypertension, diabetes, and depression (Carmichael et al., 2007b). In later work, Carmichael et al. (2007c) used a multivariate model to analyze the rate of change in lateral ventricle-to-brain ratio in 145 longitudinal pairs of MR images, accounting for dementia status, age, sex, education, race, white matter lesions, depression severity, baseline ventricular volume, and cardiovascular risk factors. Taken together, these efforts suggest that ventricular maps and volumes are useful for tracking AD and factors that modulate AD progression. Nestor et al. (2008) used a region growing method to segment the lateral ventricles and examined the cross-sectional and longitudinal ventricular volume differences in a large ADNI subset of 152 normal elderly controls, 247 MCI and 105 AD subjects after six months. The AD group had a significantly greater rate of ventricular enlargement than both subjects with MCI and controls, and the MCI group had a greater rate of enlargement than controls. MCI subjects at baseline who progressed to clinical AD after six months had greater ventricular enlargement than stable MCI subjects. Ventricular enlargement was different between ApoE4 genotypes within the AD group. The number of subjects required to demonstrate a 20% change in ventricular enlargement was substantially lower than that required to demonstrate a 20% improvement in cognitive scores.

In our study, we aimed to improve on the single-atlas ventricular segmentation method of Carmichael et al. by using multi-atlas segmentation, which can yield more accurate segmentations (Chou et al., 2008); we also calculated minimal numbers of subjects needed to detect correlations between clinical scores and ventricular maps. We also assessed correlations between emerging CSF biomarkers of AD pathology and localizable deficits in the brain.

To better understand ventricular correlates of AD progression, we automatically mapped ventricular geometry to analyze disease-related dilation in 80 AD patients, 80 individuals with MCI, and 80 healthy subjects. We automatically extracted surface-based 3D anatomical models from the 240 MRI scans. We hypothesized that (1) ventricular morphology would correlate with baseline and future (1-year) change scores on the Mini-Mental State Exam and Clinical Dementia Rating scale (both global and sum-of-boxes scores); and (2) ventricular morphology at baseline would correlate with ApoE genotype, educational level and depression severity, albeit with lower effect sizes than the primary clinical correlates. Finally, as an exploratory hypothesis, we expected that (3) ventricular dilation would correlate with biomarkers of AD pathology including CSF levels of tau protein (Tau), 181-phosphorylated tau protein (pTau_181p), beta amyloid (Aβ_1–42), and ratios of Tau/Aβ_1–42 and PTau/Aβ_1–42 (Andreasen et al. 2001; Itoh et al., 2001; Verbeek et al., 2003; Hampel et al., 2004; Lee and Trojanowski, 2006).

For each correlation, we evaluated the statistical power of our method by reducing the sample size to determine how many subjects were sufficient to detect the correlation using voxel-based statistical analyses, in conjunction with false discovery rate methods. The overarching goal of this work is to discover which map-based measures of disease burden can (1) best predict cognitive deterioration in normal, MCI and AD subjects, and (2) correlate best with CSF-based measures of pathology, an alternative objective measure of disease progression. It is not yet known whether differences on brain MRI occur along with elevated pathology in the CSF, and whether the two measures of disease are correlated. Following the intriguing pilot data of Wahlund and Blennow (2003), we hypothesized that CSF levels of beta amyloid (Aβ_1–42), but not Tau-derived measures, would be associated with ventricular expansion.¹

Materials and methods

Subjects

The Alzheimer’s Disease Neuroimaging Initiative (ADNI; Mueller et al., 2005a,b; Jack et al., 2008; http://www.loni.ucla.edu/ADNI/) is a large multi-center longitudinal MRI and FDG-PET (fluorodeoxyglucose positron emission tomography) study of 800 adults, ages 55 to 90, including 200 elderly controls, 400 MCI subjects, and 200 AD patients. The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessments acquired in a multi-site manner mirroring enrollment methods used in clinical trials, can replicate results from smaller single site studies measuring the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

At the time of writing this report, data collection for the ADNI project was in progress. The 240 subjects in this study included 80 healthy, 80 individuals with MCI and 80 individuals with Alzheimer’s disease evaluated at baseline (longitudinal follow-up data collection is now in progress). This subset of the ADNI baseline sample was assembled to age-, gender, and education-match all of the three groups (AD, MCI, and controls) as closely as possible (Table 1). As part of a thorough clinical/cognitive assessment at the time of scan acquisition, each subject’s mini-mental state examination (MMSE) score, and global and “sum-of-boxes” clinical dementia ratings (Morris, 1993) were assessed. Global CDR scores are discrete values of 0, 0.5, 1, 2, and 3, indicating no dementia, very mild, mild, moderate, and severe dementia. The sum-of-boxes CDR scores run from 0 to 18 in 0.5 intervals, (0 is no dementia; 18, very severe dementia). All AD patients met NINCDS/ADRDA criteria for probable AD (McKhann et al., 1984) with an MMSE score between 20 and 26, a global CDR of 0.5 or 1, and a sum-of-boxes CDR of 1.0–9.0. As such, these subjects would be considered as having mild, but not severe, AD. Detailed exclusion criteria, e.g., regarding concurrent use of psychoactive medications, may be found in the ADNI protocol (Mueller et al., 2005a,b). Briefly, subjects were excluded if they had any serious neurological disease other than incipient AD, any history of brain lesions or head trauma, or psychoactive medication use (including antidepressants, neuroleptics, chronic anxiolytics or sedative hypnotics, etc.). Table 1 summarizes demographic and clinical measures for all covariates tested here, including diagnosis (normal, MCI, AD), the mini-mental state exam (MMSE) (Folstein et al., 1975), global clinical dementia rating (CDR) (Morris, 1993), and sum-of-boxes CDR, change (over one year) in MMSE, change in global CDR, change in sum-of-boxes CDR, the ApoE genotype (which confers risk for AD), depression severity measured using the Geriatric Depression Scale (GDS; Yesavage et al., 1982), educational level (in years) and CSF biomarkers (detailed below).

Table 1.

Demographic and clinical scores [mean (SD)] for all covariates examined.

	N	Males/females	Age (years)	MMSE	Global CDR	Sum-of-boxes CDR
Normal	80	40/40	75.49 (5.50)	29.13 (1.01)	0 (0)	0.01 (0.08)
MCI	80	40/40	76.30 (6.91)	26.94 (1.69)*	0.50 (0)*	1.46 (0.80)*
AD	80	40/40	75.79 (7.38)	23.09 (1.77)*	0.73 (0.25)*	4.28 (1.68)*
	MMSE change	Global CDR change		Sum-of-boxes CDR change	Years of education	ApoE4(%)
Normal	−0.06 (1.47)	0.01 (0.21)		0.07 (1.02)	15.65 (2.65)	28.75
MCI	−0.74 (2.75)	0.03 (0.21)		0.67 (1.07)*	15.56 (2.52)	47.5
AD	−2.22 (4.42)*	0.21 (0.49)*		1.28 (2.24)*	14.96 (3.14)	70

^*p<0.05.

This dataset was downloaded by April 1, 2007, and reflects the status of the database at that point; as data collection is ongoing, we focused on analyzing all available baseline scans, together with baseline and 1-year follow-up clinical and cognitive scores, as well as information on conversion from MCI to AD over the 1-year follow-up period.

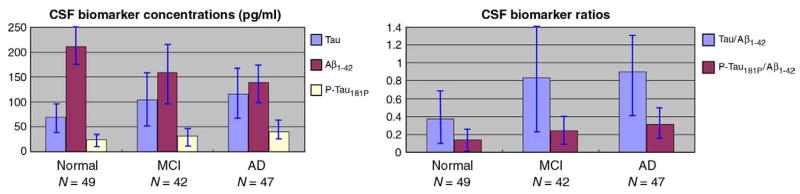
In addition, several biomarkers obtained from CSF were also included for assessing correlations, including beta amyloid 1–42 (Aβ_1–42), tau protein (Tau), phosphorylated tau protein 181 (pTau_181p), the tau and Aβ_1–42 ratio (Tau/Aβ_1–42), and pTau Aβ_1–42 ratio (pTau_181p/Aβ_1–42). Biomarker measurements were performed by Drs. Leslie Shaw and John Trojanowski of the ADNI Biomarker Core at the University of Pennsylvania School of Medicine, which collects and banks biological samples (DNA, blood, urine and CSF) from all participating sites, and conducts studies of selected AD biomarkers, including apolipoprotein E (ApoE) genotype, isoprostanes, tau, Abeta, sulphatides and homocysteine levels (Shaw et al., 2007). CSF biomarker testing was performed using the INNO-BIA AlzBio3 assay (Innogenetics, Ghent, Belgium), a procedure designed for research use only, not for use in diagnostic procedures. Fig. 1 shows summary statistics for the biomarker profiles of the AD, MCI and normal study groups. Biomarker data was assessed in 138 of the 240 subjects (49 normal, 42 MCI, and 47 AD).

Fig. 1.

CSF levels of Tau, Aβ_1–42, pTau_181p and ratios of Tau/Aβ_1–42, pTau_181p/Aβ_1–42 in the three diagnostic groups. Error bars denote standard deviations. There were significant differences between groups (AD>MCI>normal) for the pTau_181p and pTau_181p/Aβ_1–42 measures (p < 0.05). The differences between AD and MCI were not significant for CSF levels of Tau, Aβ_1–42 and ratios of Tau/Aβ_1–42.

CSF is in direct contact with brain and thus reflects brain-associated biochemical events better than any other biological fluid. CSF Aβ_1–42, Tau and pTau_181p are linked to AD-associated neuropathological changes, and they have been the most widely studied potential biomarkers for AD. It has been found that CSF Aβ_1–42 levels are consistently lower in AD (Motter et al. 1995), and can distinguish patients with mild AD from healthy controls with reasonable accuracy (Blennow and Hampel 2003).

Image acquisition and pre-processing

High-resolution T1-weighted MRI scans were acquired on 1.5 Tesla MRI scanners from Siemens and General Electric Health-care with the standard ADNI MRI protocol (Jack et al., 2008). (ADNI also collects a smaller subset of data at 3 Tesla but it was not analyzed here to avoid the additional complications of combining data across scanner field strengths). Each subject was scanned with a sagittal 3D MP-RAGE sequence, with acquisition parameters: inversion time (TI)/repetition time (TR): 1000/2400 ms; flip angle: 8°; 24 cm field of view; 192×192×166 acquisition matrix, and a voxel size of 1.25×1.25×1.2 mm³. In plane, zero-filled reconstruction yielded a 256×256 matrix for a reconstructed voxel size of 0.9375×0.9375×1.2 mm³. Images were calibrated with phantom-based geometric corrections to ensure consistency among scans acquired at different sites (Gunter et al., 2006). Additional image corrections were also applied, to adjust for scanner- and session-specific calibration errors (detailed in Jack et al., 2008). In addition to the original uncorrected image files, images with all of these corrections already applied (GradWarp, B1, phantom scaling, and N3) are available to the general scientific community (at www.loni.ucla.edu/ADNI).

To adjust for global differences in brain positioning and scale, we spatially normalized all images to the ICBM-53 average brain template with a 9-parameter linear transformation using the Minctracc algorithm (Collins et al., 1994). Aligned images were re-sampled in an isotropic space of 220³ voxels with a final voxel size of 1 mm³. To equalize image intensities across subjects, registered scans were histogram-matched.

Semi-automated lateral ventricle segmentation and shape modeling

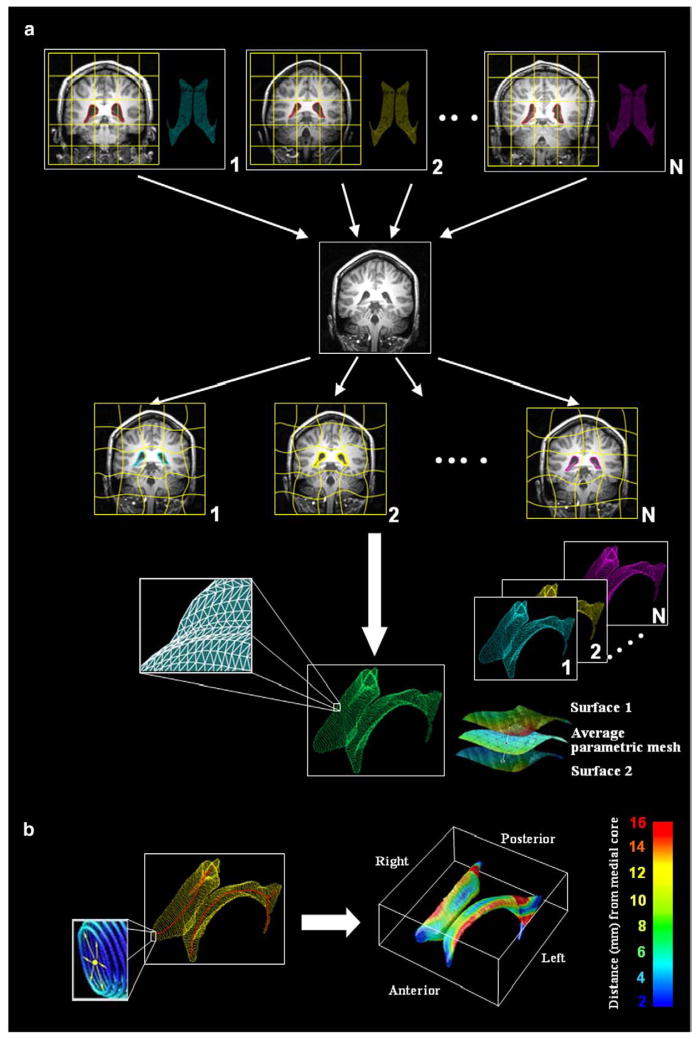
Lateral ventricular volumes were semi-automatically estimated for all scans using a “multi-atlas” technique we recently validated (Chou et al., 2008). Fig. 2(a) shows the steps used to map multiple surface-based atlases into each scan via fluid registration, before combining multiple segmentations of the same scan into a single average surface mesh. Briefly, a small subgroup of 6 images (2 AD, 2 MCI and 2 normal) were randomly chosen and the lateral ventricles were manually traced in contiguous coronal brain sections, following previously described criteria with established inter- and intra-rater reliability (Narr et al., 2001). Lateral ventricular surface models were converted into parametric meshes (we refer to these labeled images as ‘atlases’) (Thompson et al., 1996). We fluidly registered each atlas and the embedded mesh models to all other subjects, treating the deforming image as a Navier–Stokes viscous fluid (as pioneered by Christensen et al., 1996, and Gramkow, 1996), guaranteeing a diffeomorphic mapping. Fluid transforms were applied to the manually traced ventricular boundary using tri-linear interpolation, generating a propagated contour on the unlabeled images. Sets of points representing the tissue boundaries were re-sampled and made spatially uniform by stretching a regular rectangular grid (100×150 surface points) over each surface. This scheme provides a means for converting dense systems of points, sampled during outlining, into fully parametric surfaces and allows homologous points from the ventricular surfaces could be matched between subjects. The scheme we used (detailed in Thompson et al., 2004a,b) involves cutting the ventricles into 3 pieces (superior, temporal and occipital horns), as the branching structure of the ventricles makes it difficult to map the entire structure onto a single 2D domain. As such, the first coronal section in which the superior and temporal horns appear is used as a boundary between the 3 parts of the structure. We are also investigating other methods for parameterizing the ventricles, that do not involve making a planar cut between the 3 anatomically named horns. In Wang et al. (2009a), we use a holomorphic flow method, which can create parameterizations of complex branching objects such that the induced parametric coordinates are also smooth (differentiable) at the junctions between the horns. This differentiability can be useful if tensor-based morphometry is being performed in surface coordinates (as in Wang et al., 2009b), which we do not do here, as we are examining radial expansion. For each surface model, a medial curve was defined as the 3D curve traced out by the centroid of the ventricular boundary. The medial curve was defined separately in each individual, before averaging the surfaces. The operations of averaging surfaces and defining the medial curve from a surface are not commutative, as a medial curve derived from an average surface would not be the same as the average of the medial curves derived from each individual. Because we wanted to measure radial ventricular expansion in each individual, we computed these measures in each subject with reference to their own medial curve, but plotted the resulting statistics on the average surface for the groups being compared (Fig. 2(b)).

Fig. 2.

Methods flowchart. (a) Multiple surface meshes are mapped into new subjects’ scans via fluid registration. N images (subsequently called atlases) were randomly selected from the sample and the lateral ventricles were manually traced and converted into surface mesh models. N new ventricular models were then produced by fluid registration of each image to a different atlas. The N surface meshes per subject were integrated by simple mesh averaging for each individual subject (see Chou et al., 2008, for details). (b) Medial curves (red) are extracted, and the radial distance of each ventricular boundary point to a medial curve may be interpreted as a local thickness. These distance measures are then averaged across subjects at each boundary point and plotted in color to produce a regional measure of radial expansion or contraction of the ventricles. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

By integrating multiple propagated labels, random digitization errors from each hand-traced segmentation are significantly reduced. The resulting average model is also robust to inaccuracies in individual registrations that may occur when non-global minima of the intensity-based cost function are reached.

The key-time saving step in our approach is based on embedding the mesh models from the 6 randomly picked images into all the remaining scans. This has several benefits: (1) it avoids bias associated with just tracing one model and deforming it onto the other scans; (2) it is automated, after the initial tracing of a few scans whose labels are propagated into all the others; (3) it improves segmentation accuracy and the power to detect disease effects by combining multiple estimates for each scan (Chou et al., 2008); and (4) it superimposes the same mesh geometry and surface-based grid structure on the anatomy of many subjects, so that operations such as averaging and population statistics can be computed.

Our method is best described as “semi-automatic” because a small number of expert segmentations are required for the method to work, but there is no added manual effort per scan once these few expertly segmented images have been created. This is comparable to some segmentation approaches based on machine learning (e.g. Morra et al., 2008a,b) that require an expert user to delineate a small training set of images before a large number of others are automatically segmented with no further manual interaction.

Ventricular statistical maps and analysis

Surface contractions and expansions were statistically compared between groups at equivalent locations using Student’s t-tests (2-tailed), and were correlated with different clinical characteristics including diagnosis, cognitive scores, ApoE genotype, clinical scores, and future decline, as well as CSF biomarkers including levels of tau protein (Tau), 181-phosphorylated tau protein (pTau_181p), beta amyloid (Aβ_1–42), and ratios of Tau/Aβ_1–42 and pTau/Aβ_1–42. The associated p-values describing the uncorrected significance of these statistics were plotted onto the average surface model, as a color-coded map.

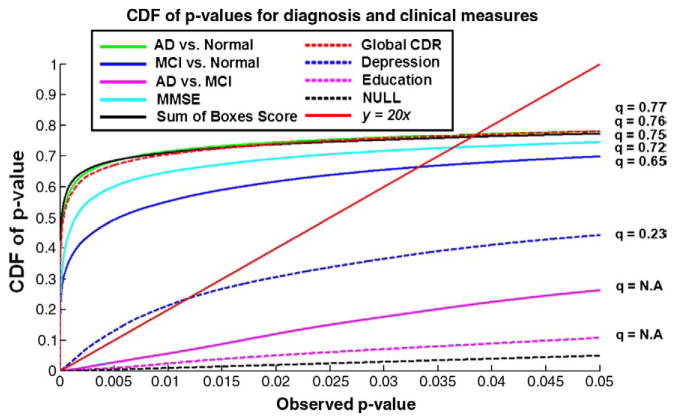
To assess the power of our method to establish linkages between morphology and different disease measures, we created cumulative distribution function (CDF) plots of the p-values. For purposes of clarification, we note that in using a CDF, this is not exactly the same as the CDF that most statisticians use; the p-values are not independent realizations of a random variable over many trials, but come from different ventricular surface locations in the same imaging dataset. We used the false discovery rate (FDR) method (Benjamini and Hochberg, 1995) to assign overall significance values to each statistical map, based on the expected proportions of voxels with intensity above the threshold under the null hypothesis. The value for which the CDF plot intersects with the y = 20x line represents the highest value for which at most 5% false positives are expected in the map. The use of the y = 20x line is related to the fact that significance is declared when the volume of suprathreshold statistics is more than 20 times that which would be expected to be observed by chance in null data. This intersection point is called the q-value. The q-value gives a single overall measure of significance for each p-map. If there is no such intersection point (other than the origin), there is no evidence to reject the null hypothesis. Our empirical CDF of p-values is the flip of the more common FDR PP plot. We have used this procedure to study statistical maps in several prior papers (Morra et al., 2008b; Hua et al., 2008a).

Results

Overall ventricular volumes

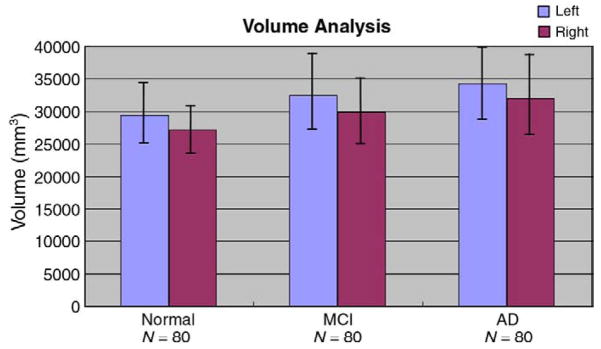
Fig. 3 shows the pattern of mean ventricular volumes in the AD, MCI and control groups, and is largely in line with prior studies. On average MCI volumes were 10.59% higher than the control averages for the left ventricles (p = 0.00012, t-test) and 10.08% higher than the control averages for the right ventricles (p = 0.00028). The AD group’s ventricles were 16.18% larger than controls on the left (p<0.0001) and 17.82% larger than controls on the right (p<0.0001). When the MCI and AD groups were directly compared with each other, the left ventricle showed a trend for being larger in AD (p = 0.069), and the right ventricle was significantly larger in AD than MCI (p = 0.018).

Fig. 3.

Mean ventricular volumes in the control, MCI, and AD groups. As expected, there is greater ventricular expansion in MCI than controls, and greater expansion in AD than MCI and controls. There is also a well known ventricular asymmetry (left larger than right) in all groups (Grossman et al., 1990). Error bars denote standard deviations.

Linking ventricular morphology and clinical characteristics

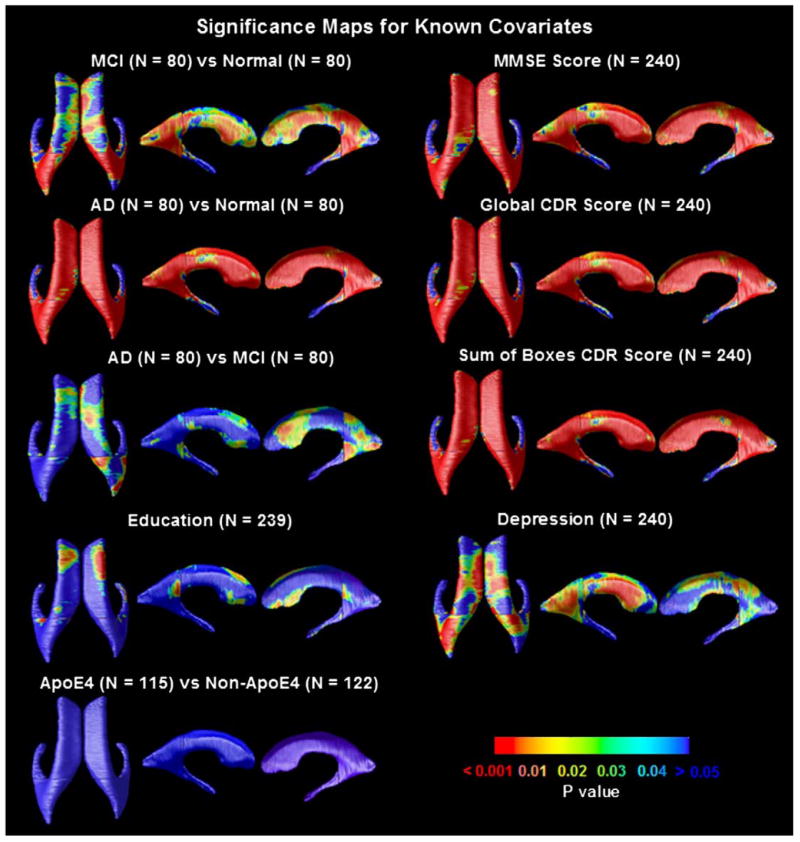
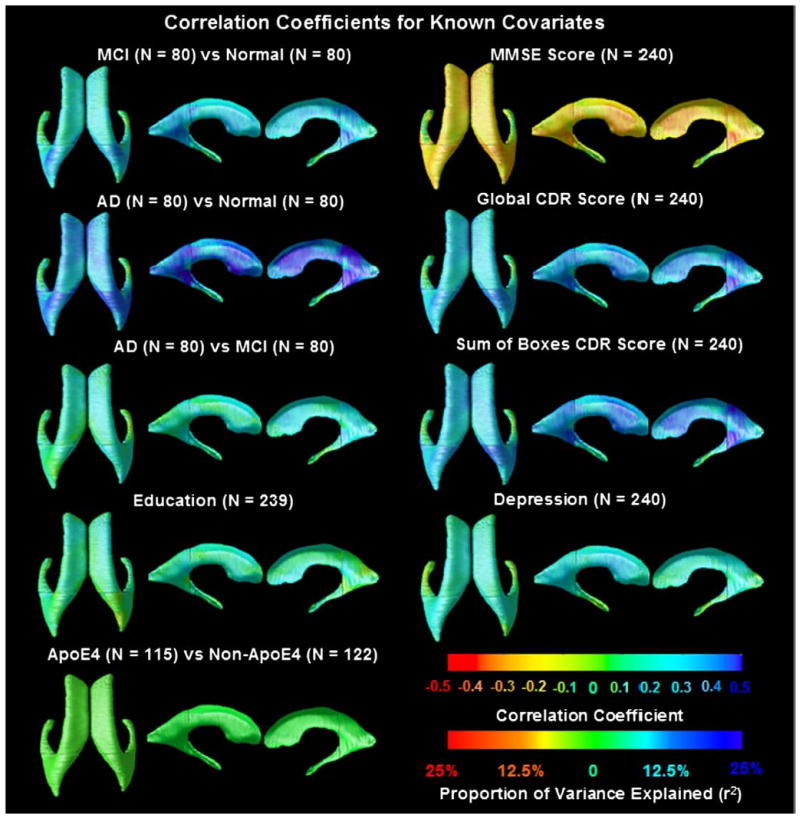
Fig. 4 shows p-maps for each pairwise diagnostic comparison (AD/MCI/normal), and correlations between ventricular morphology and MMSE scores, global CDR, sum-of-boxes CDR scores, ApoE genotype (coded as 1 for the presence of an E4 allele; 0 otherwise), educational level and clinical depression severity, as covariates. The degree of ventricular expansion was strongly associated with diagnosis (with greatest effects for the AD vs. normal comparison), MMSE scores and clinical depression scores. The overall significance of these mapping results was confirmed by FDR analysis (Fig. 5), and the Correlation coefficients (r-maps) are shown in Fig. 6.

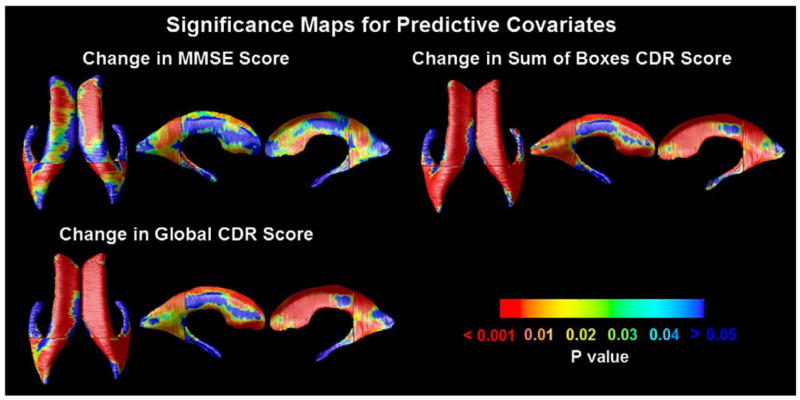
Fig. 4.

Significance maps for correlations between local ventricular enlargement and (1) diagnosis (MCI vs. normal, AD vs. normal and AD vs. MCI); (2) cognitive scores (MMSE, global CDR, and sum-of-boxes CDR); (3) ApoE genotype, (4) educational level and (5) clinical depression scores. Figs. 5 and 6 show the corrected significance and correlation coefficients of these maps respectively. One MCI subject was missing data on educational level, so they were excluded from the maps assessing that covariate.

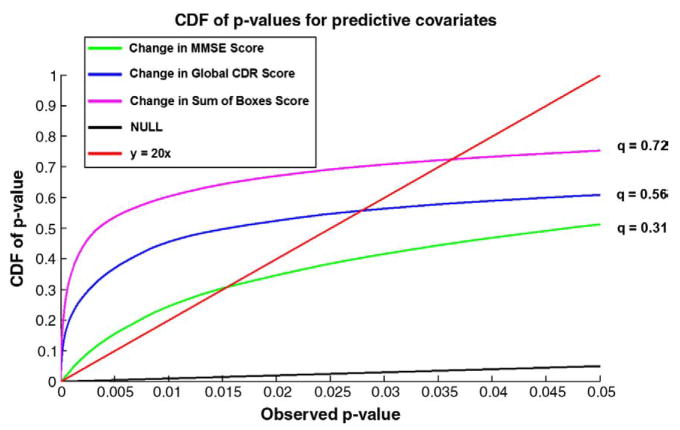
Fig. 5.

Cumulative Distribution Functions (CDFs) of significance maps associating ventricular enlargement with diagnosis and clinical measures. Based on FDR q-values, the AD vs. control and MCI vs. control contrast are significant, as is the link between ventricular dilation and (1) MMSE, global CDR, and sum-of-boxes CDR scores, and (2) depression severity. This type of plot means that all covariates examined, apart from educational level and the AD-MCI comparison, were significantly associated with ventricular expansion. The suprathreshold area in the correlation maps was higher than would be expected by chance (red line) for all statistical thresholds ranging from 0 to 0.05 (and even as high as 0.7 in some cases). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Correlation coefficients (r-maps) and proportion of variance explained (r²) for the 3 diagnostic comparisons, showing the strength of association between radial ventricular size and diagnosis, as well as with cognitive and clinical scores. The correlations in the MMSE map are negative (red colors) because a higher MMSE score is associated with less degeneration (opposite to all the other ones). It is of interest that the correlations with the MMSE scores, across the full sample, are higher than those with the CDR ratings, including the sum-of-boxes CDR scores. A correlation with an absolute value of around 0.2–0.3 for MMSE suggests that around 10% of the variation in the MMSE scores is accounted for by the ventricular enlargement. It is likely that atrophy (and the resulting ventricular enlargement) caused cognitive decline, hence changes in MMSE score. This would be regarded as a moderate to weak correlation, but is highly significant in a sample of this size. These maps are visually in very strong agreement with the corresponding p-maps, and so they are not shown for the other covariates. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Correlations of ventricular morphology and CSF biomarkers

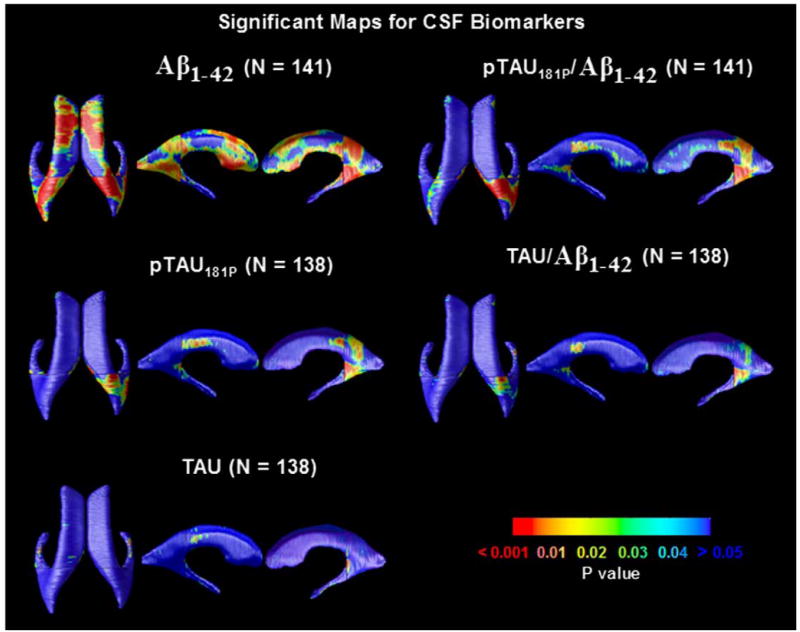
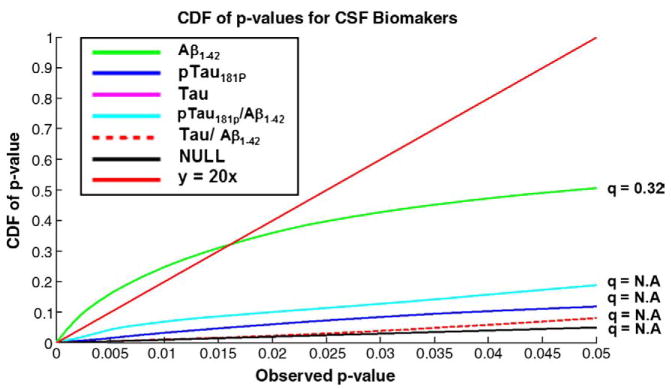
We investigated whether these cross-sectional measures of lateral ventricular expansion were correlated with the levels of CSF biomarkers. Our results in Fig. 7 indicated that higher CSF Aβ_1–42 was associated with ventricular expansion and the levels of pTau_181p, and ratios of Tau/Aβ_1–42 and pTau/Aβ_1–42 were strongly associated with right posterior horn expansion; an FDR analysis is shown in Fig. 8.

Fig. 7.

Significance maps revealing the profile of correlations between local ventricular enlargement and CSF biomarkers, including levels of Aβ_1–42, pTau_181p, Tau, and ratios of Tau/Aβ_1–42 and pTau/Aβ_1–42. Fig. 8 shows the corrected significance of these maps.

Fig. 8.

Corrected significance for correlation between lateral ventricular expansion with CSF biomarkers by FDR analysis. Of all the plasma measures, levels of Aβ_1–42 correlated best with the morphometric differences.

Predicting future cognitive change

One goal of ADNI is to determine which brain imaging measures predict future clinical decline, primarily for drug trial “enrichment”, a statistical strategy that empowers drug trials by selecting as candidates those at highest estimated risk of imminent decline in cognition. We correlated baseline ventricular morphology with subsequent change over 1 year, in MMSE, global CDR and sum-of-boxes CDR scores. Fig. 9 reveals regions where ventricular expansion at baseline correlated with future outcomes; all maps were significant overall after multiple comparisons correction with CDF-based FDR (Fig. 10).

Fig. 9.

Significance maps correlate baseline ventricular shape with subsequent decline, over the following year, in 3 commonly used clinical scores.

Fig. 10.

FDR analysis of correlations with future cognitive changes. Correlations were significant between baseline ventricular enlargement and future 1-year changes in MMSE, global CDR and sum-of-boxes scores. The baseline measures are therefore good predictors of future cognitive decline, at least at the group level.

Minimal effective sample sizes

To determine how many subjects would suffice to detect statistically significant correlations of ventricular enlargement with diagnosis and with clinical test scores, we randomly threw out subjects from our initial samples, yielding additional groups with reduced sample sizes, N. These groups were chosen to preserve the 1:1:1 ratio among normal, MCI and AD sample sizes, while maintaining the sex balance in all groups. As shown in Table 2, 40 and 120 subjects, respectively, were sufficient to discriminate AD and MCI from normal groups. 120 subjects were required to correlate ventricular enlargement with MMSE, global CDR, sum-of-boxes CDR scores and depression severity. These results offer a guide to estimate sample sizes with adequate power to detect group differences in future studies using this method.

Table 2.

Effects of varying the sample size.

	Minimal N	q-value for the minimal N	q-value for the full sample
AD vs. normal	40	0.09	0.75
MCI vs. normal	120	0.19	0.67
MMSE	120	0.37	0.72
Sum-of-boxes score	120	0.57	0.76
Global CDR score	120	0.48	0.77
Depression	120	0.10	0.38

The minimal sample size, N, and the corresponding q-value, based on using the full available sample, for discriminating AD and MCI from normal subjects and for other covariates (MMSE, global CDR, sum-of-boxes CDR and depression scores). Sample sizes smaller than N are inadequate to detect the effect of interest, meaning that no FDR threshold detects significant findings that control the false discovery rate at the conventional 5% level. In these maps, higher q-values typically denote greater effect sizes; if q is defined at all, then its value is the highest statistical threshold for which the thresholded region is expected to control the false discovery rate at the conventional 5% level.

Non-parametric versus parametric testing

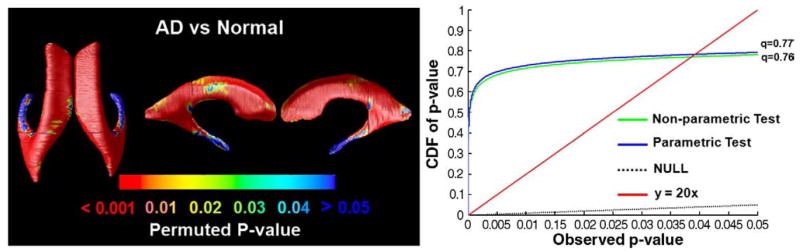
Given the distribution of radial measurements in the two groups, we used a Student’s t-test to compare the groups. Even so, we wanted to assess whether the choice of a parametric test was justified, so we re-ran the statistical maps using a non-parametric (permutation-based) test at each voxel. This test does not assume that the radial distances are normally distributed in each group. The statistical maps and cumulative plot of p-values (see Fig. 11) were almost identical to the results obtained using parametric statistics, and the q-value was also almost identical (q = 0.76 for the non-parametric test and q = 0.77 for the parametric test). These values indicate that whenever the statistical threshold applied to the maps lies in the range 0 to 0.76 (or 0.77), then the false discovery rate (expected proportion of false positives) in the thresholded region does not exceed the conventional rate of 5%. This very high q-value occurs mainly because the two groups (AD subjects and controls) differ substantially at almost every point in the maps.

Fig. 11.

Comparison of parametric versus non-parametric tests. Here we show the p-values for the comparison of ventricular surface anatomy in AD versus normal subjects (left panel) based on a non-parametric test. This test permutes the assignment of subjects to groups and computes a non-parametric null distribution for the resulting Student’s t statistics, rather than assuming that the underlying distributions are Gaussian. As the cumulative plots of p-values show, parametric and non-parametric tests give almost identical results for both the cumulative p-value plot and the q-value derived from the plot. The q-value is the highest statistical threshold at which the expected false discovery rate is kept below the conventional 5% rate.

Predictive accuracy

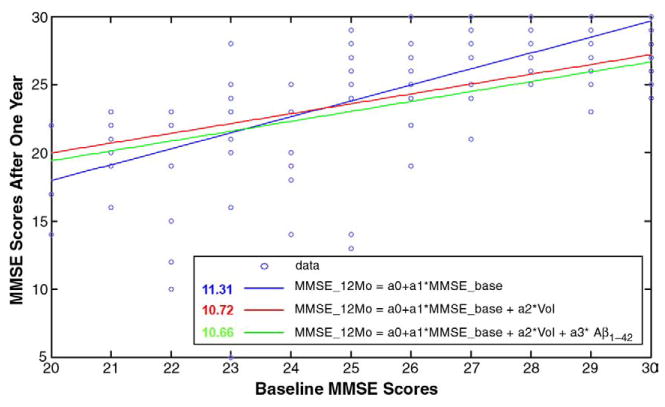
Fig. 12 shows how well cognitive performance (on the MMSE) one-year after baseline assessment could be predicted from (1) MMSE scores at baseline, (2) MMSE scores plus ventricular volumes at baseline, and (3) MMSE, ventricular volume, and CSF-derived measures of the Aβ_1–42 biomarker derived from lumbar puncture. As seen in the least-squares regression lines, the prediction errors were successively reduced as each more invasive measure was added. Even so, it must be conceded that in moderate stages of amnestic MCI, standardized cognitive tests may provide better predictive accuracy than measures of whole brain, ventricular, entorhinal cortex, or hippocampal volumes for assessing progression to Alzheimer disease (Fleisher et al., 2008).

Fig. 12.

Predicting later cognitive decline from baseline measures of MMSE, ventricular volumes and the Aβ_1–42 biomarker using least-squares regression models. MMSE_12Mo, MMSE_base, Vol and Aβ_1–42 denote MMSE scores after a one-year follow-up interval, the baseline MMSE score, ventricular volumes and Aβ_1–42 protein levels, respectively. The values shown in the legend represent the mean square of the deviations of the data from the predictive models, showing that prediction errors were successively reduced (but only by about 5%) as each more invasive measure was added to the predictive model.

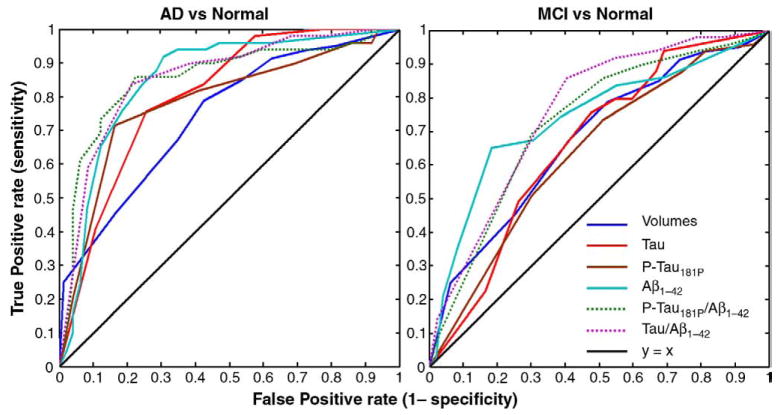
ROC curves

In Fig. 13, we compiled receiver operating characteristic (ROC) curves for predicting clinical diagnosis based on ventricular volumes, compared with other CSF biomarkers derived from lumbar puncture. Using clinical diagnosis as a gold standard, these ROC plots show the true positive rate versus the false positive rate (the two “operating characteristics”) for each binary classifier, as its discrimination threshold is varied. Ventricular volumes and CSF-derived biomarkers performed about equally well in distinguishing MCI subjects from controls, but the CSF-derived biomarkers all outperformed ventricular volumes in discriminating AD subjects from controls (see Fig. 13, right panel). Each measure provides potentially independent predictive power, so it may be possible in future to maximize the area under the ROC curve even further by combining each of these features into a single diagnostic classifier. If all domains render unique pieces of information that are not collinear, then adding them should help the diagnosis. Methods to combine these features into composite classifiers include support vector machines and adaptive boosting (Adaboost). Adaboost and SVM may be used together to adaptively combine many weak classifiers to produce a strong classifier that outperforms all of them (see Morra et al., 2009, for a review of these methods). In all of these approaches, cross-validation is vital, to determine how well brain-behavior relationships obtained from one part of the data hold up in the remaining non-overlapping part.

Fig. 13.

ROC curves for regression models predicting clinical diagnosis (here treated as the gold standard) based on ventricular volume and various CSF-derived biomarkers. The line of no discrimination (based on random guessing) is diagonal, and all the ROC curves lie above it, suggesting that all measures have some discriminative power. The curves that lie above the others represent the best classifiers. The area under the ROC curve represents the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one. In this sample, all of the CSF-derived biomarkers discriminate AD from normality better than ventricular volumes do. Ventricular volumes and CSF-derived biomarkers perform about equally well in distinguishing MCI subjects from controls, and, as expected, MCI is harder to differentiate from normality than AD is.

Discussion

In this paper, we investigated the correlations between ventricular morphology and baseline and future change in scores on the MMSE and CDR scales, ApoE genotype, educational level and depression severity, as well as CSF biomarkers. We measured ventricular morphology using a multi-atlas fluid image alignment method—a semi-automated mapping technique that uses a fluid deformation of expertly segmented mesh models to derive morphological markers of disease. Although the resulting ventricular maps give only a partial indication of the atrophy occurring throughout the brain, such an approach is easy to apply to large numbers of scans.

The study had 4 main findings. First, AD versus control groups as well as MCI versus control groups were easily differentiated using maps with sample sizes as low as 40 and 120 subjects, respectively. Posterior regions of the ventricles tended to expand between normalcy and MCI, while more frontal regions of the superior horns tended to expand further between MCI and AD. This suggests that, as with the cortex, there may be a topographic sequence of ventricular expansion with disease progression, rather than just an intensification of expansion in the same regions. Second, ventricular expansion correlated highly with MMSE, global CDR, and sum-of-boxes CDR scores and with depression severity across the entire sample, requiring only 120 subjects to detect these correlations, and confirming that the observed morphometric difference is linked with cognition. The CDF plots suggested that, of all the clinical measures, the sum-of-boxes CDR scores were the measures that were most tightly associated with ventricular expansion. In CDF plots, the associations with greatest effect sizes are those with the curves that rise most rapidly and remain higher than those for other associations. Third, lower CSF levels of the Aβ_1–42 protein, a biomarker of AD pathology, were correlated with ventricular expansion. Fourth, ventricular expansion at baseline strongly predicted future clinical decline over the following year, whether the decline was measured using 1-year changes in MMSE, global CDR or sum-of-boxes CDR.

Regarding biochemical markers, we found that Aβ_1–42 levels correlated with ventricular expansion maps in 138 subjects, corroborating earlier work by Wahlund and Blennow (2003) on a sample of 47 subjects with wide variations in cognitive impairment-ranging from MCI to manifest AD. Wahlund and Blennow (2003) found that lower Aβ_1–42 was associated with lower overall brain volumes (r = 0.55; p<0.0001) and larger ventricular volumes (r = −0.53; p<0.001). They also found, as we did, that Tau-derived measures were not detectably correlated with baseline ventricular morphology, suggesting that Aβ_1–42 may be a better correlate of disease burden as reflected on MRI. By examining CSF at baseline and MRI at both baseline and 16 months follow-up, Wahlund and Blennow (2003) also noted that significantly higher T-tau (r = 0.47; p<0.001) and pTau (r = 0.41; p=0.005) levels were associated with more marked progressive ventricular widening over time during the follow-up interval, perhaps reflecting the intensity of the disease process. This leads to the intriguing hypothesis that Tau measures may index active progression of the disease while Aβ_1–42 may instead reflect the cumulative disease burden at any given time. In support of the Tau-derived measures, CSF pTau_181p levels have been found to be lower in cognitively healthy subjects who developed dementia after three years follow-up versus those who did not (Skoog et al. 2003). CSF Tau has been consistently found to be increased in AD versus healthy subjects (Jensen et al.,1995), whereas CSF levels of Aβ_1–42 are reduced. The association between AD and increased Tau levels has also been corroborated in neuropathologically confirmed patients (Clark et al. 2003), and CSF tau has been established as one of the most promising biomarkers for AD (Blennow and Hampel, 2003). In AD, as well as in some other neurodegenerative diseases associated with Tau pathology, Tau is phosphorylated beyond the normal functional level (Avila, 2006). Elevated pTau_181p levels have been found in MCI patients who progress to AD (Arai et al. 2000) and pTau_181p levels correlate with points lost per year in MMSE (Buerger et al. 2002a,b). In advanced stages of AD, clinical diagnosis is relatively accurate, so the relative value of these invasive CSF samples is greater in normals and those with MCI.

It is also important not to infer that Tau levels and measures of structural brain atrophy are not correlated, even though our study of 240 subjects (with biomarker information available in 138 subjects) did not detect any association. In one recent study, we related cortical levels of plaque and tangles to cognitive variations in normal subjects, and in those with MCI and AD, aiming to detect correlations between pathology and atrophy (Braskie et al., 2008).

In that study, the cortical pathology, as quantified with a PET tracer sensitive to AD pathology, was not correlated with cortical thickness measures, which are also known to decline in MCI and AD (see Thompson and Apostolova, 2007 for a review). Pathology and atrophy may therefore vary most actively at slightly different times, or they may only correlate in samples that include very advanced AD subjects. Alternatively, there may be too much measurement error (including registration error) for a true correlation to be detected in current samples.

The very recently published study by Nestor et al. (2008) also examines the ventricles in an ADNI dataset, but does not provide any maps of the associations between ventricular morphology and clinical correlates, and does not associate ventricular differences with serum biomarkers, as we did here. Even so, some comparison between the two studies is warranted. Nestor et al. (2008) used a region growing method to segment the lateral ventricles and examined the cross-sectional and longitudinal ventricular volume differences in a large ADNI subset of 152 normal elderly controls, 247 MCI and 105 AD subjects after six months. In line with our findings, they also found that the AD group had greater ventricular enlargement at baseline than the MCI group, and the MCI group had greater enlargement than controls, although they did not provide maps of these effects as we did in the current study. The mean ventricular expansion over six months was 1.5%, 3.4% and 5.7% for control, MCI, and AD groups respectively in the Nestor et al. study, which supports the notion that ventricular measures may be useful for group discrimination even in very short interval follow-up studies (e.g., 6 months). Nestor et al. also found that the 18 of the 247 MCI subjects who progressed to AD in six months had higher rates of ventricular expansion than the stable MCI subjects, and the expansion rate for MCI group in aggregate exceeded that in controls. We did not examine longitudinal changes in this study, but the findings of Nestor et al. (2008) are consistent with our maps of changes over time in the hippocampus in 490 ADNI subjects scanned over a 1-year interval (Morra et al., 2008a,b). In that study, we found the same rank ordering of the diagnostic groups with respect to mean rates of longitudinal hippocampal atrophy over 1 year as did Nestor et al. (2008) did for ventricular expansion over 6 months, i.e. MCI converters showed greater changes than stable MCI subjects, and controls showed least changes.

Using mapping approaches, it would make sense in the future to determine exactly where on the ventricles these longitudinal changes are taking place. If these changes discriminate MCI converters from nonconverters, it would be useful to hone in on any specific areas of the ventricles that are most discriminative, assuming that the changes are not uniform across the ventricular surface, an assumption that is suggested by our baseline mapping data here. This approach is advocated by Ferrarini et al. (2008a,b), who used a machine learning approach to distinguish AD patients from controls, using specific subregions (termed “biomarker nodes”) on the ventricular surface to give best group discrimination.

Mapping of morphological differences in the ventricles may provide added benefit relative to simpler measures of ventricular volume. One benefit of the 3D models is that they provide spatially detailed maps of effects, and can be used to derive such measures as radial thickness, which vary across the surface. The resulting maps can implicate subregions that maximally discriminate groups for diagnostic classification. Ferrarini et al. (2008a,b) thresholded their statistical maps and used the displacements in the remaining subregions as features for a statistical classifier to differentiate AD from controls. Their classifier was more accurate when a smaller ventricular region was used for the classification, based on thresholding the map more stringently. As such, maps can define anatomical subregions to increase classification accuracy on unseen scans. Maps may outperform statistics derived from regions of interest, especially when the statistical effects are spatially concentrated. In one study of the hippocampus (in 490 subjects; Morra et al., 2008a,b), where changes over 1 year were diffuse, our 3D maps did not outperform simple volumetric summaries in separating AD and MCI groups from controls. In other studies, our maps sometimes found effects not detectable with volumetric summaries (Nicolson et al., 2006). Finally, some additional effort is required for making surface-based maps versus computing simple volumetric summaries. When a large database is examined automatically, this additional effort may pay off. When effect sizes are expected to be very large, simple volumetric assessments may be sufficient.

The correlation between ventricular expansion and depression is of interest. In a prior study of 400 subjects from the Alzheimer’s Disease Neuroimaging Initiative (Morra et al., 2008b; 100 AD, 200 MCI and 100 controls; 395 had clinical depression ratings available), we found that right but not left hippocampal atrophy was associated with geriatric depression scores (p = 0.004, corrected). This was largely attributable to an association between depression severity and atrophy of the hippocampal head, consistent with most earlier studies (Bell-McGinty et al. 2002; Hickie et al. 2005; Lloyd et al. 2004; Ballmaier et al., 2004, 2008) showing smaller hippocampal volumes in elderly depressed patients compared to controls.

Because we detected correlations with hippocampal atrophy only in the right hemisphere in a larger ADNI sample, consistent with other reports that have shown differences as being more pronounced for the right than for the left hemisphere (Bell-McGinty et al., 2002), we were interested in whether ventricular expansion was either lateralized (greater on the right) or if the correlation with depression would be found in the left hemisphere only. In Fig. 4 (last panel), it is clear that depression severity is correlated with expansion all over the ventricular surface, suggesting that depression is correlated with atrophy in general but that there is less power to detect it in the left hippocampus than in the left ventricle (this would be inferred by considering the results of Morra et al., 2008b and this paper together).

For practical application of any type of atlas-based segmentation, it is beneficial to know whether it is better to propagate atlases that are matched by age or diagnosis to the individuals whose anatomy is being studied, or to reduce this bias by picking a range of labeled atlases with varying geometries. Our recent studies examined a highly related problem, i.e., in a group study, whether normalization of images to a single individual’s scan results in greater effect sizes, or better labeling accuracy, compared with normalizing images to a group-specific template (defined using appropriate deformation and intensity-based metrics; Lepore et al., 2007), or an optimized individual template (Chiang et al., 2006). In Chiang et al. (2006) we found that greater effect sizes were obtainable in a morphometric study of HIV/AIDS if data were aligned to a geometrically optimized individual template (as in Kochunov et al., 2001) rather than aligning data to a population-based average image, perhaps because features in the individual template were more sharply defined and were not blurred away by intensity averaging (especially at the cortex). Even so, aligning data to any one individual atlas image risks a bias effect in which images that more closely resemble the template may be more accurately registered to it. They may lead to a “registration error by group” interaction that may cause bias and inflate the probability of false positive findings. To avoid this registration bias, in Lepore et al. (2008), we found that a geometrically centered template, defined using Lie group statistics on the deformation tensors, to have the mean geometry for a group of subjects, gave marginally higher effect sizes in an HIV morphometry study, relative to using an individual template. They avoided statistical bias that might result from randomly picking a template from a population.

When multiple atlases are used, as in this paper, this concern of bias in alignment to the atlas (based on the particular geometry of the atlas) is partially alleviated by deliberately using atlas templates from multiple subjects. This reduces the concern that the new anatomies to be labeled will differ severely from the labeled template. Although this is a theoretical argument, there is also empirical data supporting it. We recently found (Chou et al., 2008) that the labeling accuracy for individual structures was improved (i.e., the labeling error was decreased) when multiple atlases are used for segmentation versus a single atlas. If the choice of the atlas did not affect the registration error, then it would not be possible to reduce this error by combining multiple registrations. As the opposite is true, this has led to an increase in popularity of multi-atlas approaches (Kochunov et al., 2005, Twining et al., 2005, Chou et al., 2008), which can avoid the bias in picking a single registration target.

In this study we note that multi-atlas segmentations tend to give rise to higher effect sizes, and in Lepore et al. (2008) we noted that using a geometrically centered template gave rise to marginally higher effect sizes in tensor-based morphometry. The question then arises as to whether these higher effect sizes directly imply that the atlas is “better”, in the sense of giving more accurate results, or avoiding biases or confounds, or satisfying certain desirable axioms (e.g., avoiding possible “registration error×group” interactions). Clearly, an atlas that gives better effect sizes does not automatically imply that results are more accurate, for 3 reasons. First, we recently found that a method that directly aligns geometrically centered group mean templates, in tensor-based morphometry, gives better effect sizes for detecting Alzheimer’s disease than the standard approach, which aligns all images to a common template (Hua et al., 2008a,b). However, as we argued in Hua et al., (2008a,b), the former method is invalid and incorrectly detects differences between two randomly selected groups of controls when, by construction, no differences are present. In other words, a method that detects higher effect sizes should be tested on null data to make sure that the false positive rate is correctly controlled, and without that, higher effect sizes do not, in themselves, entail greater accuracy. Second, a higher effect size may provide good evidence for higher anatomical labeling accuracy, even if it does not logically entail it, if some convincing reason can be found as to why the error variance of the method is reduced. In the case of multi-atlas registration, random errors in the manual tracing of the ventricle surfaces are certainly reduced by averaging surface models from several subjects, so this averaging step decreases a known source of error. And, although it cannot be verified as there is no independent data on the ground truth, it may also be that the average registration error is less when using multiple templates to label anatomy than when relying on a single atlas, which may not reflect the anatomy of all subjects. Thirdly, there is a somewhat obscure situation in which more accurate registration methods may in fact produce lesser effect sizes when used for morphometry. Every morphometric method based on nonlinear registration tends to pick up differences at a certain scale, such as a few tens of voxels if deformation fields are very smooth, or even at the voxel level if deformation fields have a very high number of degrees of freedom. The scale at which effects are detected depends on the level of smoothing, the weight on the regularization term, or (in continuum-mechanical registration approaches), the autocorrelation or Green’s function of the elastic or fluid operator governing the deformation. In a specific dataset, group difference effects may be detectable with greatest effect sizes when more smoothing of the registration field is used, while a more accurate registration method, which labels anatomy more precisely, could either fail to detect them or detect them with lesser effect sizes. Increased labeling accuracy does not entail greater effect sizes. If, for instance, the small-scale details of structures do not differ between groups, but the larger-scale shape characteristics do differ, then a less accurate registration method can (at least logically) provide a higher effect size in detecting the group differences, as matching the small-scale features may just add noise to the statistics on group differences. As such, it seems fair to consider both the effect size and labeling accuracy in choosing the best morphometric method, because the scale at which greatest errors occur in the method may not match the scale at which signals are present in the empirical data. We have been studying this effect (Chou et al., 2009).

This paper has some limitations, some of which should be addressable when the full ADNI sample is collected. First, of the 240 subjects in the study, only a limited number had CSF-based assessments of the biochemical biomarkers (49 NC, 42 MCI, 47 AD). While this is one of the first studies, to our knowledge, to correlate ventricular structure with biochemical markers, and certainly the first study to use maps to do so, this rather small subsample with biochemical biomarkers may be a limiting factor in their utility here. Second, this is a cross-sectional rather than longitudinal study, and the dynamic relationship between cognition, biomarkers and ventricular morphology may become clearer as follow-up data is collected. Thirdly, our estimates of minimal sample sizes to detect group differences or covariate effects are a little different than conventional power estimates for a clinical trial. In a clinical trial, it is typical to estimate, based on longitudinal data, the expected sample size required to detect a 25% decrease in the rate of disease progression (as quantified by the method), with 80 or 90% power. Using false discovery rate curves, we are beginning to examine the minimal sample sizes to detect a 25% slowing of disease progression; longitudinal data are vital to answer this question definitively. If we were measuring the rate of change in ventricular surfaces over time, we could determine the power of this method to detect a 25% slowing of the rate of change, over a one-year interval, for example.

Another limitation of this study, taken in isolation, is that it is restricted to the ventricles, whereas a number of studies during the past few years have investigated gray and white matter atrophy in MCI and AD, and have also shown good predictions of clinical progression. A caveat is also necessary regarding the interpretation that baseline data predicts (or correlates with) future clinical decline. When we correlated baseline ventricular morphology with subsequent change over 1 year, in MMSE, global CDR and sum-of-boxes CDR scores, all maps were highly significant. This is a useful observation, as it shows that all regions of the ventricles, not just selective regions, have the characteristic expansion that is predictive of future decline. Even so, this correlation is to be expected, as subjects who are more impaired are much more likely to have future cognitive decline than subjects who are less impaired. In other words, cognitive impairment measured by MMSE, global CDR or CDR sum-of-boxes, predicts (or correlates with) future cognitive decline on the same measures. Furthermore, the ApoE4 gene and increasing age are risk factors for developing AD, so that in any sufficiently large group of controls, MCI, or AD subjects, the ApoE4 gene (and age) will also correlate with future cognitive decline. So, although it is of interest that increased ventricular volume alone predicts cognitive decline, it must also be conceded that identifying covariates in an atlas has little utility if there is no method to take them into account. In our initial efforts fitting multiple predictors to maps of hippocampal and caudate atrophy (Apostolova et al., submitted for publication (a),b; Schuff et al., 2009), we found that very large samples are needed to detect to what extent imaging measures predict future cognitive decline after baseline cognition, ApoE4 status, age (and potentially other clinical covariates) are taken into account. The stable fitting of multiple predictors with small effects is difficult unless the sample is very large. Once the full ADNI sample has been collected, we plan to set up a general linear model with multiple predictors including baseline cognition, age, and ApoE4 status. From this, we will be able to test the hypothesis that any proposed imaging measures (such as ventricular maps) have an additional value for predicting cognitive decline beyond those measures obtainable without imaging.

As noted in Weiner (2008), ventricular expansion correlates more strongly with changes on cognitive tests than medial temporal lobe (MTL) atrophy rates (Jack et al., 2004). Abnormally fast ventricular dilation over time has also been linked to the accumulation of AD pathological markers such as cortical neurofibrillary tangles and amyloid plaques (Silbert et al., 2003), and to rates of cognitive decline in AD patients and controls (Adak et al., 2004). Ventricular changes reflect atrophy in surrounding structures (Powell et al., 1991), providing somewhat indirect assessments of tissue reduction, that correlate with cognitive deterioration. Some studies suggest that ventricular enlargement is quite highly correlated with gray matter atrophy but not with white matter hyperintensities (Hsu et al., 2002). In 62 AD patients (24 with lacunar infarcts in the subcortical white matter and 38 without), Hsu et al. (2002) found that ventricular CSF volume correlated inversely with cortical GM volume (r = 0.35) but not with total WM volume. Contrary to ventricular CSF, sulcal CSF correlated inversely with cortical GM (r = 0.47) and with total WM (r = 0.75) in AD patients. No significant correlation was found between the volume of white matter hyperintensities and ventricular or sulcal CSF. Even if ventricular expansion is just an indirect reflection of diffuse gray matter atrophy that could be measured more directly, there may be circumstances where ventricular volumes are easier or more reproducible to measure than gray or white matter changes. First, accurate cortical gray matter segmentation requires a 3D MRI sequence with sufficient gray/white matter contrast and spatial resolution to resolve the cortical mantle. Scans used clinically or in neuroscience research do not always provide superior gray/white matter differentiation in many cortical regions, either due to partial volume effects, susceptibility artifacts, SNR fall-offs near the brain parenchyma, radio-frequency bias field effects, and confounding effects of meninges, whose signal resembles that of gray matter on T1-weighted scans. By contrast, ventricular segmentation is relatively easy even in low resolution scans, as the ventricular CSF has high contrast relative to surrounding tissues. Whether or not the ventricular measures are more useful than gray and white matter quantitation for diagnostic accuracy or for clinical trials depends on the expected effect sizes, the cost of acquiring scans with sufficient contrast for accurate GM/WM differentiation, and the ability to performing reproducible GM/WM segmentation across scanners and across time.

It may seem more natural to focus on segmenting the inferior horns of the lateral ventricles, given their proximity to the gray matter structures of the medial temporal lobe, which are susceptible to early atrophy in AD. Unfortunately, our deformation-based segmentation method is not optimal for mapping the inferior horns of the ventricles, since healthy subjects typically have very low CSF volumes of in the inferior horns, and their geometry appears narrow on coronally-resliced MRI (typically a millimeter or less in width). Fortunately, the other ventricular horns do show very high effect sizes for disease and genetic effects, partly because the error in segmenting them is much less as a proportion of their overall volume, and the expected percent volume difference in disease is extremely large. In theory, an inferior horn template could be propagated into new scans using a fluid registration approach, but it would be hard to propagate accurately onto controls in regions with very limited CSF, as large localized contractions (i.e., compressions of the template) would be needed. The fluid prior in the registration enforces a spatial smoothness in the deformation that limits very large localized compressions.

Some comparison with the maximally discriminative regions in other studies is warranted. In the largest ventricular mapping study to date (Carmichael et al., 2006; N =339), we applied a single-atlas segmentation approach to data from an independent sample of 40 AD, 74 MCI and 225 control subjects, drawn from the Cardiovascular Health Study (CHS). In that study, we were not able to examine the effects of the many covariates studies here (e.g., education, depression, ApoE status, and tau pathology in the CSF). Instead we focused on defining the location of maximal differences between AD, MCI and control groups, using pairwise contrasts between groups to create statistical maps of radial ventricular expansion. As observed here, contrasts between normal and demented subjects showed dramatic ventricular atrophy throughout the lateral ventricles, especially along the frontal and temporal horns, but essentially all regions of the lateral ventricles provided discriminative power. This is in line with the known neurobiology of AD, in which all lobes are somewhat affected by atrophy; this atrophy allows the CSF spaces to expand in all ventricular horns. In Carmichael et al. (2006) and in our current study, the MCI group showed prominent expansion relative to controls along the lateral boundaries of the frontal horns near their posterior limit, but the AD group showed expansions relative to MCI subjects along the superior and lateral surfaces of the frontal horns, adjacent to the head of the caudate nucleus. In our current study, consistent with our maps in Carmichael et al. (2006), the main MCI-normal differences were found not in the anterior regions of the frontal horns, but in the more posterior regions, around the junction with the occipital horns (a region sometimes called the atrium or trigone of the lateral ventricles, because it is the “3-sided” region where all 3 horns join). If the trigone of the ventricles is sensitive to MCI, then both the current study and that of Carmichael et al. (2006) suggest that the maximally discriminative region is much more restricted than the region that differs between AD and controls. This is also plausible anatomically, because extensive atrophy of the caudate head–which contributes to expansion in the anterior portion of the frontal horn–is not typically found in MCI, and although it is found in late AD, it is more typical of Parkinsonian-type dementias (Apostolova et al., 2008). If there is truly an anatomical sequence in which the discriminative region of the ventricles expands forwards along the frontal horn as AD progresses, then it makes sense for future studies to more heavily weight or focus on specific subregions of interest for detecting discriminative changes in the ventricles (see Ferrarini et al. 2008a,b). The use of statistically based regions of interest from prior independent studies is likely to empower future population studies by emphasizing regions where effect sizes are expected to be the greatest.

Ferrarini et al. (2008a) also used a shape modeling method based on “Growing and Adaptive Meshes” (GAMEs) and Support Vector Machines (SVM) to discriminate and classify 58 AD subjects and 28 age-matched healthy elderly controls. In their study, the left inferior medial temporal horn, the right (superior and inferior) medial temporal horn, and areas close to the genu of the left side of the corpus callosum and the head of the right caudate nucleus showed a consistent pattern of features that helped to discriminate AD patients from controls. Ferrarini et al. (2008a,b) went on to identify the maximally discriminative region on the ventricles for distinguishing AD from controls, by thresholding the statistical maps. By entering the 3D displacement values at these points into a support vector machine classifier, they correctly classified 76% of a group of unseen AD patients. The more stringent the thresholding of the maps (i.e., the smaller the region of interest), the more accurately they were able to classify the patients from controls. This further motivates the focus on localized regions with greatest effects in statistical maps.

In conclusion, brain mapping methods are now being evaluated for tracking AD in terms of statistical power, predictive validity, and automation. Ventricular measures show a relatively high effect sizes in distinguishing disease from normality. The FDR curve ranking method adopted here, while not the only method to evaluate effects in statistical maps, is an attractive approach for algorithm developers to compare the power of different map-based methods head-to-head, in an effort to further reduce the minimal sample sizes.