Phase matching of high harmonic generation in the soft and hard X-ray regions of the spectrum

Abstract

We show how bright, tabletop, fully coherent hard X-ray beams can be generated through nonlinear upconversion of femtosecond laser light. By driving the high-order harmonic generation process using longer-wavelength midinfrared light, we show that, in theory, fully phase-matched frequency upconversion can extend into the hard X-ray region of the spectrum. We verify our scaling predictions experimentally by demonstrating phase matching in the soft X-ray region of the spectrum around 330 eV, using ultrafast driving laser pulses at 1.3-μm wavelength, in an extended, high-pressure, weakly ionized gas medium. We also show through calculations that scaling of the overall conversion efficiency is surprisingly favorable as the wavelength of the driving laser is increased, making tabletop, fully coherent, multi-keV X-ray sources feasible. The rapidly decreasing microscopic single-atom yield, predicted for harmonics driven by longer-wavelength lasers, is compensated macroscopically by an increased optimal pressure for phase matching and a rapidly decreasing reabsorption of the generated X-rays.

Advances in X-ray science and technology have resulted in breakthrough discoveries ranging from unraveling the structure of DNA and proteins to visualizing atoms, molecules, and materials at the nanoscale level. These continuing successes have spurred the development of X-ray free-electron laser sources that promise to create superexcited states of matter or to capture the structure of a single biomolecule. Another very exciting advance in X-ray science has been the ability to generate ultrafast (0.1–10 fs), coherent X-rays from a tabletop-scale apparatus, by using the extreme nonlinear optical process of high-order harmonic generation (HHG). In HHG, the output of a tabletop femtosecond laser is upconverted into the extreme-UV and soft X-ray regions of the spectrum. The unique characteristics of HHG soft X-rays have opened up many new scientific opportunities. The femtosecond-to-attosecond pulse duration has made it possible to capture the coupled motions of electrons, atoms, and molecules in real time (1–7). Moreover, the low divergence and capability to produce light with full spatial coherence (8) have enabled static and dynamic diffraction and imaging with resolutions of tens of nanometers (9, 10).

The microscopic physics of the high harmonic generation process can be understood in terms of an intuitive recollision model (11, 12). In this model, an electron is first ripped from an atom by the strong electric field of a focused laser beam. Once liberated, the electron is accelerated to high energies by the oscillating laser field and can violently recollide with its parent ion. Finally, if the electron recombines, any excess kinetic energy acquired in the external field is emitted as a high-energy photon. This simple physics can be used to determine a maximum photon energy that can be generated, or a so-called single-atom cutoff (12, 13):

Here, U_p is the average kinetic energy of a free electron oscillating in the field of a laser [U_p (eV) = 9.33 × 10⁻¹⁴I_L (Wcm⁻²) λ_L² (μm²), where I_L and λ_L are the laser intensity and wavelength), whereas I_p is the ionization potential of the atom. In this highly nonlinear frequency upconversion, the energy scale (up to hν ≈ keV emitted from a single atom), time-scale (the emission is in a train of attosecond (10⁻¹⁶ to 10⁻¹⁸ s) bursts), and spatial scale (Å) all represent physical extremes for a controlled, fully coherent process. To date, however, most applications of HHG sources have used relatively low-energy photons at hν ≲ 100 eV. This is because, although each atom emits harmonics over a broad range of photon energies, to generate a bright output beam, the emission of a large number of atoms over an extended region of the nonlinear medium must add in phase (Fig. 1) (14–16). This phase matching condition is met when the driving laser and the generated X-rays travel at the same phase velocity in the nonlinear medium. For low photon energies <130 eV, HHG can be perfectly phase matched by balancing the neutral atom dispersion with the dispersion of the free-electron plasma that is created as the medium is ionized, including any geometric contributions (15, 16). Under these conditions, phase-matched conversion over centimeter lengths can result in an EUV light source with microwatts of coherent power, by using a modest ≈1-W driving laser. This corresponds to a flux of 10¹² photons per second (conversion efficiency ≈10⁻⁵)—sufficient for a host of applications in science and technology (1–7, 9, 10).

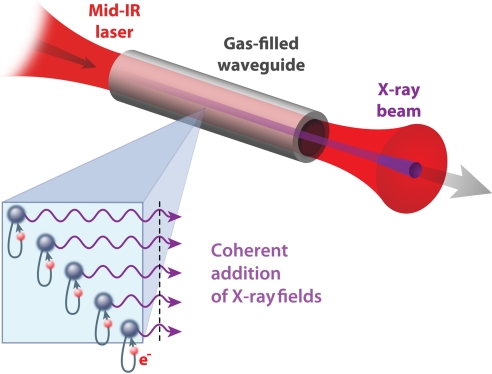
Fig. 1.

Extreme nonlinear upconversion of a femtosecond laser light to shorter wavelengths. Phase-matched (coherent) addition of the high harmonic X-ray fields emitted by many atoms in the medium is shown.

However, higher photon energies are generated at higher laser intensities (see Eq. 1) that strongly ionize the gas medium. The dispersion of the resulting plasma increases the phase velocity of the driving laser and induces a phase slip relative to that of the harmonic field. Thus, for photon energies >130 eV, conventional phase matching of the HHG process is not possible by using 0.8-μm driving lasers, and coherent addition of the harmonic field is limited to very short distances in the medium. Therefore, the HHG output could be enhanced by orders of magnitude if a scheme could be found to correct for this phase slip. Practical approaches for implementing phase matched HHG at high photon energies thus represent a grand challenge—the high-energy frontier in nonlinear optics.

To solve the phase-matching problem for HHG at high photon energies, quasiphase-matching (QPM) schemes can either adjust the phase or eliminate emission for harmonics from regions of the medium that would otherwise contribute destructively to the signal. This can be accomplished by using either modulated wave guides (17) or periodic patterns of light that modulate the emission amplitude and phase (6, 18). Partial QPM (over approximately millimeter distances) has been experimentally demonstrated up to photon energies of ≈300 eV and, in theory, can work even at keV photon energies (18). However, QPM schemes are necessarily complex to implement, requiring the use of multiple laser beams or carefully engineered geometries.

More recently, calculations and experiments (19) have explored how full phase matching scales with the driving laser wavelength. It has long been known that the single-atom cutoff scales as I_Lλ_L² (Eq. 1). Thus, somewhat counterintuitively, using a longer-wavelength infrared (IR) driving laser allows one to generate shorter-wavelength high-harmonic light for any given laser intensity (20). Recent quantum-mechanical analyses, however, have shown that this scaling to shorter X-ray wavelengths comes at a high cost in terms of photon flux, because the effective brightness of a single atom emitter scales as ≈λ_L^−5.5 (21). This unfavorable scaling arises mainly because of a combination of the spatial spreading of the recolliding electron wave packet (which gives a factor of λ_L⁻³), and the quadratic increase in the cutoff energy (which results in an additional factor of λ_L⁻² for a fixed energy interval). Fortunately, by using a longer-wavelength laser, a given harmonic can be generated at much lower laser intensity, reducing ionization of the nonlinear medium. This dramatically increases the photon energy range over which the HHG process can be phase matched (19). Past work from our group demonstrated that by shifting the driving laser wavelength from 0.8 to 1.3 μm, full phase matching over centimeter distances in Ar extends from 50 eV (0.8 μm) to 100 eV (1.3 μm). Similar more recent experimental work demonstrated enhanced harmonic emission from approximately millimeter regions of a supersonically expanding neutral gas at photon energies ≈300 eV (in Ne) and 450 eV (in He) (22). Other calculations have suggested that by using the cycle-to-cycle variation in the electric field of very short-duration laser pulses, one can also extend the phase-matching process to shorter X-ray wavelengths (23, 24).

Here, we show that by using mid-IR driving lasers of moderate intensity (10¹⁴ to 10¹⁵ W/cm²), high harmonic generation presents an experimentally feasible and straightforward route for generating bright, fully coherent beams up to several keV photon energies. Experimentally, using a driving laser wavelength of λ_L = 1.3 μm, we verify our predictions by demonstrating full phase-matched harmonic emission over approximately centimeter distances at high gas pressures (≫atm), reaching into the water window region of the spectrum ≈330 eV. Moreover, phase-matched conversion in this weakly ionized regime is quite advantageous because the driving laser experiences minimal nonlinear distortion, resulting in excellent spatial coherence of the HHG beam (8). Through direct comparison of theory and experiment, we quantitatively test our conceptual understanding of phase matching of the HHG process (15, 16): Namely, full phase matching is achieved through a balance between the neutral atom and plasma dispersions in a weakly ionized gas, including any geometric terms. This is similar to the case for phase matching of HHG using 0.8-μm lasers. Finally, we show that the predicted macroscopic conversion efficiency scales very favorably into the multi-keV hard X-ray region of the spectrum. This unique regime using mid-IR light and a high-pressure, weakly ionized (10¹ to10⁻³%) gas, contrasts with all other approaches for generating harmonics at high photon energies to date, which produce very low flux levels (non-phase-matched) from multiply ionized species at low densities (25, 26).

Phase Matching of HHG

A schematic of the experimental setup is illustrated in Fig. 1. The driving laser is focused into a gas-filled hollow wave guide, which facilitates near-plane-wave propagation over an extended distance [see supporting information (SI) Text]. The phase mismatch between the fundamental laser and the HHG light, Δk, is a sum of contributions from the pressure-dependent neutral atom and free-electron dispersions as well as from the pressure-independent geometric dispersion, which in our geometry is (15, 16):

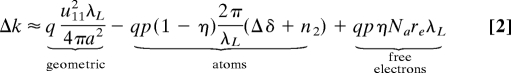Here, q denotes the harmonic order, u₁₁ is the mode factor, a is the inner radius of the hollow wave guide, p is the pressure, η is the ionization level, r_e is the classical electron radius, N_a is the number density of atoms per atm, Δδ(λ_L) is the difference between the indices of refraction of the gas per atmosphere at the fundamental and X-ray wavelengths, and n₂ = ñ₂ I_L is the nonlinear index of refraction per atmosphere at λ_L. Phase matching, or Δk → 0, can be achieved by varying the gas pressure inside the wave guide, because the neutral atom dispersion has a sign opposite to that of the generated free-electron plasma (15, 16). This dispersion balance mechanism has recently been directly verified through in situ measurements of the coherence length of the HHG process (27).

From Eq. 2, phase matching is possible only if the ionization η is less than a critical ionization level given by η_CR(λ_L) = [λ_L²N_ar_e/(2πΔδ(λ_L)) +1]⁻¹ (15, 16). Values for η_CR are on the order of a few percent in the near-IR region, or ≈4% (1.5%) for Ar, 1% (0.4%) for Ne, and 0.5% (0.2%) for He at 0.8-μm (1.3-μm) driving laser wavelengths. This critical ionization level monotonically decreases as the driving laser wavelength increases.

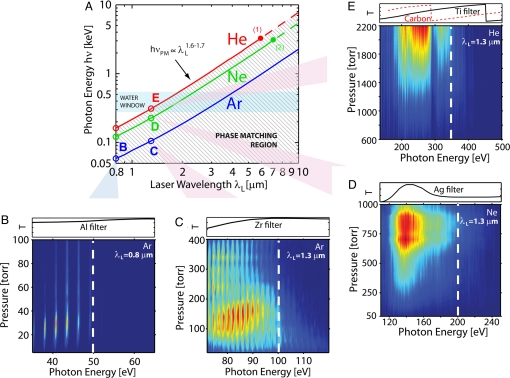
Under the illumination conditions considered here (I_L = 10¹⁴ to 10¹⁵ W/cm², 8-cycle laser pulses), intense-field ionization of an atom is well-described by the Ammosov–Delone–Krainov (ADK) tunneling ionization model, particularly when using longer-wavelength driving lasers (28). Using ADK, we can estimate the laser intensity at which the medium ionization approaches η_CR. This defines a phase-matching cutoff photon energy hν_PM(λ_L) ∝ I_L(η_CR) λ_L² (neglecting I_p) (19), which corresponds to the maximum photon energy that can be generated from a macroscopic medium with near-optimum conversion efficiency (full phase matching). Fig. 2A plots the phase-matching cutoff hν_PM(λ_L) for values of λ_L up to 10 μm, assuming a hyperbolic-secant laser pulse with 8 optical cycles FWHM (21 fs at λ_L = 0.8 μm; 35 fs at λ_L = 1.3 μm). This plot shows that phase matching of HHG can extend to 1 keV for laser wavelengths approaching 3 μm and extends even to the multi-keV region when longer mid-IR driving lasers are used. Use of a shorter 3-cycle pulse (FWHM) can increase these phase-matching cutoffs by an additional 15% because of decreased ionization levels for shorter laser pulses. Finally, the phase-matching cutoff may increase by an additional small increment (a few percent) due to nonadiabatic effects (29) that are not captured by the quasistatic ADK approximation.

Fig. 2.

Full phase matching of HHG. (A) Theoretical predictions for scaling of the phase matching cutoffs in Ar, Ne, and He gases, showing that full-phase matching of HHG emission can extend into the multi-keV X-ray region. (B) Experimentally, phase-matched emission (linear intensity scale) extends to 50 eV in Ar for 0.8-μm driving lasers. (C–E) Experimental data verifying significant extension of the phase matching cutoffs as λ_L increased from 0.8 to 1.3 μm in Ar (C), Ne (D), and He (E). In He, phase matching extends into the water window. (Above B–E, the filter transmission curves of the filters used to eliminate the driving laser light are shown.)

Phase-Matched Conversion into the Water Window using an Extended, High-Density Medium

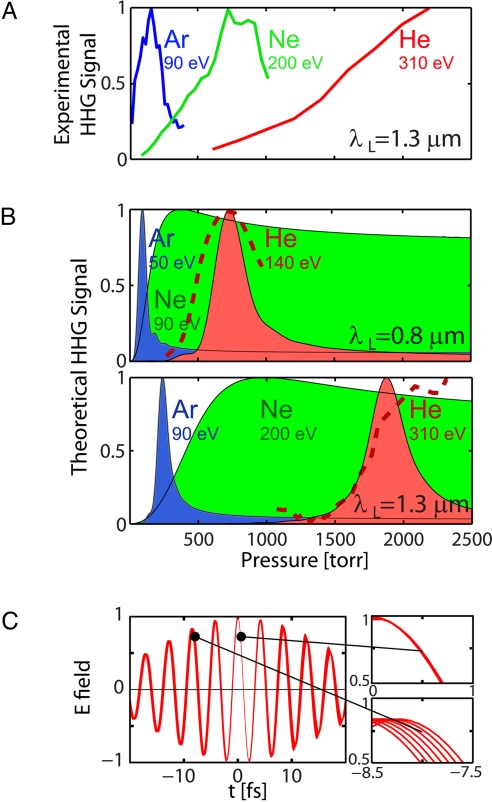
To experimentally verify the predictions of Fig. 2A, we compared HHG emission driven either by an ultrafast Ti:sapphire laser amplifier (λ_L = 0.8 μm), or an optical parametric amplifier tuned to λ_L = 1.3 μm. The driving laser was focused into a wave guide filled with Ar, Ne, or He gas (see SI Text). Using λ_L = 0.8 μm, the phase-matching cutoff extends to 50, 90, and 130 eV in Ar, Ne, and He, respectively (15, 16). Fig. 2B illustrates a typical 2D plot of the observed spectrum as a function of pressure (Ar, λ_L = 0.8 μm). As shown on a linear scale, the bright HHG extends to ≈50 eV. Fig. 2 C–E shows equivalent pressure-tuned phase-matching spectra by using a 1.3-μm driving laser. The phase-matching cutoffs in Ar (19) and Ne extend to ≈100 and 200 eV respectively, whereas for He, phase matching extends into the water window region of the soft X-ray spectrum, to ≈330 eV. These phase-matching cutoff values are all beyond what can be achieved by using a 0.8-μm driving laser. Moreover, in all cases, the observed hν_PM for different wavelengths (λ_L = 0.8 and 1.3 μm) and nonlinear media (He, Ne, and Ar), are in good agreement with the theoretical predictions of Eq. 2. The optimum peak focused laser intensity on-target also agrees with our calculations.

Additional comparison between theory and experiment can be made by evaluating the optimal phase-matching pressures, which scale very favorably with driving laser wavelength. For Ar driven by 0.8-μm light, phase matching occurs at an optimal pressure of 20–40 torr (Fig. 2B) (27). Remarkably, for longer-wavelength IR lasers, the experimentally observed optimal pressure increases significantly from ≈30 torr (0.8 μm) to 100–200 torr (1.3 μm) for Ar, from ≈100 torr (0.8 μm) to 600–900 torr (1.3 μm) for Ne, and from ≈500 torr (0.8 μm) to >2,200 torr (1.3 μm) for He (Fig. 3A). Calculations using a simple semianalytical model shown in Fig. 3B (see discussion in the following section) confirm that higher optimal pressure is needed for phase matching as the laser wavelength increases from 0.8 to 1.3 μm (this calculation was done for photon energies close to the phase matching cutoffs hν_PM, i.e., harmonics generated in a narrow time window at an ionization level slightly below η_CR). More realistic calculations of the pressure dependence of the HHG signal near the phase-matching cutoff, using the strong field approximation (SFA) (30), also confirm that the optimal pressure for phase matching increases at longer laser wavelengths (Fig. 3B). Experimentally, high pressures in the interaction region are convenient to achieve by using a wave guide geometry, because a gas jet geometry would require prohibitively large pumping capacity.

Fig. 3.

Scaling of phase matching parameters. (A) Experimental macroscopic HHG signal growth versus pressure at photon energies close to the phase-matching cutoffs for 1.3-μm lasers. (B) Theoretical predictions of the pressure required for phase matching by using 0.8- and 1.3-μm lasers, based on a simple semianalytical model (solid lines). Quantum calculations for He are shown in dashed lines. (C) Evolution of the laser field in He, represented as a temporal overlap of the field at different distances along the wave guide for a pressure of 1,500 torr and for a propagation distance of 1 cm. The macroscopic in-phase HHG emission is confined within the central cycle of the laser pulse.

In our numerical simulations, we include dispersion of the neutral atoms, transient plasma formation, geometric dispersion, ohmic power dissipation due to ionization, and reabsorption of the harmonics by the gas. Phase matching of the HHG process was determined numerically by superimposing the driving electric field at consecutive positions along the wave guide, calculated in a frame moving at the speed of light in vacuum, c (Fig. 3C). In this picture, the dispersion of the neutral atoms and the wave guide results in a phase variation at the leading edge of the pulse, whereas the intrinsic plasma formation leads to a phase variation at the trailing edge. Because the highest-energy photons are generated only during the most intense central half-cycle of the laser pulse, and propagate at phase velocity of c, phase-matched emission at the cutoff manifests itself in an absence of phase slip within this peak half-cycle of the laser (Fig. 3C, upper Inset).

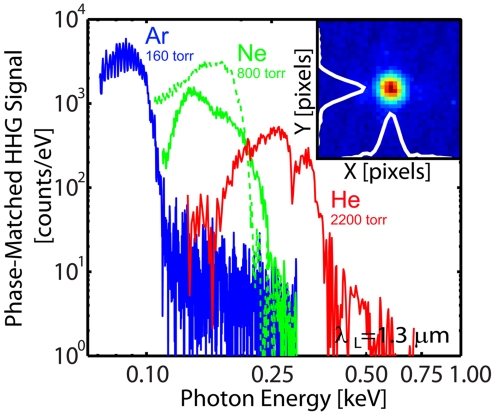
Fig. 4 compares the experimentally measured phase-matched HHG flux for different gases by using a driving laser wavelength of 1.3 μm (note that different thin-film filters are used to block the fundamental light). The emission from Ar is ≈1.5 times higher than from Ne when optimized for absorption-limited propagation lengths (31) (≈1 cm in Ar, ≈0.5 cm in Ne). The emission in He, although not fully optimized because of the very high gas load on the vacuum system, is only 8 times lower than that from Ne for the same propagation length. Thus, although the single atom effective high-order nonlinear susceptibility for HHG emission from He is much lower than for Ne, the higher relative transparency of He to soft X-rays allows larger density-length products to be used.

Fig. 4.

Characteristics of phase-matched HHG. Experimental phase-matched HHG emission from He, Ne (Ag/Zr filters, solid/dashed line), and Ar driven by λ_L = 1.3 μm, illustrating the sharp HHG cutoffs. (Inset) Raw image of the near-perfect Gaussian soft X-ray beam generated in He, for a broad band of photon energies (200–330 eV), spanning into the water window.

We also note that from Fig. 2, λ_L ≈ 1.3 μm is the shortest driving laser wavelength that can be used to fully phase match HHG into the water window region of the spectrum, above the carbon K-edge at 284 eV. This driving laser wavelength is likely to be optimal for generating bright harmonics from He in this photon energy region because of the rapidly diminishing λ_L^−5.5 effective single-atom susceptibility (for Ne, the optimal wavelength would be ≈1.6 μm for generating water window HHG photons). Plotted on a logarithmic scale, these HHG spectra exhibit several characteristics of phase-matched HHG emission—a well-defined plateau region followed by a sharp cutoff, good agreement between the measured and calculated phase matching pressures (Fig. 3), and finally, a well-defined, low-divergence (<mrad), HHG beam profile, even for very high gas pressures >2,200 torr (Fig. 4B). The soft X-ray beam generated under phase-matching conditions in He (Fig. 4B) fits very well to a Gaussian profile, suggesting high spatial coherence (8). At low gas pressure and high laser intensities in a non-phase-matched regime, we find that HHG emission using λ_L = 1.3 μm extends to 200, 400, and 500 eV in Ar, Ne, and He, respectively. However, a much reduced HHG flux is observed in the spectral region above hν_PM.

Scaling of Phase Matching to keV Photon Energies

Because our experimental results agree very well with our theoretical calculations, it is useful to predict how phase matching scales to even higher photon energies. The critical ionization level η_CR decreases to 0.1–0.001% for driving lasers in the mid-IR wavelength range (Fig. S1A). Because Δδ(λ_L) in Eq. 2 changes only by 0.35% in the range of λ_L = 0.8–10 μm, the wavelength scaling can be approximated as η_CR ∝ λ_L⁻². ADK ionization rates are wavelength independent and strongly depend on the laser intensity. Thus, the driving laser intensity required to reach η_CR decreases slightly from ≈10¹⁵ to ≈10¹⁴ W/cm² as one moves to longer laser wavelength (Fig. S1B). As a result, the phase-matching cutoff effectively scales as hν_PM ∝ λ_L^1.6–1.7 (see Fig. 2A). This is slightly less than the λ_L² scaling of the single-atom HHG cutoff but nevertheless represents a strongly favorable scaling.

It is also instructive to describe the behavior of each contributions in Eq. 2 under phase-matching conditions as the laser wavelength increases. In a simple analytical model, the wave guide dispersion scales linearly with λ_L, and therefore, the pressure-dependent dispersion terms exhibit the same scaling. In fact, harmonics near hν_PM are generated at ionization levels close to η_CR ∝ λ_L⁻². Therefore, for fully phase-matched HHG, Eq. 2 predicts that the optimal pressure will scale as p_opt ∝ λ_L² (almost independent of the gas species). This quadratic scaling results in an effective linear dependence on λ_L for both the atomic and free-electron dispersions. It is important to note that in this scaling of phase matching into the keV region, the density of the free electrons, n_e = η_CRp_optN_a, remains the same. Thus, the number of atoms being ionized can even increase—a requisite step for efficient HHG—if the medium allows for both longer laser and X-ray propagation. Finally, the increase of the dispersion from the near-IR to the mid-IR results in stronger phase variation for the leading- and trailing-edge cycles compared with the central cycle, illustrated in Fig. 3D. In practice, this may lead to a simple macroscopic isolation of a subcycle X-ray burst even by using a multicycle driving laser pulse, consistent with recent measurements that demonstrate isolated attosecond pulses by using similar phase-matching gating (32, 33).

We next predict how the overall flux of phase matched high harmonics scales as we move to longer-wavelength driving lasers and shorter-wavelength X-rays. To capture the primary scaling of the macroscopic phase-matched HHG flux, here, we use a simple model for the intensity of a single harmonic dI_q per unit interaction area dA and time dt (16, 31):

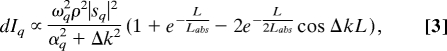where ρ is the gas density, s_q is the amplitude of the single-atom response at harmonic frequency of ω_q, α_q = ρσ_q/2, and σ_q are the harmonic field absorption coefficient and absorption cross section, and L and L_abs = (ρσ_q)⁻¹ are the propagation and absorption lengths. In this semianalytical model, the single-atom response s_q is determined numerically by using SFA, taking into account up to 8 electron trajectories. This model was verified to reproduce the λ_L^x scaling of the single-atom yield, where x ≈ −5.5 (for a fixed photon energy interval and at constant I_L), as predicted by the SFA model and more accurate time-dependent Schrödinger equation analyses reported in ref. 21. However, because of the decreasing laser intensity (Fig. S1B) at increasing photon energies along the phase matching cutoffs (Fig. 2A), the scaling for the single-atom yield exhibits a stronger power dependence that varies slightly depending on the gas species, i.e., x ≈ −6.4, considering emission within a fixed bandwidth of λ/Δλ = 100 close to hν_PM. If instead of a fixed fractional bandwidth, emission strength of a single harmonic order is considered, the power dependence is x ≈ − (9–8.4) (see SI Text and Table S1).

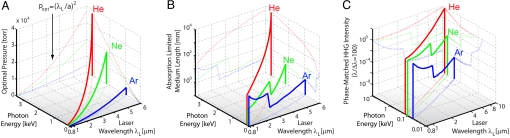
The predicted optimum phase-matching pressure is plotted in Fig. 5A. It is interesting to note how mid-IR phase matching compares with all previous work—above 12 atm of He are required for phase matching at 1 keV, assuming a wave guide radius of a = 125 μm. At longer laser wavelengths and even higher multi-keV photon energies, the optimum pressure may become too high to confine in a differentially pumped geometry. However, differential pumping may no longer be necessary because higher photon energies can penetrate a thicker window. Furthermore, the phase-matching pressure can be reduced by increasing the wave guide radius a: p_opt ∝ (λ_L/a)².

Fig. 5.

Scaling of the pressures-length products required for efficient phase-matched HHG emission at the phase-matching cutoffs for laser wavelengths up to λ_L = 6 μm and corresponding phase-matching limits up to 3 keV. (A) Predicted optimal pressure showing quadratic growth with λ_L. (B) Absorption-limited medium length for reaching 90% of the asymptotic limit of the macroscopic harmonic signal, determined by reabsorption. (C) Absorption-limited intensity of phase-matched HHG in a line width of λ/Δλ = 100 at the phase-matching cutoffs for laser wavelengths between 0.8 and 10.0 μm. The curves are normalized to the phase-matched HHG emission at λ_L = 0.8 μm. For high photon energies, group velocity mismatch and magnetic field effects reduce the HHG flux below these predictions (see SI Text for details).

In absorptive media and under phase-matching conditions, the intensity of a single harmonic dI_q grows asymptotically to a value that scales as dI_qmax ∝ ∣ω_qs_q /σ_q∣² (see Eq. 2). The signal builds to 90% of its asymptotic value for a medium length of L_med ≈ 6L_abs (16, 31). In general, at very high photon energies, the absorption cross-section drops rapidly. Thus, the higher optimum pressure does not reduce the medium length required to reach significant flux (the pressure-length products are identical for HHG in a loosely focused geometry, see SI Text). In this context, the use of He as the nonlinear medium for very high photon energies is of particular interest. Because of the absence of inner-shell absorption, He exhibits a qualitatively different scaling of the absorption-limited propagation length (∝λ_L^3.7) compared with Ar and Ne, as shown in Fig. 5B. For example, at pressures >12 atm (a = 125 μm) and a phase-matching cutoff of 1 keV, the absorption-limited length for He is L_med > 50 cm. This macroscopic density-length product will allow for orders-of-magnitude-greater conversion efficiency than has been demonstrated to date at keV energies.

Finally, the scaling of the resulting macroscopic HHG intensity under optimal phase-matching conditions (Fig. 5C and Fig. S2) suggests that He is the best medium for extending bright harmonic emission to keV photon energies, whereas Ne is a good medium for generating harmonics up to 0.87 keV. Very remarkably, for a fixed-emission spectral bandwidth of λ/Δλ = 100 (which is realistic for imaging experiments), the macroscopic, absorption-limited HHG flux from He does not change significantly up to a phase-matching cutoff of 1 keV, and may even increase in the multi-keV X-ray region (Fig. 5C). These scaling predictions also indicate that Ar is a practical HHG medium only when near-IR driving fields are used. The qualitatively different behavior of the macroscopic emission in Ne and Ar compared with He is due to the presence of L-shell absorption edges around 870 eV (Ne) and 250 eV (Ar), leading to a strong increase in the absorption cross-section. Group velocity mismatch will reduce the HHG flux below the predicted absorption-limited signal (see SI Text). This is most relevant for HHG in He for driving laser wavelengths >2 μm, because the absorption limited length in this gas becomes much longer than the group velocity walk-off length L_GV at high photon energies. In contrast, in Ne and Ar, the absorption-limited length is comparable with L_GV, and the HHG signal growth is mainly restricted by reabsorption. Also, at much longer laser wavelengths (6 and 7 μm for He and Ne, respectively, or hν_PM = 3 keV in Fig. 2), the magnetic field component of the laser field start to play an important role (see SI Text and Fig. S3) because of the longer excursion time of the electron. This will lead to a reduction in HHG efficiency, which could be addressed, however, by manipulating the electron wave packet by using external light fields. Ultimately, the phase-matched HHG flux can be further increased (linearly) by using higher repetition rate lasers (10–100 kHz) as well as higher laser energies to increase the interaction area.

Outlook

The implications of these scaling predictions are worthy of elaboration. HHG driven by mid-IR lasers results in closely separated harmonics because of the lower energy of the fundamental photons. This has the advantage of a nearly continuous spectrum that is semicontinuously tunable, making it suitable for broad applications in spectroscopy, approaching synchrotron-based light sources.

The fact that X-ray upconversion occurs at moderate laser intensity in a weakly ionized gas means that the laser propagation is likely to be well controlled with minimal nonlinear effects and lower ionization-induced energy loss (see SI Text). This fact also makes the regime amenable to the use of more sophisticated phase-matching techniques that make use of the attosecond time-scale quantum dynamics of the process. Therefore, QPM techniques (6, 17) can be combined with mid-IR driving laser, to extend the region of bright emission beyond the phase-matching cutoffs discussed here. Furthermore, QPM can be used to selectively phase match a narrow spectral range, resulting in a tunable, nearly monochromatic ultrafast coherent X-ray source (6). Finally, the low peak intensities and long driving wavelengths required, along with the long nonlinear medium lengths and high pressures, also make it advantageous to use wave guides to confine the laser light and the gas. Wave guides coated with metals, metal-dielectric structures, and dielectric layers, or photonic band-gap structures can work very well to guide infrared laser light, avoid diffraction losses, and phase match the HHG process (34). In terms of laser technology, the required pulse energies, peak focused intensities and laser pulse durations are all very accessible.

Another interesting area for future studies is the generation of bright attosecond pulses by using mid-IR driving lasers. The relatively rapid variation in phase-matching conditions also raises the possibility that emission will be predominantly in the form of a single burst, as indicated in Fig. 3D and in recent experiments at photon energies ≈45 eV (32, 33).

The resulting infrared laser-driven high-harmonic source has potential for great impact and widespread use because coherent, ultrafast, soft and hard X-ray beams can be generated from a desktop-scale femtosecond laser. Many applications from magnetic to bio-, nano-, and materials imaging and spectroscopy will be enabled. Free-electron laser sources will also benefit from the availability of these fully coherent X-rays as seeding beams to improve the spatial and temporal coherence of their output.