Text-based over-representation analysis of microarray gene lists with annotation bias

Abstract

A major challenge in microarray data analysis is the functional interpretation of gene lists. A common approach to address this is over-representation analysis (ORA), which uses the hypergeometric test (or its variants) to evaluate whether a particular functionally defined group of genes is represented more than expected by chance within a gene list. Existing applications of ORA have been largely limited to pre-defined terminologies such as GO and KEGG. We report our explorations of whether ORA can be applied to a wider mining of free-text. We found that a hitherto underappreciated feature of experimentally derived gene lists is that the constituents have substantially more annotation associated with them, as they have been researched upon for a longer period of time. This bias, a result of patterns of research activity within the biomedical community, is a major problem for classical hypergeometric test-based ORA approaches, which cannot account for such bias. We have therefore developed three approaches to overcome this bias, and demonstrate their usability in a wide range of published datasets covering different species. A comparison with existing tools that use GO terms suggests that mining PubMed abstracts can reveal additional biological insight that may not be possible by mining pre-defined ontologies alone.

INTRODUCTION

The output of a microarray experiment is typically one or more lists of genes that show an ‘interesting’ change in expression in the context of that experiment. This is often not the end point of the analysis, but the starting point of a complex process of deriving biological interpretation. Many researchers interpret their results by manually reviewing the function of each gene based on literature or database searches, or by prior familiarity with the gene and a plausible link to the biology under study. This ad hoc annotation process is both time-consuming and prone to user bias. The need to formalise this interpretation process has led to the development of a range of tools, of which a family of statistical methods collectively known as over-representation analysis (ORA) is becoming increasingly popular among researchers undertaking microarray analysis. The fundamental question asked by ORA is: what biological terms or functional categories are represented in the gene list more often than expected by chance. The most common approach to test this statistically is by using the hypergeometric test (or its variants such as Fisher's exact test) to calculate the probability of seeing at least a particular number of genes containing the biological term of interest in the gene list. This mode of analysis has been implemented (with minor variations) in several publicly available software tools, including DAVID/EASEonline (1), FatiGO (2), GenMAPP (3), GoMiner (4) and OntoTools (5).

Currently, the applications of ORA are largely limited to the mining of pre-defined ontologies (e.g. GO, MeSH) or pathway annotation (e.g. KEGG, BioCarta). These resources are, to a large extent, generated from manual literature reading by experts, with the aim of providing a structured, condensed and reduced description of the biological knowledge about genes in the scientific literature. However, due to its labour-intensive nature, such pre-defined functional annotations are inevitably limited in scope and flexibility, and cannot fully reflect the detail of all areas of biology that might be of interest. A much greater wealth of biological knowledge about genes is present only in the primary, text-based biomedical literature, which is readily accessed in the form of abstracts, and increasingly as full-text articles from selected biomedical journals.

We were therefore interested to determine whether the successful applications of ORA can be extended beyond the mining of controlled vocabularies to a wider mining of free-text, initially in the form of PubMed abstracts. Our initial exploration into this approach was based on a simple tokenisation of PubMed abstracts, followed by the identification of over-represented tokens using the classical hypergeometric test. When this approach was tested on 52 literature-derived gene lists, we discovered a dramatic and hitherto underappreciated feature—gene lists derived from a typical microarray experiment tend to have more annotation (i.e. PubMed abstracts) associated with them than would be expected by chance. This bias can lead to a marked over-representation of many common (and likely uninformative) terms, interspersed with terms that appear to convey real biological insight.

We have developed several solutions to this issue. The first is based on the use of a permutation test, but is hampered by being computationally intensive. Therefore two computationally tractable approaches for performing ORA mining on PubMed abstracts, based on the detection of outliers and the extended hypergeometric distribution, were developed. Here, we describe the unique features of these methods and illustrate their utility by applying them to several diverse biological datasets.

MATERIALS AND METHODS

Public datasets

We used publicly available microarray datasets to evaluate the performance of the ORA methods described in this work. In total, 354 different gene lists were collected from 146 scientific papers, which cover experiments performed on 10 major Affymetrix platforms, including HG-U133A, HG-U133 Plus 2.0, Mouse 430 2.0, Rat 230 2.0, Arabidopsis ATH1, DrosGenome1, Drosophila 2.0, Xenopus laevis, C. elegans and Zebrafish. These gene lists are collectively referred to as the ‘literature gene lists’ and their details can be found in Supplementary Data 2. Two gene lists were selected to evaluate in more detail the performance of the ORA methods presented here:

1. ISG gene list: This gene list was extracted from the gene expression study of Sanda et al. (6). We applied the regularised t-test method (7) to MAS5 expression data and used the false discovery rate (FDR) method to correct for multiple hypothesis testing. Genes that were differentially regulated following treatment with type I interferon at both 6 and 24 h were identified (FDR P ≤ 0.05). This produces a gene list consisting of 77 interferon-stimulated genes (ISG).

2. Nishimura gene list: This gene list was as reported in Nishimura et al. (8). It contains 685 probesets on the Affymetrix Arabidopsis ATH1 array, representing 679 different genes that were differentially expressed in pmr4 mutant relative to wild-type plants.

Text corpus creation

The methods described here require the initial creation of a text corpus that connects the textual information stored in PubMed abstracts with genes included in the microarray analysis. First, we mapped all the genes represented on an array to their corresponding EntrezGene identifiers (EGID) based on the mapping schemes provided by the appropriate Bioconductor metadata packages. Then, PubMed articles associated with these genes were obtained from the gene2pubmed file downloaded from NCBI (ftp://ftp.ncbi.nih.gov/gene/DATA; time stamp: 25 October 2007) in the form of EGID to PubMed identifier (PMID) mappings. PMIDs that are associated with more than one EGID were omitted because, based on manual inspection, these tend to be large-scale sequencing reports that contain information largely irrelevant to gene function. This lack of specificity can affect the performance of the text mining algorithms. PubMed articles passing this criterion were retrieved from the PubMed database using a customised Perl script implementing modules from the Entrez Programming Utilities (http://eutils.ncbi.nlm.nih.gov/entrez/query/static/eutils_help.html).

Upon retrieval, the abstracts were tokenised on white space to produce single-word terms. Any redundancies were removed to produce a unique set of tokens for each gene. Terms composed exclusively of numbers were removed from the text corpus. Then, a simple stemming operation was applied to reduce plural to singular forms (e.g. ‘kinases’ becomes ‘kinase’). Verb tenses were stemmed to their root (e.g. ‘phosphorylates’ and ‘phosphorylated’ become ‘phosphorylate’). Other more elaborate analysis of spelling variants (e.g. catalyze, catalyse) and composite words (e.g. cell cycle, DNA polymerase) were not explored. Porter's stemming algorithm (http://tartarus.org/~martin/PorterStemmer/; Perl version, release 1) was adapted for this analysis.

Definitions of Chip and List frequencies

For each token associated with a given gene list, we calculated two values. The first one, called Chip frequency, is defined as the number of genes that contains the token of interest on the entire chip (i.e. background). The second value, called List frequency, represents the number of genes that are associated with the token of interest in the query gene list.

Classical hypergeometric distribution-based ORA approach

Suppose that the total number of genes in the background population is N, of which M are associated with a certain token of interest T. If we select K genes randomly from the entire microarray without replacement, the probability of seeing exactly x genes associated with T in K can be modelled by the hypergeometric distribution (9). Hence, the probability of seeing x or more genes containing token T in a random gene list of K genes can be calculated as the cumulative probability:

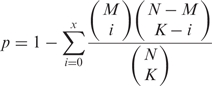This is a one-sided test for over-representation. In this study, a token is considered significantly enriched if its P-value is less than 0.05 after adjusting for multiple hypothesis testing (i.e. at 95% confidence level).

Permutation test

The fundamental idea underlying this permutation approach is to create random gene list that matches the experimentally derived gene list not only in the number of genes but also the amount of associated PMIDs. This is achieved by replacing the abstracts for each gene in the experimentally derived gene list with other abstracts selected randomly (without replacement) from the text corpus. As such, the number of genes and abstracts (hence PMID) for each random gene list are kept the same as that of the experimentally derived gene list. This permutation procedure is repeated n = 100 000 times. An empirical P-value of over-representation can then be calculated for each token in the gene list as the fraction of times its frequency in the random gene list (r) is equal to or greater than that seen in the experimentally defined gene list (x):

In this study a token is considered significantly enriched, if its P-value is less than 0.05 after Bonferroni multiple hypothesis correction.

Outlier: Outlier detection-based ORA

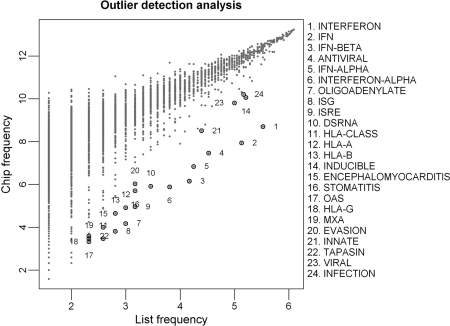
This method is motivated by the observation that, on a scatter plot of Chip versus List frequencies, there are a set of biologically plausible terms that deviate substantially from the main data cluster and appear as outliers (see Figure 2 for an example). An explanation underlying this observation is that the majority of the tokens in a gene list will not be over-represented because they are either: (i) common words or non-specific biological terms that are shared by most abstracts, or (ii) rare words that are not biologically interesting. These will form the main cloud of data points. On the other hand, biologically plausible terms are associated with more genes in the gene list and have different token frequency distributions, thus appear to be separated from other observations in the background.

Figure 2.

A scatter plot of Chip versus List frequencies for tokens in the ISG gene list. Each data point represents an abstract term. Terms that were identified as significantly enriched (i.e. Bonferroni P ≤ 0.05) in the ISG gene list by using the Outlier method are circled and the adjacent numbers corresponding to their rankings. Chip (y-axis) represents the number of genes associated with each term on the whole chip. List (x-axis) represents the number of genes associated with each term in the ISG gene list. The log 2-transformed List and Chip frequencies are plotted.

We developed an outlier detection procedure that determines within a group of tokens corresponding to the same List frequencies any tokens that have lower than expected Chip frequencies. Formally, we derive a Z-score for each token based on its Chip frequency and infer the statistical significance of this Z-score against the normal distribution as follows.

1. Local mean and standard deviation (SD) estimation: The Chip and List frequencies were log-transformed to base 2. Then, all tokens in the gene list were stratified into groups according to their List frequencies. Consider a group of n tokens corresponding to List frequency L and their Chip frequencies are given by (x₁, …, x_n). For this group of tokens, the parameters that define the outlier region, i.e. mean and SD, are estimated based on the following: If n ≥ 10, mean and SD are calculated directly from (x₁, …, x_n). If 1 < n < 10, we borrow information from neighbouring observations to give a better estimation of the local mean and SD. This is done by capturing (10 – n) tokens from the adjacent group for which the corresponding List frequency is less than L and combine the Chip frequencies from them with (x₁, …, x_n). Then, a local mean and SD are derived from the combined data.

2. Local mean and SD smoothing: The means and SDs estimated in step (1) are smoothed as a function of List frequency by fitting polynomial curves to the frequency data (see panels (a) and (b) in Supplementary Data 1 Figure S5). Locally smoothed mean and SD are computed for each group based on the fitted values derived from the best-fitting curves. The purpose of smoothing is to stabilise the variance in the data so that we can find representative mean and SD for calculating Z-score. The effect of smoothing is shown in panels (c) and (d) in Supplementary Data 1 Figure S5.

3. Z-score and P-value calculation: The Z-score for token i is

   

   where x is the Chip frequency, μ is the locally smoothed mean, and sd is the locally smoothed SD. The Z-score reflects the number of standard deviations an observed Chip frequency is above or below the local mean. A P-value was calculated from the Z-score using the normal distribution (for a justification for this approach see Supplementary Data 4). A token is labelled as an outlier and considered over-represented in the gene list if it has a significant P-value (Bonferroni P ≤ 0.05) and a negative Z-score (indicative of a lower Chip frequency than the local mean).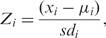

ExtendedHG: extended hypergeometric distribution-based ORA

The extended hypergeometric distribution, also known as the Fisher non-central hypergeometric distribution, is a generalization of the classical hypergeometric distribution where the sampling procedure is biased (9–11). Assume that we draw out n balls without replacement from an urn containing N balls, of which m₁ are red and m₂ are white. The balls have different weights, where the weight for each red and white ball is w₁ and w₂, respectively. When sampling is unbiased (i.e. w₁ = w₂), the balls have equal probability of being taken (i.e. p₁ = p₂) and the results will follow the classical hypergeometric distribution. However, if sampling is biased such that the probability of taking ball of one colour is proportional to its weight but independent of the other balls, then the number of balls of a particular colour drawn will follow the binomial distribution:

On the condition that the sum of the independent binomial variables is fixed (i.e. ∑ x_i = n), the number of red balls in our sample x will follow the extended hypergeometric distribution and the probability of seeing x red balls simply by chance is given by

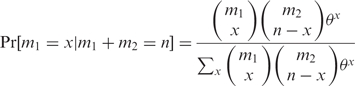where max(0, n − m₂) ≤ x ≤ min (m₁, n). The odds ratio, θ, is a measure of bias and is equivalent to the probability ratio of red over white balls:

We reasoned that when the amount of annotation associated with a gene list is higher than expected by chance, the sampling will be biased in favour of certain types of tokens. As a consequence, some common words or non-specific terms shared by most abstracts, such as ‘cell’, ‘analysis’ and ‘molecule’, will have higher probabilities of being selected along with genes in the gene list. As such, token significance inferred from the classical hypergeometric distribution is likely to be misleading and erroneous because this approach does not account for the excess annotation. Here, we propose a solution to this problem, which is based on the extended hyper-geometric distribution model:

1. Odds ratio estimation: Let the number of genes annotated by token T in the background be m₁, and the number of genes associated with tokens other than T in the background be m₂. Given a gene list of size n, the odds ratio of T can be calculated empirically by:

   

   where y is the mean number of genes we expect to see in the gene list just by chance. We determine y by fitting a polynomial regression line through the token frequencies data: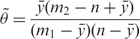

   

   In this model, the explanatory variable x represents Chip frequency (equivalent to m₁); the response variable y represents List frequency. The best-fitting curve is obtained by the method of least squares implemented in the R function lm. For each token, the fitted value of List frequency expected for a given Chip frequency is determined from the best-fitting curve. This fitted value is a good approximation for y and is used to calculate the odds ratio.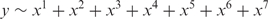

2. P-value calculation: Once the odds ratio has been determined, we use the pFNCHypergeo function implemented in the BiasedUrn R package to calculate a P-value for each token based on the extended hypergeometric distribution.

Consensus gene age computation

In order to gain an approximate measure of the ‘age’ (i.e. the length of time a gene has been known and researched upon) for genes on the HG-U133A array we used a combination of PubMed, OMIM (Online Mendelian Inheritance in Man) and HGNC (HUGO Gene Nomenclature Committee) to collate the following information for each gene: (1) the date of the earliest PubMed article that described the gene, (2) the date of the earliest article cited in an OMIM record for which the gene is described, (3) the date on which the gene first appeared in an OMIM record and (4) the date on which the gene first approved by HGNC.

Based on these dates, we derived two ‘age estimates’ for each gene: literature- and database-based age. Literature-based age was calculated by averaging the values from (1) and (2), and it represents the date on which a gene was first referred to in the scientific literature. Database-based age was calculated as the mean of (3) and (4), and represents the date when a gene symbol was first approved or integrated into the public databases. There is a good correlation between the literature- and database-based ages (data not shown); therefore we calculated a final consensus age for each gene by taking average of the literature- and database-based ages.

Platform and availability

The algorithms for Outlier and ExtendedHG have been implemented in a public web server PAKORA (http://www.pakora.cf.ac.uk/pakora.php) for interactive use. The source codes (written in R and Perl) are available from the author upon request. A summary of the literature-derived gene lists that we have used in this project can be found in Supplementary Data 2. These gene lists are available for download from PAKORA. The R scripts used in this analysis were developed and tested under R-2.6 and BioConductor-2.1. The Perl scripts were developed and tested under Perl v5.8.7. All analysis was performed on a Windows PC with a 2.8 GHz processor and 2 GB of RAM.

RESULTS

We began by analysing a list of interferon-stimulated genes (ISG) derived from the biological data reported in Sanda et al. (6), using the classical hypergeometric distribution-based ORA approach. The ISG gene list was used as a testbed because it constitutes a relatively simple and well-studied example of transcriptional regulation. PubMed articles associated with genes represented on the Affymetrix HG-U133A array were collected and filtered to give a text corpus consisting of 107 517 abstracts (70% of the unfiltered collection). These abstracts were tokenised and stemmed to produce 220 290 unique single-word tokens for mining. Of these, 9486 tokens are associated with the ISG gene list.

Classical hypergeometric test-based ORA is affected by annotation bias

Initial use of the classical hypergeometric distribution-based method produced encouraging results when applied to the ISG gene list. In total, 94 tokens were called significantly enriched after Bonferroni correction (Table 1). Biologically plausible terms such as ‘interferon’, ‘IFN’, ‘antiviral’, ‘IFN-alpha’, ‘IFN-beta’, ‘inducible’ and ‘immune’, were amongst the most significant hits being called over-represented. These terms are related in principle to the role of interferon in modulating host immune responses against viruses and infection. However, these biologically relevant terms were interspersed with relatively uninformative terms for which it was less plausible that they were specifically associated with the biology of interferon-regulated gene expression. These include common words (such as ‘after’, ‘each’, ‘also’) and non-specific biological words (such as ‘synthesis’, ‘molecule’, ‘beta’). A similar mix of specific and non-specific tokens was generally seen for other gene lists that we have analysed (data not shown).

Table 1.

Significantly over-represented abstract terms in the ISG gene list identified using the classical hypergeometric test

Rank	Term	Rank	Term	Rank	Term
1	INTERFERON	33	INFECT	65	LYSIS
2	IFN	34	INDUCE	66	AUTOIMMUNE
3	ANTIVIRAL	35	HLA-B	67	INDIGENOUS
4	IFN-BETA	36	HISTOCOMPATIBILITY	68	PROTEASOME
5	IFN-ALPHA	37	LINE	69	LMP2
6	INDUCIBLE	38	HEPATITIS	70	LMP7
7	INTERFERON-ALPHA	39	MELANOMA	71	PKR
8	INFECTION	40	ENCEPHALOMYOCARDITIS	72	INDUCIBILITY
9	VIRAL	41	REPLICATION	73	CORRESPONDING
10	IMMUNE	42	AFTER	74	MOLECULE
11	TREAT	43	MONOCLONAL	75	DEFENSE
12	INNATE	44	EPSTEIN-BARR	76	DIFFERENTIAL
13	IFN-GAMMA	45	UPREGULATE	77	ACTION
14	VIRUS	46	SYNTHESIS	78	TAP
15	IMMUNITY	47	BETA2-MICROGLOBULIN	79	STIMULATE
16	DSRNA	48	EBV	80	CONFER
17	INDUCTION	49	GAMMA-INTERFERON	81	LOAD
18	OLIGOADENYLATE	50	HLA	82	REACTIVITY
19	LYMPHOBLASTOID	51	INTERFERON-GAMMA	83	OR-C
20	ISRE	53	OAS	84	MEDIATE
21	HOST	52	HLA-G	85	RECOMBINANT
22	ISG	54	TYPE	86	CTL
23	MHC	55	MXA	87	MICROGLOBULIN
24	TREATMENT	56	ALPHA	88	STRAND
25	HLA-A	57	DEFINE	89	RECOGNIZE
26	STOMATITIS	58	IMMUNODEFICIENCY	90	ALSO
27	BETA	59	PROMYELOCYTIC	91	DERIVE
28	RESPONSE	60	INTACT	92	P69
29	HLA-CLASS	61	LEUKEMIA	93	VSV
30	EVASION	62	INDEPENDENT	94	DOUBLE
31	CYTOKINE	63	EACH
32	ANTIGEN	64	TAPASIN

Over-represented abstract terms are defined as those tokens with P ≤ 0.05 after Bonferroni correction. The most significant hits are ranked at the top of the table. See Supplementary Data 1, Table S1 for term frequencies and P-values associated with the individual terms.

Some areas of biology have, historically, been subject to greater levels of research activity and this is reflected in the biological literature. We reasoned that if a particular experiment were focused on a particularly well-studied area of biology this might therefore lead to a greater number of PMIDs associated with the resultant gene list than might otherwise occur. This in turn would introduce a bias that would affect the application of the classical hypergeometric test.

The interferon response is an example of a well-researched area and the 77 genes in the ISG gene list are annotated by 1514 PMIDs. However, if we were to create a 77-gene list by random sampling from the same set of background genes on the chip we would expect to see, on average, only 660 PMIDs associated with such a random gene list. Thus, in this example the ‘real world’ ISG gene list has 2.3 times more PMIDs associated with it than would be expected by chance. The consequence of this on the classical hypergeometric distribution-based ORA approach is that, for some tokens, there is a general shift towards appearing over-represented, simply because the background frequency is artefactually under-estimated. Therefore, even a relatively modest increase in token frequency of a common word would produce a significant P-value.

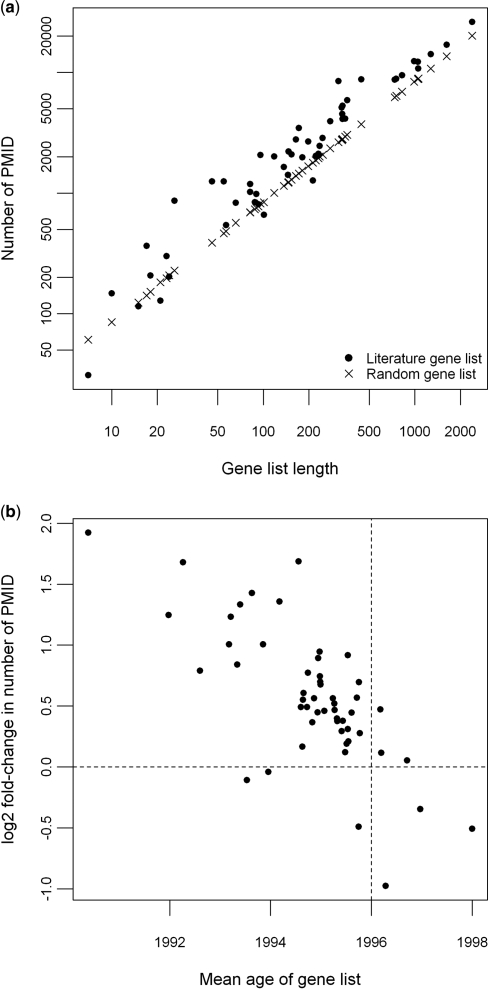
To explore this further we collated 52 gene lists from the published literature that were based on use of the human HG-U133A array (see Supplementary Data 2 for details of these literature gene lists), and then compared the amount of PMIDs in them with that in an equivalent set of random gene lists. We found that gene lists derived by experimental means (i.e. the result of mining a real biological dataset) tend to have a greater number of associated PMIDs than equivalently sized random gene lists (Figure 1a). A similar trend was also seen for other species, such as mouse and rat, for which sufficient data were available (data not shown). These findings suggest that there is an excess of annotation inherent with highly annotated gene lists. This in turn provides an explanation for the distorted token frequency distribution and skewed hypergeometric P-values that result in a mixture of specific and non-informative terms to be called significantly over-represented by the classical hypergeometric distribution-based ORA approach.

Figure 1.

The relationship between annotation bias and gene age. (a) 52 gene lists from the HG-U133A chip were collated from published literature and for each of these equivalently sized random gene lists were created. The numbers of PMIDs associated with them were calculated and plotted against the size of the gene lists. Both axes are on logarithmic scale. (b) A mean age was calculated for each of the 52 literature gene lists by averaging the consensus ages of its constituent genes. Fold-change in PMID was calculated by dividing the number of PMIDs associated with a literature gene list by the average PMID count in an equivalently sized random gene list. The vertical dashed line represents the mean age of a random gene list, which is 1996 in this case; the horizontal dashed line represents the level at which there is no difference between the numbers of PMIDs associated with the literature and random gene lists.

Annotation bias and consensus gene age

A ‘well-studied’ gene may in part reflect one that has been known for many years, thus allowing a substantial corpus of literature regarding it to be accumulated. To investigate the possible effect of this aspect of the history of recent scientific research we determined the ‘age’ of each gene represented on the HG-U133A chip. Here, gene age is defined as an approximate measure of how long a gene has been known and researched upon relative to other genes, and should not be confused with the molecular timescale of evolution in the genome. We derived a consensus age for each gene represented on the HG-U133A chip based on two criteria: (1) when the gene was first cited in the published literature and (2) when the gene was first integrated into the OMIM and HGNC public databases. The consensus gene age was computed as the average of these two measures (see ‘Materials and Methods’ section for more details), and ranges from year 1939 to 2007. In the context of this analysis, a gene with a consensus age of 1990 implies that it was discovered in approximately 1990, so it is considered older and has been studied for longer compared to a gene with a consensus age of 1998.

We stratified all the genes by their consensus age and compared the amount of PMIDs associated with them. As expected, younger genes that have only recently been described have markedly fewer PMIDs associated with them; whereas older genes are generally better studied and cited by more PMIDs (Supplementary Data 1 Figure S1). This effect seen on individual genes is also translated into an effect on the mean age of genes in biologically derived gene lists. As can be seen in Figure 1b, there is a strong trend whereby those gene lists that show excess PMID annotation are also those whose constituent genes have been known for longer.

Overcoming annotation bias by permutation test

Our initial attempt to address the effects of annotation bias used a permutation test that makes no assumptions about the underlying data distribution. The significance of a token was assessed by calculating an empirical P-value based on the creation of 100 000 random gene lists, each of which was matched for the number of genes and the amount of associated PMIDs. Tokens with List frequency equal to 1 were removed before they were subjected to permutation test because a token can only be useful in defining relationships among genes if it is shared by at least two of them. After this filtering, 4840 tokens remained for testing.

This approach produced an improvement over the classical hypergeometric distribution-based approach when tested on the ISG gene list, insofar as it successfully retained those biologically plausible terms such as ‘interferon’, ‘IFN’, ‘antiviral’, whilst no longer called those less-specific terms as significant (Table 2). However, one limitation of this approach is the precision of the P-values, the smallest of which is determined by the number of permutations carried out. In this analysis, the best possible Bonferroni P-value attainable is 10^–5 × 4840 = 0.0484. This could be improved by increasing the number of permutations, but as with many permutation-based methods, this approach is extremely computationally intensive, requiring six hours on a standard desktop computer to analyse the ISG gene list. To address this issue we developed two computationally efficient methods capable of handling the annotation bias problem.

Table 2.

A comparison of the results from different methods when applied to the ISG gene list

Abstract term	Chip	List	Bonferroni P-value
			Permutation	Outlier	ExtendedHG
INTERFERON	414	46	<0.0484	9.81 × 10−34	2.12 × 10−31
IFN	245	35	<0.0484	8.90 × 10−19	1.35 × 10−25
IFN-BETA	71	18	<0.0484	5.60 × 10−11	1.34 × 10−14
ANTIVIRAL	176	23	<0.0484	2.24 × 10−8	1.03 × 10−13
IFN-ALPHA	114	19	<0.0484	3.00 × 10−8	2.49 × 10−12
INTERFERON-ALPHA	59	14	<0.0484	6.08 × 10−8	5.85 × 10−10
OLIGOADENYLATE	18	8	<0.0484	2.26 × 10−6	8.29 × 10−6
ISG	14	7	<0.0484	1.41 × 10−5	9.05 × 10−5
ISRE	31	9	<0.0484	2.06 × 10−5	1.62 × 10−5
DSRNA	60	11	<0.0484	0.0001	1.03 × 10−5
HLA-CLASS	11	6	<0.0484	0.0002	0.0015
HLA-A	30	8	1	0.0003	0.0005
HLA-B	25	7	1	0.0024	0.0048
INDUCIBLE	1068	37	<0.0484	0.0025	1.29 × 10−7
ENCEPHALOMYOCARDITIS	16	6	<0.0484	0.0036	0.0136
STOMATITIS	52	9	<0.0484	0.0036	0.0013
OAS	10	5	0.0968	0.0145	0.1047
HLA-G	10	5	1	0.0145	0.1047
MXA	11	5	1	0.0257	0.1624
EVASION	65	9	<0.0484	0.0258	0.0074
INNATE	363	21	0.0484	0.0311	1.35 × 10−5
TAPASIN	12	5	1	0.0427	0.2407
VIRAL	892	32	0.0484	0.0447	4.25 × 10−6
INFECTION	1177	36	0.0968	0.0477	9.61 × 10−6
OR-C	5	4	<0.0484	0.0717	0.5133
LYMPHOBLASTOID	239	16	<0.0484	0.0872	0.0004
IFN-GAMMA	443	22	0.1936	0.1113	6.38 × 10−5
IMMUNITY	387	20	0.0968	0.1799	0.0002
IMMUNE	1275	35	0.6776	0.4363	0.0003
TREAT	1817	40	<0.0484	0.9165	0.0033
MHC	353	17	1	1	0.0115
VIRUS	1408	34	1	1	0.0089

Abstract terms that are identified as over-represented by the corresponding method are shown in bold. The cutoff used is P ≤ 0.05 after Bonferroni correction. 100 000 randomisations were performed for the permutation test. 4840 tokens were being tested during the permutation test and the best possible Bonferroni P-value attainable is 10^–5 × 4840 = 0.0484. Any term with an empirical P-value less than 10^–5 is provisionally assigned a value of <10^–5, and the corresponding Bonferroni P-value is set to be <0.0484. The unadjusted P-values and other details (e.g. Z-scores and odds ratio) can be found in Supplementary Data 1, Table S1. Chip is the number of genes that contains a given term on the entire chip; List is the number of genes that are associated with a given term in the ISG gene list.

Outlier: an empirical outlier detection method for finding over-represented terms in PubMed abstracts

This method exploits observations made when plotting the number of genes that contains a token of interest on the entire chip (the Chip frequency) versus the number of genes that are associated with a token in the query gene list (the List frequency). On such plots (see Figure 2 for an example) we observed that there are typically a set of biologically plausible tokens that lie far away from the main data cluster formed by the remaining tokens and appear as outliers. We reasoned that most tokens in a gene list would be largely irrelevant to the biology under study (e.g. common English words), thus forming the background cloud of points, with enriched and thus potentially interesting tokens appearing as outliers. We further reasoned that the annotation bias effect should, in principle, also affect the background distribution, and thus an outlier-detection approach may intrinsically compensate for the underlying annotation bias.

To test this we developed an outlier detection method denoted here as Outlier. The detailed methodology is described in the Materials and Methods section but briefly, we use a plot such as Figure 2 and calculate a Z-score for each token based on the local Chip mean and standard deviation. Using this method, 24 tokens were called significantly over-represented in the ISG gene list (Table 2), all of which appear relevant to the biology of an interferon-regulated response and are very similar to those tokens produced by the permutation-based method. However, Outlier is much more computationally efficient than the permutation-based test (typically runtimes of 20–30 s on a desktop PC).

ExtendedHG: identify over-represented terms in PubMed abstracts using the extended hypergeometric test

The second method, called ExtendedHG, is a parametric approach based on the extended hypergeometric distribution. The key concept underlying this approach is that annotation bias will cause common, non-specific terms to have higher probabilities of being selected than expected by chance. Therefore the sampling procedure is biased, with the token frequency distribution following the extended hypergeometric distribution. The degree of bias is measured by the odds ratio, which is equivalent to the probability ratio of seeing a token of interest over other tokens simply by chance, and a P-value for each token can therefore be calculated.

ExtendedHG produced results similar to the permutation test (Table 2). All 27 tokens identified as over-represented in the ISG gene list by ExtendedHG are biologically plausible, while those non-specific words that were called significant by the classical hypergeometric test-based approach such as ‘synthesis’, ‘molecule’, ‘after’ were not selected. As with Outlier, a typical runtime for ExtendedHG is ∼20–30 s when applied to a 500-gene list. A comparison of the rankings between the top 100 most significant terms in ISG gene list shows that, despite minor differences in rank order, there is a good concordance between Outlier and ExtendedHG (Supplementary Data 1 Figure S2).

False positive rates under the null hypothesis

From the specificity perspective, an ideal ORA method should not find any significant terms in a random gene list. To estimate the false positive rates associated with the proposed methods, we created 1000 random gene lists by randomly sampling 50–2000 unique genes from the HG-U133A array and analysed them with Outlier and ExtendedHG. The false positive rate of Outlier ranges from 0.18 to 1.84, with shorter gene lists (<300 genes) being more susceptible to false positives. This is because the Z-scores distribution from the outlier detection procedure tends to show a slight negative skewness for short gene lists, but is closer to being normally distributed for longer gene lists (see Supplementary Data 4). ExtendedHG shows a low false positive rate (<0.01) even for short gene lists.

Comparison with existing ORA tools

Using the ISG gene list as the benchmarking dataset, we observed a good agreement between the biology associated with the enriched GO terms reported by the functional annotation tool DAVID 2.0 (http://david.abcc.ncifcrf.gov/home.jsp) and the PubMed abstract terms produced by our methods, with concepts related to immune response highly ranked by both approaches (Tables 2 and 3). As an illustration of the limitations of ontologies such as GO we noted that none of the significant GO terms gives an indication of the involvement of interferon, thus demonstrating how mining of PubMed abstracts can potentially reveal additional biological insight that is not possible by mining pre-defined ontologies alone.

Table 3.

Significantly over-represented GO terms in the ISG gene list identified by DAVID

GO term	Chip	List	Bonferroni P-value
Response to biotic stimulus	853	49	6.40E–33
Immune response	737	44	8.30E–29
Defense response	816	45	2.90E–28
Response to stimulus	1765	52	1.10E–21
Organismal physiological process	1660	46	2.00E–16
Response to virus	70	14	2.20E–12
Response to pest, pathogen or parasite	503	25	2.40E–11
Response to other organism	514	25	3.90E–11
Response to stress	956	27	6.00E–07
MHC protein complex	18	6	6.30E–05
MHC class I protein complex	18	6	6.30E–05
Antigen presentation, endogenous antigen	27	7	6.70E–05
Antigen processing, endogenous antigen via MHC class I	28	7	8.50E–05
MHC class I receptor activity	36	7	2.00E–04
Antigen processing	36	7	4.20E–04
Antigen presentation	42	7	1.10E–03
Immunological synapse	31	6	1.20E–03

The ontological tool DAVID 2.0 was used to identify over-represented GO terms in the ISG gene list. The analysis was performed using all levels of GO terms and HG-U133A chip as background (database version as of 19 December 2007). Over-represented GO terms were defined as having Bonferroni P-value ≤0.05 based on Fisher's exact test (threshold settings: Count = 2, EASE = 0.1).

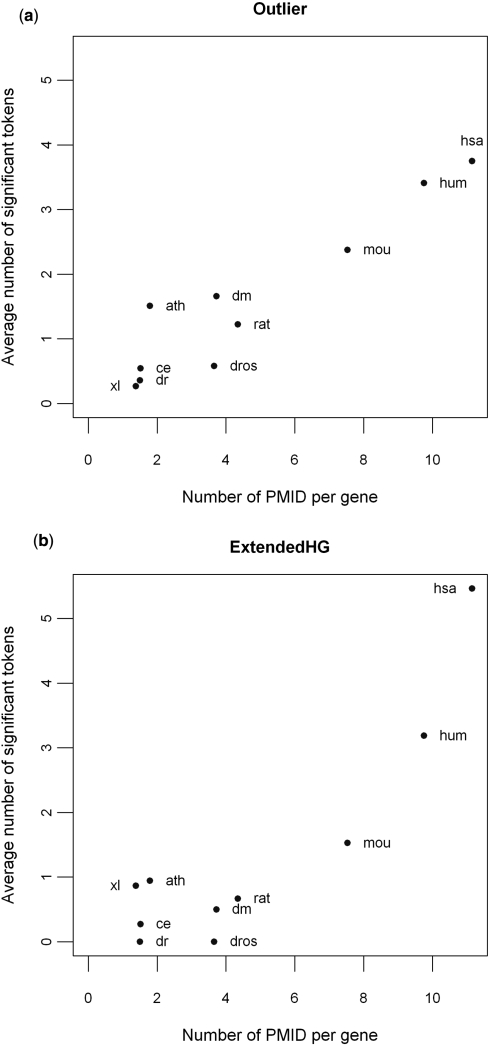
Performance across different species

Outlier and ExtendedHG can be readily extended to other species for which an associated corpus of PubMed abstracts is available, although their power will depend on the extent and quality of annotation. To test this, we analysed 354 gene lists collected from published literature spanning 10 major Affymetrix chip types and eight model organisms including human, mouse, rat, Arabidopsis, Drosophila, C. elegans, Xenopus and Zebrafish (see Supplementary Data 2 for details of these gene lists). We found that the number of tokens identified as over-represented by the two methods varies substantially between species (Supplementary Data Figures S3 and S4). This appears to be related to the amount of annotation available to each species in the text corpus used. Those species with a higher amount of overall annotation per gene tend to produce, on average, more significant tokens per gene list tested (Figure 3). Therefore at this moment gene lists based on well-researched species such as human and mouse produce more detailed insight than those from less well-studied organisms. Nevertheless, useful information can still be obtained from species such as Arabidopsis, as shown by an analysis of data presented in Nishimura et al. (8). They studied the effect of the pmr4 mutation on pathogen response in Arabidopsis and concluded that the basis for the resistance in pmr4 mutant plant to pathogens was due to an enhanced activation of the salicylic-acid (SA) signal transduction pathway. We re-analysed the list of differentially expressed genes reported by the authors using a ‘trimmed’ version of the text corpus built from only those papers published before 2003, so as to mine no more than the knowledge that was available to the authors of the original paper. Two tokens, ‘salicylic’ and ‘SA’, were identified as over-represented in the gene list, hence recapitulating the conclusions by the authors. Both tokens were called significant by Outlier; whilst only ‘salicylic’ was called significant by ExtendedHG. This shows that despite the lower level of annotation, plausible results can still be obtained for less well-annotated species by using the text-based ORA approaches described here.

Figure 3.

A comparison of the performance of Outlier (a) and ExtendedHG (b) across different species. The average number of tokens called significant by the two approaches, Outlier and ExtendedHG, is plotted against the annotation density (i.e. number of PMID per gene) for experimentally derived gene lists that were performed on 10 Affymetrix platforms representing eight different species, including HG-U133A (hsa), HG-U133 Plus 2.0 (hum), Mouse 430 2.0 (mou), Rat 230 2.0 (rat), Arabidopsis ATH1 (ath); DrosGenome1 (dm), Drosophila 2.0 (dros), Xenopus laevis (xl), C. elegans (ce) and Zebrafish (dr).

DISCUSSION

We have presented several approaches for mining literature-based information associated with a list of differentially expressed genes (DEG) and to search within them for terms or biological concepts that are significantly over-represented. Our initial explorations using the classical hypergeometric distribution revealed a hitherto unexpected bias in the degree of PubMed annotation associated with gene lists derived from ‘real’ biological experiments. We hypothesised that gene lists generated from real-life biological experiments are likely to be biased towards older genes (i.e. known for a longer period of time) from more established areas of biology. Indeed, as shown in Figure 1b, most literature-derived gene lists have an overall consensus age that is older than the mean age of a random gene list (in this case 1996). It thus seems that gene lists derived from a typical microarray experiment tends to favour groups of genes and areas of biology that have been studied for longer and have a greater amount of associated published literature. Whilst giving an insight into trends within biological research and the progress of scientific endeavour, the consequence for text-based ORA approaches is an annotation bias that has a negative effect on the performance of simple hypergeometric-based approaches. Both Blaschke et al. (12), Khatri and Draghici (13) have pointed out that such bias constitutes a real problem and should be taken into account during enrichment analysis. However, no solution has been proposed to address this problem and it has generally been overlooked by existing ontological tools that implement ORA. Although illustrated here using PubMed tokens, such bias may have a similar influence on other ORA-based functional analysis tools that mine different annotation resources.

To address this annotation bias we have implemented three different approaches to ORA using PubMed tokens, based on a permutation test, an outlier detection method, and the use of the extended hypergeometric distribution. The latter two are computational tractable and this enabled us to benchmark them against 354 literature-derived gene lists. We find that tokens plausibly relevant to each study are often called significantly enriched, whilst the apparent over-representation of common terms due to annotation bias are successfully avoided. The results produced by the proposed methods generally show a good concordance in most analyses that we have performed. These tools provided a similar but distinct insight into the themes over-represented in a gene list compared to the results from undertaking ORA using GO terms, and can be successfully applied not only to well-annotated species but also to model species such as Arabidopsis.

Evaluating the performance of any exploratory approach such as those proposed herein is a challenging task because it is difficult to find datasets for which the ground truth is known. We have therefore undertaken a more focused approach to assess the performance of the proposed methods. Specifically, we focused on gene lists based on the HG-U133A array, and compared the outcome from Outlier and ExtendedHG with those obtained from a standard ORA approach that mines GO terms. The biological relevance and plausibility of the over-represented tokens and GO terms were then assessed against the perceived biology of the original publication. These set of data are presented as Supplementary Data 3. For literature gene lists derived from other arrays, their token- and GO-based ORA results are readily accessible via our website for review by researchers with the relevant biological background.

Several groups have undertaken the challenge of incorporating literature-based information into data mining algorithms to interpret the underlying biological significance of a list of DEGs (12,14,15); their approaches differ fundamentally from our methods. The closest in spirit to ours is the GEISHA (Gene Expression Information System for Human Analysis) system developed by Blaschke et al., which evaluates the significance of terms associated with a gene cluster by comparing their frequency of abstracts with the frequency of abstracts containing these terms in different gene clusters. However, the online version of this system was only implemented for E. coli and yeast. Therefore, it has not been possible to perform a direct comparison between this tool and our methods.

Like other ORA approaches, our methods require an initial selection of DEGs by an arbitrarily chosen cut-off threshold. A major criticism to such ‘threshold-based’ approach is that different choices of the cut-off value will produce different lists of DEGs and alter the result of the enrichment analysis. Moreover, many genes with moderate but meaningful expression changes may be discarded by the selected threshold regardless of their relative position in the ranked list, leading to a loss in statistical power. In recent years, an alternative mode of analysis that does not involve an initial gene selection step has been proposed. Examples of these include Gene Set Enrichment Analysis (GSEA) (16–18) and Functional Class Scoring (FCS) (19). These methods consider the distribution of a functionally defined group of genes in the ranked list of genes and allow adjustments for their correlation structure. While a few studies have shown that such threshold-free approach enables the detection of more subtle functional categories that were overlooked by ORA (19,20), Manoli and coworkers (21) found that ORA produced more consistent results than GSEA with respect to the concordance between analyses on DEG obtained by different statistical methods from three prostate cancer data sets. Although it would be computationally challenging in scale, it may be possible to develop threshold-free methods that can accommodate annotation bias and thus be applied to the mining of PubMed tokens and we are currently exploring this question.

The methods described here depend on a corpus of articles relevant to the genes being studied (e.g. all genes appearing on an array), and an index that links the articles to the appropriate genes. We used the manually curated citations provided by NCBI to retrieve the relevant gene-related PubMed abstracts. Although such curation provides for high quality, this process together with the volume of research activity in different areas means that the coverage of less heavily studied species is still limited and this has a direct effect on the power of our method. Incorporation of additional gene-citation links, perhaps from species-specific databases, would increase the amount of textual information in the corpus and improve the power of the proposed methods. Our methods are currently based on a simple processing and analysis of the text corpus. There are several areas where this could be made more sophisticated and complex in the future, such as the removal of stopwords, the use of thesauri to allow for the identification of multi-word biological concepts and synonyms mapped to the same gene. These steps should reduce the noise caused by natural language variation and improve the information content of the over-represented tokens.

To conclude, we have described the problems and challenges associated with existing ORA methods when adapting them for mining text-based information, and three novel approaches have been proposed to address some of these problems. Analysis performed on several independent datasets show that the proposed methods produce biologically meaningful results that are in good agreement with the manually determined annotations (Supplementary Data 3). These examples also demonstrate that a coherent picture that exists within complex group of genes can be discerned by incorporating textual information embedded in literature as a knowledge source into the analysis of gene expression data. We believe that the proposed text-based ORA approaches can be used to complement and extend existing ontology-based functional analysis tools for guiding the biological interpretation of complex microarray data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Cancer Research UK (grant number C8731/A5579). Funding for open access charge: Cancer Research UK (grant number C8731/A5579).

Conflict of interest statement. None declared.