Microfabricated tissue gauges to measure and manipulate forces from 3D microtissues

Abstract

Physical forces generated by cells drive morphologic changes during development and can feedback to regulate cellular phenotypes. Because these phenomena typically occur within a 3-dimensional (3D) matrix in vivo, we used microelectromechanical systems (MEMS) technology to generate arrays of microtissues consisting of cells encapsulated within 3D micropatterned matrices. Microcantilevers were used to simultaneously constrain the remodeling of a collagen gel and to report forces generated during this process. By concurrently measuring forces and observing matrix remodeling at cellular length scales, we report an initial correlation and later decoupling between cellular contractile forces and changes in tissue morphology. Independently varying the mechanical stiffness of the cantilevers and collagen matrix revealed that cellular forces increased with boundary or matrix rigidity whereas levels of cytoskeletal and extracellular matrix (ECM) proteins correlated with levels of mechanical stress. By mapping these relationships between cellular and matrix mechanics, cellular forces, and protein expression onto a bio-chemo-mechanical model of microtissue contractility, we demonstrate how intratissue gradients of mechanical stress can emerge from collective cellular contractility and finally, how such gradients can be used to engineer protein composition and organization within a 3D tissue. Together, these findings highlight a complex and dynamic relationship between cellular forces, ECM remodeling, and cellular phenotype and describe a system to study and apply this relationship within engineered 3D microtissues.

It has long been appreciated that the generation and transduction of mechanical force by cells can drive the buckling, extension, or contraction of multicellular tissues during development (1–3) and is essential for wound healing and tissue homeostasis in adult organisms (4, 5). In addition to physically driving tissue assembly, these forces also regulate cell signaling and gene expression, thereby coordinating tissue morphogenesis with cellular differentiation (6, 7). Yet, although cellular forces are known to contribute to tissue morphogenesis and tissue repair, a more detailed picture of how tissue mechanics link to morphogenetic phenomena has been hindered by a lack of model systems in which both mechanics and remodeling can be simultaneously examined.

Centimeter scale encapsulations of cells in ECM analogues are widely used as model systems for many morphogenetic processes (8–11). However, although such systems can recapitulate many developmental processes, the cellular forces within these encapsulations are typically inferred only indirectly by measuring the volumetric contraction of free-floating constructs, or from the population average of constructs pulling against rigid strain gauges (12, 13). Moreover, the scale of these encapsulations often necessitates histological sectioning to visualize fine scale cellular structures and protein distributions within the construct. Because such sections are incompatible with live cell microscopy and provide information about only a small region of a much larger construct, it has been difficult to fully map cellular contractility, tissue mechanics and cellular phenotype simultaneously within a 3D encapsulation.

To obtain quantitative, spatially resolved measurements of cellular traction forces, investigators have cultured cells on the surface of specially engineered 2-dimensional (2D) substrates including elastic hydrogels and arrays of microfabricated pillars (14, 15). These methods have been instrumental in defining the soluble and mechanical regulators of myosin generated contractility (15, 16). Moreover, the amount of cytoskeletal tension generated against these substrates has been shown to modulate numerous cellular functions such as proliferation and differentiation (17–19). However, although these approaches have highlighted an important connection between cell mechanics and cell phenotype, the 2D nature of such techniques inherently limits the extent to which 3D morphogenetic phenomena can be described.

Here, we present an approach to measure forces from microscale constructs of cells embedded within 3D matrices. These microfabricated tissue gauges (μTUGs) incorporate MEMS cantilevers, which simultaneously constrain and report forces generated by micropatterned 3D constructs in real time. Using this system, we simultaneously monitored matrix remodeling events and microtissue force generation, and reported rapid changes in microtissue force in response to soluble stimuli. We demonstrated that both the mechanical stiffness of the cantilevers and collagen matrix influence tissue remodeling by altering cellular contractile forces and matrix protein deposition. Using these findings, we generated a computational model of multicellular contractility that predicted that fine scale gradients of mechanical stress could be used to engineer patterned protein levels within microtissues of controlled geometry. Together, these studies highlight a unique approach to examine an important mechanical interplay between cellular contractility, ECM mechanics, and tissue organization within 3D matrices.

Results

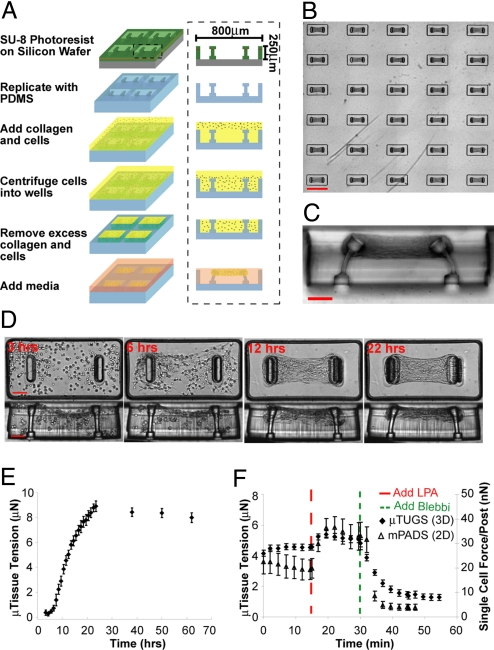
To miniaturize cultures of cells embedded within 3D collagen matrices, we microfabricated arrays of wells within a PDMS mold (Fig. 1A). The mold was immersed in a suspension of cells and unpolymerized type I collagen and centrifuged to drive cells into the recessed wells. Excess solution was removed and the remaining constructs were polymerized. Within hours, we observed the spontaneous contraction of the collagen matrix by the cells. Raised cantilevers incorporated within each template spatially restricted the contraction of the collagen matrix and resulted in a large array of microtissues anchored to the tips of the cantilevers (Fig. 1B). We used a multilayer photolithography process to generate wide heads at the tips of the cantilevers, which ensured that microtissues remained anchored even in highly deflected configurations (Fig. 1C). Because adhesion of the tissue was limited to the upper cantilever section, the stiffness of each cantilever could be controlled by altering the thickness of the lower sections. We used linear bending theory and experimental measurements, using calibrated glass micropipettes, to report the load-displacement relationship for 2 different cantilever geometries with measured spring constants of 0.098 ± 0.017 μN/μm and 0.397 ± 0.039 μN/μm (Fig. S1). These spring constants were then used to link the measured cantilever deflections to the amount of force generated by microtissues under varying conditions.

Fig. 1.

Fabrication method and temporal response of microtissues. (A) Process flow diagram for the creation of μTUG arrays. (B) Large arrays of microtissues are simultaneously generated on a substrate. (C) Cross section view of a single μTUG well. (D) Representative images depicting the time course of a contracting microtissue. (E) Time course of forces generated during microtissue contraction. Data points represent the average force for 5 microtissues ± SEM. (F) The temporal response of microtissues (closed diamonds) and single cells on mPADs (open triangles) in response to 10 μg/mL LPA and 50 μM blebbistatin. Data points represent the average force for 10 microtissues or 5 individual cells ± SEM. (Scale bars: B, 800 μm; C and D, 100 μm.)

Shortly after seeding, we observed that NIH 3T3 cells embedded within a collagen matrix extended and retracted thin protrusions and compacted the matrix around the cell periphery (Movie S1). Because cells were distributed throughout the tissue, the collective action of these local processes resulted in bulk contraction of the collagen gel (Fig. 1D). This bulk contraction first became evident 3 h after seeding and was nearly complete after 12 h. In that same time frame, microtissue tension increased nearly 8-fold and then continued to increase another 2-fold over the next 12 h in absence of gross changes in bulk tissue morphology (Fig. 1E).

In addition to driving long-term morphologic changes, more rapid dynamics in cellular contractility, which may be triggered in response to soluble factors, can play critical roles in settings such as vascular homeostasis (20). However, diffusion limited concentration gradients may complicate the interpretation of such responses within traditional, centimeter-scale, 3D cultures (21, 22). For simple diffusion (i.e., that governed by Fick's 2nd Law) the time required for diffusion of soluble factors scales with the thickness of the construct squared; therefore, concentration gradients in microtissues (thickness ≈100 μm) should equilibrate 100 times faster than those in bulk gels (thickness ≈1 mm). To illustrate the experimental relevance of this effect, we compared the dynamic contractile response of microtissues in response to a soluble factor stimulus to that of cells cultured on 2D microneedle arrays (mPADs), which lack any diffusion barrier (15) (Fig. 1F). We found that both 3D microtissues and single cells in 2D increased or decreased contractile forces within 5–10 min of treatment with lysophosphatidic acid (LPA), a known stimulant for myosin activity, or with blebbistatin, a myosin ATPase inhibitor, respectively. In contrast, centimeter-scale constructs have been shown to require substantially longer (>30 min) to reach equilibrium after a similar stimulus (23).

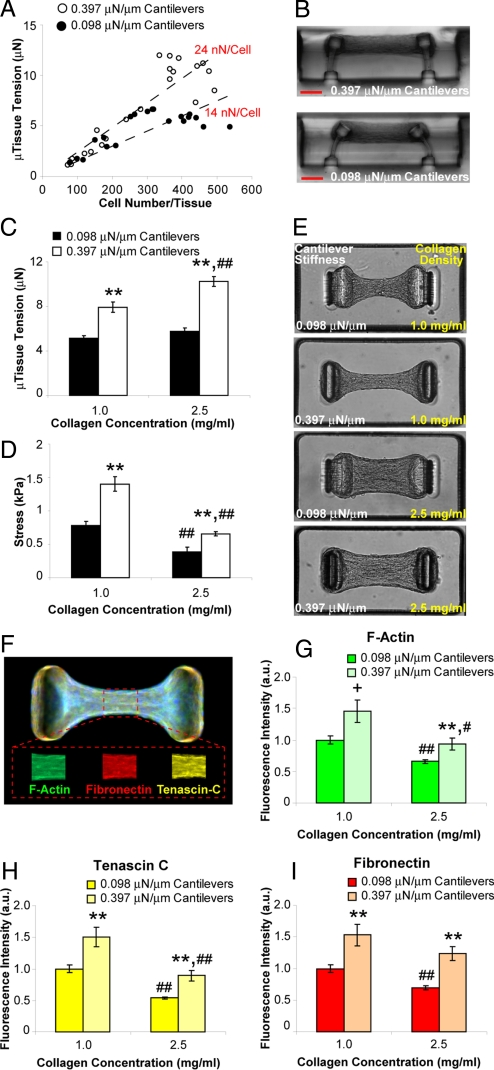
Although the contraction of a tissue arises from the actions of its constituent cells, it is currently unclear how tissue mechanics can feedback to affect cellular force generation. When we created microtissues with a range of cell densities, we observed an approximately linear relationship between microtissue tension and cell density (Fig. 2A), which provided an estimate of the average force generated per cell within each construct. Interestingly, the stiffness of the cantilevers impacted the magnitude of force generated by cells. Cells within microtissues tethered to flexible cantilevers (k = 0.098 μN/μm) generated ≈14 nN per cell whereas cells within microtissues tethered to more rigid cantilevers (k = 0.397 μN/μm) generated ≈1.7-fold more force (Fig. 2 A and B). These values for cellular contractile forces are in the range of those measured previously (see compilation in ref. 24).

Fig. 2.

Boundary and matrix mechanics regulate cellular contractility and protein deposition. (A) Plot of microtissue tension vs. number of cells per tissue for constructs tethered to rigid (0.397 μN/μm, open circles) or flexible (0.098 μN/μm, closed circles) cantilevers. (B) Representative cross sections of microtissues tethered to rigid or flexible cantilevers. (C) Plot of average microtissue tension for tissues constructed from 1.0 mg/mL or 2.5 mg/mL collagen gels tethered to rigid or flexible cantilevers. (D) Plot of average midpoint stress for tissues constructed from 1.0 mg/mL or 2.5 mg/mL collagen tethered to rigid or flexible cantilevers. (E) Phase contrast images of microtissues in each of the 4 combinations of collagen density and cantilever stiffness. (F) Representative immunofluorescence overlay of cytoskeletal and ECM proteins within microtissues. Mean fluorophore intensity was measured over a 30-μm long segment at the tissue midsection using distinct fluorphores for each protein (Inset). (G–I) Plots of average relative fibrillar actin, fibronectin and tenascin C levels under each of the 4 combinations of collagen density and cantilever stiffness. Data from (C and D) are the average of 15 microtissues from each condition ± SEM. Data from (G–I) are the average of 40 microtissues for each condition ± SEM. **, P < 0.01; *, P < 0.05; +, P < 0.05 (Student's t test) P = 0.15 (MWU) for 0.397 vs. 0.098 μN/μm cantilevers; ##, P < 0.01; #, P < 0.05 for 2.5 vs. 1.0 mg/mL collagen. (Scale bar: 100 μm.)

In addition to boundary mechanics, the bulk modulus of the matrix within which the cells are embedded may be another means by which tissue mechanics can feedback to influence cellular contractile forces. To compare the relative impact of these 2 effects, we independently varied collagen density (1.0 mg/mL vs. 2.5 mg/mL) and cantilever stiffness (0.098 μN/μm vs. 0.397 μN/μm) while controlling for cell density (Fig. 2 C–E). We observed that microtissue tension increased both with increased cantilever stiffness and increased collagen density (Fig. 2C). Normalizing the measured forces by the cross-sectional areas of the microtissues in these 4 conditions further revealed that mechanical stress increased with increased cantilever stiffness, but decreased with increased collagen density (Fig. 2D). This decreased stress with collagen density may result from the decreased compaction of denser gels and provides an interesting divergence in the relative impact of boundary rigidity versus matrix stiffness.

Because specific cytoskeletal and ECM protein levels are altered in mechanically aberrant conditions such as wound healing and hypertension (4, 25), we investigated whether mechanical feedback may be a means to regulate such changes in protein expression in microtissues. Interestingly, using quantitative immunofluorescence, we found that changes in the amounts of fibrillar actin and ECM proteins fibronectin and tenascin C qualitatively mirrored the changes in mechanical stress within microtissues under each condition (Fig. 2 F–I). These results suggest that multiple mechanical inputs (e.g., tissue boundary mechanics, matrix rigidity, and mechanical stress) can feedback to regulate cellular contractile forces and protein deposition, 2 key factors in maintaining tissue homeostasis.

Although we observed that average protein levels in microtissues correlated with average mechanical stress, the emergence of complex tissue forms in vivo relies on intricately patterned ECMs and fine scale gradients of mechanical stresses to guide cell migration and differentiation (26–28). To determine whether our microtissue approach could be used to study the effects of spatially patterned mechanical stresses, we developed a computational model to predict how such stresses may be distributed within individual microtissues. We adapted a bio-chemo-mechanical model based on actin/myosin force generation, which was originally used to describe the distribution of proteins and forces within single cells (29, 30). A full description of the equations and assumptions governing this model is provided in SI Appendix. Briefly, the microtissue is modeled as a continuum in which actin fibers are free to polymerize in any direction. Once formed, actin fibers contract according to a modified version of the Hill equation (31), which describes actin-myosin contractility in muscle. This contraction generates stresses within the tissue that then feedback to stabilize the actin fibers themselves and ultimately modulate tissue morphogenesis. Experimental measurements of the effects of cantilever and matrix stiffness were used to calibrate parameters for the initial mechanical properties of the collagen–cell composite and to set limits on the maximal stress capable of being generated by an actin/myosin element.

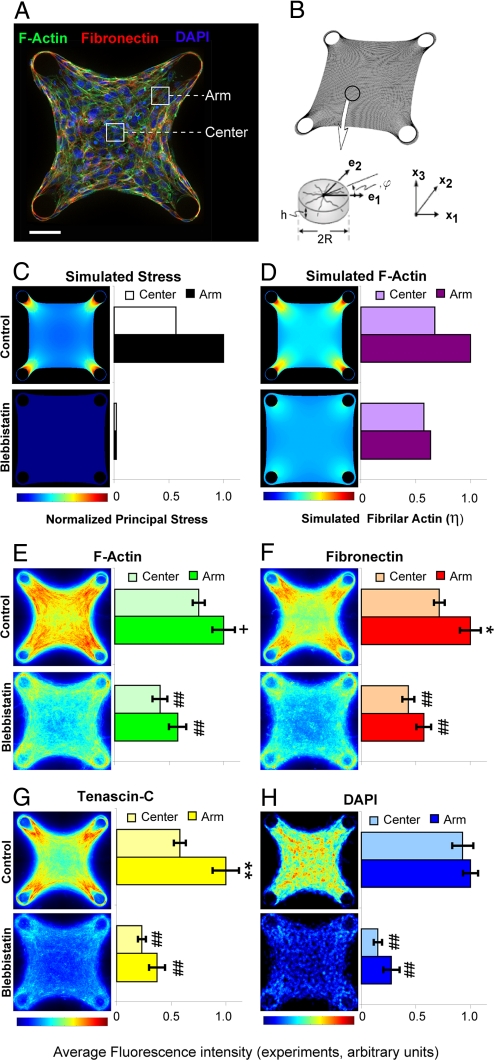
The model recapitulated the observed increase in microtissue tension in response to increased cantilever stiffness and matrix density (Table S1). We then applied the model to microtissues with 4 rigid cylindrical cantilevers forming a square tissue, to observe the effects of enhanced internal variations in stress (Fig. 3B). For such geometries, the model predicted the generation of large gradients of intratissue stress and filamentous actin with peak levels that propagate away from the cantilevers (Fig. 3 C and D). Based on these computational results, we generated the same geometries in our microtissue platform (Fig. 3A). In agreement with our predictions, we observed patterned levels of filamentous actin, fibronectin and tenascin C within the microtissue that correlated with the degree of predicted mechanical stress (Fig. 3 E–G). This effect was not due to heterogeneous cell density as cells were uniformly distributed throughout the tissue (Fig. 3H). Moreover, when we reduced stress in precontracted microtissues by treatment with blebbistatin, the protein levels decreased and were concentrated mainly around the anchors rather than propagating inward (Fig. 3 E–G). To confirm that differences in protein expression between control and blebbistatin treated samples were not simply due to differences in cell proliferation, we inhibited proliferation in both conditions, using aphidicolin and observed similar distributions of protein accumulation without altering cell density between the 2 conditions (Fig. S2). We simulated the effect of blebbistatin in our model by reducing the parameter for actin/myosin contractility to 10% of maximal, and found reduced levels and more uniform patterns of mechanical stress and filamentous actin that correlated with the observed lower peak expression and more diffuse distributions of protein staining (Fig. 3 C and D).

Fig. 3.

Predicted stress gradients within microtissues mirror patterned intratissue protein levels. (A) Immunofluorescence optical section of a microtissue tethered to 4 cylindrical posts showing: filamentous actin-green, fibronectin-red, and DAPI-blue. Arm and center regions used for quantification are indicated. (B) Finite element mesh and representative volume element for stress fiber formation used in a computational model of actin-myosin contraction. (C) Simulated distribution of principal stresses within a microtissue under 100% (control) and 10% (blebbistatin) conditions for simulated stress fiber contraction. (D) Simulated distribution of fibrillar actin within a microtissue under 100% (control) and 10% (blebbistatin) conditions for simulated stress fiber contraction. (E–G) Heat maps showing distribution of filamentous actin, fibronectin and tenascin C constructed from optical sections of microtissues under control and blebbistatin (50 μΜ) conditions. (H) Heat map of DAPI staining within microtissues under control and blebbistatin (50 μΜ) conditions. Heat maps are 2D projections of immunofluorescence staining from 120 optical sections (≈10 sections per microtissue for 12 different microtissues in each condition). **, P < 0.01; *, P < 0.05; +, P = 0.06 (Student's t test and MWU) for arm vs. center; ##, P < 0.01, for blebbistatin vs. control. (Scale bar: 50 μm.)

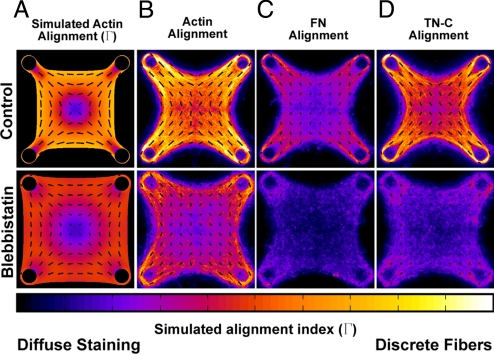
Another prediction of our model was that actin fibers would preferentially form and orient at the periphery of microtissues and in the direction of high stress gradients (Fig. 4A). Because patterned ECM alignment can play a critical and functional role in how forces and stresses are distributed within different tissues (32), we sought to investigate whether our model predictions would be confirmed experimentally. We found that actin was more fibrillar around the periphery of microtissues and was aligned in the direction of predicted principal stresses (Fig. 4B). Inhibiting myosin activity in precontracted tissues with blebbistatin reduced the overall amount of fibrillar actin and shifted the orientation to qualitatively match that which would be predicted by limiting actin/myosin contractility to 10% in our model (Fig. 4 A and B). Interestingly, both tenascin C, and to a lesser extent fibronectin, demonstrated patterned fibrillar regions and alignment in parallel with actin (Fig. 4 C and D) suggesting that mechanical stress may be a potent modulator of the organization of both cytoskeletal and ECM proteins.

Fig. 4.

Tension induced alignment of cytoskeletal and ECM proteins within patterned microtissues. (A) Simulated bundling (Γ) and alignment of actin fibers within a microtissue under 100% (control) and 10% (blebbistatin) conditions for simulated stress fiber contraction. (B–D) Heat maps depicting degree of bundling and alignment of actin, fibronectin and tenascin C based on fluorescence images of microtissues under control and blebbistatin (50 μΜ) conditions. In all cases, quiver orientation indicates orientation of the simulated or observed fibrils. Quiver length and heat map colors depict how distinctly these proteins are bundled (clustered into discrete fibers). Alignment data for each protein was quantified from immunofluorescence staining of 120 optical sections (≈10 sections per microtissue for 12 different microtissues in each condition).

Discussion

It has been suggested that a complex interplay between cellular contractile forces, matrix mechanics, and ECM remodeling contributes to developmental morphogenesis and tissue remodeling (1–3). Blocking myosin activity or surgically manipulating contractile cells via laser microdissection can alter or prevent morphogenesis at numerous stages of development (33, 34). Similarly, altering cellular forces or matrix mechanics in vitro has implicated a role for mechanics in model systems for the development of tendons and muscles, and more intricate structures such as mammary ducts and vascular networks (8–10, 35, 36). Here, we provide a simple approach to measure these cellular forces and mechanical stresses during microtissue remodeling events.

Previous studies using 2D substrates have demonstrated that substrate stiffness can regulate cellular contractile forces (16, 37) and protein expression (38), among other effects (19). Cells encapsulated in attached versus floating collagen gels also modulate expression of cytoskeletal and ECM proteins, illustrating the importance of mechanics in 3D settings (39–41). Here, by constraining microtissues, using flexible cantilevers, we simultaneously varied boundary and matrix stiffness with quantitative precision, and demonstrated that in 3D matrices, cellular contractility is regulated by overall stiffness whereas protein expression correlates with mechanical stress. The mechanical stiffness of the cantilevers that anchor the tissue may represent the rigidity of the external structure against which a tissue is contracting, such as the stiffness of bone against a ligament or blood pressure against smooth muscle in the vessel wall. In an analogous manner, collagen density may represent varying degrees of tissue fibrosis. These findings could have implications for the treatment of hypertensive and fibrotic disorders where elevated mechanical stress is associated with ECM stiffening (25, 42). Our study suggests that such stiffening may feedback to locally increase cellular contractility and matrix deposition, thereby creating a positive feedback loop between mechanical stress and disease progression. Molecules that target this feedback by modulating mechanotransduction pathways may hold promise as future therapeutics.

The ability of the μTUG system to generate large arrays of spatially isolated microtissues, each created from 80 nanoliters of starting material, may be readily extended to high throughput, low volume screening applications. Although 2D assays still provide substantially higher spatial resolution of the forces generated by individual cells, our μTUG system together with our mathematical model of multicellular contractility present a technique to study such mappings when cells are embedded within 3D matrices. The small dimensions of the microtissue constructs allow for rapid penetration of soluble effectors into the constructs in absence of substantial diffusion barriers. Although our initial studies focused on mesenchymal cell contractions that occur on the time scale of minutes, the measurement of 3D cellular forces over much faster time scales is an important functional readout for engineered physiologic or pathologic cardiac, skeletal, and smooth muscles. To illustrate that μTUGs could be used for such studies, we created microtissues of neonatal rat cardiomyocytes and observed periodic cantilever deflections in response to synchronous beating of the constituent cells (Movie S2).

By mapping the relationships between stress, cellular contractility and protein expression onto a bio-chemo-mechanical model of microtissue contractility, and coupling this model to finite element methods, we demonstrated how micropatterned gradients of mechanical stress can be used to generate patterned responses in a 3D tissue in vitro. Thus, although similar mechanical gradients have been shown to effect gene expression and contribute to tissue formation in vivo (6, 7), our studies highlight the possibility of exploiting mechanical patterning for the in vitro engineering of complex tissues. Studies that compare the extent to which data from 2D and 3D systems correlate as well as advancements in the spatial resolution of 3D force mapping will be instrumental in linking changes in cellular and matrix mechanics to in vivo phenomena. Such methods will hopefully lead not only to more effective approaches to engineer replacement organs and tissues, but also to a more complete understanding of the role of mechanical equilibrium in tissue homeostasis and disease.

Materials and Methods

Device Fabrication and Microtissue Seeding.

Single layer and multilayer templates were created by photopatterning SU-8 photoresist (Microchem) on silicon wafers. Multilayer SU-8 masters were created using successive spin coat, alignment, exposure and baking steps. All exposure steps were performed on a Karl Suss MJB3 mask aligner (Suss Microtec) using a U-360 band pass filter (HOYA). To prevent bleed through of the top cantilever lip into the lower segments, we used a modified version of the technique described in ref. 43. We spun a thin interstitial layer consisting of 15% S1813 (Shipley) and 85% SU-8, which strongly absorbed UV light. This served as a lithographic-stop layer and prevented unwanted cross-linking of the underlying SU-8 layers. All masters were developed in a single step in propylene glycol methyl ether acetate (PGMEA, Sigma) followed by hard bake. A full listing of fabrication parameters is available in SI Appendix (Table S2). To generate substrates for the microtissues, SU-8 masters were cast with a prepolymer of poly(dimethylsiloxane) (PDMS; Sylgard 184; Dow-Corning) as described in ref. 15. Before cell seeding, the PDMS templates were sterilized in 70% ethanol followed by UV irradiation for 15 min and treated with 0.2% Pluronic F127 (BASF) to reduce cell adhesion. Liquid neutralized collagen I from rat tail (BD Biosciences) was then added to the surface of the substrates on ice and templates were degassed under vacuum to remove bubbles in the liquid. A cooled suspension of cell laden neutralized collagen was then added to the substrate and the entire assembly was centrifuged to drive the cells into the micropatterned wells. Excess collagen and cells were removed by dewetting the surface of the substrate before incubating at 37 °C to induce collagen polymerization. The appropriate media was then added to each substrate.

Force Quantification.

For quantifying microtissue forces, microtissues were cultured for 24 h before brightfield images were taken of the cantilevers within each template (15 total, 5 each from 3 independent experiments), using an A-Plan10X objective on a Zeiss Axiovert 200M (Carl Zeiss MicroImaging, Inc.) with live cell incubator. Only tissues that were uniformly anchored to the tips of the cantilevers were included in the analysis. Masks were generated in Adobe Photoshop (Adobe Systems) outlining the base and cap regions of each cantilever and analyzed in MATLAB (The MathWorks) to compute the cantilever deflection. To account for errors in microfabrication, which may cause the cantilevers to deviate from perfectly vertical positions in absence of loading, baseline cantilever deflections were calibrated for cell free collagen gels. Cantilevers with a spring constant of 0.098 μN/μm had an inward baseline deflection of 1.19 ± 1.36 μm. Cantilevers with a spring constant of 0.397 μN/μm had an inward baseline deflection of 3.17 ± .38 μm. These baseline deflections were subtracted from the computed displacement of the cantilevers with attached microtissues for all force measurements.

To measure dynamic changes in contractility between microtissues and single cells, microtissues and cells on mPADs were cultured for 24 h in standard growth media, starved for 24 h in media containing 0.1% bovine serum, and then treated with 10 μg/mL LPA (Avanti Polar Lipids) followed by 50 μM blebbistatin (EMD Biosciences).

Finite Element Simulation of Microtissue Contractility.

The model for microtissue contractility was implemented in the commercial finite element package ABAQUS (Dassault Systemes) as a user-defined material as described in refs. 29 and 30 and in more detail in SI Appendix. Unless otherwise specified, the reference material parameters used in this study were the same as those published in ref. 29. To capture the effects of the collagen matrix density and cantilever stiffness as well as variance in tissue type specific contractility, parametric analysis was conducted for the passive Young's modulus (E) and the maximum tension capable of being exerted by the stress fibers (σ_max); refer to ref. 29 and SI Appendix for further details about these parameters. Suitable agreement to experimental results was found using E = 5 kPa, 15 kPa, and 25 kPa for microtissues constructed from 1.0, 1.75, and 2.5 mg/mL collagen respectively (Table S1). These values gave near perfect agreement with experimental measurements of microtissue forces under each condition and are in the range of published values for tissue-populated collagen matrices (24). Maximum isometric stress, σ_max, was determined to be 250 kPa. To correlate observations of protein alignment with model predictions, we used the circular variance (Γ) described in ref. 30 that provides an estimate of how tightly simulated stress fibers are clustered around a particular orientation. The value of Γ varies from 0 to 1, corresponding to uniformly distributed and totally aligned distributions respectively.

Immunofluorescence, Quantitative Immunofluorescent Microscopy, and Image Analysis.

Microtissues were fixed with 4% paraformaldehyde in PBS, permeabilized with 0.2% Triton X-100 in PBS, incubated with antibodies against fibronectin (MP Biomedicals) or tenascin C (Millipore/Chemicon) and detected with fluorophore-conjugated, isotype-specific, anti-IgG antibodies and counterstained with DAPI (Invitrogen). Filamentous actin was visualized by incubating samples with fluorophore conjugated phalloidin (Invitrogen). To quantify average protein composition, microtissues were cultured for 3 days, fixed and imaged with an A-Plan10X objective. Protein density was quantified by measuring the average fluorophore intensity within the microtissue (40 tissues total, 10 each from 4 independent experiments) for a 30-μm wide segment at the tissue midpoint, using distinct fluorophores for each protein, dividing by the volume of the tissue defined by this region and normalizing by DAPI staining intensity. Heat maps of protein expression were created within individual microtissues created from 1.75 mg/mL collagen and tethered to rigid cylindrical cantilevers. Microtissues were cultured for 5 days, fixed and optically sectioned under high magnification with a Plan-Neofluar 40X objective in 6-μm slices, using an Apotome structured illumination unit (Carl Zeiss MicroImaging, Inc.). Masks were generated in Adobe Photoshop labeling the positions of each cantilever and used to align and crop the z-stacks for each microtissue. To determine cell density, DAPI images were binarized within MATLAB, using a user determined threshold that was consistent between all conditions. Optical slices from each tissue (12 tissues total, 4 each from 3 independent experiments) were then averaged to quantify protein and cell distributions for each condition. All microtissues selected for protein analysis were randomly chosen from brightfield images of tissues that were uniformly anchored to the cantilever tips.

To quantify the alignment of cytoskeletal and matrix proteins, we implemented principal component analysis filtering on the image gradients as described in ref. 44. The alignment information from each optical slice was then compiled using a second implementation of principal component analysis to determine the dominant orientation.

Statistical Comparisons.

All reported statistical comparisons were performed by student t test on the mean and verified with a Mann–Whitney U test (MWU) on the median with certainty of P < 0.05 unless otherwise noted.

Cell Culture and Reagents.

NIH 3T3 cells obtained from ATCC were cultured in high glucose DMEM containing 10% bovine serum, 2 mM l-glutamine, 100 units/mL penicillin, and 100 mg/mL streptomycin (all from Invitrogen). Depending on experimental conditions, microtissues were incubated with ascorbic acid 50 μg/mL (Sigma) with DMSO (control), blebbistatin 50 μM (EMD Biosciences) and/or aphidicolin 1 μg/mL (Sigma). Cardiomyocyte cells were isolated from day 0 c57bl/6 mouse embryos (Harlan Laboratories) and cultured in DMEM:M199 (4:1) containing 10% horse serum, 1% (1M) Hepes buffer, 100 units/mL penicillin, and 100 mg/mL streptomycin (all from Invitrogen), and 5% FBS (Fisher Scientific). Cell culture media was changed every 3 days unless otherwise noted.