A Robust Unified Approach to Analyzing Methylation and Gene Expression Data

Abstract

Microarray technology has made it possible to investigate expression levels, and more recently methylation signatures, of thousands of genes simultaneously, in a biological sample. Since more and more data from different biological systems or technological platforms are being generated at an incredible rate, there is an increasing need to develop statistical methods that are applicable to multiple data types and platforms. Motivated by such a need, a flexible finite mixture model that is applicable to methylation, gene expression, and potentially data from other biological systems, is proposed. Two major thrusts of this approach are to allow for a variable number of components in the mixture to capture non-biological variation and small biases, and to use a robust procedure for parameter estimation and probe classification. The method was applied to the analysis of methylation signatures of three breast cancer cell lines. It was also tested on three sets of expression microarray data to study its power and type I error rates. Comparison with a number of existing methods in the literature yielded very encouraging results; lower type I error rates and comparable/better power were achieved based on the limited study. Furthermore, the method also leads to more biologically interpretable results for the three breast cancer cell lines.

1 Introduction

The explosion of interest in epigenetics over the past few years has had a profound impact on many areas of genetic and genomic research. Several groundbreaking studies have provided strong evidence that a wide variety of human diseases, such as cancer (Laird, 2005), have an epigenetic component. Epigenetic is the study of heritable changes in gene function that occur without a change in the DNA sequence. DNA methylation is essential for the normal development of mammals. However, evidence is mounting that aberrant DNA methylation in promoter CpG islands is linked to cancer by causing inactivation of tumor suppressor genes. These discoveries are made possible, in part, thanks to the availability of high-throughput technologies, allowing one to interrogate specific CpG sites or to profile methylation patterns of the entire genome (Piotrowski et al., 2006; Shen et al., 2006; Yan et al., 2002).

There is an extensive literature on methods for detecting genes that are differentially expressed. One of the earliest methods used in this context is the rule of two (Schena et al., 1996) in which genes with expression ratios greater than two or less than half are considered to be differentially expressed. This method is very simple to use, and is applicable to single-slide data, however it is not grounded in statistical principles. There are numerous modifications of the classical t-test statistic, including the significance analysis of microarray (SAM) (Tusher et al., 2001). Empirical Bayes methods (Efron et al., 2001, Newton and Kendziorski, 2003) are also popular ones, including the Log-Normal-Normal (LNN) and the Gamma-Gamma (GG) models that have been implemented in the EBarray software. Many other sophisticated methods have also been developed (Parmigiani et al., 2002, Pan et al., 2003, Newton et al., 2004, Dean and Raftery, 2005, Bhowmick et al., 2006, McLachlan et al., 2006). However, despite a large number of literature on the topic of identifying genes that are differentially expressed, only a very limited number of them, for example, the rule of two and the Normal-Uniform Differential Gene Expression (NUDGE) method (Dean and Raftery, 2005), are applicable to analyzing single-slide data.

Compared to expression arrays, methylation microarray technologies are still in their infancy, and thus it is still quite expensive, and some requires a large quantity of biological material, in order to profile whole genome methylation signatures. Interestingly, this mirrors the infancy stage of the expression array technologies, when replicates were hard to come by. To further complicate the matter, it is believed that methylation signatures can be highly heterogeneous, even for tumors of the same subtype (Khalili et al., 2007). As such, statistical methods for analyzing both single-slide and multi-slide (with either biological or technical replicates) data are in demand.

Since both gene expression and methylation data generated by microarrays are intensity measurements, methods proposed for gene expression analysis would appear to be applicable for methylation data too. However, due to different features and/or different experimental variation of these two biological systems and technological platforms, a method suitable for gene expression analysis may prove to be poor for methylation data. Since methylation microarray platforms are relatively new technologies, statistical methods proposed specifically for analyzing data generated from them are limited (Siegmund and Lin, 2007).

For the problem of identifying gene promoters that are differentially methylated, a recently proposed method based on finite mixture modeling (Khalili et al., 2007) appears to be the only one that was especially designed for such a purpose with single-slide data. Specifically, a three-component finite mixture model, the Gamma-Normal-Gamma (GNG) model, was proposed, where the two gamma components were used to model differential methylation while the normal component was intended to capture the rest of the data. However, since there was neither positive nor negative control data for methylation, the absolute performance of GNG was not evaluated in terms of power and type I error rates (Khalili et al., 2007). Driven by the desire to assess the absolute performance of the method, we explored whether the GNG model would fit gene expression profiles, where data with both positive and negative controls are available. This exercise led us to conclude that a single normal component is unlikely to be able to account for a variety of sources of non-biological variation present in the data. Furthermore, a potential problem with the GNG method, and similarly for many other methods proposed for the gene expression data analysis, is that the inference is based on the log-ratios of the red to green intensities. In doing so, the information about the individual red and green intensities is ignored.

Motivated by these findings, we propose, in the current paper, a robust unified method for analyzing both methylation and gene expression data. This method has two unique features that distinguish it from other methods in the literature. First, it allows for a flexible choice of the component that models non-biological variation and small biases in the data. Second, the method uses a robust procedure for parameter estimation and probe/gene classification. By doing so, the data are more fully utilized, and probes with different intensities but the same log ratio can be distinguished. Although the method is geared toward single-slide data, the type of data for which methods are still lacking, it can also be applied to multi-slide data, as we have demonstrated through several examples.

2 Methods

2.1 The Finite Mixture Model

Consider the log ratio of normalized data under two experimental conditions, e.g. healthy and diseased. In what follows we describe our mixture model focusing on methylation for ease of presentation, although the model and methods in the subsequent sections are applicable to other platforms such as gene expression. Furthermore, we assume that our data are normalized appropriately depending on the platform from which the data are generated.

In the proposed mixture model we assume that probes (loci) come from three different groups: hypomethylated, undifferentiated, and hypermethylated. Probes from the first and third groups are also collectively referred to as differentially methylated. For the hypermethylated probes, the normalized log ratio, Y, is positive and hence an Exponential distribution is a reasonable choice for modeling this group of probes. The choice of the Exponential distribution, a special case of the Gamma distribution, is mainly due to our observation (Khalili et al., 2007) that the characteristics of the distribution match well with the biological data the distribution models. In fact, the Gamma distribution has a long history in statistical ecology (e.g., Fisher et al., 1943) due to both its analytical convenience and its possession of a potential deeper biological interpretation. On the flip side, the log ratios corresponding to the hypomethylated probes are negative, and we choose to use the mirror image of the Exponential distribution for this group of probes, with a different intensity parameter. For the undifferentiated probes, since their theoretical log ratios are zero, a Normal distribution with zero mean would seem an appropriate choice for modeling their observed values. However, even after appropriate normalization, there may still be small biases due to different non-biological causes, and as such, a single normal distribution with a zero mean may not be sufficient to capture all the non-differentiated probes well. Instead, we propose to use a combination of K (unknown) Normal distributions with different location and scale parameters to model the undifferentiated probes. The resulted model would increase the versatility of the method, making it feasible for analyzing not just methylation data, but data from other platforms as well, such as those of gene expression. Thus, overall, a mixture of K Normals and two Exponential distributions is used to model the normalized log ratio Y. In the rest of the paper, the K is referred to as the order of the model. The choice of K will be discussed in Section 2.3.

Let f(y) be the unknown density function of the measurement Y. We propose to approximate f(y) by the parametric model

$$f(y;\Psi )=f_0(y;{\Psi }_0)+f_1(y;{\Psi }_1),$$ (1)

where the f₁(·; Ψ₁) component is designed to capture probes that are differentially methylated, and f₀(·; Ψ₀) is used to model the undifferentiated probes. The vector Ψ = (Ψ₀, Ψ₁) contains all the unknown parameters, to be specified in the following. The f₀(·; Ψ₀) and f₁(·; Ψ₀) functions are not by themselves probability density functions. Instead, f₁(·; Ψ₁) is further decomposed as

$$f_1(y;{\Psi }_1)={\pi }_1{E}_1(y;{\beta }_1)+{\pi }_2{E}_2(y;{\beta }_2),$$ (2)

where π₁, π₂ > 0, and π₁ + π₂ < 1. Furthermore, E₁(·; β₁) and E₂(·; β₂) are the location-Exponential density functions:

$$E_1(y;{\beta }_1)=I\{y<-{\xi }_1\}\frac{1}{{\beta }_1}\mathit{exp}\{-\frac{(-y-{\xi }_1)}{{\beta }_1}\}$$

and

$$E_2(y;{\beta }_2)=1\{y>{\xi }_2\}\frac{1}{{\beta }_2}\mathit{exp}\{-\frac{(y-{\xi }_2)}{{\beta }_2}\},$$

where I{.} is an indicator function that takes the value of 1 if the condition specified in {} is satisfied, otherwise it is 0. The vector of unknown parameters is Ψ₁ = (β₁, β₂, π₁, π₂); the location parameters ξ₁, ξ₂ ≥ 0 are assumed to be known. In applications, one may use ξ̂₁ = |max_1≤i≤p(y_i < 0)| and ξ̂₂ = min_1≤i≤p(y_i > 0) as the estimates of ξ₁ and ξ₂, respectively. Note that ξ̂₁ and ξ̂₂ would be the MLEs had we only focus on data for which Y < 0 or Y > 0, respectively. In (2), the π₁ + π₂ represents the proportion of differentially (hypo- + hyper-) methylated probes. Whatever is left is treated as the proportion of undifferentiated probes specified by the f₀(y; Ψ₀) component in (1), which is modeled by

$$f_0(y;{\Psi }_0)=\underset{k=1}{\overset{K}{\Sigma }}{\gamma }_k\varphi (y;{\mu }_k,{\sigma }_k^2),$$ (3)

where ${\Psi }_0=({\mu }_1,{\sigma }_1^2,{\mu }_2,{\sigma }_2^2,\dots ,{\mu }_K,{\sigma }_K^2,{\gamma }_1,\dots ,{\gamma }_K)$ represents the vector of parameters, with 0 ≤ γ_k ≤ 1, 1 ≤ k ≤ K, and K(≥ 1) is an integer denoting the number of normal components. The $\varphi (\cdot ;{\mu }_k,{\sigma }_k^2)$ stands for the density function of the Normal distribution with mean μ_k and variance ${\sigma }_k^2,k=1,\dots ,K$. The proportions π₁, π₂ and γ_k's in (2) and (3) are related through the equation ${\Sigma }_{k=1}^K{\gamma }_k=1-({\pi }_1+{\pi }_2)$, where ${\Sigma }_{k=1}^K{\gamma }_k$ is interpreted as the proportion of undifferentiated probes.

We note in passing that the proposed mixture model, hereafter referred to as the Exponential-Normal (EN) model, is a finite mixture of density functions from two different exponential families, i.e. Normal and Exponential. These types of finite mixture models have been used in other applications mainly because they are more flexible and provide a better fit to data, compared to the finite mixture models based on a single exponential family (Atienza et al., 2007)

2.2 Robust Parameter Estimation

A common method for estimating the parameter vector Ψ = (Ψ₀, Ψ₁) is the maximum likelihood estimate (MLE) through maximizing the likelihood function. However, in this paper, we will use a robust estimation method through the weighted likelihood function. Let y_i, i = 1, 2, …, n, be the normalized log ratios corresponding to n (methylation) probes on a single array. We assume that the y_i's are statistically independent. We will elaborate more on this assumption in the Discussion section. For a given K, i.e., the order of the mixture model, the weighted log-likelihood function of Ψ based on model (1) is given by

$$l_w\left(\Psi \right)=\underset{i=1}{\overset{n}{\Sigma }}{w}_i\log f(y_i;\Psi ),$$ (4)

where 0 ≤ w_i ≤ 1 are some pre-specified weights. The rationale for using a weighted likelihood and the choice of the weights (w_i's) will be discussed in the next subsection. The maximum weighted likelihood estimate (MWLE) of Ψ is then given by Ψ̂ = arg max_Ψ l_w(Ψ). The Expectation-Maximization (EM) algorithm (Dempster et al., 1977) provides a convenient approach to obtain the MWLE Ψ̂. Starting from an initial value Ψ⁽⁰⁾, the algorithm proceeds iteratively in two steps as follows.

Let Ψ^(m) be the estimate of Ψ after the mth iteration. The E-step computes the quantities

$$u_{\mathit{ij}}^{\left(m\right)}=\frac{{\pi }_j^{\left(m\right)}{E}_j(y_i;{\beta }_1^{\left(m\right)})}{f(y_i;{\Psi }^{\left(m\right)})},j=1,2$$

and

$$v_{\mathit{ik}}^{\left(m\right)}=\frac{{\gamma }_k^{\left(m\right)}\varphi (y_i;{\mu }_k^{\left(m\right)},{\left({\sigma }_k^2\right)}^{\left(m\right)})}{f(y_i;{\Psi }^{\left(m\right)})},k=1,2,\dots ,K,$$

which are the conditional expectations of the mixture component membership indicators conditional on the observed data. We note that, according to the definitions of E₁(y; β₁) and E₂(y; β₂) in (2), $u_{i1}^{\left(m\right)}=0,\text{if}{y}_i>-{\widehat{\xi }}_1$, and $u_{i2}^{\left(m\right)}=0,\text{if}{y}_i<{\widehat{\xi }}_2$.

The M-step on the (m+1)th iteration updates the estimates of the parameters for the Exponential components by

$${\pi }_j^{(m+1)}=\frac{{\Sigma }_{i=1}^n{w}_i{u}_{\mathit{ij}}^{\left(m\right)}}{{\Sigma }_{i=1}^n{w}_i}$$

and

$${\beta }_j^{(m+1)}=\frac{{\Sigma }_{i=1}^n{w}_i{u}_{\mathit{ij}}^{\left(m\right)}\{{(-1)}^j{y}_i-{\widehat{\xi }}_j\}}{{\Sigma }_{i=1}^n{w}_i{u}_{\mathit{ij}}^{\left(m\right)}};j=1,2.$$

For the Normal components, the updated estimates of the parameters are

$${\gamma }_k^{(m+1)}=\frac{{\Sigma }_{i=1}^n{w}_i{v}_{\mathit{ik}}^{\left(m\right)}}{{\Sigma }_{i=1}^n{w}_i},$$

$${\mu }_k^{(m+1)}=\frac{{\Sigma }_{i=1}^n{w}_i{v}_{\mathit{ik}}^{\left(m\right)}{y}_i}{{\Sigma }_{i=1}^n{w}_i{v}_{\mathit{ik}}^{\left(m\right)}}$$

and

$${\left({\sigma }_k^2\right)}^{(m+1)}=\frac{{\Sigma }_{i=1}^n{w}_i{v}_{\mathit{ik}}^{\left(m\right)}{(y_i-{\mu }_k^{(m+1)})}^2}{{\Sigma }_{i=1}^n{w}_i{v}_{\mathit{ik}}^{\left(m\right)}};k=1,2,\dots ,K.$$

The algorithm iterates between the E and M-steps until some convergence criterion is satisfied. For example, for a pre-specified value ∊ > 0, the algorithm will stop if ∥Ψ^(m+1)−Ψ^(m)∥ < ∊. This was the criterion used in the analysis carried out in this paper, with ∊ = 10⁻¹² and the use of the L² norm. Regarding the choice of the initial value Ψ⁽⁰⁾, one may start with several random initial values, and then choose the one that gives the highest value of the log-likelihood function.

As a technical aside, we wish to point out that it is well known that the log-likelihood function of the finite mixture of Normal distributions with different variance parameters is un-bounded (Kiefer and Wolfowitz, 1956, McLachlan and Peel, 2000). There are a number of ways suggested in the literature to deal with the unboundedness issue when maximizing the log-likelihood function. One popular method (Hathaway, 1985) is to maximize the log-likelihood function on the constrained parameter space

$$\Gamma =\{\Psi ;\underset{1\le k,k^{\prime }\le K}{\min }({\sigma }_k∕{\sigma }_{k^{\prime }})\ge c>0\},$$

where σ_k, σ_k′ are given in (3), and c > 0 is a fixed constant. Since we did not encounter this problem in our real data analysis, we did not resolve to maximizing on the constrained parameter space.

2.3 The Weighting Scheme

The idea for using the weighted likelihood instead of the customary unweighted likelihood is due to the desire to make fuller usage of the data and to downweigh the contributions from probes with relatively small intensity measures. An usual criticism of modeling log-ratio (say red to green) instead of using the red and green intensities directly is the lost of information as well as the non-discrimination of probes with the same log ratio but vastly different magnitudes in their individual red and green intensities. It is frequently argued that a fold change of, say two, is much more meaningful for probes with high intensities than those with low ones. In the current paper, we seek a compromise as follows. We would still use the log ratio as our basic data unit for ease of modeling, but in the mean time, we would also weigh each observation by a function of both the red and green intensities. By doing so, we make fuller use of the data available and can downweigh the influence of probes with low intensities, for example, by setting the weight function to be an increasing function of intensity. As we discuss in section 2.5, such a weighting scheme can also be used to enhance our classification rule.

In the regression context, Huber's weight function and Tukey's Bi-square functions are most common used in robust least square estimation (Huber, 1981). The weight functions are used to downweigh outliers. In the current context, we would like to downweigh those ratios for which the red and green intensities are small. More specifically, let u = g(R, G) be a given function of the red and green intensities. A reasonable choice for the function g(R, G) is

$$u=g(R,G)-\frac{1}{2}\{{\log }_2\left(R\right)+{\log }_2\left(G\right)\},$$

the average log intensity, which was what we used in our analysis. Furthermore, we used a half Huber's weight function defined as follows:

$$w\left(u^{\prime }\right)=\{\begin{array}{cc}1,\hfill & \text{if}{u}^{\prime }>-c\hfill \\ \frac{c}{\left|u^{\prime }\right|}\hfill & \text{if}{u}^{\prime }\le -c,\hfill \end{array}\phantom{\}}$$

where c = 1.345, and the u′'s are the corresponding values of the u's after they are standardized to mean zero and variance 1. Note that, in Huber's original weight function, both the upper and lower tails are downweighted. Our half Huber's weight function, on the other hand, is simply a modification of Huber's weight function to downweigh just the probes with low intensities; those having high intensities are valuable ones, and therefore are not downweighted.

2.4 Order Identification of the Mixture Model

In order to use our mixture model framework in applications, one needs to first determine K, the number of Normal components in the model. The problem of order selection in finite mixture models is a long standing one. Many statistical methods for order selection have been proposed and investigated in the past few decades (McLachlan and Peel, 2000, Chen and Khalili, 2006). In our analysis we used the Akaike information criterion (AIC, Akaike, 1973) to choose the order K. Mathematically, the criterion is defined as follows. Consider the weighted log-likelihood function (4). For a candidate model with order K, the AIC is given by

$$\mathit{AIC}\left(K\right)=l_w\left(\widehat{\Psi }\right)=d_K,$$

where Ψ̂ is the MWLE of Ψ under the model with order K, and d_K is the total number of parameters in the finite mixture model of order K. In an application, models with orders K = 1, 2, …, are examined and the best model is chosen to be the one that maximizes the AIC. Since the penalty function in AIC is a non-decreasing function of the number of parameters, it discourages the selection of models with an excessive number of components. For our applications, we set the upper limit for K to be 5.

2.5 Classification

The finite mixture EN model provides a model-based approach for classification. Let Ψ̂ be the MWLE of the parameter Ψ. Further, let C₁ be the class of differentially methylated probes, and C₀ be the class of undifferentiated probes. To identify probes belonging to classes C₀ and C₁, we borrow the idea of local false discovery rate (fdr) (Efron, 2004). Following the formulation therein, for any given probe i with log ratio Y_i, the f(y_i; Ψ̂) in (1) can also be written in the form

$$f(y_i;\widehat{\Psi })=\widehat{\alpha }{f}_0\left(y_i\right)+(1-\widehat{\alpha })f_1\left(y_i\right),$$

where $\widehat{\alpha }={\Sigma }_{k=1}^K{\widehat{\gamma }}_k,f_0\left(y_i\right)=f_0(y_i;{\widehat{\Psi }}_0)∕\widehat{\alpha }$ and f₁(y_i) = f₁(y_i; Ψ̂₁)/(1 − α̂). The local fdr is then given by

$$f\mathit{dr}\left(y_i\right)=\frac{f_0\left(y_i\right)}{f(y_i;\widehat{\Psi })}=\frac{f_0(y_i;{\widehat{\Psi }}_0)}{f(y_i;\widehat{\Psi })}\times \frac{1}{{\Sigma }_{k=1}^K{\widehat{\gamma }}_k},$$

which is in fact the upper bound for the posterior probability that probe i belongs to class C₀, given y_i. Therefore, we classify probe i with associated weight w_i to C₁ if fdr(y_i)/w_i ≤ z₀, for some threshold value z₀; otherwise it is regarded as from C₀. Following the original recommendation (Efron, 2004), we chose the threshold value z₀ = 0.1 in our data analysis. It is important to note that, for a probe with low intensities, its associated weight may be less than 1, and thus it would have a more stringent threshold in terms of the fdr to be declared as differentially methylated.

The program that implements the EN algorithm can be downloaded from the website http://www.stat.osu.edu/~statgen/SOFTWARE/GNG.

3 Data Analysis

We analyzed data sets from methylation signatures as well as gene expression. For more information about the DNA methylation datasets and the methods used in pre-processing, including normalization to obtain log ratios, see Khalili et al. (2007). For the gene expression datasets and normalization methods, see Dean and Raftery (2005).

3.1 DNA Methylation Data

In what follows we describe our data analysis for identifying differentially methylated genes in three single-slide datasets from three breast cancer cell lines: MCF-7, T47D and MDA-MB-361. Uniquely methylated loci for each of the cell lines are expected since they are known to be heterogeneous, but we also anticipate some shared methylated loci since all three cell lines are hormone-receptor positive. The age of the patients from which the three cell lines are derived are: 69, 54, and 40 for MCF-7, T47D, and MDA-MB-361, respectively. Since recent studies of selected CpG sequences have found age-related increases in DNA methylation (Ahuja et al., 1998; Toyota et al., 1999), we would expect more methylation in MCF-7, followed by T47D, and the least in MDA-MB-361.

The effect of weight

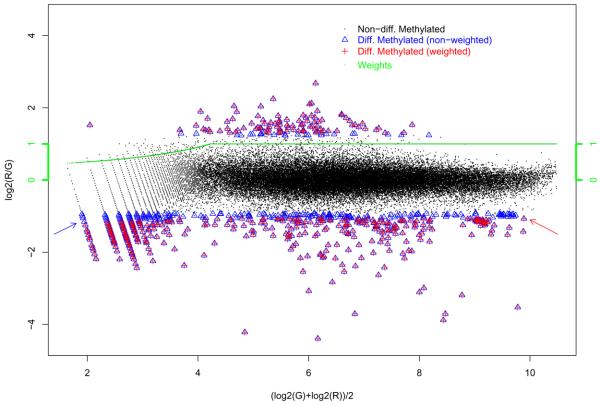
To understand the effect of our robust estimation and classification procedure empirically, EN was fitted to each of the three cell lines both with the weighting scheme as described in section 2.3 and with all weights set to 1. The latter is referred to as the unweighted procedure, and can, in fact, be viewed as a special case of the weighted procedure when the weight function is set to be independent of methylation intensity. As an example, Figure 1 shows the results for the cell line MCF-7, wherein the black dots, blue triangles, and red crosses denote probes that are undifferentiated, differentially methylated under the unweighted, and the weighted scheme, respectively. The green curve is the half Huber's weight function: probes with low average red and green log intensities are given a lower weight (< 1), and smaller weights are associated with smaller average intensities.

Fig. 1.

EN results for MCF-7 showing the effects of the weighted procedure when compared to the unweighted procedure.

As can be seen from the figure, there is a significant proportion of probes that were classified as differentially methylated under the unweighted scheme but not under the weighted procedure, especially for those with smaller average intensities. This observation is made apparent from the very dense clumps of blue triangles in the lower left quadrant of the figure where the weights are less than 1. Furthermore, under the weighted procedure, a probe with a larger average intensity is more likely to be classified as differentially methylated compared to a probe with the same log ratio but with smaller average intensity. This property, by design, can be observed empirically from the figure: the probe that have the largest average intensity among those that are classified as differentially methylated (pointed to by the red arrow) has a smaller absolute log ratio than one with a larger absolute log ratio but much smaller average intensity (among the blue clump pointed to by the blue arrow). In contrast, under the unweighted scheme, probes with the same log ratio receive the same classification.

Comparison of results between EN and NUDGE

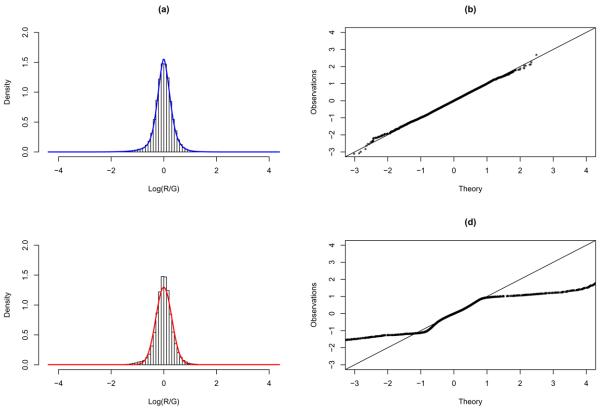
In addition to EN, the NUDGE model (Dean and Raftery, 2005) was also fitted to the methylation data from each of the three cell lines. Since NUDGE does not allow for the specification of weights, we use the unweighted results from EN to make the comparison as fair as possible. As an example, Figure 2 shows the histogram of the normalized data of the cell line MCF-7 superimposed by the fitted densities of EN and NUDGE, along with their QQ-plots. We can see that the fit by EN is much better than that by NUDGE. The number of normal components (K) are estimated to be 2, 3, and 2, for the MCF-7, T47D, and MDA-MB-361, respectively, all indicating the need to have more than just a single component to capture normal variability and small biases. Furthermore, the number of probes identified to be differentially methylated are 1712, 646, and 507 (among more than 44K probes), for MCF-7, T47D, and MDA-MB-361, respectively, consistent with what one would expect with respect to age, as discussed earlier. However, the positive correlation between age and amount of promoter methylation is not being observed with NUDGE, which identified the most differentially methylated probes for T47D (733), followed by MCF-7 (590), and then MDA-MB-361 (544).

Fig. 2.

Results from fitting the EN and NUDGE models to the normalized MCF-7 data. Left panel: histograms superimposed by the fitted EN (a) and NUDGE (c) models. Right panel: QQ-plot of the fitted EN (b) and NUDGE (d) models.

3.2 Gene Expression Data

Dean and Raftery (2005) analyzed three known gene expression data sets for which it is possible to check the false positive or false negative discovery rates. In this section we analyzed the same three data sets using the EN model and compare the results with those from NUDGE and others as presented in Dean and Raftery (2005). Again, to make the comparison as fair as possible, we use the EN results from the unweighted procedure since none of the other methods incorporate weights.

Dataset I: Apo AI

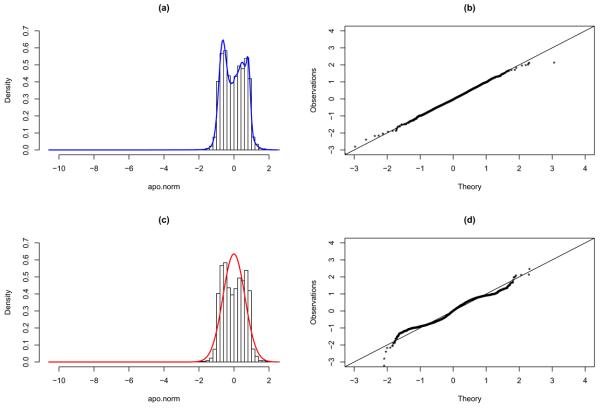
In this experiment the data was obtained from 8 mice with the Apo AI gene knocked out and 8 normal mice. According to Dudoit et al. (2002), 8 genes were suggested to be differentially expressed. The histogram of the data is as given in Figure 3. The fitted densities from EN and NUDGE are superimposed over the data histogram in Figure 3, which clearly shows the deficiency of a single normal component (as in NUDGE) for capturing the bimodal nature of the data. This lack of fit of NUDGE is also reflected in the accompanying QQ-plot, while its EN counterpart, with K̂ = 4, fits the data satisfactorily. In terms of inferences, EN identified 12 genes as differentially expressed, which includes the 8 genes suggested by Dudoit et al. (2002). Table 1, adapted from Dean and Raftery (2005) to include the results from EN, shows the comparisons of different methods regarding the identification of the 8 genes suggested. Except for SAM (delta=3.53), which is very conservative, all the other methods, including EN and NUDGE, were able to uncover the 8 genes. Also included in the table (last column) are the number of other genes identified as differentially expressed by each of the methods. As it is commonly agreed, Bonferroni correction is a very conservative procedure, and as such, it is observed that NUDGE is even more conservative as it did not identify any other genes as differentially expressed while the t-test with Bonferroni correction identified 2. NUDGE does suggest 8 other genes as potentially interesting, but none exceeds the threshold to be declared differentially expressed. On the other hand, EN identified 4 additional genes, all of which are included in the 8 additional genes suggested by NUDGE.

Fig. 3.

Results from fitting the EN and NUDGE models to the normalized Apo AI data. Left panel: histograms superimposed by the fitted EN (a) and NUDGE (c) models. Right panel: QQ-plot of the fitted EN (b) and NUDGE (d) models.

Table 1.

Results for the Apo data for the 8 control genes.

Method	Num. of the 8 genes	Num. of other genes
Rule of Two	8	134
NUDGE	8	0
SAM(delta= 0.61)	8	7
SAM(delta= 3.53)	6	0
t test	8	852
Bonfer. correc. t test	8	2
EN	8	4

Dataset II: Like-Like Experiment

The data is from a microarray experiment where the same samples (with different dyes) were hybridized to an array with 7680 genes. The gene expression levels were prepared at the University of Washington (Dean and Raftery, 2005). Since the two samples are identical, the genes should be equally expressed in the red and the green channel if there is no experimental variation, and thus the log ratios will all be around 0. Ideally a reasonable method should label only a few genes as differentially expressed. We fitted EN to the data (resulted in K̂ = 3) so that our results can be compared to those from other methods, as we had done with the Apo AI data. Table 2 shows the false positive rate from EN, along with its counterparts from NUDGE and the rule-of-two (Dean and Raftery, 2005). EN identified 7 genes that are differentially expressed, amounting to a false positive rate of about 0.1%, which is much lower than that from the rule-of-two, and is also lower than that from NUDGE. Note that this is a single-slide dataset, and as such methods available for analyzing such data are limited and the rule-of-two was the only additional method employed (Dean and Raftery, 2005).

Table 2.

Results for the Like-Like Experiment

Method	Estimated False Positive Rates
Rule of Two	1.4%
NUDGE	0.4%
EN	0.1%

Dataset III: HIV Data

The data set consists of four slides in total with the same RNA preparation hybridized to each (van't Wout et al., 2003). There are 13 genes known to be differentially expressed (and thus can be used as positive controls) and 29 genes known to be similarly expressed (negative controls). Thus, the data set is useful for checking the ability of a method for its power to detect differentially expressed genes and its control of false positive rate. As in Dean and Raftery (2005), we used the average gene expression levels among the four slides for analysis. The EN model, with K estimated to be 3, identified 16 genes as differentially expressed. These 16 genes include all the 13 positive controls. Furthermore, all the 29 negative controls were classified as non-differentially expressed. Table 3 is adapted from Dean and Raftery (2005), but also includes the results from EN, and further contains information for comparing the performances of several methods on this dataset. As we can see from the table, NUDGE, EBarrays (GG) and EN all had perfect performance on the control genes.

Table 3.

Results for the HIV data for the control genes.

Method	Num. of false neg.	Num. of false pos.
Bonfer. correc. t test	1	0
t test	0	1
Rule of Two	0	1
NUDGE	0	0
SAM	0	2
EBarrays (GG)	0	0
EBarrays (LNN)	0	1
EN	0	0

4 Discussion

In this paper we introduced a robust unified approach for capturing differentially methylated probes or differentially expressed genes through finite mixture modeling. By allowing for multiple Normal components in the model, it increases the flexibility in modeling different sources of variation and small biases, even for “normalized” data. This added flexibility enables it to be effective in analyzing not only data from methylation and gene expression, but also potentially data from other platforms. Furthermore, compared to the GNG model (Khalili et al., 2007), the components for modeling differential methylaton/expression in the current paper are more parsimonious, which further improves the tractability of our model without sacrificing its fit. The most important features of our method, however, are the robust procedures for the estimation of the parameters and for the classifications of probes/genes. By using a weight function that is based on the average log intensities, the data are more fully utilized. In fact, we note that the average (used for weight) and the difference (used in the likelihood) of the log intensities have a 1-1 correspondence with the individual red and green intensities. Moreover, through downweighting probes that have small average intensities, differentiation in the contributions to the parameter estimation among probes having the same log ratio can be made. Differentiation among such probes can also be made in their classification, with a probe having smaller average intensities less likely to be classified as differentially methylated/expressed. These prescribed benefits using the weights appear to be materialized by inspections of the results from the three methylation applications.

In our data analysis we compared our proposed method with the NUDGE model (Dean and Raftery, 2005), and by extension, other methods compared therein. It is apparent that the EN model performs better than the NUDGE in terms of fit to the data, and for our methylation data analysis EN provides more biologically interpretable results. It also appears that the proposed method is more powerful and less conservative than NUDGE yet still keeping error rates as low. By extension, the EN mixture model is competitive or better than the other methods NUDGE was compared to (Dean and Raftery, 2005).

Like other methods, our proposed method has its own limitations. It is a common practice in microarray data analysis to assume independence of the genes (or probes) on one array. This is obviously an unrealistic assumption. However, it has been shown by several authors (e.g., Dudoit et al., 2002) that ignoring correlations between genes may even lead to better classification results. There are also related works in machine learning practice (Lewis, 1998, Domingos and Pazzani, 1997, Bickel and Levina, 2004). In this paper we follow the existing literature and assume independence of the genes or probes. From a biological standpoint and evidence gathered from our data analysis, assuming a common mixture distribution for log ratios appears to be quite reasonable.

In the case of multi-slide data, averaging over the slides, as it is done in our HIV example, may lead to loss of information. We opted for doing this in the current paper so that our results are directly comparable to those presented in Dean and Raftery (2005). Alternatively, one could construct the likelihood function of the parameters of the new mixture model based on multiple slides and conduct the analysis. It is also possible to include random effects to the current model to take into account of possible correlation between genes.

Finally, it is worth noting again that, although the proposed method was applied to analyze methylation and gene expression data in the current paper, the method can be readily adapted for analyzing data from other microarray techniques, such as chromatin immunoprecipitation on microarray (ChIP-chip) and antibody microarrays. In particular, this approach can be used to interrogate data derived from different microarray approaches on the same cell system, such as interrogating differential chromatin modifications and microRNA profiling in MCF-7 cells treated and untreated with estrogen. Due to our observations that an Exponential distribution would fit gene expression and methylation data as well as a Gamma distribution, we opted for the former mainly because of its computational efficiency. Although the methodological development with Gamma would to identical to that with Exponential, and Gamma might provide a somewhat better fit to data of other types and/or from other platforms, whether the gain is worth the extra computational burden (use of numerical methods such as Newton-Raphson for parameter estimation) needs to be carefully evaluated.