Structure and Dynamics of Ca²⁺-Binding Domain 1 of the Na⁺/Ca²⁺ Exchanger in the Presence and Absence of Ca²⁺

Summary

The Na⁺/Ca²⁺ exchanger (NCX) is the major exporter of Ca²⁺ across the cell membrane of cardiomyocytes. The activity of the exchanger is regulated by a large intracellular loop that contains two Ca²⁺-binding domains, CBD1 and CBD2. CBD1 binds Ca²⁺ with much higher affinity than CBD2 and is considered to be the primary Ca²⁺ sensor. The effect of Ca²⁺ on the structure and dynamics of CBD1 has been characterized by NMR spectroscopy using chemical shifts, residual dipolar couplings, and spin relaxation. Residual dipolar couplings are used in a new way for residue selection in the determination of the anisotropic rotational diffusion tensor from spin relaxation data. The results provide a highly consistent description across these complementary data sets and show that Ca²⁺ binding is accompanied by a selective conformational change among the binding site residues. Residues that exhibit a significant conformational change are also sites of altered dynamics. In particular, Ca²⁺ binding restricts the mobility of the major acidic segment as well as several nearby binding loops. These observations indicate that Ca²⁺ elicits a local transition to a well-ordered coordination geometry in the CBD1 binding site.

Introduction

Calcium ions (Ca²⁺) act as universal second messengers that regulate many different cellular functions.^{1; 2} In the heart, for example, an influx of Ca²⁺ into the cytosol leads to muscle contraction. In order for the heart to function optimally, the same amount of Ca²⁺ that enters the cytosol at the start of the cardiac cycle must be efficiently removed from the cytosol, allowing the heart to relax and refill with blood. Defects in Ca²⁺ cycling result in smaller and slower Ca²⁺ transients that are characteristic of heart failure.³ The major exporter of Ca²⁺ across the plasma membrane is the Na⁺/Ca²⁺ exchanger (NCX) whose dominant mode of transport is the export of one Ca²⁺ ion for the uptake of three Na⁺ ions.^{4; 5; 6}

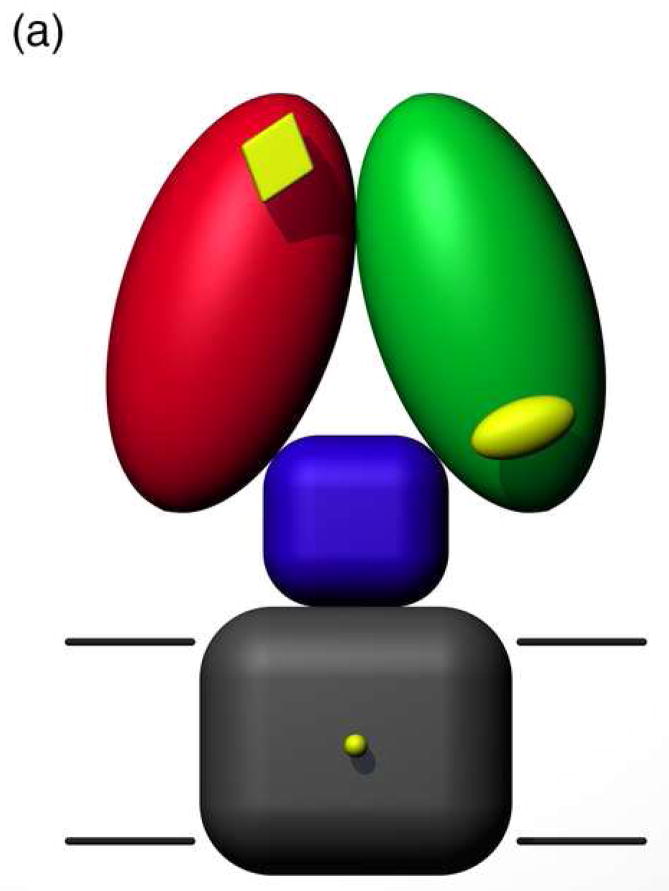
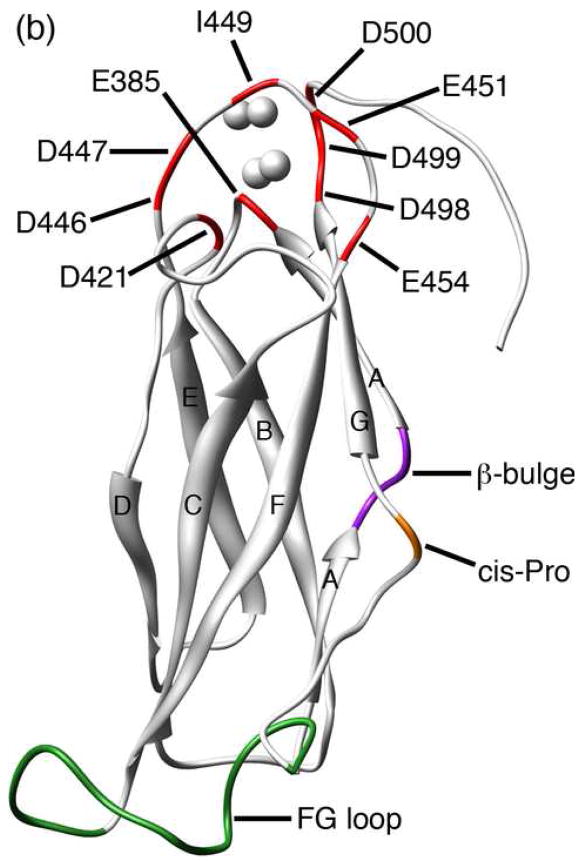
A simplified topology model for the NCX predicts nine transmembrane α-helices and a large intracellular loop of approximately 500 residues located between helices 5 and 6.^{7; 8} A more detailed description of the intracellular loop in solution was recently obtained by NMR structure determination of two Ca²⁺-binding domains, CBD1 and CBD2, present in the NCX.⁹ This study also provided evidence of a third intracellular domain that relays the Ca²⁺ signal from the regulatory domains CBD1 and CBD2 to the Ca²⁺ transport sites located within the transmembrane segments (Figure 1a). The structures of Ca²⁺-bound CBD1 and CBD2 both exhibit an immunoglobulin fold whose core consists of two antiparallel β-sheets that form a compact β-sandwich with a large unstructured loop, the FG loop, connecting strands F and G (Figure 1b). The structure of CBD1 has also been determined by X-ray crystallography, which revealed four bound Ca²⁺ ions coordinated primarily by side-chain carboxylate groups from two acidic segments located in the EF loop (D446-E454) and near the G-strand at the C-terminus (D498-D500).¹⁰ It was previously suggested that the upper half of CBD1 is unstructured in the absence of Ca²⁺, while CBD2 maintains its structural integrity in the Ca²⁺-free (apo) state.⁹ A fluorescent resonance energy transfer (FRET) study in which two fluorophores were linked to CBD1 indicates that Ca²⁺ binding elicits a conformational change in this domain.¹¹ Based on these structural observations, together with the fact that CBD1 exhibits a higher affinity for Ca²⁺ than CBD2,⁹ it has been suggested that CBD1 is the primary Ca²⁺ sensor in the NCX.

Figure 1.

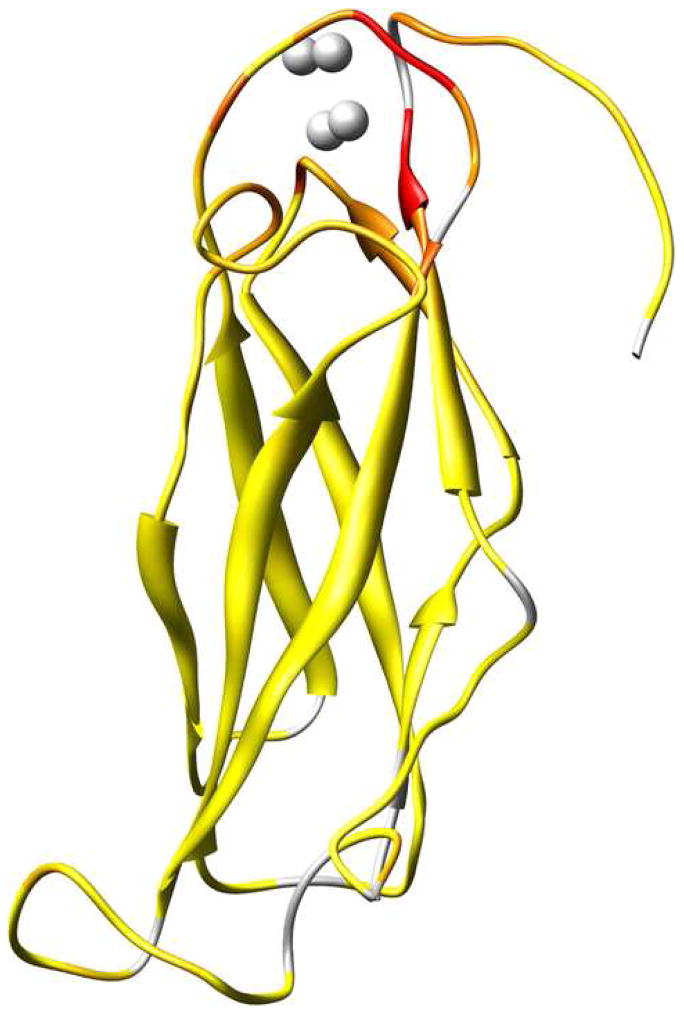
(a) Model of the intact exchanger composed of CBD1 (red), CBD2 (green), a third intracellular domain (blue), and the transmembrane segments (gray). Ca²⁺-binding sites are represented in yellow. (b) Representative member (lowest energy) of the NMR structural ensemble (2FWS). The positions of the four Ca²⁺ ions (represented as spheres) are derived from the corresponding crystal structure (2DPK). Selected structural elements are labeled and color-coded as follows: 1) residues that contribute Ca²⁺-binding ligands (red), 2) β-bulge (purple), 3) cis-Pro (orange), and 4) FG loop (green). β-strands are labeled A-G. Molecular graphics were produced using the UCSF Chimera package (supported by NIH P41 RR-01081).⁸⁸

There is currently no structure available for the apo state of CBD1. X-ray crystallographic studies of Ca²⁺-binding proteins are often hindered by an inability to obtain suitable crystals in both the presence and absence of Ca²⁺. NMR spectroscopic studies are not limited in this regard as they are performed in solution where the Ca²⁺ concentration can be freely adjusted. This capability has enabled several comparison studies between structural data from Ca²⁺-bound and apo states.^{12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29} In the case of CBD1, the quantitative comparison between the two states has been deemed challenging due to a significant amount of disorder attributed to the apo state.⁹ A detailed comparison of the two states, however, has been achieved in the current study through the use of multiple NMR observables. NMR chemical shifts and residual dipolar couplings identify sites where the apo structure differs significantly from that of the Ca²⁺-bound state. In addition, NMR relaxation methods provide a detailed characterization of the protein’s conformational dynamics in the two states.^{30; 31; 32} If Ca²⁺ binding does in fact elicit an order-disorder transition, then the dynamics amplitudes of the Ca²⁺-bound state should be significantly reduced compared to the apo state.

Backbone NMR relaxation methods have been successfully applied to several other Ca²⁺-binding proteins.^{33; 34; 35; 36; 37; 38; 39; 40; 41; 42; 43; 44; 45; 46; 47} Many of these protein systems belong to the EF-hand family. The EF-hand motif is represented in some of the most extensively studied proteins by NMR, including calbindin D_9k, calmodulin, and the regulatory domain of troponin C.^{48; 49; 50; 51} These proteins exhibit a helix-loop-helix motif whose fold and binding geometry are significantly different from that of CBD1. The β-sandwich and binding loops of CBD1 are more closely associated with the C₂-domain family, which represents another common Ca²⁺-binding motif.^{52; 53} C₂-domains often play significant roles in signal transduction and membrane traffic.⁵⁴ Although the C₂-domain is present in several published structures,^{26; 55; 56; 57} little is known about the effects of Ca²⁺ on the fast time scale dynamics of this domain. The present study aims to provide a quantitative description of the structure and dynamics of this common Ca²⁺-binding motif with the goal to better understand its binding mechanism at atomic detail.

Results and Discussion

Analytical ultracentrifugation

Potential partial oligomerization of both the Ca²⁺-bound and the apo state of CBD1 was assessed by analytical ultracentrifugation at 400 μM, i.e. at NMR concentrations. The results show that both states exist as single species whose molecular weights are consistent with that of the monomer (see Supplementary Materials). These findings are also corroborated by ¹⁵N relaxation data (vide infra).

Chemical shift analysis

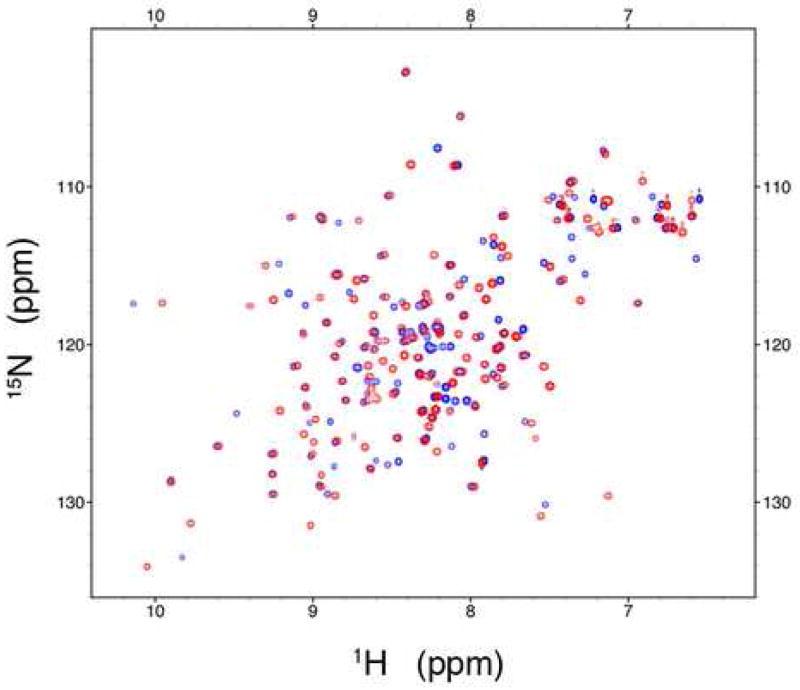
A superposition of the [¹H,¹⁵N]-HSQC spectra at 800 MHz for CBD1 in the Ca²⁺-bound (red) and apo (blue) states is represented in Figure 2. Both states exhibit high quality spectra with good peak dispersion for a protein of this size (15.2 kDa). The [¹H,¹⁵N]-HSQC spectra indicate that only 22 of the 139 total residues are missing or overlapping in both states. One of the overlapping residues (D499) directly participates in Ca²⁺ binding, i.e. it contributes a Ca²⁺-binding ligand. An additional five residues are overlapped in the Ca²⁺-bound state only, while an additional 12 residues, including residues E454, D498, and D500 of the acidic segments, are overlapped in the apo state only.

Figure 2.

Overlay of the [¹H,¹⁵N]-HSQC spectra. The Ca²⁺-bound and apo states are represented in red and blue, respectively.

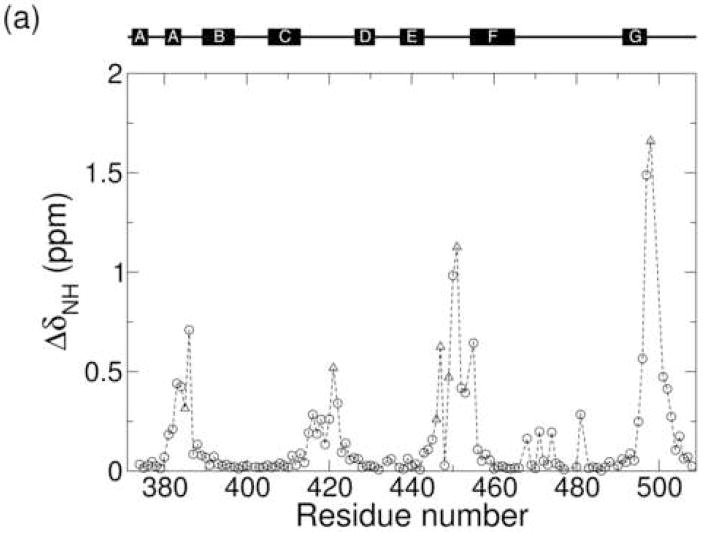
Resonance assignments for the Ca²⁺-bound state of CBD1 were previously reported by Hilge et al.⁹ Resonance assignments for the apo state were determined in the present study by working at a lower protein concentration and a higher salt concentration, which improves the sample stability. The results indicate that many nuclei experience similar structures and surroundings in the Ca²⁺-bound and apo states. Residues for which Ca²⁺ binding elicits a substantial change in chemical environment are indicated by large values of the amide chemical shift change $\mathrm{\Delta }{\delta }_{NH,i}={\left[\mathrm{\Delta }{\delta }_{H,i}^2+{(\mathrm{\Delta }{\delta }_{N,i}/5)}^2\right]}^{1/2}$ where Δδ_H,i and Δδ_N,i are the amide ¹H and ¹⁵N chemical shift differences between the two states for residue i.⁵⁸ In Figure 3a the amide chemical shift change is plotted as a function of residue number. Figure 3b maps this same information onto the CBD1 structure using color-coding from yellow (for Δδ_NH,i = 0 ppm) to red (for Δδ_NH,i ≥ 1 ppm). Ca²⁺-binding residues are represented in Figure 3a by triangles. The largest amide chemical shift changes cluster in four regions of the protein sequence, each of which contributes one or more Ca²⁺-binding ligands. The acidic segments near residues 450 and 500 exhibit particularly large Δδ_NH,i values across multiple consecutive residues.

Figure 3.

(a) Plot of the amide chemical shift change Δδ_NH as a function of residue number. Residues that contribute a Ca²⁺-binding ligand are represented by triangles. (b) Structural context for the amide chemical shift change. The color gradient extends from yellow for Δδ_NH,i = 0 to red for Δδ_NH,i ≥ 1.

Residual dipolar coupling analysis

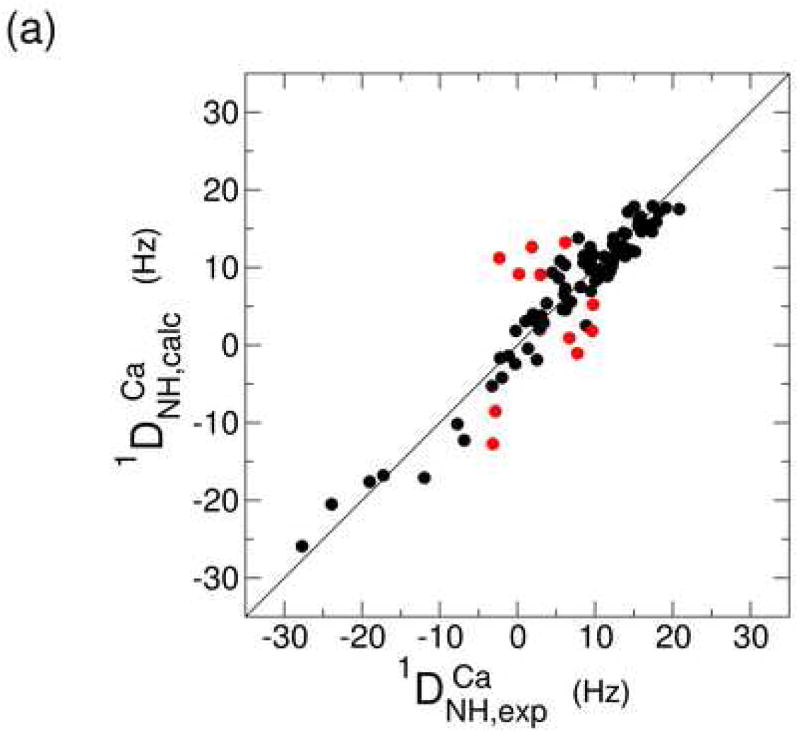
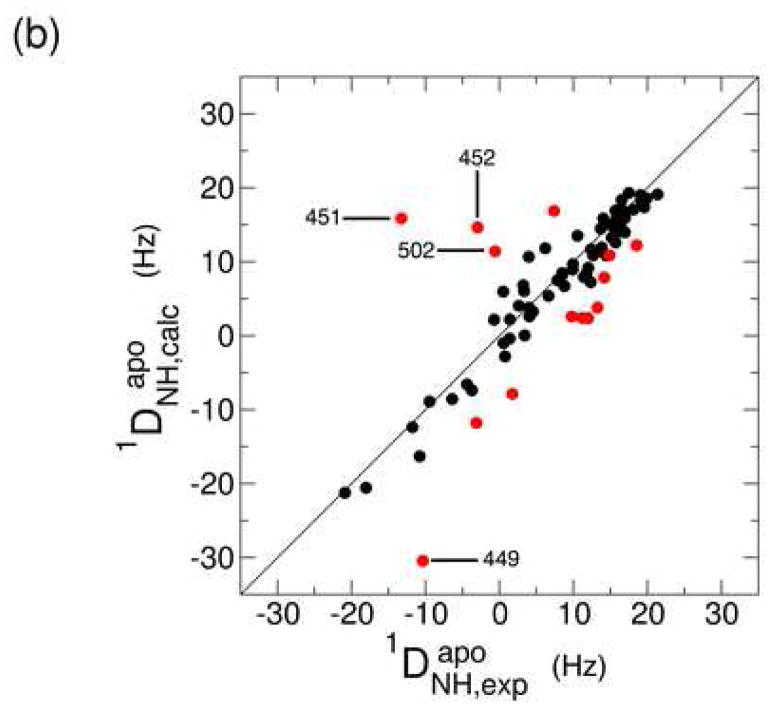
One-bond backbone ¹⁵N-¹H residual dipolar couplings (RDCs) were measured for the Ca²⁺-bound and apo states in a liquid crystalline medium containing C12E5/hexanol.^{59; 60; 61; 62; 63; 64} The use of a liquid crystalline medium results in weak alignment of the protein molecules with respect to the external magnetic field leading to the observed RDCs. This information provides a set of restraints on bond vector orientations that is commonly used in structure validation studies. The RDCs for both states were fit to the Ca²⁺-bound crystal structure in order to probe for a Ca²⁺-dependent conformational change. Figures 4a and b show the correlation between the RDCs observed experimentally and the values that are calculated from the CBD1 crystal structure. The red points correspond to residues that were excluded from the calculation of the alignment tensor due to relatively poor agreement with the crystal structure (details provided in the Materials and Methods section).

Figure 4.

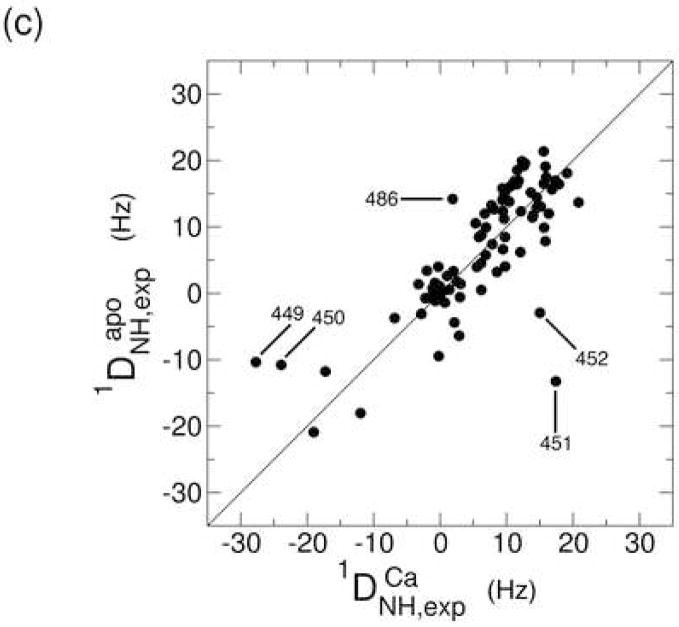
Correlation plot between the experimental and back-calculated one-bond ¹⁵N-¹H residual dipolar couplings for the Ca²⁺-bound (a) and apo (b) states. In both cases, the experimental data were fit to the Ca²⁺-bound crystal structure (2DPK). Residues that were excluded from the alignment tensor calculation are represented in red. The correlation between the experimental RDCs for both states is represented in (c).

The level of agreement between the experimental and calculated RDCs is expressed in terms of a Q value, which depends on the resolution of the available structure. In the present case, the crystal structure was determined at 2.5 Å resolution, which is expected to yield a Q value of around 0.40.⁶⁰ The Q values for the Ca²⁺-bound and apo states are 0.31 and 0.49, respectively, indicating that the RDCs for the core domain of both states are largely consistent with the crystal structure. The RDCs of the Ca²⁺-bound state are expected to provide a lower Q value (i.e. better agreement) due to the fact that the crystal structure corresponds to the Ca²⁺-loaded form. The agreement is still relatively good, however, for the apo state, suggesting only limited changes in the core β-sandwich structure. Consistent with this finding is the similarity of the alignment tensors for the two states. The axial components are 14.1 and 15.4 Hz, while the rhombicities amount to 0.18 and 0.17 for the Ca²⁺-bound and apo states, respectively (for definitions of these quantities see reference ⁶⁵). There are clear site-specific differences between the two states that are apparent in a correlation plot of the experimental RDCs (Figure 4c). Residues 449, 450, 451, and 452 exhibit particularly large differences. These residues are located in the middle of the major acidic segment that includes five of the ten residues that contribute Ca²⁺-binding ligands. The absolute value of the N-H RDC for each residue in this segment is uniformly higher in the Ca²⁺-bound state than in the apo state (Figure 4c), which is consistent with the presence of significant motional averaging of these RDCs.⁶⁵ Together with the large chemical shift differences observed in the region centered near residue 450, these observations indicate that Ca²⁺ binding requires a localized conformational and dynamic change involving several of the binding site residues.

¹⁵N relaxation analysis of overall tumbling motion

¹⁵N NMR relaxation data report on fast time scale (picosecond-nanosecond) reorientational motions.^{30; 31; 32} In order to characterize the effects of Ca²⁺ binding on the backbone dynamics of CBD1, longitudinal (T₁) and transverse (T₂) relaxation times, as well as {¹H}-¹⁵N steady-state nuclear Overhauser effects (NOEs) were measured both in the presence and absence of Ca²⁺ (relaxation data provided in the Supplementary Materials). The relaxation data were then analyzed using the model-free method of Lipari and Szabo.⁶⁶ The Lipari-Szabo method provides a generalized order parameter S² and an internal correlation time τ_int which indicate the amplitude and time scale, respectively, of internal motion at a given site. Extraction of meaningful model-free parameters requires the accurate description of the overall rotational diffusion tensor with an average correlation time τ_c. This aspect of the analysis is particularly critical in the case of molecules whose tumbling is highly anisotropic, such as CBD1. In order to optimize the rotational diffusion tensor,⁶⁷ a set of core residues was selected that satisfied the following criteria: 1) good RDC agreement with the crystal structure, 2) no signs of conformational exchange, and 3) small τ_int values (details provided in the Materials and Methods section). The cylindrical shape of the 3D structure of CBD1 suggests that a prolate, axially symmetric ellipsoid applies in good approximation for this molecule.

When using the crystal structure as a reference, the combination of the Lipari-Szabo approach with Woessner’s equations gives τ_c values of 12.30±0.01 and 11.03±0.02 ns and D_||/D_⊥ ratios of 2.10±0.02 and 1.84±0.03 for the Ca²⁺-bound and apo states, respectively. Similar values are obtained by the quadric method, which provides an alternative route to the global diffusion parameters.⁶⁸ Although the quadric method is best-suited for diffusion tensors with relatively small anisotropies, it provides results for CBD1 that are remarkably consistent with those of the Woessner method.⁶⁹ The quadric method gives τ_c values of 12.57±0.01 and 11.14±0.02 ns and D_||/D_⊥ ratios of 2.00±0.01 and 1.78±0.02 for the Ca²⁺-bound and apo states, respectively. The quality of the fits is high, providing additional evidence that the Ca²⁺-bound crystal structure is a reasonable model for the core of both the Ca²⁺-bound and apo states. The apo state, however, is slightly more sensitive to the criteria used to select residues for the diffusion tensor optimization, due to the fact that the number of available bond vectors is limited by the lack of a high-resolution apo structure. The present results demonstrate, however, that the rotational diffusion of CBD1 is slower and more anisotropic in the presence of Ca²⁺, which is likely caused by the structuring of the binding site loops upon Ca²⁺ binding. The higher mobility of the Ca²⁺-binding loop of the apo state, on the other hand, renders its effective hydrodynamic volume smaller and its shape more isotropic.

Flexible regions outside of the binding loops

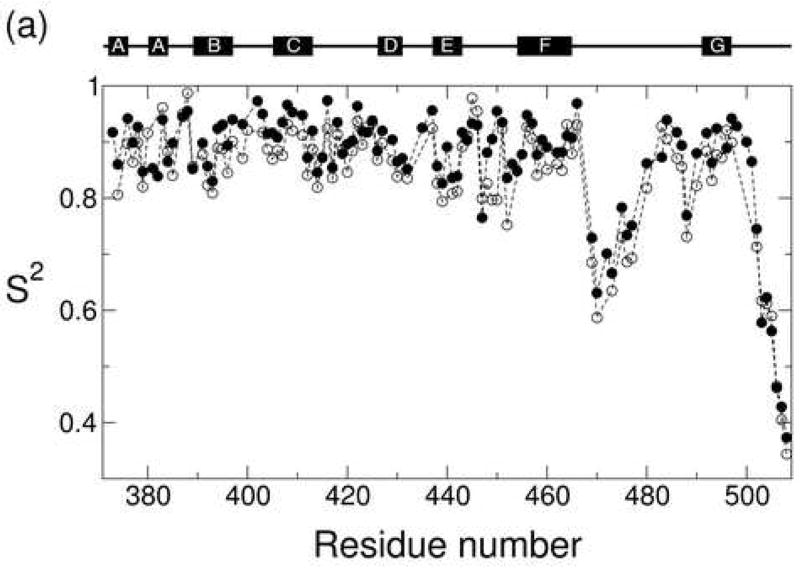
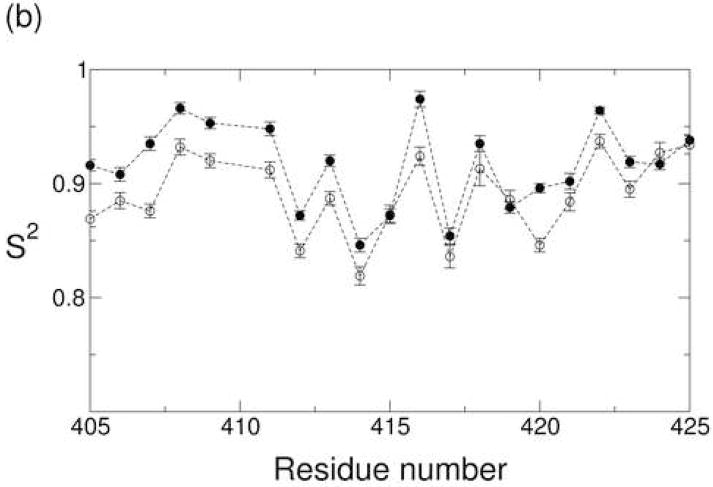
The generalized N-H order parameters S² for both states were determined with Woessner’s model for anisotropic tumbling and are plotted as a function of residue number in Figure 5a. The two states exhibit very similar S² profiles across large segments of the molecule. There is a consistent trend, however, in which the S² values for residues in the core of the domain are slightly higher (around 0.025) in the Ca²⁺-bound state than in the apo state (Figure 5b). It is considered unlikely that a uniform offset reflects an actual difference in the internal dynamics of the two states. Rather the S² difference is more likely attributed to the aforementioned uncertainty in the apo diffusion tensor. Model calculations confirm that for the majority of bond vector orientations a small increase in the apparent diffusion tensor anisotropy is reflected in a small systematic increase in the resulting order parameters. Several residues, however, exhibit changes in S² that are much larger than this overall effect (vide infra).

Figure 5.

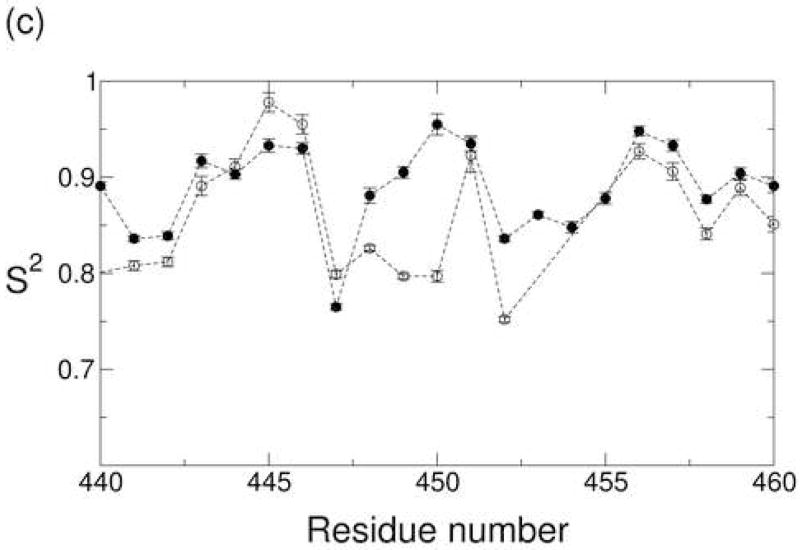
(a) The generalized order parameter S² plotted as a function of residue number for the Ca²⁺-bound state (closed circle) and apo state (open circle). Order parameters for residues near strand C are highlighted in (b), while order parameters for the major acidic segment are highlighted in (c).

The low S² values in the FG loop (residues 467-491) and C-terminus indicate that these regions are highly flexible, in agreement with their poor definitions in the NMR structural ensemble and the missing electron density in the crystal structure. It is not yet known if the high mobility at these sites is preserved in the intact exchanger. A model of the intact exchanger suggests that the FG loop and C-terminus may be subject to additional steric constraints in the NCX that are not present in the isolated domain,⁹ suggesting that the S² values for these sites might actually be higher in the intact exchanger. Previous studies of other proteins with the immunoglobulin fold indicate that the mobility of the FG loop determines the specificity of binding for various receptors. High mobility is observed in cases where the FG loop binds to multiple receptors, while more restricted dynamics are observed in cases where the FG loop exhibits higher specificity.^{70; 71} It is presently unknown whether the mobility of the FG loop plays a similar role in CBD1. To address this point, dynamics studies need to be carried out using larger NCX constructs.

In addition to the local minimum in the order parameter profile of the FG loop at Ser 470, a second local minimum is found at Ser 488. Although this residue is well-defined in the crystal structure, the S² values indicate that Ser 488 is highly flexible in both states. This observation is consistent with a high level of structural uncertainty in this region as reflected by the RDCs. Several nearby residues exhibit poor RDC agreement with the crystal structure (residues 483, 486, and 491 in the Ca²⁺-bound state and residue 486 in the apo state). In addition, superposition of the NMR and crystal structures reveals that the distance between the corresponding C^α atoms in the two structures is particularly high in the region (>4 Å for residues 481, 483, 484, 485). The relationship between average structure and dynamics is further elucidated by the local sequence context. Ser 488 is located near strand G between a glycine and a cis-proline. The cis-proline at residue 489 induces a protrusion that is commonly observed in immunoglobulin folds.⁷² It has been suggested that this structural distortion represents a natural element of negative design.^{10; 73} Disruption of the outer strand G disfavors the formation of intermolecular hydrogen bonds, which thereby inhibits aggregation of CBD1 with other β-sheet proteins. The fact that this structural distortion is accompanied by large amplitude dynamics suggests that both structure and dynamics may serve a protective role. From a thermodynamic perspective, the inability to form stable hydrogen bonds disfavors intermolecular association by increasing the enthalpy change of the process. In addition, edge-to-edge aggregation would restrict the large amplitude dynamics that are currently observed at Ser 488, which would disfavor intermolecular association by decreasing the corresponding entropy change. Such an entropic penalty represents a novel element of negative design, suggesting that evolution may actually employ a dual protective strategy that includes both structural (enthalpic) as well as dynamic (entropic) effects.

Dynamics changes in the binding loops

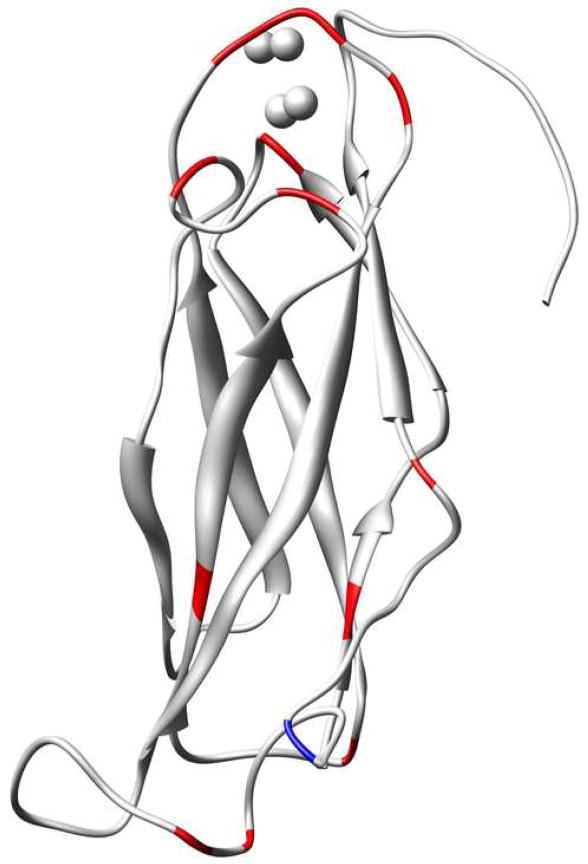
Although the Ca²⁺-bound and apo states exhibit similar backbone dynamics across large segments of the molecule, the two states exhibit substantial differences in the dynamics of the major acidic segment (Figure 5c). Five residues in this segment (D446, D447, I449, E451, and E454) contribute Ca²⁺-binding ligands. Of these five, D447 and I449 are particularly relevant to the current study due to the fact that they coordinate Ca²⁺ ions 4 and 3, respectively, via backbone carbonyl oxygens. These backbone-ion interactions are expected to restrict the mobility of the corresponding amide planes, which include the backbone N-H groups of D448 and F450. Immobilization of these residues is reflected by their S² values, which are significantly higher in the Ca²⁺-bound state than in the apo state. Ca²⁺ binding also appears to restrict the mobility of residues I449 and E452 as is visualized in Figure 6 with residues colored red if the quantity $\mathrm{\Delta }{S}^2=S_{Ca}^2-S_{\mathit{apo}}^2$ is greater than 0.05.

Figure 6.

Structural context for the change in S² that accompanies Ca²⁺ binding. Residues for which ΔS² > 0.05 are colored red. The residue for which ΔS² < -0.05 is colored blue.

Ca²⁺ binding also affects the time scale of motions in the major acidic segment. While the τ_int values are less than 20 picoseconds for most residues in both states, large τ_int values are found for residues F450 and E451 in the apo state of 1048 and 444 ps, respectively. Transverse ¹⁵N chemical shift anisotropy-dipolar cross-correlation rates η_xy indicate that neither of these residues exhibits conformational exchange on the microsecond-millisecond time scale. Note, however, that fits for both of these residues are susceptible to the effects of structural uncertainty in this region. E451, for example, is one of thirteen residues that were excluded from the characterization of the diffusion tensor due to poor RDC agreement with the crystal structure. These residues were fit using a site-specific τ_loc value (see equation 1 of the Materials and Methods section). F450 was not excluded from the diffusion tensor optimization, but the angle between the F450 N-H bond vector and the unique axis of the diffusion tensor is relatively small (θ = 29.5°). In this case, the fitting parameters are more susceptible to the effects of structural uncertainty, particularly in molecules such as CBD1 whose tumbling is highly anisotropic.

Three residues in the proximity of the major acidic segment also exhibit large ΔS² values. They are E385, whose side-chain carboxylate group acts as a Ca²⁺ -binding ligand, as well as A416 and S420, which are near the Ca²⁺-binding residue D421. A small number of residues outside of the binding loops also exhibit ΔS² values greater than 0.05. In most cases, these long-range effects map to isolated positions in the loops located at the opposite end of the domain. Only a few residues exhibit the opposite trend in ΔS². Leu 483, which is colored blue in Figure 6, is the only case where ΔS² is less than −0.05. Collectively, the order parameters demonstrate that Ca²⁺ binding rigidifies the binding site residues, which is accompanied by a few (isolated) changes at the opposite end of the molecule.

S² comparison with other Ca²⁺-binding proteins

The mean order parameter change, $\mathrm{\Delta }{S}^2=S_{Ca}^2-S_{\mathit{apo}}^2$, across the major acidic segment (residues 446-454) and other binding site residues (385 and 421) is 0.048. This value is comparable to the changes observed in the Ca²⁺-binding proteins calbindin D_9k and the N-domain of cardiac troponin C (cNTnC), both of which have been extensively studied by ¹⁵N relaxation spectroscopy. The mean ΔS² value of the binding site residues 14-27 and 54-65 of calbindin D_9k is 0.047 according to Table S4 of Ref. 74 Similarly, Table 2 of Ref. 41 yields a mean ΔS² value of 0.034 for binding sites residues 29-40 and 65-76 of cNTnC. In order to relate these dynamic changes to changes in actual thermodynamics, it is common to calculate the conformational entropy associated with a given order parameter. The two methods that are most commonly used for this purpose are those by Akke et al.⁷⁵ and Yang and Kay.⁷⁶ When applied to the order parameters of the binding site residues, the latter method, which was used in Refs. ^{41; 74}, yields -TΔS values of 2.1, 3.4, and 2.7 kcal·mol⁻¹ for CBD1, calbindin D_9k, and cNTnC, respectively, which are very similar to the values obtained by the approach of Akke et al. On a per residue basis, the relevant values are 0.23, 0.13, and 0.12 kcal·mol⁻¹·residue⁻¹. These results indicate that Ca²⁺ binding is accompanied by a local decrease in backbone conformational entropy for all three systems. Interestingly, the entropy change per binding-site residue can very significantly between the different Ca²⁺-binding motifs. The larger entropy change per residue that is obtained for CBD1 originates in part from the fact that the average order parameters for CBD1 are slightly higher than for the other two systems. As a result, the entropy change falls into the steeper portion of the order parameter-entropy relationship.^{75; 76}

While the comparison between CBD1 and the EF-hand proteins is useful, the difference between CBD1’s β-sandwich structure of the C₂-domain family and the EF-hand structure must be taken into account. Two of the most extensively studied C₂-domains are C₂A and C₂B, which are located in tandem as part of a large cytoplasmic segment of the integral membrane protein synaptotagmin I. This arrangement is analogous in many ways to the structural context of CBD1 and CBD2 in the cytoplasmic loop of the NCX. Both C₂A and C₂B exhibit local structural changes in the binding loops in response to Ca²⁺, but neither domain exhibits a large conformational change.^{26; 77} Future NMR relaxation studies of C₂A and C₂B would provide additional information about the role of dynamics in the binding mechanism of other C₂-domains. Further studies are also needed in order to characterize the effects of Ca²⁺ on the intramolecular interactions between CBD1 and CBD2 in the NCX and between C₂A and C₂B in synaptotagmin I. Of note, a FRET study of synaptotagmin I indicates that the two C₂ domains are in closer proximity when Ca²⁺ is bound.⁷⁸ This finding is consistent with a previously developed model of the NCX that includes an extended interaction interface between CBD1 and CBD2 in the presence of Ca^2+.9 Future NMR studies will test this model and determine how the changes identified here in the CBD1 binding site are transmitted to other parts of the molecule.

Conclusions

The effect of Ca²⁺ on the structure and dynamics of CBD1 has been studied by NMR chemical shifts, residual dipolar couplings, and generalized order parameters at 800 MHz field strength. These quantities provide a highly consistent, site-specific description of the changes that accompany Ca²⁺ binding. The data indicate that the two states share a common structure and dynamics within the core of the domain. Structural changes at the binding sites, however, are indicated by differences in chemical shifts and residual dipolar couplings between the two states. Spin relaxation measurements confirm that residues that exhibit a significant conformational change are in many cases sites of altered dynamics. Ca²⁺ binding restricts the mobility of the major acidic segment as well as the other nearby binding loops. Collectively, these findings indicate that the structural and dynamic changes that accompany Ca²⁺ binding map predominantly to the binding site residues and their vicinity. In the intact exchanger, the presence of the second Ca²⁺-binding domain CBD2 may induce additional structural and dynamic effects that contribute to the allosteric regulation of the NCX. Such effects will be investigated in future studies of constructs containing both CBD1 and CBD2 using approaches similar to the ones employed here.

Materials and Methods

Sample preparation

Canine NCX1 (residues 371-509) was expressed from a pET23b vector in Escherichia coli BL21(DE3) cells at 37°C for 5 hours using 0.5 mM IPTG for induction. In addition to the native sequence, the protein contained an eight-residue N-terminal His tag that facilitated purification with a Ni-NTA column (Qiagen). Samples were uniformly ¹⁵N/¹³C labeled for chemical shift assignments of the apo state and for RDC measurements of the Ca²⁺-bound state. All other measurements were performed on uniformly ¹⁵N labeled protein. NMR samples contained ~0.4 mM protein, 20 mM HEPES (pH 7.0), 20 mM β-mercaptoethanol, and 0.02% NaN₃ in 90% H₂O/10% D₂O. The Ca²⁺-bound CBD1 samples also contained 20 mM CaCl₂. Alternatively, the apo samples contained 15 mM EDTA and 100 mM NaCl. Compared to previous studies, it was found that the sample integrity of apo CBD1 was much prolonged under these conditions, in particular for protein concentrations around 0.4 mM. The liquid crystalline medium used for residual dipolar coupling (RDC) measurements contained 3% C12E5/hexanol at a molar ratio r = 0.96.⁵⁹ Sedimentation velocity experiments were performed with a Beckman XL-I ProteomeLab analytical ultracentrifuge equipped with an absorbance optical system. Samples conditions for the sedimentation velocity experiments matched those of the NMR sample conditions, including both protein concentration and temperature. The program SEDFIT⁷⁹ was used to determine the sedimentation coefficient distributions, which indicate the presence of a single monomeric species in both states (see Supplementary Materials).

NMR spectroscopy

Experiments were performed at 306 K on a Bruker 800 MHz spectrometer equipped with a TCI cryoprobe. Chemical shift assignments for the apo state were obtained from HNCO, HN(CA)CO, HNCA, HN(CO)CA, and CBCA(CO)NH spectra.⁸⁰ RDCs were obtained from [¹⁵N,¹H]-HSQC-IPAP spectra.⁸¹ Longitudinal (T₁) and transverse (T₂) relaxation times, as well as {1H}-15N steady-state nuclear Overhauser effects (NOEs) were measured using standard ¹⁵N relaxation methods.^{82; 83} Transverse ¹⁵N chemical shift anisotropy-dipolar cross-correlation rates (η_xy) were measured using an IPAP-type spectrum.⁸⁴ Spectra were processed by NMRPipe⁸⁵ and analyzed within Sparky (T. D. Goddard & D. G. Kneller, SPARKY 3, University of California, San Francisco).

Data Analysis

RDCs and diffusion tensors using the quadric approach were fit to the crystal structure (2DPK) via singular value decomposition using the MATLAB software.^{68; 86} The calculation of the alignment tensor was initially performed with all of the available residues. The procedure was then repeated with a subset of residues for which the quantity |RDC_calc − RDC_exp|/rms(RDC_exp)<0.5 where rms is the root mean square function. Relaxation rate constants were obtained by fitting the cross-peak intensities to a single exponential function using the program CurveFit. (A. G. Palmer, CurveFit, Columbia University.) Duplicate time points provided a measure of the random error in the peak intensities. Monte Carlo simulations were subsequently performed in order to estimate the uncertainty in the rate constants from the measured peak intensity errors. Model-free calculations were performed with the program ModelFree4. (A. G. Palmer, ModelFree, Columbia University.) An initial model-free analysis was performed using the following spectral density function:^{39; 66; 68}

$$\begin{array}{l}J(\omega )=\frac{2}{5}\left[S^2\frac{{\tau }_{\mathit{loc}}}{1+{(\omega {\tau }_{\mathit{loc}})}^2}+(1-S^2)\frac{\tau }{1+{(\omega \tau )}^2}\right]\\ {\tau }^{-1}={\tau }_{\mathit{loc}}^{-1}+{\tau }_{int}^{-1}\end{array}$$ (1)

where S² is the generalized order parameter, τ_int is the internal correlation time, and τ_loc is the overall correlation time sensed locally by an individual bond vector. Model-free calculations were performed with an N-H bond length of r_NH = 1.02 Å and a chemical shift anisotropy of Δσ = −172 ppm. Following the initial model-free fit, a set of core residues was selected in order to characterize the rotational diffusion tensor. A residue was included in this set of core residues if all of the following criteria were met. 1) The bond vector orientation was consistent with the Ca²⁺-bound crystal structure. This criterion was met if the quantity |RDC_calc − RDC_exp|/rms(RDC_exp)< 0.5. 2) The residue showed no signs of conformational exchange. This criterion was met if the quantity η_xy/R₂ > 0.65 where $R_2=T_2^{-1}$. 3) The residue showed no signs of long time scale internal dynamics in the initial model-free fit with equation (1), i.e. when τ_int < 100 ps. The model-free analysis was then repeated with this set of core residues using the spectral density function for an axially symmetric diffusion tensor:^{66; 67}

$$\begin{array}{l}J(\omega )=\frac{2}{5}\sum _{j=0}^2{A}_j\lfloor S^2\frac{{\tau }_j}{1+{(\omega {\tau }_j)}^2}+(1-S^2)\frac{{\tau }_j^{\prime }}{1+{\left(\omega {\tau }_j^{\prime }\right)}^2}\rfloor \\ {\tau }_j^{\prime }={({\tau }_j^{-1}+{\tau }_{int}^{-1})}^{-1}\end{array}$$ (2)

where ${\tau }_j^{-1}=6D_{\perp }-j^2(D_{\perp }-D_{\left|\right|})$, D_|| and D_⊥ are the diffusion coefficients; A₀ = (3cos² θ −1)²/4, A₁ = 3sin²θ cos²θ, A₂ = (3/4)sin⁴θ, and θ is the angle between the bond vector and the unique axis of the diffusion tensor. The Ca²⁺-bound crystal structure was used as a reference structure, which was rotated into the principal axis frame of the diffusion tensor as part of this procedure. Errors in the model-free parameters were estimated by Monte Carlo analysis. The optimized diffusion tensor was verified for this set of core residues by the quadric method^{68; 87} using the program quadric_diffusion. (A. G. Palmer, quadric_diffusion, Columbia University.) Residues that met criterion 1, but not criterion 2 or 3 were included in a final round of model-free calculations using the spectral density function in equation 2, but with the previously optimized diffusion tensor fixed. In order to account for the effects of conformational exchange, R_ex terms were included in the fitting procedure for residues that were excluded by criterion 2. Note, however, that residue G399 is the only residue for which a large R_ex term is observed (10.55 and 10.19 s⁻¹ in the Ca²⁺-bound and apo states, respectively). Residues that did not meet criterion 1 or that were absent in the crystal structure due to weak electron density were excluded from the final round of model-free calculations due to their large orientational uncertainty. For these residues, the S² and τ_int values that are reported correspond to the results originally obtained using the spectral density function in equation 1.

Abbreviations

CBD1

calcium-binding domain 1

NCX

Na⁺/Ca²⁺ exchanger

RDC

residual dipolar coupling