Abstract
The polarizable empirical CHARMM force field based on the classical Drude oscillator has been extended to the nitrogen-containing heteroaromatic compounds pyridine, pyrimidine, pyrrole, imidazole, indole and purine. Initial parameters for the 6-membered rings were based on benzene with non-bond parameter optimization focused on the nitrogen atoms and adjacent carbons and attached hydrogens. In the case of 5-member rings, parameters were first developed for imidazole and transferred to pyrrole. Optimization of all parameters was performed against an extensive set of quantum mechanical and experimental data. Ab initio data was used for determination of the initial electrostatic parameters, the vibrational analysis, and in the optimization of the relative magnitudes of the Lennard-Jones parameters, through computations of the interactions of dimers of model compounds, model compound-water interactions and interactions of rare gases with model compounds. The absolute values of the Lennard-Jones parameters were determined targeting experimental heats of vaporization, molecular volumes, heats of sublimation, crystal lattice parameters and free energies of hydration. Final scaling of the polarizabilities from the gas phase values by 0.85 was determined by reproduction of the dielectric constants of pyridine and pyrrole. The developed parameter set was extensively validated against additional experimental data such as diffusion constants, heat capacities and isothermal compressibilities, including data as a function of temperature.
Introduction
Aromatic heterocyclic compounds are organic substances that have an aromatic ring that includes nitrogen, oxygen or sulfur atoms in addition to carbon and hydrogen. Naturally occurring heteroaromatic compounds that contain nitrogen are found in, for example, proteins, nucleic acids, enzymatic co-factors, plant pigments, anthrocyanins and antibiotics (eg. penicillin and streptomycin).1 Thus, in the context of empirical force fields, a necessary step towards development of a comprehensive biological force field is the development of parameters for N-containing heteroaromatics.
The simplest 6-member N-containing heteroaromatic compound is pyridine, which is derived from benzene by substituting one of the CH groups by nitrogen. Natural compounds with pyridine include niacin, nicotinic acid, NAD, and nicotine.1 Accordingly, this molecule represents an ideal initial model compound for parametrization of N-containing heterocycles.† Pyrimidines are a class of compounds related to benzene and pyridine that include nitrogen atoms at the 1 and 3 positions. The simplest member, pyrimidine itself (C4H4N2), is not common in biological systems but its derivatives are present in thiamine (vitamin B1), barbiturates and three nucleic acid bases: cytosine, thymine and uracil.
Of the 5-membered, N-containing heteroaromatic compounds pyrrole is the simplest. It has the formula C4H4N and structurally has two C=C double bonds.2 Pyrroles are components of a number of biological molecules including porphyrins, chorines and bacteriochorins, chlorophyll and porphyrogens. It is also present in the dye indigo. Therefore, pyrrole also represents an ideal starting point for the development of a force field for N-containing heteroaromatics. Imidazole, or 1,3-diazine, is an essential component of many biologically relevant compounds, for example the biogenic amine, histamine, the amino acid histidine, and the nucleic acid bases adenine and guanine. Imidazole has a 5-member ring aromatic structure with N1 contributing two p electrons and N3 and the carbons each contributing one p electron to form the sextet aromatic π system. N3 also has a lone pair of electrons in the plane of the molecule. This is responsible to the coordinating properties of imidazole and its derivatives. For example, histidine is commonly found coordinated to metal ions in metalloenzymes.3
Indole (C8H9N) is an aromatic compound with a bicyclic structure with a pyrrole-like moiety fused with a benzene ring. It is found in the amino acid tryptophan and in a variety of alkaloids and pigments. Another heteroaromatic bicyclic compound is purine. It consists of an imidazole ring fused to a pyrimidine ring. Purine derivatives are notable compounds in the chemistry of life, with 50% of all nucleic acid bases being purines. Purine has two tautomers associated with protonation of the nitrogens of the imidazole moiety.
Based on their general importance, N-containing hetero aromatic compounds have been subjected to a multitude of experimental studies in all phases: crystalline, liquid and gaseous. The use of spectroscopic methods is ubiquitous, and techniques ranging from vibrational spectroscopy4–7 to neutron scattering8,9 and nuclear spin resonance10–13 have been applied to study this class of compounds. While experimental methods allow for measurements of the properties of these compounds, in order to probe molecular details of the structure and dynamics of these molecules theoretical approaches hold great promise. Information from computational studies may be used to study the molecular and electronic structures and, retrospectively, to interpret the spectroscopic parameters of aromatic heterocyclic molecules and complexes. First-principles ab initio and Density Functional Theory (DFT) calculations have been extensively used to study both their ground and excited state properties in the gas phase. The tractable size of these molecules allow studies using DFT, MP2 and CCSD(T) methods. Many of the studies focus on the study of noncovalent interactions between dimers and sometimes trimers of aromatic heterocycles and a number of studies have focused on the π–π stacking interactions. Many of these studies use standard ab initio methods for the treatment of electron correlation including both MP2 or CCSD(T) methods.14–20 Recent studies have used DFT methods that include corrections for the dispersion terms. Lin et al. 21 have used the London-Dispersion-Corrected DFT method,22 and Piacenza and Grimme23 used the so-called DFT-D method.24 In addition, a number of studies of excited states of this class of molecules have been published.25–29
Going beyond gas phase theoretical studies are a variety of condensed phase simulation studies of aromatic compounds using molecular dynamics (MD)30–34 or Monte-Carlo35–39 methods based on empirical force fields.40–43 These models have proved their usefulness by accurately reproducing a variety of experimental observables including phase change properties, free energies of solvation, transport properties and structural properties of the fluids or solids. The majority of models used to date are nonpolarizable or additive, and include the CHARMM,44,45 GROMOS,46 OPLS,40,47 and AMBER48 force fields, among others. Force fields are commonly used in other scientific areas, for example chemical engineering. An example is the NERD force field of Nath and co-workers used to predict vapor-liquid phase equilibria.49–52 The majority of these force fields have been optimized based on the reproduction of experimental enthalpies of vaporization and densities, as pioneered by Jorgensen.40 Further improvements in additive models have included the incorporation of free energies of hydration in the target data53–55 and MacKerell and co-workers have introduced a protocol for Lennard-Jones (LJ) parameter optimization using a combined ab initio/empirical approach that provides better balanced LJ parameters.53 Such advances are expected to further improve the accuracy of additive force fields, although the limitation associated with the additive approximation in the treatment of electrostatics as well as other approximations in the energy functions will hinder significant further development of such models. Accordingly extending force fields for heteraromatics beyond the additive approximation to include electronic polarizability is desirable.
Empirical models of aromatic molecules using nonadditive, polarizable models are still scarce in the literature. Patel and Brooks presented a model based on a fluctuating charge model that reproduced the heat of vaporization and crystal properties of benzene, imidazole and indole.43 Ren and Ponder developed a polarizable model (AMOEBA) based on atomic multipoles along with induced dipoles to treat the polarizability.56–58 Work in our laboratory developed a classical Drude-based polarizable model of benzene and toluene that was shown to satisfactorily reproduce a number of experimental observables including heats of vaporization, densities, heat capacities, diffusion coefficients and dielectric constants of the pure solvent as well as the free energy of solvation.59 In the present work this model is extended to N-containing heterocycles including pyridine, pyrimidine, pyrrole, imidazole, indole and purine (Figure 1). The developed force field is shown to reproduce a variety of experimental and quantum mechanical (QM) target data, including condensed phase properties. This work represents an additional step towards the development of a comprehensive polarizable force field for biological macromolecules.
Figure 1.
Model compounds including atom numbering.
Computational Methods
QM calculations were performed with NWChem60,61 and the Gaussian 0362 suite of programs. Geometry optimizations were performed at the MP2(fc)/6-31G(d) level of theory. This level of theory provides molecular geometries consistent with available gas phase experimental data (see the Table S1 of the Supporting Information) and it has been previously utilized during optimization of the latest version of the latest all-atom additive CHARMM force field (CHARMM27).63,64 QM calculations of the molecular electrostatic potentials (ESP) were performed on MP2 optimized geometries using the B3LYP hybrid functional65–67 and the correlation-consistent double-ζ Dunning aug-cc-pVDZ basis set,68 as previously discussed.69,70 Single-point energy B3LYP calculations were performed with the tight convergence criteria producing the target QM ESP maps. QM calculations on complexes between the model compounds and the rare gas atoms were performed at the MP3/6-311++G(3d,3p) level.53
Empirical force field calculations were performed with the program CHARMM.45,71 The SWM4-NDP water model72 was used in all calculations involving water. The functional form of the potential energy function from the pairwise additive CHARMM all-atom force field45 was used with polarizability introduced using the classical Drude oscillator model with some modification. In the classical Drude oscillator model the polarizability is introduced by attaching a massless charged particle to each polarizable atom (i.e., only non-hydrogen atoms in the present model) via a harmonic spring with the force constant kD. The magnitudes of the Drude charges, qD, can be unambiguously determined from the atomic polarizabilities using the relationship α=qD2/kD. The sign of the charges on Drude particles qD, in principle, has minimal impact due to the point dipole approximation; qD is chosen to be negative by analogy with the electron charge.69 The charge on the atomic core of a polarizable atom, qc, is the partial atomic charges minus qD, such that each atom-Drude pair forms a dipole qD·d, where d is the displacement vector going the atomic center to its Drude particle. Thus, the electrostatic energy term in the additive potential energy function is supplemented to include interactions between atomic cores and the Drude particles, and the self-energy of the polarizable atoms is calculated using the harmonic term 1/2kD·d2, which is also included in the potential energy function.69 Recently, the CHARMM Drude model was extended to include anistoropic atomic polarizability along with the inclusion of lone pairs on selected atoms, typically hydrogen bond acceptors.70
In the polarizable model electrostatic interactions between covalently bonded atoms and atoms at the termini of valence angles (i.e., 1–2 and 1–3 pairs, respectively) are excluded, as common in additive force fields. However, the electrostatic term is modified to allow 1–2 and 1–3 screened dipole-dipole interactions, as suggested by Thole.73,74 The screening is implemented through smearing of the charges associated with the dipole moments on the Drude particle and the real atom using a Slater distribution, from which the electrostatic interactions between the 1,2 and 1,3 atomic pairs are calculated. The Thole model has been extended by including atom-atom specific Thole scale factors, the terms describing the extent of charge smearing, 74,75 this extension is applied in the present study.
Partial atomic charges and atomic polarizabilities for the Drude polarizable force field for the aromatic compounds were determined from restrained fitting to QM response ESP maps, as per previous protocol.69 Briefly, the ESP grid points were located on concentric non intersecting Connolly surfaces around the molecules. To determine both atomic polarizabilities and partial atomic charges from the single fitting procedure, a series of perturbed ESP maps was generated, representing the electronic response of the molecule in the presence of a background point charge of magnitude +0.5e placed on Connolly surfaces along chemical bonds and in the gaps between the initial perturbation charges to achieve nearly equidistant coverage of the molecular shape. Five alternating Connolly surfaces of perturbation charges and grid points were generated with size factors 2.2 (charges), 3.0 (grid), 4.0 (charges), 5.0 (grid), and 6.0 (charges), where the size factor multiplied by the vdW radius of the corresponding atom determines its distance from the corresponding surface. Fitting was performed using parabolic restraints to the initial values of both the charges and polarizabilities with a weighting factor of 10−5 Å−2. Additionally, a flat well potential with a half-width of 0.1 e was used for atomic polarizabilities. (The penalty is applied directly on the charges of the Drude particles.) Fitting to the same charge and polarizability values was imposed for chemically equivalent atoms.
Molecular dynamics (MD) simulations were performed in the isothermal, isobaric ensemble (NPT) at 1 ATM pressure using the new velocity Verlet integrator76 implemented in CHARMM. The integrater was extended to include a number of crystal lattice types as part of the present work. Details of the extension are presented in the appendix. A Nose-Hoover thermostat with a relaxation time of 0.1 ps was applied to all real atoms to control the global temperature of the system. A modified Andersen-Hoover barostat with a relaxation time of 0.1 ps was used to maintain the system at constant pressure. All simulations were performed by at 298.2 K unless noted. Condensed-phase MD simulations were performed using periodic boundary conditions and SHAKE to constrain covalent bonds involving hydrogens.77 Electrostatic interactions were treated using particle-mesh Ewald (PME) summation78 with a coupling parameter 0.34 and a 6th order spline for mesh interpolation. Nonbond pair lists were maintained out to 16 Å, and a real space cutoff of 12 Å was used for the electrostatic and Lennard-Jones terms. Long-range contributions to the van der Waals terms were corrected for as previously described.79,80 The extended Lagrangian double-thermostat formalism76 was used in all polarizable MD simulations where a mass of 0.4 amu was transferred from real atoms to the corresponding Drude particles. The amplitude of their oscillation was controlled with a separate low-temperature thermostat (at T = 1.0 K) to ensure that their time course approximates the SCF regimen.76 All simulations using the extended Lagrangian formalism were performed with 1.0 fs time step and force constant of 500 kcal/(mol•Å2) on the Drude particles.
All simulations of the neat fluids were performed with cubic periodic boxes containing 128 molecules. These simulations were used for calculation of densities, enthalpies of vaporization, self-diffusion coefficient, isothermal compressibilities, specific heat capacities and the dielectric constants. Boxes of 1000 molecules were used to study the structure and dynamics of the pure liquids in order to recover the full layered structure of the liquids as required for analysis of radial or spatial distribution functions. Simulations in the aqueous phase were performed in cubic boxes containing 128 water molecules with one solute molecule. This was used, for example, in the computational determinations of the free energies of hydration and in the analysis of hydration through the use of radial or spatial distribution functions. The total length and the number of simulations used in the parametrization work varied according to the observable being simulated and the stage of the parameterization work. During the optimization stages, in particular during optimization of LJ parameters using neat liquid simulations, a high rate of turnover was required in order to probe many combinations of LJ parameters. In this case simulations to compute enthalpies of vaporization were performed with total lengths of 600 ps, of which the final 300 ps were used for analysis. Free energies of hydration were carried out initially with runs of 20 ps for equilibration and 80 ps for analysis in each simulation window. Final validation of the developed parameters made use of longer simulation times, as follows; (a) densities, enthalpies of vaporization, isothermal compressibilities, specific heat capacities and the dielectric constants were obtained from simulations of 5 ns of which the last 4 ns were taken for analysis. Each system was run multiple times (n = 8) using different random number seeds to assign the initial velocities and the results from the individual simulations used for statistical analysis. Coordinates sets from the trajectories were saved every 0.1 ps in the case of the dielectric constants and every 0.5 ps otherwise when required; (b) simulations in each window for the computation of the final free energies of solvation were run for a total of 130 ps with the first 30 ps used for equilibration and the final 100 ps for the production run.
Heats of vaporization, ΔHvap, were determined following the protocol previously described.59 The values were corrected for the different volumes between the liquid and gas phases by the term RT.81 Crystal calculations were performed for all compounds and variations of the cell parameters were used to verify the quality of the parameters. Heats of sublimation were also calculated for molecules that exist in crystalline form at 298 K. Crystal calculations were prepared by obtaining the coordinates for the asymmetric units from the CSD database82 for all compounds except indole. The unit cells were then prepared for all compounds following which supercells were were generated by replicating the primitive unit cells twice along all vectors (2×2×2). Indole was a special case since the structure is disordered and coordinates were extracted from the original paper.83 Images were generated based on transformation for the experimental lattices. Lennard-Jones (LJ) interactions were treated with force vswitch smoothing84 applied between 24 and 26 Å. Nonbonded pair lists were maintained out to 30 Å and long range corrections80 were applied. Electrostatics were treated using the Particle-Mesh-Ewald method78 with a coefficient of 0.34 Å and a sixth-order interpolation spline. After crystal generation the protocol consisted of an initial minimization of the systems, including lattice parameters, for 200 adopted-basis Newton-Raphson steps. This was followed by 300 ps of molecular dynamics. The last 200 ps were considered as the production run and used for analysis.
Free energies of hydration were computed through the free energy perturbation85 (FEP) protocol of Deng and Roux.86 The solvation free energies were computed as a sum of the electrostatic, dispersive, and repulsive contributions and each term was obtained as a difference in the free energy of the solute in water and in a vacuum. The weighted histogram analysis method (WHAM)87 was used to obtain the repulsive contribution and thermodynamic integration (TI) was used to compute the dispersive and electrostatic contributions.
Methods used for the calculation of the various properties presented in the Results and Discussion had been presented in detail in a previous study.59
Results and Discussion
Optimization steps and validation of the force field
Optimization of the parameters for the different model compounds (Figure 1) targeted both QM and experimental data. Internal parameters, including the bond, valence angle, dihedral angle and improper dihedral terms, were optimized to reproduce experimental82,88–91 and QM geometries and vibrational spectra from QM and experimental IR and RAMAN experiments. Partial atomic charges and atomic polarizabilities were determined sequentially from fittings to perturbed QM ESP maps followed by a refinement step where charges were manually adjusted to reproduce QM or, when available, experimental dipole and quadrupole moments. LJ parameters were based on the interactions with rare gases, reproduction of experimental densities and enthalpies of vaporization and free energies of hydration at room temperature when data are available for the liquid phase at that temperature and 1 atm (pyridine, pyrimidine, pyrrole). Alternatively, when data is available for the substances in the solid phase at room temperature and 1 atm, the LJ parameters were optimized to reproduce experimental enthalpies of sublimation and crystal lattice parameters and free energies of hydration at room temperature, as in the case of imidazole, indole and purine. As generally done in the CHARMM force fields, optimization was performed in an iterative manner as required due to the interdependence of the different terms in the energy function.53,64,92
To assure that the optimized parameters are transferable to analogs of the targeted model compounds a hierarchical and iterative optimization procedure was applied. For the compounds with 5-membered rings, this involved initial optimization of the parameters based on imidazole followed by application of those parameters to pyrrole. For example the NH and the adjacent carbons LJ parameters from imidazole were applied to pyrrole. The parameters were then applied to calculations of pyrrole and adjustments made if required. This was continued until satisfactory agreement with the target data was obtained for both model compounds. Similarly, for the 6-membered rings, optimization was initially based on pyridine, with initial parameters for the aromatic carbons and hydrogens not adjacent to the nitrogen atom transferred from benzene.59 This was followed by application of the resulting parameters to pyrimidine with iterative optimization. Finally, the appropriate benzene, 5-membered ring heteroaromatic and 6-membered ring heteroaromatic parameters were then applied to purine and indole.
An important aspect of force field development in CHARMM is validation of the newly developed parameters. For compounds that exist in the liquid phase at room temperature and 1 atm of pressure, additional thermodynamic and transport properties were calculated. These included densities and heats of vaporization as a function of temperature, the isothermal compressibility, specific heat capacity and the dielectric constants.
Determination of the electrostatic parameters
Electrostatic parameter determination, (i.e. the partial atomic charges, atomic polarizabilities and the atom-atom Thole scale factors), is the first step in the parametrization protocol of the Drude polarizable force field. For molecules of C2v symmetry coordinate systems were chosen to keep the molecule in the xy-plane and the positive x-axis along the 2-fold rotation axis. This choice corresponds to a principal axis system that diagonalizes the polarizability tensor. For compounds with Cs symmetry, only the z-axis is a principal axis. Thus, this coordinate system leads to block diagonal quadrupole moment and polarizability tensors, the 2×2 blocks for the in-plane (x,y) and the 1×1 blocks for the out of plane z components. Initial values of the partial atomic charges and polarizabilities were taken from the C22 additive all-atom force field44 and from adjusted Miller’s atomic hybrid polarizabilities (ahp) values, respectively.69,93 The fitted values of atomic polarizabilities were scaled to reflect the reduced polarization expected for the condensed media. In this work polarizabilities were scaled by 0.85. This value is intermediate between the full gas phase polarizability and the 0.7 scaling of the Drude polarizable water model94 and was selected based on reproduction of the dielectric constants of pyridine and pyrrole (see below). Manual optimization of the partial atomic charges was then performed based on reproduction of the QM and experimental95 dipole (μ) and quadrupole moments, θ (Table 1). The dipole moments of the C2v molecules coincide with the 2-fold rotation axis but in case of species with Cs symmetry (imidazole, indole and purine) the dipole lies on the molecular plane, with its orientation indicated by φ, the angle between the dipole vector and one of the inertial axis of the molecular plane. Components of the quadrupole moment tensor are also indicated. For compounds of C2v symmetry the quadrupole moment tensor is purely diagonal whereas for Cs molecules it has a 2×2 block component with non-zero θxy (and also θyx) elements. The agreement between the calculated and reference data is excellent (Table 1). This emphasizes the importance of polarization in the model. Contrary to the requirement of additive force fields to have enhanced gas-phase dipole moments to be able to reproduce condensed phase properties accurately, the Drude polarizable model is able to simultaneously reproduce the gas phase dipole and quadrupole moments and condensed phase properties (see below). Thus, the polarizable model is able to capture the response from the environment in condensed phase (liquid or solid).
Table 1.
Dipole (in Debye) and quadrupole moments (in Buckingham) for pyridine, pyrimidine, imidazole, 4-methyl-imidazole, pyrrole, indole and purine. (1 au ≈ 4.4866 × 10 −40 C·m2 ≈ 1.3450 Buckingham).
| Method | μ | θαα | θββ | θχχ | φ(°)d |
|---|---|---|---|---|---|
| Pyridine | |||||
| Drudea | 2.211 | −2.66 | 6.38 | −3.72 | 0 |
| Drudeb | 2.189 | −2.98 | 6.71 | −3.73 | 0 |
| CRCc | 2.215 | ||||
| Zeeman | −2.60 | 7.21 | −4.61 | ||
| Zeeman | −1.71 | 6.91 | −5.13 | ||
| Zeeman | −1.93 | 5.95 | −4.01 | ||
| QM (MP2) | 2.206 | −2.62 | 7.13 | −4.51 | 0 |
|
| |||||
| Pyrimidine | |||||
| Drudea | 2.286 | −4.17 | 5.69 | −1.52 | 0 |
| Drudeb | 2.322 | −4.39 | 5.88 | −1.50 | 0 |
| CRCc | 2.334 | ||||
| QM (MP2) | 2.300 | −3.81 | 5.59 | −1.79 | 0 |
|
| |||||
| Pyrrole | |||||
| Drudea | 1.715 | −6.56 | 1.36 | 5.20 | 0 |
| Drudeb | 1.667 | −6.68 | 1.42 | 5.26 | 0 |
| CRCc | 1.767 | ||||
| Zeeman | −9.22 | 4.31 | 4.91 | ||
| QM (MP2) | 1.740 | −8.40 | 1.78 | 6.61 | 0 |
|
| |||||
| Imidazole | |||||
| Drudea | 3.755 | −0.77 | 5.90 | −5.13 | 9.8 |
| Drudeb | 3.707 | −0.75 | 5.96 | −5.21 | |
| CRCc | 3.8±0.4 | ||||
| QM (MP2) | 3.755 | −0.38 | 5.94 | −5.55 | 9.8 |
|
| |||||
| 4-methyl-imidazole | |||||
| Drudea | 3.943 | −2.89 | 5.69 | −2.80 | 29.7 |
| Drudeb | 3.745 | −2.90 | 5.76 | −2.85 | |
| QM (MP2) | 3.946 | −2.96 | 7.09 | −4.13 | 29.7 |
|
| |||||
| Indole | |||||
| Drudea | 2.253 | 5.74 | 4.76 | −10.49 | 53.9 |
| Drudeb | 2.119 | 5.63 | 4.88 | −10.51 | |
| QM (MP2) | 2.210 | 5.64 | 6.73 | −12.38 | 45.6 |
|
| |||||
| Methyl-indole | |||||
| Drudea | 1.968 | 1.42 | 9.89 | −11.31 | 62.8 |
| Drudeb | 1.841 | 1.27 | 10.08 | −11.35 | |
| QM (MP2) | 2.071 | 1.52 | 10.36 | −11.88 | 63.0 |
|
| |||||
| Purine | |||||
| Drudea | 5.875 | −0.80 | 2.83 | −2.03 | 17.8 |
| Drudeb | 5.691 | −0.74 | 2.75 | −2.01 | |
| QM (MP2) | 5.839 | −2.37 | 4.84 | −2.46 | 15.6 |
Polarizable model with polarizabilities scaled by 0.85.
Polarizable model with unscaled polarizabilities.
Methodology unknown.95
φ is the angle between the dipole vector and one of the inertial axis of the molecular plane
Dielectric constants are extremely important not only from the macroscopic point of view, because of their role in determining the solubility properties of the substances, but also at the atomic level. The charge redistribution occurring when a particle is subjected to an electric field is determined largely by the polarizability. The new charge distribution can be written in terms of electric multipole moments, the lowest-order moment of a neutral molecule being the dipole moment M. In a uniform electric field E the dipole moment the particle is written as
| (4) |
Where the term M0 represents the permanent dipole moment. The polarizability α is a Cartesian tensor that characterizes the lowest-order induced dipole moment in the atom or molecule. Among the physical quantities that depend on the polarizabilities is the dielectric constant. Thus, reproduction of experimental dielectric constants is important not only as another property the polarizable force field is able to reproduce, but mainly because it has a direct relation to the atomic properties of the compounds. During the development of the Drude polarizable model for water it was observed that use of the gas phase polarizability of water led to the dielectric constant being systematically too large.94 Based on this overestimation the polarizability was included as a parameter and optimized as part of the model, leading to determination of a scale factor of approximately 0.7 for the water model.72,94 The need for such scaling was initially suggested to be due to Pauli exclusion in the condensed phase, effectively damping the polarization response, although more recently QM calculations have shown that the scaling may actually be compensating for inhomogeneties in the electric field in the excluded volume of water96 or, in the case of lipid analogs, due to “charge stabilization” due to interactions with surrounding water molecules.97 Accordingly in subsequent parameter optimization studies in our laboratory the polarizability was treated as a fit parameter, with the target data being the dielectric constant of the pure solvent. This procedure was applied in the present study to determine the appropriate scaling factor for the N-containing heterocycles.
A useful expression to calculate the static dielectric constant ε in terms of properties of the fluid accessible from molecular simulations with periodic boundary conditions is
| (5) |
where ε is calculated from the dipole moment fluctuations of the box, M is the total dipole moment of the box ( ), <V> is the average volume of the box, andε∞ is the high-frequency or optical dielectric constant ε∞.98 Time series of M were obtained from 8 independent simulations of 5 ns using data from the last 4 ns of each simulation and then concatenated into one large time series, which was used for the ε calculation from eq 5. The high-frequency optical dielectric constant ε∞ was estimated from the Clausius-Mossotti equation, which relates ε∞ to the molecular polarizability: 94,99
| (6) |
Comparison of calculated and experimental dielectric constants is presented in Table 2 for pyridine95 and pyrrole,100 the two compounds for which experimental dielectric constants are available. Using the full polarizabilities leads to the dielectric constants being significantly overestimated for pyrrole. A number of scale factors were then tried from which 0.85 was selected for the final model. For consistency this value was applied to pyridine as well as the rest of the N-containing heterocycles. As is evident the agreement of the Drude model with experiment is very good. In the case of pyrrole, ε is slightly overestimated while the value for pyridine lies between the reported experimental values.
Table 2.
Comparison of experimental and calculated dielectric constant of liquid pyridine and pyrrole.
Polarizabilities of all the model compounds were computed and compared to QM values. It is useful to report quantities that are invariant to coordinate choices, and three quantities are reported. One is the mean polarizability, given by the trace of the polarization tensor:
| (1) |
in which a1=azz ≤ a2 ≤ a3 are the eigenvalues or principal values of the polarization tensor. A measure of the polarizability anisotropy is the difference between the in-plane and out-of-plane components given by
| (2) |
Another invariant quantity that is related to the Kerr effect is given by
| (3) |
Comparison of ab initio reference values, equivalent quantities calculated with the polarizable Drude model and experimental values is presented in Table 3. Overall, the discrepancies between the polarizable Drude model and the ab initio values is small, evidencing the ability of the polarizable model to reproduce subtle aspects of the electrostatic behavior of the molecules under study. Scaling of the polarizabilities decreases the magnitude of the components of the polarizability tensors, but leaves the relative magnitudes of the derived quantities mostly unchanged. Experimental polarizabilites for pyrrole and imidazole were reported by LeFèvre et al.101 at a wavelength of 5893 Å based on measurements of depolarization ratios, refraction and dielectric polarization in a carbon tetrachloride solvent. Calder et al102 determined polarizabilities from the Kerr effect for pyrrole and imidazole. Their anisotropy values are less accurate though, due to their choice of the coordinate axis. In both cases, there is a good agreement to the Drude computed values.
Table 3.
Polarizabilities (in Å3) for pyridine, pyrimidine, imidazole, pyrrole, 4-methyl-imidazole, indole and purine.
| Method | α1 | α2 | α3 | ᾱ | Δ1α | Δ2α |
|---|---|---|---|---|---|---|
| Pyridine | ||||||
| Drudea | 9.43 | 9.65 | 4.92 | 8.00 | −2.15 | 4.62 |
| Drudeb | 10.08 | 11.45 | 5.50 | 9.01 | −1.61 | 5.40 |
| QM (MP2) | 10.96 | 11.62 | 6.06 | 9.55 | −2.12 | 5.26 |
|
| ||||||
| Pyrimidine | ||||||
| Drudea | 8.55 | 8.07 | 4.93 | 7.18 | −2.05 | 3.41 |
| Drudeb | 9.85 | 9.35 | 5.55 | 8.25 | −2.40 | 4.07 |
| QM (MP2) | 10.07 | 10.52 | 5.50 | 8.70 | −2.06 | 4.81 |
|
| ||||||
| Pyrrole | ||||||
| Drudea | 7.26 | 7.23 | 5.30 | 6.60 | −1.00 | 1.95 |
| Drudeb | 8.45 | 8.30 | 6.08 | 7.61 | −1.26 | 2.30 |
| QM (MP2) | 9.15 | 9.57 | 5.82 | 8.18 | −1.46 | 3.56 |
|
| ||||||
| Imidazole | ||||||
| Drudea | 6.78 | 7.21 | 4.31 | 6.10 | −1.02 | 2.71 |
| Drudeb | 7.76 | 8.30 | 4.88 | 6.98 | −1.17 | 3.18 |
| QM (MP2) | 8.32 | 8.65 | 5.07 | 7.35 | −1.46 | 3.43 |
|
| ||||||
| 4-methyl-imidazole | ||||||
| Drudea | 9.40 | 7.92 | 5.08 | 7.47 | −2.90 | 3.80 |
| Drudeb | 10.88 | 9.02 | 5.75 | 8.55 | −3.50 | 4.50 |
| QM (MP2) | 11.66 | 9.92 | 6.47 | 9.35 | −3.47 | 4.58 |
|
| ||||||
| Indole | ||||||
| Drudea | 18.53 | 13.66 | 6.62 | 12.94 | −8.39 | 10.37 |
| Drudeb | 22.55 | 16.19 | 7.35 | 15.36 | −10.78 | 13.22 |
| QM (MP2) | 21.17 | 15.99 | 8.90 | 15.35 | −8.73 | 10.67 |
|
| ||||||
| Methyl-indole | ||||||
| Drudea | 22.61 | 17.16 | 7.74 | 15.84 | −10.16 | 13.03 |
| Drudeb | 29.16 | 20.43 | 8.63 | 19.41 | −14.63 | 17.85 |
| QM (MP2) | 23.01 | 18.33 | 10.21 | 17.18 | −8.74 | 11.22 |
|
| ||||||
| Purine (7H) | ||||||
| Drudea | 13.98 | 10.32 | 5.90 | 10.07 | −5.87 | 7.01 |
| Drudeb | 16.42 | 11.82 | 6.61 | 11.62 | −7.21 | 8.50 |
| QM (MP2) | 17.56 | 13.13 | 7.11 | 12.60 | −7.44 | 9.08 |
Polarizable model with polarizabilities scaled by 0.85.
Polarizable model with unscaled polarizabilities.
Methodology unknown
The anisotropy of the polarization of the nitrogen atoms was adjusted to reproduce the QM polarization response along arcs surrounding those atoms. QM ESP maps were calculated at B3LYP/aug-cc-pVDZ level on MP2 optimized geometries, as previously described.69,70 The resulting anisotropies satisfactorily reproduced the QM data as a function of orientation as shown in Figure 2. Validation of those anisotropies was performed by computation of in-plane and out-of-plane interaction energies of the 5 and 6-membered ring model compounds with a sodium cation. Sodium cations were placed 4 Å from the nitrogen and neighboring carbon atoms of pyridine, pyrimidine and imidazole. This distance was selected as it was found that no significant charge transfer occurs based on analysis of Mulliken populations. For the nitrogen atoms two geometries were considered: along the lone pair and perpendicular to the molecular plane. The individual interaction energies are presented in Table 4, and the corresponding geometries are shown in Figure S1 of the supporting information. RMS variations in the interaction energy differences with respect to the QM values were 0.11, 0.30 and 0.44 for pyridine, pyrimidine and imidazole. The relative orders of the interaction energies are correct around the nitrogens as well as the neighboring carbon atoms. It should be emphasized that the interaction energies with sodium were not used in fitting the electrostatic parameters, but only to test the newly developed parameters.
Figure 2.
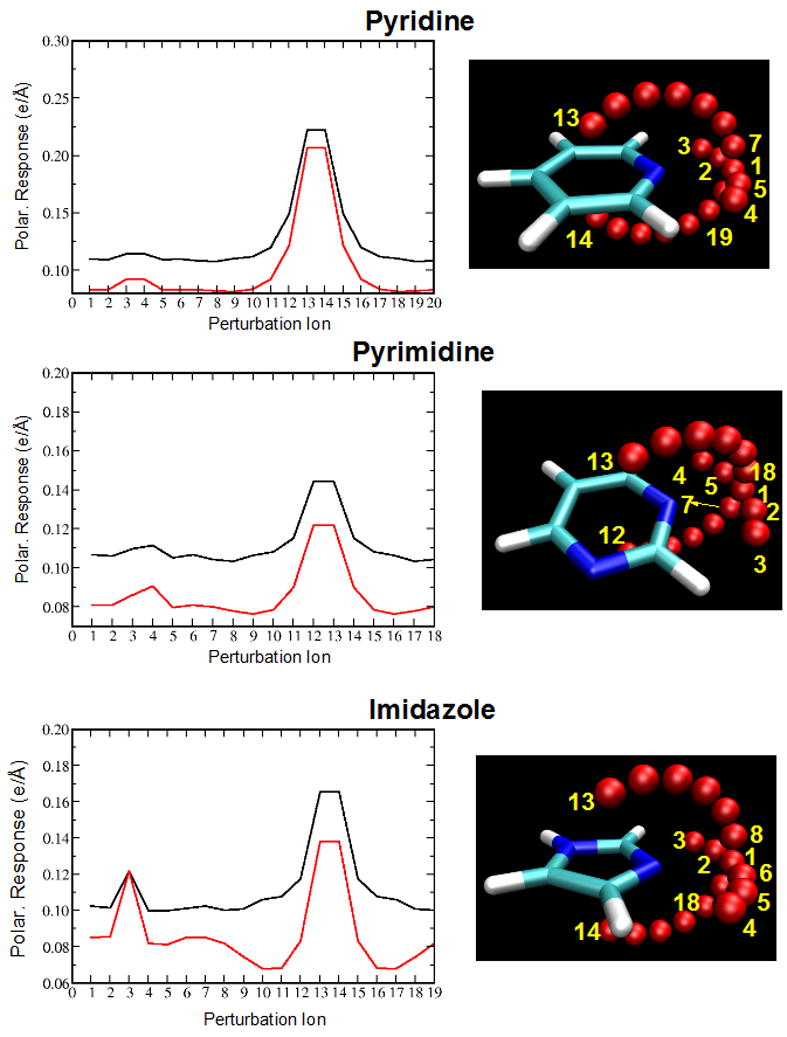
Polarization response as a function of orientation (left) on selected sites (red spheres). Perturbation ion positions are represented by red spheres
Table 4.
Interaction energies of a sodium cation with the models compounds as a function of orientation.
| Drude | ab initio | Difference | |
|---|---|---|---|
| Energy (kcal mol−1) | Energy (kcal mol−1) | Energy (kcal mol−1) | |
| Pyridine | |||
| NZ in | −10.45 | −12.30 | 1.85 |
| NZ out | −6.62 | −8.24 | 1.62 |
| CG | −5.38 | −7.12 | 1.74 |
| CE1 | −3.61 | −5.17 | 1.57 |
| Pyrimidine | |||
| N1 in | −7.89 | −9.51 | 1.62 |
| N2 out | −4.36 | −5.32 | 0.96 |
| C2 | −4.49 | −5.54 | 1.05 |
| C4 | −2.77 | −3.61 | 0.84 |
| Imidazole | |||
| NE2 in | −12.97 | −14.97 | 2.00 |
| NE2 out | −8.91 | −9.75 | 0.84 |
| CG | −4.77 | −5.75 | 0.98 |
| CD2 | −5.70 | −6.64 | 0.94 |
| ND1 | −3.15 | −4.02 | 0.87 |
| CE1 | −7.81 | −8.75 | 0.84 |
See Figure S1 of the supporting information for images of the sodium-model compound orientations.
Optimization of Internal Parameters
Optimization of the internal parameters was done by reproducing target data on the geometry and vibrational spectra of pyridine, pyrimidine, pyrrole and imidazole. Internal parameters for purine and indole were transferred from the constituent fragments (benzene,59 pyrimidine, pyrrole and imidazole) and complemented with specific terms for the unique connectivities and atom types at the intersections of the 5- and 6-membered rings. Target data for the geometries included the optimized structure of the compounds at the MP2/6-31G(d) level along with a survey of the Cambridge Structural Database (CSD)82 and gas phase geometries from microwave spectroscopy88,90 or electron diffraction.89 RMS differences of the bonds and angles with respect to the target data are shown in Table 5. The absolute values of all bond distances and angles are shown in Table S1 of the Supporting Information. Specific bonds and angles are identified following the numbering of Figure 1. The agreement between calculated and the target values is excellent. The larger RMS differences occur for imidazole and are 0.011 Å for distances and 0.91° for angles, which is well within the targeted differences of 0.02 Å for bonds and 2° for angles that is commonly used for the CHARMM force fields.
Table 5.
RMS differences between the empirical and target data for the intramolecular bond lengths (Å) and valence angles (degrees).
| Geometrical data | ||||
|---|---|---|---|---|
| RMS | Pyridine | Pyrimidine | Pyrrole | Imidazole |
| Distances | 0.002 | 0.004 | 0.010 | 0.011 |
| Angles | 0.228 | 0.272 | 0.603 | 0.912 |
Force constants were primarily optimized to reproduce experimental and QM vibrational spectra. Emphasis was placed on the magnitude of the frequencies along with the reproduction of the assignments based on the potential energy distributions determined via the MOLVIB module in CHARMM. In addition, for the bicyclic molecules potential energy surfaces were calculated for the out-of-plane butterfly modes, with the QM and empirical results shown on Figure 3. The quality of the level agreement for these energy surfaces along with the level of agreement for the lowest frequency modes indicates that the empirical model will correctly treat out-of-plane distortions of the ring systems that occur in MD simulations. All vibrational frequencies and assignments for the model compounds are shown in Table S2 of the supporting information. The final internal parameters developed in this work are shown in Table S6.
Figure 3.
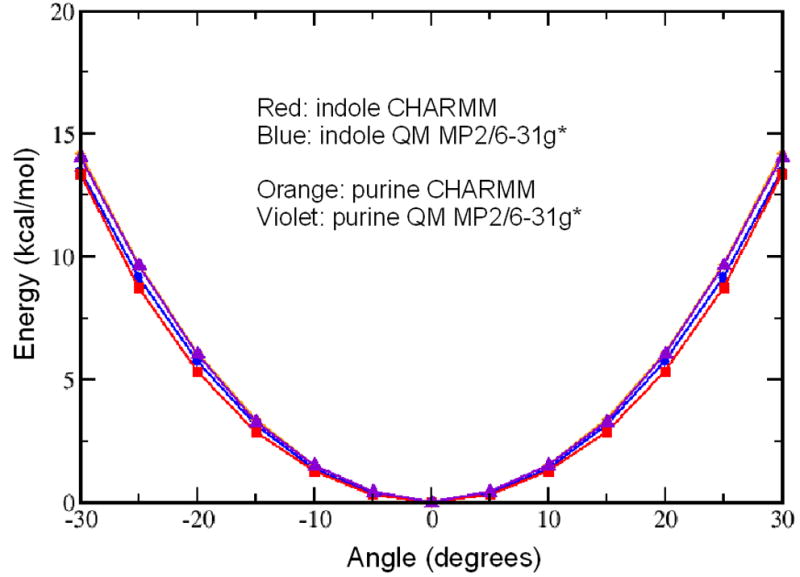
Potential energy surfaces of the out-of-plane butterfly motions of the bicyclic model compounds.
Optimization of Lennard-Jones Parameters
LJ parameters were optimized iteratively based on a procedure described in detail in ref 53. It involves two steps: the relative and absolute optimizations. The relative procedure, aimed at yielding parameters in which the relative values of the LJ parameters for different atom types (e.g., different nitrogens, carbons and hydrogens in the aromatic ring of purine) were able to reproduce relative QM minimum interaction energies and geometries for different rare gas to model compound interactions, was initially applied. Target data for this optimization includes RMS fluctuations about average differences or ratios between the QM and empirical models for selected interaction orientations between He or Ne and the model compounds. The second aspect, the absolute optimization procedure is included to ensure that the values of the LJ parameters yield condensed-phase properties, such as enthalpies of vaporization or sublimation, in good agreement with experiment. The newly developed parameters were then validated by comparing computed and experimental thermodynamic and transport properties at different temperatures. Thermodynamic properties included enthalpies of vaporization, free energies of solvation, isothermal compressibilities and heat capacities at constant pressure.
The relative LJ optimization step, based on interactions with rare gases allows the resulting empirical interactions to be systematically offset from the QM values while reproducing the relative values of the QM target data for different interaction orientations. For example, in an ideal case all minimum interaction distances may be offset by 0.1 Å such that the RMS fluctuation of the average distance over all interaction orientations is zero, with the resulting parameters simultaneously yielding the correct density and heat of vaporization of the pure solvent. Presented in Table 6 are the RMS fluctuations about the average differences and ratios between the QM and empirical models for the interactions with the rare gases. Data are based on the interaction orientations shown in Figure S2. In Table S3 of the Supporting Information absolute values for the individual interactions are presented. Only results with scaled polarizabilities are shown since RMS fluctuations of both the ratios and differences of the rare gas interactions were similar for both the polarizable models. Such a small change is expected given that the use of rare gas atoms is designed to primarily probe repulsion/dispersion interactions. The same trend was observed previously.59 Analysis of the individual interactions reveals that the main contributors that increase the RMS fluctuations are associated with interactions with hydrogen atoms. Ideally these interactions would require larger values of Rmin but reproduction of QM data for interactions of water and the model compounds required significantly lower values of Rmin and thus a compromise was made. This compromise is largely associated with the spherical representation of atoms by the LJ function used to describe the vdW interactions in the force field.
Table 6.
RMS fluctuations about the average differences and ratios between the QM and CHARMM minimum interaction energies and distances for interactions with rare gases.*
| Rmin (Å) | Emin (kcal/mol) | |||
|---|---|---|---|---|
| Complex | Difference | Ratio | Difference | Ratio |
| Pyridine/He | 0.1882 | 0.0686 | 0.0143 | 0.1122 |
| Pyridine/Ne | 0.1580 | 0.0595 | 0.0289 | 0.0720 |
| Pyrimidine/He | 0.1100 | 0.0415 | 0.0197 | 0.1220 |
| Pyrimidine/Ne | 0.1397 | 0.0522 | 0.0329 | 0.0704 |
| Imidazole/He | 0.0657 | 0.0228 | 0.0218 | 0.1670 |
| Imidazole/Ne | 0.0149 | 0.0083 | 0.0405 | 0.0933 |
| Pyrrole/He | 0.1042 | 0.0376 | 0.0195 | 0.2313 |
| Pyrrole/Ne | 0.0172 | 0.0166 | 0.0604 | 0.1178 |
RMS fluctuations were calculated as in Yin and MacKerell.53
Energies and geometries for the interaction of several model compound homodimers were also incorporated in the optimization of the LJ parameters. Reference data for this work was taken from QM calculations. Geometries were obtained from constrained geometry optimizations at the MP2/6-31g(d) level and energies from single point calculations at the RIMP2 level103,104,105 with the cc-pVQZ basis set.68,106,107 This level of the theory is computationally accessible yet provides accurate geometries and energies, in particular for the complexes considered in this work that involve in-plane hydrogen bonds of the type N···H-X(X=C, N. Basis set superposition error (BSSE) corrections were included following the scheme of Boys and Bernardi.108 Three dimers of pyridine, five of pyrimidine and three of imidazole were considered and the results are shown on Table 7. Their respective geometries are shown in Figure S3 of the Supplementary Information.
Table 7.
Minimum interaction energies and distances for homodimers of pyridine, pyrimidine and imidazole.
| Drude | ab initio | Difference | ||||
|---|---|---|---|---|---|---|
| Energy (kcal mol−1) | Distance (Å) | Energy (kcal mol−1) | Distance (Å) | Energy (kcal mol−1) | Distance (Å) | |
| Pyridine | ||||||
| 1 | −2.63 | 4.94 | −2.98 | 4.90 | 0.35 | 0.04 |
| 2 | −2.35 | 5.89 | −4.00 | 5.83 | 1.65 | 0.06 |
| 3 | −1.52 | 6.25 | −2.14 | 6.29 | 0.62 | −0.04 |
| Pyrimidine | ||||||
| 1 | −2.82 | 5.80 | −3.81 | 5.81 | 0.99 | −0.01 |
| 2 | −3.61 | 5.76 | −4.59 | 5.79 | 0.98 | −0.03 |
| 3 | −2.70 | 6.23 | −2.94 | 6.23 | 0.24 | 0.00 |
| 4 | −2.26 | 6.14 | −2.41 | 6.26 | 0.15 | −0.12 |
| 5 | −1.51 | 6.20 | −1.85 | 6.27 | 0.34 | −0.07 |
| Imidazole | ||||||
| 1 | −4.25 | 5.42 | −6.30 | 5.17 | 2.05 | 0.25 |
| 2 | −3.00 | 5.55 | −5.01 | 5.24 | 2.00 | 0.31 |
| 3 | −8.62 | 5.18 | −9.75 | 5.33 | 1.14 | −0.15 |
See Figure S3 of the supporting information for images of the model compound dimer orientations.
Compared to the QM results, with the newly developed parameter set minimum interaction distances are in good agreement for pyridine and pyrimidine while with imidazole the distance are too long for in-plane geometries (orientations 1 and 2) and too short for the directional hydrogen bond type of interaction. With the interaction energies, the empirical values are systematically less favorable than the QM target data. This trend is smaller for the hydrogen bond types of interactions, even between nonpolar C-H donors and nitrogen acceptors while the stacking types of interactions are significantly less favorable than the QM data. These differences to some extent may be due to limitations in the QM data, including the treatment of electron correlation and BSSE. For example studies have shown that more rigorous treatment of electron correlation leads to stacking interactions becoming less favorable (see following paragraph) In addition, inherent limitations in the potential energy function, in particular the treatment of the dispersive and repulsive terms also are expected to limit the extent of agreement between the QM and empirical models.
The study of nonbonded interactions by QM ab initio methods is an active area of research. However, only few studies comparing the behavior of different theoretical approaches to calculate nonbonded interactions exist. An early study by Rappé and Bernstein109 compared various small dimers (methane dimer, ammonia dimer, water dimer, H2O•NH3, CH4•(NH3) and (FHF)− at different computational approximations: Hartree-Fock, density functional theory (B3LYP), Moller-Plesset perturbation theory (MP2, LMP2, MP3, MP4D, MP4QD) and coupled-cluster (CCSD and CCSD(T)) with various basis sets (6-31G and cc-pVXZ, X=D, T, Q,5). The results show that the interaction energies become more favorable with increasingly larger basis sets and higher levels of the theory. This study did not take in account the effect of the different computational approaches on the equilibrium separations of the monomers. A number of studies have addressed the impact of basis set, including extrapolations to a complete basis set (CBS) and the inclusion of electron correlation via couple cluster methods (eg. CCSD(T)).110–112 These studies have focused on hydrogen bonded and dispersion bound complexes. Increasing the size of the basis set led, typically, to a decrease in the interaction energies, with the inclusion of higher level correlation treatment having the largest impact on stacking types of interactions. One drawback of these studies is that geometries were usually taken from calculations at the MP2 level. To our knowledge no systematic study has been performed on the influence of the basis set and level of theory on both the energetics and geometry of the interactions. A recent trend is the inclusion of corrections to DFT methods to treat dispersion interactions.21,23 In a related work, Sherrill and co-workers113,114 have studied benzene dimers at different levels of theory and using different theoretical approaches. Their results include effects on the intermolecular separation and indicate that interaction energies are less favorable and separations are longer at the highest level of the theory (CCSD(T)/aug-cc-pVQZ). Assuming that these results also apply to the heteroaromatic dimers, it seems that reproduction of condensed phase properties in the optimization protocol is driving CHARMM results in the correct direction.
Absolute values of the LJ parameters are dominated by the reproduction of condensed phase properties. Heats of vaporization and molecular volumes for the final empirical models of pyridine*, pyrimidine and pyrrole are shown in Table 8. For all compounds the Drude model reproduces the experimental target data within 2% of the experimental value, our targeted limit. The only significant discrepancy may occur with the molecular volume of pyrimidine; however, the ambiguity of the experimental data100,116 disallows a more detailed comparison. For the final model, parameters for carbon atoms and their covalently bound hydrogens not adjacent to nitrogen were transferred directly from benzene. Transferability of parameters is a key aspect of a force field and the current combination of LJ and internal parameters yield satisfactory condensed phase properties when applied to all compounds. As will be shown below, the model also yields excellent agreement at temperatures above room temperature, which were not considered in the optimization procedure, highlighting the quality of the Drude polarizable model and the developed parameter set.
Table 8.
Comparison of experimental and calculated pure solvent properties for pyridine, pyrimidine and pyrrole.
Optimization of LJ parameters (Table S7) also relied on experimental data on crystals of imidazole, indole and purine. For these molecules optimization of the absolute values of the LJ parameters was based on reproduction of the cell parameters and of heats of sublimation from crystal simulations. All crystal simulations were performed with the native lattice types.
The crystal structure of purine required special treatment. In the experimental crystal117 hydrogen is attached to N(7) (tautomer 7H) instead of N(9) (tautomer 9H) as occurs in nucleic acid bases. This required generation of an additional set of charges and polarizabilities since the same LJ and internal parameters may be applied to both tautomers. Purine molecules pack on top of each other as a result of the stabilization offered by the π–π stacking interactions and form chains due to strong N-H• • •N hydrogen bonds.
The most recent crystal structures of imidazole are from 1977 and 1979.118,119 Imidazole crystallizes in the monoclinic space group P21/c with four molecules per unit cell and structures were determined at the temperatures −123 and 293 K (Ref. 118) and 170 K (Ref 119) The most important structural feature is the presence of a strong hydrogen bond between N-H•••N. The H•••N distances are 1.83 Å at 293 K and 1.81 Å at −123 K. Comparison of the lattice parameters determined at the two temperatures show no significant difference in the lattice parameter c, which appears to be due to the similarity in the distances of the hydrogen bonds that link the molecules in chains along c. Lattice parameters a and b are roughly 0.2 Å longer at 293 K.
The crystal structure of indole was studied in 1975 by Roychowdhury and Basak.83 Indole crystallizes in the orthorhombic space group Pna21 with unit cell parameters a=7.86, b=5.66 and c=14.89 Å with four molecules per unit cell. The crystal structure was found to be disordered with indole being able to assume two alternative orientations. Orientation A was assigned a weight of 0.66 and orientation B 0.33. For the present study all calculations were performed using orientation A.
The simulation results are compared in Table 9 with the corresponding experimental data taken from the literature as indicated. For imidazole, indole and purine, the calculated and experimental lattice volumes exhibit deviations smaller than 2%, the largest being indole. These deviations are similar to those obtained in this study for the compounds that exist in the liquid phase at room temperature. In general, in the MD simulations the experimental unit cell dimensions and angles were reproduced with deviations less than 3%, the exception being purine. In purine the largest deviation occurs along cell vector a (+6.6% relative to the experimental value) but that is compensated by changes in the opposite direction for b and c (−3.0 and −3.9% respectively). Globally the newly developed force field performs very well. It is noteworthy that all MD data presented in Table 9 (cell parameters and volume of the cell) were obtained by direct averaging of the simulation results. Experimental enthalpies of sublimation are accurately reproduced for imidazole and indole with differences with respect to experiment less that 1%.
Table 9.
Comparison of simulated and experimental results with the corresponding structural and energetic data for imidazole, indole and purine.
| Crystallographic Properties | |||||
|---|---|---|---|---|---|
| Imidazole118 | Indole83 | Purine117 | |||
| Ref Code | IMAZOL04 | IMAZOL13 | INDOLE | PURINE01 | |
| Space Group | P21/c | P21/c | Pna21 | Pna21 | |
| Simulation Details | |||||
| No. molecules | 32 | 32 | 32 | 32 | |
| No. cells | 2×2×2 | 2×2×2 | 2×2×2 | 2×2×2 | |
| T/K | 123 K | 293 K | 298 K | 298 K | |
| Crystallographic vs Simulated Data | |||||
| a/Å | Drude Exp. | 15.58±0.07 15.16 |
15.91±0.19 15.46 |
15.97±0.13 15.72 |
29.02±0.24 31.1 |
| b/Å | Drude Exp. | 10.57±0.03 10.74 |
10.68±0.10 10.92 |
11.52±0.15 11.20 |
19.02±0.38 18.75 |
| c/Å | Drude Exp. | 19.27±0.02 19.58 |
19.20±0.05 19.56 |
28.83±0.39 29.78 |
7.71±0.04 7.33 |
| β/deg | Drude Exp. | 117.65±0.33 118.98 |
115.75±0.95 117.26 |
NA | NA |
| Physical and Thermodynamic properties | |||||
| ΔHsub/kcal·mol−1(298 K) | Drude Exp. | NA NA |
19.86 19.90 |
18.45 18.30 |
NA |
| Δ(ΔHsub)/% | NA | −0.20 | 0.82 | NA | |
| Vm/Å3 | Drude Exp. | 91.82±0.47 91.71 |
165.71±1.18 163.85 |
133.05±0.84 133.51 |
|
| ΔVm/% | 0.12 | 1.14 | −0.34 | ||
Free energies of hydration were computed for the model compounds (Table 10). In the case of pyridine and pyrrole values for the unsubstituted compounds were used whereas for imidazole and indole their methylated derivatives, 4-methyl-imidazole and 3-methyl-indole, were used. Pyrimidine is a special case and to our knowledge no experimental value has been published. However, pyrimidine is extremely important due to its central role in nucleic acid bases. Accordingly, its free energy of hydration was estimated using several QM methods.
Table 10.
Free energies of hydration, kcal/mol.
Results for the free energies of hydration were obtained for two sets of parameters. Set one is based on LJ parameters optimized to reproduce the pure solvent or crystal properties, as described above. The second, corrected set, includes off-diagonal LJ parameters between the heteroaromatic C or N atoms and the water oxygen; the off-diagonal LJ terms for carbons taken directly from benzene (i.e. atom type CD2R6A) were those optimized for that molecule. The specific off-diagonal LJ terms were implemented using the NBFIX keyword of CHARMM. The need for the special LJ terms is seen in the systematic overestimation of the free energies of solvation for the first set of parameters. This trend has previously been seen with the Drude parameters for alkanes120 and alcohols75 and is due to the assumption associated with the use of combining rules to generate the Rmin,ij and εij values for atom type i to atom type j LJ interactions.
Reproduction of interactions directed at the hydrogen atoms calculated by QM require much smaller LJ radii than the regular values developed from condensed phase properties and interactions with rare gases. A compromise was reached between the two and common set of hydrogen parameters was used in all simulations. For 5-membered molecules these parameters were satisfactory for the free energies of hydration as the agreement between experimental and computed values is excellent, emphasizing the ability of the newly developed polarizable model in describing hydration. With the 6-membered compounds, the systematic overestimation of the free energies of hydration required the development of off-diagonal terms, with the final model yielding excellent agreement with experiment. Notably, the use of the off-diagonal terms led to improvements in the reproduction of QM interactions with water. Presented in Table S4 of the supporting information are the individual interaction energies and distances of the model compounds with water and the RMS fluctuations about the average differences and ratios between the QM and empirical models are shown in Table S5. The corresponding geometries are shown in Figure S4. Importantly, the use of off-diagonal terms lead to a significant improvement of the RMS differences and ratios of the interactions of the 6-membered compounds with water, providing an additional physical basis for using the correction.
Force field validation
A number of additional pure solvent and crystal properties were calculated to validate the model. These include the heat capacity and isothermal compressibilities as well as crystal simulations for those compounds that are liquids at room temperature for which the pure liquid properties were used as target data for the LJ optimization.
Isothermal compressibilties121,122 and heat capacities123–127 were calculated for pyridine and pyrrole, with the results presented in Table 11. For pyridine the absolute value of the calculated and experimental heat capacities is somewhat overestimated, a trend already observed with the Drude polarizable model of benzene and toluene.59 For the isothermal compressibilities the polarizable model slightly underestimates the experimental values for both pyridine and pyrrole although the calculated values for pyridine approach the experimental values at higher temperatures. The same trend was also observed for benzene and toluene.59 Precision of the calculated values is higher at 298K due to the use of additional and longer simulations to calculate the isothermal compressibility.
Table 11.
Comparison of experimental and calculated heat capacities and isothermal compressibilities of liquid pyridine and pyrrole.
| Isothermal Compressibilities (GPa−1) | |||
|---|---|---|---|
| Temperature (K) | Drude | Exp. | |
| Pyridinea | 293.2 | 0.515±0.066 | 0.649* 0.673 0.682 |
| 298.2 | 0.613±0.034 | 0.670* 0.700 0.704 0.706 |
|
| 303.2 | 0.606±0.105 | 0.692* 0.720 0.726 |
|
| 308.2 | 0.704±0.234 | 0.714* 0.748 |
|
| Pyrroleb | 298.2 | 0.558±0.046 | 0.652 (293K) |
| Heat capacity (cal mol−1 K−1) | |||
| Drude | Exp. | ||
| Pyridine | 37.39 | 31.73123–126 | |
| Pyrrole | 30.53127 | ||
Further validation of the developed Drude polarizable model was obtained via crystal simulations of pyridine, pyrimidine and pyrrole (Table 12). The crystal structure of pyridine was determined at 153 K by Mootz and Wussow in 1981.128 There are 16 pyridine molecules in the unit cell, the crystal system is orthorhombic with space group Pna21, a = 1.75, b = 8.97 and c = 1.14 Å. The volume of the unit cell is very well conserved by the Drude model, with cell vectors a and b being longer than the experimental equivalents and c smaller. The final snapshot of the simulated crystal and the corresponding experimental coordinates are superimposed in Figure S5(a), illustrating the similarity between the two.
Table 12.
Comparison of simulated and experimental results for crystals of pyridine, pyrimidine and pyrrole.
| Crystallographic Properties | ||||
|---|---|---|---|---|
| Pyridine128 | Pyrimidine129 | Pyrrole130 | ||
| Crystallographic Properties | ||||
| Ref Code | PYRDNA01 | PRMDIN01 | RUVQII | |
| Space Group | Pna21 | Pna21 | Pnma | |
| Simulation Details | ||||
| No. molecules | 16 | 32 | 32 | |
| No. cells | 1×1×1 | 2×2×2 | 2×2×2 | |
| T/K | 153 K | 107 K | 103 K | |
| Crystallographic vs Simulated Data | ||||
| a/Å | Drude Exp. | 18.11±0.08 17.52 |
23.30±0.03 23.11 |
14.53±0.05 14.56 |
| b/Å | Drude Exp. | 9.18±0.05 8.97 |
18.32±0.03 18.92 |
20.66±0.06 20.57 |
| c/Å | Drude Exp. | 10.73±0.08 11.35 |
7.34±0.02 6.78 |
10.10±0.06 10.14 |
| Vm/Å3 | Drude Exp. | 111.36 111.48 |
98.16 92.54 |
95.40 94.94 |
| ΔVm/% | −0.11 | 6.07 | 0.48 | |
The crystal structure of pyrimidine was solved by Wheatley129 and several interesting observations were made in that study: (1) work should be done at lower temperatures to minimize the effects of thermal motion; (2) the thermal parameters indicate that there is considerable thermal motion around the normal axis to the molecular plane and normal to the plane of the molecule. Crystal simulations were carried out at 107 K. In the simulations at 107 K the volume of the unit cell is reasonably well conserved although cell vectors b and c have their magnitudes significantly reversed compared to the experimental value. Figure S5(b) shows the similarity between the computed and experimental structures.
The crystal structure of pyrrole was solved by Goddard and co-workers.130 It crystallizes in the Pnma space group, the crystal system is orthorhombic with a = 7.29, b = 10.29 and c = 5.07 Å. The most important interaction in the crystal is a N-···π interaction between neighboring molecules. Crystal simulations were carried out at the experimental temperature (103 K) and the final snapshot is shown in Figure S5(c). As is evident for this molecules as well as pyridine and pyrimidine (Table 12), the parameters perform well in these test systems, validating the utility of the model.
Conclusions
Presented is a polarizable model of 5 and 6-membered N-containing heteroaromatic molecules and derived bicyclic compounds based on the classical Drude oscillator formalism. The model was optimized to reproduce a variety of gas and condensed phase target data. Transferability of the optimized parameters was tested via their application to indole, methyl-indole and purine, with the required methyl parameters being transferred from the previously published alkane force field. The quality of the resulting indoles and purine models in treating various condensed phase properties supports the transferability of the parameters. Additional validation of the developed force field was performed via calculation of additional condensed phase data, including heat capacities and isothermal compressibilities. Significant care was taken in the optimization of the electrostatic properties around the nitrogen atoms, including the use of anisotropic polarizabilties on those atoms. Moreover, partial charges were optimized to reproduce values of dipole and quadrupole moments obtained from QM methods or obtained from experiment. These qualities along with the ability of the polarizable model in reproducing condensed phase properties, including the experimental dielectric constant, indicate that the model will be useful for force field based studies of a variety of heterocycles.
Supplementary Material
Acknowledgments
Financial support from the NIH (GM51501 and GM72558) is acknowledged
Footnotes
See the Experimental Section for details.
Experimental data at 313.2 K from Ref. 115
Bibliography
- 1.Katritzky AR, Pozharskii AF. Handbook of Heterocyclic Chemistry. Pergamon Press; 2000. [Google Scholar]
- 2.Loudon MG. Organic Chemistry. Oxford University Press; New York: 2002. [Google Scholar]
- 3.Messerschmidt A, Huber R, Wieghardt K, Poulos T. Handbook of Metalloproteins. Wiley; New York: 2001. [Google Scholar]
- 4.Breda S, Reva ID, Lapinski L, Nowak MJ, Fausto R. J Mol Struct. 2006;786(2–3):193–206. [Google Scholar]
- 5.Chen JX, Park J, Hochstrasser RM. J Phys Chem A. 2003;107(49):10660–10666. [Google Scholar]
- 6.Urena FP, Gomez MF, Gonzalez JJL, Torres EM. Spectroc Acta Pt A-Molec Biomolec Spectr. 2003;59(12):2815–2839. doi: 10.1016/s1386-1425(03)00082-9. [DOI] [PubMed] [Google Scholar]
- 7.Wrzeszcz W, Czarnik-Matusewicz B, Hawranek JP. Pol J Chem. 1998;72(2):302–313. [Google Scholar]
- 8.Nicolai B, Kaiser E, Fillaux F, Kearley GJ, Cousson A, Paulus W. Chem Phys. 1998;226(1–2):1–13. [Google Scholar]
- 9.Navarro A, Fernandez-Gomez M, Lopez-Gonzalez JJ, Fernandez-Liencres MP, Martinez-Torres E, Tomkinson J, Kearley GJ. J Phys Chem A. 1999;103(29):5833–5840. [Google Scholar]
- 10.Kintzinger JP. Mol Phys. 1971;22:273. [Google Scholar]
- 11.Litchman WM. J Magn Resn. 1974;14:286. [Google Scholar]
- 12.Megiel E, Kasprzycka-Guttman T, Jagielska A, Wroblewska L. J Mol Struct. 2001;569(1–3):111–119. [Google Scholar]
- 13.Salman SR, Farrant RD, Glen RC, Lindon JC. Spectr Lett. 1998;31(2):269–274. [Google Scholar]
- 14.Mishra BK, Sathyamurthy N. J Phys Chem A. 2005;109(1):6–8. doi: 10.1021/jp045218c. [DOI] [PubMed] [Google Scholar]
- 15.Hobza P, Sponer J. J Am Chem Soc. 2002;124(39):11802–11808. doi: 10.1021/ja026759n. [DOI] [PubMed] [Google Scholar]
- 16.Sponer J, Hobza P. Chem Phys Lett. 1997;267(3–4):263–270. [Google Scholar]
- 17.Hopkins BW, Tschumper GS. J Phys Chem A. 2004;108(15):2941–2948. [Google Scholar]
- 18.Muller-Dethlefs K, Hobza P. Chem Rev. 2000;100(1):143–167. doi: 10.1021/cr9900331. [DOI] [PubMed] [Google Scholar]
- 19.Hobza P, Sponer J. Chem Rev. 1999;99(11):3247–3276. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
- 20.Braun J, Neusser HJ, Hobza P. J Phys Chem A. 2003;107(19):3918–3924. [Google Scholar]
- 21.Lin IC, von Lilienfeld A, Coutinho-Neto MD, Tavernelli I, Rothlisberger U. J Phys Chem B. 2007;111(51):14346–14354. doi: 10.1021/jp0750102. [DOI] [PubMed] [Google Scholar]
- 22.von Lilienfeld OA, Tavernelli I, Rothlisberger U, Sebastiani DP. Rev Lett. 2004;93(15) doi: 10.1103/PhysRevLett.93.153004. [DOI] [PubMed] [Google Scholar]
- 23.Piacenza M, Grimme S. Chemphyschem. 2005;6(8):1554–1558. doi: 10.1002/cphc.200500100. [DOI] [PubMed] [Google Scholar]
- 24.Grimme S. J Comp Chem. 2004;25(12):1463–1473. doi: 10.1002/jcc.20078. [DOI] [PubMed] [Google Scholar]
- 25.Fischer G, Cai ZL, Reimers JR, Wormell P. J Phys Chem A. 2003;107(17):3093–3106. [Google Scholar]
- 26.Cai ZL, Reimers JR. J Phys Chem A. 2002;106(37):8769–8778. [Google Scholar]
- 27.Fischer G, Wormell P. Chem Phys. 2000;257(1):1–20. [Google Scholar]
- 28.Cai ZL, Reimers JR. J Phys Chem A. 2000;104(36):8389–8408. [Google Scholar]
- 29.Becucci M, Lakin NM, Pietraperzia G, Salvi PR, Castellucci E, Kerstel ERT. J Chem Phys. 1997;107(24):10399–10405. [Google Scholar]
- 30.Baker CM, Grant GH. J Chem Theory Comput. 2007;3(2):530–548. doi: 10.1021/ct600218f. [DOI] [PubMed] [Google Scholar]
- 31.Zoidis E, Besnard M, Yarwood J. Chem Phys. 1996;203(2):233–243. [Google Scholar]
- 32.Gamba Z, Klein ML. Chem Phys. 1989;130(1–3):15–22. [Google Scholar]
- 33.Parbhoo B, Nagy OB. J Mol Struct. 1988;177:393–399. [Google Scholar]
- 34.Sagarik K, Spohr E. Chem Phys. 1995;199(1):73–82. [Google Scholar]
- 35.Coutinho K, Saavedra N, Serrano A, Canuto S. Theochem-J Mol Struct. 2001;539:171–179. [Google Scholar]
- 36.de Almeida KJ, Coutinho K, de Almeida WB, Rocha WR, Canuto S. Phys Chem Chem Phys. 2001;3(9):1583–1587. [Google Scholar]
- 37.Sinoti ALL, Politi J, Freitas LCG. J Braz Chem Soc. 1996;7(2):133–141. [Google Scholar]
- 38.Sinoti ALL, Politi JRS, Freitas LCG. Theochem-J Mol Struct. 1996;366(3):249–258. [Google Scholar]
- 39.Nagy PI, Durant GJ, Smith DA. J Am Chem Soc. 1993;115(7):2912–2922. [Google Scholar]
- 40.Jorgensen WL, Maxwell DS, TiradoRives J. J Am Chem Soc. 1996;118(45):11225–11236. [Google Scholar]
- 41.Sun H. J Phys Chem B. 1998;102(38):7338–7364. [Google Scholar]
- 42.Kaminski GA, Stern HA, Berne BJ, Friesner RA. J Phys Chem A. 2004;108(4):621–627. [Google Scholar]
- 43.Patel S, Brooks CL. J Comp Chem. 2004;25(1):1–15. doi: 10.1002/jcc.10355. [DOI] [PubMed] [Google Scholar]
- 44.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 45.MacKerell AD, Jr, Brooks B, Brooks CL, III, Nilsson L, Roux B, Won Y, Karplus M. In: Encyclopedia of Computational Chemistry. Schleyer PvR, Allinger NL, Clark T, Gasteiger J, Kollman PA, Schaefer HF, III, Schreiner PR., editors. John Wiley & Sons; Chichester, UK: 1998. p. 271. [Google Scholar]
- 46.Scott WRP, Hunenberger PH, Tironi IG, Mark AE, Billeter SR, Fennen J, Torda AE, Huber T, Kruger P, van Gunsteren WF. J Phys Chem A. 1999;103(19):3596–3607. [Google Scholar]
- 47.Jorgensen WL, TiradoRives J. J Am Chem Soc. 1988;110(6):1657–1666. doi: 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
- 48.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1996;118(9):2309–2309. [Google Scholar]
- 49.Nath SK, Escobedo FA, de Pablo JJ, Patramai I. Ind Eng Chem Res. 1998;37(8):3195–3202. [Google Scholar]
- 50.Nath SK, De Pablo JJ. Mol Phys. 2000;98(4):231–238. [Google Scholar]
- 51.Nath SK, Khare R. J Chem Phys. 2001;115(23):10837–10844. [Google Scholar]
- 52.Nath SK, Banaszak BJ, de Pablo JJ. J Chem Phys. 2001;114(8):3612–3616. [Google Scholar]
- 53.Yin DX, Mackerell AD. J Comp Chem. 1998;19(3):334–348. [Google Scholar]
- 54.Chen IJ, Yin D, MacKerell AD. J Comp Chem. 2002;23(2):199–213. doi: 10.1002/jcc.1166. [DOI] [PubMed] [Google Scholar]
- 55.Oostenbrink C, Villa A, Mark AE, Van Gunsteren WF. J Comp Chem. 2004;25(13):1656–1676. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 56.Ren PY, Ponder JW. J Comput Chem. 2002;23(16):1497–1506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 57.Ren PY, Ponder JW. J Phys Chem B. 2003;107(24):5933–5947. [Google Scholar]
- 58.Schnieders MJ, Baker NA, Ren PY, Ponder JW. J Chem Phys. 2007;126(12) doi: 10.1063/1.2714528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lopes PEM, Lamoureux G, Roux B, MacKerell AD. J Phys Chem B. 2007;111(11):2873–2885. doi: 10.1021/jp0663614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bylaska EJ, de Jong WA, Govind N, Kowalski K, Straatsma TP, Valiev M, Wang D, Apra E, Windus TL, Hammond J, Nichols P, Hirata S, Hackler MT, Zhao Y, Fan P-D, Harrison RJ, Dupuis M, Smith DMA, Nieplocha J, Tipparaju V, Krishnan M, Wu Q, Van Voorhis T, Auer AA, Nooijen M, Brown E, Cisneros G, Fann GI, Fruchtl H, Garza J, Hirao K, Kendall R, Nichols JA, Tsemekhman K, Wolinski K, Anchell J, Bernholdt D, Borowski P, Clark T, Clerc D, Dachsel H, Deegan M, Dyall K, Elwood D, Glendening E, Gutowski M, Hess A, Jaffe J, Johnson B, Ju J, Kobayashi R, Kutteh R, Lin Z, Littlefield R, Long X, Meng B, Nakajima T, Niu S, Pollack L, Rosing M, Sandrone G, Stave M, Taylor H, Thomas G, van Lenthe J, Wong A, Zhang Z. Pacific Northwest National Laboratory; Richland, Washington 99352–0999, USA: 2007. [Google Scholar]
- 61.Kendall RA, Apra E, Bernholdt DE, Bylaska EJ, Dupuis M, Fann GI, Harrison RJ, Ju J, Nichols JA, Nieplocha J, Straatsma TP, Windus TL, Wong AT. Computer Phys Comm. 2000;128:260–283. [Google Scholar]
- 62.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian, Inc.; Wallingford CT: 2004. [Google Scholar]
- 63.Foloppe N, MacKerell AD. J Phys Chem B. 1998;102(34):6669–6678. [Google Scholar]
- 64.Foloppe N, MacKerell AD. J Comp Chem. 2000;21(2):86–104. [Google Scholar]
- 65.Becke AD. Physical Review A. 1988;38(6):3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 66.Becke AD. Journal Of Chemical Physics. 1993;98(7):5648–5652. [Google Scholar]
- 67.Lee CT, Yang WT, Parr RG. Theochem-Journal Of Molecular Structure. 1988;40:305–313. [Google Scholar]
- 68.Dunning TH. Journal Of Chemical Physics. 1989;90(2):1007–1023. [Google Scholar]
- 69.Anisimov VM, Lamoureux G, Vorobyov IV, Huang N, Roux B, MacKerell AD. J Chem Theory Comput. 2005;1(1):153–168. doi: 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]
- 70.Harder E, Anisimov VM, Vorobyov IV, Lopes PEM, Noskov SY, MacKerell AD, Roux B. J Chem Theory Comput. 2006;2(6):1587–1597. doi: 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- 71.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan SKM. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 72.Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD. Chem Phys Lett. 2006;418(1–3):245–249. [Google Scholar]
- 73.Thole BT. Chem Phys. 1981;59(3):341. [Google Scholar]
- 74.van Duijnen PT, Swart M. J Phys Chem A. 1998;102(14):2399–2407. [Google Scholar]
- 75.Anisimov VM, Vorobyov IV, Roux B, MacKerell AD. J Chem Theory Comput. 2007;3(6):1927–1946. doi: 10.1021/ct700100a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Lamoureux G, Roux B. J Chem Phys. 2003;119(6):3025–3039. [Google Scholar]
- 77.Ryckaert JP, Ciccotti G, Berendsen HJC. J Comp Phys. 1977;23(3):327–341. [Google Scholar]
- 78.Darden T, York D, Pedersen L. J Chem Phys. 1993;98(12):10089–10092. [Google Scholar]
- 79.Lague P, Pastor RW, Brooks BR. J Phys Chem B. 2004;108(1):363–368. [Google Scholar]
- 80.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Clarendon Press; Oxford: 1994. [Google Scholar]
- 81.Levine IN. Physical Chemistry. McGraw-Hill; 2001. [Google Scholar]
- 82.Allen FH. Acta Crystallogr Sect B-Struct Sci. 2002;58:380–388. doi: 10.1107/s0108768102003890. [DOI] [PubMed] [Google Scholar]
- 83.Roychowdhury P, Basak BS. Acta Crystallogr Sect B-Struct Sci. 1975;31(6):1559–1563. [Google Scholar]
- 84.Steinbach PJ, Brooks BR. J Comp Chem. 1994;15(7):667–683. [Google Scholar]
- 85.Kollman P. Chem Rev. 1993;93(7):2395–2417. [Google Scholar]
- 86.Deng YQ, Roux B. J Phys Chem B. 2004;108(42):16567–16576. [Google Scholar]
- 87.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. J Comput Chem. 1992;13(8):1011–1021. [Google Scholar]
- 88.Innes KK, Ross IG, Moomaw WR. J Mol Spectrosc. 1988;132(2):492–544. [Google Scholar]
- 89.Cradock S, Liescheski PB, Rankin DWH, Robertson HE. J Am Chem Soc. 1988;110(9):2758–2763. [Google Scholar]
- 90.Nygaard U, Nielsen JT, Kirchheiner J, Maltesen G, Rastrup-Andersen J, Sorensen GO. J Mol Struct. 1969;3(6):491. [Google Scholar]
- 91.Blackman GL, Brown RD, Burden FR, Elsum IR. J Mol Spectrosc. 1976;60(1–3):63. [Google Scholar]
- 92.Feller SE, MacKerell AD. J Phys Chem B. 2000;104(31):7510–7515. [Google Scholar]
- 93.Miller KJ. J Am Chem Soc. 1990;112(23):8533–8542. [Google Scholar]
- 94.Lamoureux G, MacKerell AD, Roux B. J Chem Phys. 2003;119(10):5185–5197. [Google Scholar]
- 95.Lide DR, editor. CRC Handbook of Chemistry and Physics. Taylor and Francis; Boca Raton, FL: 2003. [Google Scholar]
- 96.Schropp B, Tavan P. J Phys Chem B. 2008;112(19):6233–6240. doi: 10.1021/jp0757356. [DOI] [PubMed] [Google Scholar]
- 97.Botek E, Giribet C, Ruiz de AM, Negri RM, Bernik D. J Phys Chem A. 2008;112(30):6992–6998. doi: 10.1021/jp711620m. [DOI] [PubMed] [Google Scholar]
- 98.Boresch S, Willensdorfer M, Steinhauser O. J Chem Phys. 2004;120(7):3333–3347. doi: 10.1063/1.1640996. [DOI] [PubMed] [Google Scholar]
- 99.Bonin KD, Kresin VV. Electric-Dipole Polarizabilities of Atoms, Molecules and Clusters. World Scientific River Edge; NJ: 1997. [Google Scholar]
- 100.Gokel GW. Dean’s Handbook of Organic Chemistry. McGraw-Hill; New York: 2004. [Google Scholar]
- 101.Le Fèvre CG, Le Fevre RJW, Plurnachandra Rao B, Smith MR. J Chem Soc. 1959:1188 – 1192. [Google Scholar]
- 102.Calder KE, Calvert RL, Lukins PB, Ritchie GLD. Aust J Chem. 1981;34(9):1835–1844. [Google Scholar]
- 103.Feyereisen M, Fitzgerald G, Komornicki A. Chem Phys Lett. 1993;208(5–6):359. [Google Scholar]
- 104.Vahtras O, Almlof J, Feyereisen MW. Chem Phys Lett. 1993;213(5–6):514–518. [Google Scholar]
- 105.Bernholdt DE, Harrison RJ. Chem Phys Lett. 1996;250(5–6):477–484. [Google Scholar]
- 106.Kendall RA, Dunning TH, Harrison RJ. J Chem Phys. 1992;96(9):6796–6806. [Google Scholar]
- 107.Woon DE, Dunning TH. J Chem Phys. 1993;98(2):1358–1371. [Google Scholar]
- 108.Boys SF, Bernardi F. Mol Phys. 1970;19(4):553 – 566. [Google Scholar]
- 109.Rappe AK, Bernstein ER. J Phys Chem A. 2000;104(26):6117–6128. [Google Scholar]
- 110.Leininger ML, Nielsen IMB, Colvin ME, Janssen CL. J Phys Chem A. 2002;106(15):3850–3854. [Google Scholar]
- 111.Riley KE, Hobza P. J Phys Chem A. 2007;111(33):8257–8263. doi: 10.1021/jp073358r. [DOI] [PubMed] [Google Scholar]
- 112.Hesselmann A, Jansen G, Schutz M. J Am Chem Soc. 2006;128(36):11730–11731. doi: 10.1021/ja0633363. [DOI] [PubMed] [Google Scholar]
- 113.Sinnokrot MO, Sherrill CD. J Phys Chem A. 2004;108(46):10200–10207. [Google Scholar]
- 114.Sinnokrot MO, Sherrill CD. J Phys Chem A. 2006;110(37):10656–10668. doi: 10.1021/jp0610416. [DOI] [PubMed] [Google Scholar]
- 115.Linstrom PJ, Mallard WG, editors. National Institute of Standards and Technology; Gaithersburg, MD: 2005. p. 20899. [Google Scholar]
- 116.Nabavian M, Sabbah R, Chastel R, Laffitte M. J Chim Phys. 1977;74(1):115–126. [Google Scholar]
- 117.Watson DG, Sweet RM, Marsh RE. Acta Crystallographica. 1965;19(4):573–580. doi: 10.1107/s0365110x65003900. [DOI] [PubMed] [Google Scholar]
- 118.Craven BM, McMullan RK, Bell JD, Freeman HC. Acta Crystallogr Section B. 1977;33(8):2585–2589. [Google Scholar]
- 119.McMullan RK, Epstein J, Ruble JR, Craven BM. Acta Crystallogr Section B. 1979;35(3):688–691. [Google Scholar]
- 120.Vorobyov IV, Anisimov VM, MacKerell AD. J Phys Chem B. 2005;109(40):18988–18999. doi: 10.1021/jp053182y. [DOI] [PubMed] [Google Scholar]
- 121.Cibulka I, Takagi T. J Chem Eng Data. 2002;47(5):1037–1070. [Google Scholar]
- 122.Marcus Y, Hefter GT. J Mol Liq. 1997;73–4:61–74. [Google Scholar]
- 123.Domalski ES, Hearing ED. J Phys Chem Ref Data. 1996;25(1):1–525. [Google Scholar]
- 124.Domalski ES, Hearing ED. J Phys Chem Ref Data. 1997;26(6):1501–1505. [Google Scholar]
- 125.Chirico RD, Steele WV. J Chem Therm. 1996;28(8):819–841. [Google Scholar]
- 126.Chirico RD, Steele WV, Nguyen A, Klots TD, Knipmeyer SE. J Chem Therm. 1996;28(8):797–818. [Google Scholar]
- 127.Scott DW, Berg WT, Hossenlopp IA, Hubbard WN, Messerly JF, Todd SS, Douslin DR, McCullough JP, Waddington G. J Phys Chem. 1967;71(7):2263–2270. [Google Scholar]
- 128.Mootz D, Wussow HG. J Chem Phys. 1981;75(3):1517. [Google Scholar]
- 129.Wheatley P. Acta Crystallographica. 1960;13(2):80–85. [Google Scholar]
- 130.Goddard R, Heinemann O, Kruger C. Acta Crystallogr Section C. 1997;53(12):1846–1850. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


