DNA Repair and DNA Triplet Repeat Expansion: The Impact of Abasic Lesions on Triplet Repeat DNA Energetics

Abstract

Enhanced levels of DNA triplet expansion are observed when base excision repair (BER) of oxidative DNA base damage (e.g., 8-oxo-dG) occurs at or near CAG repeat sequences. This observation suggests an interplay between processing mechanisms required for DNA repair and expansion pathways that yield genotypes associated with many neurological/developmental disorders. It has been proposed that DNA expansion involves the transient formation within the triplet repeat domains of non-native slipped DNA structures that are incorrectly processed by the BER machinery of repair during DNA synthesis. We show here that replacement within a triplet repeat bulge loop domain of a guanosine residue by an abasic site, the universal BER intermediate, increases the population of slipped/looped DNA structures relative to the corresponding lesion-free construct. Such abasic lesion-induced energetic enhancement of slipped/looped structures provides a linkage between BER and DNA expansion. We discuss how the BER machinery of repair may be influenced by abasic-induced energetic alterations in the properties of regions proximal to and/or within triplet repeat domains, thereby potentially modulating levels of DNA expansion.

DNA expansion of triplet repeat sequences can lead to the development of debilitating neurological disorders commonly referred to as DNA expansion diseases.¹⁻⁵ It has been suggested that expansion involves the transient formation of non-native slipped DNA structures within the triplet repeat domain that then are incorrectly processed during de novo DNA synthesis.⁶⁻¹⁶ It recently has been shown that base excision repair (BER) of oxidatively damaged guanines at or near CAG triplet repeat sequences enhances the probability of DNA expansion.^17,18 In the BER pathway, base repair initially proceeds via glycosylase-mediated glycosidic bond cleavage to yield an intermediate abasic site.^19,20 The abasic lesion, which is toxic and mutagenic if not repaired, is further processed by endonucleases which excise the abasic lesion, with the remaining gap being filled using specialized repair polymerases, such as pol β.²¹⁻³⁴

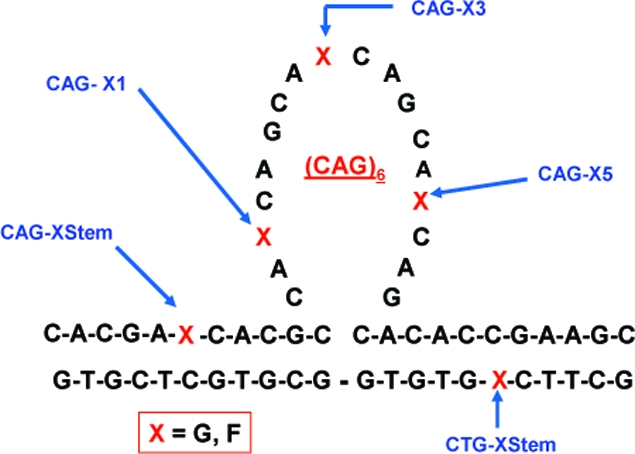
The observation that BER of oxidative damage at or near CAG repeats facilitates DNA triplet expansion suggests that the presence of the abasic repair intermediate may influence the ability of repeat DNA sequences to form non-native slipped DNA structures.^17,35 To assess this possibility, we report here the impact of abasic sites on the overall stability and conformational preferences of a CAG triplet repeat bulge loop structure that models slipped DNA states. The specific system investigated and the five locations of the guanine-to-abasic lesion site “mutations” studied here are shown in Scheme 1. We previously demonstrated that the unmodified versions of these so-called Ω-DNA constructs correspond to metastable states on a rough energy landscape.^36,37 We showed that the “single-stranded”, loop domains form ordered self-structures that enthalpically stabilize the overall Ω-DNA structure.

Scheme 1. Schematic Representation of the CAG Ω-DNA Construct.

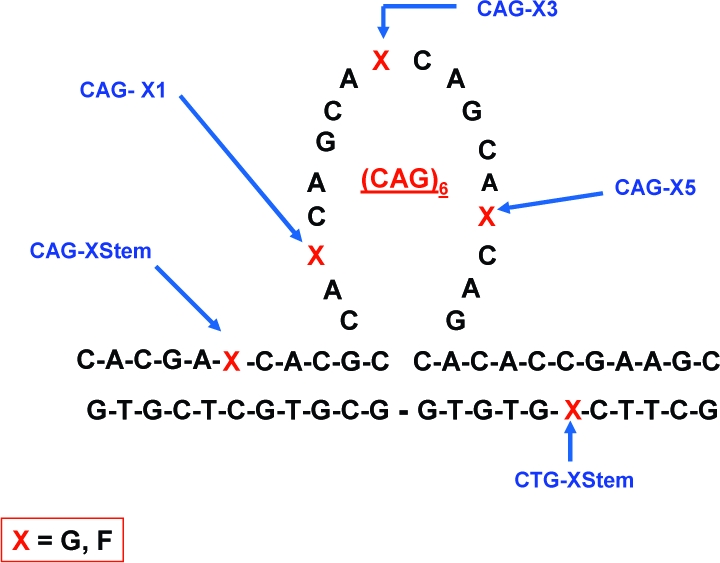
The positions where a single guanine base was replaced by a tetrahydrofuran abasic site analogue (F) are indicated by the letter X, where X can be either G or F. Also shown are the corresponding designations/names for these modified constructs. Lesion sites upstream (CAG-FStem) or downstream (CTG-FStem) of the loop domain are defined by the orientation shown here. Although the schematic represents the CAG loop domain as unstructured, experimental evidence suggests these bases adopt a structured/base-paired conformation. The nature of the pairing interactions in the loop and at the loop duplex junction is unknown.

In the present study we have incorporated the tetrahydrofuran abasic lesion analogue (F) in place of guanine at select positions within our bulge loop Ω-DNA construct, as shown in Scheme 1. We adopt nomenclature that positionally distinguishes between lesions (X = F) within the loop domains (CAG-F1, CAG-F3, CAG-F5) and lesions located in the Watson−Crick base-paired domains, either immediately upstream (CAG-FStem) or downstream (CTG-FStem) from the loop. The CAG designation for the lesion in the upstream stem duplex domain reflects the fact that the upper strand contains the CAG triplet repeat loop. By analogy, the designation for the lesion in the downstream stem duplex domain reflects the complementary nature of the lower strand. We have selected the specific lesion sites in consideration of both the 3D topology of the Ω constructs and future studies with repair enzymes that process such substrates.

Materials and Methods

Materials

Oligonucleotides were synthesized on a 10 μmol scale by standard phosphoramidite chemistry using an Äkta DNA synthesizer and were purified by repeated DMT-on/DMT-off reverse-phase HPLC, as previously described.^38,39 The purities of the oligonucleotides were assessed by analytical HPLC and ion spray mass spectroscopy and were found to be better than 98% by mass spectroscopy. Purified oligonucleotides were dialyzed against at least two changes of buffer containing NaCl, 10 mM cacodylic acid/sodium cacodylate, and 0.1 mM Na₂EDTA to yield a final concentration of 100 mM in Na⁺ cations using dispo-dialyzers with MWCO = 500 Da (Spectrum, Rancho Dominguez, CA). DNA extinction coefficients of the unmodified parent sequences were determined by phosphate assay under denaturing conditions (90 °C).^40,41 For the abasic-site-containing oligonucleotides, extinction coefficients were determined from continuous variation titrations (Job plots) with the complementary parent oligonucleotides and were found to be ϵ_{X(CAG)6Y(260nm,90°C)} = 368 400 M⁻¹ cm⁻¹, ϵ_{Y′(CTG)6X′(260nm,90°C)} = 342 900 M⁻¹ cm⁻¹, ϵ_{XY(260nm,90°C)} = 190 400 M⁻¹ cm⁻¹, ϵ_{Y′X′(260nm,90°C)} = 186 200 M⁻¹ cm⁻¹, ϵ_{X(CAG)6Y-F(260nm,90°C)} = 368 400 M⁻¹ cm⁻¹, ϵ_{XY-F(260nm,90°C)} = 180 000 M⁻¹ cm⁻¹, and ϵ_{Y′X′-F(260nm,90°C)} = 176 000 M⁻¹ cm⁻¹. As expected, for the 40mers, the impact of a single abasic site lesion in place of guanine is independent of lesion position and too small to result in a measurable change in extinction coefficient compared to the parent 40mer.

DSC Studies

DSC studies were conducted using a NanoDSCII differential scanning calorimeter (Calorimetry Science Corp., Lindon, UT) with a nominal cell volume of 0.3 mL.(42) Oligonucleotides, at a concentration of 50 μM in strand, were repeatedly scanned between 0 and 90/95 °C with a constant heating rate of 1 °C /min, while continuously recording the excess power required to maintain sample and reference cells at the same temperature. For the strand exchange measurements, preformed complementary Ω-DNAs were kept at 5 °C and mixed 1:1 immediately prior to loading and starting the DSC instrument. After conversion of the measured excess power values to heat capacity units and subtractions of buffer/buffer scans, the raw DSC traces were normalized for DNA concentration and analyzed using Origin software, as previously described.(36) The calorimetric enthalpy (ΔH_cal) was derived by integration of the excess heat capacity curve, and ΔC_p was derived from the difference in the linearly extrapolated pre- and post-transition baselines at T_m. ΔS was derived by ΔH/T_m, assuming “pseudomonomolecular” behavior in which propagation dominates initiation. Although our constructs formally are bimolecular complexes, their concentration-dependent denaturation deviates from a molecularity of two, as generally is the case for complexes of this size.(43) The theoretical entropy correction for a strictly bimolecular reaction of 21 cal mol⁻¹ K⁻¹ at C_t = 50 μM falls within the uncertainties of our entropy values and is the same for all our constructs. As a result, inclusion of such a molecularity contribution simply scales the magnitudes, while not altering the relative differences in ΔS and ΔG between our constructs. ΔG at the reference temperature was calculated using standard equations taking into account the nonzero heat capacity changes. T_m is defined as the temperature at the midpoint of the integrated excess heat capacity curve for a given conformational transition. At this temperature, for a process that exhibits pseudomonomolecular behavior, the sample is 50% denatured.

CD Melting Studies

CD spectra as a function of temperature were recorded using an AVIV model 400 spectropolarimeter (Aviv Biomedical, Lakewood, NJ). Spectra were recorded in steps of 1 nm between 360 and 200 nm with an averaging time of 10 s using a 1 mm cell, between 0 and 95 °C in 5 °C intervals. After subtraction of the relevant buffer scans, spectra were normalized for DNA concentration as previously described(44) and analyzed further. The oligonucleotide concentration was 10 μM in strand.

Results and Discussion

The Primary Abasic Lesion-Induced Impact Is Energetic Rather than Structural

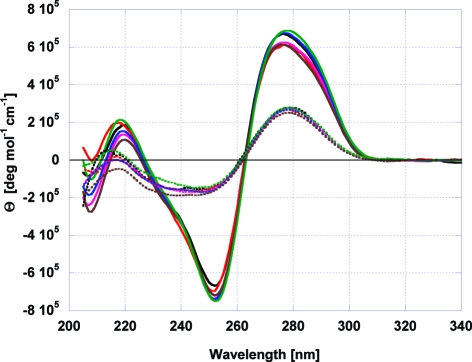
Figure 1 shows the CD spectra, at both low and high temperatures, for the different DNA constructs shown in Scheme 1, including the corresponding lesion-free system. The general similarity of these spectra suggests that the presence of the lesion and its position do not significantly alter the global Ω-DNA structure, at least within the resolution of the CD profile. Small differences in the intensity of the spectra near the positive and negative peak maxima may indicate modest lesion-induced local conformational adjustments in DNA structure to accommodate the absence of the guanine base. By contrast, calorimetric melting experiments reveal that the lesion can substantially alter the thermal and thermodynamic properties of the Ω-DNA construct in a manner that depends on the position of the lesion. We discuss below the position-dependent differential impact of the lesion on Ω-DNA stability, as part of our global effort to define lesion-induced energetic alterations that may modulate the processing of potential BER substrates.

Figure 1.

CD spectra for the DNA constructs shown in Scheme 1: spectra for the native (solid lines, 0 °C) and denatured (stippled lines, 95 °C) Ω-DNA constructs with and without F abasic site lesion. The unmodified parent sequence is shown in black, whereas the spectrum of the Ω-DNA with the lesion upstream of the loop domain (CAG-FStem) is shown in red and that of the lesion downstream of the loop (CTG-FStem) is in green. The spectra of the constructs with the lesion in the loop domain are shown in magenta (CAG-F1), blue (CAG-F3), and purple (CAG-F5). Note the overall similarities in the native spectra at 0 °C, indicating that the global structure is not significantly perturbed by the F lesion.

Abasic Lesions in the Watson−Crick Stem Duplex Domains Are Destabilizing and Alter the Heat Capacity of the Initial Ω States

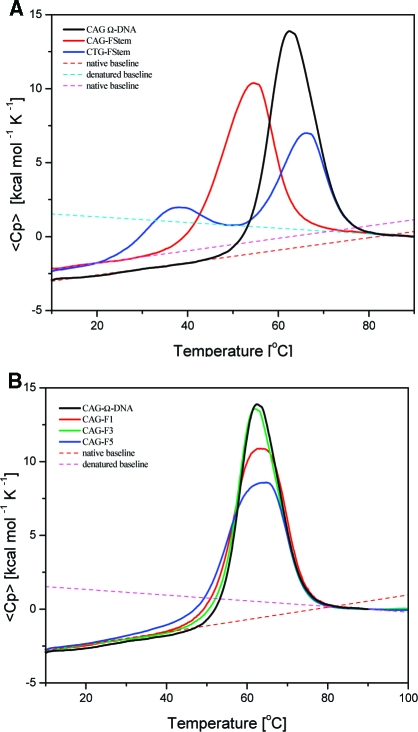
Inspection of the DSC curves presented in Figure 2A and the data listed in Table 1A reveals that a THF lesion (F) in either of the two Watson−Crick stem duplex domains adjacent to the bulge loop results in a net destabilization of the entire Ω-DNA construct, relative to the corresponding lesion-free construct. Furthermore, the presence of the lesion in either duplex domain causes the apparent heat capacities of the two lesion-containing initial states, the blue and red traces, to be similar to each other and “higher” than that of the corresponding lesion-free Ω-DNA construct, the black trace (see figure legend). Such behavior suggests that the abasic lesion induces an increase in DNA flexibility, or degrees of freedom, relative to the corresponding lesion-free construct; that is to say, the presence of the lesions causes the initial states to more resemble the disorder of the final state.⁴⁵⁻⁴⁷ This lesion-induced enhanced flexibility may be relevant to the differential recognition of such domains by repair enzymes relative to undamaged structures.

Figure 2.

DSC of Ω-DNAs (A) with a F abasic site in a stem duplex domain and (B) with the F lesion present at different positions in the loop. (A) Excess heat capacity curves measured for the Ω-DNAs with F lesion upstream (red, CAG-FStem) or downstream (blue, CTG-FStem) of the loop domain. Also shown is the excess heat capacity curve for the unperturbed parent (black) for comparison. To allow comparison, all excess heat capacity curves are set to ⟨C_p⟩ = 0 kcal mol⁻¹ K⁻¹ at 90 °C. The linear upper (denatured state) and lower (native state) baselines are indicated as stippled lines, revealing significant differences in C_p (ΔC_p) between the native and denatured states for each Ω-DNA construct.⁴⁸⁻⁵¹ Note also the distinct difference in magnitude of the apparent heat capacities (Y-axis) of the native state of the lesion containing Ω-DNAs compared to the unmodified parent Ω-DNAs at low temperature, reflecting the increased flexibility of the lesion-containing construct. (B) Excess heat capacity curves measured for the Ω-DNAs with the F lesion within the loop domain (red, CAG-F1; green, CAG-F3; blue, CAG-F5). The excess heat capacity curve for the unperturbed parent Ω-DNA (black) is also shown for comparison. To facilitate comparison, all excess heat capacity curves are set to ⟨C_p⟩ = 0 kcal mol⁻¹ K⁻¹ at 90 °C. The linear upper (denatured state) and lower (native state) baselines are indicated as stippled lines, revealing significant differences in ΔC_p between the native and denatured states of each complex.⁴⁸⁻⁵¹ Note also the change in shape of the denaturation curve not reflected in changes in T_m, ΔH, or ΔS for the lesion-containing Ω-DNAs relative to the parent Ω-DNA construct. Note further the similarity in magnitude of the apparent heat capacities of the native state of the lesion-containing Ω-DNAs compared to the unmodified parent construct.

Table 1. Thermodynamic Parameters for F Lesion (A) in the Watson−Crick Stem and (B) in the Bulge Loop Domain of the CAG Ω-DNA.

Ω construct	Tm (°C)	ΔHcal (kcal mol−1)	ΔScal (cal mol −1 K−1)	ΔCp (cal mol −1 K−1)	ΔGcal(25 °C) (kcal mol−1)
(A) Watson−Crick Stem
CAG-FStem	54.1 ± 0.3	145.7 ± 7.3	445 ± 22	1050 ± 100	11.55 ± 0.6
CTG-Fstem	37.2 ± 0.3	145.0 ± 7.2	428 ± 21	N/D
	65.9 ± 0.3			N/D
CAG	62.3 ± 0.3	172.7 ± 8.6	515 ± 25	1350 ± 140	16.29 ± 0.8
(B) Bulge Loop Domain
CAG-F1	62.5 ± 0.3	172.4 ± 8.6	514 ± 25	1120 ± 110	16.82 ± 0.8
CAG-F3	61.8 ± 0.3	177.0 ± 8.8	528 ± 26	1170 ± 120	16.98 ± 0.8
CAG-F5	63.2 ± 0.3	151.3 ± 7.5	450 ± 23	1080 ± 110	14.74 ± 0.7
CAG	62.3 ± 0.3	172.7 ± 8.6	515 ± 25	1350 ± 140	16.29 ± 0.8

In contrast to the heat capacity similarity of the Ω constructs with a F lesion in one of the stem duplex domains, the details of the lesion-induced impact on overall Ω-DNA stability are position dependent. Specifically, the lesion-induced impact depends on whether the lesion is located upstream of the loop and on the same strand as the loop (the CAG-FStem construct), or downstream of the loop and on the opposing strand from the loop (the CTG-FStem construct); again, this energetic distinction may be relevant to their possible differential recognition by the machinery of repair.

When the lesion is positioned upstream and on the loop strand (CAG-FStem), our measurements reveal three consequences (see Figure 2A and data in Table 1A): the overall Ω structure is destabilized (ΔT_m = −8.2 °C); the enthalpy and entropy values for melting the lesion-containing constructs are reduced relative to the unmodified CAG Ω-DNA structure (ΔΔH = −27 kcal mol⁻¹, ΔΔS = −70 cal mol⁻¹ K⁻¹); and an apparent single melting transition is observed, albeit at lower temperature. By contrast, when the lesion is positioned downstream of the loop and on the opposite strand (CTG-FStem), the melting transition visually resolves into two domains. In these circumstances, we list in Table 1A single thermodynamic parameters for the combined two transitions. The lower-temperature melting transition reflects destabilization which is even greater than that induced by the upstream lesion (ΔT_m1 = −30°C). The higher-temperature melting transition reflects a less perturbed domain, exhibiting a thermal stability quite similar to that of the lesion-free construct (ΔT_m2 = +3.6 °C).

Interpretations of the upstream versus downstream position-dependent, lesion-induced differential behavior should take into consideration the following realities. B-DNA helical topology causes the lesion that is 5 base pairs upstream (half a helical turn) to be on the opposite side of the bulge loop domain in the overall Ω DNA helical construct, despite being on the same strand of the structure. By contrast, the opposing strand lesion that is 5 base pairs downstream (half a helical turn) topologically is on the same side as the bulge loop. For molecular interpretations of the data reported here, one must be cognizant of these perhaps counterintuitive topological facts. Another consideration is that Ω-DNA bulge loop constructs resemble imperfect three-way junctions, where one of the arms, namely the bulge loop “arm”, is partially denatured. DNA three-way junctions are known to be stabilized by stacking of two of the three arms to form a continuous helix.^52,53 Such stacking also may influence the observed Ω-DNA differential stabilities. Furthermore, curve fitting of the apparent heat capacity curves allows one to resolve the experimentally observed melting profiles into multiple subtransitions.^54,55 Each resolved subtransition, however, does not necessarily reflect an independently populated discrete ensemble. Accordingly, caution should be exercised when assigning subtransitions to specific conformational states as part of efforts to characterize the energy landscapes of biopolymers. Nevertheless, this deconvolution exercise provides insight into the origins of the lesion-induced alterations in the distribution of states, as noted in the Supporting Information.

Independent of the details of the position-dependent differential behavior we observe, the upstream abasic site and the average impact of the downstream abasic site result in a net destabilization of the Ω duplex structures relative to the corresponding lesion-free construct. This result is consistent with expectations based on our previous studies of the impact of abasic lesions on duplex stability.⁵⁶⁻⁶¹ However, in the Ω-DNA constructs studied here, the F-induced destabilization is greater than that observed when the lesion is present in an otherwise fully bonded Watson−Crick duplex. Such enhanced lesion-induced destabilization in the Ω construct may reflect synergistic energy coupling between the destabilizing influence of the lesion and the proximal destabilizing impact of the loop domain.(62)

Abasic Lesions in the Loop Domains Are Energetically Much Less Perturbing than the Same Lesion in Duplex Domains

Figure 2B shows the experimental heat capacity melting profiles for the Ω-DNA construct with the THF lesion (F) present in one of three positions within the CAG loop domain. The relevant thermodynamic parameters derived by integration of these experimental excess heat capacity curves are listed in Table 1B for each of the Ω-DNA constructs. By contrast to the results observed for F lesions within the stem duplex domains, we find that placing the lesion within the loop does not destabilize the melting transition relative to the unmodified parent Ω-DNA, nor does it alter the heat capacity of the initial states. The thermal and thermodynamic properties of these lesion-containing Ω-DNA constructs are essentially identical to those of the corresponding lesion-free structure, although there is some modest change in shape of the overall melting curves. Specifically, we measure the differences for the lesion at the 5′ end of the loop to be ΔT_m = 0.2 °C, ΔΔH = −0.3 kcal mol⁻¹, and ΔΔS = −1 cal mol⁻¹ K⁻¹, while for the lesion in the middle of the loop we measured the differences to be ΔT_m = −0.5 °C, ΔΔH = +4.3 kcal mol⁻¹, and ΔΔS = +13 cal mol⁻¹ K⁻¹. Interestingly, based on the data listed in Table 1B and the heat capacity curves shown in Figure 2B, when the F lesion is near the 3′ end of the loop, a significant enthalpic destabilization is observed, but it is exactly balanced by a decrease in entropy, resulting in no net T_m shift (ΔT_m = −0.1 °C, ΔΔH = −21.4 kcal mol⁻¹, and ΔΔS = −65 cal mol⁻¹ K⁻¹). The reasons for the difference in thermodynamic impact of F at the 3′ end of the bulge loop compared to the other two loop positions are not known, but it may reflect differential lesion-induced distributions of microstates within the Ω-DNA macrostates, as discussed below.

Origins of Position-Dependent Lesion Impact on Looped Structures

We previously have shown the lesion-free CAG Ω-DNA macrostate to be composed of an ensemble of discrete microstates with significant energy barriers between them.^37,63 We propose here that the F lesion can lead to an altered distribution of these microstates without significantly affecting the ensemble average properties. The absence of a guanine base at a single site may be accommodated within an ensemble of heterogeneous structural and energetic microstates without a net change in global thermodynamics through redistribution between these microstates. In other words, we propose that the Ω-DNA state is sufficiently plastic to accommodate deletion of an individual base without a net change in global energetics.

We previously have shown in the absence of abasic lesions that single-stranded CAG triplet repeat loops form self-structures that enthalpically and entropically stabilize Ω and hairpin DNA structures.^36,39,63 While atomic-level structural information for such CAG self-structure is lacking, it has been argued that CAG repeat structures consist of G·C and C·G base pairs separated by A·A mismatches. This view is based on NMR measurements on isolated (CAG)/(CAG) segments within duplex DNA, and on the known thermodynamic stability of G·C base pairs in duplex DNA.^4,64−74 In this model, deletion of a G base within the loop domain, as we do here with the abasic lesion, should significantly destabilize the Ω-DNA loop, and thereby the entire Ω-DNA construct, particularly since such a “disrupted” nonpairing lesion site would be situated next to an already destabilizing AA mismatch. The fact that we do not observe any net impact of the loop-positioned abasic lesion on overall Ω-DNA thermodynamics (other than a modest modulation in the melting curve shape) suggests that the CAG loop is able to accommodate the lesion without loss of the loop-stabilizing interactions observed in the corresponding lesion-free construct. As a result, our data do not support the “G·C and C·G base pairs separated by A·A mismatches” single-stranded order model of CAG repeats that is popular in the literature. Nevertheless, this base-pairing model may play a role in some of the different microstates populated in the loop, thereby explaining the presence of the relevant fingerprint signals in 1D proton NMR spectra of simple CAG repeats.

In general, depending on where the F lesion is located in the loop, different microstates may be differentially populated, although the ensemble average value could remain essentially constant. Such redistribution between microstates should be reflected in the shape of the calorimetric melting curve, as indeed we observed. The altered distribution of microstates may not be detected in spectroscopic measures of nucleic acid structure, such as CD measurements, due to a lack of resolution and the averaging of the signal. The ability of the Ω-DNA to accommodate base deletions through redistribution between different energetic/structural microstates represents a reasonable working hypothesis, particularly given the repetitive nature of the CAG repeat sequences, the relatively small energy penalties for a plethora of non-Watson−Crick base-pairing arrangements involving A, G, and C bases, and the inherent flexibility of single-stranded loops. The strand exchange reaction from Ω-DNA to complementary duplex discussed in the following section provides additional support for this hypothesis, as does the curve fitting resolution into multiple subtransitions of the experimental heat capacity curves (see Supporting Information).

Abasic Lesions Differentially Modulate Ω-DNA Strand Exchange in a Position-Dependent Manner

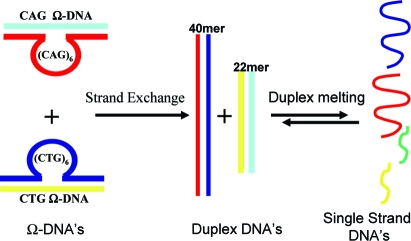
We previously have demonstrated that the lesion-free CAG Ω-DNA construct and its complementary lesion-free CTG Ω-DNA are metastable.^36,37 As shown in Scheme 2, these two complementary lesion-free Ω constructs can undergo thermally induced strand exchange to form fully paired 22mer and 40mer Watson−Crick duplexes.

Scheme 2. Different DNA Conformations and the Transformation between Them.

The corresponding experimental heat capacity melting profiles reflective of these transformations in the presence and in the absence of the lesions located within the stem duplex domains and in the looped domain of the CAG Ω-DNA construct are shown in Figure 3. The same lesion-free CTG Ω-DNA construct is used for all exchange measurements.

Figure 3.

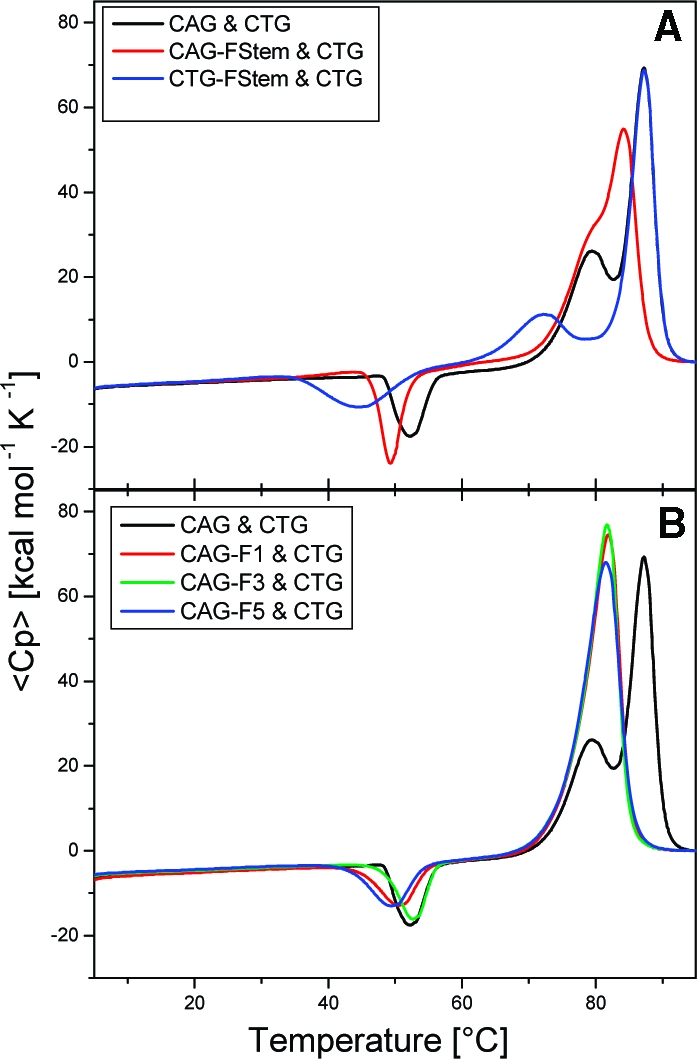
Strand exchange heat capacity profiles of Ω-DNA constructs with and without the F lesion in the stem domains (A) and in the loop domain (B). The excess heat capacity curves were obtained for a 1:1 mixture of the CAG Ω-DNA with and without lesions and its complementary CTG -Ω-DNA. Note the unusual exotherm near 50 °C present in all traces that indicates strand exchange from the metastable Ω-DNA states to the thermodynamically stable duplex states. The conventional endotherms observed at higher temperatures in these traces correspond to the melting of the 22mer and 40mer duplexes that are formed by the exchange process. (A) Strand exchange when the F lesion is located in the duplex domain upstream (red, CAG-FStem) or downstream (blue, CTG-FStem) of the loop domain. For comparison, the strand exchange of the unmodified parent Ω-DNAs is shown in black. (B) Strand exchange when the F lesion is located within the loop domain (red, CAG-F1; green, CAG-F3; blue, CAG-F5). The strand exchange of the unmodified parent Ω-DNAs is shown in black for comparison.

Note the presence in the heat capacity profiles of the exotherms prior to endothermic global duplex melting, consistent with the general behavior observed for the corresponding lesion-free Ω-DNA constructs.^36,37 This exothermic trough reflects the thermally induced strand exchange event between the two complementary metastable Ω-DNA states to form the two thermodynamically more stable Watson−Crick duplexes, which subsequently melt, exhibiting their characteristic endothermic peaks. Using these experimental heat capacity profiles and the differential positions, breadths, and magnitudes of the exothermic peak, we can distinguish between the exchange behavior of those CAG Ω-DNAs which contain the lesion in the Watson−Crick duplex domains and those which contain the lesion in the single-stranded loop domain.

F Lesion in the CAG Ω-DNA Duplex Domains: Position-Dependent Coupling of Strand Exchange with Ω-DNA Melting

When the lesion is downstream of the loop in the CAG Ω-DNA duplex domain, designated as CTG-FStem, strand exchange occurs in a temperature range where a significant fraction of the overall lesion-containing CAG Ω-DNA already has melted, but where melting of the lesion-free complementary CTG Ω-DNA construct has yet to occur. Under such circumstances, the exchange process may be influenced by the properties of the (partially) denatured lesion-containing CAG Ω-DNA state, making this event similar to a strand displacement process, as we previously have reported.(36) This perspective also is consistent with the broad temperature range of strand exchange observed in Figure 3A (the blue exotherm) for the lesion-containing CAG Ω-DNA.

By contrast, when the lesion is positioned upstream of the loop in the CAG duplex domain (CAG-FStem), the exchange transition partially overlaps the global melting of the lesion-containing CAG Ω-DNA construct. As a result of this thermal overlap, one observes apparent coupling between CAG Ω-DNA melting and the overall strand exchange, as reflected by the narrow transition exotherm observed in Figure 3A (the red curve). Collectively, these results suggest that, in addition to lesion-induced alterations (destabilizations) of local Ω-DNA energy minima, the presence of a F lesion in duplex domains of metastable Ω-DNA constructs also modulates the overall energy landscape, influencing the strand exchange trajectory/pathway leading from the metastable Ω-DNA states to the final thermodynamically more stable duplex states.

F Lesion in the Looped Domain: Decoupling of Strand Exchange with Global Ω-DNA Melting

For Ω-DNAs with the F lesion in the loop domain, we find strand exchange to occur below the onset of global melting of the Ω-DNAs. This observation is consistent with an energetic decoupling of these two events, as we have observed for the lesion-free construct.^36,37 We also find the exchange temperature and shape of the exotherm to exhibit subtle but real differences. These differences depend on the position of the F lesion within the loop, although the overall temperature range of strand exchange is similar, particularly compared to the impact of the lesion in the duplex domains. Collectively, these observations suggest that the energy barrier between the metastable Ω-DNA states and the final duplex states is not consequentially altered by the presence of the F lesion within the loop, in contrast to the impact when the lesion is in the duplex domains. We do find, however, that the F lesion impacts the thermal and thermodynamic properties of the lesion-containing duplex products formed by the exchange process. Given that strand exchange occurs from a metastable initial state and is dominated by the necessity to form a stable initiation complex, the energetics of the final state will only impact the overall driving force. This topic will be the subject of a subsequent report.

Below we propose an overall interpretation of the differences just noted for the influence of looped lesions on the exchange temperatures, the thermal ranges, and the shapes of the Ω-DNA exchange exotherms observed in Figure 3B.

Lesion-Induced Microstate Redistribution

Consistent with our previous interpretation of the corresponding lesion-free Ω-DNA construct, we propose that the subtle differences in exchange temperature and shape of the exchange exotherm seen in Figure 3B reflect lesion-induced energetic differences and population redistribution of microstates that make up the metastable Ω-DNA macrostate.(37) We observe that, for the Ω-DNA containing the F lesion near the center of the loop domain, strand exchange occurs at a slightly higher temperature and over a narrower temperature range than strand exchange for those Ω-DNAs containing the F lesion near the 3′ or 5′ end of the loop domain. Perhaps an abasic lesion near the center of a loop domain reduces the number of microstates that can be populated. The centered lesion also may favor the population of the lower energy microstates, resulting in a narrower temperature range during the exchange process at higher temperatures. By contrast, an abasic site either 3′ or 5′ of the center of the loop may increase the number of microstates that can be populated, resulting in an increase in the population of higher energy microstates, thereby giving rise to the experimental outcomes we observe. Collectively, these results provide further evidence for the roughness of the Ω-DNA energy landscape and the distribution of energetically/structurally discrete microstates that make up the Ω-DNA macrostate. In the following section, we discuss the biological implications of our observations.

Biological Implications

We report here a position-dependent, differential impact of abasic lesions on the population of slipped DNA structures. Replacement of a guanosine by an abasic lesion within a double-helical domain destabilizes the duplex state, either for the Ω constructs studied here or for a fully bonded duplex (unpublished results). By contrast, replacement of a guanosine by an abasic lesion within a CAG single-stranded, bulge loop domain does not alter the stability of the Ω DNA state. As a consequence of this differential impact, the presence of an abasic lesion favors the CAG bulge loop state relative to the duplex state, thereby increasing the probability that such “damaged” repeat sequences form slipped DNA structures. This observation may, in part, explain why activation of BER processes results in increases in DNA expansion.(17)

In general, within an extended iterative sequence, migration of a looped domain can occur. When loop migration encounters an abasic lesion site, our data demonstrate that the lesion-containing looped structures will be energetically favored over those with the lesions in the adjacent duplex domains. In other words, abasic sites create thermodynamic sinks for migrating loops that trap or enhance the occupancy of slipped, bulged structures. In addition, the presence of abasic lesions in the flanking duplex domains produces regions of instability which, as we previously have shown, provide sites for enhanced protein binding and, by extension, BER activity.^75,76 We also note that the interactions of proteins (e.g., pol β) on regions immediately upstream or downstream of repeat domains may further enhance repeat loop formation through mechanical stress on the DNA helix.⁷⁷⁻⁷⁹

The results presented here reinforce the notion that CAG repeat loops are energetically and perhaps structurally heterogeneous, thereby providing a challenge for proteins that have evolved to deal with double-stranded substrates. Our proposal that an abasic lesion within CAG repeat loops results in an altered distribution of microstates may be biologically relevant, since some of these energetic/structural microstates could pose challenges to or opportunities for DNA processing enzymes. A lesion-induced increase in population of these states may lead to erroneous expansion of the repeat sequences, the hallmark of DNA expansion diseases.

The results reported here also reinforce our previous proposal of a rough energy landscape for triple repeat DNAs and the potential impact of such rough landscapes on biological processes.(37) In the aggregate, our data provide a potential rationale for the in vivo observation of BER-induced enhancement of DNA expansion.(17)

Concluding Remarks

To probe potential origins for the observation of BER-induced DNA expansion, we have studied the impact of inserting a BER intermediate (an abasic site) either adjacent to or within an ordered bulge loop triplet repeat domain embedded within a DNA duplex structure. Specifically, we replaced select guanosine residues with an analogue of an abasic site, since such sites are the common intermediate created by initial glycosylase activity in BER pathways.^{20,24,27,29,80} Using calorimetric and spectroscopic techniques, we found that a single guanosine-to-abasic site substitution in the duplex regions of a bulge loop DNA structure, either 5′ or 3′ to a (CAG)₆ repeat loop, causes substantial overall destabilization, with a secondary dependence on the specific location of the lesion. By contrast, a guanosine-to-abasic site substitution within the single-stranded, triplet repeat loop domain has relatively little, if any, impact on the stability of the overall DNA structure, suggestive of energetic plasticity for the loop permitting accommodation of this site alteration in a free energy neutral fashion. As a result of these differential effects, the presence of an abasic lesion in the bulged domain favors formation of slipped/looped DNA structures. It has been suggested that expansion involves the transient formation of such non-native slipped DNA structures within the triplet repeat domain that are incorrectly processed during de novo DNA synthesis.^{6−11,66,81,82} Consequently, the BER machinery of repair may be influenced by such differential abasic-induced energetic alterations in the properties of regions proximal to and/or within triplet repeat domains, thereby potentially modulating levels of DNA expansion.

Supporting Information Available

Description of the model used to fit the experimental heat capacity curves and the corresponding results. This material is available free of charge via the Internet at http://pubs.acs.org.