Collective dynamics of social annotation

Abstract

The enormous increase of popularity and use of the worldwide web has led in the recent years to important changes in the ways people communicate. An interesting example of this fact is provided by the now very popular social annotation systems, through which users annotate resources (such as web pages or digital photographs) with keywords known as “tags.” Understanding the rich emergent structures resulting from the uncoordinated actions of users calls for an interdisciplinary effort. In particular concepts borrowed from statistical physics, such as random walks (RWs), and complex networks theory, can effectively contribute to the mathematical modeling of social annotation systems. Here, we show that the process of social annotation can be seen as a collective but uncoordinated exploration of an underlying semantic space, pictured as a graph, through a series of RWs. This modeling framework reproduces several aspects, thus far unexplained, of social annotation, among which are the peculiar growth of the size of the vocabulary used by the community and its complex network structure that represents an externalization of semantic structures grounded in cognition and that are typically hard to access.

The rise of Web 2.0 has dramatically changed the way in which information is stored and accessed and the relationship between information and online users. This is prompting the need for a research agenda about “web science,” as put forward in ref. 1. A central role is played by user-driven information networks, i.e., networks of online resources built in a bottom-up fashion by web users. These networks entangle cognitive, behavioral and social aspects of human agents with the structure of the underlying technological system, effectively creating technosocial systems that display rich emergent features and emergent semantics (2, 3). Understanding their structure and evolution brings forth new challenges.

Many popular web applications are now exploiting user-driven information networks built by means of social annotations (4, 5). Social annotations are freely established associations between web resources and metadata (keywords, categories, ratings) performed by a community of web users with little or no central coordination. A mechanism of this kind that has swiftly become well established is that of collaborative tagging (see www.adammathes.com/academic/computer-mediated-communication/folksonomies.html) (6), whereby web users associate freeform keywords—called “tags”—with online content such as web pages, digital photographs, bibliographic references, and other media. The product of the users' tagging activity is an open-ended information network—commonly referred to as “folksonomy”—which can be used for navigation and recommendation of content and has been the object of many recent investigations across different disciplines (7, 8). Here, we show how simple concepts borrowed from statistical physics and the study of complex networks can provide a modeling framework for the dynamics of collaborative tagging and the structure of the ensuing folksonomy.

Two main aspects of the social annotation process, so far unexplained, deserve special attention. One striking feature is the so-called Heaps' law (9) (also known as Herdan's law in linguistics), originally studied in information retrieval for its relevance for indexing schemes (10). Heaps' law is an empirical law that describes the growth in a text of the number of distinct words as a function of the number of total words scanned. It describes, thus, the rate of innovation in a stream of words, where innovation means the adoption for the first time in the text of a given word. This law, also experimentally observed in streams of tags, consists of a power law with a sublinear behavior (8, 11). In this case, the rate of innovation is the rate of introduction of new tags, and a sublinear behavior corresponds to a rate of adoption of new words or tags decreasing with the total number of words (or tags) scanned. Most existing studies about Heaps' law, either in information retrieval or in linguistics, explained it as a consequence of the so-called Zipf's law (12) [see ref. 10 and supporting information (SI)]. It would instead be highly desirable to have an explanation for it relying only on very basic assumptions on the mechanisms behind social annotation.

Another important way to analyze user-driven information networks is given by the framework of complex networks (13–15). These structures are, indeed, user-driven information networks (16), i.e., networks linking (for instance) online resources, tags, and users, built in a bottom-up fashion through the uncoordinated activity of thousands to millions of web users. We shall focus in particular on the particular structure of the so-called cooccurrence network. The cooccurrence network is a weighted network where nodes are tags, and 2 tags are linked if they were used together by at least 1 user, the weight being larger when this simultaneous use is shared by many users. Correlations between tag occurrences are (at least partially) an externalization of the relations between the corresponding meanings (17, 18) and have been used to infer formal representations of knowledge from social annotations (19). Notice that cooccurrence of 2 tags is not a priori equivalent to a semantic link between the meanings/concepts associated with those tags and that understanding what cooccurrence precisely means, in terms of semantic relations of the cooccurring tags, is an open question that is investigated in more applied contexts (20, 21).

On these aspects of social annotation systems, a certain number of stylized facts about, e.g., tag frequencies (6, 8) or the growth of the tag vocabulary (11), have been reported, but no modeling framework exists that can naturally account for them while reproducing the cooccurrence network structure. Here, we ask whether the structure of the cooccurrence network can be explained in terms of a generative model and how the structure of the experimentally observed cooccurrence network is related to the underlying hypotheses of the modeling scheme. We show in particular that the idea of social exploration of a semantic space has more than a metaphorical value and actually allows us to reproduce simultaneously a set of independent correlations and fine observables of tag cooccurrence networks as well as robust stylized facts of collaborative tagging systems.

User-Driven Information Networks.

We investigate user-driven information networks using data from 2 social bookmarking systems: del.icio.us^† and BibSonomy.^‡ Del.icio.us is a very popular system for bookmarking web pages and pioneered the mechanisms of collaborative tagging. It hosts a large body of social annotations that have been used for several scientific investigations. BibSonomy is a smaller system for bookmarking bibliographic references and web pages (22). Both del.icio.us and BibSonomy are broad folksonomies (see www.personalinfocloud.com/2005/02/), in which users provide metadata about preexisting resources and multiple annotations are possible for the same resource, making the ensuing tagging patterns truly “social” and allowing their statistical characterization. A more detailed description of the datasets is given in the SI.

A single user annotation, also known as a post, is a triple of the form (u, r, T), where u is a user identification, r is the unique identification of a resource (a URL pointing to a web page, for the systems under study), and T = {t₁, t₂, … } is a set of tags represented as text strings. We define the tag cooccurrence network based on post cooccurrence. That is, given a set of posts, we create an undirected and weighted network where nodes are tags and 2 tags, t₁ and t₂ are connected by an edge if and only if there exists 1 post in which they were used in conjunction. The weight w_t1t2 of an edge between tags t₁ and t₂ can be naturally defined as the number of distinct posts where t₁ and t₂ cooccur. This construction reflects the existence of semantic correlations between tags and translates the fact that these correlations are stronger between tags cooccurring more frequently. We emphasize once again that the cooccurrence network is an externalization of hidden semantic links and therefore distinct from underlying semantic lexicons or networks.

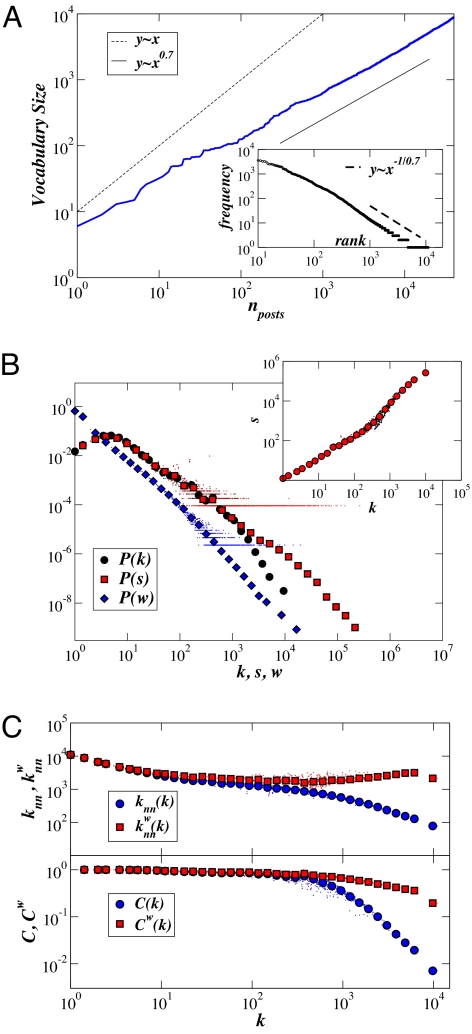
The study of the global properties of the tagging system, and in particular of the global cooccurrence network, is of interest but mixes potentially many different phenomena. We therefore consider a narrower semantic context, defined as the set of posts containing 1 given tag. We define the vocabulary associated with a given tag t* as the set of all tags occurring in a post together with t*, and the time is counted as the number of posts in which t* has appeared. The size of the vocabulary follows a sublinear power-law growth (Fig. 1), similar to the Heaps' law (9) observed for the vocabulary associated with a given resource and for the global vocabulary (11). Fig. 1 also displays the main properties of the cooccurrence network, as measured by the quantities customarily used to characterize statistically complex networks and to validate models (14, 15). These quantities can be separated in 2 groups. On the one hand, they include the distributions of single node or single link quantities, whose investigations allow one to distinguish between homogeneous and heterogeneous systems. Fig. 1 shows that the cooccurrence networks display broad distributions of node degrees k_t (number of neighbors of node t), node strengths s_t (sum of the weights of the links connected to t, s_t = Σ_t′w_tt′), and link weights. The average strength s(k) of vertices with degree k, s(k) = 1/N_kΣ_t/kt=ks_t, where N_k is the number of nodes of degree k, also shows that correlations between topological information and weights are present. On the other hand, these distributions by themselves are not sufficient to fully characterize a network, and higher-order correlations have to be investigated. In particular, the average nearest-neighbor degree of a vertex t, k_nn,t = 1/k_tΣ_{t′∈𝒱(t)}k_t′, where 𝒱(t) is the set of t's neighbors, gives information on correlations between the degrees of neighboring nodes. Moreover, the clustering coefficient c_t = e_t/(k_t(k_t − 1)/2) of a node t measures local cohesiveness through the ratio between the number e_t of links between the k_t neighbors of t and the maximum number of such links (23). The functions k_nn(k) = 1/N_kΣ_t/kt=kk_nn,t and C(k) = 1/N_kΣ_t/kt=kc_t are convenient summaries of these quantities, that can also be generalized to include weights [see SI for the definitions of k_nn^w(k) and C^w(k)]. Fig. 1 shows that broad distributions and nontrivial correlations are observed. All of the measured features are robust across tags within 1 tagging system and across the tagging systems we investigated (see SI).

Fig. 1.

Data corresponding to the posts containing the tag Folksonomy in del.icio.us. (A) Heaps' law: growth of the vocabulary size associated with the tag t* = Folksonomy, measured as the number of distinct tags cooccurring with t*, as a function of the number n_posts of posts containing t*. The dotted line corresponds to a linear growth law, whereas the continuous line is a power-law growth with exponent 0.7. (Inset) Frequency-rank plot for the tags. The dashed line corresponds to a power law −1.42 ≃ −1./0.7. (B and C) Main properties of the cooccurrence network of the tags cooccurring with the tag Folksonomy in del.icio.us, built as described in User-Driven Information Networks. (B) Broad distributions of degrees k, strengths s and weights w are observed. The Inset shows the average strength of nodes of degree k, with a superlinear growth at large k. (C) Weighted (k_nn^w) and unweighted (k_nn) average degree of nearest neighbors (Upper) and weighted (C^w) and unweighted (C) (Lower) average clustering coefficients of nodes of degree k. k_nn displays a disassortative trend, and a strong clustering is observed. At small k, the weights are close to 1 (s(k) ≈ k, see B Inset), and k_nn^w ≈ k_nn, C^w ≈ C. At large k instead, k_nn^w > k_nn and C^w > C, showing that large weights are preferentially connecting nodes with large degree: Large-degree nodes are joined by links of large weight, i.e., they cooccur frequently. In B and C both raw and logarithmically binned data are shown.

Modeling Social Annotation.

The observed features are emergent characteristics of the uncoordinated action of a user community, which call for a rationalization and for a modeling framework. We now present a simple mechanism able to reproduce the complex evolution and structure of the empirical data.

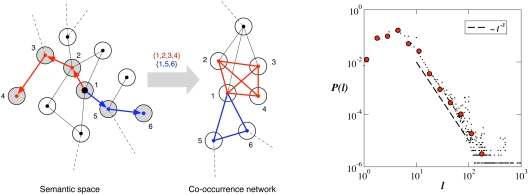
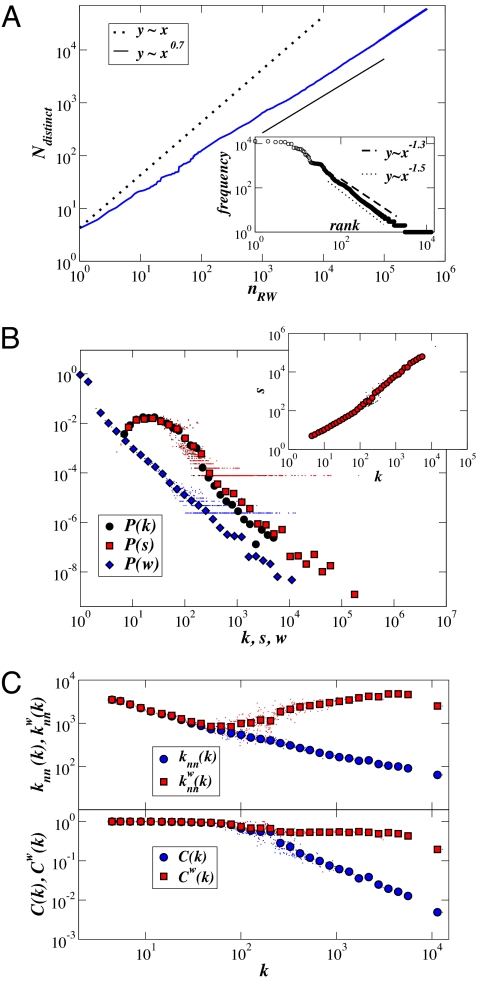
The fundamental idea underlying our approach, illustrated in Fig. 2, is that a post corresponds to a random walk (RW) of the user in a “semantic space” modeled as a graph. Starting from a given tag, the user adds other tags, going from 1 tag to another by semantic association. It is then natural to picture the semantic space as network-like, with nodes representing tags, and links representing the possibility of a semantic link (24). A precise and complete description of such a semantic network being out of reach, we make very general hypothesis about its structure and we have checked the robustness of our results with respect to different plausible choices of the graph structure (24). Nevertheless, as we shall see later on, our results help fixing some constraints on the structural properties of such a semantic space: it should have a finite average degree together with a small graph diameter, which ensures that RWs starting from a fixed node and of limited length can potentially reach all nodes of the graph. In this framework, the vocabulary cooccurring with a tag is associated with the ensemble of nodes reached by successive RWs starting from a given node, and its size with the number of distinct visited nodes, N_distinct, which grows as a function of the number n_RW of performed RWs. Empirical evidence on the distribution of post lengths (Fig. 2) suggests that one consider RWs of random lengths, distributed according to a broad law (see SI for the case of walks of fixed length). Analytical and numerical investigations show that sublinear power law-like growths of N_distinct are then generically observed, mimicking the Heaps' law observed in tagging systems (Fig. 3 and SI).

Fig. 2.

(Left) Illustration of the proposed mechanism of social annotation. The semantic space is pictured as a network in which nodes represent tags, and a link corresponds to the possibility of a semantic association between tags. A post is then represented as a RW on the network. Successive RWs starting from the same node allow the exploration of the network associated with a tag (here pictured as node 1). The artificial cooccurrence network is built by creating a clique between all nodes visited by a RW. (Right) Empirical distribution of posts' lengths P(l). A power-law decay ≈l⁻³ (dashed line) is observed.

Fig. 3.

Synthetic data produced through the proposed mechanism. (A) Growth of the number of distinct visited sites as a function of the number of RWs performed on a Watts–Strogatz network (see SI) of size 5 × 10⁴ nodes and average degree 8, rewiring probability P = 0.1. Each RW has a random length l taken from a distribution P(l) ≈ l⁻³. The dotted line corresponds to a linear growth law, whereas the continuous line is a power-law growth with exponent 0.7. (Inset) Frequency-rank plot. The dashed and dotted line have slope −1.3 and −1.5, respectively. (B and C) Properties of the synthetic cooccurrence network obtained for n_RW = 5 × 10⁴, to be compared with the empirical data of Fig. 1.

Synthetic Cooccurrence Networks.

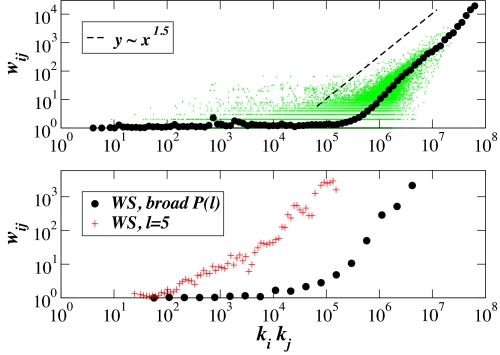
Vocabulary growth is only one aspect of the dynamics of tagging systems. Networks of cooccurrence carry much more information and exhibit very specific features (Fig. 1). Our approach allows one to construct synthetic cooccurrence networks: We associate to each RW a clique formed by the nodes visited (see Fig. 2) and consider the union of the n_RW such cliques. Moreover, each link i–j built in this way receives a weight equal to the number of times nodes i and j appear together in a RW. This construction mimics precisely the construction of the empirical cooccurrence network and reflects the idea that tags that are far apart in the underlying semantic network are visited together less often than tags that are semantically closer. Figs. 3 and 4 show how the synthetic networks reproduce all statistical characteristics of the empirical data (Fig. 1), both topological and weighted, including highly nontrivial correlations between topology and weights. Fig. 4 in particular explores how the weight w_ij of a link is correlated with its extremities' degrees k_i and k_j. The peculiar shape of the curve can be understood within our framework. First, the broad distribution in l is responsible for the plateau ≈1 at small values of k_ik_j, because it corresponds to long RWs that occur rarely and visit nodes that will be typically reached a very small number of times (hence small weights). Moreover, w_ij ≈ (k_ik_j)^a at large weights. Denoting by f_i the number of times node i is visited, w_ij ≈ f_if_j in a mean-field approximation that neglects correlations. On the other hand, k_i is by definition the number of distinct nodes visited together with node i. Restricting the RWs to the only processes that visit i, it is reasonable to assume that such sampling preserves Heaps' law, so that k_i ∝ f_i^α, where α is the growth exponent for the global process. This leads to w_ij ≈ (k_ik_j)^a with a = 1/α. Because α ≃ 0.7–0.8, we obtain a close to 1.3–1.5, consistently with the numerics.

Fig. 4.

Correlations between the weights of the links in the cooccurrence networks and the degrees of the links' endpoints, as measured by plotting the weight w_ij of a link i–j versus the product of the degrees k_ik_j. (Upper) Cooccurrence network of the tag Folksonomy of del.icio.us; each green dot corresponds to a link; the black circles represent the average over all links i–j with given product k_ik_j. (Lower) Synthetic cooccurrence networks obtained from n_RW = 5 × 10⁴ RWs performed on a Watts–Strogatz network of 10⁵ nodes. The black circles correspond to RWs of random lengths distributed according to P(l) ≈ l⁻³ and the red crosses to fixed-length RWs (l = 5).

Strikingly, the synthetic cooccurrence networks reproduce also other, more subtle observables, such as the distribution of cosine similarities between nodes. In a weighted network, the similarity of 2 nodes i₁ and i₂ can be defined as

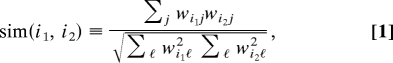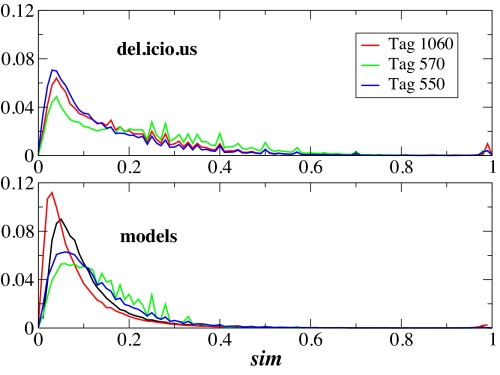
which is the scalar product of the vectors of normalized weights of nodes i₁ and i₂. This quantity, which measures the similarities between neighborhoods of nodes, contains semantic information that can be used to detect synonymy relations between tags or to uncover “concepts” from social annotations (20). Fig. 5 shows the histograms of pairwise similarities between nodes in real and synthetic cooccurrence networks. The distributions are very similar, with a skewed behavior and a peak for low values of the similarities. In the SI, we report the similarity distributions for other tags and provide a more detailed discussion on their properties.

Fig. 5.

Distribution of tag similarities for real (Upper) and synthetic (Lower) cooccurrence networks. For del.icio.us, the tag number represents its popularity rank in the database. For the synthetic cooccurrence networks, the different curves correspond to different underlying networks on which the RWs are performed (see SI).

Whereas the data shown in Figs. 3 and 4 correspond to a particular example of underlying network (a Watts–Strogatz network, see ref. 23 and SI), taken as a sketch for the semantic space, we investigate in the SI the dependence of the synthetic network properties on the structure of the semantic space and on the other parameters, such as n_RW or the distribution of the RW lengths. Interestingly, we find an overall extremely robust behavior for the diverse synthetic networks, showing that the proposed mechanism reproduces the empirical data without any need for strong hypotheses on the semantic space structure. The only general constraints implied by the mechanism proposed here are the existence of an underlying semantic graph with a small diameter and a finite average degree (RWs on a fully connected graph would not work, for instance) and a broad distribution of post lengths. This lack of strong constraints on the precise structure of the underlying semantic network is actually a remarkable feature of the proposed mechanism. The details of the underlying network will unavoidably depend on the context, namely on the specific choice of the central tag t*, and the robustness of the generative model matches the robustness of the features observed in cooccurrence networks from real systems. Of course, given an empiric cooccurrence network, a careful simultaneous fitting procedure of the various observables would be needed to choose the most general class of semantic network structures that generate that specific network by means of the mechanism introduced here. This delicate issue goes beyond the goal of this article and raises the open question of the definition of the minimal set of statistical observables needed to specify a graph (25).

Conclusions

Investigating the interplay of human and technological factors in user-driven systems is crucial to understand the evolution and the potential impact these systems will have on our societies. Here, we have shown that sophisticated features of the information networks stemming from social annotations can be captured by regarding the process of social annotation as a collective exploration of a semantic space, modeled as a graph, by means of a series of RWs. The proposed generative mechanism naturally yields an explanation for the Heaps' law observed for the growth of tag vocabularies. The properties of the cooccurrence networks generated by this mechanism are robust with respect to the details of the underlying graph, provided it has a small diameter and a small average degree. This mirrors the robustness of the stylized facts observed in the experimental data, across different systems.

Networks of resources, users, and metadata such as tags have become a central collective artifact of the information society. These networks expose aspects of semantics and of human dynamics, and are situated at the core of innovative applications. Because of their novelty, research about their structure and evolution has been mostly confined to applicative contexts. The results presented here are a definite step toward a fundamental understanding of user-driven information networks that can prompt interesting developments, because they involve the application of recently developed tools from complex networks theory to this new domain. An open problem, for instance, is the generalization of our modeling approach to the case of the full hypergraph of social annotations, of which the cooccurrence network is a projection. Moreover, user-driven information networks lend themselves to the investigation of the interplay between social behavior and semantics, with theoretical and applicative outcomes such as node ranking (i.e., for search and recommendation), detection of nonsocial behavior (such as spam), and the development of algorithms to learn semantic relations from a large-scale dataset of social annotations.