Temporal lenses for attosecond and femtosecond electron pulses

Abstract

Here, we describe the “temporal lens” concept that can be used for the focus and magnification of ultrashort electron packets in the time domain. The temporal lenses are created by appropriately synthesizing optical pulses that interact with electrons through the ponderomotive force. With such an arrangement, a temporal lens equation with a form identical to that of conventional light optics is derived. The analog of ray diagrams, but for electrons, are constructed to help the visualization of the process of compressing electron packets. It is shown that such temporal lenses not only compensate for electron pulse broadening due to velocity dispersion but also allow compression of the packets to durations much shorter than their initial widths. With these capabilities, ultrafast electron diffraction and microscopy can be extended to new domains,and, just as importantly, electron pulses can be delivered directly on an ultrafast techniques target specimen.

With electrons, progress has recently been made in imaging structural dynamics with ultrashort time resolution in both microscopy and diffraction (ref. 1 and references therein). Earlier, nuclear motions in chemical reactions were shown to be resolvable on the femtosecond (fs) time scale using pulses of laser light (ref. 2 and references therein), and the recent achievement of attosecond (as) light pulses (for recent reviews, see refs. 3–6) has opened up this temporal regime for possible mapping of electron dynamics. Electron pulses of femtosecond and attosecond duration, if achievable, are powerful tools in imaging. The “electron recombination” techniques used to generate such attosecond electron pulses require the probing electron to be created from the parent ions (to date no attosecond electron pulses have been delivered on an arbitrary target) and for general applications it is essential that the electron pulse be delivered directly to the specimen.

In ultrafast electron microscopy (UEM) (7), the electron packet duration is determined by the initiating laser pulse, the dispersion of the electron packet due to an initial energy spread and electron-electron interactions (see, e.g., ref. 8). Because packets with a single electron can be used to image (1, 7), and the initiating laser pulse can in principle be made very short (<10 fs), the limiting factor for the electron pulse duration is the initial energy spread. In photoelectron sources this spread is primarily due to the excess energy above the work function of the cathode (8), and is inherent to both traditional photocathode sources (9) and optically induced field emission sources (10–13). Energy-time uncertainty will also cause a measurable broadening of the electron energy spread, when the initiating laser pulse is decreased below ≈10 fs. For ultrafast imaging techniques to be advanced into the attosecond temporal regime, methods for dispersion compensation and new techniques to further compress electron pulses to the attosecond regime need to be developed.

A recent article by Baum and Zewail (14) has proposed a new technique for compressing free electron packets, from durations of hundreds of femtoseconds to tens of attoseconds, using spatially dependent ponderomotive potentials. The numerical results showed that a train of attosecond pulses can be created and used in ultrafast electron imaging. Because they are generated independent of the target they can be delivered to a specimen for studies of transient structures and electronic excitations on the attosecond time scale. In reference (14), the proposed compression concept was examined using numerical, electron trajectory calculations. The deflection of electrons [as in the Kapitza–Dirac effect (15)] by the ponderomotive potential of intense lasers (16) and the diffraction (17) of electrons in standing waves of laser light have been observed, and so is the possibility (described through computer modeling) of spatial/temporal focusing with combined time-dependent electric and static magnetic fields (18).

This article develops the “temporal lens” description that analytically expresses how ponderomotive compression can be used to both compensate for the dispersion and magnify (in this case compress) the temporal duration of electron packets. We obtain simple lens equations that have analogies in optics and the results of “electron ray optics” of temporal lenses reported here are entirely consistent with the findings of ref. 14, but now allow for analytical expressions and for the design of different schemes using geometrical optics. Here, we consider 2 types of temporal lenses: thin and thick.

For the realization of the temporal thin lens, a laser beam with a Laguerre–Gaussian transverse mode, radial index ρ = 0 and azimuthal index l = 0 [or, in common nomenclature, a “donut” mode (19–21)], is used. In the center of the donut mode, electrons will experience a spatially varying ponderomotive potential (intensity) that is approximately parabolic. This potential corresponds to a linear spatial force that, for chirped electron pulses, can lead to compression from hundreds of femtoseconds to <10 fs. The second type, that of a thick lens, which is the concept outlined in ref. 14, is based on the use of 2 counterpropagating laser beams to produce a spatially dependent standing wave that copropagates with the electrons. A train of ponderomotive potential wells are produced at the nodes of the standing wave, leading to compression but now with much “tighter focus” (thick lens). Because the electron copropagates with the laser fields the velocity mismatch is no longer a problem (14). Here, analytical expressions are derived showing that this lens has the potential to reach foci with attosecond duration, in agreement with the results of ref. 14. Finally, we discuss methods for creating tunable standing waves for attosecond pulse compression, and techniques for measuring the temporal durations of the compressed pulses. Space-charge dispersed packets of electrons that have a linear spatial velocity chirp (22, 23) may also be compressed with the temporal lenses described here.

Results and Discussion

Preliminaries: Temporal Lens Concepts.

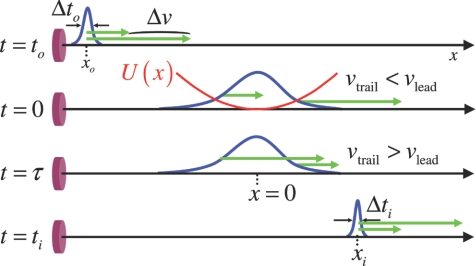
All electron sources, both cw and pulsed, have an initial energy spread. For pulsed electron sources this is particularly relevant as electron packets created in a short time disperse as they propagate. The initial energy spread leads to an initial spread in velocities. These different velocities cause the initial packet to spread temporally, with the faster electrons traveling a further distance and the slower electrons traveling a shorter distance in a given amount of time. The dispersion leads to a correlation between position (along the propagation direction) and electron velocity (see Fig. 1). The linear spatial velocity “chirp” can be corrected for with a spatially dependent linear impulsive force (or a parabolic potential). Thus, if a pulsed, spatially dependent parabolic potential can be made to coincide appropriately with the dispersed electron packet, the slow trailing electrons can be sped up and the faster leading electrons can be slowed down. The trailing electrons, now traveling faster, can catch the leading electrons and the electron pulse will thus be compressed.

Fig. 1.

Dispersion of an ultrashort electron packet. At t = t_o, the packet is created from a photocathode and travels with a velocity v₀. As it propagates along the x axis it disperses, with the faster electrons traveling further, and the slower ones trailing for a given propagation time t. At t = 0 a parabolic potential is pulsed on, giving an impulsive “kick” to the dispersed electron packet. After the potential is turned off, t > τ, the trailing electrons now have a greater velocity than the leading electrons. After a propagation time t = t_i, the pulse is fully compressed.

Consider a packet of electrons, propagating at a speed v₀ along the x axis, with a spread in positions of Δx_o = v₀Δt_o, at time t = t_o; see Fig. 1. At t = 0, a potential of the form U(x) = ½Kx² interacts with the electron packet for a duration τ in the lab frame. The waist, or spatial extent of the potential (temporal lens) is chosen to be w, whereas the duration τ is chosen such that it is short compared with w/v₀. When this condition is met the impulse approximation holds, and the change in velocity is Δv = −τ/m(dU(x)/dx) = −τKx/m, for x <w, where m is the electron mass. After the potential is turned off, t>τ, the electrons will pass through the same position, x_f − x = (v₀ +Δv)t_f, at the focal time t_f = −x/Δv = m/(Kτ). To include an initial velocity spread around v₀ (due to an initial ΔE), consider electrons that all emanate from a source located at a fixed position on the x axis. An electron traveling exactly at v₀ will take a time t₀ to reach the center of the potential well at x = 0. Electrons leaving the source with other velocities v₀+v_k will reach a location x = v_kt_o at t = 0 (Fig. 2). The image is formed at a location where electrons traveling with a velocity v₀ and a velocity v₀ + v_k intersect, this is, when v₀t_i = x + (v₀ + Δv + v_k)t_i. The image time t_i is then t_i = −x/(Δv + v_k).

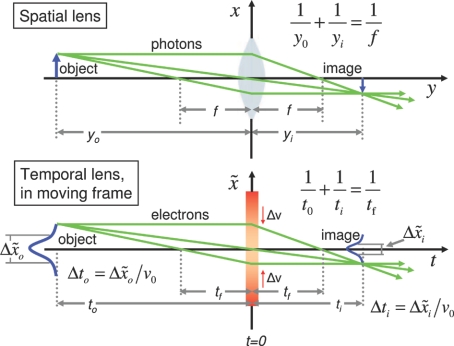
Fig. 2.

Ray diagrams for spatial and temporal lenses. (Upper) Depicts 3 primary rays for an optical thin spatial lens. The object is located at y_o, and the spatial lens has a focal length, f. A real image of the object is created at the image plane, position y_i. (Lower) Ray diagram for a temporal thin lens. The diagram is drawn in a frame moving with the average speed v₀ of the electron packet. The slopes of the different rays in the temporal diagram correspond to different initial velocities that are present in the electron packet. As shown in the diagram a temporal image of the original electron packet is created at the image time t_i. The initial packet (object) is created at a time t_o with Δt_o = Δx_o/v₀, where the spatial extend of the pulse is directly related to the temporal duration of the object. The lens is pulsed on at t = 0 and the temporal focal length of the lens is t_f. The lens represents the ponderomotive potential and in this case is on for the very short time τ.

For the object time, t_o = x/v_k, image time t_i = −x/(Δv + v_k) and the focal time t_f = −x/Δv, the temporal lens equation holds,

Ray tracing for optical lenses is often used to visualize how different ray paths form an image, and is also useful for visualizing how temporal lenses work, see Fig. 2. As derived in later sections the magnification M is defined as the ratio of the electron pulse duration (Δt_i) at the image position to the electron pulse duration (Δt_o), and is directly proportional to the ratio of the object and image times (−t_i/t_o) and distances (−x_i/x_o).

Femtosecond Thin Lens.

In polar coordinates a Laguerre–Gaussian (LG₀¹) mode has a transverse intensity profile given by, I(r,ϕ) = I₀exp (1)2r²exp(−2(r/w)²)/w² where w is the waist of the focus and I₀ the maximum intensity (19–21). This “donut” mode has an intensity maximum located at r = $\sqrt{2}$|w|/2 with a value of I₀ = 2E_P$\sqrt{\ln 2/{\pi }^3}$/(w²τ) where E_P is the energy of the laser pulse and τ is the full-width-at-half-maximum of the pulse duration, assuming a Gaussian temporal profile given by exp(−4ln2(t/τ)²). The ponderomotive energy U_P(x) is proportional to intensity (24),

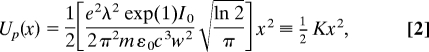where m is the electron mass, e is the electron charge and λ the central wavelength of the laser radiation and replacing r with x. Near the center of the donut mode focus (or x ≪ w) the intensity distribution is approximately parabolic, and hence the ponderomotive energy near the donut center is also parabolic. In analogy with a mechanical harmonic oscillator, the quantity in the square brackets of Eq. 2 can be referred to as the stiffness K; it has units of J/m² = N/m, and at 800 nm has the numerical value of, K≈3.1 × 10⁻³⁶E_P/(w⁴τ). For this parabolic approximation to be applicable, the spatial extent of the dispersed electron pulse, at t = 0, Δx (0) = v₀Δt_o + Δv_ot_o must be much smaller than the laser waist, where the object velocity spread is Δv_o = ΔE/$\sqrt{2mE}$ (8).

The effect of this parabolic potential on an ensemble of electrons emitted from a source will now be analyzed (for detailed derivation, see SI Appendix). The velocity distribution of the ensemble is centered around v₀, with an emission time distribution centered on −t_o, where all electrons are emitted from the same location x_o = −v₀t_o. Assuming a single donut-shaped laser pulse is applied at t = 0, and centered at x = 0, the electron ensemble is then influenced by the potential U(x) = (1/2)Kx². The k^th electron in the ensemble has an initial velocity v₀ + v_k and emission time −t_o + t_k. Using a Galilean transformation to a frame moving with velocity v₀, the propagation coordinate x (lab frame) is replaced with the moving frame coordinate x̃ = x − v₀t. At t = 0 the potential exists for the ultrashort laser pulse duration τ, giving the electron an impulse (or ‘kick’) dependent on its instantaneous position in the parabolic potential. In both frames, the position of the electron at t = 0 is x_k (0) = x̃_k (0) −v₀t_k + v_kt_o − v_kt_k, where x_k(t) and x̃_k(t) are in the lab and moving frames, respectively. Using the impulse approximation the electron trajectory immediately after the potential is turned off becomes,

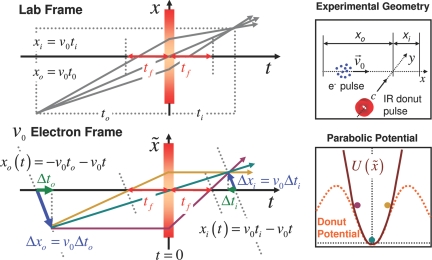
where t_f = m/(Kτ) is the focal time. The electron trajectories, before and after t = 0, can be plotted in both frames to give the equivalent of a ray diagram, Fig. 3. Electrons emitted at the same time, i.e., t_k = 0, but with different velocities, will meet at the image position, x̃_k = 0 in the moving frame at the image time t_i. The image time is found by setting x̃_k(t_i) = 0, from Eq. 3, with t_k = 0, x̃_k(t_i) = v_kt_i + v_kt_o(1 − t_i/t_f) = 0, which is equivalent to the lens equation, Eq. 1: t_o⁻¹ + t_i⁻¹ = t_f⁻¹.

Fig. 3.

Thin lens temporal ray diagrams for the lab and copropagating frames. (Upper Left) Ray diagram drawn in the lab frame showing how different initial velocities can be imaged to a single position/time. The gray lines are rays representing electrons with different velocities. (Lower Left) Ray diagram drawn in a frame moving with the average velocity v₀ of the electron packet. The rays represent velocities of v₀/67, v₀/100, and 0. In the copropagating frame, the relationship between Δt_o and Δt_i can be visualized as Δt_i = −Δt_ot_i/t_o. One major difference between the lab frame and the moving frame is that in the latter the position of the object and image are moving. The lines representing the object and the image positions are drawn with slopes of −v₀. (Upper Right) Experimental geometry for the implementation of a thin temporal lens. Note that the laser pulse and electron packet propagate perpendicular to each other, and that the interception point between the electrons and photons is at x = 0 and t = 0. (Lower Right) Shows how the parabolic (idealized) potential compares to the experimentally realizable donut potential. The colored dots indicate the position of electrons following the rays indicated in Lower Left.

An expression for the magnification can be obtained when electrons that are emitted at different times t_k and different velocities v_k are considered (see SI Appendix for detailed derivation). If the magnification is defined as M = −t_i/t_o then the temporal duration at the image time becomes,

where Δt_o and Δt_i are the duration of the electron packet at the object and image time, respectively. Durations achievable with a thin temporal lens follow from Eq. 4.

An experimentally realistic temporal lens would use a 50-fs, 800-nm laser pulse with 350 μJ energy, focused to a waist of w = 25 μm. These values result in a stiffness of K = 5.5 × 10⁻⁸ N/m and a focal time of t_f = 0.3 ns; t_f = m/(Kτ). If the lens is applied 10 cm from the source, electrons emitted at v₀ = c/10 (3 keV) would have an object time of t_o = x_o/v₀ = 0.1/(c/10) = 3.0 ns. Using the temporal lens equation, Eq. 1, t_i is obtained to be 0.33 ns. Hence, a magnification of M = −t_i/t_o = 0.1. Consequently, a thin temporal lens can compress an electron packet with an initial temporal duration of Δt_o≈100 fs, after it has dispersed, to an image duration of Δt_i≈10 fs. Although the example presented here is for 3 keV electrons, the thin lens approximation holds for higher energy electrons as long as τ is chosen to be short compared with w/v₀. Experimentally, the thin temporal lens can be used in ultrafast diffraction experiments (25), which operate at kHz repetition rates with lasers that typically possess power that exceeds the value needed for the ponderomotive compression.

Attosecond Thick Lens.

In the previous section it was analytically shown that free electron packets can be compressed from hundreds to tens of femtoseconds using a temporal thin lens, which would correspond to a magnification of ≈0.1. However, the analytic solutions used rely on an impulse approximation that may not generally hold for the temporal lens described in ref. 14. For example, ref. 14 numerically showed that a ≈300-fs duration electron packet can be compressed to a train of ≈15 as pulses, which corresponds to a magnification of M≈5 × 10⁻⁵; the associated image time of t_i = 2 ps is comparable with the laser pulse duration of τ = 0.3 ps. Because M ≪ 1 and t_i and τ are the same order, it is unclear whether the impulse approximation would accurately describe the results.

Another issue that needs to be addressed is how an initial source velocity spread and dispersion affects the ability for the temporal lens in ref. 14 to compress electron packets. The simulation done in ref. 14 predicted ≈15 as electron pulses, where the duration was determined solely by the sinusoidal deviation from the optimal parabolic potential, and did not allow the electron packet to disperse before compression. In the thin lens case, an initial velocity spread results in a nonzero pulse duration even with a parabolic potential. Developing a model incorporating an electron packet that is allowed to disperse before encountering a parabolic potential will answer whether or not an initial velocity spread is detrimental to attosecond pulse compression.

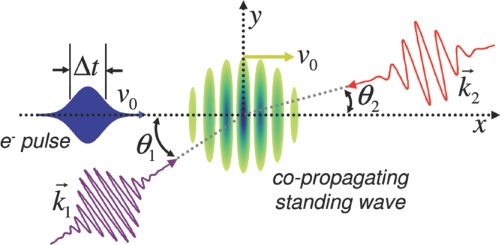
The attosecond compression scheme presented in ref. 14 relies on the presence of a standing wave that copropagates with an ultrashort electron pulse. The copropagating standing wave is created by using 2 different optical frequencies, constructed by having a higher frequency (ω₁) optical pulse traveling in the same direction as the electron packet and a lower frequency (ω₂) traveling in the opposite direction. When the optical frequencies ω₁, ω₂, and the electron velocity v₀ are chosen according to v₀ = c(ω₁ − ω₂)/(ω₁ + ω₂), a standing wave is produced in the rest frame of the electron (14) (see Fig. 4). If the electron has a velocity v₀ = c/3, and ω₁ = 2ω₂ then the copropagating standing wave has a ponderomotive potential of the form (24),

where E₀ is the peak electric field, λ̃ the Doppler shifted wavelength (14). The envelopes of the laser pulses are ignored in this derivation, but they can be engineered so that the standing wave contrast is optimized (26).

Fig. 4.

2D schematic of tilted laser pulse concept for copropagating standing wave used for attosecond electron compression (thick temporal lens). When θ₁ = θ₂ = 0, then v₀ = c/3 for ω and 2ω beams (14). With frequencies of ω and 2ω the velocity of the copropagating standing wave can be tuned by tilting the 2 laser pulses angles θ₁ and θ₂. When the 2 angles are chosen according to θ₂ = arcsin(2sinθ₁), the wells in the standing wave are perpendicular to the electron propagation.

To find an analytic solution in the thick lens geometry, each individual potential well in the standing wave is approximated by a parabolic potential that matches the curvature of the sinusoidal potential, U_P(x) = (1/2)[e²E₀²/(2mc²)]x² (1/2)Kx². Using the exact solution to the harmonic oscillator the focal time is,

where ω_p = $\sqrt{Km}$ and τ is the duration that the lens is on. For τ → 0, t_f → m/(Kτ), which is identical to the thin lens definition. The image time, t_i, has a form,

and after the 2 assumptions, τ → 0 and t_o≫1/(t_fω_p²) becomes equivalent to Eq. 1, the lens equation: t_o⁻¹ + t_i⁻¹ = t_f⁻¹.

The standard deviation of the compressed electron pulse at arbitrary time t_a is,

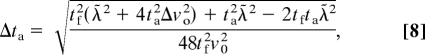which is valid for an individual well (detailed derivation in the SI Appendix). The time when the minimum pulse duration occurs is t_a = t_fλ̃²/(λ̃²+4t_f²Δv_o²) ≈ t_f and for experimentally realistic parameters is equal to t_f. This implies that the thick lens does not image the initial temporal pulse; it temporally focuses the electrons that enter each individual well. Because there is no image in the thick lens regime, the minimum temporal duration is not determined by the magnification M as in the thin lens section, but is a given by,

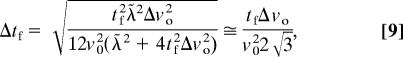which is equivalent to Eq. 6 in ref. 14. It should be noted that neither the temporal focal length nor the temporal duration are directly dependent on the Doppler shifted wavelength λ̃, as long as the condition t_o < v₀Δt_o/Δv_o is met.

An example illustrates what temporal foci are obtainable. A source emits electrons with an energy distribution of 1 eV and a temporal distribution of 100 fs. Electrons traveling at v₀ = c/3 and having an energy E = 31 keV gives a velocity distribution of Δv_o = 1670 m/s. If the distance between the source and the temporal lens is 10 cm, t_o = 1.0 ns is less than v₀Δt_o/Δv_o ≈ 6.0 ns, satisfying the condition t_o < v₀Δt_o/Δv_o and Eq. 9 is then valid. If the 2 colors used for the laser beams are 520 nm and 1040 nm, the Doppler-shifted wavelength is λ̃ = 740 nm. For a laser intensity of 3 × 10¹² Wcm⁻² (available with repetition rates up to megahertz), the oscillation frequency in the potential well is ω_p ≈ 2 × 10¹² rad/s, which gives a focal time of t_f ≈ 1 ps. With these parameters, Eq. 9 gives a temporal duration at the focus of Δt_f ≈ 5 as. To support this ≈5 as electron pulse, time-energy uncertainty demands an energy spread of ≈50 eV. The ponderomotive compression imparts an energy spread to the electron pulse, which can be estimated from ΔE ≈ mv₀λ̃(2t_f), giving ≈50 eV similar to the uncertainty limit. This ΔE is very small relative to the accelerating voltage in microscopy (200 keV) and only contributes to a decrease of the temporal coherence. In optical spectroscopy such pulses can still be used as attosecond probes despite the relatively large ΔE when the chirp is well characterized (27). Combining the anharmonicity broadening of 15 as (as discussed in ref. 14), we conclude that ultimately temporal pulse durations in the attosecond regime can be reached.

Tunable Thick Lens.

In the temporal thick lens case, the use of ω and 2ω to create a copropagating standing wave requires v₀ = c/3. However, the velocity of the electrons, v₀, can be tuned by changing the angle of the 2 laser pulses. A copropagating standing wave can still be obtained by forcing the Doppler-shifted frequencies of both tilted laser pulses to be equal. A laser pulse that propagates at an angle θ with the respect to the electron propagation direction has a Doppler-shifted frequency ω̃ = γω(1 ± (v/c)cosθ), where ω is the angular frequency in the lab frame, v→ = vx̂ is the electron velocity, and γ = 1/$\sqrt{1-v^2/c^2}$ (28). When the 2 laser pulses are directed as shown in Fig. 4, a copropagating standing wave occurs for an electron with a velocity v₀ = c(k₁ − k₂)/(k₁cosθ₁ + k₂cosθ₂), where the laser pulse traveling with the electron packet has a wave vector of magnitude k₁ and makes an angle of θ₁ with the electron propagation axis; the second laser pulse traveling against has a wave vector magnitude of k₂ and angle θ₂, in the lab frame. An electron moving at v₀ will see a standing wave with an angular frequency,

where 2k = k₁ = 2k₂ for experimental convenience, ω = kc, and the wavelength is λ̃ = 2πc/λ̃ = 2π/λ̃.

The standing wave created with arbitrary angles θ₁ and θ₂ will be tilted with respect to the electron propagation direction, which will temporally smear the electron pulse. This tilting of the standing wave can be corrected for by constraining the angles θ₁ and θ₂ to be: θ₂ = arcsin(2sin θ₁).

For θ₁ = 15⁰ (forcing θ₂ ≈ 31⁰), electrons with velocity v₀ = 0.36c (E ≈ 33 keV) see a standing wave. A 1 eV electron energy distribution at the source gives a velocity distribution of Δv₀≈1630 m/s, at 33 keV. Using the same laser intensity as in the thick lens case, and the new v₀ and Δv_o, the condition t_o < v₀Δt_o/Δv_o is still satisfied, allowing Eq. 10 to be used, resulting in a duration at the focus of Δt_f ≈ 4.6 as. Using the tunable thick lens makes the experimental realization more practical, allowing for easy optical access and electron energy tuning, while at the same time keeping Δt_f approximately the same. For additional tunability, an optical parametric amplifier can be used so that the laser pulse frequencies are not restricted to ω and 2ω.

Detection Proposals.

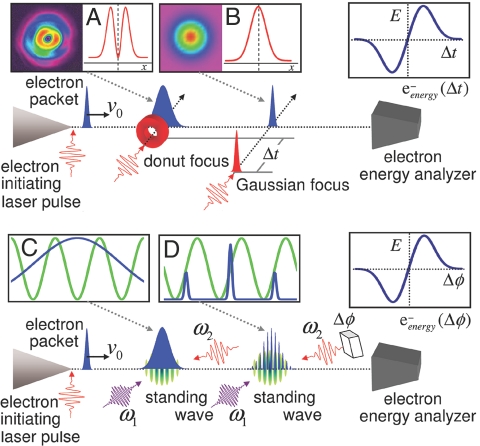
The ability to create electron pulses with duration from ≈10 fs to ≈10 as raises a challenge regarding the measuring of their duration and shape. Two different schemes are presented here for measuring pulses compressed by thick and thin temporal lenses. For measuring the thin lens compressed electron packet, the focused packet could be intersected by a laser pulse with a Gaussian spatial focus (Fig. 5). An optical delay line would control the time delay between the measuring laser pulse and the compressed electron packet. As the time delay, Δt, is varied, so is the average energy of the electrons, as shown in Fig. 5. If the delay time is zero, then the average electron energy will be unaffected, because there is no force. If the delay line is changed so that the Gaussian pulse arrives early (late), then the average energy will decrease (increase). The change in the average energy depends on the duration of the electron pulse, and the intensity of the probing laser pulse. If the electron pulse is longer than the duration of the measuring laser pulse, then the change in the average energy will be reduced. The steepness of the average energy as a function of delay time, Ē(Δt), is a direct measure of the electron pulse duration, and by using femtosecond-pulsed electron energy loss spectra (29) this scheme can be realized.

Fig. 5.

Detection schemes for measuring femtosecond and attosecond compressed electron packets. (Upper) Depicts how femtosecond electron packets can be measured by intersecting the packet at the image position/time. (A) Spatial profile of the donut mode temporal lens. (B) Gaussian profile of the measuring laser pulse. As the time delay, Δt, between the measuring Gaussian laser pulse and the electron packet is varied the average energy of the electron pulse changes. (Lower) depicts the scheme for measuring the duration of attosecond pulses. (C) The spatial profile of the temporal lens at t = 0 is shown (green). (D) The second standing wave that is used to measure the pulse duration of the attosecond electron packets at t = t_f is displayed. The blue lines in C and D give the spatial distribution of the electron packets at t = 0 and t = t_f, respectively. To measure the duration of the attosecond pulses, a second copropagating standing wave is made to coincide with the electron pulse at the focal position. Instead of using a temporal delay a phase shift, Δϕ, is introduced into one of the laser pulses that creates the probing standing wave. By varying this phase shift the nodes of the standing wave shift position. The average electron energy can thus be plotted versus this phase shift. As the electron pulses become shorter than the period of the standing wave the change in the average energy will increase.

For the thick lens a similar method was proposed in ref. 14 and described in more detail here. At the focal position and time of the compressed temporal electron packet, a second copropagating potential is introduced. The positions of the individual wells in the second copropagating standing wave can be moved by phase shifting one of the two laser beams that create the probing potential (Fig. 5). By varying the phase shift, the potential slope (and hence the force) that the electrons encounter at the focus is changed. If no phase shift is given to the probing standing wave, no average energy shift results. When a phase shift is introduced, the electrons will be accelerated (or decelerated) by the slope of an individual well in the standing wave, and as long as the phase stability between the electrons and the probing standing wave is appropriate, attosecond resolution can be achieved. As the electron pulse duration becomes less than the period of the standing wave, the average electron energy change increases. The electron temporal duration of the compressed electron packet can be determined directly by the steepness of the Ē(ϕ) curve.

Conclusion and Outlook.

The attosecond electron imaging regime is possible only when the electron pulses are compressed to the attosecond duration. Current efforts in employing attosecond technologies (primarily electron recombination) require the target specimen to be part of the electron generation, causing the pump and the probe to be coupled. Here, we have described 2 temporal lens designs and obtained analytical expressions consistent with the proposal of Baum and Zewail (14). With a thin temporal lens, the capability to image an electron packet temporally is illustrated with compressibility (or magnification) of the pulse duration from 100 fs to 10 fs. A thick temporal lens can focus an initial dispersed electron packet (hundreds of femtoseconds) into a train of attosecond pulses; this case is discussed in ref. 14 using electron trajectory simulations.

The ultrashort pulses produced by the temporal lenses described here, or by using other compression schemes (18, 30, 31), will have a wide range of applications in UEM (1, 7) and femtosecond-pulsed electron energy loss spectroscopy (29). Although single electron packets develop a linear velocity chirp due to dispersion, packets with linear chirp can be imaged with the temporal lenses described in this article. For an initial packet with an ellipsoidal distribution of electrons, electron-electron interactions (space charge) result in a linear spatial chirp in the propagation direction (23). This linear chirp due to space charge can be used to increase the temporal resolution of ultrafast electron diffraction experiments through energy filtering (22) or pulse compression with radio-frequency fields (32). In principle, the concepts presented here can also be used to compress space-charge dominated pulses of electrons extending the range of applicability for temporal lenses.

Finally, temporal lenses have the potential to increase by orders of magnitude the quantum degeneracy of an electron packet (33). The first use of electron quantum degeneracy in free space—the demonstration of the Hanbury Brown and Twiss effect for electrons (antibunching)–reached a degeneracy value of 10⁻⁴ (34, 35) and in other sources could be 10⁻⁶ or less. This was done with a continuous electron beam from a field emission tip (34). By using pulsed sources and temporal lenses the degeneracy factor can become significantly closer to the quantum limit of one because of the increased current density during the pulse duration. In this limit, the potential for “electron quantum optics” becomes real.