Abstract
The dynamical systems arising from gene regulatory, signalling and metabolic networks are strongly nonlinear, have high-dimensional state spaces and depend on large numbers of parameters. Understanding the relation between the structure and the function for such systems is a considerable challenge. We need tools to identify key points of regulation, illuminate such issues as robustness and control and aid in the design of experiments. Here, I tackle this by developing new techniques for sensitivity analysis. In particular, I show how to globally analyse the sensitivity of a complex system by means of two new graphical objects: the sensitivity heat map and the parameter sensitivity spectrum. The approach to sensitivity analysis is global in the sense that it studies the variation in the whole of the model's solution rather than focusing on output variables one at a time, as in classical sensitivity analysis. This viewpoint relies on the discovery of local geometric rigidity for such systems, the mathematical insight that makes a practicable approach to such problems feasible for highly complex systems. In addition, we demonstrate a new summation theorem that substantially generalizes previous results for oscillatory and other dynamical phenomena. This theorem can be interpreted as a mathematical law stating the need for a balance between fragility and robustness in such systems.
Keywords: sensitivity, robustness, mathematical models, circadian clocks, signalling networks, regulatory networks
1. Introduction
It has recently been emphasized that uncovering the design principles behind complex regulatory and signalling systems requires an analysis of degrees of complexity that cannot be grasped by intuition alone (Csete & Doyle 2002; Kitano 2002, 2004; Stelling et al. 2004b). This task requires some form of mathematical analysis and the discovery of some more universal principles. In particular, this is true of two related key aspects of the design principles problem: firstly, determining how such systems address the need for robustness and trade-off robustness of some aspects against fragility of others; and, secondly, determining the key points of regulation in such systems, aspects of the network that are crucial to its behaviour and control.
Because it identifies which parameters a given particular aspect of the system is most sensitive to, classical sensitivity analysis (Hwang et al. 1978; Kacser et al. 1995; Heinrich & Schuster 1996; Campolongo et al. 2000; Stelling et al. 2004a) is a very useful tool that has been used to address both of these aspects. However, apart from some summation theorems about the control coefficients for period and amplitude of free-running oscillators that are analogous to those derived as in metabolic control analysis (Kacser et al. 1995; Heinrich & Schuster 1996; Fell 1997), there is currently rather little general theory about general non-equilibrium networks. There is a great need to develop tools that give a more integrated picture of all the sensitivities of a system and to develop more coherent universal or widely applicable general principles underlying these sensitivities. To this end, we provide a compact and easily comprehensible representation of all the sensitivities and a precise statement of the robustness–fragility balance (a global summation theorem).
Control coefficients have been widely used particularly in the engineering sciences and metabolic control theory. In such applications, it is natural to fix a particular observable or performance measure Q of interest and then ask how sensitive this is to the various parameters. However, in many systems biology applications there are multiple performance measures of interest. For example, in the study of circadian oscillators one is interested in many aspects such as the free-running period, the strength of entrainment and the consequent phases of the various molecular products, the phase response curves, period and phase as a function of temperature and the response to different day lengths. For signalling systems such as that of the NF-κB system, one is interested in multiple aspects of the response to a signal related to its strength, timing, persistence, decay and transient, equilibrium or oscillatory structure. Moreover, in the search for key points of regulation there may be aspects, where the system is particularly sensitive, that do not correspond to obvious performance measures. Therefore, it would be extremely useful to have an effective approach that will find the sensitivity of all the performance measures and operating aspects of a given model.
The approach to sensitivity analysis developed here is a global one that studies the variation of the whole solution rather than focusing on just one output variable. In addition, this more global approach allows us to address which observable variables Q (henceforth called observables) are affected by which parameters kj without having to choose the variable or parameter in advance. The results of this analysis can be summarized in
the sensitivity heat map (SHM) from which one is able to effectively identify those observables Q that are sensitive to some parameter, and
the parameter sensitivity spectrum (PSS) that characterizes the sensitivity of these observables and the system as a whole with respect to each parameter.
The crucial observation that makes the theory applicable in practice by ensuring that for a given tolerance the above objects are compact and manageable is that such network systems are rigid in the following sense. The map from parameters to the corresponding solutions of interest (a map from a high-dimensional space s to an infinite-dimensional solution space) locally maps round balls to ellipsoids with axes lengths where the lengths σi decrease very rapidly. This is rigidity because random jiggling of the parameter vector in the high-dimensional parameter space results in the variation of the solution of interest that effectively occupies a space of much lower dimension.
The sensitivity principal components (PCs) Ui(t) that we present in §2 are key components of our theory. These are multidimensional time series from which all system derivatives can be calculated and whose importance rapidly decreases as i increases. We show that, when the parameters being varied are a full set of linear parameters, the sensitivity PCs satisfy a global summation theorem which says that a certain linear combination of them sums to a function that is simply related to the original differential equation. This global summation theorem contains within it the other known simple summation theorems for dynamic systems such as those for the period and amplitude of an oscillatory solution of an unforced oscillator. However, it is a substantial generalization because it relates a set of functions rather than a set of numbers and thus is effectively an infinite number of simple summation conditions. Moreover, unlike the classical summation theorems, it applies to non-autonomous systems such as forced oscillators as well as to autonomous systems.
I have applied the theory to a broad range of examples (table 1), but for the purposes of discussion and illustration in this paper we will mainly consider two representative examples: a model of the mammalian circadian oscillator (Leloup & Goldbeter 2003) and a version of the Hoffmann model for the NF-κB signalling system (Hoffmann et al. 2002). The former is a reasonably representative example of a periodically oscillating system and for the latter the solution of interest is a transient solution produced by an incoming signal.
Table 1.
A list of some models analysed together with the number of state variables n, the number of parameters s and the rate of decay α of the singular values σi (i.e. ). (The superscripts ‘u’ and ‘f’ for the circadian oscillators indicate, respectively, the values for the cases where the oscillator is unforced and forced by light.)
| model | n | s | α |
|---|---|---|---|
| Neurospora clock; Leloup et al. (1999) | 3 | 10 | 0.30u/0.26f |
| Drosophila clock; Leloup et al. (1999) | 10 | 38 | 0.24u/0.19f |
| Drosophila clock; Ueda et al. (2001) | 10 | 55 | 0.15u/0.20f |
| Drosophila clock; Tyson et al. (1999) | 2 | 9 | 0.48u |
| mammalian clock; Leloup & Goldbeter (2003) | 16 | 53 | 0.21u/0.17f |
| mammalian clock; Forger & Peskin (2003) | 73 | 36 | 1.63f |
| yeast cell cycle; Tyson et al. (2002) | 9 | 26 | 0.27 |
| full NF-κB model; Hoffmann et al. (2002) and Nelson (2004) | 24 | 35 | 0.45 |
| glycolytic oscillations; Ruoff et al. (2003) | 9 | 10 | 0.44 |
2. Results
Suppose we are considering a regulatory or signalling system modelled by the differential equation
| (2.1) |
where t is time; are the state variables of the system; and is a vector of parameters. The vector k may contain all the parameters but we will also consider the case where it only contains some and where the other parameters are held fixed and only are varied. For example, k may consist of just those parameters that the system is particularly sensitive to or may consist of just the linear parameters as defined in §2.5.
In general, there will be a solution or a class of solutions defined for a specific time range that are of particular interest. For example, for circadian oscillations the primary object of interest is an attracting periodic orbit of equation (2.1) and T will be the period of this orbit. On the other hand, for models of signalling systems, one is often interested in a solution that is not periodic but is defined by a given initial condition x0. Such a signalling system is usually also subject to a given perturbation caused by an incoming signal and this will typically be modelled by a sudden change in a system parameter or by the time dependence of the r.h.s. of equation (2.1).
In regulatory and signalling systems, the values of two parameters may differ by an order of magnitude or more. Therefore, it is usually not appropriate to consider the absolute changes in the parameters kj, but instead to consider the relative changes. A good way to do this is to introduce new parameters because absolute changes in ηj correspond to relative changes in kj. Then, for small changes δk to the parameters, , so the changes δηj are scaled and non-dimensional.
2.1 Fundamental observation
There are two aspects to the fundamental observation behind the tools and analysis presented here. The first is that for such regulatory and signalling systems there are the following easily computable objects:
a set of n-dimensional time series , defined for , which are of unit length and orthogonal to each other in the sense of equation (2.3),
a decreasing sequence of s positive numbers called sensitivity singular values, and
a special set of new parameters that are related to the original (scaled) parameter variations δη by an orthogonal linear transformation W (i.e. ),
with the following key property that connects them: if δη is any change in the (scaled) parameter vector then the change δg in the solution g of interest is given by
| (2.2) |
The second aspect is that for a broad range of networks such as those in table 1, the amplitudes actually decrease very rapidly, usually exponentially in the sense that decreases linearly with i, i.e. , α>0.
The Ui are of unit length and orthogonal to each other in the following sense
| (2.3) |
where if i≠j and equals 1 if i=j. These are called sensitivity PCs.
We stress two points here: (i) that the given system and solution of interest determine the Ui, the σi, W and the λi and (ii) that the change δg is described by (2.2) in terms of these for any parameter perturbations δη.
It can easily be shown (see the electronic supplementary material) that the derivatives of the solution g with respect to the parameters ηj are given by
| (2.4) |
where .
One can regard equation (2.3) as saying that Ui and Uj (i≠j) are uncorrelated as functions of time t. The derivatives and will in general be correlated with each other and writing them as in equation (2.4) is a decomposition of them into uncorrelated time series. Since the σi decay rapidly from a significant value we see that, in fact, the derivatives are highly correlated and their correlation is concentrated in a few components Ui with low values of i.
The usefulness of the Ui, the σi and the Sij arises from a combination of the following facts:
they are straightforward to compute (see §3), even for very complex models,
classical sensitivity coefficients can be expressed in terms of them,
when represented in a heat map (see below), one can rapidly map out all the sensitivities of a complex model, and
since the amplitudes σi get small very quickly, for a broad class of network models it is usually necessary to consider only a small number of the dominant Ui.
Let us illustrate the fundamental observation by considering the two models mentioned above. For the modified Hoffmann model (Hoffmann et al. 2002), there are n=10 state variables corresponding to the concentrations of nuclear and cytoplasmic NF-κB and IκBα and their complexes plus IKK, and s=42 parameters most of which are rate constants. This is a simplified version of the model in Hoffmann et al. (2002) in which, of the IκB's, only IκBα is included and not IκBβ and IκBϵ. The solution g(t) considered is the transient orbit produced when an incoming signal at t=0 increases the level of IKK above the equilibrium level. The IKK is washed out at t=600 min. The mammalian clock model (Leloup & Goldbeter 2003) has n=16 state variables and s=53 parameters. Both have rapidly decreasing sensitivity spectra as is shown in figure 1. The σ1-scaled sensitivity PC for the above model of the mammalian oscillator is shown in figure 2 as a heat map. Although these two models have a large number of state variables and parameters, to study all their sensitivities that are no smaller than 5% of the biggest it is enough to consider only the first five Ui.
Figure 1.
The plot shows log10 σi for the largest singular values of the models in table 1. The case shown is for relative changes in both parameters and the solution (as explained in §2.4). We see that, for all these examples, the σi decay exponentially like and that the rate of decay α>0 varies significantly from model to model. The models are listed in the same order as in table 1, which are as follows: open circle, Neurospora; open square, Drosophila 1; open diamond, Drosophila 2; open down triangle, Drosophila 3; open up triangle, mammalian 1; filled circle, mammalian 2; filled square, cell cycle; filled diamond, full NF-κB; filled down triangle, glycolytic oscillations.
Figure 2.
C1(t)=σ1U1(t) for the model of the mammalian circadian clock due to Leloup & Goldbeter (2003) with no forcing by light (i.e. in DD). Each of the 16 components C1,m=σ1U1,m is represented by a coloured strip that shows the value of C1,m(t) at the corresponding time 0≤t≤T, where T is the period of the oscillation. In order to highlight their structure the C1,m are scaled by a factor 1/am so that the values taken by C1,m(t) fill a maximal range of the interval from minm′,tC1,m′(t) to maxm′,tC1,m′(t). They are shown in order of decreasing am and the values of am are shown in the column headed ratio. Thus one sees that the amplitude am of C1,m for CRY protein is more than 100 times that of phosphorylated cytoplasmic PER CRY complexes or phosphorylated cytoplasmic BMAL1 protein. A glance shows that CRY is the most sensitive in that am is largest, followed by cytoplasmic PER CRY complexes (cyto PER:CRY), nuclear PER CRY complexes (nuc PER:CRY), Per mRNA and PER protein in that order. We can also quickly see at what times or phases these variables are fragile or robust. Thus we see that CRY is most fragile at times close to t=14.5 hours and relatively fragile over a broad band of phases centred on this time, while the variable for nuclear PER CRY complexes is most fragile close to t=18 hours, but even there, much less so than CRY. On the other hand since their amplitude is so small, the last six variables are relatively insensitive at all phases. In calculating these sensitivity PCs no scaling of the dynamical variables is carried out but the scaled parameters ηj=log kj have been used. In cases where these variables have significantly different scales, it is usually preferable to scale the variables to concentrate on relative changes rather than absolute ones. As is explained in §3, this scaled approach is very easy to implement. In (b), the curves are as follows: dark blue, CRY; green, cyto PER:CRY; red, nuc PER:CRY; light blue, Per mRNA; purple, PER.
The results behind this observation about the rapid decay of the σi were first developed independently in Brown & Sethna (2003), Brown et al. (2004) and Rand et al. (2004, 2006). In the former work, the σi appeared as the square roots of the eigenvalues of the Hessian of the function that has to be minimized when doing least-squares fitting of parameters to data for such models. In the latter reference they arose as part of an argument about the complex structure of circadian clocks being a result of the inflexibility of such systems despite the large number of parameters. The link between these two approaches is provided by the matrix defined above (see equation (2.4)) by . The square is an example of a Fisher information matrix and its eigenvalues are the . It can be shown that under certain conditions it is the mean value of the abovementioned Hessians (see electronic supplementary material). In Waterfall et al. (2006), it is argued that such systems form a universality class and it will be important to determine whether this is true or whether there is a more mundane reason for this decay. More evidence for the seemingly universal ubiquity of the rapid decay of the σi in tightly coupled systems biology models and the consequences for parameter estimation are discussed in Gutenkunst et al. (2007).
2.2 Classical sensitivity coefficients from the Ui
Typical classical sensitivity coefficients can be written in terms of the Ui and Sij. As explained in the electronic supplementary material many can be written either as a sum
| (2.5) |
for some finite set of times tℓ or as an integral over a interval of times
where is either
| (2.6) |
and is the derivative of Ui,m with respect to time t. Examples involving a sum include the control coefficients of phase and amplitude for forced oscillators and the time for signals to peak in signalling systems. Examples involving an integral include the Fourier transforms of the components of the solution (reflecting changes in the shapes of the time series). Thus, we conclude that the control coefficients of interest are all linear sums or integrals over tℓ of terms that are of the form given in (2.6). This fact is key to understanding the use of the SHMs.
In the electronic supplementary material the reader will find a table listing some key observables for oscillators and signalling systems and giving the expressions for their control coefficients in terms of the Ui,m using formula (2.5).
2.3 SHM and parameters sensitivities graphically summarize all the system's sensitivities
We now discuss how to analyse the sensitivity of such a complex dynamical system globally using the SHM and the PSS (figures 3 and 6). They allow us to graphically analyse what observables are significantly changed by what parameters. We do not have to fix the observable or parameter in advance but let the model decide what the most salient observables are. The SHM and PSS are intrinsic to the system and characterize its sensitivity in a global fashion.
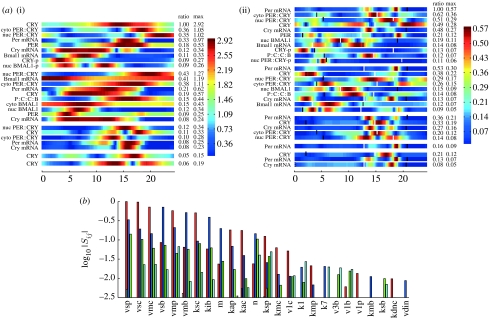
Figure 3.
(a) The SHMs for the model of the mammalian circadian clock discussed in figure 2: (i) fi,m and (ii) . The threshold for the fi,m is set to be 5% of the global maximum of the fi,m(t). For the (t) heat map, the corresponding threshold is 7.5%. These were chosen to keep the figure size small and smaller thresholds can be used. The only values of i (the sensitivity PC index) and m (the variable index) for which maxt fi,m(t) or (t) is greater than this threshold have i=1, 2, 3, 4 or 5. Each block of variables corresponds to one value of i. Thus, in (i), the first block of nine variables corresponds to i=1. The plotted fi,m are coloured on the scale shown after scaling each of them by a factor 1/ai,m to make all their amplitudes the same as that with maximum amplitude. These factors ai,m are in the column marked ratio. (b) The PSS where each group of bars corresponds to the value of log10 |Sij| for a particular parameter kj. These are only plotted for those i for which |Sij| is significant (in this case i=1–4). They are coloured as follows: red (pc 1), i=1; blue (pc 2), i=2; green (pc 3), i=3; light blue (pc 4), i=4. The parameters kj are ordered by maxi=1–4|Sij| and only the 25 most sensitive are plotted. To demonstrate how the heat maps can be used, we consider the sensitivity of the 32 phases of the maxima and minima of the various products. We see from table 1 of the electronic supplementary material that the control coefficient of such a phase for xm(t) is proportional to a linear sum of the , and we therefore need to check whether the phases of the maxima or minima are hot times for the . We have therefore plotted the maxima and minima on the heat map (black, minima; white, maxima). We immediately see that some of the maxima are sensitive, notably Per mRNA and cytoplasmic PER–CRY complexes that are the most sensitive. Following these, approximately one-third as sensitive are nuclear PER–CRY complexes, Cry mRNA and CRY protein. Of the minima, only those of cytoplasmic PER–CRY complexes and CRY protein appear to be significantly sensitive. Using the software described in the electronic supplementary material, one can quickly turn this into quantitative information. For the most sensitive phases ϕ, the high values of occur when i=1. Therefore, to see what parameters these most sensitive phases are sensitive to, we check the red bars in the PSS in the second row of the figure, since these are the values of log10 |S1j|. We quickly see that four parameters dominate (vsp, vsc, vmp and kib) and three others have a sensitivity a little above 10% of the maximum. Only 12 out of the 56 parameters have more than 1% of the maximum sensitivity for these phases.
Figure 6.
(a) The SHMs and (b) the parameter sensitivity spectra (PSS) for the modified Hoffmann model. (a) The analysis when the time domain is restricted to (i, iii) 0≤t≤200 (i.e. T=200) and (ii,iv) when this is 0≤t≤1000. (b) The PSS show that in both cases ((i) 0≤t≤200 and (ii) 0≤t≤1000), only very few parameters kj have sensitivities greater than one thousandth of the maximum one. However, the dominant parameters for the two cases are different. In (b(i)), we note that ka4, k1, ka7, ka1 and klr2 are the most sensitive and that these primarily affect the variables at the times that are coloured red in (a(iii)). As for figure 3, the maxima and minima have been marked with pink and white bars, respectively, on the heat maps for the so that one can quickly check which are sensitive to any parameter and then determine which parameters using the PSS.
The strategy is to
use the SHM to identify all those times tℓ and indices i and m that correspond to the terms, which are significantly large, of the form given in equation (2.6) and thus to effectively determine which observables Q have significantly large for some parameters kj, and then to
use the PSS to identify, for those Q from (i), which of the parameter indices j have significantly large.
2.3.1 Sensitivity heat map
Suppose
| (2.7) |
and
| (2.8) |
(Note that , , and the σi are decreasing rapidly for the systems of interest.)
Then and . Thus, if is a linear combination of terms as in equation (2.6) using a given m and a given set of times tℓ, the following is true: if and are small for all those values of tℓ, then must be small.
Therefore to determine which observables can have a significant control coefficient we need to determine all i, m and tℓ such that either or have significant values. To do this we fix a small threshold τ (e.g. 1% of the maximum value achieved by all the fi,m and ) and identify all pairs (i,m) such that either or is greater than τ. Luckily, since these sizes are comparable to σi, there are relatively few pairs (i,m) for which fi,m or have to be plotted: in the examples studied so far about twice the number of state variables.
These fi,m and are then plotted in the SHM. Since relatively few fi,m or have to be plotted, the heat map is compact and therefore convenient. For each such pair (i,m) we inspect the fi,m plotted in the SHM to determine the set Ti,m of times such that fi,m(t) or is significantly large. This achieves step (i) above.
SHMs for the mammalian clock model and the NF-κB signalling systems are shown in figures 3 and 6.
2.3.2 Parameter sensitivity spectrum
The matrix characterizes the sensitivity of the system with respect to each parameter. Recall that, up to second-order terms that are , the variation δg produced by a parameter variation is
since . We see that Sij completely determines the effect of small changes δηj in the jth parameter ηj. Moreover, since the Ui(t) are orthogonal in time-series space, the Sij act in independent directions and efficiently parametrize the derivatives . In fact, the Sij give a representation of the derivatives that is optimal in that it maximizes the effect of terms with low i (for a precise statement see the electronic supplementary material).
In figure 4 we see that, for the model of the mammalian circadian clock, the magnitude of the Sij decreases rapidly with i and relatively few of them have . In figures 3 and 6, the are plotted as a grouped bar chart with the parameters kj reordered according to the size of their sensitivity. Using this for a given value of i we can immediately identify the strength of each parameter in moving the solution g in the direction of Ui. Although not monotonically decreasing in i, the Sij nevertheless rapidly get small as i increases. This can be seen in figure 4 where we plot and see that very few of the Sij have a magnitude greater than one per cent of . Therefore, we only have to consider the Sij for a few values of i and the grouped bar chart can be restricted to these.
Figure 4.
(a, b) The values of (for the same systems as in figure 2) are shown as a bar chart, showing only those Sij whose magnitude is greater than 10−3. We note the generally fast decline in as i increases and the large variation in these values with the parameter index j.
Thus, if we (i) use the SHM to determine the set Ti,m of times t such that either fi,m(t) or is significantly large, and (ii) use the PSS to identify those parameters ηj such that |Sij| is significantly large we obtain a set of triples (i,m,j) that give the significant terms of the form in equation (2.6). These are called hot. We can then conclude that the control coefficients that are significant are those which involve terms of the form given in equation (2.6) where (i,m,j) is hot and the times tℓ are in Ti,m.
2.4 Signalling: the NF-κB system
There are now a number of models of the NF-κB system (see the references in Tiana et al. 2007). For illustrative purposes, we consider a modified version of the model due to Hoffmann et al. (2002) although a similar analysis can, and, in most cases, has been applied to the other models. There are n=10 state variables corresponding to the concentrations of nuclear and cytoplasmic NF-κB and IκBα and their complexes plus IKK, and s=42 parameters kj most of which are rate constants. The solution g(t) considered is the transient orbit produced when at t=0 an incoming signal increases the level of IKK above the equilibrium level. The IKK is washed out at t=600 min. A conventional sensitivity analysis of a related model was carried out in Ihekwaba et al. (2004) and Cox (2005) and an analysis based on the variation in the full solution was carried out in Yue et al. (2006).
The solution of interest is shown in figure 5. For oscillators it is clear how to choose the length T of the time period under consideration. For signalling systems like this, the choice of T depends upon the problem being considered. For example, if one is only interested in the initial response, then T will be chosen small, while if one is interested in the full response, then a longer period will be chosen.
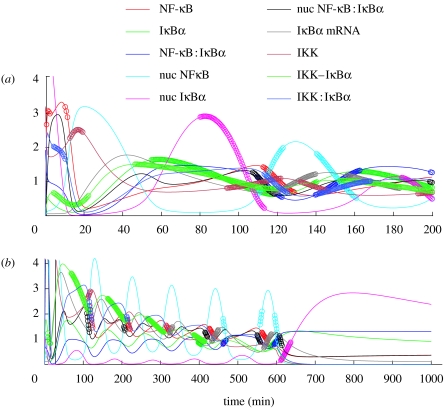
Figure 5.
The trajectories of the simplified Hoffmann model with parameter values as in Hoffmann et al. (2002). The system is first allowed to equilibrate and then the level of IKK is increased at t=0. This is washed out at t=600 min. There are 10 state variables corresponding to IKK, nuclear and cytoplasmic NF-κB and IκBα and their complexes.
For the purposes of illustration let us suppose that we are interested in the first two oscillations (i.e. until t=200) and in the full trajectory (i.e. until t=1000).
We see from figure 5 that the different components gi(t) of the solution have very different amplitudes. This raises the problem that parameter changes will tend to produce larger absolute changes to those variables with larger magnitudes. Therefore, it will usually be the case that, in situations like this, relative changes in the gi are more appropriate than absolute ones. One way to allow for this is to use instead of . However, this is not sensible in this case as for some times t, gi(t) is very close to 0. When this is the case it is usually more appropriate to normalize and non-dimensionalize the gi by dividing by the mean value or some other appropriate measure to obtain a scaled solution and then to consider the control coefficient .
Using the software described in the electronic supplementary material the analysis of this system takes a few seconds and in figure 6 we show the SHM and the appropriate rows of the sensitivity matrix. We apply this to discuss the sensitivity of the peak values and their timing for the sequence of oscillations (figure 7).
Figure 7.
For the two cases ((a) 0≤t≤200 and (b) 0≤t≤1000) of the Hoffmann model considered in figure 6, we plot the trajectories of the differential equation and mark those times when for the corresponding value of m and some i. Using the software associated with this paper, one can effectively and instantaneously produce such plots, changing τ and seeing which aspects of the trajectories are sensitive.
2.5 Summation law
Like certain metabolic control coefficients, the sensitivity PCs satisfy a summation law. This law can be interpreted as a mathematical statement of the idea (e.g. Csete & Doyle 2002; Kitano 2002, 2004) that there is a balance between fragility and robustness in systems like those we study and that increasing robustness in parts will increase fragility in others.
This result holds when the parameters being considered are a full set of linear parameters, i.e. are the parameters in front of the terms which make up f with such a parameter in front of every term. A precise definition of such a set is as follows: it satisfies for all ρ>0. There may be other parameters but we consider here the case where these are held fixed and only the linear parameters are varied so that the parameter vector k just consists of these parameters.
We first consider (i) autonomous systems (i.e. when f does not depend explicitly on t) and (ii) non-autonomous systems where the solution of interest g(t) is defined by its initial condition as in signalling systems (i.e. is the solution of the differential equation with a given fixed initial condition). Then the summation law is
| (2.9) |
The function Φ is given by
| (2.10) |
where X(s,t) is the n×n matrix solution of the variational equation
with initial condition given by X(s,s) being the identity matrix. In the above equation, J(t) is the Jacobian evaluated at .
In the remaining case where the solution of interest is a periodic solution of a non-autonomous system, the summation law is
| (2.11) |
where Φ is as above and τ is the period.
When the system is autonomous then and therefore and the summation law reduces to
| (2.12) |
From equation (2.12), one can deduce the following known summation laws for free-running oscillations with period τ and amplitude Am for the mth state variable (see §5.8.5 of Heinrich & Schuster 1996):
However, these can also be proved in a much easier manner using the fact that scaling the linear parameters corresponds to scaling time. Again the sums are over just the linear parameters.
Note that for autonomous systems (sum over all i and j). Thus, if we have exponential decay of the σi,
because . Therefore, if σ2 is small compared to σ1, as is often the case, we deduce that U1(t) is approximately proportional to . But, for oscillators, is the infinitesimal generator of a change in the period of g, i.e. is the derivative at φ=1 of . Thus, in this case U1(t) is roughly proportional to an infinitesimal period change.
3. Methods
The mathematical object underlying this analysis is a matrix M that is made up from the partial derivatives , where . We restrict time t to a discrete set of equally spaced values and for each parameter kj and each state variable xm consider the column vectors . For each j we concatenate the rm,j into a single column vector rj and then consider the matrix M whose jth column is rj.
This matrix is a time-discretized version of the linear operator that associates with each change of scaled parameters the linearized change δg in the solution of interest g that is in the infinite-dimensional space of appropriate n-dimensional time series.
In order to ensure that in the limit Δt→0 the singular value decomposition (SVD) of M is independent of the choice of the time discretization (assumed for the moment to be independent of i), we normalize M by and consider instead .
We use the version of SVD that is often called thin SVD. Since M1 has nN rows and s columns (i.e. is nN×s), this thin SVD is a decomposition into a product of the form (superscript ‘t’ denotes transpose), where U is a nN×s orthonormal matrix ( and UtU=Is), V is a s×s orthonormal matrix and is a diagonal matrix. The elements are the singular values of M. The matrix W is the inverse of V and since V is orthogonal .
The columns Uj of U are orthogonal unit vectors and can be augmented to provide an orthonormal basis for the space of discretized time series. As for rj they are in the concatenated form. To restore them to their form as time series in n-dimensional space, the concatenation must be undone but this is straightforward. The Uj(ti) then approximate the . From one immediately deduces that , where Vj is the jth column of V. The fundamental equation (2.2) follows directly from this.
If it is appropriate to scale the solution g as above in §2.4 then, in the definition of M, we use the derivatives for the scaled rather than those for g. If it is preferred to use the original variables kj instead of the scaled ones , then we just use the derivatives with respect to kj instead of ηj in the definition of M.
4. Discussion
There is a pressing need for effective tools with which to probe how a network's function depends upon its structure and parameters. The development of such tools presents many challenges because typically (even when they have relatively few components) these networks have significant complexity, are highly nonlinear and the states of interest are dynamical and non-equilibrium. In particular, they involve large numbers of state variables and even larger numbers of parameters. The paper by Kitano (2007) points out that a solid theoretical foundation of biological robustness is yet to be established and represents a key challenge in systems biology, and starts a discussion of how this can be achieved.
However, Brown & Sethna (2003), Brown et al. (2004) and Rand et al. (2004, 2006) uncovered a surprising property of such systems that aids the construction of such tools. This is the local geometric rigidity described in §2.1: variation in the high-dimensional parameter space causes variations of the solution of interest that effectively occupies a space of much lower dimension.
We have shown that the fundamental observation enables a more global approach to sensitivity analysis in which we do not have to fix an observable function in advance but can instead effectively consider the effect of all the parameters on all reasonable observables. As a result we are able to represent all the sensitivities of these complex dynamical systems in terms of a pair of relatively simple graphical objects, the SHM and the PSS.
Since F=S*S is intimately related to the Fisher information matrix for such systems, it is clear that the approach presented here will be useful in developing techniques for experimental optimization (Brown et al. 2004).
Our approach is local in phase space, estimating the structure of the model in a small neighbourhood of a given set of parameter values. An important task for the future is to extend this to a theory that is more global in parameter space. This will require the development of tools that allow one to sew together the local domains. Luckily, all the computations used in this paper are very fast and can be carried out on relatively small computers. Moreover, many of the computations can be effectively parallelized. Thus, it is probable that this task is quite practical from a computational point of view. This more global approach will be of relevance to algorithms that search parameter or structure space. These spaces are very high dimensional and one needs help in determining in which direction to move. The current theory suggests how to do this since only movement in the directions of the dominant PCs produces substantial changes in the system.
Another limitation is that the approach presented here, being deterministic in nature, does not make any use of the significant amount of information contained in the stochastic fluctuations in data. The ability to incorporate this into the approach would be a significant addition.
We mentioned above that in order to allow for the fact that different parameters and different components gi(t) of the solution may differ in size by an order of magnitude or more, it is usually appropriate to scale the parameters (i.e. take as the parameters) and/or to scale the components gi(t). The choice of whether to scale one or other or both of these depends upon the context. It is also sometimes natural not to scale either; for example, this is sometimes the case when using this approach for experimental optimization.
Acknowledgments
The software used in my analysis was developed with Paul Brown and much of it was originally developed in collaboration with Boris Shulgin. I am very grateful to both of them and also to Nigel Burroughs and How Sun Jow for their discussions on the experimental optimizations that are related to some aspects discussed here. I had some very useful discussions with David Broomhead and Mark Muldoon about how to prove the fundamental observation. I am very grateful to Hugo van den Berg for a critical reading of a draft manuscript. I also thank Sanyi Tang, Andrew Millar, Bärbel Finkenstadt, Isabelle Carré and John Tyson for their useful discussions on these topics, the KITP for its hospitality and the BBSRC, EPSRC and EU (BioSim Network Contract no. 005137) for funding. I currently hold an EPSRC Senior Research Fellowship.
Footnotes
One contribution of 10 to a Theme Supplement ‘Biological switches and clocks’.
Supplementary Material
Mapping sensitivity
References
- Brown K.S., Sethna J.P. Statistical mechanical approaches to models with many poorly known parameters. Phys. Rev. E. 2003;68(Pt 1):021904. doi: 10.1103/PhysRevE.68.021904. doi:10.1103/PhysRevE.68.021904 [DOI] [PubMed] [Google Scholar]
- Brown K.S., Hill C.C., Calero G.A., Myers C.R., Lee K.H., Sethna J.P., Cerione R.A. The statistical mechanics of complex signaling networks: nerve growth factor signaling. Phys. Biol. 2004;1:184–195. doi: 10.1088/1478-3967/1/3/006. doi:10.1088/1478-3967/1/3/006 [DOI] [PubMed] [Google Scholar]
- Campolongo F., Saltelli A., Sorensen T., Tarantola S. Hitchhiker's guide to sensitivity analysis. In: Saltelli A., Chan K., Scott E.M., editors. Sensitivity analysis. Wiley series in probability and statistics. Wiley; New York, NY: 2000. pp. 15–47. [Google Scholar]
- Cox, L. G. E. 2005 A comparison study of sensitivity analyses on two different models concerning the NFκB regulatory module. Technische Universiteit Eindhoven report 05/BMT/S01.
- Csete M.E., Doyle J.C. Reverse engineering of biological complexity. Science. 2002;295:1664–1669. doi: 10.1126/science.1069981. doi:10.1126/science.1069981 [DOI] [PubMed] [Google Scholar]
- Fell D.A. Portland Press; London, UK: 1997. Understanding the control of metabolism. [Google Scholar]
- Forger D.B., Peskin C.S. A detailed predictive model of the mammalian circadian clock. Proc. Natl Acad. Sci. USA. 2003;100:14 806–14 811. doi: 10.1073/pnas.2036281100. doi:10.1073/pnas.2036281100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst R.N., Waterfall J.J., Casey F.P., Brown K.S., Myers C.R., Sethna J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007;3:e189. doi: 10.1371/journal.pcbi.0030189. doi:10.1371/journal.pcbi.0030189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinrich R., Schuster S. Chapman and Hall; New York, NY: 1996. The regulation of cellular systems. [Google Scholar]
- Hoffmann A., Levchenko A., Scott M.L., Baltimore D. The IκB-NF-κB signaling module: temporal control and selective gene activation. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. doi:10.1126/science.1071914 [DOI] [PubMed] [Google Scholar]
- Hwang J.T., Dougherty E.P., Rabitz S., Rabitz H. The Green's function method of sensitivity analysis in chemical kinetics. J. Chem. Phys. 1978;69:5180–5191. doi:10.1063/1.436465 [Google Scholar]
- Ihekwaba A.E.C., Broomhead D.S., Grimley R., Benson N., Kell D.B. Sensitivity analysis of parameters controlling oscillatory signalling in the NF-κB pathway: the roles of IKK and IκBα. IEE Syst. Biol. 2004;1:93–103. doi: 10.1049/sb:20045009. doi:10.1049/sb:20045009 [DOI] [PubMed] [Google Scholar]
- Kacser H., Burns J.A., Fell D.A. The control of flux. Biochem. Soc. Trans. 1995;23:341–366. doi: 10.1042/bst0230341. [DOI] [PubMed] [Google Scholar]
- Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–1664. doi: 10.1126/science.1069492. doi:10.1126/science.1069492 [DOI] [PubMed] [Google Scholar]
- Kitano H. Opinon: cancer as a robust system: implications for anticancer therapy. Nat. Rev. Cancer. 2004;4:227–235. doi: 10.1038/nrc1300. doi:10.1038/nrc1300 [DOI] [PubMed] [Google Scholar]
- Kitano H. Towards a theory of biological robustness. Mol. Syst. Biol. 2007;3:137. doi: 10.1038/msb4100179. doi:10.1038/msb4100179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup J.C., Goldbeter A. Toward a detailed computational model for the mammalian circadian clock. Proc. Natl Acad. Sci. USA. 2003;100:7051–7056. doi: 10.1073/pnas.1132112100. doi:10.1073/pnas.1132112100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup J.C., Gonze D., Goldbeter A. Limit cycle models for circadian rhythms based on transcriptional regulation in Drosophila and Neurospora. J. Biol. Rhythm. 1999;14:433–448. doi: 10.1177/074873099129000948. doi:10.1177/074873099129000948 [DOI] [PubMed] [Google Scholar]
- Nelson D.E., et al. Oscillations in NF-κB signaling control the dynamics of gene expression. Science. 2004;306:704–708. doi: 10.1126/science.1099962. doi:10.1126/science.1099962 [DOI] [PubMed] [Google Scholar]
- Rand D.A., Shulgin B.V., Salazar D., Millar A.J. Design principles underlying circadian clocks. J. R. Soc. Interface. 2004;1:119–130. doi: 10.1098/rsif.2004.0014. doi:10.1098/rsif.2004.0014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rand D.A., Shulgin B.V., Salazar J.D., Millar A.J. Uncovering the design principles of circadian clocks: mathematical analysis of flexibility and evolutionary goals. J. Theor. Biol. 2006;238:616–635. doi: 10.1016/j.jtbi.2005.06.026. doi:10.1016/j.jtbi.2005.06.026 [DOI] [PubMed] [Google Scholar]
- Ruoff P., Christensen M.K., Wolf J., Heinrich R. Temperature dependency and temperature compensation in a model of yeast glycolytic oscillations. Biophys. Chem. 2003;106:179–192. doi: 10.1016/s0301-4622(03)00191-1. doi:10.1016/S0301-4622(03)00191-1 [DOI] [PubMed] [Google Scholar]
- Stelling J., Gilles E.D., Doyle F.J. Robustness properties of circadian clock architectures. Proc. Natl Acad. Sci. USA. 2004a;101:13 210–13 215. doi: 10.1073/pnas.0401463101. doi:10.1073/pnas.0401463101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J., Sauer U., Szallasi Z., Doyle F.J., Doyle J. Robustness of cellular functions. Cell. 2004b;118:675–685. doi: 10.1016/j.cell.2004.09.008. doi:10.1016/j.cell.2004.09.008 [DOI] [PubMed] [Google Scholar]
- Tiana G., Krishna S., Pigolotti S., Jensen M.H., Sneppen K. Oscillations and temporal signalling in cells. Phys. Biol. 2007;4:R1–R17. doi: 10.1088/1478-3975/4/2/R01. doi:10.1088/1478-3975/4/2/R01 [DOI] [PubMed] [Google Scholar]
- Tyson J.J., Hong C.I., Thron C.D., Novak B. A simple model of circadian rhythms based on dimerization and proteolysis of PER and TIM. Biophys. J. 1999;77:2411–2417. doi: 10.1016/S0006-3495(99)77078-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson J.J., Csikasz-Nagy A., Novak B. The dynamics of cell cycle regulation. Bioessays. 2002;24:1095–1109. doi: 10.1002/bies.10191. doi:10.1002/bies.10191 [DOI] [PubMed] [Google Scholar]
- Ueda H.R., Hagiwara M., Kitano H. Robust oscillations within the interlocked feedback model of Drosophila circadian rhythm. J. Theor. Biol. 2001;210:401–406. doi: 10.1006/jtbi.2000.2226. doi:10.1006/jtbi.2000.2226 [DOI] [PubMed] [Google Scholar]
- Waterfall J.J., Casey F.P., Gutenkunst R.N., Brown K.S., Myers C.R., Brouwer P.W., Elser V., Sethna J.P. Sloppy-model universality class and the Vandermonde matrix. Phys. Rev. Lett. 2006;97:150601. doi: 10.1103/PhysRevLett.97.150601. doi:10.1103/PhysRevLett.97.150601 [DOI] [PubMed] [Google Scholar]
- Yue H., Brown M., Knowles J., Wang H., Broomhead D.S., Kell D.B. Insights into the behaviour of systems biology models from dynamic sensitivity and identifiability analysis: a case study of a NF-κB signalling pathway. Mol. BioSyst. 2006;2:640–649. doi: 10.1039/b609442b. doi:10.1039/b609442b [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Mapping sensitivity