Diffusion of nitric oxide can facilitate cerebellar learning: A simulation study

Abstract

The gaseous second messenger nitric oxide (NO), which readily diffuses in brain tissue, has been implicated in cerebellar long-term depression (LTD), a form of synaptic plasticity thought to be involved in cerebellar learning. Can NO diffusion facilitate cerebellar learning? The inferior olive (IO) cells, which provide the error signals necessary for modifying the granule cell–Purkinje cell (PC) synapses by LTD, fire at ultra-low firing rates in vivo, rarely more than 2–4 spikes within a second. In this paper, we show that NO diffusion can improve the transmission of sporadic IO error signals to PCs within cerebellar cortical functional units, or microzones. To relate NO diffusion to adaptive behavior, we add NO diffusion and a “volumic” LTD learning rule, i.e., a learning rule that depends both on the synaptic activity and on the NO concentration at the synapse, to a cerebellar model for arm movement control. Our results show that biologically plausible diffusion leads to an increase in information transfer of the error signals to the PCs when the IO firing rate is ultra-low. This, in turn, enhances cerebellar learning as shown by improved performance in an arm-reaching task.

The gaseous second messenger nitric oxide (NO), which readily diffuses in brain tissue irrespective of cell membranes or processes, has been implicated in cerebellar long-term depression (LTD), a form of synaptic plasticity thought to be involved in cerebellar learning. It is not clear, however, what could be the advantage of NO diffusion for learning in general, and cerebellar learning in particular, because it appears at first that it should decrease synaptic specificity, the hallmark of Hebbian learning (1).

From its anatomy, the cerebellum can be analyzed in terms of small structural and functional units, or microcomplexes (2), which are defined by one-to-one relationships between inferior olive (IO) cell assemblies, groups of deep nuclear cells, and overlying microzones (3), which are narrow longitudinal strips of cerebellar cortex. The cerebellum has been proposed to be an associative learning device (4, 5), where each microcomplex is an adaptive unit associated with a unique bodily function (2). In this learning hypothesis, the granule cells (GCs) provide a sensori-motor context to the Purkinje cells (PCs) of the microzone, whereas the climbing fibers—the axons of the IO neurons—carry the error signals that modify the GC-PC synapses in a supervised manner. This theory is supported by experiments showing that the coactivation of GCs and climbing fiber inputs induces LTD of the GC-PC synapses (6), which is thought to be caused by the phosphorylation of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors (7). Furthermore, it has been shown that IO neurons carry teaching or error signals that are used for the acquisition of motor skills (8–11) and for conditioned motor behavior (12). In addition, according to modern computational theories of cerebellar motor learning (13, 14), the IO must transmit error signals with good temporal and spatial resolution so that individual microcomplexes can acquire internal models of sensory motor transformation (15). The ultra-low firing rates of IO neurons in vivo, rarely more than two or four spikes within a second (16), is consistent with these learning theories. Because, in these theories, the IO carries error signals only for learning and not for on-line control, the interference of the PC responses to the IO spikes (i.e., the complex spikes) with real-time motor control [carried by the simple spikes generated by parallel fibers (PFs)] should be minimal (9). However, the low firing rate challenges the assumption that the IO output carries rich information error signals necessary to learn complex internal models: during each movement, each PC will receive only one or two spikes. How can such a sporadic error signal lead to efficient cerebellar learning?

NO plays a role in cerebellar LTD (17, 18), as increased levels of NO ultimately inhibit phosphatases, thus preventing dephosphorylation (7). Cerebellar NO also has been directly related to adaptive behavior: the injection of NO synthesis inhibitors or NO scavengers impairs eye blink conditioning (19, 20), adaptation in a walking task (21), and adaptive changes in vestibulo-ocular reflex (22, 23). Although NO can be produced by PF stimulation (24–26), there is strong evidence that climbing fiber stimulation results in a large amount of NO production (27–29). This has been confirmed by experiments showing that a strong activation of the IO by harmaline results in a large amount of NO release in the cerebellar cortex (30, 31). Furthermore, electrical stimulation of the climbing fiber input seems to result in larger quantities of released NO in wider areas of the cerebellar cortex than that that occurs with PF stimulation alone (32).

NO directly diffuses away from the site of production (33) because it is extremely permeant, and can cross cell membranes, irrespective of the cellular processes. Because the sphere of influence of NO includes the synaptic terminal where it is released as well as terminals farther away, it can influence distant neurons. Given a diffusion coefficient of 3,800 μm²/s and a half-life of about 4 s (33), NO can diffuse 160 μm in all directions in 4 s (1). This sphere of NO diffusion is to be compared with the Purkinje soma width of 35 μm. Thus, even if the diffusion coefficient is smaller in vivo, it is highly probable that the NO released by a PC can affect several neighboring PCs.

In this paper, we examine how NO diffusion influences cerebellar learning. We first show that, when the mean IO firing is low, NO diffusion can improve the transmission of sporadic IO error signals to PCs within a microzone. Second, to investigate the relationship between NO diffusion, LTD, and adaptive behavior, we add NO diffusion and a “volumic” LTD learning rule (34) to a biologically plausible cerebellar model for adaptive arm movement control (35). Our simulation results show that NO diffusion can enhance cerebellar adaptive control.

Methods

Cerebellar Neural Model.

Testing whether NO diffusion can enhance cerebellar adaptive control requires a task that is sufficiently difficult to learn but still computationally tractable. Learning the inverse dynamics of a six-muscle, two-joint arm has this proper balance. Schweighofer et al. (35, 36) studied the role of the cerebellum in adaptive movement control by inserting a detailed cerebellar model into a basic control system model (cerebral cortex and spinal network) that fed crude motor commands to a six-muscle, two-joint arm. The cerebellar neural model could learn how to compensate for interaction torques that occur during reaching movements (37). The inputs to the mossy fibers were kinematic variables and the IO carried feedback errors. After learning the inverse dynamics of the arm, the outputs of the cerebellar neural network were the interaction torques necessary for precise control.

We simplified the architecture of the real cerebellar cortex by only considering a two-dimensional surface. The PC dendritic trees were thus flattened and reduced to rectangles. Here we slightly modified the architecture of the Schweighofer et al. model (35) to better take into account the anatomy of the cerebellar cortex. In the real cerebellum, microzones' widths range from under 500 μm to 1,500 μm and their lengths are up to several millimeters. For computational tractability, a microzone was modeled by a 315 × 630-μm surface and contained 27 PCs, each occupying a 35 × 210-μm rectangle; thus, there were nine columns and three rows of PCs per microzone (as drawn in the shoulder extensor microzone, left of Fig. 1). The cells were distributed in a shifted manner such that the same set of PFs crossed one PC dendritic tree of three along the PF beam. Furthermore, each PC domain was divided into 216 5 × 5-μm synaptic domains, which corresponded to GC synapses. To reflect the cerebellar connectivity of the previous model (35), the 27 PCs of a microzone then projected onto nine deep nuclear cells.

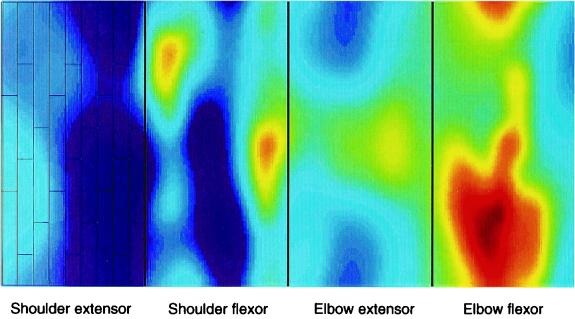
Figure 1.

Structure of the model of the cerebellar cortex and example of NO diffusion. We modeled four microzones: a flexor and an extensor microzone for the shoulder and the elbow joints. Each microzone contained nine columns and three rows of PCs as drawn on the left (shoulder extensor microzone). The color picture shows an example of the spatial aspect of NO diffusion in the model (k = 0.3 s⁻¹, D = 3,300 μm²/s); light colors show high NO concentrations. The large NO concentration in the most rightward microzone (elbow flexor microzone) was caused by a large error in the elbow flexor during this movement; conversely, low concentration in the most leftward microzone (shoulder extensor microzone) was caused by a small error in the shoulder extensor.

We modeled four microzones (35): a flexor and an extensor microzone for the shoulder and elbow joints. The microzones were innervated by a group of IO cells that received signals that reflected the errors in motor performance in joint coordinates (13, 35). Each error signal was distributed to 27 IO cells, i.e., there were as many IO cell as PCs, with a one-to-one connection. (Note that an alternative view is that different IO cells receive different signals, appropriate to different forms of error relevant to the task the microcomplex contributes to). Because the IO cells fire at a very low rate, they were modeled as spiking neurons. It has been shown by simulation that irregular, desynchronized firing caused by the electrical coupling of IO cells enhances input-output information transmission¶; in addition, successful cerebellar learning occurs best if the IO neuron firings are irregular (38). This hypothesis is supported by the apparently random IO firing in behaving animals at rest (39) and during ocular following response (9). Thus, to generate in vivo-like IO spikes, we used stochastic Poisson spike generators whose mean frequency was modulated by the error signals (1). The spikes lasted for 10 ms and, unless otherwise noted, we scaled the input signals such that the average firing rate was 0.5 spikes/s. Although this value might underestimate real IO firing rates, IO cells recorded during simulated arm movements before learning (see below) had maximum mean firing rates between 2 and 4 spikes/s, in line with biological data (8). Cerebellar connectivity and cellular parameters for the rest of the neural circuitry, which notably comprised 9 × 9 mossy fibers, 54 × 54 GCs, 3 × 3 Golgi cells, have been described (35).

NO Diffusion and Cerebellar Learning.

The equation that governs NO diffusion is the Fick's law and is given by:

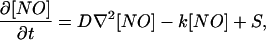1

where [NO] is the NO concentration, D the diffusion coefficient, ∇² the Laplacian operator, k the first-order kinetic decay, and S the source term. ∇²[NO] represents the rate of diffusion into/out of a given location, k[NO] is the rate at which NO disappears by reaction. We approximated the solution to this equation by considering the stationarity hypothesis: during a short time, the NO concentration is constant on the (very small) surface of each PF-PC synapse. After discretizing the Fick's law (40), we could simulate the concentration at GC-PC synapses. Because the time step needed to solve the NO concentration evolution equation depends on the diffusion and absorption constants, we adjusted the time step for NO diffusion so that the variation in NO at each synapse would not be more than 20% from one time step to the next. The time step for neural and arm dynamics was 5 ms. The time step for NO diffusion was typically 10 or 50 times smaller.

We assumed that NO is necessary for LTD induction and that NO arises solely from IO discharge (see below for an alternative). Because coactivation of PF and IO inputs induces LTD at the PF-PC synapses, LTD expression has been modeled by the negative product of the PF activity and the increment of the climbing fiber from its mean level (13). Here, we replaced the climbing fiber activity by the synaptic NO concentration, which was normalized by the maximum concentration. At each time step, the GC-PC synaptic efficacies are updated by the following “volumic” learning rule (34):

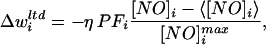2

where PF_i(t) is the PF activity, [NO]_j is the concentration of NO at the synapses, 〈[NO]_j〉 is the running average, and [NO]_i^max is the maximum concentration at this synapse recorded during a test trial before learning (see below). Dividing by the maximum concentration was necessary to compare learning results when varying the diffusion parameters, because large amounts of NO would artificially increase the learning rate. A subtractive normalization term was included in the learning rule to keep the sum of the weights constant for each PC. In a first approximation, we assumed that NO production is purely caused by climbing fiber activity, i.e., when the IO discharges, S = 1 in Eq. 1, and S = 0 otherwise. Fig. 1 shows an example of the spatial aspect of NO diffusion in the cerebellar cortical model (k = 0.3 s⁻¹, D = 3,300 μm²/s). Note the large NO concentration in the elbow flexor microzone, which was produced by a large elbow flexor error during this particular movement.

Finally, we considered a second learning rule for which PF also releases NO: the learning rule was the same as Eq. 2, but NO was produced by both IO cells and the GC synapses, in variable proportions. We scaled the NO produced by the average firing rates.

Task 1: Transmitting Sinusoidal Inputs at Various Frequencies.

In this first experiment, we assessed the information content of the NO signals by computing the mutual information (41) between the NO concentration at a particular synapse and a sinusoid input to the IO Poisson spike generators. The results did not depend on the cell recorded because all of the IO cells received the same input and there was symmetry in the connections. For each computation of the mutual information, both the NO concentration and the input variable were placed in 1,000 bins, thus creating 1,000 levels. Because of the delay between the excitation and the NO response, the mutual information reached a maximal value with a 20-ms delay. We then normalized this mutual information by the entropy of the input (the ratio is 1 for no information loss) and ran 10 series of 100 3-s trials for variable IO mean firing rates and for variable sinusoidal input frequencies.

Task 2: Learning to Control Reaching Movements.

We simulated planar reaching movements (duration 0.7 s) to eight targets on a circle of radius 20 cm around the start position. The target to the right of the start position was defined as the 0° direction, and targets at successive counterclockwise positions were given in 45° increments. At t < 0, the hand was on the 90° target. At t = 0 s, the target was first moved to the central position. At t = 1.2 s (i.e., 0.5 s after the end of the desired movement), the target was displaced to a new position, and so on. The straight, desired trajectories were generated by a minimum-jerk trajectory generator in extra-personal space and then converted to joint angles by an inverse kinematics transformation (35). To assess performance, we computed the mean square error (MSE) between the real and the desired trajectory during a test trial in which every target is visited once, sequentially (there were 16 movements in a test trial: eight to the targets and eight back to the initial position). We show the MSE after 200 movements normalized by the MSE before learning, which was 7.63 cm².

Results

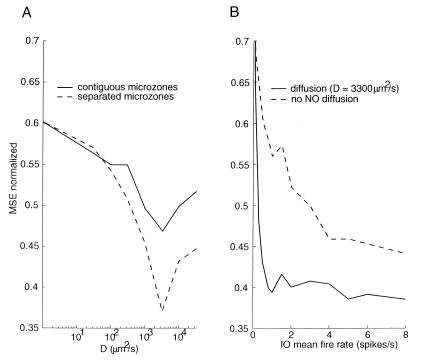
We first varied the mean firing rate of IO cells, which all received the same sinusoidal inputs. We then computed the mutual information between the excitation and NO concentration at a randomly chosen synapse with and without diffusion (D = 3,300 μm²/s; k = 0.3 s⁻¹ in both cases). As shown in Fig. 2A, when the IO mean firing rate was low, like in the real cerebellum (<3 spikes/s), diffusion provided better information transmission of the error signal to the PC. When the mean firing rate was high (>3 spikes/s), the nondiffusive system was more efficient because the PCs received enough information to rebuild the whole error message. Note that the diffusive system was more robust regarding changes in the firing rate than the nondiffusive system, which was very sensitive to such changes. For low firing rates, the diffusive system transmitted more than twice as much information as the nondiffusive system.

Figure 2.

Mutual information between sinusoidal excitation and NO concentration with and without diffusion. (A) As a function of IO mean firing rate. When the mean firing rate is low, diffusion provides better information to the learning synapses. (B) As a function of the sinusoidal input frequency. NO diffusion process is a low-frequency pass filter and it cannot carry high-frequency signals, so the efficiency of the error information transmission by NO decreased when the signal frequency increased.

To investigate the performance of the NO diffusive system in response to diverse inputs, we then varied the frequency of the sinusoidal excitation input (Fig. 2B). When the input frequency was less than 2 Hz, more than 60% of the information was transmitted after 100 trials. However, the information transmitted by NO decreased when the frequency of the signal was increased, because the NO diffusion process has a low-frequency tuning.

The most important parameters in our model were the diffusion coefficient D, and the first-order kinetic decay k in Eq. 1. We, therefore, performed extensive simulations of the arm movement task to find the values that gave the best learning performance. The best learning was obtained with k = 0.3 s⁻¹ (corresponding to a half-life of 3.33 s) and 2,000 < D < 3,300 μm²/s. These values are well within the biologically plausible range, at least in vitro (33). In Fig. 3A, we plotted the MSE after 200 movements as a function of the diffusion constant D for k = 0.3 s⁻¹; for values lower than D = 2,000 μm²/s; NO did not diffuse far enough and learning was poor. Conversely, for larger values, NO was too spread out and the input signals were too filtered for good learning.

Figure 3.

MSE for an arm reaching learning task after 200 movements. (A) As a function of the diffusion constant D for k = 0.3 s^-1 for the normal cerebellar cortex (plain line) and an idealized cerebellar cortex in which the microzones were artificially separated for NO diffusion (dashed line). (B) As a function of the inferior olive mean firing rate.

From its release point, NO can diffuse in any direction, so one synapse in a given microzone may receive, via diffusion, an error signal that originally was sent to a neighboring microzone. To evaluate the effect of these interferences in learning, we artificially separated all of the microzones (to limit the edge effects, each microzone was wrapped around), varied the diffusion constant, and computed the normalized MSE. The dashed curve in Fig. 3A shows that when the diffusion constant was increased, the separated model gave, as expected, better results than that obtained by the regular model: the error was almost half that of the nondiffusive system. Furthermore, the learning loss caused by microzone interference became higher when the diffusion constant increased.

We then computed the normalized MSE in the arm reaching task after 200 movements as a function of the IO firing rate for both a diffusing (D = 3,300 μm²/s) and a nondiffusing system (D = 0 μm²/s). As shown in Fig. 3B, for ultra-low (0.5–2 Hz) firing rates, diffusion dramatically enhanced learning. When the mean firing rate was higher than 4 spikes/s, however, the performance of the diffusive system was not much better than that of the nondiffusive system.

In the above experiments, NO was released solely from IO activity. Because several studies have indicated that NO also can be released through GC activity, we ran simulations to measure the MSE after 200 training movements while varying the amount of NO released from PF activity. We found that as long as the percentage of NO released by each PF spike was less than 20% of the NO released by each IO spike, then NO diffusion enhanced learning.

Discussion

In this paper, we showed that biologically plausible NO diffusion increases the transmission of sporadic IO error signals to PCs within a microzone. Furthermore, the improvement takes place only for parameter values corresponding to biological plausibility. Thus, besides the suggested role of NO diffusion in development and memory formation (42), we propose here that NO diffusion can enhance cerebellar learning. Although NO diffuses to neighboring synapses, we suggest that the unit of computation in the cerebellar cortex is still the synapse; the whole computation (here the computation of the interaction torques), however, is not performed by a single neuron, but by an entire group of PCs in a microzone. Because the IO cell's firing rate is low (at most one or two spikes will be generated during a movement), the PCs directly receive only a poor representation of the error signal necessary at each trial, which limits the learning process. Given a diffusion coefficient of 3,300 μm²/s and a half-life of 3.33 s, NO can diffuse 148 μm in all directions in 3.33 s in a two-dimensional plane or 182 μm in the three-dimensional tissue (see equation 11.26 in ref. 1). This sphere is to be compared with the PC soma width, 35 μm. Thus, NO released from an IO discharge affects several neighboring PCs and distributes the sporadic error signal to other PCs of the microzone, which enhances learning. Note, however, that an alternative view to the one proposed here is that different PCs could receive different signals, appropriate to different forms of error relevant to the task the microcomplex contributes to. Comparing the complex spike discharges of several PCs during movements within a microzone may shed light on this issue.

We identified three limitations of NO diffusion for cerebellar learning: (i) decay in the high-frequency signal, (ii) interference between microzones, and (iii) possible error independent plasticity caused by NO release from PF activity. In the following, we address these limitations in light of our results and the assumptions we have made.

(i) Considering the results of Fig. 2B regarding the limit frequency for information transmission through NO diffusion, we performed a frequency analysis of the IO inputs during the 16 test movements. This analysis showed that the input signal energy was carried mostly by frequencies between 0 and 5 Hz. However, Fig. 2B shows that frequencies superior to 2 Hz are not properly transmitted. Thus, some high-frequency harmonics of the signal error may not be carried properly by the NO diffusion process. This result may constitute a limit to NO enhanced learning. Higher frequencies might, however, be directly transmitted via the second, NO independent, biochemical pathway that is involved in cerebellar LTD formation. Protein kinase C (PKC), which is activated by both calcium entry through voltage-gated calcium channels caused by climbing fiber activation and by diacylglycerol produced by activation of metabotropic receptors at GC-PC synapses, phosphorilates α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors, and thus depresses synaptic efficacy (7). We currently are developing a biochemical model of LTD that includes both the NO and the PKC pathways. From such a model it will be possible to derive learning rules that take into account direct PF and IO activities (by the PKC pathway) as well as NO diffusion (by the NO pathway).

(ii) We have shown that, between contiguous microzones, NO diffusion creates interferences that impede learning when compared with an ideal cerebellum in which there is no diffusion from one microzone to the next. However, this interference problem might be overestimated in the model when compared with the real cerebellum for two reasons. First, the microzones in the model were only 315 μm wide, whereas actual biological values are between 500 and 1,500 μm (2). Second, our model consisted of 108 PCs only, each of 35 μm width, whereas the PC dendritic tree in the real cerebellum is about 9 μm. Diffusive NO is thus likely to reach many more PCs than in the model.

(iii) NO also has been considered to be produced by PF stimulation (24–26). This could be a problem for our NO-enhanced learning hypothesis, as we found that NO release from GCs decreased the efficiency of cerebellar learning resulting from NO diffusion. The cause of this loss in learning efficiency is that the critical signal to be transmitted in the system is not the GC activity but the error signal, which is of ultra-low frequency. The presence of NO released from GCs is a noise worse than uncorrelated noise added to the error signal, and it therefore degrades the system's global learning performance. This issue could be resolved by performing precise quantitative measurements of NO release after climbing fiber and PF stimulation. Finally, an assumption we made in the model was that all nearby PFs carry relevant information. However, because this is unlikely, a volumic learning rule such as Eq. 2 would create wrong associations between the irrelevant PF inputs and the errors carried by NO diffusing from nearby PCs. It has been proposed that metaplasticity at the PF-PC synapses, i.e., plasticity of the individual learning rates, could allow the PCs to ignore irrelevant PF inputs (43). Thus, we propose that an extended version of our volumic learning rule that includes metaplasticity could lead to efficient cerebellar learning even when nearby PFs carry irrelevant information.

It is possible to test our volumic LTD learning rule by the following experiment. Recent advances in optical imaging allow for the study of both the temporal and the spatial extent of NO diffusion at the surface of the cerebellar cortex‖. We propose to stimulate the PF beam and climbing fiber input with a protocol that induces LTD while simultaneously monitoring the spread of NO diffusion with optical recording. Then by testing for synaptic depression in neighboring Purkinje neurons on beams that were not excited by the IO stimulation but within the range of NO diffusion, evidence supporting the LTD volumic learning rule could be obtained.

Abbreviations

LTD

long-term potentiation

IO

inferior olive

PC

Purkinje cell

GC

granule cell

PF

parallel fibers

MSE

mean square error