Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2009 Jul;182(3):899–910. doi: 10.1534/genetics.109.102756

Association Studies Identify Natural Variation at PHYC Linked to Flowering Time and Morphological Variation in Pearl Millet

Abdoul-Aziz Saïdou *,†,‡, Cédric Mariac *,†, Vivianne Luong *, Jean-Louis Pham *, Gilles Bezançon †, Yves Vigouroux *,†,1
PMCID: PMC2710168  PMID: 19433627

Abstract

The identification of genes selected during and after plant domestication is an important research topic to enhance knowledge on adaptative evolution. Adaptation to different climates was a key factor in the spread of domesticated crops. We conducted a study to identify genes responsible for these adaptations in pearl millet and developed an association framework to identify genetic variations associated with the phenotype in this species. A set of 90 inbred lines genotyped using microsatellite loci and AFLP markers was used. The population structure was assessed using two different Bayesian approaches that allow inbreeding or not. Association studies were performed using a linear mixed model considering both the population structure and familial relationships between inbred lines. We assessed the ability of the method to limit the number of false positive associations on the basis of the two different Bayesian methods, the number of populations considered and different morphological traits while also assessing the power of the methodology to detect given additive effects. Finally, we applied this methodology to a set of eight pearl millet genes homologous to cereal flowering pathway genes. We found significant associations between several polymorphisms of the pearl millet PHYC gene and flowering time, spike length, and stem diameter in the inbred line panel. To validate this association, we performed a second association analysis in a different set of pearl millet individuals from Niger. We confirmed a significant association between genetic variation in this gene and these characters.

DOMESTICATION and dispersion of cultivated plants were associated with their adaptation to the agricultural environment. These adaptations led to genetic changes shared by all individuals of a cultivated species (domestication genes) or to variations between varieties within a cultivated species (genes controlling varietal differences). Domestication genes like tb1 (Doebley et al. 1997; Wang et al. 1999) in maize (Zea mays) were selected very early by human populations (Jaenicke-Després et al. 2003). After the first early selection, adaptation of the flowering phenotype to different climatic conditions was certainly a key innovation that enabled colonization of new environments. One of the most well-known examples was the adaptation of maize—a tropical plant—to northern climates. Maize cultivation spread late to northeastern America. By 1000 YBP, only maize was an established staple crop (Fritz 1995). A genetic variant of the Dwarf8 gene led to an earlier flowering phenotype (Thornsberry et al. 2001). This early allele was present at a high frequency in North America and was certainly selected after the domestication of maize under northern climatic conditions (Camus-Kulandaivelu et al. 2006).

Pearl millet (Pennisetum glaucum [(L.) R. Br.]), one of the most important West African cereals, was most likely domesticated once in the Sahelian zone of West Africa (Oumar et al. 2008). By 3500 YBP, it was already being cultivated throughout Sahelian and tropical West African countries (D'Andrea et al. 2001; D'Andrea and Casey 2002). The adaptation of pearl millet in West Africa was also associated with an environmental gradient (Haussmann et al. 2006). Pearl millet varieties from tropical coastal West Africa flower very late (up to 160 days from planting to female flowering) as compared to varieties from Sahelian West Africa, which may have a flowering time as short as 45 days (Haussmann et al. 2006). The genetic factors underlying the differences between these varieties are still unknown.

Association studies offer new opportunities for assessing the role of a particular gene on a phenotype. Contrary to QTL analysis, association studies have the challenging task of taking an unknown evolutionary history of studied individuals into account. For example, population structure is a common confounding effect in association studies (Pritchard et al. 2000a). Allele frequencies evolve between divergent structured populations via drift, mutation, and selection. Differences in allele frequencies may be correlated with any morphological traits that differentiate two populations. Then a statistical correlation between a gene and a trait is not necessarily associated with a “causative” relationship between the gene and the morphology, which can lead to a high number of false positives. The use of population structure to correct the number of false positives was a significant breakthrough in plant studies (Thornsberry et al. 2001). This approach was recently further refined by also using a matrix of kinship coefficients, which proves efficient when there is a complex structure and familial relationship between individuals (Yu et al. 2006; Kang et al. 2008; Stich et al. 2008). Complex structures and familial relationships are common in inbred cultivated crop material. In the current association study framework (Thornsberry et al. 2001; Yu et al. 2006; Casa et al. 2008; Kang et al. 2008; Stich et al. 2008), population structure was assessed using STRUCTURE software (Pritchard et al. 2000b). This tool is not implemented to deal with selfed inbred materials or inbred species (Pritchard et al. 2000b). Through new methodological developments, population structure analysis can now be performed using Bayesian methods in these particular cases (Gao et al. 2007). The extent to which the power of association studies will differ when dealing with inbred material or selfing species using either Bayesian method has yet to be evaluated.

In this study, we developed an association framework for pearl millet to assess the role of flowering pathway genes. We assessed the ability of the method to control the number of false positives, while taking different methodological inferences of population structure that allow inbreeding or not into account. We also assessed the power of the association framework to detect given additive genetic effects. Finally, we applied this method to a set of eight flowering time gene homologs sequenced in pearl millet. We assessed sequence variation in light perception genes (PHYA, PHYB, PHYC, and CRY2) and downstream regulators of flowering (GI, Hd6, Hd1, and FLORICAULA). Variation was detected in the PHYC gene associated with variations in flowering time and morphological traits. This association was noted in two different data sets.

MATERIALS AND METHODS

Field experiments:

For the association framework, a set of 90 pearl millet inbred lines was used (supporting information, Table S1). These inbred lines had diverse origins: India and West and East Africa. They were obtained from T. Hash [International Crops Research Institute for the Semi-Arid Tropics (ICRISAT), Hiderabad, India], J. Chantereau (Centre de Cooperation Internationale en Recherche Agronomique pour le Développement, Montpellier, France), and T. Robert and A. Sarr (University Paris XI, Paris).

These inbred lines were characterized in three experimental field trials during the rainy season. Planting dates were July 9, 2005, June 16, 2006, and July 13, 2006. Hereafter, we refer to these three different field trials as 2005, 2006a, and 2006b, respectively. The experiments were performed at the ICRISAT field station in Sadore, Niger. The plant spacing was 0.7 × 0.7 m. Inbred individuals from given inbred lines were sown in a row and the locations of inbred lines were randomized. For each pearl millet inbred line, data from 6–10 individuals were separately scored for days from planting to the female flowering stage (FT), the number of basal tillers at head emergence (NTHE), plant height (PH), stem diameter (SD), basal primary spike diameter (BSpD), primary spike length (SpL), and primary spike diameter (SpD). Average values of each inbred line were calculated for each field trial and each morphological and phenological trait. To obtain an inbred line average trait effect for the total field trials, we fitted the mixed model yijkl = μ + xi + zj + vjk + ɛijk, where yijkl was the phenotype of individual l of the i inbred line, in the j field trial, in the k subplot. The value ɛijk was the residual error and μ the grand mean. Inbred lines (xi) were considered as fixed effects and field trial (zj) and subplot (vjk) were considered as random effects. For each trait, the best linear unbiased effect (BLUE) was estimated for each inbred line i as 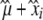Inline graphic. The model was fitted using R (http://cran.r-project.org/) and the lmer() function. The BLUE of each trait was then used for association studies.

We also used a set of 598 different pearl millet varieties originating from Niger. These landraces were sampled throughout the country from 0°E to 13.3°E latitude and from 12°N to 15°N longitude (Table S1). Each landrace was sown in 2004 and 2005 during the rainy season at the ICRISAT field station in Sadore, Niger. The plant spacing was 0.7 × 0.7 m. For each accession, data from five individuals were recorded on flowering time from planting to female flowering stage, the number of tillers at head emergence, plant height, stem diameter, primary spike length, primary spike diameter, and thousand seed weight (TSW). The averages for each trait were calculated per accession for each field trial and used for association studies. We also used a BLUE estimate of each trait, using the procedure previously described for inbred lines.

SSR and AFLP genotyping:

DNA was extracted from inbred lines and pearl millet varieties as previously described (Mariac et al. 2006b). Pearl millet inbred lines were genotyped three to four times, using a set of 27 microsatellite loci (Oumar et al. 2008) on plants from 2005 and 2006 field trials. The PCR conditions and methods were previously described (Oumar et al. 2008). Consensus genotypes were obtained as follows. If one of the four multilocus genotypes was markedly different from the three others, this genotype was excluded and classified as erroneous. If, for an inbred line, the multilocus was identical at most of the loci but a variation was observed at a given locus, the most frequent genotype was conserved. This variation was attributed to genotyping errors or to residual diversity segregating in the inbred lines. The same inbred lines were also genotyped with AFLP markers (Vos et al. 1995), using the method previously described in pearl millet (Allinne et al. 2008). A total of six primer pair combinations with three specific bases were used (E-AAC/M-CTT, E-ACA/M-CTT, E-AGC/M-CTT, E-ACA/M-CTG, E-AGC/M-CTG, and E-AAC/M-CTG). The letters E and M represent the sequences ACTGCGTACCAATTCAG and GATGACTCCTGAGTAA corresponding to EcoRI and TruI adapters, respectively. AFLP-Quantar (Keygen) software was used to identify and count the number of polymorphic bands. Two independent readings were performed per gel and only reliable loci were used. A total of 306 locus markers were identified.

For the second association population, an individual of each variety was genotyped with 25 microsatellite loci. A total of 598 different plants were genotyped. All varieties were genotyped according to a previously published (Mariac et al. 2006a) protocol and this data set has already been partially published (Mariac et al. 2006a).

Sequencing:

Primers for partial amplification of eight flowering genes (Table S3) were designed or obtained from previously published studies (Mathews et al. 2000). Fragments ranging from 200 to 1175 bp in size were amplified by PCR with 0.2–0.4 μm of each primer, 0.5 units of Taq polymerase, 1× GoTaq Buffer (Promega, Madison, WI), 0.200 mm dNTP, and 20 ng genomic DNA in a 30-μl final volume. Amplifications were performed as follows: 35 cycles of 30 sec at 94°, 90 sec at 50°–64° (depending on the primer Tm), and 60 sec at 72°, ending with 10 min at 72°. PCR products were purified using Ampure kits (Agencourt Bioscience) and sequence reactions were performed using the BigDye v3.1 Terminator kit (Applied Biosystems, Foster City, CA). Sequence reactions were purified with CleanSeq kits (Agencourt Bioscience) and read on an ABI 3130 XL automated sequencer (Applied Biosystems). Forward and reverse sequences were obtained for inbred lines.

Sequence data analysis:

To confirm amplification of the targeted gene, all gene sequence data obtained in pearl millet were confirmed using Blastn (MegaBlast) analysis. We calculated the percentage of polymorphic sites, the pairwise nucleotide diversity (π), Watterson's estimator (θ) of diversity, Tajima's D (Tajima 1989), and Fu and Li's D* and F* (Fu and Li 1993) using DNAsp version 4.10.3 (Rozas et al. 2003). All SNP and indel polymorphic sites were used for this analysis. The linkage disequilibrium and its significance were estimated on the basis of r2, using TASSEL software version 2.0.1 (Buckler et al. 2007).

SNP genotyping:

To genotype pearl millet varieties, a restriction assay using PvuII was performed to recognize an SNP C/G at position 697 on the amplified PHYC fragment. The PHYC gene was amplified by PCR with 0.2 μm of each forward and reverse primer (Table S3), 0.5 units of Taq polymerase, 1× GoTaq buffer (Promega), 0.200 mm dNTP, and 20 ng genomic DNA in a 30-μl final volume. Amplifications were performed as follows: 35 cycles of 30 sec at 94°, 30 sec at 55°, and 60 sec at 72°, ending with 10 min at 72°. PCR reactions were digested with PvuII as recommended by the supplier (Fermentas) immediately following amplification. About 10 μl of the digestion were loaded on a 2% (w/v) agarose gel for genotyping. Genotypes were scored as C/C, G/G, and C/G according to the digestion pattern.

Population structure analysis:

Bayesian methods:

For inbred lines, we analyzed the population structure using STRUCTURE (Pritchard et al. 2000b; Falush et al. 2003) and INSTRUCT (Gao et al. 2007) software. The number of populations tested ranged from K = 1 to K = 10. STRUCTURE runs were performed with 106 iterations and a burn-in period of 30,000. Ten independent simulations were performed. INSTRUCT parameters involved 200,000 iterations, including a burn-in of 100,000. INSTRUCT allows a different selfing rate for each individual plant and seems more appropriate for inbred line materials. For landraces, we used only the STRUCTURE method as pearl millet is an outcrossing cereal species. We varied the number of populations from K = 1 to K = 5 and 10 independent simulations were performed.

Choice of K and comparison of methods:

For STRUCTURE, we used the method of Evanno et al. (2005) based on the second-order rate of change of likelihood. For INSTRUCT, we used the deviance information criterion (DIC) to infer optimal K (Gao et al. 2007). The results obtained by both methodologies were compared for each K value. To measure differences between INSTRUCT and STRUCTURE results, we compared the ancestry values for each population obtained with each method. For an individual i, let qik and q′ik be the ancestry of individual i from STRUCTURE and INSTRUCT, respectively, where k is the population. The two methods gave relatively similar results and it was easy in the present case to associate the qik and q′ik values to “the same population,” i.e., a population that pooled a common set of individuals in the STRUCTURE and INSTRUCT results. We calculated a similarity index of ancestry per individual: 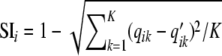Inline graphic. We then calculated the average similarity index for all inbred lines: 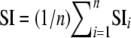Inline graphic. This index ranged from 0 if individuals were associated with different groups to 1 if the results obtained by both methods were identical. To compare the STRUCTURE and INSTRUCT results, we used the ancestry Q matrix obtained with the highest likelihood run.

Association studies:

Model:

We used a linear mixed model to determine associations between morphological traits and genetic variations (Yu et al. 2006). This model took into account (1) the population structure of the inbred lines based on the ancestry Q matrix of each individual inbred line in K − 1 populations and (2) the family relationship between individuals through the kinship coefficient matrix.

The association model was y = Xβ + Sα + Qv + Zu + e, where y was the phenotype vector, β was a fixed effect other than SNP or population structure, α was the vector of a given SNP fixed effect, v was the vector of population structure fixed effects, u was the vector of background genetic effects, and e was the residual error vector (Yu et al. 2006). Q was the population ancestry matrix. X, S, and Z were 0/1 matrices relating y to β, α, and u vectors. The variance of the random effect u was expected to be Var(u) = KM V, where KM is the kinship matrix and V the variance (Yu et al. 2006).

We used the kinship package (Atkinson and Therneau 2008; Ingvarsson et al. 2008) to implement the mixed-model approach. The mixed model was fitted using a maximum-likelihood method. Different nested models were assessed: the most complete model that included population structure ancestry and kinship matrix, models without kinship matrix or population structure, and a null model that disregards the population structure and kinship matrix. The different models were compared to the complete model by calculating a likelihood ratio Λ, and the −2 ln Λ value was statistically assessed for significance using a χ2-distribution with the number of degrees of freedom equal to the difference in the number of parameters between the two models.

For the association analysis of an SNP with a trait, we used either the kinship package or the mixed-model method implemented in TASSEL (Buckler et al. 2007). The two methods gave similar results but the method implemented in TASSEL was particularly user friendly with respect to managing SNP, trait, matrix, and population structure data sets. For inbred lines, we used microsatellite loci to infer population structures and AFLP markers to calculate the kinship matrix. Kinship coefficients were calculated using SPAGeDI (Hardy and Vekemans 2002). Kinship coefficients lower than zero were set at zero. For pearl millet varieties, the kinship coefficient was calculated using the method of Loiselle et al. (1995) implemented in SPAGeDI (Hardy and Vekemans 2002). This method is adapted to heterozygote diploid individuals in the case of multiallele and multilocus data sets.

For the mixed-model analysis of the kinship package, the kinship matrix needs to be positive definite (Atkinson and Therneau 2008); i.e., all the matrix's eigenvalues need to be positive. However, kinship matrix estimations might lead to non-positive-definite matrices (Atkinson and Therneau 2008). To obtain a positive-definite matrix, we adapted an ad hoc procedure from Hayes and Hill (1981). With M being the non-positive-definite matrix, we need to find M′, i.e., a matrix highly correlated to M but positive definite with diagonal elements of 1 and only positive values for all elements. To obtain such a matrix, we decomposed the M matrix into its eigenvectors and eigenvalues. Eigenvalues lower than an arbitrary threshold of 10−4 times the higher eigenvalue were set to this threshold. There is at least one such element since a non-positive-definite matrix is defined as having a least one negative eigenvalue. A new matrix M′ could then be rebuilt using the new eigenvalues and eigenvectors. The problem of this method is that the new matrix M′ might have small negative values. To avoid this problem, we did not apply the procedure to M but rather to M − ɛ, with ɛ being a square matrix of the same size as M with all elements equal to a small negative value ɛ. A possible value for ɛ is the minimum value of M′ (if negative) or 0. Using the previously described procedure, we obtained the matrix (M − ɛ)′. Each row of this new positive-definite matrix (M − ɛ)′ was then standardized, so the diagonal was 1. To measure the extent of the modification, a Spearman correlation between the initial matrix M and standardized (M − ɛ)′ matrix was calculated and compared using the Mantel test (Sokal and Rohlf 1991).

Assessment of type I error:

We performed an analysis using microsatellite and AFLP alleles to assess the ability of the linear mixed-model (LMM) method to reduce type I errors for the inbred lines data set. We used all microsatellites of AFLP alleles having a frequency >2.5% to perform association studies. For each allele, the association between the presence or the absence of the allele and a trait was assessed. When the allele occurrence and phenotype are strictly independent, 5% of the alleles could be expected to have a significant association at the 5% level. This analysis was performed independently for three different phenotypic traits: flowering time, primary spike length, and primary spike diameter. We wanted to assess the extent to which taking the population structure and family relationship into account reduced the type I error. We thus considered a population number ranging from K = 1 (no structure) to K = 7 using the Q matrix obtained by the STRUCTURE and INSTRUCT methodological approaches. The kinship matrix (KM) obtained from AFLP data or a noninformative kinship matrix was also used. The uninformative matrix (UKM) was built by setting the relationship between two different individuals at 0 (no relatedness). The analysis output is a percentage of false positives for different inferences of population structure and family relationship (STRUCTURE + UKM, INSTRUCT + UKM, STRUCTURE + KM, and INSTRUCT + KM), for a different number of accepted populations, K (K = 1 to K = 7), for different phenotypic traits (FT, SpD, and SpL), and for the three field trials. The number of false positives was compared using the Kruskal–Wallis test. Paired data from AFLP-based false positive rates and SSR-based false positive rates were compared using Wilcoxon's paired tests.

Empirical P-value threshold:

Taking the population structure and family relationship into account could, however, lead to a higher type I error rate than the commonly used 5% threshold. We therefore also calculated an empirical threshold. To do so, we used AFLP and microsatellite allele data to perform association studies taking the population structure (K = 7) and kinship matrix into account. To calculate a corrected threshold, the P-values associated with AFLP and microsatellite alleles were ordered from the lowest to the highest value. The corrected P-value threshold corresponded to the P-value associated with microsatellite or AFLP alleles having a rank of 5%. This value was specific to each phenotype/field trial, and we calculated a separate threshold on the basis of the AFLP and microsatellite data sets.

Power analysis:

We performed a simulation analysis to assess the power of this methodology for detecting an additive effect in pearl millet. A set of inbred lines was used to create an SNP data set having a given flowering time effect. We first randomly attributed the causative SNP to an inbred line. Then, for each inbred line having the causative SNP, the flowering time value was increased by adding a certain amount of flowering time (in days). We used the best linear estimates of flowering times for all field trials. This additive effect ranged from 0 to 22 days. We also calculated this additive effect in terms of genetic effect ratio (Yu et al. 2006), i.e., as a percentage of the flowering time standard deviation. The genetic effect ratio ranged from 0 to 2.9. We varied the frequency of the causative SNP allele in the inbred lines: frequencies of 50, 25, 12.5, 6.25, and 3.12%. One hundred random data sets were created for each given set of parameters (SNP frequency, a given additive effect). Association analyses using these data sets were performed to detect the SNP effect, using the mixed linear model with the INSTRUCT or STRUCTURE Q matrix for K = 7 and the kinship matrix. The percentage of tests that were significant (out of 100 data sets) at the 5% level was used as a measurement of the probability of detecting the SNP effect on the phenotype. This value was obtained for each SNP frequency (5 different values) and additive effect (21 values).

RESULTS

Pearl millet diversity and structure:

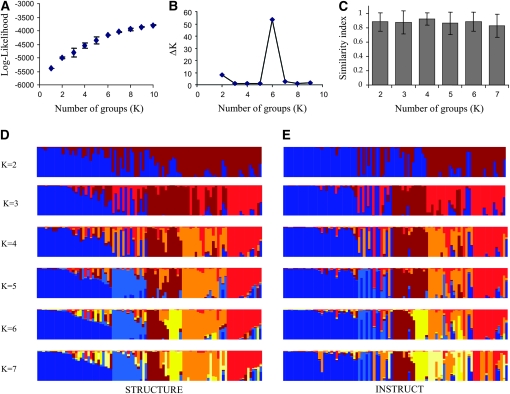
Of the 27 microsatellite loci, 25 were polymorphic enough on the 90 inbred lines to be used for subsequent analyses. The total number of alleles detected was 188. An average number of 7.5 alleles per locus were found with an average gene diversity of 0.56. The observed heterozygosity was low (0.059) as expected for inbred materials. The data set structure was first estimated using STRUCTURE. The log-likelihood increased as K increased and did not show evidence of a maximum (Figure 1A). We calculated the second-order change in log-likelihood (Figure 1B) and found a strong signal for K = 6. On the basis of this result, we considered K = 6 as being the supported number of populations. INSTRUCT uses a deviance criterion to infer K. The DIC value was lowest for K = 7 (DICK=7 = 6116.08). We calculated a similarity index to assess the difference between the results of the two methods (Figure 1C). The average similarity index for all individuals was >82.5% regardless of the number of K populations. The highest value was obtained for K = 4 at 92% but then the similarity index tended to decrease to 82.5% for K = 7. Visual comparison of the output of STRUCTURE and INSTRUCT (Figure 1, D and E) showed an apparent similarity. However, numerous differences were noted and some individuals were grouped with different clusters.

Figure 1.—

Figure 1.—

Open in a new tab

Analysis of the population structure of pearl millet inbred lines. The analysis of population structure in inbred lines was performed using STRUCTURE (Pritchard et al. 2000b; Falush et al. 2003) and INSTRUCT (Gao et al. 2007). (A) The average log-likelihood and the standard error of 10 different runs of STRUCTURE were calculated. The log-likelihood showed a steady increase as the number of groups (K) increased, and no clear maxima were detected. (B) To assess the number of groups (K) supported by the analysis, we also calculated the second-order change in the log-likelihood ΔK (Evanno et al. 2005). A clear change was detected for K = 6, suggesting six was the number of groups supported by the STRUCTURE analysis. To allow a comparison of the two Bayesian structure inference methods of STRUCTURE and INSTRUCT, we calculated a similarity index (see text for details). (C) The average similarity index and standard error values for each individual were reported. The average similarity index was >80% in most cases, suggesting similar inference of ancestry results for each plant. We finally represented the results of a run of STRUCTURE (D) and INSTRUCT (E) to enable direct visual comparison of the two methods. The graph (D) represents the run with the highest likelihood of STRUCTURE for a number of populations (K), and E represents the run of INSTRUCT that showed the lowest deviance information criterion (DIC). The ancestry (q) of each of the inbred lines in a population is represented by a different color. The different colors correspond to the different populations identified by STRUCTURE and INSTRUCT. The global visual comparison highlighted a global similarity, but some differences were clearly observed between the two analyses.

A total of 306 AFLP markers were identified. The average gene diversity was 0.29. Kinship coefficients between 0 and 0.35 represented 99% of the data points of the distribution (Figure S1). A total of 67.5% of the kinship coefficients suggested that there was no or low relatedness between inbred lines with kinship values ranging from 0 to 0.05. A significant fraction (31.5%) showed various degrees of relatedness, with kinship ranging from 0.05 to 0.35. Finally, only 1% showed relatedness >0.35. This relatedness was illustrated in a phylogenetic relationship between inbred lines (Figure S2). Few inbred lines showed weak genetic dissimilarity (and so high kinship), but a large share of the inbred lines were weakly related.

Morphological traits:

The days to female flowering of inbred lines ranged from 35.0 to 98.0 days, with a mean of 58.8 (SE ±0.54) days for all field trials. The mean spike morphological values were 0.46 (SE ±0.54), 2.20 (SE ±0.034), and 25.6 (SE ±0.79) for basal primary spike diameter, primary spike diameter, and spike length, respectively. The number of basal tillers at heading date was 8.50 (SE ±0.20). Finally, the mean stem diameter was 1.04 (SE ±0.016) and the mean plant height was 83.9 (SE ±0.016).

Association study:

We reported the likelihood for the different models considered, using STRUCTURE or INSTRUCT (Table 1). The complete model, including population structure and kinship matrix, is generally better than models with structure only or kinship only and always better than a null model (Table 1). Comparisons of nonnested models are generally based on the Akaike information criterion (AIC), with AIC = −2 log-likelihood + 2k, with k being the number of parameters. For our purposes, we wanted to compare models with STRUCTURE or INSTRUCT considering the same number of populations. So the highest likelihood would lead to the lowest AIC for the same number of k parameters. We noted that for K = 7, STRUCTURE always gave a better fit. However, when comparing the likelihood for different K values (Figure S3), the INSTRUCT and STRUCTURE results were similar, or sometimes better with INSTRUCT (for flowering time), for K < 4. However, as K increased, STRUCTURE always performed better for each of the considered traits (Figure S3). In summary, STRUCTURE led to a better likelihood for the highest number of assumed populations (K = 7).

TABLE 1.

−2 log-likelihood of the different statistical models

INSTRUCT
STRUCTURE
Model FT SpL SpD FT SpL SpD
Null 576.86*** 678.20*** 84.96*** 576.86*** 678.20*** 84.96***
KM 551.76** 638.26*** 60.46 (NS) 551.76*** 638.26*** 60.46***
Q7 533.76 (NS) 625.54*** 57.76* 526.78(ns) 597.56*** 40.80***
KM + Q7 531.26 607.98 52.06 526.78 586.18 32.76
Open in a new tab

The models tested include the null model, where neither population structure nor family relatedness are considered, the model where only family relatedness is considered (KM), structure only (Q7), and both KM + Q7. Q7 corresponds to ancestry obtained with STRUCTURE or INSTRUCT with seven populations. Comparison of the most complete model (KM + Q7) to other models is based on a χ2-test. Significance is noted as follows: NS, nonsignificant; *P < 0.05, **P < 0.01, and ***P < 0.001.

Using microsatellite allele data, the population inference method (INSTRUCT/STRUCTURE) and an informative or noninformative kinship matrix did not have a significant effect on the rate of false positives for flowering time (Kruskal–Wallis test, P = 0.97), spike diameter (Kruskal–Wallis test, P = 0.95), or spike length (Kruskal–Wallis test, P = 0.76). The effect of the population number (Figure S4) was highly significant regardless of the character considered: flowering time (Kruskal–Wallis test, P < 0.001), spike length (Kruskal–Wallis test, P < 0.001), or spike diameter (Kruskal–Wallis test, P < 0.001). For flowering time, the type I error rate ranged from 18.1% (K = 1, no structure) to 5.6% for K = 3 (Figure S4). The type I error rate increased as K increased from K = 4 to K = 7, while for K = 7 the type I error rate was 7.2%. For spike diameter (Figure S4), the type I error rate decreased from 16.5% (K = 1) to 7.8% (K = 7). Finally, the spike length showed the highest rate of false positives (Figure S4), with values of 27.2% at K = 1 and 11.9% at K = 7. We observed similar results when we used AFLP alleles rather than SSR alleles (Figure S4, statistical analysis not shown). However, although no overall difference in false positive rate was observed between AFLP and SSR allele-based distributions for spike diameter (P = 0.28), the AFLP data showed a significantly higher global false positive rate for spike length (Wilcoxon's test, P < 0.004) and flowering time (Wilcoxon's test, P < 10−6).

We analyzed how these three characters (spike length, spike diameter, and flowering time) were associated with the population structure. We thus considered only K = 3 to have enough individual plants in the different groups and set the ancestry threshold at 0.70 to determine whether the plants belong to one of the three groups. We then performed a Kruskal–Wallis test for each field experiment and used a Fisher combining probability to obtain a statistical test pooling the results of the three field experiments. All characters covaried with the population structure. Spike length showed the strongest covariation signal with respect to the population structure (χ2 = 92.3, P < 10−17), then flowering time (χ2 = 74.4, P < 6 × 10−14), and finally spike diameter (χ2 = 28.5, P < 8 × 10−5).

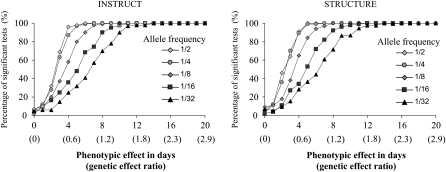
The power of the method for detecting a given additive effect on the flowering time character was assessed with different allele frequencies (Figure 2). The given additive effect was a number of days or a genetic effect ratio (Yu et al. 2006; Stich et al. 2008). The genetic effect ratio was the number of days divided by the standard deviation. Modest effects of <2 days (a genetic effect ratio of 0.22) could not be easily detected regardless of the allele frequency of the SNP. An effect of 6 days was easily detected even for alleles with a frequency of 12.5%. Alleles present at low or very low frequency (1/16 or 1/32) were detected only if they had a strong effect on the phenotype (12–16 days). Some authors have presented this effect as a percentage of the explained variance, which depends both on the standard deviation of the studied trait and on the allele frequency (Yu et al. 2006; Stich et al. 2008). For comparison, with an SNP frequency of 20% in our simulation, the percentages of explained variance for differences of 2 days, 6 days, and 10 days were 1.4, 11.1, and 25.8%, respectively. The analysis performed using ancestry, as estimated with INSTRUCT, did not show a marked difference with respect to the STRUCTURE findings (Figure 2).

Figure 2.—

Figure 2.—

Open in a new tab

Power to detect a given flowering phenotypic effect as a function of the allele frequencies. We calculated the probability of finding a significant association at P < 0.05 for a simulated allele having a given flowering phenotypic effect. The allele frequency ranged from 50% (1/2) to 3% (1/32). The additive effect was number of days to flowering from 0 to 22 days. Weak phenotypic effects of <2 days were difficult to identify regardless of the allele frequency. For an additive effect of 6 days, the probability of detection of the effect was high when alleles had a frequency of 12.5–50%. It was, however, only 60% for alleles with a frequency 6% and 40% for alleles with a frequency of 3%. Low-frequency alleles were detected only when they had a large phenotypic effect (≥16 days).

Gene sequence diversity:

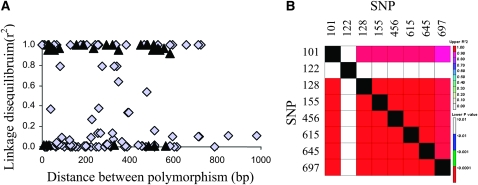
All primers designed in this study led to sequences with high Blast values with respect to the targeted gene (Table S4). The average percentage of polymorphic sites was 0.64% (Table 2). Polymorphic site indels and SNPs were considered in the present analysis. The average θ-value was 1.1 × 10−3 and the average π-value was 1.6 × 10−3. The average Tajima's D value for all eight loci was 0.66, with a slight bias toward positive values. Two loci exhibited significant Tajima's D values: PHYC (Tajima's D = 2.38, P < 0.05) and PHYA (Tajima's D = 2.16, P < 0.05). The PHYC gene also showed significant Fu and Li's D* (D* = 1.81, P < 0.05) and F* (F* = 1.13, P < 0.05) test values. The linkage disequilibrium (LD) was calculated on the basis of r2 (Figure 3). LD varied according to the SNP considered. Strong or weak LDs were observed for the short sequence considered here (<1000 bp between two polymorphisms). Some SNPs separated by only a few hundred base pairs presented no LD. LD was particularly high for PHYC, while all polymorphisms except one were strongly linked.

TABLE 2.

Diversity of pearl millet genes

Name Size (bp) Polymorphic site (%) π (10−3) ⊝ (10−3) Tajima's D Fu and Li's D* Fu and Li's F*
Floricaula 819 0.24 0.82 0.51 1.00 0.72 0.94
CRY2 848 0.24 0.60 0.49 0.38 −0.99 −0.67
GI 1417 0.92 1.64 2.07 −0.59 1.51* 0.94
Hd3a 917 0.76 2.00 0.16 0.65 1.21 1.21
Hd6 652 0.92 2.27 1.78 0.61 1.06 1.07
PHYA 1051 0.29 1.24 0.58 2.12* 0.84 1.45
PHYB 1175 0.51 0.49 1.06 −1.28 −0.67 −1.02
PHYC 866 0.69 3.00 1.47 2.38* 1.13* 1.82*
Mean 0.57 1.51 1.02 0.66 0.60 0.72
Open in a new tab

For each gene, the size of the amplified fragment (SNP and indels), the percentage of the polymorphic site, the value of π, the value of ⊝, Tajima's D value, and Fu and Li's D* and F* are reported. *P < 0.05.

Figure 3.—

Figure 3.—

Open in a new tab

Linkage disequilibrium in pearl millet. The linkage disequilibrium (LD) was estimated using r2 (A) between each polymorphism (SNP or indel) for each gene except PHYC (gray diamonds) and PHYC (black triangles). For PHYC, LD values are also presented as a square matrix (B) with r2 values (top matrix) and LD significance P-values (bottom matrix).

Association with candidate genes:

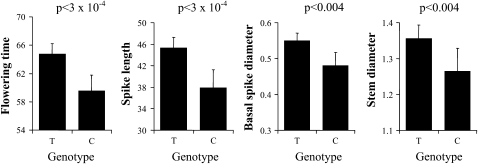
Association analyses were performed for all polymorphic sites of the eight genes (Table S2). We present results obtained with a complete mixed model including the kinship matrix and ancestry inferred for seven populations, using STRUCTURE for SNP 101 of the PHYC gene (Table 3). Analyses were performed for each field trial and on BLUE for all field trials. Significant associations (Table 3) were found for flowering time, plant, and spike morphology. Spike length and basal spike diameter were the strongest associated morphological traits. Stem diameter was associated only when the best linear unbiased effects were used. Some morphological associations were significantly detected only in one field trial (NTHE). As most of the PHYC SNPs were tightly linked, the same association was observed for the entire PHYC amplified fragment (Table S2). Estimation of the SNP effect using BLUE values was 5.2 days for flowering time, 8.3 cm for spike length, 0.070 cm for basal spike diameter, and 0.10 cm for stem diameter (Figure 4).

TABLE 3.

Association of morphological character and PHYC polymorphism

Field trials
2005
2006a
2006b
BLUE
No. of inbred lines
Traits 79 80 76 88
Flowering time
    FT P < 0.002, R2 = 6.6% P < 0.01, R2 = 6.5% P < 4 × 10−5, R2 = 15.5% P < 3 × 10−4, R2 = 8.9%
Plant morphology
    PH P = 0.59 P = 0.54 P = 0.33 P = 0.62
    SD P = 0.07 P = 0.08 P = 0.08 P < 0.004, R2 = 5.7%
    NTHE P = 0.22 P = 0.36 P < 0.04, R2 = 5.2% P = 0.09
Spike morphology
    SpD P = 0.81 P = 0.21 P = 0.74 P = 0.84
    BSpD P < 0.01, R2 = 4.2% P < 0.03, R2 = 2.9% P < 0.007, R2 = 5.2% P < 0.004, R2 = 3.8%
    SpL P < 3 × 10−4, R2 = 7.0% P < 0.003, R2 = 5.4% P < 3 × 10−4, R2 = 7.9% P < 3 × 10−4, R2 = 6.6%
Open in a new tab

For each field trial the number of inbred lines having sequence data, morphological data, and phenological data is given. The mixed model used included a kinship matrix and STRUCTURE-inferred ancestry for seven populations. The P-value and percentage of variance explained (R2) are presented for the SNP at position 101 of the amplified PHYC fragment and flowering time (FT), plant morphology (PH, SD, NTHE), and spike morphology (SpD, BSpD, SpL). The probability is presented for each field trial (2005, 2006a, and 2006b) and on best linear unbiased estimates for all field trials. The strongest significant association with PHYC was observed for flowering time, basal spike diameter, and spike length for the three field trials.

Figure 4.—

Figure 4.—

Open in a new tab

Trait effect of PHYC SNP 101 in pearl millet inbred lines. The mean value and standard errors for each genotype of the SNP 101 in the PHYC gene (C or T) are presented for flowering time (in days), spike length (in centimeters), basal spike diameter (in centimeters), and stem diameter (in centimeters). The P-value was obtained using the mixed-model method implemented in TASSEL.

Associations were also noted for PHYA polymorphism and spike length in all field trials for SNPs of the amplified fragment (Table S2). The SNP 146 of PHYA, for example, explained >4% of SpL variation in all field trials (2005, P < 0.0005, R2 = 7.8%; 2006a, P < 0.02, R2 = 4.0%; 2006b, P < 0.005, R2 = 5.9%; BLUE, P < 0.0007, R2 = 6.6%). The other two SNPs of this gene had similar association probability values.

To validate the association of SNP in the PHYC gene, we analyzed a new set of 598 pearl millet individuals from Niger. The structure analysis of this sample did not reveal a marked population structure (Figure S5). A kinship matrix was calculated and was not positive definite. We bent this matrix using an ad hoc method, using ɛ = −10−2. The new positive-definite matrix was almost identical to the initial matrix (Spearman's correlation coefficient R = 0.9999, P < 0.001), showing the adjustment only very slightly modified the original matrix. The different individuals showed only weak relatedness (Figure S6). However, the model with the kinship matrix was significantly better than a null model for most traits (Table S5). We used the model with the kinship matrix for the association between the PHYC SNP and traits.

Genotypes for the presence of the C or G alleles of PHYC were obtained for 560 of these pearl millet individuals. We found 27 individual homozygotes G/G, 120 individual C/G, and 413 C/C. We assessed associations in this data set with a mixed model considering the kinship matrix and the three genotypes (C/C, C/G, and G/G), using BLUE of trait value for all field experiments. The analysis highlighted a significant effect of the genotype on flowering time [Wald test of fixed effects, WT = 12.1, degree of freedom (dof) = 2, P < 0.003], spike length (Wald test of fixed effects, WT = 11.9, dof = 2, P < 0.003), and stem diameter (Wald test of fixed effects, WT = 13.9, dof = 2, P < 0.001). The number of tillers, plant height, spike diameter, and thousand seed weight were not significantly associated with the SNP polymorphism (Figure 5). The Bonferroni-corrected P-value for seven different tests was 0.007, so the association of flowering time, spike length, and stem diameter was significant with this corrected threshold. The association was also performed on individual field trials and led to a similar conclusion (Table S6). On the basis of BLUE, flowering time was on average 62.8 days for the G/G genotype and 65.7 days for C/C. A difference of 2.8 days was thus noted. The difference in stem diameter was 0.07 cm. The average stem diameter was 1.59 cm for G/G and 1.66 cm for C/C. The spike length difference was 8.7 cm. The average spike length was 61.4 cm for G/G and 70.1 cm for C/C.

Figure 5.—

Figure 5.—

Open in a new tab

Variation at PHYC and variation in phenology and morphology in pearl millet varieties. The mean value and standard errors for each genotype of the SNP 697 in the PHYC gene (C/C, C/G, and G/G) are presented for each morphological and phenological trait: flowering time in days (FT), number of tillers at head emergence (NTHE), plant height in centimeters (PH), stem diameter in centimeters (SD), spike length in centimeters (SpL), spike diameter in centimeters (SpD), and thousand seed weight in grams (TWS) are presented. The analysis was performed on the best linear unbiased effect of traits assessed in two different field trails (2004 and 2005). The analysis was performed using a mixed model incorporating a kinship matrix only (see text for details). We reported, for each trait and each field trial, the value of the Wald test statistics of fixed effects and the associated P-values with 2 dof. Three traits (FT, SPL, and SD) showed a significant genotypic effect even though we considered a Bonferroni-corrected significant threshold of 0.007.

DISCUSSION

Inference of population structure and association study:

The STRUCTURE Bayesian method is frequently used to infer population structures in an association framework. However, this method is not yet tailored for studies with inbred materials or selfing species. New methods like INSTRUCT have been developed very recently for this specific purpose (Gao et al. 2007). Our comparison obviously showed some differences between INSTRUCT and STRUCTURE results, as also previously noted (Gao et al. 2007). The similarity between the two methods was high (generally >90%). However, for the mixed model, STRUCTURE tends to have higher likelihood for a number of assumed populations >5, whereas INSTRUCT tends to have higher likelihood for a lower number of assumed populations. Comparative analyses of the two population structure inference methods on a type I control in association studies did not show a significant difference. Although the INSTRUCT model seems to be the most appropriate method for inbred material, our results obtained on our current data set using only 27 microsatellite loci showed that STRUCTURE led to better control of population structure. For population structure inference, we assumed a K population number ranging from 1 to 10. For STRUCTURE, the optimal K was K = 6, while for INSTRUCT it was K = 7. A question that might be addressed is, What population number gave the best control of type I error? As expected, taking the population structure into account (assuming K > 1) led to a lower number of false positives. However, using the optimal number of populations (K = 6 or K = 7) did not necessarily lead to better control of the false positive rate than K = 3, for example. The number of false positives for a given K value is certainly dependent on the relationship between the genetic structure and the phenotype differentiation between populations (Casa et al. 2008).

Traits covarying with the population structure are the most problematic for effective control of the false positive rate (Remington et al. 2001). Our results showed that spike length was most strongly linked to the population structure. For this trait, the false positive rate was never <10% regardless of the number of K populations considered. It could thus be hard to detect associations with this particular trait even if a particular SNP has an effect on the phenotype. We calculated a corrected P threshold based on microsatellite loci for each trait/field trial. This new significance threshold should partially overcome the gap between the expected 5% nominal ratio of false positive rate and the observed ≥10% for spike length.

In the present study, we used model-based Bayesian approaches to infer the population structure. Other methods like the principal components analysis (PCA)-based approach are not based on a particular model and can also be applied to detect population structures (Patterson et al. 2006). Stich et al. (2008) found that the PCA-based approach did not have better control of the false positive rate on a wheat data set. We observed—like previous studies—that taking the kinship matrix into account give a fitter model (Yu et al. 2006; Stich et al. 2008). However, considering the control of spurious associations, we actually did not detect a significant difference when using a kinship matrix or not. However, we noted that the type I error rate was slightly lower when taking the kinship matrix into account. In this study, we used SPAGeDI to infer a kinship matrix between inbred lines. A very recent study (Stich et al. 2008) showed that a restricted maximum-likelihood-based method could be used to infer this kinship matrix. This approach leads to a slight improvement in false positive control (Stich et al. 2008) over the initial approach of Yu et al. (2006).

We considered the best model using kinship and a STRUCTURE population structure. Seven clusters were used to perform all subsequent analyses. We analyzed the power of the methodology for identifying a given additive effect. From this analysis, it is clear that frequent variants (>1/8) are easily spotted for even a modest effect of 7 days (genetic effect ratio of ∼1.0). But a slight effect (<2 days, i.e., a genetic effect of ∼0.3) would be difficult to identify. The ability to detect slight effects may have been linked to the number of inbred lines considered in this study, whereas a higher number of inbred lines might be more effective for identifying such a slight effect. However, a previous power analysis study also detected a low power for a similar genetic effect, even though it considered threefold more inbred lines (Yu et al. 2006; Stich et al. 2008). Such a low effect may thus be difficult to detect, even though we used larger data set. Identification of variants using this approach in the present framework would likely be useful for flowering genes having an effect of at least 4 days; lower flowering differences were observed for allele frequencies of at least 1/8. In terms of explained variance, an effect of ≥10% is often easily detected. For the study of flowering time differences, some authors suggest that crop mutations might be more likely associated with large phenotypic effects (Roux et al. 2006). Although such alleles are relatively frequent, they could be easily spotted using this association framework.

Association of PHYC polymorphism with flowering time and morphological character:

We identified some polymorphism in the PHYC gene correlated with the flowering phenotype and other morphological traits in a pearl millet inbred data set. Using pearl millet varieties from Niger, we validated the association between PHYC polymorphism and phenological variation that we first detected in our inbred line data set. This analysis was based on an estimation of the average morphological/phenological character of each variety. The association was based on a single individual per variety associated with the average morphological/phenological value of the variety. Detection of an effect based on this design could not be very powerful since we attributed the average value of a variety to a single individual and within-variety polymorphism is expected to be very high (Allinne et al. 2008). We nevertheless detected a significant effect of PHYC polymorphism on a similar set of characters: flowering time, spike length, and stem diameter. However, the design did not allow us to draw any conclusions on the recessivity or dominance of the C and G alleles based on the mixed model results (Figure 5).

The association we detected with PHYC polymorphism was thus validated in two independent samples. The extent to which the phenotype is controlled by the PHYC gene or a neighboring gene has yet to be determined. Several studies suggest that polymorphism at PHYC is related to flowering differences in rice (Takano et al. 2005) and Arabidopsis (Balasubramanian et al. 2006). The direct causative role of PHYC (although not yet fully demonstrated) is a very likely scenario. A sequence analysis is underway to identify potential functional polymorphism within the entire PHYC gene. However, the phenotype might also be associated with differences in expression pattern. PHYA and GI genes also showed a significant association with spike length. However, the character associated with these genes is one for which false positive control was the least effective. These results should be considered with caution until they are further validated.

We found evidence based on Tajima's D statistics of two PHYA and PHYC genes, suggesting that polymorphism was balanced at these loci. These statistics were accurate if there was no population structure within the study sample. We found a significant population structure signal in the inbred lines. The average Tajima's D value for all loci was 0.66 (0.13 when PHYA and PHYB were excluded), suggesting a slight positive bias. This effect certainly inflated the Tajima's D values of the two genes. However, when considered with the PHYC association, these values might indicate a real selection signal. Wild pearl millet populations are spread in a dry area at the southern limit of the Sahara desert (Oumar et al. 2008). In West Africa, pearl millet is cultivated throughout three agro-ecological zones: the Sahel zone (200–500 mm annual rainfall), the Sudano-Sahelian zone (500–900 mm), and the Sudanian zone (900–1100 mm). The adaptation of pearl millet to a wetter climate is associated with later flowering (Haussmann et al. 2006). A likely hypothesis is this adaptation to a wetter climate was associated with selection at the two genes: different alleles of these genes are maintained in different environments, leading to genetic diversity exhibiting balanced polymorphism. A study should be carried out on a regional scale to validate this hypothesis.

The LD study highlighted a fast decrease in pearl millet inbred material, with low r2 values, as we observed here for SNPs separated by a few base pairs. The LD in Arabidopsis has a genomewide decrease to r2 < 0.20 at a distance of 10 kb (Kim et al. 2007). In inbred maize lines, a decrease has been observed at a shorter range of a few hundred base pairs (Remington et al. 2001). The results obtained here were closer to maize results. However, as expected, we also found strong locus-specific variability, which was certainly linked to each particular gene history, gene location in the genome, selection, local diversity, and recombination rate. The LD for PHYC was particularly high, as expected for a selected genomic region. As we investigated a low number of genes, it was hard to pinpoint the factor controlling this high LD in PHYC. However, a better assessment of LD in pearl millet would require an analysis of a larger number of loci and a larger chunk of DNA.

Altogether, the positive association results, significant selection test results, and high LD at PHYC suggested that this locus is under diversifying selection in pearl millet.

Five phytochrome PHYA-E genes have been found in Arabidopsis thaliana, and only three PHYA-C genes are described in monocotyledon species like Oryza or Sorghum (Mathews 2006b). The PHYC gene seems to have a relatively minor functional role in Arabidopsis development (Franklin et al. 2003; Monte et al. 2003; Mathews 2006a). However, natural variation at PHYC is associated with a latitudinal gradient (Balasubramanian et al. 2006), and there is empirical evidence that PHYC mediates photoperiod sensitivity in natural populations of A. thaliana (Samis et al. 2008). PHYC in Arabidopsis thus has an important role for the adaptation of natural populations to different climates. A recent study has also revealed natural variation at the PHYB gene in Arabidopsis accessions causes differential responses to light (Filiault et al. 2008). In Populus tremula, PHYB2 natural variations are also associated with variations in the timing of bud set (Ingvarsson et al. 2008). In rice, PHYC protein is required to delay flower initiation during long days (Takano et al. 2005). The phyB mutants have an earlier flowering phenotype similar to phyC mutants under long day conditions, but phyB and not phyC hastens the flowering time during short days (Takano et al. 2005). In sorghum, the phyB natural mutant is associated with a photoperiod-insensitive flowering time phenotype (Foster et al. 1994; Childs et al. 1997). Moreover, the PHYC in sorghum shows unusual nonsynonymous polymorphisms (White et al. 2004), which might be associated with functional effects. Overall, these results and the present study findings suggest that phytochromes might be preferential targets of selection for flowering time variation in plants (Balasubramanian et al. 2006). The upstream position of the photoreceptor gene in the flowering development network might partially explain why, in different species, variations may occur in the same set of genes associated with flowering time variation. Variations in the most upstream gene of a pathway might be associated with a lower pleiotropic effect (Roux et al. 2006).

To date, 3000 genomic DNA sequences are available for pearl millet in GenBank. This species is not a genomic research priority and is best described as an orphan crop. Pearl millet is adapted to marginal agricultural areas with low rainfall and plays a crucial role in feeding the poorest of the poorest, particularly in the Sahel. In Niger, pearl millet is grown on 65% of the total cultivated area. Conducting association studies in pearl millet provides an opportunity to rapidly validate important agronomic genes identified in other plant models and cereals for their role in the pearl millet phenotype. We hope that the identification of such key genes will favor the development of improved varieties using marker-assisted selection.

Acknowledgments

We thank T. Hash (International Crops Research Institute for the Semi-Arid Tropics), J. Chantereau (Centre de Cooperation Internationale en Recherche Agronomique pour le Développement), T. Robert, and A. Sarr (University of Orsay, Paris) for supplying us with pearl millet inbred line seeds. We thank Y. Orieux, C. Allinne, P. Sire, M. Couderc, D. Moussa, and M. Tidjani for help during the field studies and laboratory experiments. We thank Pär K. Ingvarsson for advice on R code development. This project was funded by an Institut de Recherche pour le Developpement (IRD) core grant and by a grant from the Agence Nationale de la Recherche to Y.V. (ANR-07-JCJC-0116-01). A.-A.S. is funded by an IRD Ph.D. fellowship.

Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.109.102756/DC1.

Sequence data from this article have been deposited with the EMBL/GenBank Data Libraries under accession nos. FN376885–FN377564.

References

  1. Allinne, C., C. Mariac, Y. Vigouroux, G. Bezançon, E. Couturon et al., 2008. Role of seed flow on the pattern and dynamics of pearl millet (Pennisetum glaucum [L.] R. Br.) genetic diversity assessed by AFLP markers: a study in south-western Niger. Genetica 133 167–178. [DOI] [PubMed] [Google Scholar]
  2. Atkinson, B., and T. Therneau, 2008. Kinship: mixed kinship: mixed-effects Cox models, sparse matrices, and modeling data from large pedigrees. R package, Versions 1.1.0–21. http://cran.r-project.org.
  3. Balasubramanian, S., S. Sureshkumar, M. Agrawal, T. P. Michael, C. Wessinger et al., 2006. The phytochrome C photoreceptor gene mediates natural variation in flowering and growth responses of Arabidopsis thaliana. Nat. Genet. 38 711–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Buckler, E., P. Bradbury, D. Kroon, Y. Ramdoss, T. Casstevens et al., 2007. Trait Analysis by Association, Evolution and Linkage (TASSEL). Version 2.0.1. http://www.maizegenetics.net/tassel.
  5. Camus-Kulandaivelu, L., J.-B. Veyrieras, D. Madur, V. Combes, M. Fourmann et al., 2006. Maize adaptation to temperate climate: relationship between population structure and polymorphism in the Dwarf8 gene. Genetics 172 2459–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Casa, A. M., G. Pressoir, P. J. Brown, S. E. Mitchell, W. L. Rooney et al., 2008. Community resources and strategies for association mapping in Sorghum. Crop Sci. 48 30–40. [Google Scholar]
  7. Childs, K. L., F. R. Miller, M. M. Cordonnier-Pratt, L. H. Pratt, P. W. Morgan et al., 1997. The sorghum photoperiod sensitivity gene, Ma3, encodes a phytochrome B. Plant Physiol. 113 611–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. D'Andrea, A. C., and J. Casey, 2002. Pearl millet and Kintampo subsistence. Afr. Archaeol. Rev. 19 147–173. [Google Scholar]
  9. D'Andrea, A. C., M. Klee and J. Casey, 2001. Archaeological evidence for pearl millet (Pennisetum glaucum) in sub-Saharan West Africa. Antiquity 75 341–348. [Google Scholar]
  10. Doebley, J., A. Stec and L. Hubbard, 1997. The evolution of apical dominance in maize. Nature 386 485–488. [DOI] [PubMed] [Google Scholar]
  11. Evanno, G., S. Regnaut and J. Goudet, 2005. Detecting the number of clusters of individuals using the software Structure: a simulation study. Mol. Ecol. 14 2611–2620. [DOI] [PubMed] [Google Scholar]
  12. Falush, D., M. Stephens and J. K. Pritchard, 2003. Inference of population structure using multilocus genoype data: linked loci and correlated allele frequencies. Genetics 164 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Filiault, D. L., C. A. Wessinger, J. R. Dinneny, J. Lutes, J. O. Borevitz et al., 2008. Amino acid polymorphisms in Arabidopsis phytochrome B cause differential responses to light. Proc. Natl. Acad. Sci. USA 105 3157–3162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Foster, K. R., F. R. Miller, K. L. Childs and P. W. Morgan, 1994. Genetic regulation of development in Sorghum bicolor. Plant Physiol. 105 941–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Franklin, K. A., S. J. Davis, W. M. Stoddart, R. D. Vierstra and G. C. Whitelam, 2003. Mutant analyses define multiple roles for phytochrome C in Arabidopsis photomorphogenesis. Plant Cell 15 1981–1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fritz, G. L., 1995. New dates and data on early agriculture: the legacy of complex hunter-gatherers. Ann. Mo. Bot. Gard. 82 3–15. [Google Scholar]
  17. Fu, Y.-X., and W.-H. Li, 1993. Statistical tests of neutrality of mutations. Genetics 133 693–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gao, H., S. Williamson and C. D. Bustamante, 2007. An MCMC approach for the joint inference of population structure and inbreeding rate from multi-locus genotype data. Genetics 176 1635–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hardy, O. J., and X. Vekemans, 2002. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2 618–620. [Google Scholar]
  20. Haussmann, B. I. G., A. Boubacar, S. S. Boureima and Y. Vigouroux, 2006. Multiplication and preliminary characterization of West and Central African pearl millet landraces. Int. Sorghum Millet Newsl. 47 110–112. [Google Scholar]
  21. Hayes, J. F., and W. G. Hill, 1981. Modification of estimates of parameters in the construction of genetic selection indices (“bending”). Biometrics 37 483–493. [Google Scholar]
  22. Ingvarsson, P. K., M. V. Garcia, V. Luquez, D. Hall and S. Jansson, 2008. Nucleotide polymorphism and phenotypic associations within and around the phytochrome B2 locus in European aspen (Populus tremula, Salicaceae). Genetics 178 2217–2226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jaenicke-Després, V., E. S. Buckler, B. D. Smith, M. T. Gilbert, A. Cooper et al., 2003. Early allelic selection in maize as revealed by ancient DNA. Science 302 1206–1208. [DOI] [PubMed] [Google Scholar]
  24. Kang, H. M., N. A. Zaitlen, C. M. Wade, A. Kirby, D. Heckerman et al., 2008. Efficient control of population structure in model organism association mapping. Genetics 178 1709–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kim, S., V. Plagnol, T. T. Hu, C. Toomajian, R. M. Clarck et al., 2007. Recombination and linkage disequilibrium in Arabidopsis thaliana. Nat. Genet. 39 1151–1155. [DOI] [PubMed] [Google Scholar]
  26. Loiselle, B. A., V. L. Sork, J. Nason and C. Graham, 1995. Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae). Am. J. Bot. 82 1420–1425. [Google Scholar]
  27. Mariac, C., V. Luong, I. Kapran, A. Mamadou, F. Sagnard et al., 2006. a Diversity of wild and cultivated pearl millet accessions (Pennisetum glaucum [L.] R. Br.) in Niger assessed by microsatellite markers. Theor. Appl. Genet. 114 49–58. [DOI] [PubMed] [Google Scholar]
  28. Mariac, C., T. Robert, C. Allinne, M. S. Remigereau, A. Luxereau et al., 2006. b Genetic diversity and gene flow among pearl millet crop/weed complex: a case study. Theor. Appl. Genet. 113 1003–1014. [DOI] [PubMed] [Google Scholar]
  29. Mathews, S., 2006. a Seeing the light. Nat. Genet. 38 606–608. [DOI] [PubMed] [Google Scholar]
  30. Mathews, S., 2006. b Phytochrome-mediated development in land plants: red light sensing evolves to meet the challenges of changing light environments. Mol. Ecol. 15 3483–3503. [DOI] [PubMed] [Google Scholar]
  31. Mathews, S., R. C. Tsai and E. A. Kellogg, 2000. Phylogenetic structure in the grass family (Poaceae): evidence from the nuclear gene phytochrome B. Am. J. Bot. 87 96–107. [PubMed] [Google Scholar]
  32. Monte, E., J. M. Alonso, J. R. Ecker, Y. Zhang, X. Li et al., 2003. Isolation and characterization of phyC mutants in Arabidopsis reveals complex crosstalk between phytochrome signaling pathways. Plant Cell 15 1962–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Oumar, I., C. Mariac, J.-L. Pham and Y. Vigouroux, 2008. Phylogeny and origin of Pearl Millet (Pennisetum glaucum [L.] R. Br) as revealed by microsatellite loci. Theor. Appl. Genet. 117 489–497. [DOI] [PubMed] [Google Scholar]
  34. Patterson, N., A. L. Price and D. Reich, 2006. Population structure and eigenanalysis. PLoS Genet. 2 e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pritchard, J. K., M. Stephens, N. A. Rosenberg and P. Donnelly, 2000. a Association mapping in structured populations. Am. J. Hum. Genet. 67 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pritchard, J. K., M. Stephens and P. Donnelly, 2000. b Inference of population structure using multilocus genotype data. Genetics 155 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Remington, D. L., J. M. Thornsberry, Y. Matsuoka, L. M. Wilson, S. R. Whitt et al., 2001. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98 11479–11484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Roux, F., P. Touzet, J. Cuguen and V. Le Corre, 2006. How to be early flowering: an evolutionary perspective. Trends Plant Sci. 11 375–381. [DOI] [PubMed] [Google Scholar]
  39. Rozas, J., J. C. Sanchez-DelBarrio, X. Messeguer and R. Rozas, 2003. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics 19 2496–2497. [DOI] [PubMed] [Google Scholar]
  40. Samis, K. E., K. D. Heath and J. R. Stinchcombe, 2008. Discordant longitudinal clines in flowering time and phytochrome C in Arabidopsis thaliana. Evolution 62 2971–2983. [DOI] [PubMed] [Google Scholar]
  41. Sokal, R. R., and F. J. Rohlf, 1991. Biometry, Ed. 3. W. H. Freeman, New York.
  42. Stich, B., J. Mohring, H.-P. Piepho, M. Heckenberger, E. S. Buckler et al., 2008. Comparison of mixed-model approaches for association mapping. Genetics 178 1745–1754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tajima, F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Takano, M., N. Inagaki, X. Xie, N. Yuzurihara, F. Hihara et al., 2005. Distinct and cooperative functions of phytochromes A, B, and C in the control of deetiolation and flowering in rice. Plant Cell 17 3311–3325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 28 286–289. [DOI] [PubMed] [Google Scholar]
  46. Vos, P., R. Hogers, M. Bleeker, M. Reijans, T. Van de Lee et al., 1995. AFLP: a new technique for DNA fingerprinting. Nucleic Acids Res. 23 4407–4414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wang, R. L., A. Stec, J. Hey, L. Lukens and J. Doebley, 1999. The limits of selection during maize domestication. Nature 398 236–239. [DOI] [PubMed] [Google Scholar]
  48. White, G. M., M. T. Hamblin and S. Kresovich, 2004. Molecular evolution of the phytochrome gene family in sorghum: changing rates of synonymous and replacement evolution. Mol. Biol. Evol. 21 716–723. [DOI] [PubMed] [Google Scholar]
  49. Yu, J., G. Pressoir, W. H. Briggs, I. V. Bi, M. Yamasaki et al., 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38 203–208. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES