Polymorphic Genes of Major Effect: Consequences for Variation, Selection and Evolution in Arabidopsis thaliana

Abstract

The importance of genes of major effect for evolutionary trajectories within and among natural populations has long been the subject of intense debate. For example, if allelic variation at a major-effect locus fundamentally alters the structure of quantitative trait variation, then fixation of a single locus can have rapid and profound effects on the rate or direction of subsequent evolutionary change. Using an Arabidopsis thaliana RIL mapping population, we compare G-matrix structure between lines possessing different alleles at ERECTA, a locus known to affect ecologically relevant variation in plant architecture. We find that the allele present at ERECTA significantly alters G-matrix structure—in particular the genetic correlations between branch number and flowering time traits—and may also modulate the strength of natural selection on these traits. Despite these differences, however, when we extend our analysis to determine how evolution might differ depending on the ERECTA allele, we find that predicted responses to selection are similar. To compare responses to selection between allele classes, we developed a resampling strategy that incorporates uncertainty in estimates of selection that can also be used for statistical comparisons of G matrices.

THE structure of the genetic variation that underlies phenotypic traits has important consequences for understanding the evolution of quantitative traits (Fisher 1930; Lande 1979; Bulmer 1980; Kimura 1983; Orr 1998; Agrawal et al. 2001). Despite the infinitesimal model's allure and theoretical tractability (see Orr and Coyne 1992; Orr 1998, 2005a,b for reviews of its influence), evidence has accumulated from several sources (artificial selection experiments, experimental evolution, and QTL mapping) to suggest that genes of major effect often contribute to quantitative traits. Thus, the frequency and role of genes of major effect in evolutionary quantitative genetics have been a subject of intense debate and investigation for close to 80 years (Fisher 1930; Kimura 1983; Orr 1998, 2005a,b). Beyond the conceptual implications, the prevalence of major-effect loci also affects our ability to determine the genetic basis of adaptations and species differences (e.g., Bradshaw et al. 1995, 1998).

Although the existence of genes of major effect is no longer in doubt, we still lack basic empirical data on how segregating variation at such genes affects key components of evolutionary process (but see Carrière and Roff 1995). In other words, How does polymorphism at genes of major effect alter patterns of genetic variation and covariation, natural selection, and the likely response to selection? The lack of data stems, in part, from the methods used to detect genes of major effect: experimental evolution (e.g., Bull et al. 1997; Zeyl 2005) and QTL analysis (see Erickson et al. 2004 for a review) often detect such genes retrospectively after they have become fixed in experimental populations or the species pairs used to generate the mapping population. The consequences of polymorphism at these genes on patterns of variation, covariation, selection, and the response to selection—which can be transient (Agrawal et al. 2001)—are thus often unobserved.

A partial exception to the absence of data on the effects of major genes comes from artificial selection experiments, in which a substantial evolutionary response to selection in the phenotype after a plateau is often interpreted as evidence for the fixation of a major-effect locus (Frankham et al. 1968; Yoo 1980a,b; Frankham 1980; Shrimpton and Robertson 1988a,b; Caballero et al. 1991; Keightley 1998; see Mackay 1990 and Hill and Caballero 1992 for reviews). However, many of these experiments report only data on the selected phenotype (e.g., bristle number) or, alternatively, the selected phenotype and some measure of fitness (e.g., Frankham et al. 1968, Yoo 1980b; Caballero et al. 1991; Mackay et al. 1994; Fry et al. 1995; Nuzhdin et al. 1995; Zur Lage et al. 1997), making it difficult to infer how a mutation will affect variation, covariation, selection, and evolutionary responses for a suite of traits that might affect fitness themselves. One approach is to document how variation at individual genes of major effect affects the genetic variance–covariance matrix (“G matrix”; Lande 1979), which represents the additive genetic variance and covariance between traits.

Although direct evidence for variation at major-effect genes altering patterns of genetic variation, covariation, and selection is rare, there is abundant evidence for the genetic mechanisms that could produce these dynamics. A gene of major effect could have these consequences due to any of at least three genetic mechanisms: (1) pleiotropy, where a gene of major effect influences several traits, including potentially fitness, simultaneously, (2) physical linkage or linkage disequilibrium (LD), in which a gene of major effect is either physically linked or in LD with other genes that influence other traits under selection, and (3) epistasis, in which the allele present at a major-effect gene alters the phenotypic effect of other loci and potentially phenotypes under selection. Evidence for these three evolutionary genetic mechanisms leading to changes in suites of traits comes from a variety of sources, including mutation accumulation experiments (Clark et al. 1995; Fernandez and Lopez-Fanjul 1996), mutation induction experiments (Keightley and Ohnishi 1998), artificial selection experiments (Long et al. 1995), and transposable element insertions (Rollmann et al. 2006). For pleiotropy in particular, major-effect genes that have consequences on several phenotypic traits are well known from the domestication and livestock breeding literature [e.g., myostatin mutations in Belgian blue cattle and whippets (Arthur 1995; Grobet et al. 1997; Mosher et al. 2007), halothane genes in pigs (Christian and Rothschild 1991; Fujii et al. 1991), and Booroola and Inverdale genes in sheep (Amer et al. 1999; Visscher et al. 2000)]. While these data suggest that variation at major-effect genes could—and probably does—influence variation, covariation, and selection on quantitative traits, data on the magnitude of these consequences remain lacking.

Recombinant inbred line (RIL) populations are a promising tool for investigating the influence of major-effect loci. During advancement of the lines from F₂'s to RILs, alternate alleles at major-effect genes (and most of the rest of the genome) will be made homozygous, simplifying comparisons among genotypic classes. Because of the high homozygosity, individuals within RILs are nearly genetically identical, facilitating phenotyping of many genotypes under a range of environments. In addition, because of recombination, alternative alleles are randomized across genetic backgrounds—facilitating robust comparisons between sets of lines differing at a major-effect locus.

Here we investigate how polymorphism at an artificially induced mutation, the erecta locus in Arabidopsis thaliana, affects the magnitude of these important evolutionary genetic parameters under ecologically realistic field conditions. We use the Landsberg erecta (Ler) × Columbia (Col) RIL population of A. thaliana to examine how variation at a gene of major effect influences genetic variation, covariation, and selection on quantitative traits in a field setting. The Ler × Col RIL population is particularly suitable, because it segregates for an artificially induced mutation at the erecta locus, which has been shown to influence a wide variety of plant traits. The Ler × Col population thus allows a powerful test of the effects of segregating variation at a gene—chosen a priori—with numerous pleiotropic effects. The ERECTA gene is a leucine-rich receptor-like kinase (LRR-RLK) (Torii et al. 1996) and has been shown to affect plant growth rates (El-Lithy et al. 2004), stomatal patterning and transpiration efficiency (Masle et al. 2005; Shpak et al. 2005), bacterial pathogen resistance (Godiard et al. 2003), inflorescence and floral organ size and shape (Douglas et al. 2002; Shpak et al. 2003, 2004), and leaf polarity (Xu et al. 2003; Qi et al. 2004).

Specifically, we sought to answer the following questions: (1) Is variation at erecta significantly associated with changes to the G matrix? (2) Is variation at erecta associated with changes in natural selection on genetically variable traits? And (3) is variation at erecta associated with significantly different projected evolutionary responses to selection?

MATERIALS AND METHODS

Plant material and experimental design:

A. thaliana (common name: mouse-ear cress) is a largely selfing annual plant, native to Eurasia and recently introduced to North America (Jorgensen and Mauricio 2004). Plants initially grow as a vegetative rosette until they bolt and produce a flowering inflorescence from the apical meristem. Branches are produced both on the inflorescence and from the rosette. We characterized the size, architecture, and phenology of plants from a simple set of measurements: diameter of the rosette, the number of inflorescence branches, the number of basal rosette branches (hereafter, basal branches), and bolting date. We estimated reproductive fitness from fruit number, which is highly correlated with seed number (Westerman and Lawrence 1970; Mauricio and Rausher 1997).

In this study we analyze data from a Ler × Col RIL population (Lister and Dean 1993) that was planted into a recently plowed field at Brown University's Haffenreffer Reserve, Bristol, Rhode Island. As full details of the methods are given elsewhere (Weinig et al. 2002, 2003a,b), we provide only a brief summary. Seeds were cold-stratified in the dark for 14 days, germinated in the Brown University greenhouse, and then planted into the field in early April. One replicate seedling per RIL was planted into 30 randomized blocks. Plants that died within 1 week of transplanting (presumably due to transplant shock) were scored as missing data; plants that survived transplanting yet died before setting fruit were assigned a fitness value of 0 and included in our estimates of fitness (Weinig et al. 2003a). An appreciable number of plants per RIL suffered rabbit herbivory, which in turn affected a host of phenotypic traits (Weinig et al. 2003a,b). We analyze only data from the replicates of each RIL that escaped herbivory. Sample sizes ranged from N = 8 to 28 individuals per RIL, with a median = 18 or 19 individuals, depending on the trait.

Data analysis:

To examine the effect of variation at erecta on genetic variances and covariances between the four traits (rosette diameter, bolting time, inflorescence branches, and rosette branches), we first split the data set according to which erecta allele the lines contained, as determined from the Nottingham Arabidopsis Stock Centre (http://arabidopsis.info/). RILs lacking erecta genotype information were excluded from subsequent analyses. (Recall that the Ler parent in the cross was the source of the mutant erecta allele.)

We compared genetic variance–covariance matrices for lines with alternate erecta alleles using the program CPCrand (Phillips and Arnold 1999). CPCrand tests a series of hypotheses about matrix similarity by examining whether the matrices share principal components, are proportional to each other, or are in fact equal to each other (i.e., whether G matrices are identical between groups of lines with different erecta alleles). Each of these hypotheses in the “jump-up” approach (Phillips and Arnold 1999) is tested against a null model of unrelated matrix structure by comparing the results of a likelihood-ratio test to those obtained with a large number of randomizations. CPCrand has become a common method of comparing genetic variance–covariance matrices (see Caruso et al. 2005; Stinchcombe and Schmitt 2006; Brock and Weinig 2007; Doroszuk et al. 2008). Because we elected to multiply the G matrix by biologically informative vectors (i.e., selection gradients, see below), we did not use the random skewers method (Cheverud 1996) for G-matrix comparison.

Analysis of raw phenotypic data with CPCrand required a high degree of matrix bending (because of negative eigenvalues), which has yet to be verified when used with randomization tests for hypothesis testing (CPCrand documentation). To alleviate this problem, we estimated best linear unbiased predictors (BLUPs) for each trait for all of the RILs in the experiment using restricted maximum likelihood (Proc Mixed, SAS). We then used these BLUPs in the “phenotypic analysis” option of CPCrand to estimate G matrices as if they were phenotypic variance–covariance matrices, using 5000 randomizations. Utilizing BLUPs eliminated the need for matrix bending, as the estimated matrices were positive definite. All G-matrix comparisons for the erecta locus showed similar patterns of statistical significance when using either the raw phenotypic data or the G matrices estimated from BLUPs.

The exact null distribution of test statistics to use for testing whether lines with alternate alleles at erecta (or any locus) have similar G matrices remains unclear. For instance, because we analyzed an RIL population, lines with the same erecta locus will differ at other loci throughout the genome, and, conversely, lines with alternate erecta alleles will be the same at other loci throughout the genome; how this might affect hypothesis testing for G-matrix similarity is unknown. Therefore, to address to the likelihood of obtaining significant differences in G-matrix structure simply by splitting the data according to any single marker locus, we performed similar analyses to those described above for 52 other reference loci, which were chosen to be evenly spaced throughout the genome and not underlying QTL for the traits in question in this experiment. From these analyses, we estimated a null distribution of test statistics for G-matrix similarity. Because our goal was to estimate a null distribution, we use only the test statistics for the level of the CPC hierarchy that correspond to hypothesis tests for erecta.

We also implemented a likelihood-based approach to test the null hypothesis that a single G matrix, vs. two G matrices corresponding to the erecta allele classes, adequately described our data. To do this, we estimated a multivariate G matrix in SAS using Proc Mixed (SAS v. 9.1.3), using the factor-analytic modeling approach described by Hine and Blows (2006). This approach, which estimates the effective number of principal components of the G matrix, reduces the number of parameters necessary to describe the pattern of variance–covariance (see Hunt et al. 2007; Mcguigan and Blows 2007; Doroszuk et al. 2008; Mcguigan et al. 2008). Within a factor analytic modeling framework, we evaluated whether a model allowing for separate G matrices for the two erecta allele classes, vs. a single G matrix, provided a better fit to the data using likelihood-ratio tests and the “group = ” option of the “random” statement in Proc Mixed (following Doroszuk et al. 2008).

To determine whether erecta influences natural selection, we estimated selection gradients (Rausher 1992; Stinchcombe et al. 2002). We regressed BLUPs for relative fitness on the BLUPs for the four traits; the partial regression coefficients from these models estimate directional selection gradients. Selection gradients estimated with breeding values are equal to traditional phenotypic selection gradients (Lande and Arnold 1983) in the absence of environmentally induced covariances between traits and fitness (Rausher 1992). In an initial model, we included erecta allelic class as a categorical variable and erecta × trait interaction terms. Because of a marginally significant interaction between erecta and inflorescence branch number for relative fitness in this initial model, we subsequently estimated selection gradients for each erecta allele class separately. In practice, the overlapping 95% confidence limits of these estimates will not bias quantitative predictions, as the methods we use incorporate uncertainty in the parameter estimates (see below).

To examine whether variation at erecta was associated with different responses to selection, we solved the equation 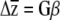for each erecta allele class, where G is the genetic variance–covariance matrix (estimated as the variances and covariances of the BLUPs), β is a vector of directional selection gradients, and 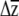is a vector describing the change in the mean phenotype. Conceivably, a similar approach could be used to examine whether the loss of genetic variation due to selection [given by ΔG = G(γ − ββ^T)G, where γ is the matrix of nonlinear selection gradients (Lande and Arnold 1983)] or the orientation of G and γ (Blows et al. 2004) is affected by variation at erecta (J. R. Stinchcombe, unpublished data).

Placing confidence limits on is rarely done (e.g., Conner and Via 1992; Etterson and Shaw 2001; Caruso 2004; but see Smith and Rausher 2008), and existing published analytical methods (Mcculloch et al. 1996) have yet to be implemented. To estimate uncertainty in , we developed a parametric bootstrapping approach. We considered each point estimate of β_i as the mean of a normal distribution, with standard deviation equal to the standard error of the regression coefficient. We then drew 999 values from each of these normal distributions independently; samples were drawn from each distribution independently, as the multiple regression used to obtain β_i (and their standard errors) estimates direct selection on the traits while statistically controlling for selection on the other traits in the regression model. For traits for which erecta was not associated with significant differences in β_i, these random draws sample highly overlapping distributions. The 999 values were assembled into β vectors, which were then multiplied with the estimated G matrices to obtain a distribution of 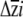. We considered the 25th and 975th values of each 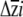, once sorted in ascending order, to represent the lower and upper 95% confidence limits for each 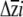. Because this approach does not capture uncertainty in the estimation of G, it underestimates of the confidence limits on .

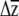RESULTS

Patterns of G-matrix similarity:

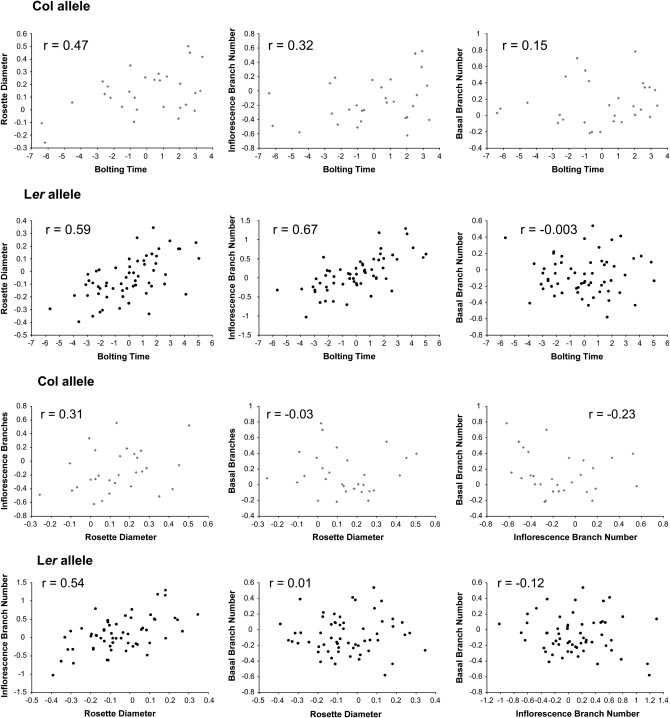
Analysis with CPCrand suggests that G matrices differ significantly depending on which erecta allele is present. Specifically, the hypothesis of 1 common principal component is rejected (likelihood ratio = 11.7386, P = 0.0174 on the basis of 5000 randomizations). The G matrices and genetic correlation matrices for the Col and Ler erecta alleles are presented in Table 1, with bivariate plots in Figure 1. Qualitatively, the differences between these matrices are likely driven by correlations/covariances involving inflorescence branches. For example, in lines with the Ler erecta allele, inflorescence branch number is highly correlated with bolting time and rosette diameter, while showing a weak negative correlation with basal branch number. In lines with the Col erecta allele, the correlations between inflorescence branch number and bolting time and rosette diameter are reduced (by approximately one-half), while the correlation between inflorescence branch number and basal branch number is approximately twice as negative (Figure 1).

TABLE 1.

Genetic variance–covariance and correlation matrices for RILs containing either Col or Ler erecta alleles

	Bolting time	Rosette diameter	Inflorescence branches	Basal branches
Bolting time	Col: 7.26	Col: 0.22	Col: 0.27	Col: 0.11
	Ler: 5.22	Ler: 0.22	Ler: 0.71	Ler: −0.0019
Rosette diameter	Col: 0.47	Col: 0.03	Col: 0.017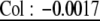
	Ler: 0.59	Ler: 0.027	Ler: 0.042	Ler: 0.00055
Inflorescence branches	Col: 0.32	Col: 0.31	Col: 0.098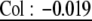
	Ler: 0.67	Ler: 0.55	Ler: 0.21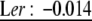
Basal branches	Col: 0.15	Col: −0.037	Col: −0.23	Col: 0.07
	Ler: −0.0036	Ler: 0.014	Ler: −0.12	Ler: 0.055

Genetic variances–covariances, estimated from BLUPs are underlined. Genetic correlations, estimated as Pearson correlations of BLUPs are not underlined. Correlations in boldface type are significant at P <0.05, while those in italics are marginally significant (P < 0.1). For the Col erecta allele, N = 29 RILs, and for the Ler erecta allele, N = 59 RILs.

Figure 1.—

Bivariate plots showing the genetic correlations between four quantitative traits for the alternate erecta allele classes. Top, Col erecta allele; bottom, Ler erecta allele.

Despite the significant differences in G matrices detected by CPCrand, principal components analysis (PCA) revealed that the angle (θ) between PC1 of the two G matrices was 5.9°, indicating close alignment of the first eigenvectors. In other words, the main direction of genetic variation in multivariate trait space is similar for the two allele classes. Nevertheless, the PCA also suggests that significant differences in the G matrices are driven by differences in genetic variances and covariances associated with inflorescence branches and basal branches between the two erecta allele groups. For both Col and Ler erecta alleles, PC1 explains >96% of the genetic variation (Table 2). For inflorescence branches, the loading on PC1 is approximately threefold higher for lines with the Ler erecta allele than for lines with the Col erecta allele. For basal branches, although this trait does not load heavily on PC1 for either allele class, the loading for lines with the Col erecta allele is higher than for lines with the Ler allele.

TABLE 2.

PCA of the estimated G matrices for Col and Ler erecta alleles

	Col erecta				Ler erecta
	PC1	PC2	PC3	PC4	PC1	PC2	PC3	PC4
Bolting time	0.9987	−0.0264	−0.0341	−0.0271	0.9895	−0.1391	−0.0293	−0.026
Rosette diameter	0.03059	0.11945	0.01396	0.99227	0.04271	0.10187	0.07858	0.99077
Inflorescence branches	0.03784	0.8223	0.55742	−0.108	0.13806	0.96435	0.19105	−0.1203
Basal branches	0.01517	−0.5557	0.82941	0.05477	−0.0007	−0.2007	0.97799	−0.0569
Percentage of variance explained	97.59	1.40	0.71	0.30	96.59	2.16	0.96	0.29

Genomewide distribution of CPCrand results:

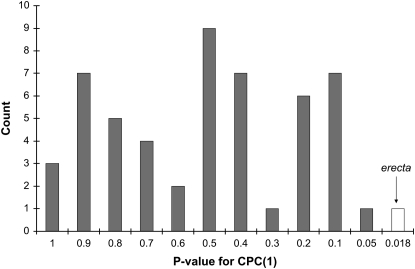
To evaluate how likely it would be to get significant CPCrand results simply by splitting the data into two allelic classes at any locus, we performed CPCrand analyses for 52 markers chosen throughout the genome. For each of these markers, we saved the P-value of the hypothesis test of 1 common principal component [CPC(1)]; all of these hypothesis tests were based on 5000 randomizations, using a genetic variance–covariance matrix estimated from BLUPs. The overall distribution of P-values suggests that rejection of 1 common principal component is rare (Figure 2)—i.e., for 98% of the markers used, lines with alternate alleles shared at least 1 principal component. The P-value for rejecting CPC(1) for the erecta locus was the most extreme P-value we obtained, and for only 1 other marker locus (mi238) was the hypothesis of CPC(1) rejected at the α = 0.05 level. These results suggest that the significant differences in G-matrix structure detected by CPCrand for erecta are rare on a genomewide basis.

Figure 2.—

Distribution of P-values for hypothesis tests of CPC(1) for 52 markers chosen throughout the genome and erecta. Note that on the x-axis, smaller P-values are to the right of the axis.

Factor-analytic modeling of the G matrix:

Factor-analytic modeling suggested that G was of full rank (i.e., all four eigenvalues were significantly different from zero). These results held whether we fit factor analytic models (FA0) using unstandardized data that included a main effect of the trait to control for the trait mean or using data where the traits were standardized to a mean of 0 and a variance of 1 (cf. Hunt et al. 2007). In both cases, decreasing from FA0(4) to FA0(3) (i.e., from four to three PCs) led to significantly worse model fit according to likelihood-ratio tests (unstandardized data, χ² = 5.8, d.f. = 1, P = 0.016; standardized data, χ² = 6.9, d.f. = 1, P = 0.0086). Moreover, for both unstandardized and standardized data, estimation of separate G matrices for different erecta allele classes significantly improved model fit (unstandardized, χ² = 26.7, d.f. = 10, P = 0.0039; standardized, χ² = 23.5, d.f. = 10, P = 0.009), suggesting that G matrices differed between erecta allele classes.

Because G matrices are frequently not of full rank (Hine and Blows 2006; Hunt et al. 2007; Mcguigan and Blows 2007; Doroszuk et al. 2008; Mcguigan et al. 2008), and PC1 of the G matrices explained such a large fraction of genetic variation (vs. PCs 3 and 4; Table 2), we also repeated the likelihood-ratio tests for scenarios where the G matrices were constrained to have only 1, 2, or 3 PCs. These analyses test the hypothesis of whether separate G matrices are supported even when all of the genetic variation and covariation is described by a reduced number of axes. In all cases, we found that estimating separate G matrices for lines with different erecta alleles provided significantly better fits to the data (χ² > 26.6, P < 0.0011 for all comparisons).

Patterns of natural selection:

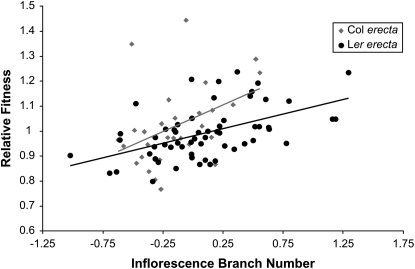
Analysis of covariance for relative fitness suggested marginally significant evidence that natural selection on inflorescence branches differed depending on the erecta locus and that variation at erecta was associated with differences in relative fitness (Table 3; Figure 3). Accordingly, we estimated selection gradients for the four traits separately for each erecta allele class (Table 4).

TABLE 3.

Analysis of covariance for relative fitness, testing the effects of erecta, phenotypic traits, and the erecta × trait interactions

Source	d.f.	F	P
erecta	1	2.70	0.104
Bolting time	1	0.41	0.53
Rosette diameter	1	16.72	0.0001
Inflorescence branches	1	18.02	<0.0001
Basal branches	1	28.50	<0.0001
erecta × bolting time	1	0.51	0.48
erecta × rosette diameter	1	2.46	0.12
erecta × inflorescence branches	1	2.84	0.096
erecta × basal branches	1	0.45	0.50
Error	78

Significant effects are shown in boldface type, and marginally significant effects (P < 0.10) are in italics.

Figure 3.—

Graphical portrayal of natural selection on inflorescence branch number, depending on the erecta locus. The difference in the slopes of the lines is marginally significant.

TABLE 4.

Genotypic selection gradients estimated from BLUPS, estimated separately for RILs with alternate erecta alleles

	Col erecta		Ler erecta
Trait	β (SE)	P	β (SE)	P	Genetic σ	Phenotypic σ
Bolting time	−0.0073 (0.01)	0.49	0.0004 (0.06)	0.95	2.41	4.35
Rosette diameter	0.415 (0.15)	0.012	0.185 (0.07)	0.015	0.19	0.47
Inflorescence branches	0.212 (0.08)	0.017	0.092 (0.03)	0.0027	0.43	1.31
Basal branches	0.258 (0.09)	0.010	0.20 (0.04)	<0.0001	0.26	2.03

For Col erecta A, N = 29 lines; for Ler erecta, N = 59 lines. For purposes of comparison, genetic and phenotypic standard deviations for the traits are also provided (calculated from the entire data set). Significant selection gradients are shown in boldface type.

For lines that contained the Col erecta allele, we detected significant directional selection to increase rosette diameter, the number of inflorescence branches, and the number of basal branches (Table 4)—bigger plants with more branches had higher relative fitness. In lines that contained the Ler erecta allele, we found a similar pattern: directional selection significantly favored larger rosette diameters and more inflorescence and basal branches. The selection gradient estimates suggest larger gradients for lines with the Col allele, although the ANCOVA indicates that these differences approached significance only for inflorescence branches.

Predicted responses to selection:

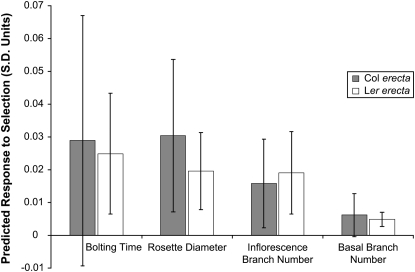
Despite significant genetic variation in the four traits, and significant natural selection on three of them, the predicted responses to natural selection remain small—both in original trait units (data not shown) and when judged relative to the phenotypic standard deviation of the traits (Figure 4). Comparison of Tables 1 and 4 reveals a likely mechanism: for the three traits under the strongest natural selection (rosette diameter, inflorescence branches, and basal branches), there is appreciably less genetic variation, in either allelic class. Conversely, the trait under the weakest natural selection (bolting time) showed the greatest genetic variance.

Figure 4.—

Predicted response to selection of the four quantitative traits, calculated separately for each erecta allele class. The response to selection for each trait 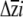is in standard deviation units. Error bars indicate the upper and lower 95% confidence intervals for the predicted response to selection based on a parametric bootstrap that incorporated uncertainty in the estimation of selection.

Despite differences between erecta allele classes in the point estimates for genetic variances, for covariances, and possibly for selection gradients, similar predicted responses to selection are obtained for these two classes (Figure 4). The apparent differences between erecta allele classes in the patterns of genetic variance/covariance for inflorescence branches (Table 1), when combined with the differences in the estimated selection gradients (Table 4), show a “canceling-out” pattern. In lines with Ler erecta (compared to those with Col), direct selection on inflorescence branch number is weaker, yet this trait has larger variance and stronger pairwise covariances and correlations with two other traits (rosette diameter and bolting time). Vice versa, inflorescence branch number is under stronger selection in lines with Col erecta, yet variance as well as the covariances and correlations between inflorescence branches and rosette diameter, and inflorescence branches and bolting time, are of smaller magnitude. Placing confidence intervals on the predicted responses to selection by incorporating variation in the estimation of β reveals that the small differences obtained in the point estimates of 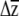are within the range of estimation uncertainty.

DISCUSSION

Our results indicate that alternate alleles at the erecta locus are associated with both significant changes in G-matrix structure and marginally significant differences in natural selection. Nevertheless, our results predict relatively minor differences in the expected response to natural selection. There appear to be multiple mechanisms behind this discrepancy. First, overall selection in this experiment was weak for the three traits that exhibited substantial genetic variances and covariances. Second, the same trait that exhibited stronger selection but lower genetic variance and covariances in one erecta allele class exhibited weaker selection but higher variance in the other allele class. Finally, detecting significant differences in the predicted response to selection is likely to be quite challenging, given estimation uncertainty. Below, we discuss these results in light of past work on the role of major genes in evolution and the challenges of statistically comparing predicted responses to natural selection.

Evolution and genes of major effect:

The last 15 years have led to an increasing acceptance that genes of major effect contribute to adaptive evolution. Orr (1998, 2005a,b) has noted that growing acceptance of this result was due, in part, to widespread QTL mapping results showing chromosomal regions of major effect and experimental evolution studies that showed mutations with large fitness effects, along with the lack of convincing data in favor of many alleles of small effect (Orr and Coyne 1992). The acceptance of genes of major effect was probably also aided by the intriguingly similar distributions of empirically detected QTL effects and Orr's (1998) theoretically derived distributions. These QTL and experimental evolution results were consistent with earlier results from Drosophila quantitative genetics and plant genetics (e.g., Frankham et al. 1968; Frankham 1980; Yoo 1980a,b; Gottlieb 1984, 1985). Likewise, Robertson (1967) predicted that the distribution of effect sizes for genes affecting a trait would be leptokurtic, with many genes having small to no effects and a few having large effects.

Despite the acceptance of the role of major genes in evolution, we still have remarkably little knowledge of how polymorphism at these genes will affect the microevolution of quantitative traits. In the study most directly comparable to ours, Carrière and Roff (1995) examined how the evolution of insecticide resistance affected the heritabilities and genetic correlations between life history traits and insecticide resistance in natural populations of the oblique-banded leaf roller [Choristoneura rosaceana (Lepiodoptera: Tortidae)]. They found that the spread of resistance allele(s) increased the additive genetic variance in larval weight and diapause propensity and decreased the genetic correlation between these traits, consistent with their theoretical predictions (Carrière and Roff 1995). Using an experimental genetic approach, Bradshaw and Schemske (2003) reciprocally introgressed YELLOW UPPER (YUP) floral color alleles derived from Mimulus lewisii and M. cardinalis into the alternate species and measured changes in pollinator attraction and visitation. Variation at this locus was sufficient to change the pollinator visitation, suggesting that reproductive isolation due to pollinator preferences could be due to a single allele. Although Bradshaw and Schemske (2003) did not report how variation at the YUP locus affected the correlations between, or selection on, floral traits, it is not difficult to envision pollinator-mediated selection on floral color and floral design.

Our results suggest that polymorphism at genes of major effect can have statistically significant effects on G-matrix structure. The most striking results we obtained were the nearly twofold differences in the genetic correlations involving inflorescence branch number and either bolting time or rosette diameter. Therefore, our results suggest that allelic variation at major-effect loci can influence the direction of trait variation available to natural selection. We might have predicted that alternate erecta alleles would affect plant architecture traits, given past findings of QTL centered on erecta [e.g., apical inflorescence and basal branch height QTL (Weinig et al. 2003b) and flowering time under short days (Weinig et al. 2002)], as well as the confirmed effects of the gene itself on organ size and shape (Douglas et al. 2002; Shpak et al. 2003, 2004; Kliebenstein 2007).

While our results for G-matrix comparisons were statistically significant by a variety of approaches and our analysis of marker loci suggested that significant G-matrix differentiation was unlikely to occur by chance alone, the quantitative magnitude of the differences detected appears small. The interpretation of slight quantitative effect on G-matrix structure is supported by the similarity of the eigenvectors of each G matrix, the close alignment of PC1 of each matrix in multivariate space (i.e., the angle between them), and the similar responses to selection produced by each G matrix. These findings point to the need for statistically significant G-matrix comparisons to be interpreted in light of their biological significance. Surprisingly, of the suite of tools available for G-matrix comparisons (see Steven et al. 2007 and Doroszuk et al. 2008 for overviews), few investigators have paired G matrices with estimates of natural selection (β vectors) to see if the predicted response to selection will differ (see below).

Our use of the ERECTA to examine the effects of a mutation at a highly pleiotropic gene on G-matrix structure, selection, and the response to selection entailed both benefits and costs. On the one hand, erecta is an induced mutation and may provide a better model of new mutations—upon which much of the theoretical work is based—than standing genetic variation. The incorporation of erecta into an RIL mapping population also breaks up associations between erecta alleles and their respective Landsberg and Columbia genomes, which would otherwise confound estimation of the effects of this ERECTA. In addition, the ERECTA gene is highly pleiotropic, and mutations to it (induced or natural) may have greater consequences on a suite of traits than mutations to typical genes throughout the genome and thus enhanced our power to detect effects on G-matrix structure and selection. On the other hand, these same factors also could represent disadvantages. For instance, it is clearly possible (perhaps likely) that the induced erecta mutation is not representative of naturally occurring mutations at this gene, and the pleiotropic nature of the ERECTA gene is not likely to be representative of all genes throughout the genome. Both of these interpretations are supported by our analyses of reference loci that indicated that most loci shared at least 1 PC and by other studies from the literature that suggest pleiotropy may be restricted and limited to functionally integrated units (e.g., Cheverud et al. 1997). The relatively small Ler × Col mapping population may have inflated the effect sizes associated with erecta and limits our ability to distinguish between the effects of erecta vs. neighboring loci. In addition, RIL crosses often estimate genetic variance associated with divergence between populations, and thus the genetic variances, covariances, and selection detected using them may not be reflective of standing genetic variation within populations (e.g., Agrawal et al. 2001; Orr 2005b). Ultimately resolving any of these issues would be a daunting empirical challenge. However, our findings that variation at erecta is significantly associated with changes in G-matrix structure and possibly natural selection nonetheless illustrate how polymorphism at major genes can affect contemporary patterns of genetic (co)variation and selection.

Predicting the response to selection:

Intensive effort over the last 25 years has been devoted to estimating natural selection in the wild (see Endler 1986; Hoekstra et al. 2001; Kingsolver et al. 2001; Geber and Griffen 2003; Hereford et al. 2004). While these efforts may have clarified the typical strength of selection, they are rarely combined with estimates of genetic variation to predict evolutionary trajectories. Houle (2007) recently noted how surprising it is that estimates of G and β are rarely (with some exception) obtained from the same population and also rarely combined to make quantitative predictions. Theoretical work (Turelli and Barton 1990, 1994; Barton and Turelli 1991) has shown that predictions based on the infinitesimal model are robust to the genetic details underlying the traits for predictions made over a short number of generations, suggesting that these predictions could be useful.

We suggest that one challenge currently inhibiting predictions of multivariate evolution—apart from obtaining the necessary data—is that there are no accepted methods for placing confidence limits on estimates of 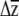or significance testing of 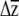. In the univariate case, investigators have compared the actual response to selection to predictions from the breeders equation (R = h²s) and placed uncertainty estimates on R by using the upper and lower confidence limits of the heritability or selection differential estimates (Galen 1996; Grant and Grant 2006). Simply using the upper and lower confidence limits of β_i is not applicable to the multivariate case, as it is unclear a priori which combinations of upper and lower estimates of β_i should be multiplied with G.

For multivariate responses to selection, several investigators have predicted 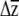(e.g., Conner and Via 1992; Mitchell et al. 1998; Etterson and Shaw 2001; Caruso 2004), yet were unable to place confidence limits on their estimates. Etterson and Shaw (2001) tested the significance of the predicted response to selection, estimated as the additive genetic covariance between a trait and fitness, with likelihood-ratio tests that compared the fitted model to one in which the correlation was constrained to equal zero. Using a different approach, Caruso (2004) compared 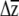to selection to β using a t-test, taking advantage of the standard error of the β-estimates obtained by regression.

The benefit of our approach is that predicted responses to selection can be compared to zero for significance testing, as well as to other specified values (e.g., 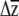for a different treatment or allelic class, to β, to univariate predictions). The approach inherits all of the assumptions of selection analyses (Mitchell-Olds and Shaw 1987) and adds the assumption that individual β_i's are themselves sampled from normal distributions. An alternative would be to bootstrap the multiple regressions used to estimate β, sample individual β_i's from these bootstrap distributions (e.g., Calsbeek and Smith 2007), and combine them with G to place confidence intervals on 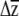. Our method is similar to the one used by Franks et al. (2007), who sampled from bootstrapped distributions of both parent–offspring regressions and selection differential estimates to produce confidence limits on R. Regardless of the method used to incorporate uncertainty in β, the confidence limits generated by our method are underestimates, as no variation in the elements of G is included in the estimation. Conceivably, families or inbred lines could be sampled with replacement to create bootstrapped estimates of G (e.g., Smith and Rausher 2008), which could then be combined with β's estimated from the parametric boostrap to produce a confidence limit, although this is likely to be computationally intensive if G is estimated with likelihood. Despite the limitation of not incorporating uncertainty in G, we argue that an underestimate of the confidence limits of 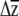is better than no estimate.

One additional benefit of placing confidence limits on 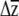is that it can be used to compare G matrices. For a given strength and pattern of selection, the evolutionary response will be determined by the patterns of variation and covariation described by G (Lande 1979). An effective means of comparing G matrices is thus to ask, for a given strength of selection, Are there differences in 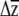? Our approach is similar to the “random skewers” method developed by Cheverud (Cheverud et al. 1983; Cheverud 1996; Cheverud and Marroig 2007) as well as to recent work by Smith and Rausher (2008) and Hansen and Houle (2008). In the random skewers method, randomly drawn vectors (with rows equal to the dimension of G) are combined with the G matrices being compared, and the distribution of vector correlations between the 's are compared. Steven et al. (2007) modify the skewers approach and compare 's for different G by multiplying them by hypothetical (yet ecologically realistic) β, a useful approach for when β is either unknown or likely to change during adaptation. Smith and Rausher (2008) compare the angles of response vectors after projecting them onto a plane, while Hansen and Houle (2008) calculate the “response difference” by multiplying two G matrices (G₁ and G₂) by a given β and calculating the vector norm of the difference between 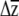₁ and 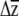₂ (i.e., |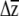₁ − ₂|). Hansen and Houle (2009) give expressions for the expectations of this norm over random selection gradients, as a general measure of response differences between G₁ and G₂ when β is unknown.

The main difference in emphasis of our approach is that we combined G with empirical estimates of β, rather than random vectors, and we used the confidence limits of 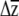for the individual traits to perform hypothesis testing, rather than using the vector correlation, angles between projections, or the vector norm. Moreover, instead of yielding a simple P-value or an angle in multivariate space, both of which can be difficult to interpret biologically, the information used by our approach to perform hypothesis testing is evolutionarily and biologically relevant—the predicted changes in the means of individual traits and an estimate of uncertainty.

Conclusions and future directions:

Understanding the role of genes of major effect in contemporary microevolution is likely to be an ongoing challenge. While intuition might suggest that genes of major effect, or those that affect several traits at once, might speed adaptation, their spread through populations will ultimately be determined by the relationship between the traits they affect and fitness and any trade-offs they generate with other traits under selection. Our results suggest that pleiotropic genes of major effect will not necessarily have dramatic effects on evolutionary trajectories, although whether this is a general pattern remains an empirical question. A major goal for future empirical work will be to determine how any naturally segregating genes of major effect influence the microevolution of quantitative traits.