Abstract
Using electron spin resonance spectroscopy (ESR), we measure the rotational mobility of probe molecules highly diluted in deeply supercooled bulk water and negligibly constrained by the possible ice fraction. The mobility increases above the putative glass transition temperature of water, Tg = 136 K, and smoothly connects to the thermodynamically stable region by traversing the so called “no man's land” (the range 150–235 K), where it is believed that the homogeneous nucleation of ice suppresses the liquid water. Two coexisting fractions of the probe molecules are evidenced. The 2 fractions exhibit different mobility and fragility; the slower one is thermally activated (low fragility) and is larger at low temperatures below a fragile-to-strong dynamic cross-over at ≈225 K. The reorientation of the probe molecules decouples from the viscosity below ≈225 K. The translational diffusion of water exhibits a corresponding decoupling at the same temperature [Chen S-H, et al. (2006) The violation of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci USA 103:12974–12978]. The present findings are consistent with key issues concerning both the statics and the dynamics of supercooled water, namely the large structural fluctuations [Poole PH, Sciortino F, Essmann U, Stanley HE (1992) Phase behavior of metastable water. Nature 360:324–328] and the fragile-to-strong dynamic cross-over at ≈228 K [Ito K, Moynihan CT, Angell CA (1999) Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water. Nature 398:492–494].
Keywords: decoupling of transport properties, dynamic cross-over in water, dynamic heterogeneity, supercooled water, polycrystalline materials
The physical properties of water are far from being completely understood. Several thermodynamic and dynamic anomalies are known or anticipated in the metastable supercooled regime that influence the equilibrium states and have deep impact in biology, astrophysics, glaciology, and atmospheric science (1–3). At ambient pressure, the supercooled regime ranges between the commonly accepted value of the glass transition temperature Tg = 136 K and the freezing temperature Tm = 273.15 K. Above Tg, amorphous water transforms into a highly viscous fluid (4, 5). Crystallization into metastable cubic ice (Ic) at TX ≈ 150 K with further transformation to the usual hexagonal form of ice Ih is reported (1, 6). On the other hand, bulk water at atmospheric pressure can be supercooled below its melting temperature down to the homogeneous nucleation temperature TH ≈ 235 K, below which it usually crystallizes to Ih. Thus, the region between TX and TH is often regarded as a region where liquid water cannot be observed [“no man's land,” NML (1)]. Nonetheless, the coexistence of crystals and deeply supercooled liquids was suspected almost 1 century ago for bulk systems (7). More recently, evidence that water and cubic ice coexist in thin films in the temperature range 140–210 K was reported (8–11). The existence of liquid water has been also shown experimentally in veins (or so-called triple junctions) of polycrystalline ice (12) that serve as interfacial reservoirs for impurities (13–15). The size of such reservoirs is thermodynamically defined by surface forces and also by the curvature of the surface (i.e., the Kelvin effect in veins) (11, 16). In pure ice, the reservoir size increases when approaching the melting point (17). Notably, recent simulations concluded that in polycrystalline materials grain boundaries exhibit the dynamics of glass-forming liquids (45).
This background motivated us to investigate the coexistence of ice and supercooled water in large volumes in an attempt to characterize the dynamical properties of the liquid, particularly in NML. Of major interest is the comparison with the results concerning the liquid behavior evidenced in small volumes, like nanopores (18–20) and nanometric films (4, 10), where homogeneous nucleation is bypassed.
NML is of paramount interest for a definitive picture of the supercooled water. Different scenarios predict their characteristic temperatures in NML, i.e., the singular temperature Ts ≈ 228 K, where most response functions appear to diverge (3), the fragile-to-strong dynamic cross-over (FSC) temperature at TFSC ≈ 228 K (6, 21, 22), the strongly suspected second critical point at Tc ≈ 220 K, Pc ≈ 108 Pa (23), and the kinetic glass transition temperature TMCT ≈ 221 K (24, 25). The existence of characteristic temperatures highlights that viscous water close to Tg and normal water under equilibrium conditions are distinct, particularly due to the different static structural heterogeneities of the low- (LDL) and the high-density (HDL) states of water, the corresponding liquids of LDA and HDA amorphs (1–3, 19, 20, 26). Viscous water is more structured and LDL-rich, whereas normal water is disordered and HDL-rich. This viewpoint is challenged by experimental results suggesting that supercooled water >Tg is an ultraviscous fragile liquid smoothly connected to the equilibrium states above the melting temperature Tm (4). As a further example of the unusual properties of water in NML, the breakdown of the Stokes–Einstein law (SE), stating the constancy of the quantity ℛSE ≡ Dη/T (T, D, and η being the temperature, the translational diffusion coefficient, and the viscosity, respectively), has been evidenced at ≈225 K by confining water in nanopores (18) and simulations (26–28). That decoupling has been attributed to the occurrence of dynamical heterogeneity (DH), i.e., a spatial distribution of mobility, in structural glass-formers and put into correspondence with the static structural heterogeneities of water (26). Orientation and reorientation of water molecules deserve consideration. There is competition between orientational entropy and bond energy in water, and the anomalies of the latter are thought to be closely related to the orientational order (26, 29). The rotation of individual water molecules, mainly occurring by large jumps (θ ≃ 60°) (30), changes constantly the connectivity of the H-bond network. Recent simulations (26–28) suggested that the SE breakdown in water must also be accompanied by the breakdown of the Debye–Stokes–Einstein law (DSE), accounting for the coupling between the viscosity and the rotational diffusion, as observed in experiments (31) and simulations (32) on molecular glass-formers.
Outine of ESR Spectroscopy
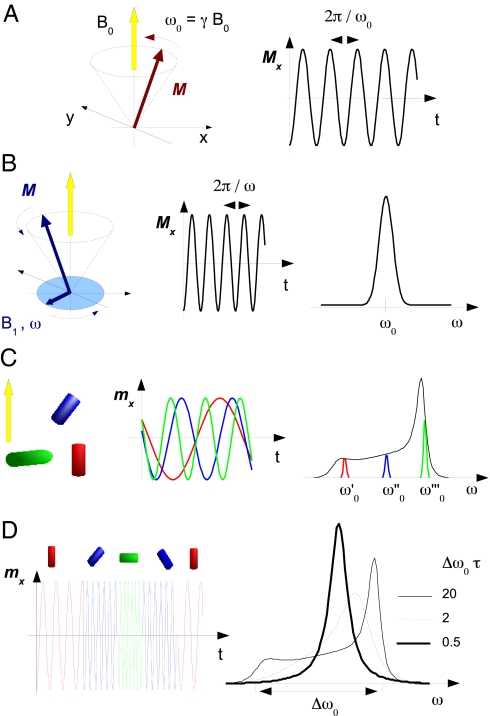
Electron spin resonance (ESR) spectroscopy detects the dynamics of the magnetization M of an ensemble of electrons in the presence of a static magnetic field B0 and under driving by (ideally) a rotating magnetic field B1(t) ⊥ B0 with angular frequency ω (typically ω/2π ≈ 9 GHz) (33). The electron has a magnetic dipole moment m that stems from its intrinsic angular moment (spin) ℏS with ℏ = h/2 π, h being the Planck constant. For a free electron m = −geβeS, where ge = 2.0023 and βe are the electron Landé g-factor and the Bohr magneton, respectively. If B1(t) = 0 and the spins are isolated, M, if misaligned with respect to B0, performs a precession around B0 with angular Larmor frequency ω0 = γB0, where γ = geβe/ℏ is the magnetogyric ratio (Fig. 1A). The ESR spectroscopy usually investigates condensed-matter systems where the electrons exchange energy with the surroundings. When the rotating field B1(t) is acted on the magnetization M, the latter undergoes a precession around B0 with angular frequency ω in the stationary state (Fig. 1B). For ω ≃ ω0, a resonance is observed corresponding to a marked power absorption by the spin system.
Fig. 1.
Aspects of the ESR spectroscopy. (A) Free precession of the magnetization M of an ensemble of isolated electrons around the static magnetic field B0 with Larmor angular frequency ω0 = γB0, γ being the magnetogyric ratio. The transverse magnetization oscillates at the same frequency. (B) In condensed matter, the electrons exchange energy with the surroundings. A rotating microwave field B1(t) ⊥ B0 with angular frequency ω forces the precession of the magnetization around B0 with the same angular frequency. When ω ≈ ω0, an absorption resonance occurs. (C) The magnetic dipoles m of immobile spin probes in a frozen liquid have different ω0 values because of their different orientations with respect to B0, thus resulting in a broad line with width Δω0 (black line), usually referred to as rigid-limit or powder lineshape. (D) If the spin probe undergoes rotation (sketched as instantaneous clockwise jumps at random times), ω0 fluctuates. When the rotational rate 1/τ is larger than the width of the ω0 distribution Δω0, the different precession frequencies become indistinguishable and an average value is seen, i.e., the ESR lineshape coalesces (motional narrowing).
Spin Probes.
Liquids are usually diamagnetic and thus provide no ESR signal. The issue is circumvented by dissolving paramagnetic guest molecules (spin probes), usually nitroxide free radicals with 1 unpaired electron, at an extremely low concentration to make their influence on the host and their mutual interactions vanishingly small (33). The unpaired electron is localized in a highly directional, i.e., anisotropic, molecular bond (see Fig. 2). On this basis, a quantum-mechanical analysis shows that the Larmor frequency of the dipole moment of the spin probe depends on the orientation of the latter with respect to B0 [see supporting information (SI) Appendix].
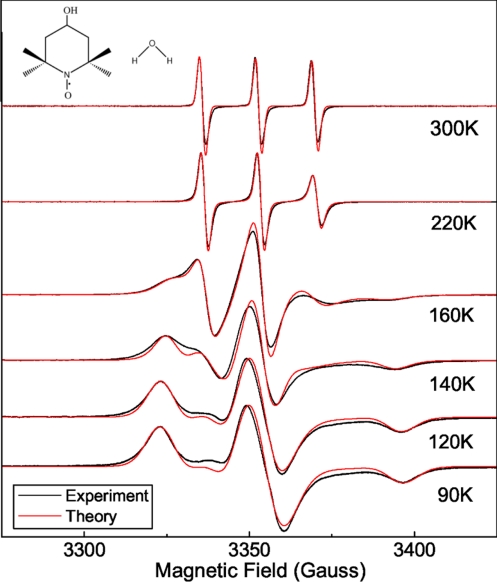
Fig. 2.
Selected ESR lineshapes of the spin probe TEMPOL in quenched bulk water and subsequent reheating at the indicated temperature. Note that: (i) for technical convenience the static magnetic field B0, and not the microwave frequency ω as in Fig. 1, is swept; (ii) the phase-sensitive detection displays the lineshape in derivative mode. The chemical structures of TEMPOL (molecular size rTEMPOL ≈ 0.34 nm) and water (rH2O ≈ 0.14 nm) molecules are sketched. The unpaired electron of TEMPOL (drawn as a dot) is localized in the NO bond. The theoretical predictions considering the reorientation of TEMPOL with (140 K, 160 K) and without dynamical heterogeneity are also shown.
Rigid-Limit and Motional Narrowing of the Lineshape.
We now illustrate how the ESR lineshape conveys information on the rotational dynamics of the spin probe (33–35). Additional details are found in SI Appendix. We first consider an ensemble of immobile spin probes, e.g., like in a frozen host, with different fixed orientations. The different resonances of their magnetic dipole moments are detected by sweeping the ω frequency of B1(t), and their superposition gives rise to a broad absorption with width Δω0, usually referred to as rigid-limit or powder lineshape (Fig. 1C). If the spin probe undergoes a rotational motion, the Larmor frequency of the associated dipole changes randomly in time. Fig. 1D pictures the case of a reorientation occurring by sudden jumps separated by random waiting times with average value τ (τ denotes the rotational correlation time, i.e., the area below the normalized correlation function of the spherical harmonic Y2,0 (34), see SI Appendix). The fluctuation gives rise to frequency averaging. In fact, let us consider 2 Larmor frequencies differing by δω0. If the accumulated phase difference in a time τ, δω0τ, is <1, the 2 frequencies cannot be distinguished and are replaced by their average. This process distorts the rigid-limit lineshape to an extent that is controlled by the product τΔω0. Illustrative cases are shown in Fig. 1D. If τΔω0 ≫ 1, the rigid-limit lineshape is rounded off on the frequency scale 1/τ. If τΔω0 ≈ 1, the average process manifests as a coalescence of the lineshape (“motional narrowing”) that becomes extreme for τΔω0 ≪ 1. In the latter case, the width of a single line is approximately given by Δω02τ (34).
Accessible Range of the Rotational Dynamics.
The longest detectable τ value of a nitroxide spin probe by ESR, τmax, is set by the changes of the Larmor frequency, occurring each T2★ ≈ 0.1 μs on average, because of the magnetic field produced by the rotating methyl groups close to the unpaired electron (33). If τ ≫ τmax ≡ T2★, the spin probe does not rotate within T2★ appreciably, the lineshape is independent of the reorientation rate 1/τ and virtually coincident with the rigid-limit lineshape. On the other hand, in the extreme narrowing regime, the line coalescence cannot lead to line width less than ≈1/T2★ in that T2★ is the upper limit of the lifetime of the coherent oscillation of the magnetization (33). Then, the shortest detectable τ value, τmin, is found when the line width Δω2τmin ≈ 1/T2★. For nitroxide spin probes τmin ≈ 10 ps.
Results and Discussion
Samples were prepared in a capillary (diameter ≈100 μm) by doping a small amount of triple-distilled water with approximately 0.1% by weight of the polar spin probe 4-hydroxy-2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPOL), see Fig. 2. The ESR signal of TEMPOL is recorded during the slow reheating of the quenched sample. Details are given in Materials and Methods.
Influence of Crystallization.
In occasional runs, the crystallization occurring during the thermal cycle affects the ESR signal of the spin probes. The resulting artifacts are well known in aqueous solutions (13, 14, 36) and because of the possible strong confinement of the radicals in interstices between the ice grains with subsequent strong reduction of their mutual distance (see Materials and Methods). However, in most runs, the signal is flawless. Henceforth, we focus on these cases where strong arguments lead to the conclusion that the ice loosely confines TEMPOL in liquid pockets.
Spin-Probe Mobility Above 130 K.
Fig. 2 presents the temperature dependence of the ESR signal of the spin probe. As usual, the lineshape, because of phase detection, is displayed in derivative mode by sweeping the static magnetic field B0 with constant microwave frequency ω.* The lineshapes in Fig. 2 are strikingly similar to the usual ones of spin probes dissolved in viscous liquids (14, 31, 33, 36–38). At low temperatures (≤90 K) the ESR lineshape exhibits the rigid-limit pattern, namely the reorientation of TEMPOL is very slow (rotational correlation time τ ≳ τmax ≈ 0.1 μs). Above 120 K, the ESR lineshape changes and its “motional narrowing” becomes apparent, signaling the increased mobility of the spin probe. For T ≳ 220 K, narrowing is extreme, and the lineshape collapses to 3 lines. The 3-line pattern connects smoothly to the one detected in equilibrium condition at 300 K. Note that the observed narrowing of the lineshape is opposite to the crystallization-driven broadening discussed above.
The temperature dependence of the ESR lineshape shown in Fig. 2 excludes the possibility that the spin probes are trapped into the solid crystalline matrix developed during the initial quench-cooling or the subsequent slow reheating (when the ESR data are collected). In fact, if trapping occurs during the quench, the rigid-limit ESR lineshape at 90 K should be observed upon heating up to Tm, where a sudden collapse to a 3-line pattern much similar to the one observed at 300 K should occur because of the large increase in mobility. Instead, one notes the continuous narrowing of the lineshape, i.e., the progressively increasing mobility of TEMPOL, across the supercooled region from, say, 120 K up to 300 K. Moreover, the motionally narrowed lineshape at 220 K, pointing to fast reorientation, is almost identical to the one at 300 K indicating that TEMPOL has similar mobility at that temperatures. Because fast reorientation is also seen between 220 K and Tm (see below), the trapping of the spin probes into the ice fraction can be safely ruled out. Instead, it has to be concluded that, when ice freezes, TEMPOL, as are most impurities (13–15), is expelled from the ice and accumulate in liquid pockets (7–12, 16, 17). The volume fraction of the liquid water φw is estimated to be φw ≥ 0.04–0.07 (see Materials and Methods).
Dynamical Heterogeneities.
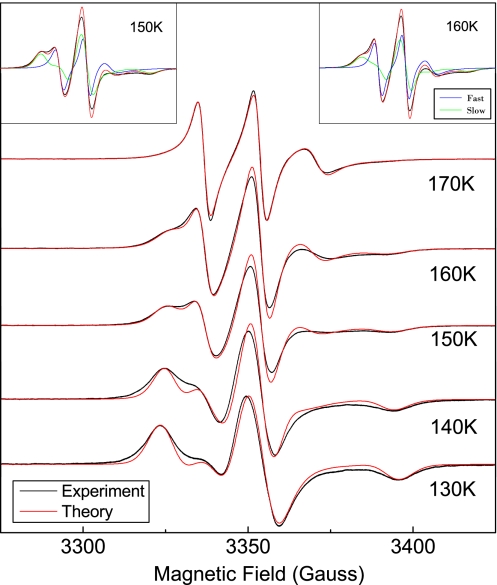
In-depth numerical analysis of the ESR lineshape was first carried out by modeling the jump reorientation of TEMPOL in terms of the jump angle θ and the rotational correlation time τ (see Materials and Methods). When fitted to the experiment, the model, relying on a homogeneous mobility scenario, worked nicely except in the temperature region 140–180 K, and typical results are shown in Fig. 2. In the temperature region 140–180 K, dynamical heterogeneity (DH) is apparent. In fact, entering the DH regime on heating, a second component, to be ascribed to a TEMPOL fraction with greater rotational mobility, appears (Fig. 3). In the DH regime, the lineshape was evaluated as a weighted sum of 2 components, i.e., the “fast” (F) component with weight wf and the “slow” (S) component with weight ws = 1 − wf. Upon increasing the temperature, wf increases and above 180 K, still well inside NML, wf ≃ 1 (see Inset b of Fig. 4). The missing evidence of heterogeneous dynamics >180 K is due to the limited ability of the ESR spectroscopy to discriminate between different TEMPOL rotational mobilities if the correlation times are too short (τ ≲ 1 ns) and cannot be taken as evidence of no actual DH.
Fig. 3.
ESR lineshapes of TEMPOL in DH regime. Note the growth of the narrow component (fast TEMPOL) that superimposes to the broader one (slow TEMPOL) with increasing temperature. The Insets show the fast (blue) and slow (green) components of the overall lineshape (red) at 2 temperatures.
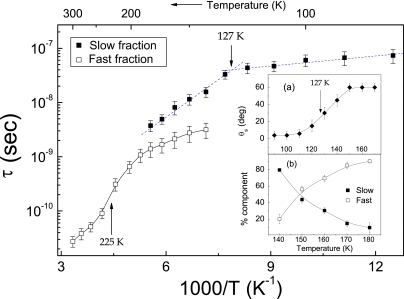
Fig. 4.
Temperature dependence of the rotational parameters of the fast (F) and the slow (S) fractions of TEMPOL in deeply supercooled bulk water. Shown are rotational correlation times τs and τf. (Inset a) average jump angle of the S fraction. (Inset b) weights of the F and S fractions. Note in the main image : (i) the knee at ≈127 K close to Tg = 136 K, (ii) the DH regime (140–180 K) where the 2 coexisting TEMPOL fractions with different mobilities are evidenced, (iii) the inflection close to TFSC ≈ 228 K.
Temperature Dependence of the Spin-Probe Reorientation.
Fig. 4 presents the temperature dependence of the model parameters describing the reorientation of the 2 TEMPOL fractions. It is seen that at the lowest temperatures the dominant S fraction of TEMPOL undergoes small-size diffusive rotational jumps with nearly constant τs correlation times. Crossing over 127 K, τs starts to drop, and the jump size to increase, which is consistent with a more mobile and open structure of the surroundings of TEMPOL consequent to the glass transition. At 140 K, the F component becomes apparent in the ESR lineshape, and its weight increases with the temperature. The presence of the F fraction leads to no anomaly in the rotational dynamics of TEMPOL molecules belonging to the S fraction. In particular, θs levels off to ≃60° (see Fig. 4, Inset a) in agreement with simulations on water (30). The DH region ends at ≈180 K, above which only the F component is seen. The correlation time τf decreases with the temperature and shows an inflection point at ≈225 K. At higher temperatures, τf connects smoothly to the equilibrium value at 300 K.
We note that the temperature dependence of the TEMPOL correlation times in Fig. 4 shows a cross-over at 225 K from a high-temperature “fragile” behavior (non-Arrhenius) to a lower-temperature “strong” one (Arrhenius) that strongly resembles the FSC cross-over that has been hypothesized for water at TFSC ≈ 228 K (6) with recent support from simulation (21) and experiments in confined environments (22). The observation of fragile behavior in weakly supercooled water is fully consistent with the views that the water–glass transition is kinetic in nature (24, 25),
Breakdown of the Debye–Stokes–Einstein Law.
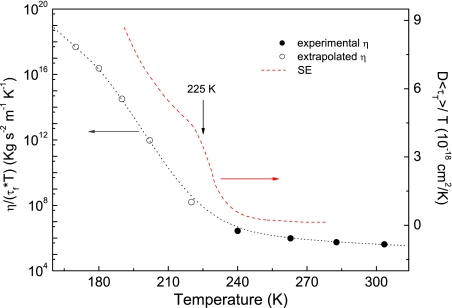
Both the FSC and DH in supercooled water drive the breakdown of the SE and DSE relations (18, 26–28). The DSE breakdown was already observed by ESR in supercooled liquids (31). We evaluated the DSE ratio ℛDSE ≡ η/(τfT) (to be constant according to the DSE law). To evaluate the water viscosity below TH ≈ 235 K, we resorted to, after proper consideration (see Materials and Methods), a thermodynamic construction (39) based on the entropy-based Adam–Gibbs equation (40, 41). Owing to several thermodynamic constraints on the entropy of water, the construction provides tight bounds on η(T) below TH, provided that a maximum in the specific heat occurs at ≈225 K (39). The latter has been recently observed (42). Fig. 5 shows the results about ℛDSE that are compared with the corresponding SE ratio ℛSE for nanoconfined water (18). At high temperatures, both SE and DSE are weakly violated. In fact, the ratio ℛDSE increases by ≈5.1 times from 280 K down to 240 K [the water viscosity increases by ≈16 times (39)], whereas ℛSE increases by ≈4.4 times for nanoconfined water (18). By decreasing the temperature below ≈225 K, one observes that both ℛDSE and ℛSE increase much more than at high temperature, i.e., the violations of both SE and DSE are much more apparent. So, we note that DSE, as SE (see also figure 3 of ref. 18), undergoes a 2-stage decoupling, i.e., a weak violation above ≈225 K, followed by a stronger decoupling at lower temperatures. The larger increase of ℛDSE with respect to ℛSE at lower temperatures is in agreement with simulations of water (27, 28) and molecular liquids (see ref. 32 and reference 22 of that article).
Fig. 5.
Breakdown of the DSE law. Data are compared with the SE breakdown from ref. 18. Filled dots refer to temperatures where experimental values of the viscosity are available. Open dots are based on a thermodynamic extrapolation of the viscosity (39). The line across the dots is a guide for the eye.
Spin-Probe Sensing of the Water Static Heterogeneities.
The correspondence between DH, the breakdown of SE and DSE and the presence of static heterogeneities in supercooled water, characterized by large fluctuations spanning a range of structures from HDL-like to LDL-like, has been explored, with particular attention to the local orientational order (26–28). It is interesting to put the evidence concerning the heterogeneous dynamics of TEMPOL within this context. In the low-temperature region of the supercooled regime, the LDL fraction, characterized by better organization of the local tetrahedrally coordinated hydrogen-bonded network, is higher than the HDL fraction, where the network is not fully developed (19, 20). One expects that LDL exhibits slower rearrangements and lower fragility (i.e., more Arrhenius-like temperature dependence) than HDL. The HDL fraction is larger at higher temperatures and connects smoothly to the equilibrium states above Tm (19, 20). This scenario suggests that TEMPOL senses the distribution of static structures of supercooled water. In particular, the S fraction senses LDL, and the F fraction senses HDL. In fact, (i) the S fraction of TEMPOL reorients with Arrhenius behavior, whereas the F fraction is more fragile, i.e., τf exhibits a non-Arrhenius temperature dependence (see Fig. 4); (ii) the weight of the F fraction increases with the temperature and connects smoothly to the reorientation regime of TEMPOL above Tm.
ESR evidences LDL and HDL states of water in an indirect way via their influence on the spin-probe reorientation. This leads to the possibility of their direct identification in the supercooled water–ice mixture. To do that, one needs a technique with good discrimination among the 3 distinct coexisting contributions, i.e., ice, LDL, and HDL. In this respect, promising opportunities are offered by (i) the measurement of the vibrational spectra (HOH-bending and OH-stretching modes) via Fourier transform infrared spectroscopy (see figure 1B of ref. 19) and (ii) the measurement of the proton chemical shift δNMR by NMR, providing a picture of the intermolecular geometry [compare the data of figure 1A of ref. 42 with δNMR = 7.4 ppm for a single crystal of hexagonal ice (43)].
In conclusion, ESR investigations of the rotational mobility of probe molecules dissolved in deeply supercooled bulk water provide evidence for 2 coexisting liquid phases between ≈130 K and the thermodynamically stable region, including the NML (the range 150–235 K). Two distinct fractions of the probe molecules with different mobility and fragility are observed. It is argued that they sense the low- and high-density states of supercooled water. The reorientation of the probe molecules exhibits fragile, i.e., non-Arrhenius, character at high temperature with a cross-over to a strong behavior below ≈225 K. An analogous cross-over has been hypothesized for water at TFSC ≈ 228 K (6). The temperature dependence of the correlation time of the slow component shows a change in slope at ≈127 K, close to the putative glass transition temperature of water at ≈136 K. The reorientation of the probe molecules decouples from the viscosity below ≈225 K (DSE breakdown), paralleling the behavior of the translational diffusion of water (18).
Materials and Methods
Samples were prepared in a capillary (diameter ≈100 μm) by doping a small amount of triple-distilled water with ≈0.1% by weight of the polar radical TEMPOL (spin probe). TEMPOL accommodates well in water because of hydrogen bonds and the moderate size (rTEMPOL ≈ 0.34 nm to be compared with rH2O ≈ 0.14 nm). The amorphous water samples were prepared by direct exposition to liquid helium (4.2 K) in situ in the ESR low-temperature cryostat. The liquid helium transfer tube was modified such that a burst of liquid helium hits the capillary, cooling it to 4.2 K almost instantaneously, leading to the formation of vitrified water. The ESR signal of TEMPOL are recorded by using a X-band Bruker ER 200 CW EPR spectrometer. Data are collected upon heating the quenched samples. At a selected temperature, no aging, i.e., no sample evolution, was ever detected.
The ESR lineshape provides information on the conditions of the sample during the experiment, particularly the degree of confinement of the spin probe between the ice grains and the amount of the interstitial liquid water >130 K. In fact, the spin probes, as are most impurities (13–15), are expelled from the ice grains and accumulate in the interstitial liquid fraction. This process reduces the mutual distances between the radicals and, if the confinement is strong, leads to the huge increase of the ESR line width (13, 14, 36). In fact, at short distances, the magnetic field B(sp) created by 1 spin probe is not negligible [∣B(sp)∣ ≈ 150 G at 0.5 nm (33)]. Then, each spin probe sees an effective total magnetic field because of the surrounding ones B0★ ≈ B0 + ΣjBj(sp). Because of the randomness of both the direction and the modulus of Bi(sp), ∣B0★∣ exhibits a distribution centered at B0 and width approximately ∣Bsp∣ resulting in a very wide distribution of the Larmor frequencies ω0 ∝ ∣B0★∣, i.e., an apparent line broadening much larger than the one observed under diluted conditions.
In our experiments, the line broadening because of the crystallization was observed only occasionally during several experimental runs. This points to the conclusion that the crystallization does not yield a marked increase of the spin probe concentration in the liquid fraction of the water–ice mixture. The minimum liquid fraction φw of the sample that is needed so that crystallization effects on the ESR lineshape are not observed may be estimated. Let us assume that, because of the increased spin-probe concentration, the magnetic field B(sp) acted by 1 spin probe on the close ones is large enough to exceed any other broadening effect. At 220 K, the narrowest line of the observed triplet has width of ≈1–2 G (see Fig. 2). If the spin probes, with magnetic dipole equal to approximately the Bohr magneton μB, have mutual average distance d, B(sp) ∝ μBd−3 and B(sp) ≈ 1–2 G if d ≈ 2.1–2.6 nm. If no ice is present, TEMPOL molecules are homogeneously dispersed in water with, given the adopted concentration, average distance d′ ≃ 6.4 nm. Then, φw ≥ (d/d′)3 ≈ 0.04–0.07.
The lineshape is evaluated by a stochastic memory-function approach (see SI Appendix and ref 35). The reorientation of TEMPOL, because of its globular shape, is modeled by instantaneous random jumps with fixed size θ after a mean residence time τ0 (38). Under this hypothesis, the rotational correlation time τ [the area below the normalized correlation function of the spherical harmonic Y2,0 (34)] is given by τ = τ0/[1 − sin(5θ/2)/(5 sin(θ/2))]. The temperature-independent magnetic parameters of TEMPOL were determined by the rigid-limit lineshape recorded at low temperature according to a procedure detailed in ref. 44 and outlined in SI Appendix. The number of adjustable parameters of the theoretical lineshape changes over the temperature range under investigation. In general, the ESR lineshape is fitted by using 2 components, corresponding to the F and slow S fractions of TEMPOL, with weights wf and ws = 1 − wf, respectively. The S component depends on 2 adjustable parameters, i.e., τs and θs, whereas, because of rapid motion, the F component depends on τf only. Therefore, to fit the ESR lineshape in the temperature region 140–180 K (DH regime), one needs 4 adjustable parameters (τs, θs, τf, and wf). These reduce to 2 (τs, θs) at lower temperatures where ws ≃ 1 and to 1 (τf) at higher temperatures where wf ≃ 1. The theoretical lineshape was convoluted by a Gaussian curve with width 1/T2★ to account for the magnetic field produced by the rotating methyl groups close to the unpaired electron. T2★ increases with the temperature from ≈30 ns up to ≈40 ns in the temperature range 90 K–300 K .
To get confidence on the thermodynamic extrapolation of the viscosity at temperatures below TH ≈ 235 K (39), we compared the DSE violation of TEMPOL in water with that of the spin-probe TEMPO (virtually identical to TEMPOL) in the prototypical fragile glass-former o-terphenyl (OTP) where η is known (31). At the temperature where the DSE violation takes place (225 K for TEMPOL in water and 290 K for TEMPO in OTP), ℛDSE(TEMPO)/ℛDSE(TEMPOL) ≈ 1.33. If one considers temperatures where water and OTP have viscosities 1011 times larger than the ones where the DSE breakdown is observed (≈170 K for water and 240 K for OTP), one has ℛDSE(TEMPO)/ℛDSE(TEMPOL) ≈ 1.08. This comparison shows that the magnitude of the DSE breakdown in water and OTP is quite similar and reassured us on the robustness of extrapolation.
Supplementary Material
Acknowledgments.
Discussions with G. Carini, J. F. Douglas, F. Mallamace, F. Sciortino, S. N. Shore, and R. Torre are gratefully acknowledged by D.L.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0900734106/DCSupplemental.
This results in a different pattern with respect to the one in Fig. 1d where for clarity's sake ω is swept with B0 constant, no derivative operation is performed, and the coupling of the unpaired electron with the nuclear magnetic dipoles has been neglected (see SI for details).
References
- 1.Mishima O, Stanley HE. The relation between liquid, supercooled and glassy water. Nature. 1998;396:329–335. [Google Scholar]
- 2.Debenedetti PG. Supercooled and glassy water. J Phys Condens Matter. 2003;15:R1669–R1726. [Google Scholar]
- 3.Angell CA. Insights into phases of liquid water from study of its unusual glass-forming properties. Science. 2008;319:582–587. doi: 10.1126/science.1131939. [DOI] [PubMed] [Google Scholar]
- 4.Smith RS, Kay BD. The existence of supercooled liquid water at 150 K. Nature. 1999;398:788–791. [Google Scholar]
- 5.Johari GP. Liquid state of low-density pressure-amorphized ice above its Tg. J Phys Chem B. 1998;102:4711–4714. [Google Scholar]
- 6.Ito K, Moynihan CT, Angell CA. Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water. Nature. 1999;398:492–495. [Google Scholar]
- 7.Rosenhain W, Ewen D. The intercrystalline cohesion of metals. J Inst Metals. 1913;10:119–148. [Google Scholar]
- 8.Dowell LG, Rinfret AP. Low-temperature forms of ice as studied by X-ray diffraction. Nature. 1960;188:1144–1148. [Google Scholar]
- 9.Jenniskens P, Banham SF, Blake DF, McCoustra MRS. Liquid water in the domain of cubic crystalline ice Ic. J Chem Phys. 1997;107:1232–1241. doi: 10.1063/1.474468. [DOI] [PubMed] [Google Scholar]
- 10.Souda R. Two liquid phases of water in the deeply supercooled region and their roles in crystallization and formation of LiCl solution. J Phys Chem B. 2007;111:5628–5634. doi: 10.1021/jp0672050. [DOI] [PubMed] [Google Scholar]
- 11.Johari GP. Thermodynamics of water-cubic ice and other liquid–solid coexistence in nanometer-size particles. J Chem Phys. 1998;109:1070–1073. [Google Scholar]
- 12.Mader HJ. The thermal behaviour of the water-vein system in polycrystalline ice. J Glaciol. 1992;38:359–374. [Google Scholar]
- 13.Ross RT. Dipolar broadening of EPR spectra due to solute segregation in frozen aqueous solution. J Chem Phys. 1965;42:3919–3922. [Google Scholar]
- 14.Leigh JS, Jr, Reed GH. Electron paramagnetic resonance studies in frozen aqueous solutions. Elimination of freezing artifacts. J Phys Chem. 1971;75:1202–1204. [Google Scholar]
- 15.Mulvaney R, Wolff EW, Oates K. Sulphuric acid at grain boundaries in Antarctic ice. Nature. 1988;331:247–249. [Google Scholar]
- 16.Nye JF. Thermal behaviour of glacier and laboratory ice. J Glaciol. 1991;37:401–413. [Google Scholar]
- 17.Wettlaufer JS, Grae Worster M. Premelting dynamics. Annu Rev Fluid Mech. 2006;38:427–452. [Google Scholar]
- 18.Chen S-H, et al. The violation of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci USA. 2006;103:12974–12978. doi: 10.1073/pnas.0603253103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mallamace F, et al. Evidence of the existence of the low-density liquid phase in supercooled, confined water. Proc Natl Acad Sci USA. 2007;104:424–428. doi: 10.1073/pnas.0607138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mallamace F, et al. The anomalous behavior of the density of water in the range 30 K < T < 373 K. Proc Natl Acad Sci USA. 2007;104:18387–18391. doi: 10.1073/pnas.0706504104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu L, et al. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc Natl Acad Sci USA. 2005;102:16558–16562. doi: 10.1073/pnas.0507870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu L, Chen S-H, Faraone A, Yen C-W, Mou C-Y. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys Rev Lett. 2005;95:117802–4. doi: 10.1103/PhysRevLett.95.117802. [DOI] [PubMed] [Google Scholar]
- 23.Poole PH, Sciortino F, Essmann U, Stanley HE. Phase behaviour of metastable water. Nature. 1992;360:324–328. [Google Scholar]
- 24.Sciortino F, Gallo P, Tartaglia P, Chen S-H. Supercooled water and the kinetic glass transition. Phys Rev E. 1996;54:6331–6343. doi: 10.1103/physreve.54.6331. [DOI] [PubMed] [Google Scholar]
- 25.Torre R, Bartolini P, Righini R. Structural relaxation in supercooled water by time-resolved spectroscopy. Nature. 2004;428:296–299. doi: 10.1038/nature02409. [DOI] [PubMed] [Google Scholar]
- 26.Kumar P, et al. Relation between the Widom line and the breakdown of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci USA. 2007;104:9575–9579. doi: 10.1073/pnas.0605880103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Becker SR, Poole PH, Starr FW. Fractional Stokes–Einstein and Debye–Stokes–Einstein relations in a network-forming liquid. Phys Rev Lett. 2006;97 doi: 10.1103/PhysRevLett.97.055901. 055901–4. [DOI] [PubMed] [Google Scholar]
- 28.Mazza MG, Giovambattista N, Stanley HE, Starr F.W. Connection of translational and rotational dynamical heterogeneities with the breakdown of the Stokes–Einstein and Stokes–Einstein–Debye relations in water. Phys Rev E. 2007;76 doi: 10.1103/PhysRevE.76.031203. 031203–031212. [DOI] [PubMed] [Google Scholar]
- 29.Errington JR, Debenedetti PG. Relationship between structural order and the anomalies of liquid water. Nature. 2001;409:318–321. doi: 10.1038/35053024. [DOI] [PubMed] [Google Scholar]
- 30.Laage D, Hynes JT. A molecular jump mechanism of water reorientation. Science. 2006;311:832–835. doi: 10.1126/science.1122154. [DOI] [PubMed] [Google Scholar]
- 31.Andreozzi L, Di Schino A, Giordano M, Leporini D. Evidence of a fractional Debye–Stokes–Einstein law in supercooled o-terphenyl. Europhys Lett. 1997;38:669–674. [Google Scholar]
- 32.De Michele C, Leporini D. Viscous flow and jump dynamics in molecular supercooled liquids. II. Rotations. Phys Rev E. 2001;63 doi: 10.1103/PhysRevE.63.036702. 036702–036710. [DOI] [PubMed] [Google Scholar]
- 33.Weil JA, Bolton JR. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications. New York: Wiley–Interscience; 2006. [Google Scholar]
- 34.Nordio PL. In: Spin Labeling: Theory and Applications. Berliner LJ, editor. New York: Academic; 1976. pp. 5–52. [Google Scholar]
- 35.Giordano M, Grigolini P, Leporini D, Marin P. Fast computational approach to the evaluation of slow motion EPR spectra in terms of a generalized Langevin equation. Phys Rev A. 1983;28:2474–2481. [Google Scholar]
- 36.Bhat SN, Sharma A, Bhat SV. Vitrification and glass transition of water; insights from spin probe ESR. Phys Rev Lett. 2005;95:235702. doi: 10.1103/PhysRevLett.95.235702. [DOI] [PubMed] [Google Scholar]
- 37.Polnaszek CF, Bruno GV, Freed JH. ESR lineshapes in the slow-motional region: Anisotropic liquids. J Chem Phys. 1973;58:3185–3199. [Google Scholar]
- 38.Andreozzi L, Cianflone F, Donati C, Leporini D. Jump reorientation of a molecular probe in the glass transition region of o-terphenyl. J Phys Condens Matter. 1996;8:3795–3809. [Google Scholar]
- 39.Starr FW, Angell CA, Stanley HE. Prediction of entropy and dynamic properties of water below the homogeneous nucleation temperature. Physica A. 2003;323:51–66. [Google Scholar]
- 40.Angell CA. Entropy and fragility in supercooling liquids. J Res NIST. 1997;102:171–185. doi: 10.6028/jres.102.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Scala A, Starr FW, La Nave E, Sciortino F, Stanley HE. Configurational entropy and diffusivity of supercooled water. Nature. 2000;406:166–169. doi: 10.1038/35018034. [DOI] [PubMed] [Google Scholar]
- 42.Mallamace F, et al. NMR evidence of a sharp change in a measure of local order in deeply supercooled confined water. Proc Natl Acad Sci USA. 2008;105:12725–12729. doi: 10.1073/pnas.0805032105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pfrommer BG, Mauri F, Louie SG. NMR chemical shifts of ice and liquid water: the effects of condensation. J Am Chem Soc. 2000;122:123–129. [Google Scholar]
- 44.Andreozzi L, Giordano M, Leporini D. Efficient characterization of the orientational ordering of ESR-active probes in supermolecular fluids. Appl Magn Reson. 1993;4:279–295. [Google Scholar]
- 45.Zhang H, Srolovitz DJ, Douglas JF, Warren JA. Grain boundaries exhibit the dynamics of glass-forming liquids. Proc Natl Acad Sci USA. 2009;106:7735–7740. doi: 10.1073/pnas.0900227106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.