Translational switch for long-term maintenance of synaptic plasticity

Abstract

Memory can last a lifetime, yet synaptic contacts that contribute to the storage of memory are composed of proteins that have much shorter lifetimes. A physiological model of memory formation, long-term potentiation (LTP), has a late protein-synthesis-dependent phase (L-LTP) that can last for many hours in slices or even for days in vivo. Could the activity-dependent synthesis of new proteins account for the persistence of L-LTP and memory? Here, we examine the proposal that a self-sustaining regulation of translation can form a bistable switch that can persistently regulate the on-site synthesis of plasticity-related proteins. We show that an αCaMKII–CPEB1 molecular pair can operate as a bistable switch. Our results imply that L-LTP should produce an increase in the total amount of αCaMKII at potentiated synapses. This study also proposes an explanation for why the application of protein synthesis and αCaMKII inhibitors at the induction and maintenance phases of L-LTP result in very different outcomes.

Introduction

Synaptic plasticity, the experience-dependent change in synaptic efficacies, provides a physiological basis for learning and memory storage (Bliss and Lomo, 1973; Bliss and Collingride, 1993; Bear, 1996; Morris et al, 2000). Theoretical considerations require that synaptic plasticity must be synapse specific if it is to provide sufficient neuronal selectivity, but must also be long lasting if it is indeed the basis for long-lasting learning and memory. However, synapses are composed of proteins that turnover at rates that are much faster than memory lifetimes (Crick, 1984; Lisman and Goldring, 1988). Therefore, there must be a synapse-specific biological mechanism to preserve synaptic efficacies in the face of protein turnover.

Long-term potentiation (LTP), a long-lasting cellular manifestation of synaptic plasticity, can be divided into two forms: early-phase LTP (E-LTP) is induced by a ‘weak' stimulus, is protein synthesis independent, and lasts for 2–4 h, whereas late-phase LTP (L-LTP), which requires a ‘strong' stimulus, lasts much longer and depends on the synthesis of new proteins (Frey et al, 1988; Kang and Schuman, 1996). Although both transcription and translation have been implicated in L-LTP, we concentrate here on the effect of translation because nuclear transcription cannot account for synapse specificity.

A popular theory is that the maintenance of long-term memory and synaptic plasticity is accomplished through a bistable molecular switch. Specifically, most attention has been given to theory that autophosphorylation of αCaMKII can form a bistable switch that is resistant to phosphatases and protein turnover (Lisman and Goldring, 1988; Zhabotinsky, 2000; Lisman and Zhabotinsky, 2001; Miller et al, 2005). There are several significant challenges to this theory, which include the following observations: First, this theory does not depend on protein synthesis and cannot account for the protein synthesis dependence of long-term memory and plasticity (Frey et al, 1988; Kang and Schuman, 1996); second, this theory assumes a conserved amount of total αCaMKII and therefore cannot account for the observed increase in synaptic levels of αCaMKII (Ouyang et al, 1997, 1999; Otmakhov et al, 2004); third, a key biochemical experiment of αCaMKII phosphorylation did not find bistability (Bradshaw et al, 2003). In addition, there is a dispute whether blocking αCaMKII activity during the maintenance phase reverses L-LTP (Malinow et al, 1989; Otmakhov et al, 1997; Sanhueza et al, 2007). Therefore, it makes sense to examine alternative theories that might be able to account for these experimental observations.

The main objective of this work is to explore a possible link between activity-dependent temporal and spatial regulation of post-transcriptional gene expression and lifelong stability of some memories, despite the rapid turnover of their molecular substrates. This study is motivated by the following experimental observations: (1) L-LTP requires new protein synthesis (Stanton and Sarvey, 1984; Frey et al, 1988). (2) Almost all the components of translational machinery are constitutively localized in dendrites (Gardiol et al, 1999; Pierce et al, 2000; Ostroff et al, 2002; Tang et al, 2002). (3) The translation of proteins important for synaptic plasticity, such as αCaMKII, can be controlled locally in dendrites and synapses (Wu et al, 1998; Miller et al, 2002). Here, we examine a hypothesis that a molecular loop between a kinase and a translation regulation factor acts as a bistable switch to stabilize activity-induced synaptic plasticity over long periods of time. Various regions of the brain, including hippocampus and neocortex, are involved in different phases of memory consolidation (McClelland et al, 1995; Wiltgen et al, 2004), indicating that the maintenance of memory includes system-level components that are beyond cellular and molecular substrates. Discussions on these system-level components are beyond the scope of this study.

One regulatory mechanism for mRNA translation is cytoplasmic polyadenylation (Wells et al, 2000, 2001), in which the translation of mRNAs is modulated by regulating the length of the 3′ poly(A) tail (Wilutz et al, 2001). A shorter poly(A) tail entails lower translational efficiency (Sheets and Wickens, 1989). The length of the poly(A) tail is increased through cytoplasmic polyadenylation, thus enhancing the efficiency of translation (Gallie, 1991). The translation of mRNAs that contain a short nucleotide sequence known as cytoplasmic polyadenylation elements (CPEs) in their 3′ UTR is regulated through polyadenylation. The CPE binds a CPE-binding protein (CPEB1), which represses translation through its dual interactions with CPEs and other mRNA-binding proteins. The phosphorylation of CPEB1 changes its interactions with these other proteins, promotes polyadenylation, and increases translation efficiency (Du and Richter, 2005).

A key molecule linked to the induction of LTP is αCaMKII (Soderling, 2000; Hudmon and Schulman, 2002); however, its link to the maintenance phase of LTP is less clear (Silva et al, 1992; Bagni et al, 2000). The αCaMKII protein is highly enriched at synapses and a significant amount of αCaMKII mRNA is localized in dendrites (Wells et al, 2001). Recent experimental evidence indicates that almost 83% of αCaMKII found in dendrites during normal brain function is synthesized locally in dendrites (Miller et al, 2002). The αCaMKII mRNA contains two CPE elements in its 3′UTR, and its translation can be regulated through a CPEB1-dependent polyadenylation process. Recent studies (Atkins et al, 2004, 2005) have shown that αCaMKII can phosphorylate and therefore possibly modulate its own translation at synapses in a CPE-dependent manner.

In this study, we examine the hypothesis that a kinase translation-factor loop acts as a bistable switch and study a specific instantiation of such a loop, the αCaMKII–CPEB1 molecular pair. Here, using a computational model, we show that the proposed αCaMKII–CPEB1 molecular loop can act as a bistable switch and thus stabilize the synaptic efficacies in a synapse-specific manner despite a continual turnover of its molecular constituents. We also show that with the application of a stimulus pulse (of (Ca²⁺)₄–CaM), we can induce a long-lasting elevation of total αCaMKII levels consistent with experimental observations (Ouyang et al, 1997, 1999; Otmakhov et al, 2004). The induction of L-LTP also produces a moderate, persistent elevation in the fraction of phosphorylated αCaMKII, in contrast to saturated levels of phosphorylated αCaMKII in post-translational models (Lisman and Zhabotinsky, 2001). In this study, we concentrate on the maintenance of the total amount of αCaMKII and the fraction of phosphorylated αCaMKII. We assume that these variables are directly correlated with synaptic efficacy, as shown in previous theoretical studies (Lisman, 1989; Castellani et al, 2005).

Experimental results show that protein synthesis inhibitors that are applied during the induction of L-LTP can block L-LTP, but if they are applied during the maintenance of L-LTP, they do not reverse the potentiation (Frey et al, 1988; Fonseca et al, 2006). Similarly, several results show that the inhibition of αCaMKII activity blocks the induction of L-LTP, but not its maintenance (Malinow et al, 1989; Otmakhov et al, 1997). These results might indicate that a basic assumption of the model, that protein synthesis of new αCaMKII during maintenance is required for maintenance, does not hold, potentially invalidating the model. However, by simulating a large, but not complete, inhibition of protein synthesis and αCaMKII activity, we show a very different effect during the induction and maintenance phases of L-LTP, which is not only consistent with experimental observations but might also account for an apparent discrepancy between different experiments (Malinow et al, 1989; Otmakhov et al, 1997; Sanhueza et al, 2007).

Results

A molecular model of αCaMKII interaction loop

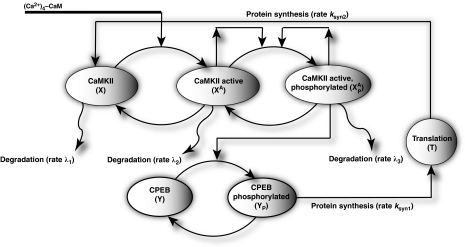
The model that we propose for a translation-factor kinase loop (Figure 1) is composed of two molecular components: (1) the αCaMKII protein, which can be in one of three states: inactive, active, or phosphorylated; (2) the CPEB1 translation factor, which can be either in the phosphorylated or unphosphorylated state, binds to the CPE domain of the αCaMKII mRNA, and represses its translation if unphosphorylated. These two components interact through a closed loop. Here, we assume that CPEB1 is phosphorylated by active and phosphorylated αCaMKII (Atkins et al, 2004, 2005). Once CPEB1 is phosphorylated by a kinase, it initiates the translation of a new αCaMKII protein from αCaMKII mRNA through a CPE-dependent polyadenylation process. In addition to new protein synthesis, the proposed molecular model also assumes that the αCaMKII protein undergoes degradation. This degradation is a combination of several processes, including protein turnover and permanent diffusion of non-bound proteins out of synapses. All of the processes modeled herein are complex, but we have approximated them by simpler processes that maintain their key qualitative features. An implicit assumption of this model is that αCaMKII levels are related to synaptic efficacy, although this relationship might not be linear.

Figure 1.

The proposed model of the local αCaMKII synthesis through the αCaMKII–CPEB1 molecular loop. Here, the αCaMKII molecule can be in inactive, active or active and phosphorylated state, whereas CPEB1 can be in unphosphorylated or phosphorylated state. The αCaMKII molecule in each of the three states has a finite turnover time. A new αCaMKII molecule is produced by CPEB1-dependent polyadenylation of αCaMKII mRNA, which is represented by translation stage (T).

Our model of αCaMKII activation and autophosphorylation (Figure 1) assumes that the αCaMKII protein can reside in three distinct states: an inactive state that cannot phosphorylate substrates, an active state, which is obtained when inactive αCaMKII binds to calcium–calmodulin ((Ca²⁺)₄–CaM); this active state can phosphorylate substrates, including other αCaMKII molecules. The third state is the phosphorylated state of αCaMKII, which is constitutively active, independent of the level of (Ca²⁺)₄–CaM. The active phosphorylated state can be dephosphorylated by a phosphatase. A faithful activation, autophosphorylation model of αCaMKII is more complex than the three-state model assumed here (Zhabotinsky, 2000; Lisman and Zhabotinsky, 2001); in particular, it must take into account the structure of αCaMKII holoenzymes. In our simulations, we assumed a non-negligible basal level of inactive αCaMKII (10 μM) (Chen et al, 2005), whereas the basal concentrations for active αCaMKII is considered to be negligibly small. The biochemical reaction rates for the αCaMKII molecular loop are taken from previous work (Kubota and Bower, 2001). For determining the degradation rates of αCaMKII, we used constants consistent with experimentally measured rates (Ehlers, 2003). It has been suggested that the αCaMKII loop is itself a bistable molecular loop (Zhabotinsky, 2000; Lisman and Zhabotinsky, 2001) However, the isolated αCaMKII molecular loop of our model has only one stable steady state (Supplementary Figure S₁) in accordance with experimental results (Bradshaw et al, 2003). Therefore, the bistability of this translation–phosphorylation model originates from the overall structure of the αCaMKII–CPEB1 molecular loop and not from the isolated αCaMKII structure, in contrast to previous models (Zhabotinsky, 2000; Lisman and Zhabotinsky, 2001).

The synthesis of new proteins in our proposed molecular model is controlled by the phosphorylation of CPEB1 molecules. Once CPEB1 is phosphorylated, it initiates the polyadenylation process, which leads to the synthesis of a new αCaMKII molecule. In our model, the rate of new protein synthesis is controlled by the fraction of phosphorylated CPEB1 through a simple model of translation (see Materials and methods). In our translation model (Figure 1), the phosphorylated CPEB1 (Y_P) binds to the translation machinery (T) with a forward constant, k_SYN1, a backward constant, k₍₋₁₂₎, and produces a new protein with a synthesis rate, k_SYN2. Although this model is clearly a very simplified representation of the translation processes, we presume that it captures the qualitative features essential for this work. Although our simplified model might be sufficient for capturing the qualitative behavior of this loop, its simplified nature implies that it may not account quantitatively for experimental results. We assume that αCaMKII is synthesized in its inactive state. This model differs qualitatively from most previous models of molecular bistability (Kholodenko, 2000; Tyson et al, 2003) in that it does not assume conserved quantities of molecules and includes both protein synthesis and degradation.

In this study, although we are primarily focused on the maintenance phase of L-LTP, we modeled the induction of L-LTP by using a brief pulse of increased (Ca²⁺)₄–CaM concentration. This is used to mimic the high-frequency stimulation (HFS) induction protocol of L-LTP. This is a very simple approach that ignores many of the details of induction protocols and the complex signal-transduction pathways that are involved. However, as maintenance and not induction is the focus of our work, we chose a simple model so as not to obscure the essence of our results with details. Nevertheless, the cost of this simple approach is that our results have qualitative, but not quantitative, significance.

Bistable molecular switch

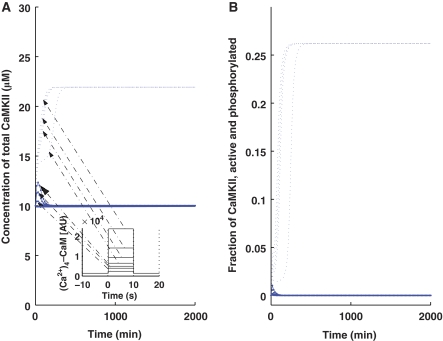
We next determined whether the kinase translation-factor loop can operate as a bistable switch. We implemented the induction of L-LTP through a (Ca²⁺)₄–CaM pulse as mentioned in a previous section. In the absence of a pulse (Figure 2, solid lines), the system stays in the lower steady state, wherein the total concentration of αCaMKII is 10 μM (Figure 2A, solid line), as the rest of the cell and the fraction of phosphorylated αCaMKII is 0% (Figure 2B, solid line). On application of a pulse (10 s), there is a sustained increase in the total amount of αCaMKII to approximately twice the basal-level concentration (Figure 2A, dotted line) and the fraction of phosphorylated αCaMKII is elevated (Figure 2B, dotted line), but is far from saturation. These results are consistent with experimental observations (Ouyang et al, 1997, 1999). The temporal dynamics depicted in Figure 2 clearly show two phases of L-LTP: an early phase in which the concentration of αCaMKII rapidly increases (30–40 min), followed by a persistent phase in which the concentration of αCaMKII is maintained over a long period of time. The system depicted here is bistable because we can provide stimulus of different amplitudes, but they will converge to one of only two possible stable states, depending on the amplitude and duration of stimulus (Figure 2). We call these two stable states the ‘up' and ‘down' states. The sustained increase in the αCaMKII amount and activity is believed to be linked with synaptic potentiation. Previous models have investigated the connections between the signal transduction networks and changes in synaptic efficacy during the induction phase (Castellani et al, 2001, 2005; Shouval et al, 2002; D'Alcantara et al, 2003), and although similar components can be used here, it is beyond the scope of this study.

Figure 2.

Bistability characteristics of the αCaMKII–CPEB1-positive feedback loop. A brief (Ca²⁺)₄–CaM concentration pulse is used to mimic the induction of L-LTP through the application of HFS. The solid line represents the αCaMKII concentration at the basal level (without the application of pulse) and the dashed line represents the αCaMKII concentration after the application of pulse. (A) Total αCaMKII concentration (μM) with a lower steady state at 10 μM and an upper steady state at ∼22 μM. (B) Fraction of active and phosphorylated αCaMKII with a lower steady state at ∼0 and an upper steady state at ∼25%. This figure also shows the bistability characteristics of the αCaMKII–CPEB loop at different amplitudes of the (Ca²⁺)₄–CaM pulse for 10 s duration. These results show that even with different amplitudes of pulse stimulus, the αCaMKII–CPEB loop converges to the same up- or downregulated state, thus indicating that this system is bistable, that is, with a sufficiently strong stimulus, it is upregulated and without enough stimulus it is downregulated.

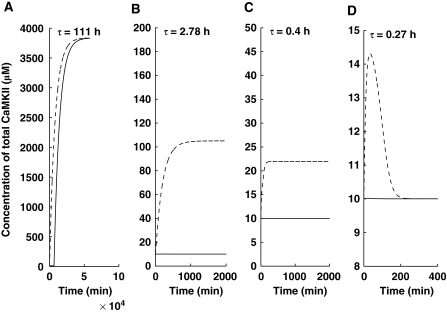
Two key processes that might control the stability of the proposed molecular model are protein synthesis and protein degradation (Figure 1). In our simple model of degradation, protein turnover is characterized by turnover rates. To simplify further, we assume that the turnover rates for the different states of αCaMKII are identical (λ₁=λ₂=λ₃), and to facilitate a comparison with experimental results, we use the protein degradation time constant, τ=1/λ. In Figure 3, we present the results of simulations with different degradation time constants. At a large degradation time constant, the system is monostable (Figure 3A). As degradation time constant decreases, the system becomes bistable (Figures 3B and C) and the difference between the ‘up' and ‘down' states decreases (Figure 3A–C). Once the degradation rate is high enough, the system loses its bistability and becomes monostable (Figure 3D).

Figure 3.

Bistable and monostable characteristics of the αCaMKII–CPEB1-positive feedback loop. Solid line represents αCaMKII concentration, without the application of (Ca²⁺)₄–CaM pulse and the dashed line represents αCaMKII concentration on application of a brief (Ca²⁺)₄–CaM pulse. All simulations are carried out with identical parameters, except the αCaMKII turnover rate (A) τ=111.0 h (B) τ=2.78 h (C) τ=0.4 h (D) τ=0.27 h. For a slow turnover rate, the switch is monostable (A), as the turnover rate is increased, the switch becomes bistable (B and C), and at a faster turnover rate, the switch becomes monostable again (D).

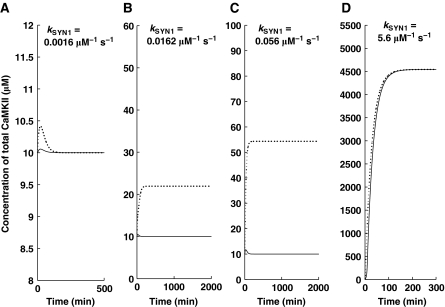
Bistability critically depends also on the rate of protein synthesis. Protein synthesis is characterized in our simple model by several parameters. In Figure 4, we show how one of these parameters, k_SYN1, affects the dynamics of our model. These results are obtained at the αCaMKII turnover rate of 1 h. Here, we show that at low k_SYN1, the molecular switch has a monostable character (Figure 4A), which implies that at a lower synthesis rate, the new protein synthesis is not sufficient to provide a replacement for protein loss due to degradation, and therefore, the upregulated state of αCaMKII cannot be maintained for a long period of time, leading to a gradual loss of synaptic strength. However, at high k_SYN1, the synthesis of a new αCaMKII molecule sufficiently compensates for loss due to protein turnover. We also show that a higher synthesis rate of new proteins leads to higher steady-state levels of αCaMKII (Figure 4B–D).

Figure 4.

Bistable and monostable characteristics of the αCaMKII–CPEB1-positive feedback loop. The simulations are implemented using a brief (Ca²⁺)₄–CaM pulse. The solid line represents αCaMKII at the basal condition and the dashed line represents the application of pulse. All simulations are carried out with identical parameters, except the synthesis rate of new proteins (A) k_SYN1=0.0016 μM⁻¹ sec⁻¹ (B) k_SYN1=0.0162 μM⁻¹ sec⁻¹ (C) k_SYN1=0.056 μM⁻¹ sec⁻¹ (D) k_SYN1=5.6 μM⁻¹ sec⁻¹. The switch is monostable for slow protein synthesis rate (A), as the protein-synthesis rate is increased, the switch becomes bistable (B, C), and as the protein-synthesis rate is further increased, it becomes monostable again (D).

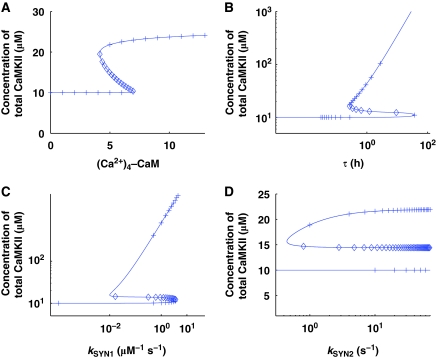
To systematically evaluate the influence of physiologically significant parameters on the stable states of this dynamic system, we developed bifurcation diagrams for several of the key parameters: Ca²⁺–calmodulin signal (Ca²⁺)₄–CaM, degradation rate (λ₁), and synthesis rate (k_SYN1, k_SYN2) (Figure 5). All these bifurcation diagrams show regions of bistability in which there are three fixed points, two of them stable (solid line) and one unstable (dashed line). The bifurcation diagram with the (Ca²⁺)₄–CaM signal (Figure 5A) shows that at a lower signal intensity, the molecular switch has only a ‘down' state and as the (Ca²⁺)₄–CaM signal intensity increases, the molecular switch has both ‘up' and ‘down' states. The X-axis of Figure 5A is in arbitrary units [AU], as available experimental data do not provide sufficient information for determining realistic physical units. We have attempted to set other parameters in the system so that the units fall in the μM range; however, there is uncertainty with regard to some of the kinetic coefficients in this system, which does not allow us to definitely set the scale. Determining the lower cutoff of the bistable region (Figure 5A) in numerical values and comparing with experimental estimates of free (Ca²⁺)₄–CaM (Persechini and Stemmer, 2002) is crucial for determining whether this system can be bistable under realistic conditions. The bifurcation diagram for the degradation parameter, τ=1/λ₁ (λ₁=λ₂=λ₃), shows that, at intermediate degradation rates, there are three fixed points (Figure 5B), two of them are stable (solid lines) and are termed the ‘down' and ‘up' states, respectively. For very fast degradation (small τ), only the ‘down' state survives, suggesting that protein degradation rates are so fast that protein synthesis rates cannot reach the ‘up' state. For slow degradation (large τ), only the ‘up' state survives. Similarly, the bifurcation diagram with the protein synthesis parameters, k_SYN1 and k_SYN2, (Figure 5C and D) shows both bistable and monostable regions depending on the parameters. These bifurcation diagrams have wide bistability regions, suggesting that this is a robust system. In this system, when the total concentration of αCaMKII is in the upregulated state, so is the total concentration of active and phosphorylated αCaMKII, as shown in Supplementary Figure S₂.

Figure 5.

Numerical and analytical bifurcation diagrams represent the steady-state solutions of this dynamic system with respect to model parameters. Numerically (solid lines), these steady-state solutions are tracked with a nonlinear global continuation-based solver. The analytical bifurcation diagrams (cross and diamond signs, where cross represents the stable analytical branches (‘up' and ‘down' states) and diamond sign represents the unstable analytical branch) are generated using an analytical expression, which is obtained by analytically solving all the equations and converting them into a single nonlinear expression. Both numerical and analytical bifurcation diagrams completely match each other. Four key parameters are selected for generating bifurcation diagrams. (A) The intensity of the [(Ca²⁺)₄–CaM] signal, (B) turnover rate (τ), (C) protein synthesis rate (k_SYN1), (D) protein synthesis rate (k_SYN2).

We find that the steady states of this complex dynamic system, described in equations 8–18, can be determined analytically. The system can be reduced to a fifth-order polynomial (Supplementary information). The fixed points of this dynamic system are the zero crossings of this polynomial. As this is a fifth-order polynomial, it has at most five real roots, two of which fall in the non-physiological regime (negative). On the basis of the analytical expression, we also developed the analytical bifurcation diagrams (Figure 5—cross and diamond symbols, where cross represents stable steady-state solutions and diamond represents the unstable steady-state solution). Our comparison of the analytical and numerical results shows an exact match between the two approaches (Figure 5). A transition from a bistable to a monostable system means that as we change a parameter, the number of positive real zeros of the polynomial changes from 3 to 1.

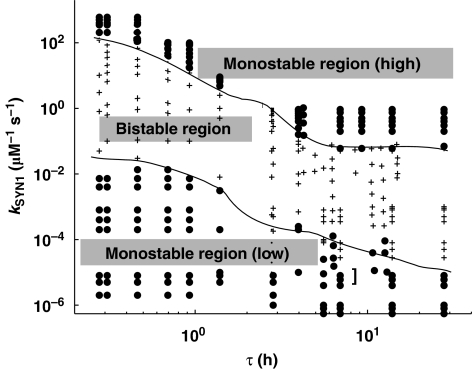
In the bifurcation diagrams presented, one parameter is changed, whereas the others remain fixed. However, this phosphorylation–synthesis loop is a high-dimensional system, and the different types of behaviors (bistable and monostable) exist in a subspace of the high-dimensional parameters space. Mapping out such high-dimensional spaces is very difficult and showing it is not possible. We can, however, show two dimensional slices of these high-dimension spaces. We used τ and k_SYN1 as two physiologically significant parameters to develop this two-dimensional phase diagram. This phase diagram (Figure 6) is divided into three distinct regions: a low monostable region, a bistable region, and a high monostable region. These results show that for a given value of k_SYN1, the lower monostable region is found at lower turnover rates and the higher monostable region is found at high turnover rates. This specific phase diagram shows a wide parameter region in which bistability can be sustained and therefore indicates that this system is robust.

Figure 6.

Phase diagram of the αCaMKII–CPEB1 loop. Two key parameters are selected for phase envelope: (i) the αCaMKII turnover rate, τ and (ii) the new protein synthesis rate, k_SYN1. This phase diagram is characterized by three regions: a low monostable region with only one downregulated steady state; a high monostable region with only an upregulated steady state; and a bistable region that has both up- and downregulated steady states.

Blocking protein synthesis during the induction and maintenance of L-LTP

The translation inhibitors used during the induction and maintenance phases of L-LTP produce very different outcomes. When translation inhibitors are applied during the induction phase, L-LTP is compromised (Kang and Schuman, 1996; Frey and Morris, 1997). However, when applied later, after the induction phase of L-LTP is complete, translation inhibitors do not reverse the potentiation (Frey and Morris, 1997; Fonseca et al, 2006). Thus, the effective blocking of L-LTP can only be accomplished during a transient window, that is, during induction. This might be taken to imply that protein synthesis is important for induction but not for the maintenance of L-LTP, posing a significant fundamental challenge to the theory. Here, we implemented protein-synthesis-blocking experiments through our mechanistic model, by manipulating the kinetic parameter, k_SYN2, during different temporal windows, to model the effects of protein synthesis blockers on the induction and maintenance of L-LTP.

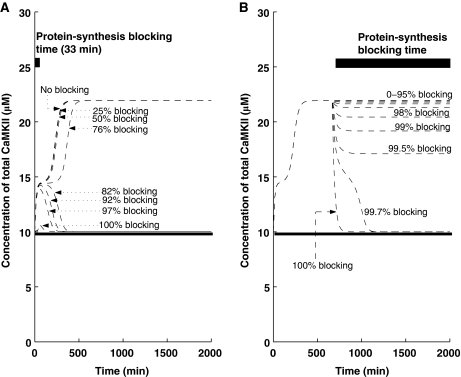
First, we simulate the application of protein synthesis inhibitors during the induction phase of L-LTP (the first 33 min of L-LTP) by reducing the value of k_SYN2. We find that (Figure 7A) the outcome depends on the effectiveness of the protein synthesis inhibitor. When the protein synthesis inhibitor reduces the protein synthesis rate constant by less than 78%, the inhibitor does not produce any effect on L-LTP maintenance. However, as blocking levels are increased beyond 82%, the induction of L-LTP is disrupted.

Figure 7.

Blocking of protein synthesis in early and late phases. Simulations are implemented with and without a (Ca²⁺)₄–CaM pulse. The solid line indicates the αCaMKII concentration without any pulse stimulus, whereas the dotted line indicates the αCaMKII concentration with pulse stimulus (pulse stimulus is used to mimic the effect of HFS). (A) Protein synthesis blocking during induction for 33 min (solid thick black line shows blocking time). For different levels of blocking, L-LTP has a different outcome during the maintenance phase. (B) Protein synthesis blocking during maintenance for 1300 min (the solid thick black line shows blocking time). Even for high-percentage blocking, the upregulated state can still be maintained, suggesting that if αCaMKII is a trace for L-LTP, its expression can still be observed, even if synthesis of new proteins is blocked.

Next, we simulated the application of protein synthesis inhibitors starting 9 h after the induction of L-LTP (Figure 7B). Our results show that inhibition of protein synthesis during the maintenance phase of L-LTP does not produce a significant change in the total concentration of αCaMKII if less than 98% blocking of k_SYN2 is obtained, and the system remains in the ‘up' state. If more than 99.7% of k_SYN2 is blocked, the system reverts to the ‘down' state and is no longer bistable. This implies that a much stronger inhibition of protein synthesis is required to reverse L-LTP during the maintenance phase than to block it during the induction phase. As many aspects of our model are simplified, and many of the parameters are unknown, the model cannot be expected to make quantitative predictions, and therefore the number quoted above should not be understood as precise. However, as this system is robust, the qualitative predictions made here are likely to survive.

Inhibition of αCaMKII activity during induction and maintenance of L-LTP

Previous experimental recordings have indicated that αCaMKII activity regulates the induction of L-LTP (Kang and Schuman, 1996; Frey and Morris, 1997); however, its role in the maintenance of L-LTP is not very clear. Several experiments (Malinow et al, 1989; Otmakhov et al, 1997; Chen et al, 2001) show that blocking αCaMKII activity has no effect on the maintenance of L-LTP, whereas a recent experiment that uses a different inhibitor actually shows the reversal of L-LTP during maintenance (Sanhueza et al, 2007). Thus, we set out to address the question of activity blocking during induction and maintenance of L-LTP through our simple translation model. We implemented αCaMKII activity blocking by simultaneously inhibiting the two αCaMKII reaction rate constants (k₃ and k₅).

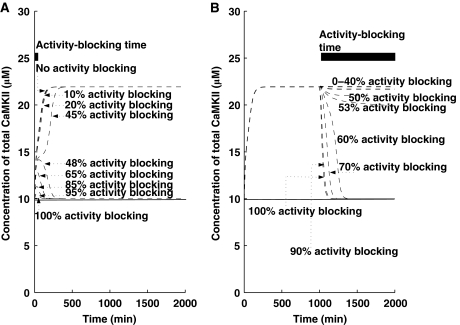
Similar to protein synthesis inhibitors, first we simulated the application of αCaMKII activity inhibitors during the induction phase of L-LTP (the first 5 min of L-LTP) by simultaneously reducing the values of k₃ and k_5. We noted that (Figure 8A), similar to protein synthesis inhibitor, the outcome of αCaMKII activity blocking depends on the effectiveness of the activity inhibitor. Our results show that 40% of αCaMKII activity blocking during induction does not have any effect on L-LTP maintenance. However, as activity-blocking levels are increased beyond 46%, the induction of L-LTP is compromised.

Figure 8.

Blocking of αCaMKII activity in early and late phases. Simulations are implemented with and without a (Ca²⁺)₄–CaM pulse. Solid line indicates the αCaMKII concentration without any pulse stimulus, whereas dotted line indicates the αCaMKII concentration with pulse stimulus (pulse stimulus is used to mimic the effect of HFS). (A) αCaMKII activity blocking during induction for 5 min (solid thick black line shows blocking time). For different levels of αCaMKII activity blocking, L-LTP has different outcomes during the maintenance phase. (B) αCaMKII activity inhibition during maintenance for 900 min (solid thick black line shows blocking time). For very high levels of αCaMKII activity blocking, the upregulated state can still be maintained, suggesting that, with a very high-level inhibition of αCaMKII activity, the L-LTP expression can still be observed, and a complete reversal of L-LTP in the maintenance phase requires a very high dose and sustained application of the αCaMKII activity inhibitor.

Next, we simulated the application of activity inhibitors starting several hours after the induction of L-LTP (Figure 8B). We showed that complete blocking of αCaMKII activity during the maintenance of L-LTP can completely abolish any increase in total αCaMKII. However, our results also indicate that a partial blocking of activity during maintenance has no effect on the total amount of αCaMKII, as blocking αCaMKII activity by less than 53% of αCaMKII does not lead to any significant change in the total amount of αCaMKII, and only inhibition above 60% completely abolishes any change in total αCaMKII concentration. It is noteworthy that the exact quantitative numbers shown here depend on the parameters of the system, many of which have not been experimentally verified. However, the qualitative results suggesting that blocking during maintenance requires much more effective inhibition than during induction are robust.

Discussion

This study proposes a general hypothesis that a feedback loop between a plasticity-related kinase and its translation factor can act as a bistable switch that stabilizes long-term memory. On the basis of experimental results (Wells et al, 2000, 2001; Miller et al, 2002; Atkins et al, 2004, 2005), we used the αCaMKII–CPEB1 molecular pair as a specific instantiation of this hypothesis. In the proposed molecular network, phosphorylation of CPEB1 regulates the synthesis of αCaMKII molecules through polyadenylation of αCaMKII mRNA, and αCaMKII phosphorylates CPEB1. Our results show that this molecular network can indeed be bistable, and that in potentiated synapses, the total αCaMKII content is significantly increased, whereas the fraction of αCaMKII phosphorylated is moderately elevated. These results are consistent with experimental observations in which tetanized slices show an elevation in the total amount of αCaMKII levels (Ouyang et al, 1997, 1999) and in which the fraction of αCaMKII phosphorylated is far from saturation.

Besides exploring the dynamics and fixed points of this system numerically, we have also reduced the complex system of differential equations to a single fifth-order polynomial, which can be used to find the fixed points of this system. We use this polynomial to generate bifurcation diagrams that are identical to those found numerically (Figure 5). Being a fifth-order polynomial, the system has at most five fixed points, but we found that, at most, three of them are real and in the physiologically plausible range (positive). In terms of the polynomial, the transition from bistability to monostability occurs when two real fixed points, one stable and one unstable, merge and then move into the complex plane. Finding the zeros of a polynomial is much simpler and computationally cheaper than numerical methods for finding zeros. Therefore, this polynomial can be used to further explore the properties of the system, for example, describing the phase diagrams in higher dimensions.

In the bistable region, this model has two stable fixed points (‘up' and ‘down') at which the amount of protein degraded is equal to the amount synthesized. At the ‘down' state, the total concentration of the αCaMKII protein is equal to its concentration in the rest of the cell. At the ‘up' state, the concentration is about twice as high as the basal level, because at this synapse, CPEB1 becomes phosphorylated and therefore the rate of protein synthesis is higher. If the system is perturbed from the ‘up' state by a small momentary reduction in the concentration of phosphorylated αCaMKII, the rate of degradation will also go down proportionately. Although the rate of protein synthesis will also decrease, it will decrease less than degradation, thus causing the system to return to the ‘up' state.

We produced bifurcation diagrams for several parameters ((Ca²⁺)₄–CaM, τ, k_SYN1, and k_SYN2) (Figure 5) and a phase diagram (Figure 6). On the basis of these bifurcation and phase diagrams, we find that this system shows robust bistability. One limitation of our results is that the proposed bistable switch requires a persistent level of (Ca²⁺)₄–CaM signal. However, our results (Figure 5A) show that even at low signal intensity, bistability is observed and can be maintained over a certain concentration range of (Ca²⁺)₄–CaM. Previous experimental measurements have shown that the basal concentration of free (Ca²⁺)₄–CaM is 50 nM (Persechini and Stemmer, 2002). Owing to the lack of sufficient experimental data, the bifurcation parameter, (Ca²⁺)₄–CaM (Figure 5A), on the X-axis was given in arbitrary units, which cannot be compared with experiments. Once sufficient data exist for producing such a curve using physical units, it will be possible to compare the lower bistability threshold of the bifurcation diagram with resting levels of (Ca²⁺)₄–CaM, to determine if bistability exists for realistic biophysical parameters. Recent results (Shifman et al, 2006) that indicate that calmodulin bound to less than four calcium molecules might be active are likely to extend the bistability region. The demonstrated robustness of this system suggests that it may still be bistable under stochastic fluctuations, which might be quite significant in the small volume of a synapse (Miller et al, 2005). Further study is needed to test at which copy number of the different molecular species this system remains bistable. The lack of bistability at very low levels of (Ca²⁺)₄–CaM is because of the structure of the αCaMKII component, and therefore must occur for post-translational models as well.

Our study shows that protein synthesis inhibitors can easily block L-LTP if applied during the induction phase, but might not reverse L-LTP if applied later. This occurs because, during the induction phase, a large amount of protein synthesis is needed to shift from the ‘down' to the ‘up' state. However, during maintenance, the amount of protein produced should only compensate for the amount of protein removed because of protein degradation. Therefore, a partial block of protein synthesis will have a much more significant effect during the induction phase. These results show that one should consider the effectiveness of protein synthesis inhibitors when considering their impact. This model predicts that if effectiveness of the protein synthesis inhibitors were controlled in experiments, as we did in the model, it would produce a dose-response curve that differs significantly in the induction and maintenance phases.

Our results also indicate a role for αCaMKII activity in the induction and maintenance of L-LTP. The activity of αCaMKII is necessary for the induction of L-LTP, and some activity is also necessary for maintaining the system in the ‘up' state once induction is achieved. However, the amount of αCaMKII activity necessary during maintenance is much lower than that during induction. These results might explain why it is hard to reverse L-LTP during the maintenance phase using αCaMKII activity inhibitors (Malinow et al, 1989; Otmakhov et al, 1997), and also possibly why different types of inhibitors produce different effects (Sanhueza et al, 2007).

Recent experimental results that use imaging of GFP-tagged αCaMKII in cultures (Lee et al, 2009) indicate that the induction of LTP only causes a transient synapse-specific increase in the activity levels of αCaMKII. Another recent study shows that local stimulation of dendritic sites in cultures increases αCaMKII levels locally by translocation from more distal sites (Rose et al, 2009). These increased levels of αCaMKII were transient and heterosynaptic. However, neither of these induction protocols in cultures was shown to produce L-LTP; neither in terms of the duration of changes nor in terms of protein synthesis dependence. These two recent results are different from previous results in which the induction of L-LTP slices produced a longer duration of increase in the levels of αCaMKII (Ouyang et al, 1999), an increase that was protein synthesis dependent. There is no obvious contradiction between the recent results in culture (Lee et al, 2009; Rose et al, 2009) and the older results in slices (Ouyang et al, 1999) because L-LTP was induced only in the latter. A transient increase in αCaMKII activity levels during E-LTP is actually consistent with this model (Figure 2), as well as with models based on the autophosphorylation of αCaMKII (Lisman and Zhabotinsky, 2001).

In our model, we did not attempt to simulate the induction phase of L-LTP in a detailed manner and only represented the whole complex induction cascade by introducing a (Ca²⁺)₄–CaM pulse. Previous biophysical models have been proposed to account for the induction phase of L-LTP (Smolen et al, 2006). Clearly, a complete model of L-LTP should model both its induction and maintenance; however, this is beyond the scope of this study. Similarly, this model assumes that the level of active αCaMKII determines the state of synapses. However, in this model, we have not explicitly modeled the downstream processes that more directly determine synaptic efficacy, which have been previously modeled in the context of induction of LTP (Lisman, 1989; Castellani et al, 2001; D'Alcantara et al, 2003; Earnshaw and Bressloff, 2006).

Some of the assumptions we made to construct this model might still be disputed. There is no consensus as to the amount of polyribosomes that exists in the spine or the PSD (Li et al, 2004; Peng et al, 2004). Some studies indicate that polyribosomes might be located close to the neck of spines, but are not normally found in spines. Such reduced localization may not completely invalidate this model but is likely to reduce the resulting synapse specificity (Ostroff et al, 2002). In addition, many of the components of this model are simplified and many of the kinetic constants are unknown. Therefore, this model cannot tell us that there is indeed a bistable CPEB1–αCaMKII switch, only that such bistability is feasible and consistent with various experimental results.

Although our model is motivated by experimental results, its assumptions as well as its consequences need to be further tested. One of the key assumptions in our proposed translation-dependent model is that de novo synthesis of αCaMKII has a significant function in the maintenance of L-LTP. This assumption is supported by the observation that, in mice, in which the 3′UTR region of the αCaMKII mRNA (which includes the CPE elements) was altered, the concentration of αCaMKII in dendrites was significantly reduced and a profound deficit in L-LTP was observed (Miller et al, 2002). This result is consistent with our assumption that dendritic protein synthesis regulation of αCaMKII is crucial for the maintenance of L-LTP. Although the mutated region includes the CPE elements, the mutation also affects the trafficking of mRNA to the dendrite and therefore this result is not specific regarding the regulation of dendritic translation by CPEB-1. Plasticity experiments with CPEB-1 knockout mice found a significant deficit in LTP only for some induction protocols, whereas other more robust protocols showed a small effect (Alarcon et al, 2004). These results might indicate that, although CPEB-1 contributes to the late phase of LTP, it is not the sole factor controlling translation, and that there are redundant pathways controlling the maintenance of plasticity. Possibly, as suggested by Richter and co workers (Alarcon et al, 2004), an independent, rapamaycin-sensitive pathway can regulate translation as well. The possibility of redundant molecular pathways is not surprising and can contribute to the system's robustness. The mechanisms of each putative pathway should be independently analyzed as we have done here for the CPEB-1-dependent pathway. However, redundancy makes hypothesis testing more difficult.

A kinase-protein synthesis loop is not the only possible mechanism for preserving synaptic efficacies for long periods of time in synapse-specific ways. Other possibilities include the post-translational molecular-switch idea (Roberson and Sweatt, 1999; Zhabotinsky, 2000; Lisman and Zhabotinsky, 2001; Hayer and Bhalla, 2005). This idea, examined in various models, has produced testable predictions and some experiments to test these predictions. Our theory differs from this previous post-translational theory in that it is protein synthesis dependent and can therefore account for changes in total protein concentration, not only their conformational states, and it does not depend on the bistability of the isolated αCaMKII autophosphorylation loop, an assumption currently not supported by experimental evidence (Bradshaw et al, 2003). Various different mechanisms for bistability within the complex biochemical networks of synaptic plasticity can interact, possibly producing multistability or making the system more robust due to redundancy.

The stability of synaptic efficacies might also arise from structural changes that accompany synaptic plasticity. Such changes have been observed experimentally (Harris et al, 2003), but to the best of our knowledge have not yet been modeled. The extent of stability of such structural changes is not yet known, and the mechanisms for this possible stability have not yet been examined. Another theory, the cluster model, proposes that synapses are not bistable but can exist in long-lived metastable states (Shouval, 2005). These metastable states are formed in a non-equilibrium system in which neighborhood interactions of receptors influence their trafficking. Yet another option is that synaptic efficacies are stabilized by network activity, which tends to continuously strengthen strong synapses and weaken weak synapses. Although this is a common notion, not many formal models of this idea have been examined, and one study casts doubt whether more than one memory pattern can be maintained through this mechanism (Wittenberg et al, 2002).

The assumptions of the proposed model are motivated by experimental results regarding the importance of the synthesis of new proteins; this distinguishes it from previous models proposed for the stability of synaptic efficacies. The consequences of this theory are qualitatively consistent with actual L-LTP experiments, including its ability to account for the different impacts of protein synthesis and activity inhibitors during the induction and maintenance phase.

Materials and methods

Biochemical reactions

The biochemical reactions for αCaMKII molecular loop (Figure 1) are based on standard Michaelis–Menten-type kinetics. The following set of reactions is used to describe the molecular interactions of this loop. The dynamic variables used are X to represent αCaMKII, Y to represent CPEB1, a P subscript to represent phosphorylation, and an A as a superscript to represent activation by (Ca²⁺)₄–CaM. The phosphatase P is approximated as a fixed parameter, not as a dynamic variable, to simplify the bifurcation analysis; in simulations, this does not significantly alter the results. The signal, (Ca²⁺)₄–CaM, is a parameter rather than a dynamic variable. The reactions are:

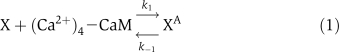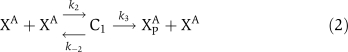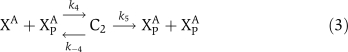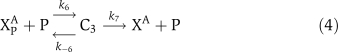
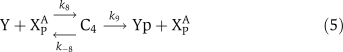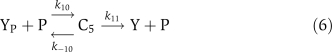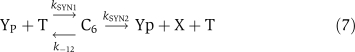The binding of (Ca²⁺)₄–CaM with inactive αCaMKII (X) drives it into an active αCaMKII state (X^A), similarly the unbinding of (Ca²⁺)₄–CaM from an active X^A molecule will result in an inactive state. This binding and unbinding event is described in equation (1). The two neighboring active αCaMKII subunits can result in the phosphorylation of active αCaMKII. Moreover, once an active αCaMKII molecule is phosphorylated (X_P^A), it can phosphorylate other active molecules in an autocatalytic manner. These steps are modeled by standard Michaelis–Menten kinetics, equations (2) and (3). The phosphatase enzyme regulates the dephosphorylation of the X_P^A molecule through equation (4). In our proposed model, the active and phosphorylated αCaMKII molecule phosphorylates the CPEB1 molecule and a phosphatase enzyme regulates the dephosphorylation of phosphorylated CPEB1. These events are also described using Michaelis–Menten kinetics, equations (5) and (6). Here, the complex process of polyadenylation is described by an enzymatic-like reaction with factor T, which interacts with phosphorylated CPEB1 to form a new αCaMKII molecule. This polyadenylation step is modeled in equation (7). The complete formulation in the form of differential equations and all the above reaction rates are described in the Supplementary information.

Induction

In our simulations, L-LTP induction is simulated by a 10 s (Ca²⁺)₄–CaM pulse (basal (Ca²⁺)₄–CaM concentration is set at 5.6 AU, and for the 10 s induction period, this concentration is raised to a level in the range of 6000–24 000 AU), which produces an upregulation in the total amount of αCaMKII from a basal concentration of 10 μM.

Temporal dynamics

We integrated these differential equations (Supplementary information) through nonlinear solvers (using Math-Works MATLAB). For αCaMKII dynamic coefficients, we used values estimated from experiments. We then scaled unknown rate constants to obtain dynamics that are comparable with experimental values. All molecular concentrations in the model are expressed in μM, except if otherwise stated, and time is represented in min.

Bifurcation diagrams

The nonlinear-coupled differential equations describing the above biochemical reactions are solved for their steady states. The steady-state solutions of these equations are determined by setting their right-hand side equal to zero and solving the corresponding system of algebraic equations through a global continuation-based solver (Aslam and Sunol, 2006). The steady states as a function of any model parameters are known as bifurcation diagrams. We tracked the bifurcation diagram of these nonlinear algebraic equations through a continuation-based algorithm (Aslam and Sunol, 2006). To further verify our results, we reproduced all the bifurcation diagrams with Matcont, a Matlab-based package for numerical bifurcation analysis of ODEs (Dhooge et al, 2003).

Supplementary Material

Supplementary Information

this file contains Supplementary figures S1-2, Supplementary table SI, and a mathematical description of the differential equations used and analytical derivations