Intrinsic Dynamics of Restriction Endonuclease EcoO109I Studied by Molecular Dynamics Simulations and X-Ray Scattering Data Analysis

Abstract

EcoO109I is a type II restriction endonuclease that functions as a dimer in solution. Upon DNA binding to the enzyme, the two subunits rotate counterclockwise relative to each other, as the two catalytic domains undergo structural changes to capture the cognate DNA. Using a 150-ns molecular dynamics simulation, we investigated the intrinsic dynamics of the DNA-free enzyme in solution to elucidate the relationship between enzyme dynamics and structural changes. The simulation revealed that the enzyme is considerably flexible, and thus exhibits large fluctuations in the radius of gyration. The small-angle x-ray scattering profile calculated from the simulation, including scattering from explicit hydration water, was in agreement with the experimentally observed profile. Principal component analysis revealed that the major dynamics were represented by the open-close and counterclockwise motions: the former is required for the enzyme to access DNA, whereas the latter corresponds to structural changes upon DNA binding. Furthermore, the intrinsic dynamics in the catalytic domains were consistent with motions capturing the cognate DNA. These results indicate that the structure of EcoO109I is intrinsically flexible in the direction of its functional movement, to facilitate effective structural changes for sequence-specific DNA recognition and processing.

Introduction

Restriction endonucleases (REases) provide antiviral protection for bacteria by degrading the foreign DNA of invading bacteriophages (1). These enzymes recognize specific nucleotide sequences, and cleave both strands of DNA. EcoO109I is a type II REase isolated from Escherichia coli, and recognizes seven basepairs of double-stranded DNA (ds-DNA). The sequence is RG↓GNCCY, where R = A or G, Y = T or C, and ↓ indicates cleavage position (2). Type II REases are classified into two families, EcoRI and EcoRV, based on their DNA cleavage pattern. EcoO109I is classified into the EcoRI family, characterized by the production of 5′-overhang DNA.

The crystal structures of both DNA-free and DNA-bound forms of EcoO109I were determined (Fig. 1), and small-angle x-ray solution scattering (SAXS) measurements of the DNA-free form revealed that the homodimer (subunits A and B in Fig. 1 A) is the functional unit of the enzyme in solution (2). The subunit of EcoO109I consists of two domains: dimerization and catalytic (Fig. 1 D). The dimerization domain consists of only α-helices (α1–3 and α9–11), and the catalytic domain, in which the active site for catalysis is located, folds into an α/β structure (α4, β1–2, α6, β3, α7, β4, and α8).

Figure 1.

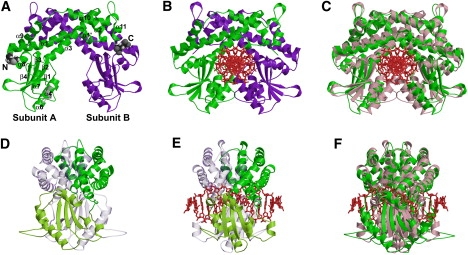
Crystal structures of EcoO109I. (A and B) DNA-free and DNA-bound forms, respectively, colored according to subunits A (green) and B (purple). (A) N-terminal and C-terminal residues are rendered in space-filling. Missing residues in crystal structure were modeled (gray). Secondary structures α1 (residues 2–23), α1′ (residues 26–32), α2 (residues 36–46), α3 (residues 51–75), α4 (residues 91–95), β1 (residues 110–113), β2 (residues 120–128), α6 (residues 133–148), β3 (residues 157–164), α7 (residues 171–178), β4 (residues 194–198), α8 (residues 200–207), α9 (residues 211–227), α10 (residues 236–252), and α11 (residues 262–267) along amino-acid sequence are labeled. (D and E) Side view of DNA-free and DNA-bound forms, respectively, colored according to dimerization (green) and catalytic (pink) domains in one subunit, and counterpart subunit (transparent representation). (C and F) Front and side views of superimposition of DNA-free form (green) and DNA-bound form (pink), respectively.

A comparison between the crystal structures of the DNA-free and DNA-bound forms of EcoO109I shows that the enzyme undergoes large structural changes upon DNA binding, to allow catalytic residues to interact with DNA. These structural changes can be explained mainly by two movements. The first is the movement of the two catalytic domains in subunits A and B closer together, allowing interactions with DNA (Fig. 1, A–C). The second is the twisting motion between the two subunits in a counterclockwise direction, making the two catalytic domains fit together on the major groove of DNA from both sides (Fig. 1, D–F). However, in the crystal structure of the DNA-free form, the intervening space between the two catalytic domains is not large enough to be accessed by DNA.

Generally, mechanisms of structural changes in proteins upon substrate binding are explained using the induced-fit model (3), in which substrates induce structural changes in proteins to make the active sites of proteins fit to the substrates. An alternative model to explain structural changes is the preexisting equilibrium model (4), in which protein conformations significantly fluctuate in the substrate-free state, and the equilibrium ensemble before substrate binding includes specific conformations complementary to the substrates as minor components. The substrates then bind selectively to the binding conformations, shifting the equilibrium toward these conformations. This model was supported by experimental studies, e.g., nuclear magnetic resonance relaxation measurements (5–7). Theoretical studies also revealed that protein motions in the substrate-free state correlate well with structural changes upon substrate binding (8–18). In a unified view of the two models, the relationship among protein fluctuations in the substrate-free state, substrate-protein interactions, and structural changes upon substrate binding was formulated using a framework of linear response theory (19). Those studies indicated that intrinsic protein flexibility, evident even in the substrate-free state, is crucial for elucidating the physical mechanisms of functionally important structural changes in proteins. Therefore, we investigated the intrinsic dynamics of EcoO109I in the DNA-free state, and examined the relationship between the intrinsic dynamics and the structural changes of EcoO109I upon DNA binding.

To probe intrinsic dynamics in proteins, all-atom molecular dynamics (MD) simulations are widely used (20,21), and can provide detailed protein motions in solution at an atomic resolution. Structural ensembles obtained by MD simulations should, however, be assessed by means of a comparison with experimental data. Small-angle x-ray solution scattering data are suitable for this purpose (22–28). In fact, whereas x-ray crystallography yields a high-resolution protein structure that is likely to differ from the solution structure, SAXS offers information on the low-resolution structure of proteins in solution (27,28). The structural information of SAXS data involves an average not only over all orientations, but also over all protein conformations. The structural data provided by SAXS are therefore complementary to those of x-ray crystallography. These characteristics of SAXS enabled us to test the structural ensemble obtained by MD simulations by comparing the calculated SAXS profile with the experimentally observed profile.

In this study, we performed a 150-ns MD simulation of the DNA-free form of the enzyme with the explicit water molecules, to elucidate the relationship between the intrinsic dynamics of EcoO109I in solution and its structural changes upon DNA binding. From the trajectory of the MD simulation, the SAXS profile, taking scattering from explicit hydration water molecules into account, was calculated and compared with the experimentally observed SAXS profile. The time-resolved analysis of the radius of gyration estimated from the Guinier plot (29) demonstrates that the structure of EcoO109I is considerably flexible. Analyses of atomic fluctuations within the subunit and in the dimer identified two rigid cores that undergo rigid-body motions relative to each other. The motions of the two rigid cores were characterized using principal component analysis, and were compared with the DNA-induced structural changes observed in a previous crystallographic study (2). Motions in the catalytic domains were also examined, using principal component analysis (30–32). Determinants of the intrinsic flexibility in EcoO109I were pursued using interresidue contact networks in the MD simulation.

Methods

MD simulations

All simulations were performed at 298 K, using MARBLE (33). The CHARMM22 potential (34) and the TIP3P model (35) were used for the proteins and water, respectively. The periodic boundary condition was applied using the particle mesh Ewald method (36). The symplectic integrator for rigid bodies was used with a time step of 2 fs, in which water and the CH_x, NH_x (x = 1, 2, 3), SH, and OH groups were treated as rigid bodies.

The initial structure for the simulation of EcoO109I was generated from the crystal structure (Protein Data Bank [PDB] accession code 1WTD) (2). The coordinates for residues 93–100 of subunit A and residues 178–182 of subunit B (Fig. 1, gray), which are missing in the PDB coordinates, were modeled after corresponding residues of the other subunit in the crystal structure. The protein and crystal water molecules were immersed in a water box, and 14 Na⁺ ions were added in bulk solution, followed by an energy minimization of 5000 steps of the whole system. The total number of atoms was 108,249. To equilibrate the size of the simulation box, a 100-ps run was performed under the NPT condition (33,37), at T = 298.15 K and P = 1.0 atm, where the positions of all atoms except solvent atoms were constrained with a harmonic force constant of 1 kcal/mol/Ų. The cube edge length of the simulation box became ∼102.1 Å.

After equilibration of the simulation box, two series of product runs were performed under the NPT condition, at T = 298.15 K and P = 1.0 atm: 1), a 150-ns run without any restraints; and 2), a 20-ns run with restraints on the positions of all atoms of the protein. The procedure for product run 1 was as follows. First, for the equilibration of the structure of the modeled residues, constraints on the positions of only these residues were gradually removed over a period of 100 ps, followed by further equilibration with constraints on the positions of atoms, except those of the modeled residues, for 5 ns. The remaining constraints were then gradually removed over a period of 100 ps, and the 150-ns run was performed without any constraints. Structures were saved every 1 ps in the product runs.

Calculation of SAXS profile

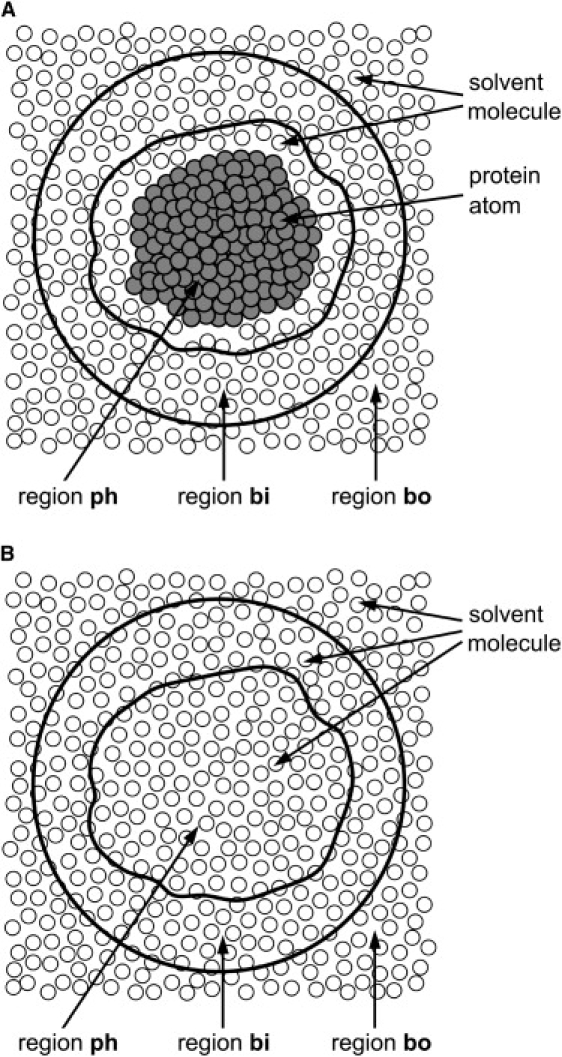
The experimental data of the SAXS profile were taken from a previous study (2). In those experiments, the SAXS profile of a protein was obtained by the subtraction of the scattering data of buffer solution from those of protein solution. In our calculations, as suggested by Seki et al. (23), we used a similar procedure, i.e., MD simulations for pure solvent were performed in addition to simulations for the protein solution, and the simulated scattering data for pure solvent were subtracted from those of the protein solution. The procedure of the SAXS-profile calculation from MD simulations is summarized as follows: 1), the average density of the bulk water region “bo” (Fig. 2 A), ${\rho }_0$, is calculated from the simulation for the protein solution; 2), the MD simulation of a pure solvent system, in which some ions are added to make the average density identical to ${\rho }_0$, is performed; and 3) the instantaneous scattering intensity $\tilde{I}\left(Q\right)$, where Q is defined as $Q=4\pi \sin \theta /\lambda$ (2θ is the scattering angle, and λ is the wavelength of x-rays), is calculated for each snapshot in the trajectories of the protein solution and pure solvent systems, using the following equation:

$$\tilde{I}\left(Q\right)=4\pi \sum _{l=0}^{\mathrm{\infty }}\sum _{m=-l}^l{\left|i^l\sum _k^N{f}_k\left(Q\right)j_l\left(Q{r}_k\right)Y_{lm}^{\ast }\left({\Omega }_{{\mathbf{r}}_k}\right)\right|}^2-{\rho }_0\sum _k^N{f}_k\left(Q\right){\int }_{\mathrm{S}}dS({\mathbf{s}}_k\cdot \mathbf{n})\frac{j_1\left(Q{s}_k\right)}{Q{s}_k}+{\rho }_0^2{\int }_{\mathrm{S}}dS\prime {\int }_{\mathrm{S}}dS\left[\frac{(\mathbf{n}\prime \cdot \mathbf{n})}{Q^2}\cdot \frac{j_1(Qs\prime )}{Qs\prime }-\left\{(\mathbf{s}\prime \cdot \mathbf{n}\prime )(\mathbf{s}\prime \cdot \mathbf{n})\right\}\frac{j_2(Qs\prime )}{{(Qs\prime )}^2}\right],$$ (1)

where N is the number of atoms within in region “v” (Fig. 2 A), r_k and ${\Omega }_{{\mathbf{r}}_k}$ are the position and the solid angle in real space of the k-th atom, respectively, and ${\mathbf{s}}_k$ and $\mathbf{s}\prime$ denote $\mathbf{r}-{\mathbf{r}}_k$ and $\mathbf{r}-\mathbf{r}\prime$, respectively. We use $f_k\left(Q\right)$ to denote the atomic form factor of the k-th atom, and $j_l$ and $Y_{lm}$ denote a spherical Bessel function and a spherical harmonic function, respectively. We use S to represent the closed surface of region v, and n is the unit normal vector outward from the infinitesimal surface element $dS$ of the surface S. The details of the derivation of Eq. 1 are described in the Appendix. Continuing the procedure of the SAXS-profile calculation, 4), $\tilde{I}\left(Q\right)$ is averaged over all the snapshots for each system, and 5), the final SAXS profile is obtained by the subtraction of the scattering data of the pure solvent from those of the protein solution.

Figure 2.

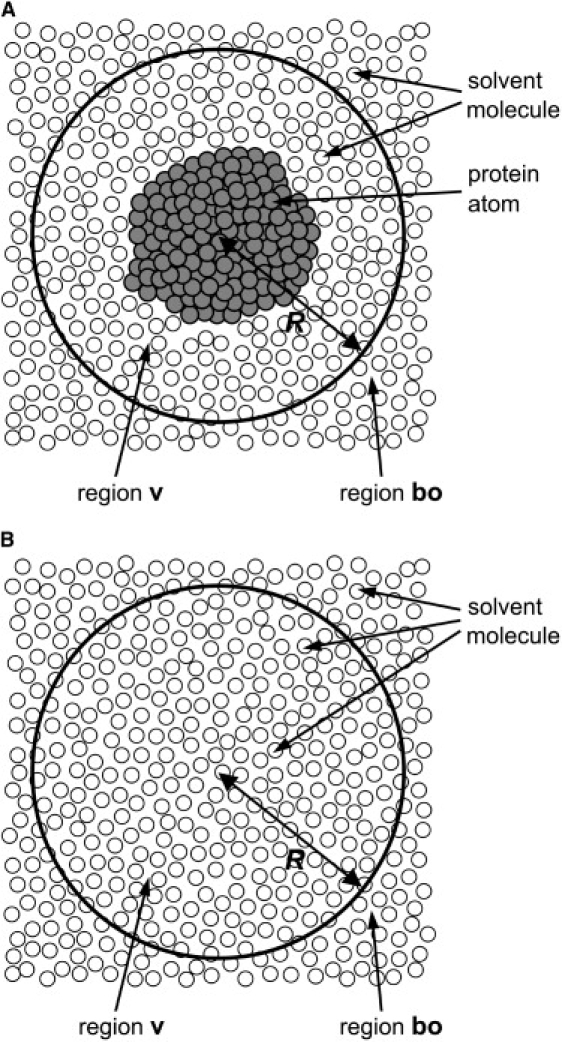
Dividing total volume of a system into two regions “v” and “bo” for a dilute solution of a protein (A) and pure solvent (B).

In our method, the calculation of scattering intensity was performed only for region v, which corresponds to the area within a sphere centered at the center of mass of the protein molecule with radius R (Fig. 2 A). In the original method, Seki et al. (23) divided region v into three regions: the protein area, its hydration shell, and the bulk water region, to estimate the contribution of scattering from the hydration water to the total scattering intensity. However, as proven theoretically in the Appendix, the final subtracted scattering intensity, calculated only from region v, exactly equals the experimentally obtained intensity if radius R is sufficiently large so that density fluctuations outside the region v (i.e., region “bo”) have no correlation with those in the protein area and its hydration shell. This fact simplifies the calculation procedure. In our calculations, we used the sphere R = 50 Å as region v, which is sufficiently large for the correct evaluation of the scattering intensity of EcoO109I (see Appendix for details).

In addition to the approach described above, we also used a multipole expansion (38) for fast computation of the SAXS profile of a snapshot in the MD trajectory. The multipole expansion is used in the program CRYSOL, developed by Svergun et al. (39), and was applied to a trajectory of MD simulation by Merzel and Smith (24). As shown in these studies, the appropriate truncation of the expansion gives the correct evaluation of a SAXS profile (see Appendix for details). The use of multipole expansion and parallelization of the program (see Appendix) enabled us to calculate the SAXS profile for every snapshot in the trajectory of the 150-ns simulation (the total number of snapshots is 150,000), and analyze the dynamics of EcoO109I in terms of the time-resolved SAXS profile.

In both the unrestrained 150-ns and restrained 20-ns MD simulations, the average electron density in the bulk water region bo,${\rho }_0$, was 0.3367 Å⁻³. We also performed a 2-ns MD simulation of a pure-solvent system, including 3 Na⁺ and 3 Cl⁻ ions, in which the average electron density was identical to ${\rho }_0$. The scattering intensities for the pure-solvent system were used in subsequent calculations.

Results and Discussion

A 150-ns MD simulation of the DNA-free form of EcoO109I was performed with explicit water molecules at 298 K. The root mean-square displacement of C^α atoms (C^α-RMSD) from the crystal structure of the DNA-free form reached ∼5.0 Å within the first 20 ns of the simulation. However, as described below, the C^α-RMSD of individual rigid cores, i.e., the elements of rigid-body motions, was ∼1.0 Å during the simulation, indicating that the rigid cores were stable during the simulation, and that there were certain rigid-body motions between them.

Comparison of SAXS profile calculated from MD simulation with experimentally observed profile

To test the validity of the structural ensemble sampled by the MD simulation, we calculated the SAXS profile from all snapshots in the trajectory, taking scattering from the explicit hydration water molecules into account (for details of the calculation, see Methods and Appendix), and compared it with the experimentally observed profile. As shown in Fig. 3 A, the simulation-derived profile was in agreement with the experimentally observed SAXS profile.

Figure 3.

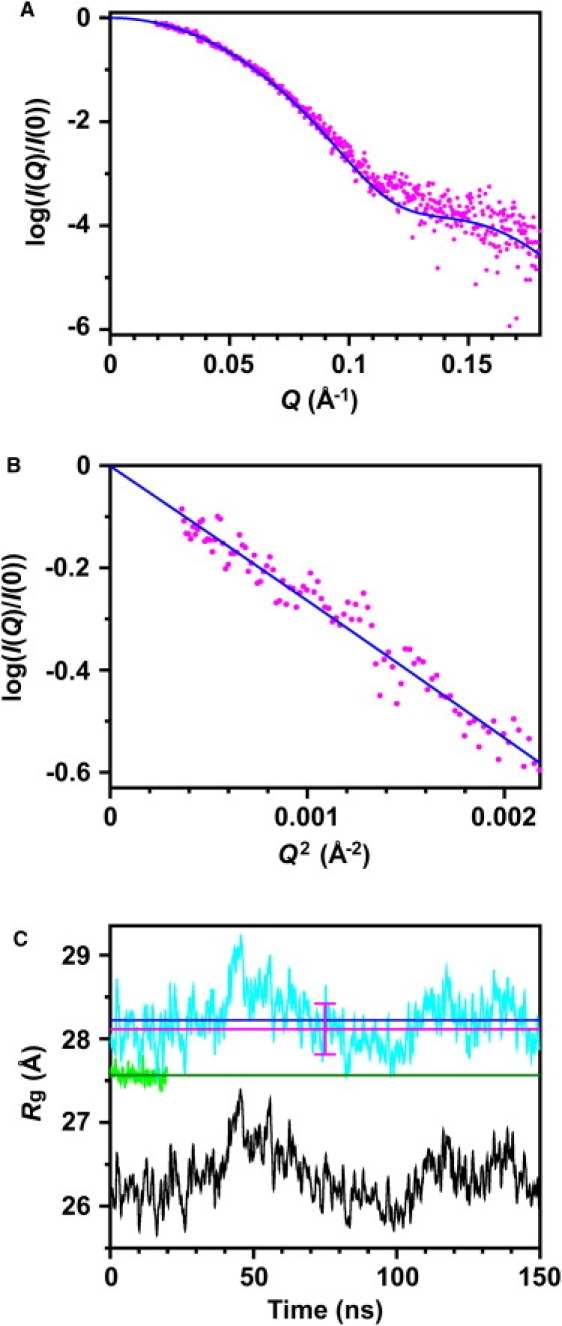
Comparison of experimental and simulation-derived SAXS profiles of DNA-free form of EcoO109I in solution. The SAXS profiles from the experiments (pink dots) and the 150-ns MD simulation (blue curves) are shown in logarithmic plot (A) and Guinier plot (range of R_gQ, <1.3) (B). (C) Time evolution of protein-water R_g estimated from Guinier plot for time-window of 500 ps shifting through 150-ns MD trajectory (cyan curve) and 20-ns restraint-MD trajectory (yellow-green curve). Average R_g is also shown for 150-ns trajectory (blue horizontal line) and 20-ns trajectory (green horizontal line). Pink horizontal line with error bar shows protein-water Rg estimated from Guinier plot of experimental SAXS profile. Protein R_g was calculated from protein structures without water molecules in 150-ns trajectory (black).

In the range of R_gQ <1.3, the scattering intensity I(Q) is approximated to the Guinier approximation,

$$I\left(Q\right)\simeq I\left(0\right)\exp (-Q^2{R}_{\mathrm{g}}^2/3),$$ (2)

where I(0) and R_g are the scattering intensity at Q = 0 (zero-angle) and the radius of gyration, respectively, as estimated from the ln[I(Q)] versus Q² plot (Guinier plot) (29). Fig. 3 B compares Guinier plots of the simulation-derived and experimentally observed SAXS profiles, showing that the R_g (referred to as “protein-water R_g” or simply “R_g”) estimated from the SAXS profile calculated from the structural ensemble sampled by the MD simulation (R_g = 28.2 Å) was in agreement with that obtained from the experimentally observed SAXS profile (R_g = 28.1 ± 0.3 Å).

We then calculated the protein-water R_g for the time window of 500 ps, shifting from t = 0–150 ns, to investigate the fluctuation of the overall structure of EcoO109I. R_g (Fig. 3 C, cyan curve) exhibited large fluctuation, with a period of ∼50–100 ns. There was an ∼1.8-Å difference in R_g between the most expanded and closed conformations. However, R_g averaged over all time windows (Fig. 3 C, blue horizontal line) is in agreement with the R_g obtained from the experimentally observed SAXS profile (Fig. 3 C, pink horizontal line). In addition, the R_g and the SAXS profile in the range of Q ≤0.18 Å⁻¹ almost converged from t = 100 ns (data not shown), indicating that at least a 100-ns time length of a simulation is needed to obtain the structural ensemble consistent with the experimentally obtained SAXS data.

We calculated another R_g (referred to as “protein R_g”) obtained from the mass-weighted atomic structure of the protein without water molecules, $R_g^2=1/M\sum _i^N{m}_i{r}_i^2$, where $M=\sum _i^N{m}_i$ (N is the number of protein atoms, and m_i is atomic weight of the ith protein atom) for the time windows described above (Fig. 3 C, black curve). The time course of protein R_g clearly shows almost the same time dependency as that of the protein-water R_g. This indicates that the fluctuation of the protein-water R_g reflects the fluctuation of the protein moiety, and a 2-Å difference between the protein-water R_g and the protein R_g is attributable to the hydration shell on the surface of the protein molecule (40,41).

To analyze the effects of structural changes on the protein-water R_g during the 150-ns MD simulation, we performed another 20-ns MD simulation in which positions of the protein atoms were restrained to the original crystal positions, and only the solvent atoms were sampled (referred to as “restraint-MD simulation”). As shown in Fig. 3 C (yellow-green curve), we calculated the protein-water R_g for the time window of 500 ps, shifting from t = 0–20 ns, for the restraint-MD simulation. In this simulation, the protein-water R_g was ∼27.6 Å, and the average of the protein-water R_g (Fig. 3 C, green horizontal line) was still smaller than the experimental value. The difference in protein-water R_g between the restraint-MD simulation and the experimental value indicates that EcoO109I adopts a more expanded conformation in solution, as observed in the 150-ns MD simulation, than in a crystalline state. All these results show the validity of the structural ensemble sampled by the 150-ns MD simulation. Next, we investigated the detailed dynamics of EcoO109I during a 150-ns MD simulation.

Dynamics within the subunit

To elucidate the dynamics of EcoO109I during the 150-ns MD simulation, we first analyzed the fluctuations occurring within the subunit in detail. Based on a superposition on the C^α best fits for each subunit structure, we calculated the root mean-square fluctuation of the C^α atom (C^α-RMSF, Fig. 4 A) and the average C^α-RMSD of each residue from the crystal structure of the DNA-free form (data not shown), using all snapshots in the trajectory. As a result, the “rigid” segments (Fig. 4 A, blue horizontal lines), defined as the segments of residues with C^α-RMSF and average C^α-RMSD values <1.2 Å and 2.0 Å, respectively, were localized and constituted one rigid part (Fig. 4 B, blue) in the center of the subunit. Interestingly, this rigid part of the subunit comprised parts of both the dimerization and catalytic domains, i.e., it comprised α1, the last half of α3 and α9 in the dimerization domain, and β1–3 and α8 in the catalytic domain.

Figure 4.

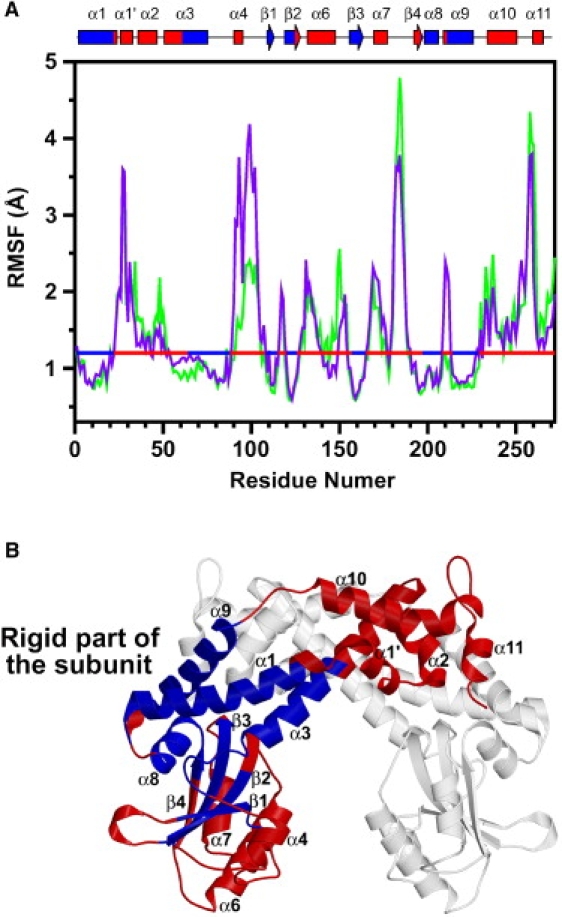
Dynamics within subunit during 150-ns simulation. (A) C^α-RMSF of subunits A (green) and B (purple). Calculation of C^α-RMSF for each subunit was performed, based on superposition using C^α best fits for its own subunit. Horizontal line indicates threshold value (1.2 Å) of C^α-RMSF, which is used in classification of segments into rigid segments (blue; residues 1–21, 64-87, 108–113, 120–125, 157–164, 198–207, and 213–229) and the others (red). Assignments of secondary structures are also shown in schematic diagram along top of A. (B) Rigid segments (blue) and others (red) of a subunit. All rigid segments are located at center of subunit, and constitute one rigid part of the subunit.

The C^α-RMSD of this rigid part of the subunit from the crystal structure of the DNA-free form was ∼0.9 Å in the simulation. In contrast, the C^α-RMSD of the dimerization domain (α1–3 and α9–11) and the catalytic domain (β1–4 and α6–8, excluding the missing residues 93–100 in α4, and 178–182 in the loop between α7 and β4) became ∼2.5 Å and ∼2.9 Å, respectively. These results indicate that the rigid part of the subunit was stable in the simulation, but the dimerization and catalytic domains exhibited certain flexibilities. Furthermore, a comparison of crystal structures between the DNA-free and DNA-bound forms showed that the C^α-RMSD of the rigid part of the subunit between the DNA-free and DNA-bound forms was ∼0.8 Å, whereas the C^α-RMSD of the dimerization and catalytic domains was ∼1.5 Å and ∼2.1 Å, respectively. These observations of structural changes in the crystal structures confirmed the results of the MD simulation, i.e., demonstrating the stability of the rigid part of the subunit, and flexibility in the dimerization and catalytic domains.

Dynamics in the dimer: identification of two rigid cores

To investigate dynamics in the dimer, we focused on the dynamics of one subunit relative to the other subunit. We compared the C^α-RMSF of the dimeric structure (Fig. 5, A and B, corresponding to subunits A and B of the dimer, respectively) between two schemes of superposition for the MD trajectory: in one scheme, all snapshots of the dimer were superimposed, using the C^α best fits for subunit A (Fig. 5, A and B, green curve); in the other scheme, we used the C^α best fits for subunit B (Fig. 5, A and B, purple curve). Interestingly, the C^α-RMSF of the two helices α2 and α11 (Fig. 5 C, cyan; also, Fig. 5, A and B, arrows) in the dimerization domain of one subunit became smaller when dimer structures were best fitted when using the other subunit rather than their own subunit. This indicates that the two helices α2 and α11 in the dimerization domain of one subunit moved collectively with the rigid part (Figs. 4 B and 5 C, blue) of the other subunit rather than with that of the same subunit. Thus, the rigid part of one subunit and the two helices α2 and α11 in the other subunit formed a rigid core (RCA and RCB for subunits A and B, respectively, in Fig. 5 C).

Figure 5.

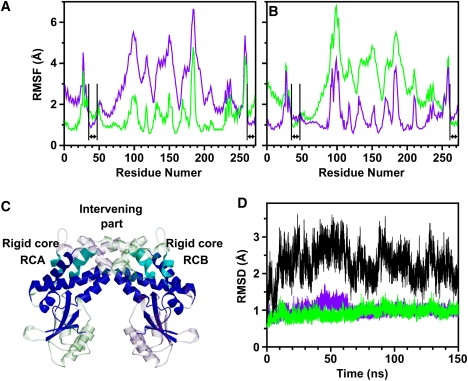
Dynamics in dimer during 150-ns simulation. (A and B) C^α-RMSF of dimer is shown for subunits A and B, respectively, calculated using two different superposition schemes. In one scheme, all dimer structures in the simulation were superimposed using C^α-atom best fits for subunit A (green), and in the other scheme, for subunit B (purple). In segments indicated by arrows corresponding to helices α2 (residues 36–46) and α11 (residues 262–272), C^α-RMSF was smaller in the case of superimposition on the other subunit than on its own subunit. (C) Rigid part of subunit (blue) and two helices α2 and α11 of other subunit (cyan) form a rigid core (rigid core RCA for subunit A, and RCB for subunit B). (D) C^α-RMSD from DNA-free crystal structure in 150-ns simulation is shown for RCA (green), RCB (purple), and a combined residue group of RCA and RCB (black).

The C^α-RMSDs of individual rigid cores RCA and RCB from the crystal structure were both ∼1.0 Å during the simulation, whereas the C^α-RMSD of a combined residue group of two rigid cores became larger than 2.0 Å within the first 10 ns (Fig. 5 D). Hence the individual rigid cores were stable in the simulation, and in contrast, there were large rigid-body motions between RCA and RCB. These individual stabilities of RCA and RCB are also supported by a comparison of the crystal structures between the DNA-free and DNA-bound forms of the enzyme. The C^α-RMSDs of RCA and RCB between the DNA-free and DNA-bound forms are both 0.8 Å, whereas the C^α-RMSD of a combined residue group of the two rigid cores is 2.4 Å, indicating that (in agreement with the results of the MD simulations) individual crystal structures of RCA and RCB remain unchanged upon DNA binding to the enzyme, whereas certain rigid-body motions occur between RCA and RCB.

Rigid-body motions between two rigid cores

For further analysis of rigid-body motions between the rigid cores RCA and RCB in the simulation, principal component analysis was applied for the trajectory of C^α atoms of the rigid cores. The first two principal modes accounted for the dominant portion of motions in RCA and RCB, i.e., 25.6% and 22.5% contributions to the total C^α-RMSF for the first and second principal modes, respectively (Fig. 6 A).

Figure 6.

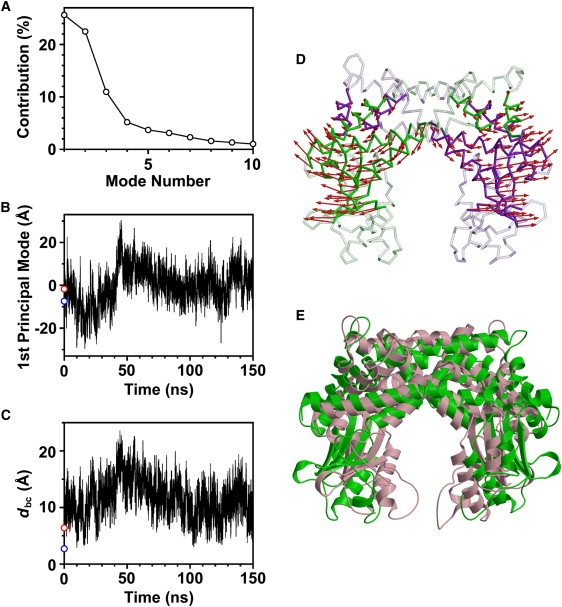
Principal component analysis for motions of RCA and RCB. (A) Individual contributions of first 10 principal components to total C^α-RMSF of rigid cores RCA and RCB. (B) Snapshots in trajectory were projected onto first principal mode. The DNA-free (red open circle) and DNA-bound (blue open circle) crystal structures are also projected onto the first principal mode. (C) Distance between two catalytic domains, d_bc, in the 150-ns simulation. (D) Amplitude (8σ) and direction of C^α displacements along first principal mode are represented by red arrows on C^α trace of the average structure of RCA and RCB in the 150-ns simulation. Other parts, except for RCA and RCB, are shown in transparent representation. Subunits A and B are shown in green and purple, respectively. (E) Superposition of structures with largest projection (green) and smallest projection (pink) onto first principal mode.

The eigenvector of the first principal mode represents the open-close motion between RCA and RCB (Fig. 6 D, red arrows). The time course of projections onto the first principal mode is shown in Fig. 6 B, in which positive and negative projection values correspond to open and closed conformations, respectively. The oscillation of projections between positive and negative values indicates frequent interchanges between open and closed conformations. Because the R_g of open conformations were larger than those of closed conformations, there was a significant correlation of time courses between projections onto the first principal mode and the time-dependent R_g shown in Fig. 3 C (correlation coefficient, 0.74). Moreover, we found that the open-close motion represented by the first principal mode changed the width of the intervening space between the two catalytic domains. The distance between the two catalytic domains, d_bc (Fig. 6 C), correlated well in the time course with the projections onto the first principal mode (Fig. 6 B) (correlation coefficient, 0.65). The domain distance d_bc was defined as the closest atomic distance between the two catalytic domains.

In Fig. 6 E, the superposition of the structures with the largest and smallest projections onto the first principal mode is shown. The structure with the largest projection value (Fig. 6 E, green) has a distance between the two catalytic domains, d_bc, of 20.9 Å, which is slightly larger than the diameter of DNA (20 Å). In contrast, the structure with the smallest projection value (Fig. 6 E, pink) has a d_bc of 5.2 Å, which is close to the d_bc of the crystal structure in the DNA-bound form (2.7 Å). Because the d_bc of the crystal structure in the DNA-free form is 6.4 Å, which is much smaller than the diameter of DNA, the open-close motion represented by the first principal mode is necessary for the enzyme to access DNA. Moreover, the small difference between the projection values of crystal structures in the DNA-free and DNA-bound forms (Fig. 6 B) indicates that the open-close motion was unexpected in terms of the previous crystallographic study (2).

The eigenvector of the second principal mode represents the twisting motion between RCA and RCB in a counterclockwise direction (Fig. 7 B, red arrows). The superposition of structures with the largest and smallest projections is shown in Fig. 7 C. As seen when comparing Fig. 1 F and Fig. 7 C, the directions of the second principal mode were significantly similar to the structural changes occurring upon DNA binding. Indeed, the correlation coefficient for the directions between the second eigenvector and the structural change in the DNA-free and DNA-bound crystal structures is 0.90 (Fig. 7 B), whereas the correlation coefficient for the first principal mode is 0.11. This indicates that structural changes upon DNA binding clearly correlate with the intrinsic dynamics of EcoO109I. In other words, the relative arrangement between RCA and RCB is specifically flexible in a counterclockwise direction in the DNA-free state, and this flexibility effectively facilitates structural changes upon DNA-binding. Furthermore, the crystal structure of the DNA-free form corresponds to the upper limit of the sampled range of the projections onto the second principal mode (Fig. 7 A), indicating that the crystal structure is slightly different in the counterclockwise direction from the average structure, although the crystal structure is within the range of equilibrium. This may be attributable to crystal packing, which was relaxed during the first few nanoseconds of the simulation.

Figure 7.

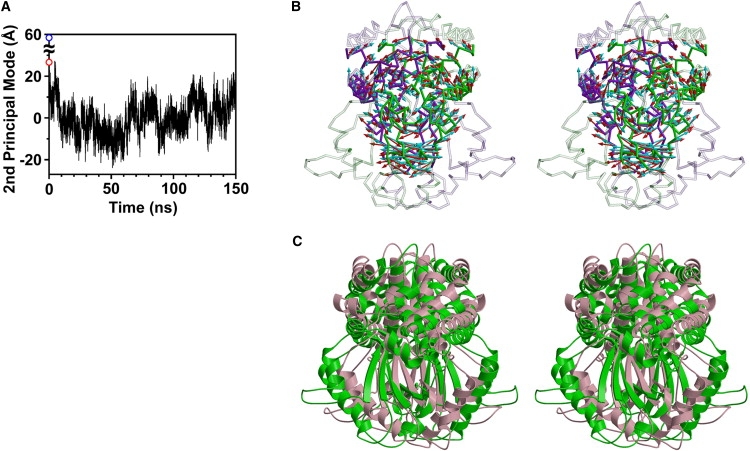
Second principal mode of principal component analysis for motions of RCA and RCB. (A) Snapshots in trajectory were projected onto second principal mode. The DNA-free (red open circle) and DNA-bound (blue open circle) crystal structures are also projected onto the second principal mode. (B) Amplitude (8σ) and direction of C^α displacements along second principal mode are represented by red arrows on C^α trace of average structure of RCA and RCB in a side view. Other parts, except for RCA and RCB, are shown in transparent representation. Subunits A and B are shown in green and purple, respectively. The difference in coordinates between the average structure and crystal structure in the DNA-bound form is represented by cyan arrows. (C) Superposition of structures with largest projection (green) and smallest projection (pink) onto second principal mode.

EcoRI is another REase in the EcoRI family, which functions as a homodimer, and shares a common structural motif in the catalytic domain with EcoO109I (42) (Fig. 8, A and B, blue). A normal mode analysis showed that EcoRI also has two low-frequency modes: an open-close motion, and a twisting motion, between the two subunits (43). However, the closing direction of the twisting mode in EcoRI is opposite to that of EcoO109I, i.e., a counterclockwise rotation in EcoO109I and a clockwise rotation in EcoRI (Fig. 8, A and B, yellow arrows). This difference is consistent with the DNA binding modes and locations of catalytic domains in EcoO109I and EcoRI. Whereas EcoO109I binds DNA from the minor groove side, EcoRI binds DNA from the major groove side (Figs. 1 and 8) (2,44). The catalytic domains of EcoO109I are located on the side of the DNA opposite the dimer interface (Fig. 8 A), and thus interact with the major groove of DNA. Therefore, counterclockwise rotation is necessary for EcoO109I to make the catalytic domains fit the major groove of DNA (Fig. 8 A, yellow arrow). In contrast, the catalytic domains of EcoRI are located on the same side of the DNA as the dimer interface (Fig. 8 B), and thus interact with the major groove of DNA. Therefore, the clockwise rotation is necessary for EcoRI to make the catalytic domains fit the major groove of DNA (Fig. 8 B, yellow arrow). As a consequence, the intrinsic twisting flexibility, which is different between EcoO109I and EcoRI, is suitable for facilitating their specific DNA binding and interaction.

Figure 8.

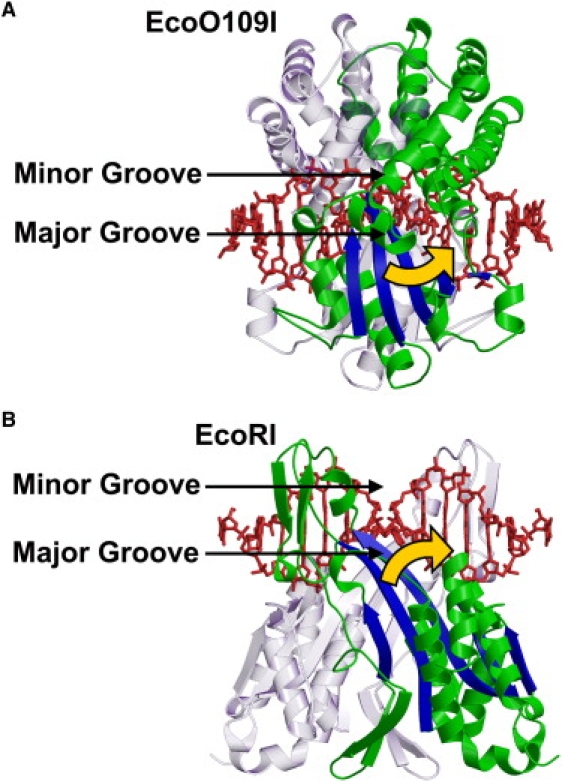
Closing direction of twisting mode in EcoO109I and EcoRI. (A and B) Side view of DNA-bound form of EcoO109I and EcoRI, respectively, colored according to common structural motif in the catalytic domain (blue) and other parts (green) in one subunit. Counterpart subunit is shown in transparent representation. DNA molecules (red) are shown, as minor groove faces upward. Yellow arrows represent closing direction of the twisting mode in EcoO109I and EcoRI, i.e., counterclockwise rotation in EcoO109I and clockwise rotation in EcoRI.

Motions of α6, α7, and β4 in the catalytic domain

Next, we focused on the dynamics within the catalytic domain in the simulation. In terms of fluctuations in the MD simulation, the catalytic domain can be divided into three parts: 1), secondary structures belonging to the rigid part of the subunit (β1–3 and α8); 2), unstructured regions (α4 and the loops between secondary structures); and 3), the rest (α6, α7, and β4), located at the bottom of the catalytic domain. Helix α4 and the loop between α7 and β4, which are missing in the crystal structure of the DNA-free form, were also unstructured in the MD simulation (Fig. 4 A).

To investigate the collective motions in the catalytic domains, principal component analysis was performed for the trajectory of the C^α atoms of α6, α7, and β4, excluding unstructured regions based on a superposition using the C^α best fits for the rigid part of the subunit, where the trajectories of both subunits A and B were used in the calculation.

As a result, the first principal mode accounted for 60.4% of the total fluctuations (Fig. 9 A). The motion represented by the eigenvector of the first principal mode (Fig. 9 C, red arrows) was the closing motion, the direction of which correlated well with that of the structural change (Fig. 9 C, cyan arrows) upon DNA binding (correlation coefficient, 0.83). As seen in Fig. 9 C, α6, α7, and β4 move collectively, relative to the rigid part of the subunit in this principal mode, and this was also evident in the structural change upon DNA binding (Fig. 9 C, cyan arrows). The small discrepancy in the direction between the first principal mode and the structural change upon DNA binding is attributable to the fact that the movement involves a hinge-bending motion, and the eigenvector points to the tangential direction of this motion.

Figure 9.

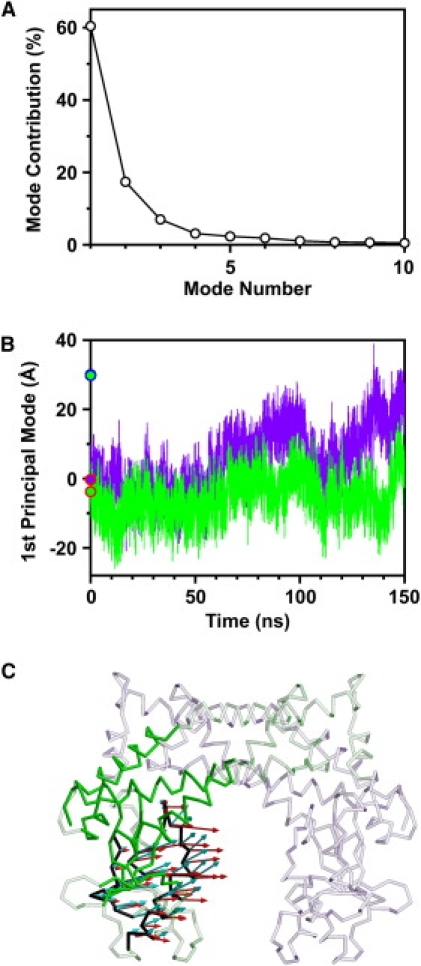
Principal component analysis for motions of secondary structures α6, α7, and β4 in catalytic domain, relative to rigid part of subunit. (A) Individual contributions of first 10 principal components to total C^α-RMSF of secondary structures α6, α7, and β4. Snapshots in trajectory of secondary structures α6, α7, and β4 in subunits A (green) and B (purple) were projected onto first principal mode (B). Blue circle shows projection value for crystal structures in the DNA-bound form. Red circles filled with green and purple show projection values for subunits A and B of the DNA-free crystal structure, respectively. (C) Amplitude (3σ) and direction of C^α displacements along first principal mode are represented by red arrows on C^α trace of average structure, in which are shown the rigid part of the subunit (green), the secondary structures α6, α7, and β4 in the catalytic domain (black), and the others (white). The difference in coordinates between the average structure and the crystal structure in the DNA-bound form is represented by cyan arrows.

Time courses of projections onto the first principal mode show no significant correlation between subunits A and B (Fig. 9 B). In addition, no significant correlation was found between the projections of α6, α7, and β4 on any principal mode and those of the rigid cores RCA and RCB (Figs. 6 B, 7 A, and 9 B). These results indicate that the collective motions of α6, α7, and β4 were independent of motions in the other parts of the structure during the simulation.

Based on all these results, we conclude that α6, α7, and β4 are intrinsically mobile in the closing direction, to capture DNA. In addition to the rigid-body motions between RCA and RCB, the intrinsic dynamics of α6, α7, and β4 also play an essential role in the function of EcoO109I. Furthermore, the DNA-bound crystal structure is located within the sampled range of projections of subunit B (Fig. 9 B), indicating that the closed conformation of the catalytic domain observed in the DNA-bound form is accessible within the range of the equilibrium fluctuations in the DNA-free state.

Relationship between intrinsic dynamics and residue interactions of EcoO109I

To investigate the relationship between the observed intrinsic dynamics of EcoO109I and the residue interactions, we calculated fractions of contacts during the simulation (Fig. 10 A). Two residues were seen to be in contact when two nonhydrogen atoms, each belonging to a different residue, were within 4.5 Å of each other. The calculated fraction of contacts was averaged over the two subunits. To identify stable interactions in the structure, a contact maintained at more than 98% during the simulation that was formed between two residues more than 15 residues apart was defined as a “permanent” contact, and was mapped onto the three-dimensional structure (Fig. 10 B).

Figure 10.

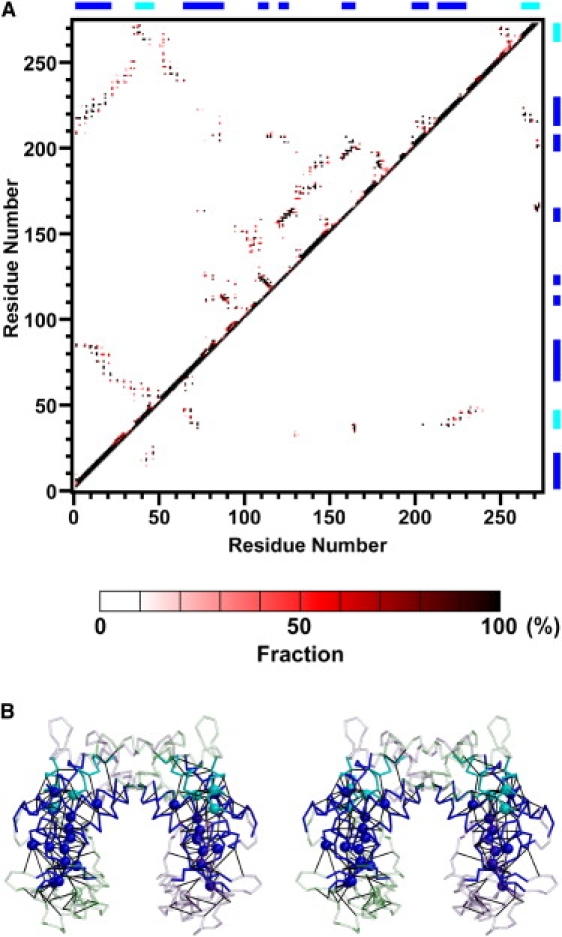
Interresidue contact analysis. (A) Fractions of contacts present in the simulation. Upper and lower triangles of contact map indicate intrasubunit contacts and intersubunit contacts, respectively. Color bar for fractions of contacts is shown along bottom. Bars along top and right sides indicate rigid part of subunit (blue) and helices α2 and α11 (cyan) in the dimerization domain. (B) Permanent contacts are mapped onto average structure in C^α trace. Rigid cores RCA and RCB, composed of the rigid part of the subunit (blue) and helices α2 and α11 (cyan), are shown in nontransparent representation. Black lines represent permanent contact formations between pairs of residues. The C^α atoms of residues with more than four permanent contacts are rendered in space-filling.

As a result, most of the permanent intrasubunit contacts formed within the rigid part of the subunit (Fig. 10 B, blue), and most of the permanent intersubunit contacts formed between the two helices α2 and α11 (Fig. 10 B, cyan) in the dimerization domain of one subunit and the rigid part (Fig. 10 B, blue) of the other subunit. In other words, permanent contacts were localized within each of the two rigid cores (RCA and RCB), forming a “contact network”. This result is consistent with the fact that RCA and RCB were rigid during the simulation.

In Fig. 10 B, the C^α atoms of residues that have more than four permanent contacts are shown in a sphere. Such residues work as “hubs” that are necessary for the maintenance of a contact network within each of the rigid cores. Interestingly, three residues (Phe-38, Leu-267, and Asn-271), located in helices α2 and α11 of subunit A, worked as hubs of the contact network within RCB (those three residues in subunit B were also hubs within RCA). This indicates that intersubunit interactions within RCA and RCB significantly contributed to the stability of the rigid cores.

In contrast to the contacts within the rigid cores, the intervening part between rigid cores RCA and RCB had few permanent contacts (Fig. 10 B), i.e., most of the contact formations in the intervening part were unstable. However, the total number of contacts within this intervening part did not significantly change during the simulation, and was similar to that of the DNA-free crystal structure, i.e., 74 ± 7 and 86 for the average of the simulation and the crystal structure, respectively. This indicates that frequent interchanges of contacts occurred in the intervening part. Most of the contacts in the intervening part were hydrophobic interactions between the side chains of residues. Few hydrogen bonds and no salt bridges were formed. The characteristics of these interactions allowed for frequent interchanges of contacts without a large change in energy, resulting in flexibility of the intervening part and enabling rigid-body motions between RCA and RCB.

In the catalytic domains, several permanent contacts were formed among α6, α7, and β4, and no significant permanent contact between the rigid part of the subunit and each of α6, α7, and β4 was evident. This is why α6, α7, and β4 moved collectively, without significant correlation with movements of the other parts of the structure in the simulation.

Conclusions

To elucidate the relationship between the intrinsic dynamics of EcoO109I and its function, we performed a 150-ns MD simulation of the DNA-free form of the enzyme, and examined the resultant trajectory in detail.

We calculated the SAXS profile from all snapshots in the trajectory, taking scattering from the explicit hydration water molecules into account. The calculated SAXS profile and R_g estimated from the Guinier plot of the profile are in agreement with the experimentally observed SAXS profile and R_g, supporting the validity of the structural ensemble sampled by the simulation presented here. In addition, a large fluctuation in R_g was observed in the simulation, which indicates considerable flexibility in the overall structure of the enzyme. There was a difference of ∼1.8 Å in R_g between its most expanded and pinched forms.

Based on further analyses of the dynamics in the trajectory, we identified two rigid cores, RCA and RCB, which are elements of rigid-body motions in the dimeric structure of EcoO109I. Interestingly, the two rigid cores were composed of the rigid part of one subunit and two helices, α2 and α11, of the other subunit. Principal component analysis, as applied to the trajectory of RCA and RCB, revealed that the rigid-body motions between the two rigid cores play an important role in the function of EcoO109I. The motion represented by the first principal mode is required for the intervening space between the catalytic domains to be accessed by DNA. The motion represented by the second principal mode has a significant correlation with the structural changes upon DNA binding, and is therefore necessary for EcoO109I to achieve effective functionality. These two functional modes accounted for a dominant portion of the fluctuations of RCA and RCB in the DNA-free state.

We also observed functional motions of α6, α7, and β4, which are located at the bottom of the catalytic domain. Principal component analysis applied to the trajectory of α6, α7, and β4 showed that the major dynamic of the catalytic domain is the closing motion relative to the rigid core, which correlates well with the structural change of this domain capturing DNA.

Analysis of contact formations revealed a relationship between intrinsic dynamics and residue interactions. A strong contact network formed within each of the rigid cores, and stable contacts between the rigid part of one subunit and the two helices α2 and α11 of the other subunit worked as hubs in the contact network. In contrast, frequent interchanges of contacts occurred in the intervening part between RCA and RCB, enabling rigid-body motions between two rigid cores. These motions are crucial for the function of the enzyme. Moreover, a small contact network formed among α6, α7, and β4 in the catalytic domain.

Our 150-ns MD simulation of EcoO109I revealed that the intrinsic dynamics of this enzyme are important for its function. To achieve functionally important structural changes upon DNA binding, the structure of EcoO109I is significantly flexible in the specific direction of functional structural changes, and this flexibility originates in its three-dimensional dimeric structure.

Appendix: Calculation of Saxs Profile from Md Trajectory

Illustration of method for calculation of SAXS profile

Here, we present a method for the calculation of scattering intensities of a solvated protein molecule in MD simulations. Let us consider a simulation box as part of a model system of dilute solution, where one protein molecule is dissolved in a large amount of solvent molecules (Fig. 2 A). The origin of the system is set to the center of mass of the protein molecule. The total volume of the model system is divided into two regions, “v” and “bo” (23,24), as illustrated in Fig. 2 A. The area corresponding to region v is within a sphere centered at the origin, and that corresponding to region bo is outside the sphere. The radius R of the sphere is chosen to be sufficiently large so that region v includes not only all of the hydration shell around the protein, but also some bulk region. The hydration shell is the area where the solvent density is perturbed from the bulk by the protein molecule.

In a dilute solution, the average electron density of the solution can be assumed to be equal to that of pure solvent, denoted as ${\rho }_0$. In our model system, the time-averaged density of the solvent in region bo was used as the ${\rho }_0$. Next, denoting electron density at position r as $\rho \left(\mathbf{r}\right)$, the instantaneous scattering amplitude of the solution is expressed as

$$\begin{array}{l}\tilde{F}\left(\mathbf{Q}\right)={\int }_{\mathrm{v}}(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}+{\int }_{\text{bo}}(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}\\ ={\tilde{F}}_{\mathrm{v}}\left(\mathbf{Q}\right)+{\tilde{F}}_{\text{bo}}\left(\mathbf{Q}\right),\end{array}$$ (3)

where Q is the scattering vector related to the scattering angle 2θ and the wavelength of the incident radiation λ by the equation $Q=\left|\mathbf{Q}\right|=4\pi \sin \theta /\lambda$. As protein molecules in solution scatter isotropically and undergo configurational changes, the instantaneous scattering intensity $\tilde{I}\left(\mathbf{Q}\right)$ must be averaged orientationally and configurationally:

$$\begin{array}{l}I\left(Q\right)={\langle {\langle \tilde{I}\left(\mathbf{Q}\right)\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{MD}}\\ =I_{\mathrm{v},\mathrm{v}}\left(Q\right)+I_{\mathrm{v},\text{bo}}\left(Q\right)+I_{\text{bo},\text{bo}}\left(Q\right),\end{array}$$ (4)

where

$$\begin{array}{l}{I}_{\lambda \lambda }\left(Q\right)={\langle {\langle F_{\lambda }^{\ast }\left(\mathbf{Q}\right)\cdot F_{\lambda }\left(\mathbf{Q}\right)\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{MD}}\hfill \\ I_{\lambda \mu }\left(Q\right)={\langle {\langle F_{\lambda }^{\ast }\left(\mathbf{Q}\right)\cdot F_{\mu }\left(\mathbf{Q}\right)+F_{\mu }^{\ast }\left(\mathbf{Q}\right)\cdot F_{\lambda }\left(\mathbf{Q}\right)\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{MD}}\hfill \\ (\lambda ,\mu =\mathrm{v},\text{bo}),\hfill \end{array}$$ (5)

where $F^{\ast }\left(\mathbf{Q}\right)$ is a complex conjugate of $F\left(\mathbf{Q}\right)$, and ${\langle \rangle }_{{\Omega }_{\mathbf{Q}}}$ and ${\langle \rangle }_{\text{MD}}$ denote the orientational average and the average over all snapshots in the trajectory of the MD simulation, respectively (${\Omega }_{\mathbf{Q}}$ is the solid angle in reciprocal space, $\mathbf{Q}=(Q,{\Omega }_{\mathbf{Q}})$).

In experiments of solution scattering, the SAXS profile of a protein is obtained by the subtraction of the scattering data of buffer solution from that of the protein solution. In our calculation method, we use the same data treatment as in the experiments, i.e., MD simulations for pure solvent are performed in addition to simulations for the protein solution, and the simulated scattering data for pure solvent are subtracted from those of protein solution.

Let us consider a pure solvent system whose average density equals ${\rho }_0$. As well as the dilute solution of the protein, this pure solvent system is divided into two regions, v and bo (Fig. 2 B). There is no difference in solvent properties between these two regions in the pure solvent system. Based on the MD simulation of the pure solvent system, the scattering intensity, $I^{\text{W}}\left(Q\right)$, is calculated. Subsequently, $I^{\text{W}}\left(Q\right)$ is subtracted from $I\left(Q\right)$, calculated from the MD simulation for protein solution:

$$\begin{array}{l}\Delta I\left(Q\right)=I\left(Q\right)-I^{\text{W}}\left(Q\right)\\ =\Delta I_{\mathrm{v},\mathrm{v}}\left(Q\right)+\Delta I_{\mathrm{v},\text{bo}}\left(Q\right)+\Delta I_{\text{bo},\text{bo}}\left(Q\right),\end{array}$$ (6)

where $\Delta I\left(Q\right)$ corresponds to the experimentally obtained scattering intensity of the protein molecule. In our study, to ensure that the average electron density of the pure solvent system is identical to ${\rho }_0$, we attempted 15 series of MD simulations for various pure-solvent systems, including different numbers of Na⁺ and Cl⁻ ions, and selected a pure-solvent system in which the average electron density was closest to ${\rho }_0$. The procedure for the i-th series is as follows: 1), i Na⁺ and i Cl⁻ ions were added into a water box with a cube edge length of 115.0 Å, followed by an energy minimization of 2000 steps; 2), a 1-ns run was performed under NPT conditions, at T = 298.15 K and P = 1.0 atm for equilibration; and 3), a 2-ns product run was performed under the same NPT conditions. The edge length of the simulation box became ∼113.5 Å in the simulation for every series. Consequently, we selected a pure-solvent system including 3 Na⁺ and 3 Cl⁻ ions, in which the average electron density was identical to ${\rho }_0$ calculated from the simulations of EcoO109I (${\rho }_0\simeq 0.3367$ Å⁻³). Numerically, the differences in scattering intensities between the buffers, which were different in terms of average density, exert negligible effects on the calculation of the final SAXS profile, $\Delta I\left(Q\right)$ (data not shown). Theoretically, however, the average density of a buffer should be equal to the ρ₀ of the protein solution (see theoretical details below).

As proved below, $\Delta I_{\mathrm{v},\text{bo}}\left(Q\right)$ and $\Delta I_{\text{bo},\text{bo}}\left(Q\right)$ equal 0 if the radius R of the sphere is sufficiently large so that the density fluctuations, $\rho \left(\mathbf{r}\right)-{\rho }_0$, in the region bo have no correlation with those in the protein area and its hydration shell. Eq. 6 then becomes

$$\begin{array}{l}\Delta I\left(Q\right)=\Delta I_{\mathrm{v},\mathrm{v}}\left(Q\right)\\ ={\langle {\langle {\int }_{\mathrm{v}}{d}^3\mathbf{r}\prime {\int }_{\mathrm{v}}{d}^3\mathbf{r}(\rho (\mathbf{r}\prime )-{\rho }_0)(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot (\mathbf{r}-\mathbf{r}\prime )}\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{MD}}\\ -{\langle {\langle {\int }_{\mathrm{v}}{d}^3\mathbf{r}\prime {\int }_{\mathrm{v}}{d}^3\mathbf{r}({\rho }^{\text{W}}(\mathbf{r}\prime )-{\rho }_0)({\rho }^{\text{W}}\left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot (\mathbf{r}-\mathbf{r}\prime )}\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{pure}\text{solvent}\text{MD}},\end{array}$$ (7)

where ${\rho }^{\text{W}}\left(\mathbf{r}\right)$ is the electron density at position r in the pure solvent system, and ${\langle \rangle }_{\text{pure}\text{solvent}\text{MD}}$ denotes the average over all snapshots in the trajectory of the MD simulation of the pure solvent.

Denoting the atomic form factor of the k-th atom at position r_k as $f_k\left(Q\right)$ (45), the instantaneous scattering intensity in the bracket ${\langle \rangle }_{\text{MD}}$ of Eq. 7 is rewritten as

$$\begin{array}{l}\tilde{I}\left(Q\right)={\langle {\int }_{\mathrm{v}}{d}^3\mathbf{r}\prime {\int }_{\mathrm{v}}{d}^3\mathbf{r}(\rho (\mathbf{r}\prime )-{\rho }_0)(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot (\mathbf{r}-\mathbf{r}\prime )}\rangle }_{{\Omega }_{\mathbf{Q}}}\\ ={\langle {\left|\sum _k^N{f}_k\left(Q\right)e^{-i\mathbf{Q}\cdot {\mathbf{r}}_k}\right|}^2\rangle }_{{\Omega }_{\mathbf{Q}}}\\ -2{\rho }_0\sum _k^N{f}_k\left(Q\right){{\int }_{\mathrm{v}}{d}^3\mathbf{r}\langle e^{-i\mathbf{Q}\cdot (\mathbf{r}-{\mathbf{r}}_k)}\rangle }_{{\Omega }_{\mathbf{Q}}}\\ +{\rho }_0^2{\int }_{\mathrm{v}}{d}^3\mathbf{r}\prime {\int }_{\mathrm{v}}{d}^3\mathbf{r}{\langle e^{-i\mathbf{Q}\cdot (\mathbf{r}-\mathbf{r}\prime )}\rangle }_{{\Omega }_{\mathbf{Q}}},\end{array}$$ (8)

where N is the number of atoms within region v. For fast computation of the SAXS profile of a snapshot, the first term on the right-hand side of Eq. 8 is calculated, based on a multipole expansion (24,38,39) that uses the following relation: (46):

$$\exp \left(-i\mathbf{Q}\cdot \mathbf{r}\right)=4\pi \sum _{l=0}^{\mathrm{\infty }}\sum _{m=-l}^l{i}^l{j}_l\left(Qr\right)Y_{lm}^{\ast }\left({\Omega }_{\mathbf{r}}\right)Y_{lm}\left({\Omega }_{\mathbf{Q}}\right),$$ (9)

where $j_l$ and $Y_{lm}$ denote a spherical Bessel function and a spherical harmonic function, respectively, and ${\Omega }_{\mathbf{r}}$ is the solid angle in real space, $\mathbf{r}=(r,{\Omega }_{\mathbf{r}})$. The volume integrals of the second and third terms on the right-hand side of Eq. 8 can be replaced by the surface integral, and this simplifies the numerical procedure of these integrals (47). Eventually, Eq. 8 is rewritten as Eq. 1. Furthermore, if region v is sufficiently large, the shape of surface S is not limited to a sphere.

In summary, the SAXS profile of a protein is obtained from MD simulations as follows: 1), the MD simulation of a protein solution system is performed; 2), the average density of the region bo, ${\rho }_0$, is calculated; 3), the MD simulation of a pure solvent system is performed, in which some ions are added to make the average density identical to ${\rho }_0$; 4), the instantaneous scattering intensity $\tilde{I}\left(Q\right)$ in Eq. 1 is calculated for each snapshot in the trajectories of the protein solution and pure solvent systems; 5), $\tilde{I}\left(Q\right)$ is averaged over all snapshots for each system; and 6), the final SAXS profile is obtained by the subtraction of the scattering data of the pure solvent from those of the protein solution.

To examine the size of region v for the correct evaluation of the SAXS profile of EcoO109I from the MD simulation, we calculated the scattering intensities $\Delta I\left(Q\right)$ by using spheres different in radius by 1 Å in a range of R = 45–51 Å. For the test calculation here, we used 500 snapshots from t = 44,001–44,500 ps, which adopted the most expanded conformations during the 150-ns simulation of EcoO109I. The maximum distance between a protein atom and the origin, $\max \left[\left|{\mathbf{r}}_k\right|\right]$, was also calculated for each snapshot, and the averages for those 500 snapshots and all snapshots were 46.9 Å and 43.7 Å, respectively. The SAXS profile calculated from the 500 snapshots turned out to converge fully at R = 50 Å, which is ∼3 Å larger than ${\langle \max \left[\left|{\mathbf{r}}_i\right|\right]\rangle }_{44001-44501\text{ps}}$. These results ensure that the sphere, the radius of which is larger than 50 Å, can be used as region v for the correct evaluation of the SAXS profile from the simulation. Therefore, we used the sphere R = 50 Å as region v for subsequent calculations and analyses.

The multipole expansion of the first term on the right-hand side of Eq. 1 fully converges for $l\le 14$, when evaluating the SAXS profile in a range of $0\le Q\le 0.18$ Å⁻¹. This is because the spherical Bessel function $j_l\left(Qr\right)$ in the expansion becomes almost 0 for $l\ge 15$ in a range of $0\le Qr\le 9$ ($0\le r\le 50$ Å). The use of the multipole expansion of $l\le 14$ makes the speed of calculation of scattering intensities ∼100 times faster than that of the Debye formula

$${\langle {\left|\sum _k^N{f}_k\left(Q\right)e^{-i\mathbf{Q}\cdot {\mathbf{r}}_k}\right|}^2\rangle }_{{\Omega }_{\mathbf{Q}}}=\sum _{i,j}^N{f}_i\left(Q\right)f_j\left(Q\right)\frac{\sin \left(Q{r}_{ij}\right)}{Q{r}_{ij}},$$ (10)

where r_ij is the distance between the i-th and j-th atoms, and N equals ∼53,800 for the sphere R = 50 Å. When calculating the scattering intensities for 138 data points of Q and using a single CPU of 3.2 GHz, the speed of calculation of the multipole expansion and the Debye formula is ∼60 and 6500 s per snapshot, respectively. To make the speed of calculation much faster, we parallelized the program, such that atoms were partitioned by order. In another strategy of parallelization, it is possible to calculate the SAXS profile independently for each snapshot, followed by averaging all profiles. The speed of calculation then becomes 2.5 s per snapshot, when using 128 CPUs. Our program enabled us to calculate the SAXS profile for every snapshot in the trajectory of the 150-ns simulation (the total number of snapshots was 150,000), and to analyze the dynamics of EcoO109I in terms of the time-resolved SAXS profile, as shown in Fig. 3 C.

Proof of $\Delta I\left(Q\right)=\Delta I_{\mathrm{v},\mathrm{v}}\left(Q\right)$

Here, we prove that if radius R of the sphere of region v is sufficiently large so that the density fluctuations in region bo have no correlation with those in the protein area and its hydration shell, $\Delta I\left(Q\right)$ equals $\Delta I_{\mathrm{v},\mathrm{v}}\left(Q\right)$.

First, let us further divide region v of both the protein solution and pure solvent systems into two regions “ph” and “bi”, as illustrated in Fig. 11. Region ph consists of the protein and its hydration shell, and the rest of region v is defined as region bi. There is no difference in solvent properties between regions bi and bo in the protein solution system, nor is there any difference among regions ph, bi, and bo in the pure solvent system. The instantaneous scattering amplitude of the protein solution of Eq. 3 is then rewritten as

$$\begin{array}{l}\tilde{F}\left(\mathbf{Q}\right)={\int }_{\text{ph}}(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}+{\int }_{\text{bi}}(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}\\ +{\int }_{\text{bo}}(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}\\ =F_{\text{ph}}\left(\mathbf{Q}\right)+F_{\text{bi}}\left(\mathbf{Q}\right)+F_{\text{bo}}\left(\mathbf{Q}\right),\end{array}$$ (11)

and the scattering intensity of Eq. 4 is rewritten as

$$\begin{array}{l}I\left(Q\right)={\langle {\langle \tilde{I}\left(\mathbf{Q}\right)\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{ens}}\\ =I_{\text{ph},\text{ph}}\left(Q\right)+I_{\text{ph},\text{bi}}\left(Q\right)+I_{\text{ph},\text{bo}}\left(Q\right)\\ +I_{\text{bi},\text{bi}}\left(Q\right)+I_{\text{bi},\text{bo}}\left(Q\right)+I_{\text{bo},\text{bo}}\left(Q\right),\end{array}$$ (12)

where ${\langle \rangle }_{\text{ens}}$ represents the configurational average over the ensemble. The subtraction of the scattering data of the pure solvent from those of the protein solution is expressed as

$$\begin{array}{l}\Delta I\left(Q\right)=I\left(Q\right)-I^{\text{W}}\left(Q\right)\\ =\Delta I_{\text{ph},\text{ph}}\left(Q\right)+\Delta I_{\text{ph},\text{bi}}\left(Q\right)+\Delta I_{\text{ph},\text{bo}}\left(Q\right)\\ +\Delta I_{\text{bi},\text{bi}}\left(Q\right)+\Delta I_{\text{bi},\text{bo}}\left(Q\right)+\Delta I_{\text{bo},\text{bo}}\left(Q\right)\\ (\Delta I_{\lambda ,\mu }\left(Q\right)=I_{\lambda ,\mu }\left(Q\right)-I_{\lambda ,\mu }^{\text{W}}\left(Q\right))\text{.}\end{array}$$ (13)

where $\Delta I\left(Q\right)$ corresponds to the experimentally obtained scattering intensity of the protein molecule. The third term of the right-hand side of Eq. 13 is given by

$$\begin{array}{l}{I}_{\text{p},\text{bo}}\left(Q\right)={\langle {\langle F_{\text{ph}}^{\ast }\left(\mathbf{Q}\right)\cdot F_{\text{bo}}\left(\mathbf{Q}\right)+F_{\text{bo}}^{\ast }\left(\mathbf{Q}\right)\cdot F_{\text{ph}}\left(\mathbf{Q}\right)\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{ens}}\\ =2{\langle {\langle {\int }_{\text{ph}}{d}^3\mathbf{r}\prime {\int }_{\text{bo}}{d}^3\mathbf{r}(\rho (\mathbf{r}\prime )-{\rho }_0)(\rho \left(\mathbf{r}\right)-{\rho }_0)e^{-i\mathbf{Q}\cdot (\mathbf{r}-\mathbf{r}\prime )}\rangle }_{{\Omega }_{\mathbf{Q}}}\rangle }_{\text{ens}}\\ =2{\langle {\int }_{\text{ph}}{d}^3\mathbf{r}\prime {\int }_{\text{bo}}{d}^3\mathbf{r}{\langle (\rho (\mathbf{r}\prime )-{\rho }_0)(\rho \left(\mathbf{r}\right)-{\rho }_0)\rangle }_{\text{ens}}{e}^{-i\mathbf{Q}\cdot \mathbf{r}}\rangle }_{{\Omega }_{\mathbf{Q}}}\text{.}\end{array}$$ (14)

Figure 11.

Dividing total volume of a system into three regions “ph”, “bi”, and “bo” produces dilute solution of a protein (A) and pure solvent (B).

If region v is sufficiently large that regions ph and bo are separated enough by region bo, there is no correlation in density fluctuations between regions ph and bo. This relationship can be expressed as

$$\begin{array}{l}{\langle (\rho (\mathbf{r}\prime )-{\rho }_0)(\rho \left(\mathbf{r}\right)-{\rho }_0)\rangle }_{\text{ens}}=0\\ (\mathbf{r}\prime \in \text{ph},\mathbf{r}\in \text{bo})\text{.}\end{array}\text{.}$$ (15)

On substituting Eq. 15 in Eq. 14, we find that

$$I_{\text{ph},\text{bo}}\left(Q\right)=0\text{.}$$ (16)

and in the pure solvent system,

$$I_{\text{ph},\text{bo}}^{\text{W}}\left(Q\right)=0\text{.}$$ (17)

Considering that there is no difference in solvent properties of regions bi and bo between the protein solution and pure solvent systems, it follows that

$$I_{\text{bi},\text{bi}}\left(Q\right)=I_{\text{bi},\text{bi}}^{\text{W}}\left(Q\right),I_{\text{bi},\text{bo}}\left(Q\right)=I_{\text{bi},\text{bo}}^{\text{W}}\left(Q\right),I_{\text{bo},\text{bo}}\left(Q\right)=I_{\text{bo},\text{bo}}^{\text{W}}\left(Q\right)\text{.}$$ (18)

On substituting Eqs. 16–18 in Eq. 13, we find that

$$\Delta I\left(Q\right)=\Delta I_{\text{ph},\text{ph}}\left(Q\right)+\Delta I_{\text{ph},\text{bi}}\left(Q\right)+\Delta I_{\text{bi},\text{bi}}\left(Q\right)=\Delta I_{\mathrm{v},\mathrm{v}}\left(Q\right),$$ (19)

where $\Delta I_{\text{bi},\text{bi}}\left(Q\right)$ equals 0.