Abstract
The role of β-sheets in the early stages of protein aggregation, specifically amyloid formation, remains unclear. Interpretations of kinetic data have led to a specific model for the role of β-sheets in polyglutamine aggregation. According to this model, monomeric polyglutamine, which is intrinsically disordered, goes through a rare conversion into an ordered, metastable, β-sheeted state that nucleates aggregation. It has also been proposed that the probability of forming the critical nucleus, a specific β-sheet conformation for the monomer, increases with increasing chain length. Here, we test this model using molecular simulations. We quantified free energy profiles in terms of β-content for monomeric polyglutamine as a function of chain length. In accord with estimates from experimental data, the free energy penalties for forming β-rich states are in the 10–20 kcal/mol range. However, the length dependence of these free energy penalties does not mirror interpretations of kinetic data. In addition, although homodimerization of disordered molecules is spontaneous, the imposition of conformational restraints on polyglutamine molecules does not enhance the spontaneity of intermolecular associations. Our data lead to the proposal that β-sheet formation is an attribute of peptide-rich phases such as high molecular weight aggregates rather than monomers or oligomers.
Introduction
Nine neurodegenerative diseases are associated with polyglutamine expansion mutations (1). Ages of onset and severity of disease at onset are inversely correlated with the lengths of polyglutamine expansions (2). Proteolysis of mutant proteins releases fragments rich in polyglutamine that aggregate to form insoluble neuronal intranuclear inclusions (3). Aggregates are fibrillar and amyloidlike (4) with high β-sheet contents. Based on fiber diffraction data, Perutz et al. proposed a model in which the individual polyglutamine molecules within aggregates are arranged in a β-helical conformation (5). The fiber diffraction data have also been shown to be consistent with flat β-sheet architectures for individual polyglutamine peptides (6).
In contrast to structures adopted by individual polyglutamine molecules in fibrillar aggregates, monomeric polyglutamine molecules have spectroscopic signals that indicate a lack of well-defined secondary structures (7,8). It has also been shown that monomeric polyglutamine forms collapsed structures in water (9), and this observation is consistent with water being a poor solvent for polyglutamine (10). Monomeric polyglutamine is intrinsically disordered, irrespective of chain length, and these molecules sample heterogeneous ensembles of collapsed structures in water.
Chen et al. (11) proposed a model to connect intrinsically disordered monomers and β-sheet structures that are prominent in fibrillar forms. Analysis of kinetic data using a homogeneous nucleation model yielded a nucleus size of one (11). The results were interpreted as follows: Monomeric polyglutamine is in a preequilibrium between a folded, toxic, β-sheet structure and the disordered ensemble. Whenever the toxic fold is adopted, the thermodynamically unfavorable nucleus is populated and the resulting ordered conformation is elongated through monomer addition. A schematic of this proposal is shown in Fig. 1. The proposal put forth by Chen et al. is difficult to test experimentally because the critical nucleus is, by definition, a rare species.
Figure 1.
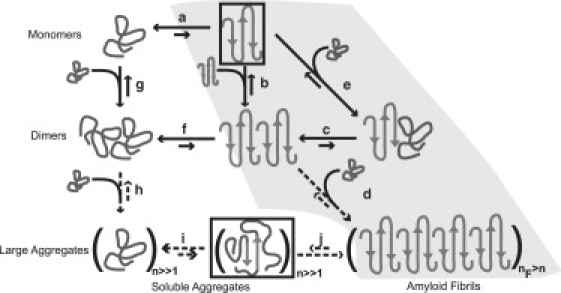
Schematic of possible aggregation pathways for polyglutamine in vitro; n denotes the number of polyglutamine molecules within a disordered aggregate and nF denotes the number of polyglutamine molecules within an ordered amyloid fibril. The ordered amyloid fibril rich in β-sheets is shown in the bottom-right corner of the schematic. The gray-shaded region encompasses steps a, e, c, and d and depicts the homogeneous nucleation proposal of Chen et al. (11). We investigated the thermodynamics of step a, which indicates that the formation of ordered conformations is thermodynamically unfavorable. Monomeric polyglutamine prefers disordered, collapsed conformations, to the left of step a. Step b pertains to the thermodynamics of interactions between chains that have been restrained to adopt ordered conformations. Associativities of restrained chains—step b—are akin to the associativities of unrestrained chains—step g. However, the likelihood that chains will sample the associations shown in step b is very small, because this is tied to the equilibria in step a, which requires the population of the conformations with high β-content. Fig. 3 shows that this is highly unlikely. Similarly, step f shows that disordered dimers are thermodynamically favored to dimers with high β-contents in individual chains. This is the result of linkage to step a as discussed above. The aggregates achieved in step h are likely to be large (in terms of n) and exhibit spherical, “liquid-like” (31,32,34) organization of polyglutamine chains around each other. Step i depicts a slow conformational conversion of individual/small numbers of chains to β-sheets. This slow step is likely to lead to the creation of an ordered template for fibril formation via monomer or oligomer addition and elongation to yield the ordered amyloid fibril. Steps a, b, and g are anchored in the collection of data generated in this work and previous studies. However, the reversible associations depicted in step h and the conformational conversions depicted in step i are yet to be tested.
Recently (12), we corroborated experimental results that polyglutamine chains spanning the pathological threshold range for Huntington's disease (N ≈ 37) adopt disordered, compact conformations at the monomer level. We also showed that they associate spontaneously to form disordered dimers. These studies were carried out using the ABSINTH implicit solvation model combined with the all atom OPLS-AA/L force field (12,13). Here we use the same combination of force field and implicit solvation model to answer a set of questions and test all aspects of the homogeneous nucleation model proposed by the analysis of Chen et al. (11) and Bhattacharya et al. (14). The questions of interest are as follows:
What is the probability that monomeric polyglutamine forms structures with high β-content under ambient conditions?
Are such species metastable states along a reaction coordinate that measures the net β-content of the chain?
How does the likelihood of forming species high in β-content vary with chain length?
If we bias individual polyglutamine chains toward structures with high β-content, do we observe a change in the spontaneity of dimer formation?
Finally, do our results support the idea of a structure-driven, homogeneous nucleation pathway for polyglutamine aggregation?
The rest of this article is organized as follows: First, we introduce the details of our methodology. This is followed by a presentation of results that allow us to answer the questions raised above and we conclude with a summary and discussion of our results.
Materials and Methods
Degrees of freedom and force field
We simulated one- or two-polyglutamine molecule n-acetyl-(Gln)N-n′-methylamide; the chains were modeled in atomic detail and the number of glutamine residues was set to N = 5, 15, 30, and 45, respectively. Chains with N glutamine residues are denoted as QN. Markov chain Metropolis Monte Carlo (MC) Simulations were performed in the canonical ensemble and molecules were enclosed in a spherical droplet of radius 200 Å, which was enforced using a stiff harmonic boundary potential. The degrees of freedom were the backbone ϕ, ψ, ω, and side-chain χ-dihedral angles. For MC simulations with two chains, rigid-body coordinates, namely center-of-mass translations and rotations, were included as additional degrees of freedom. Bond lengths and bond angles were held fixed at values prescribed by Engh and Huber (15).
We used parameters from the OPLS-AA/L force field (16) with appropriate modifications and the ABSINTH implicit solvent model (13). The energy function is
| (1) |
Here, Wsolv is the direct mean-field interaction term that captures the transfer of a polypeptide solute in a specific conformation from the gas phase into the continuum solvent. Wel denotes the mean-field electrostatic term; the dielectric constant of the solvent is set to be ɛ = 78. ULJ models van der Waals interactions using the Lennard-Jones (LJ) model. Parameters for the LJ hard-sphere radii and well depths are based on heats of fusion data for model compounds and are different from the choices made in standard force fields. This choice allows us to omit many of the torsional potentials because the rotational barriers and minima are captured by excluded volume interactions alone (13). Utor represents torsional terms applied to dihedral angles that cannot be captured by ULJ. For polyglutamine, we use torsional potentials taken from OPLS-AA/L to maintain peptide dihedral angles (ω) in predominantly trans-configurations.
Salient features of the interplay between the Wsolv and Wel terms are summarized as follows: Polypeptide chains are decomposed into a set of distinct solvation groups; for capped polyglutamine, the solvation groups are N+1 backbone secondary amides and N side-chain primary amides. Wsolv is a sum of contributions from each solvation group and for each of these groups we use experimentally measured free energies of solvation of appropriate model compound analogs as references for fully solvated states. The degree of solvent accessibility modulates the direct mean-field interaction and consequently Wsolv varies with conformation. Solvent-accessible volume fractions are used as the metric for solvent accessibility and this is used to evaluate the solvation states for atom k in solvation group i. Electrostatic interactions between nonbonded solute atoms with partial charges are fully screened by the continuum dielectric if the atoms are fully exposed to solvent. The screening of polar interactions is conformation-dependent and the solvation states of atoms determine the extent to which the screening of electrostatic interactions is modulated. ABSINTH is built upon the distinct strengths of the generalized Born (GB) (17–19) and EEF1 (20) models. In accord with EEF1, the process of transferring solutes from the gas phase into the continuum solvent is treated in “one shot” without attempting to parse the distinct contributions from the polar and nonpolar components. However, ABSINTH deviates from EEF1 in the way electrostatic interactions between solute atoms are handled. No explicit or implicit distance-dependence is assumed for the dielectric response. Instead, solvation states of individual atoms are used to determine the extent to which the screening of electrostatic interactions is to be modulated by the protein environment. ABSINTH therefore captures the main strengths of the GB model while retaining the efficiency of the EEF1 model and it may be viewed as an effective interpolation between GB and EEF1.
Sampling methodology
Move sets for MC simulations included pivots about random backbone torsions, perturbations about random dihedrals, randomized side-chain rotations, and randomized changes to rigid body coordinates. Details regarding the move sets are summarized in Table S1 in Supporting Material. One of our goals was to quantify free energy penalties associated with sampling of β-rich conformations for monomeric polyglutamine. We defined a reaction coordinate fβ to assess global β-content within a molecule and used umbrella sampling to enhance the sampling of the low-likelihood regions of conformational space. Results of independent umbrella sampling calculations were stitched together using weighted histogram analysis methods (WHAM) (21,22) to generate unbiased potentials of mean force (PMFs) as a function of fβ, which is defined as
where
| (2) |
| (3) |
Here, N is the number of glutamine residues in the sequence, mod2π terms correct for periodicity effects associated with distance calculations in angular space; (ϕβ,ψβ) define the reference (ϕ,ψ) values for an individual residue. If residue i adopts ϕ- and ψ-angles that lie within a circle of radius rβ, then the parameter fβ(i) is set to unity; otherwise, fβ(i) has a value between 0 and 1; the precise value is determined by two parameters, namely d(i)2 and τβ. The latter is the width of the Gaussian function and ensures a continuous function. We used: (ϕβ,ψβ) = (−152°, 142°), rβ = 50°, and τβ = 0.002 deg−2.
We assessed the validity of fβ as a measure of β-content by quantifying its ability to estimate β-content in proteins of known three-dimensional structures. We used PDBSelect (23) to create a database of 3693 nonredundant protein structures from the Protein Data Bank. Sequences in this dataset have <25% sequence identity with each other. For each structure in the dataset, we calculated the fβ values and their DSSP-E score (24), normalized by the number of residues, as an alternative to measure the degree of ordered β-sheet. Fig. 2 shows the correlation between fβ and fractional DSSP-E scores. The correlation coefficient is 0.83. Fig. S1 shows ribbon drawings of three-dimensional structures for five structures from the database. Since we do not have definitive prior knowledge of the type of ordered β-sheets that polyglutamine molecules adopt in fibrillar aggregates, we used fβ instead of fractional DSSP-E scores as a reaction coordinate for assessing the bias toward structures with high or low β-contents.
Figure 2.
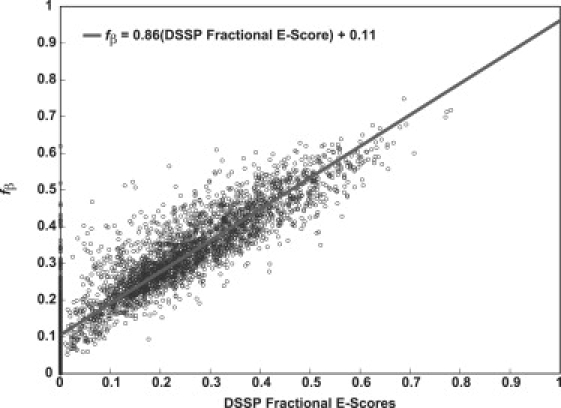
Correlation between fractional DSSP-E scores and fβ: The solid line is the line of best fit that quantifies the strength and direction of the linear correlation between fβ values and fractional DSSP-E scores. Parameters for the slope and intercept are shown in the inset. Structures that have high fractional DSSP-E scores also have high fβ values, although there is some scatter about the line of best fit. For ∼27% of the structures in the dataset, the fractional DSSP-E scores are zero. Although the fβ values for most of these structures are small (≤0.3), they span a finite range of fβ values.
Simulations for monomeric polyglutamine were carried out at 298 K. For each chain length, we performed 17 sets of distinct umbrella sampling simulations and in each simulation, fβ was restrained to one of 17 target fβ0 values: [0.0, 0.1, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.7, 0.75, 0.8, 0.9, 0.95, 1.0]. Each simulation was biased toward a target value fβ0 using a harmonic restraint potential Urestr = k(fβ − fβ0)2 that was added to the energy function shown in Eq. 1. The number of (ϕ,ψ) pairs that contribute to fβ increases with N and the value of k varied with N. We used values of k = 25 kcal/mol and 75 kcal/mol for Q5 and Q15, and k = 150 kcal/mol for Q30 and Q45, respectively. Therefore, k varies from 1.7 kcal/mol (Q45) to 2.5 kcal/mol (Q5, Q15, and Q30) per restrained degree of freedom.
For each window, the starting conformation was extracted at random from an ensemble of self-avoiding random walks. For Q5, Q15, and Q30 the first 106 MC steps were used for equilibration followed by 4 × 107 steps of production. For Q45, we used 1.5 × 106 steps of equilibration and 6 × 107 steps of production. Sampling was enhanced using replica exchange MC in fβ-space (25). For each chain length, we performed three independent replica exchange umbrella sampling MC runs. The quality of sampling was assessed by computing statistics for the extent of overlap of fβ histograms between adjacent windows and statistics for replica exchange. These details are documented in Fig. S3, Fig. S4, and Fig. S5.
The WHAM protocol has two components, namely iterative computation of relative free energies between adjacent windows and the construction of unbiased PMFs. Data from restrained simulations were analyzed using WHAM in three different ways. In the first two methods, both components of the WHAM protocol are used, with the only difference being the method used to compute error bars for the unbiased PMFs. The first method reports error bars as standard errors and the second method uses a bootstrap procedure to estimate error bars. For the third method, the relative free energies between adjacent windows were computed using thermodynamic integration (TI) and the unbiased PMF was computed using WHAM. All the details regarding error analysis and TI-WHAM are provided in the Supporting Material.
For polyglutamine dimer simulations, we combined MC simulations with thermal replica exchange. In two of the three sets of simulations, each chain was restrained to target fβ0 values of = 0.75 and 1.0, respectively, whereas the third simulation set involved unrestrained molecules. For each chain length, we carried out three independent replica exchange runs. The following Kelvin temperature schedule was used for the replica exchange simulations: [298, 305, 315, 325, 335, 345, 355, 360, 370, 380, 390]. The temperature schedule was based on data for coil-to-globule transitions of unrestrained monomeric polyglutamine. As shown in Fig. S2, temperature modulates the solvent quality. Temperatures in the range T ≤ 355 K correspond to the poor solvent regime, where monomeric polyglutamine prefers globules; temperatures in the range 355 K < T < 420 K are in the transition region between globule and coil, and higher temperatures correspond to swollen coils. The θ-point (Tθ) was found to be ∼390 K (see caption to Fig. S2). We wish to quantify the spontaneity of intermolecular associations in the poor solvent regime. The overlap between coil and globule ensembles is small and decreases with increasing N. Therefore, we set the upper limit for the replica exchange temperature schedule to be Tθ, to ensure that the replicas were used judiciously. We quantified overlap statistics and acceptance ratios for swaps between adjacent thermal replicas to demonstrate the adequacy of the protocol, and details are in Fig. S6, Fig. S7, and Fig. S8.
Results
Conformations with high β-content are thermodynamically unfavorable for monomeric polyglutamine
Fig. 3 A shows free energy profiles for monomeric polyglutamine of four chain lengths. Fig. 3, B and C, shows the same free energy profiles, except that the profile in Fig. 3 B shows the bootstrap errors, whereas Fig. 3 C shows the free energy profiles constructed using the TI-WHAM procedure. The free energy profiles along fβ are smooth and possess broad minima for N ≥ 15. For Q5, the PMF is essentially flat because the peptide is short and cannot collapse on itself. For longer chains, the minima are located at values of fβ ≈ 0.3, which is the value preferred by unrestrained polyglutamine chains. The Q15 chain possesses a tendency for forming α-helical segments (12). This helix propensity is the reason for the flatness of the free energy profile for values of fβ <0.3 for this peptide. Decreased α-helical propensities for longer chain lengths lead to an increase in the free energy penalty for fβ < 0.3.
Figure 3.
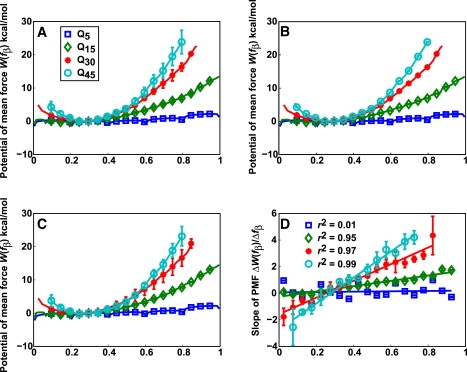
Potentials of mean force (PMFs) for monomeric polyglutamine chains of different lengths. The profiles are plotted as a function of fβ, which is a reaction coordinate that measures β-content. (A) PMFs with standard errors, (B) with bootstrap errors, and (C) PMFs that result from using TI-WHAM with a coarse fβ schedule. Details are described in the Supporting Material. (D) Lines of best fit to the data for the derivatives of the PMFs shown in panel A. The insets show the Pearson correlation coefficients—r2—that diagnose the strength and direction of the hypothesis that the PMF derivatives (forces) are linear. The slopes and intercepts for the lines of best fit are as follows: Q5 (0.25, −0.05), Q15 (2.00, −0.27), Q30 (5.74, −1.38), and Q45 (9.5, −2.65). Slopes have units of kcal/mol-fβ and intercepts have units of kcal/mol.
The free energy profiles do not show evidence for distinct local minima. This is confirmed by analyzing the derivatives of each of the PMFs. In the harmonic limit with a single minimum, a mean force profile will be a straight line and this is what we observe as shown in Fig. 3 D. Therefore, monomeric polyglutamine does not access metastable conformations with high fβ values. Bhattacharya et al. (14) estimated the nucleation free energy for Q47 to be roughly 12 kcal/mol. Beta-rich structures will have fβ values between 0.6 and 0.7 (Fig. 2 and Fig. S1). Free energy penalties associated with accessing such structures are in the range of 10–15 kcal/mol for Q45 (Fig. 3 A). This is in the range of the estimate obtained by Bhattacharya et al.
Bhattacharya et al. also proposed that aggregation rates increase with increasing chain length because free energy penalties associated with forming β-rich structures decrease with increasing chain length (11,14). The calculated free energy profiles do not support this hypothesis. The free energy penalty for forming structures with high fβ values increases with increasing chain length. However, this increase in free energy penalty levels off for Q45 because the PMFs for Q30 and Q45 resemble each other—more so than those for Q30 and Q15. We previously showed that the stability of nonspecifically collapsed states increases with increasing chain length (12). Here, we show that the likelihood of populating structures with high fβ values decreases with increasing chain length. The former observation is consistent with the physics of flexible polymers in a poor solvent, whereas the latter observation is congruent with the idea that energetic frustration (26) makes it difficult for flexible, homopolymeric polyglutamine to adopt well-ordered three-dimensional structures in their monomeric forms.
Restraining monomeric polyglutamine to high fβ values provides access to ordered β-sheet conformations
Fractional DSSP-E scores (24) based on analysis of hydrogen-bonding patterns are a complementary measure of secondary structure. Fig. 4 plots data for monomeric polyglutamine with fractional DSSP-E scores along the ordinate and fβ values along the abscissa. Data were extracted from the simulations that were performed in the presence of restraints on fβ. We do not observe any structures for which the fβ value is low when the fractional DSSP-E score is high. Structures with characteristic β-sheet hydrogen-bond patterns have high fractional DSSP-E scores as well as high fβ scores. However, for moderate to high fβ values, there is a substantial spread in the observed fractional DSSP-E scores, implying that polyglutamine samples disordered conformations lacking regular backbone-backbone hydrogen bonds even when fβ is restrained to a high value.
Figure 4.
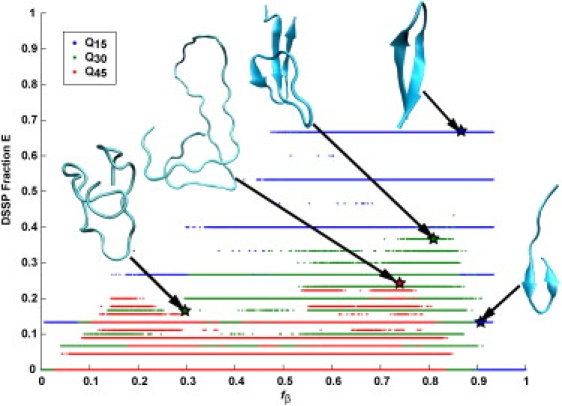
Scatter plot of all recorded snapshots in all simulations for Q15, Q30, and Q45 correlating the fractional β-content according to DSSP with the values for fβ at 298 K. Dots of different colors correspond to chains of different length. Representative points are marked using stars and the corresponding structures are shown in cartoon representation. Graphics were generated using VMD (35). Note that the fractional β-content according to DSSP is an inherently discrete quantity for chains of finite length. Q5 is not shown since the chain is too short to have nonzero DSSP-E scores.
Persistence of disorder in the presence of restraints results from a diverse registry of intramolecular hydrogen bonds
We asked whether disordered structures contain large numbers of hydrogen bonds, which are either unsatisfied or assumed to be satisfied by the solvent. In Fig. 5, we plot the average number of intramolecular hydrogen bonds per backbone and side-chain oxygen (acceptor) atom in monomeric polyglutamine as a function of chain length. All four types of hydrogen bonds including backbone acceptor to backbone donor, side-chain acceptor to side-chain donor, backbone acceptor to side-chain donor, and side-chain acceptor to backbone donor, make roughly equivalent contributions to the total hydrogen-bond inventory. No obvious preference for specific intramolecular contacts is seen, even in the presence of restraints. Summing up around the acceptor sites, the average number of hydrogen bonds per backbone side-chain acceptor is less than unity, indicating that a substantial fraction of hydrogen bonds is satisfied by the solvent. The average number of intramolecular hydrogen bonds per acceptor is generally larger for the unrestrained case. Restraints to high values of fβ increase the number of solvent-exposed acceptors leading to increased interfaces with the surrounding solvent. Despite the restraints, the peptides prefer the full spectrum of intramolecular and chain-solvent contacts.
Figure 5.

Average number of hydrogen bonds per acceptor oxygen atoms. Data are shown for hydrogen bonds around the backbone (A and C) and side-chain (B and D) acceptor oxygen atoms, respectively. BB denotes backbone and SC denotes side chains. Values are shown for T = 298 K and three different chain lengths (Q15, Q30, Q45) and restraint values. Hydrogen bonds were determined using the general definition introduced by Kabsch and Sander (24).
Dimerization of polyglutamine remains spontaneous in the presence of restraints
We asked whether the spontaneity of homodimerization is altered when each chain is restrained to adopt high values of fβ. We simulated dimerization of polyglutamine for chains of length N = 5, 15, 30, and 45 as a function of temperature and two different values for the target restraint, fβ0. If the homogeneous nucleation model applies for polyglutamine aggregation, then associations involving restrained chains should be stronger than the associations involving unrestrained chains. To quantify associativity, we computed a temperature-dependent excess interaction coefficient, B22(T), which we introduced in previous work and recapitulate below:
| (4) |
Here, FT(R) is the cumulative distribution function for the intermolecular distance at temperature T; ddroplet = 400 Å is the diameter of the simulation system. When spontaneous associations are favored compared to Tθ, B22(T) is negative. If chains interact the way they would at Tθ, then B22(T) is zero.
Fig. 6 plots B22(T) as a function of T for different chain lengths in the presence and absence of restraints on fβ. The associativity of chains is length- and temperature-dependent, but it does not vary with the presence or absence of conformational restraints. Fig. 6 A shows that the short Q5 peptide remains nonassociative across the entire simulated temperature range. For Q15, the differences in associativity with and without restraints are statistically insignificant. At the lowest temperatures, B22 is negative for restrained as well as unrestrained chains. It increases monotonically with increasing temperature and reaches zero between 320 and 340 K. This temperature range represents the stability limit for the associated dimer. Fig. 6, B and C, show the same data for Q30 and for Q45. As chain lengths increase, the stability limit for associated dimers shifts to higher temperatures. Within the statistical accuracy of the data, chains with restraints are as associative (not more associative) as unrestrained chains.
Figure 6.
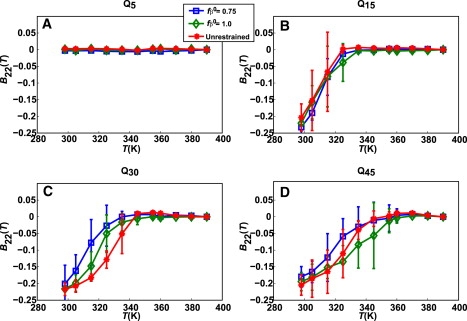
Plots of B22(T) as a function of temperature. Each panel shows B22(T) extracted from simulations with unrestrained chains and simulations where each chain in the simulation has a target restraint of fβ0 = 0.75 or fβ0 = 1.0.
For high values of fβ, the surface/volume ratio increases with respect to the unrestrained chains (see Fig. S9). This does not translate into increased associativity with respect to the unrestrained chains. Instead, the actual poorness of the solvent (the value of T) remains the main determinant of the spontaneity of intermolecular associations. This observation is confounding since solute-solvent interfaces increase for monomeric polyglutamine when restraints toward high fβ are imposed. We quantified the solvent-solute interface for monomeric polyglutamine by asking if interfacial energies were insensitive to the presence or absence of conformational restraints. We decomposed the system energies (excluding the restraint potential) into bulk (volumetric) and surface contributions (27) by fitting the system energies to the functional form shown in Eq. 5. Here, C1 and C2 measure the effective strengths of volumetric self-interactions and surface terms, respectively,
| (5) |
where N is the chain length, Utotal is the system energy, and Urestr is the restraint potential energy. Fig. 7 plots C1 and C2 as a function of temperature for different values of fβ0. When compared to the unrestrained simulations, the C1 term in the collapse regime is less favorable in the presence of restraints indicating the high free energy of structures with high values of fβ. Additionally, for a given temperature, values for C2 are more positive because larger interfaces with the surrounding solvent are more unfavorable than the smaller solute-solvent interfaces made by unrestrained chains. As T→Tθ, C2 approaches zero indicating that the interface is indifferent with respect to interactions with either solvent or the chain. This is Flory's definition of the θ-state. For temperatures >Tθ ≈ 390 K, C1 converges to a value of ∼–20 kcal/mol. This is the approximate mean-field energy for a fully solvated glutamine residue within the ABSINTH Hamiltonian (13), and is the expected limiting value for a chain preferring chain-solvent interactions to chain-chain interactions. Therefore, in the presence of restraints toward high target values of fβ, the chains swell and form energetically unfavorable interfaces with the surrounding solvent. However, these features do not translate into differences in B22 compared to the unrestrained chains.
Figure 7.
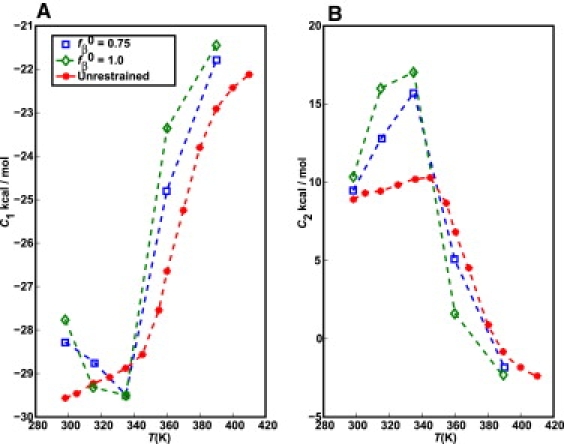
Energy density C1 (A) and surface energy term C2 (B) for monomeric polyglutamine. Data were obtained for unrestrained polyglutamine and two other simulations with restraints on fβ. The quality of the fits underlying these data cannot be accurately assessed since they are fits to data from only three chain lengths (because we exclude Q5 excluded from analysis, since it is too short for a volumetric term to contribute).
Restraints toward high values of fβ promote the formation of canonical β-sheets
Fig. 8 shows the average fractional DSSP-E scores observed in monomer and dimer simulations with fβ0=1 compared to the data obtained from simulations with unrestrained chains. When the free energy penalty for sampling high fβ values is prepaid, the resultant increase in solute-solvent interface at the monomer level results in increased β-sheet formation through a coupling between inter- and intramolecular interactions. This difference is suggestive of intermolecular interfaces being responsible for promoting β-sheet content. To provide a visual perspective of increased β-sheet content in dimers formed with restrained chains, Fig. S10 shows a scatter plot in the space of the two parameters, fβ and fractional DSSP-E scores. Fig. 9 shows a bar plot of intermolecular hydrogen bonds to quantify the interactions in intermolecular interfaces. Intermolecular hydrogen bonds predominantly involve glutamine side chains. There is a significant enhancement in intermolecular backbone-backbone hydrogen bonds for Q15 and Q30 when fβ0 = 1.0 and is congruent with data in Fig. 8. Interestingly, the per-molecule PMF obtained via WHAM for two Q30 molecules in the simulation system is virtually identical to the one obtained for the monomer (data not shown). Hence, we conjecture that larger oligomers must form to facilitate spontaneous conversion of individual chains to β-rich conformations.
Figure 8.
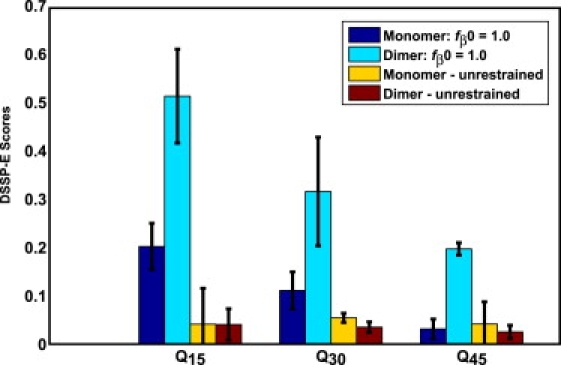
Bar plots comparing the average fractional DSSP-E scores in simulations of monomeric polyglutamine to simulations of dimeric polyglutamine at 298 K. Data are shown for three chain lengths using data from simulations with unrestrained chains as well as data from simulations for fβ0 = 1.0.
Figure 9.
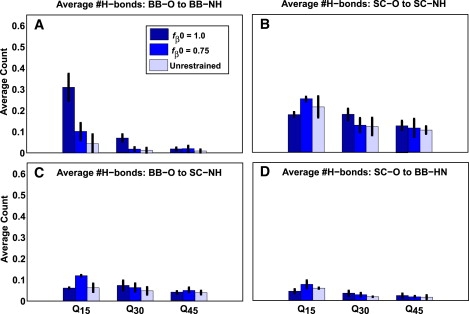
Average number of hydrogen bonds per acceptor oxygen atoms. This plot is similar to Fig. 5 except that the hydrogen-bond statistics are shown for simulations with two molecules. Only intermolecular hydrogen bonds are shown. Q5 is excluded from this plot, since no intermolecular hydrogen bonds are detected in these simulations.
Discussion
Monomeric polyglutamine encompassing the threshold length for Huntington's disease does not adopt conformations rich in β-content. Such conformations have been proposed as putative nuclei for polyglutamine aggregation (11). Our estimate of the free energy penalty associated with forming structures with high β-content is in the range of estimates proposed in the literature (14). However, these penalties increase with increasing chain length and may plateau past a certain chain length. Our observations contradict the expectations of Bhattacharya et al. (14), who proposed that the free energy penalties in question should decrease with increasing chain length if the stability of the monomeric nucleus is the source of the increased rate of aggregation with increasing chain length. In our calculations, coil-to-globule transitions for monomeric polyglutamine (Fig. S2) as well as the spontaneities of intermolecular association show clear dependence on chain length. In a poor solvent, longer chains form disordered globules of increased stability. The more stable the globules, the more favorable the dimers (12), and the harder it is to dissociate the dimers. Although conformational restraints toward high fβ values lead to increases in solute-solvent interfaces and increased β-content, these do not translate into increased spontaneity for intermolecular associations. This observation points to poorness of the solvent, as opposed to the associativities ascribed to specific structures, as the invariant and generic driving force for promoting aggregation of homopolymers. Even though high β-content remains just as thermodynamically unfavorable at the dimer level as at the monomer level, the formation of intermolecular interfaces between restrained chains promotes the formation of canonical backbone-driven β-sheet structures. Other approaches to simulating polyglutamine conformational equilibria and aggregation have been published (28,29). Clearly, comparative calculations using different models are needed to test the model dependence of our predictions and this is part of ongoing work.
Recent experiments (30) suggest that β-sheet formation is a feature of large aggregates. It was also shown that large nonspecific aggregates form before nucleated formation of ordered fibrils. These observations are consistent with extrapolations from our calculations, specifically the data shown in Fig. 9. In Fig. 1, we summarize conceivable routes from the ensemble of disordered globules to the high molecular weight, ordered fibrillar aggregates. The homogeneous nucleation model, with a monomeric nucleus, is highlighted in gray. An alternative proposal, consistent with our results and recent experimental data of Lee et al. (30), is follows: Disordered globules reversibly associate to form a broad distribution of disordered oligomers. These oligomers can be described as being “molten” (31) or “liquid-like” (32) and may be large enough to be referred to as “mesoglobules” (33). Molten oligomers are peptide-rich microphases, and chains in the interior are solvated by other chains. These peptide-peptide interfaces should be more favorable than peptide-solvent interfaces in a poor solvent. Peptides within concentrated droplets can become indifferent to preferring intramolecular interactions to intermolecular interactions and consequently, individual chains can expand. In the ensuing conformational sampling, a presumed slow step, chains can converge on energetically favorable conformations that are high in β-content. Our proposal is similar to those of others for polyglutamine (30), Aβ (34), and the N-domain Sup35 (31) but needs to be tested using appropriate simulations.
Supporting Material
Ten figures and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00906-0.
Supporting Material
Acknowledgments
This work was supported by grant No. 5R01-NS056114 from the National Institutes of Health.
Footnotes
Andreas Vitalis and Nicholas Lyle contributed equally to this work.
References
- 1.Williams A.J., Paulson H.L. Polyglutamine neurodegeneration: protein misfolding revisited. Trends Neurosci. 2008;31:521–528. doi: 10.1016/j.tins.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ross C.A. When more is less: pathogenesis of glutamine repeat neurodegenerative diseases. Neuron. 1995;15:493–496. doi: 10.1016/0896-6273(95)90138-8. [DOI] [PubMed] [Google Scholar]
- 3.Ross C.A., Poirier M.A. Protein aggregation and neurodegenerative disease. Nat. Med. 2004;10:S10–S17. doi: 10.1038/nm1066. [DOI] [PubMed] [Google Scholar]
- 4.Chen S.M., Berthelier V., Hamilton J.B., O'Nuallain B., Wetzel R. Amyloid-like features of polyglutamine aggregates and their assembly kinetics. Biochemistry. 2002;41:7391–7399. doi: 10.1021/bi011772q. [DOI] [PubMed] [Google Scholar]
- 5.Perutz M.F., Finch J.T., Berriman J., Lesk A. Amyloid fibers are water-filled nanotubes. Proc. Natl. Acad. Sci. USA. 2002;99:5591–5595. doi: 10.1073/pnas.042681399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sikorski P., Atkins E. New model for crystalline polyglutamine assemblies and their connection with amyloid fibrils. Biomacromolecules. 2005;6:425–432. doi: 10.1021/bm0494388. [DOI] [PubMed] [Google Scholar]
- 7.Chen S., Berthelier V., Yang W., Wetzel R. Polyglutamine aggregation behavior in vitro supports a recruitment mechanism of cytotoxicity. J. Mol. Biol. 2001;311:173–182. doi: 10.1006/jmbi.2001.4850. [DOI] [PubMed] [Google Scholar]
- 8.Masino L., Kelly G., Leonard K., Trottier Y., Pastore A. Solution structure of polyglutamine tracts in GST-polyglutamine fusion proteins. FEBS Lett. 2002;513:267–272. doi: 10.1016/s0014-5793(02)02335-9. [DOI] [PubMed] [Google Scholar]
- 9.Crick S.L., Jayaraman M., Frieden C., Wetzel R., Pappu R.V. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vitalis A., Wang X., Pappu R.V. Quantitative characterization of intrinsic disorder in polyglutamine: insights from analysis based on polymer theories. Biophys. J. 2007;93:1923–1937. doi: 10.1529/biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen S.M., Ferrone F.A., Wetzel R. Huntington's disease age-of-onset linked to polyglutamine aggregation nucleation. Proc. Natl. Acad. Sci. USA. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vitalis A., Wang X., Pappu R.V. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J. Mol. Biol. 2008;384:279–297. doi: 10.1016/j.jmb.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vitalis A., Pappu R.V. ABSINTH: a new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009;30:673–700. doi: 10.1002/jcc.21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bhattacharya A.M., Thakur A.K., Wetzel R. Polyglutamine aggregation nucleation: Thermodynamics of a highly unfavorable protein folding reaction. Proc. Natl. Acad. Sci. USA. 2005;102:15400–15405. doi: 10.1073/pnas.0501651102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Engh R.A., Huber R. Accurate bond and angle parameters for x-ray protein-structure refinement. Acta Crystallogr. A. 1991;47:392–400. [Google Scholar]
- 16.Kaminski G.A., Friesner R.A., Tirado-Rives J., Jorgensen W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 17.Still W.C., Tempczyk A., Hawley R.C., Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- 18.Gallicchio E., Levy R.M. AGBNP: an analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 19.Feig M., Im W., Brooks C.L. Implicit solvation based on generalized Born theory in different dielectric environments. J. Chem. Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 20.Lazaridis T., Karplus M. Effective energy function for proteins in solution. Proteins Struct. Funct. Genet. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 21.Kumar S., Rosenberg J.M., Bouzida D., Swendsen R.H., Kollman P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 22.Roux B. Calculation of the potential of mean force using computer simulations. Comput. Phys. Commun. 1995;91:275–282. [Google Scholar]
- 23.Hobohm U., Scharf M., Schneider R., Sander S. Selection of a representative set of structures from the Brookhaven Protein Data Bank. Protein Sci. 1992;1:409–417. doi: 10.1002/pro.5560010313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kabsch W., Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 25.Sugita Y., Kitao A., Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 2000;113:6042–6051. [Google Scholar]
- 26.Camacho C.J., Thirumalai D. Minimum energy compact structures of random sequences of heteropolymers. Phys. Rev. Lett. 1993;71:2505–2508. doi: 10.1103/PhysRevLett.71.2505. [DOI] [PubMed] [Google Scholar]
- 27.Milchev A., Paul W., Binder K. Off-lattice Monte Carlo simulation of dilute and concentrated polymer solutions under theta conditions. J. Chem. Phys. 1993;99:4786–4798. [Google Scholar]
- 28.Marchut A.J., Hall C.K. Effects of chain length on the aggregation of model polyglutamine peptides: molecular dynamics simulations. Proteins Struct. Funct. Bioinform. 2007;66:96–109. doi: 10.1002/prot.21132. [DOI] [PubMed] [Google Scholar]
- 29.Barton S., Jacak R., Khare S.D., Ding F., Dokholyan N.V. The length dependence of the polyQ-mediated protein aggregation. J. Biol. Chem. 2007;282:25487–25492. doi: 10.1074/jbc.M701600200. [DOI] [PubMed] [Google Scholar]
- 30.Lee C.C., Walters R.H., Murphy R.M. Reconsidering the mechanism of polyglutamine peptide aggregation. Biochemistry. 2007;46:12810–12820. doi: 10.1021/bi700806c. [DOI] [PubMed] [Google Scholar]
- 31.Krishnan R., Lindquist S.L. Structural insights into a yeast prion illuminate nucleation and strain diversity. Nature. 2005;435:765–772. doi: 10.1038/nature03679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lomakin A., Asherie N., Benedek G.B. Liquid-solid transition in nuclei of protein crystals. Proc. Natl. Acad. Sci. USA. 2003;100:10254–10257. doi: 10.1073/pnas.1334069100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pappu R.V., Wang X., Vitalis A., Crick S.L. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch. Biochem. Biophys. 2008;469:132–141. doi: 10.1016/j.abb.2007.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bitan G., Kirkitadze M.D., Lomakin A., Vollers S.S., Benedek G.B. Amyloid β-protein (Aβ) assembly: Aβ40 and Aβ42 oligomerize through distinct pathways. Proc. Natl. Acad. Sci. USA. 2003;100:330–335. doi: 10.1073/pnas.222681699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Humphrey W., Dalke A., Schulten K. VMD—visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


