Abstract
Existence and stability criteria for harmonic locking modes were derived for two reciprocally pulse coupled oscillators based on their first and second order phase resetting curves. Our theoretical methods are general in the sense that no assumptions about the strength of coupling, type of synaptic coupling, and model are made. These methods were then tested using two reciprocally inhibitory Wang and Buzsáki model neurons. The existence of bands of 2:1, 3:1, 4:1, and 5:1 phase locking in the relative frequency parameter space was predicted correctly, as was the phase of the slow neuron's spike within the cycle of the fast neuron in which it occurred. For weak coupling the bands are very narrow, but strong coupling broadens the bands. The predictions of the pulse coupled method agreed with weak coupling methods in the weak coupling regime, but extended predictability into the strong coupling regime. We show that our prediction method generalizes to pairs of neural oscillators coupled through excitatory synapses, and to networks of multiple oscillatory neurons. The main limitation of the method is the central assumption that the effect of each input dies out before the next input is received.
Introduction
In harmonic N:1 phase locking the faster oscillator exhibits an integer number (N) of oscillation cycles for every cycle of the slower oscillator. Harmonic locking, which is frequently referred to as cross-frequency synchronization, occurs in many biological systems, including harmonic phase locking between cardiovascular rhythms, breathing, blood pressure, and other rhythmic activity (1–4). For example, harmonic synchronization occurs between respiration and heartbeat (4). In the absence of temporal cues, human subjects can develop a 2:1 rhythm between their body temperature and the sleep-wake cycle (5). In this study, we focus on locking between pulse-coupled oscillators with neural applications: coupling between neural oscillators interacting through chemical synapses whose postsynaptic effects decay rapidly compared with the cycle period of the fastest oscillator can be approximated as pulsatile (6–8). Cross-frequency synchronization between different bands of brain rhythms has recently been hypothesized to be a substrate for several cognitive functions. For example, locking between theta and delta (3:1) and alpha and delta (4:1) rhythms has been proposed as a neural mechanism for the orienting response (9). Synchronization between theta and gamma has been suggested to match the information stored in working memory with incoming sensory information (10). Finally, synchronization between alpha and theta has been suggested as a mechanism for retrieving items from long-term memory and loading them in working memory (11). In this study, we apply phase resetting methods to gain insight into N:1 lockings.
A phase resetting curve (PRC) tabulates the effect of a perturbation on an oscillator as a function of the phase at which the perturbation is applied. Only the effect on cycle length is considered. PRCs are generated in the open loop condition; that is, a perturbation is applied to an isolated oscillator. Several studies (7,12–15) used open loop PRCs to predict network activity once the loop is closed and all connections in the network are active. To use PRCs for this purpose, the perturbation used in the open loop should resemble the perturbation(s) that will be received in the closed loop circuit, which in the examples in this study is a spike in the presynaptic neuron. The assumptions are then made that closing the circuit does not substantially alter the perturbation, and that the individual neurons remain oscillatory in the network; that is, they do not get stuck at a fixed point. The final assumption required is that the oscillator returns to the limit cycle between inputs because the phase resetting curve only applies to trajectories on the original limit cycle. In other words, the effect of one input must die out before the next one is received.
In this study, we focus on N:1 phase locked modes in which a fast oscillator receives an input every Nth cycle from a slow oscillator at a constant phase within that Nth cycle. Previous studies of phase-locking in mutually coupled oscillators (16) assumed weak coupling in that the phase resetting due to a perturbation of a given waveform can be characterized by the convolution of that waveform with the resetting due to an infinitesimal perturbation under an assumption of linearity, but here we dispense with that assumption. First we formulate existence and stability criteria based solely on the PRCs under the above assumptions, then we use a system of two reciprocally coupled Wang and Buzsáki model neurons to test the hypothesis that all information required to predict N:1 locking is contained in the PRCs.
Methods
Simulations
The prediction methods were tested in a network of two Wang and Buzsáki neurons coupled via inhibitory synapses (17). This single compartment model was developed originally to represent the intrinsic properties of a hippocampal interneuron. For each neuron the state variables change according to the following equations:
where Vi is the membrane potential (in mV), hi is the inactivation variable for the sodium current and ni is the activation variable for the potassium current with the subscript i indicating either the faster (F) or slower (S) neuron. The steady state activation for the sodium current is described by
The kinetics for sodium channel inactivation and potassium channel activation are given by the following rate equations:
We used the following parameter values. The conductances for the sodium, potassium and leak channels are gNa = 35 mS/cm2, gK = 9 mS/cm2, and gL = 0.1 mS/cm2 and the reversal potentials are ENa = 55 mV, EK = −90 mV, and EL = −65 mV. The dimensionless scale factor ϕ was set to 5 and the membrane capacitance C was 1 μF/cm2. The synaptic current is given by Isyn,i = gsyn si (Vi − Esyn) where gsyn is the synaptic conductance and Esyn is the reversal potential. For inhibitory synapses, Esyn = −75 mV. The reciprocal synaptic coupling has a rise time and decay time that can be controlled separately as in (15,18). The synapses are regulated by the following equations:
where Vj is the membrane potential for the cell presynaptic to cell i (j ≠ i). Heterogeneity in frequency can be obtained by using different applied currents for each neuron so that Iapp,i ≠ Iapp,j. The parameter ɛ is defined such that the faster neuron has Iapp,i = Iapp + ɛ and the slower has Iapp,i = Iapp − ɛ. Simulation of the Wang and Buzsáki model was implemented in C code and integrated with a variable step size implicit fifth order Runge Kutta method. An exhaustive search of the state space of initial conditions was not carried out, but when modes were predicted but not observed, the predictions were used to estimate initial conditions likely to lead to the predicted mode. Initial conditions between the predictions and the differential equations could be compared by selecting initial conditions along the unperturbed limit cycle at a given phase.
PRC generation
PRCs were generated as in Fig. 1 A using the change in postsynaptic conductance (lower trace) generated by an action potential in the presynaptic neuron as the perturbation. This perturbation best approximates the input received by the neuron in the network. The perturbation is applied at time ts after a spike is initiated in the postsynaptic neuron. The phase (ϕ) is defined as ts/P0, where P0 is the intrinsic period. As in previous studies (7), a phase of zero was assigned to spike initiation defined as the upward crossing of −14 mV by the membrane potential. This threshold was chosen because the activation of the postsynaptic conductance began to be observable at this presynaptic voltage. The presynaptic model neuron is initialized at its spiking threshold, then the unidirectional coupling is turned on for a single cycle of the presynaptic neuron at different phases in the cycle of the postsynaptic model neuron. This type of open loop PRC is often called a spike time response curve (19). The phase resetting is defined as fk(ϕ) = (Pk − P0)/P0, where k denotes the order of the PRC. If a cycle is defined at the elapsed time between spikes, first order resetting tabulates the change in the cycle length containing the perturbation onset, and the second order resetting tabulates the change in the length of the next cycle. Perturbations delivered immediately before the end of a cycle may span two cycles. It is important to consider second order resetting if the perturbation spans two cycles or if the trajectory has simply not yet relaxed to the limit cycle before the next spike emitted after the perturbation. Under this convention, a decrease in cycle length produces negative resetting called an advance, whereas an increase in cycle length produces positive resetting called a delay. Biologists generally use the sign convention that we chose for this study, whereas mathematicians usually use the opposite sign convention (20).
Figure 1.
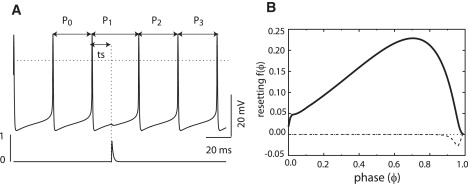
(A) PRC generation. The top trace shows the membrane potential during PRC generation. The horizontal dotted line indicates zero mV. The parameters were as in the Methods section except that Iapp = 0.5 μA/cm2 for both neurons and gsyn = 0.15 mS/cm2. The lower trace shows the perturbation in the dimensionless activation variable (s) for the synaptic conductance applied at a phase of ϕ = 0.5. The intrinsic period is P0, the cycle containing the perturbation is P1, and subsequent cycles are numbered sequentially. The stimulus time, ts, is the time between the previous spike and stimulus onset. (B) Typical phase resetting curve. The first order resetting is the solid line and the second order resetting is the dashed line. Third order resetting was not visible on this scale and is therefore negligible. The same parameters as in A were used.
Fig. 1 B illustrates the first (solid line) and second (dashed line) order PRC computed for a model neuron in the open loop configuration. The third order resetting is not used or shown because it is negligible, as it must be to satisfy the assumption that the effect of one perturbation dies out before the next one is received. The PRC was generated by tabulating the effects of a perturbation applied at 100 evenly spaced points during the cycle of a spontaneous limit cycle oscillator on the length of the cycle as a function of the phase (ϕ) at which the perturbation is applied.
Weak coupling methods
In this section, we present the well-established and widely used weak coupling methods (21–23) for studying phase oscillators for comparison with the pulsatile coupling methods explained in the Results section. Previously, Ermentrout (16) derived existence and stability conditions for N:M phase locked modes in the weak coupling limit. We repeat them here for N:1 lockings only. The assumptions underlying weak coupling are that the perturbations are small enough so that the effects of consecutive or superimposed perturbations add linearly, and that the relative phase of the oscillators varies slowly compared to the rate that they travel around their respective limit cycles (the rate that absolute phase varies). The difference between our methods and preexisting weak coupling methods is that we do not require these assumptions. Instead, we require only a return to the limit cycle between inputs. The key idea for the previous, existing weak coupling methods is that if you have a limit cycle oscillator, it can be described in terms of a single variable, its phase. For weak coupling, a system of two limit cycle oscillators can be further reduced to only account for the relative phase between the oscillators. Thus in the regime where a stable limit cycle oscillation exists, the differential equations for Wang and Buzsaki model neurons used in this study can be simplified in principle to a single variable each, the rates of change of the absolute phases
where ωF and ωS are the intrinsic frequencies of the fast and slow oscillators respectively and Hi indicates the coupling function determined as described below. The infinitesimal PRC for each oscillator (or the adjoint z(ϕi) (3)) is the phase resetting curve in the limit as perturbation in current i(ϕi,ϕj). The infinitesimal PRC can also be defined as the phase resetting in these systems normalized by the area under the perturbation as the strength and duration of the perturbation go to zero. If the intrinsic periods of the neurons are PF and PS, respectively, then the total phase resetting due to the perturbation i(ϕi,ϕj) is termed the coupling function Hi, which can be computed by convolving the coupling current waveform i(ϕi, ϕj) = gsyn s(ϕi) {V(ϕj) −Esyn} with the infinitesimal PRC, z(θj), over one complete cycle T of the uncoupled network where T = N PF = PS.
For weak coupling, the changes in the period represented by the total resetting approximate the change in frequency. The coupling functions HF, HS are periodic with period T. The iPRCs were calculated by the adjoint method (21,23) using XPPAUT (22).The coupling functions are given in terms of the relative phase ψ = ϕS − (1/N) ϕF for two neural oscillators with an intrinsic frequency ratio of N:1. Both phase and relative phase are defined modulo 1. For the coupled system, the ratio of intrinsic frequencies is no longer an exact integer because the coupling slightly changes the frequencies and the exact integral ratio applies in the N:1 coupled system. The differential equation describing the rate of change of the relative phase in the coupled system is
where the term ΔωF represents the deviation in intrinsic frequency in the fast neuron required to achieve a locking in the coupled network. The main idea with respect to finding N:1 lockings is that the ratio ωF/ωS is initially assumed to be N:1. Because the coupling functions are defined over N cycles of the fast neuron but only one cycle of the slow neuron, if HS (−ψ) = HF (ψ) then the effect of the coupling on the frequency of the slow neuron is exactly 1/N of that on the fast neuron, so an N:1 locking can be established. The locking points at which HS (−ψ) = HF (ψ) can be determined by examining the zero crossings of the function describing their difference K(ψ) = HS (−ψ) − HF (ψ). More generally, the range of frequencies of the fast neuron, ωF + ΔωF, that support a locking can be determined by determining the values of ΔωF (positive and negative) that produce a zero crossing of the function Q(ψ) = ΔωF + HS (−ψ) − HF (ψ). This gives the range of intrinsic frequencies of the fast neuron that produce an N:1 locking at a given intrinsic frequency for the slow neuron ωS.
Fig. 2 illustrates the weak coupling method with an example. The two neurons were chosen to have as close to an exact 2:1 ratio of the intrinsic frequencies as possible. This was achieved using Iapp,F = 1.842 μA/cm2 and Iapp,S = 0.77 μA/cm2. The coupling was weak with gsyn = 0.01 mS/cm2. All traces for the slower neuron are indicated by dashed lines and for the faster neuron by solid lines. Fig. 2 A displays the voltage V(ϕj) and Fig. 2 B the synaptic activation s(ϕi) traces for the two uncoupled Wang and Buzsáki oscillators. The slower neuron receives two synaptic inputs as the faster neuron spikes twice during the cycle of the slow neuron. Fig. 2 C shows the adjoint z(ϕi) for each oscillator computed for the longer period, then normalized to a period of length 1. The coupling functions shown in Fig. 2 D are computed by convolving the coupling current waveform (not shown) with the infinitesimal PRC over two cycles of the fast neuron (which is equal to one cycle of the slow neuron). The iPRCs were approximated by the adjoint method (21,23) using XPPAUT (22). To get a 2:1 locking for the coupled system, the frequency of the faster neuron over two of its cycles must be changed by the same amount as frequency of the slower neuron over a single one of its cycles to preserve the 2:1 ratio. There are no zero crossings of the function K(ϕS − ϕF/2) = HS(−(ϕS − ϕF/2)) − HF(ϕS − ϕF/2) (Fig. 3, solid curve) indicating that no 2:1 locking will be exhibited by the coupled network. To bring the frequency ratio back to an exact integer ratio, the frequency of one oscillator (in this case the faster oscillator) must be adjusted by Δω as determined by finding the values that allow the following function, Q(ψ) = ΔωF + HS (−ψ) − HF (ψ), (Fig. 3, dashed curves) to cross the x axis. The additional applied current Iadded,f that is required to change the frequency of the fast neuron can be determined by analytically using weak coupling to solve for the magnitude of square pulse of constant current that produces the correct change in frequency when convolved with the iPRC or adjoint z(ϕi) (). The sign convention is such that downward crossings are stable but upward ones are not. Details about how XPPAUT was used to compute the coupling functions can be found in the Supporting Material.
Figure 2.
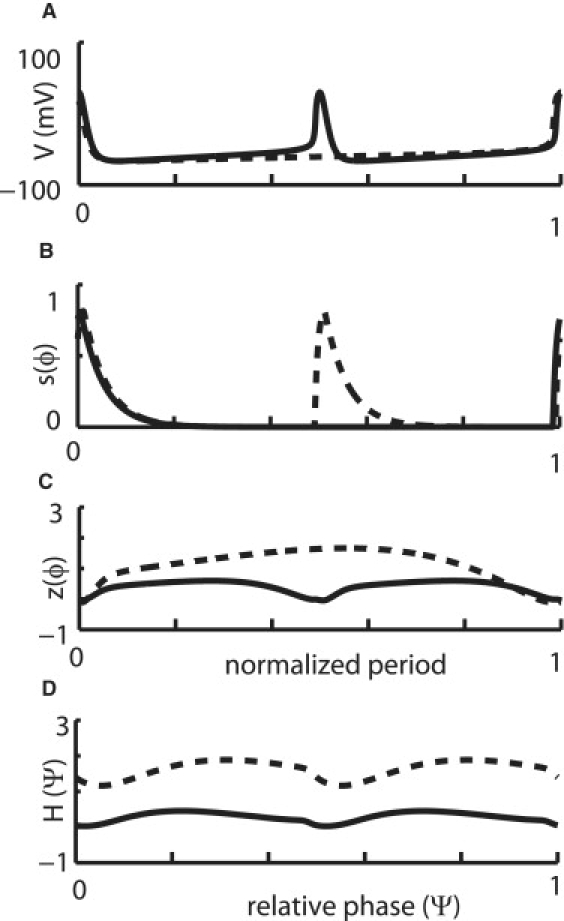
Illustration of averaged weak coupling. Iapp,F = 1.842 μA/cm2 for the fast (F) neuron (solid line) and Iapp,S = 0.77 μA/cm2 for the slow (S) neuron (dashed line). These parameter values are for two oscillators where neuron S has a free running period which is double the period of neuron F. (A) The free-running membrane potential waveforms for the fast (solid line) neuron and the slow (dashed line) neuron. This potential was used in two ways: first to obtain the postsynaptic voltage V(ϕj) to calculate the postsynaptic current i(ϕi, ϕj) = gsyns(ϕi) {V(ϕj) − Esyn} and second to calculate the presynaptic voltage V(ϕi) to drive the presynaptic activation s(ϕi). (B) The presynaptic activation calculated as described in A. Notice that the solid black trace in A drives the dotted trace in B and vice versa. (C) The adjoint (iPRC) is computed for each neuron. (D) The coupling functions computed using the averaging method for weakly coupled oscillators for each neuron are shown here. This is the only step in which the value of gsyn is taken into account. The perturbations in the synaptic current are convolved with the iPRC over the network period to calculate these functions. They were numerically calculated using XPPAUT.
Figure 3.
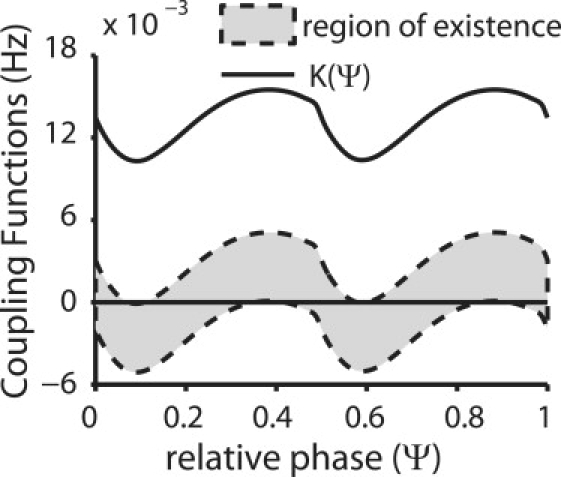
Mode prediction for weak averaged coupling. The solid black curve is the effective coupling function K(ϕ) for the system composed of the two neurons from Fig. 3 whose intrinsic periods have a ratio of exactly 2:1 for weak coupling with gsyn = 0.01 mS/cm2. The lack of zero crossing shows that they cannot lock unless the intrinsic frequency of one neuron is modified. The dashed curves are the coupling function Q(ϕ) computed with additional current to the fast neuron to change its intrinsic frequency sufficiently to enable a locking. The range of current added to the fast neuron (−0.026 μA/cm2 for the top dashed curve and −0.0385 μA/cm2 for the lower dashed curve) that enables these curves to have a zero crossing of the x axis determines the lower and upper limits of the intrinsic frequency of the fast neuron that allow a locking. The region inside the dashed curves is the existence region for this weak coupling strength. The upward zero crossings indicate the phases (separated by ∼0.5) at which the slow neuron receives an input from the fast neuron in a stable 2:1 locking for the coupled system.
Results
We develop a novel method for predicting and understanding N:1 phase locking in two neuron networks in terms of the phase response curve generated for each neuron using a perturbation similar to the input that will be received in the network. We test these methods extensively in model neurons for both inhibition and excitation, and extend the analysis to locking between populations of neurons. These results generalize to any system of pulse-coupled oscillators, not just neurons.
Existence and stability criteria for N:1 locking based on PRCs
In Fig. 4 A we define the firing intervals in an N:1 locking in a very general way, indexed by the cycle number m. The ellipsis indicate the appropriate number of spikes in the faster neuron (F) to produce an N:1 locking. The stimulus interval (tsF) is defined as the time elapsed between the most recent spike in the faster neuron and the time at which it receives the input from the slower neuron. The phase at which the faster neuron receives this input is denoted ϕF. The first recovery interval (trF1) for the fast neuron is the time elapsed between when the input is received and when the fast neuron next fires. The second recovery interval (trF2) consists of the remaining (N-1) cycles of the fast neuron. The recovery interval (trS) for the slow neuron (S) is defined as the interval between when the slow neuron receives the last (Nth) input in a given slow neuron cycle and when the slow neuron fires next. The first stimulus interval (tsS1) is defined as the time elapsed between when the slower neuron fires and when it receives the first input from the faster neuron at a phase of ϕS1. The second stimulus interval (tsS2) begins with the arrival of the first input and terminates with the Nth input received at a phase of ϕSN. By definition the following equalities must be satisfied in any N:1 phase locked mode: tsF [m] = trS [m], trF1 [m + 1] = tsS1 [m + 1], and trF2 [m + 1] = tsS2 [m + 1], hence they constitute the periodicity, or existence criteria.
Figure 4.
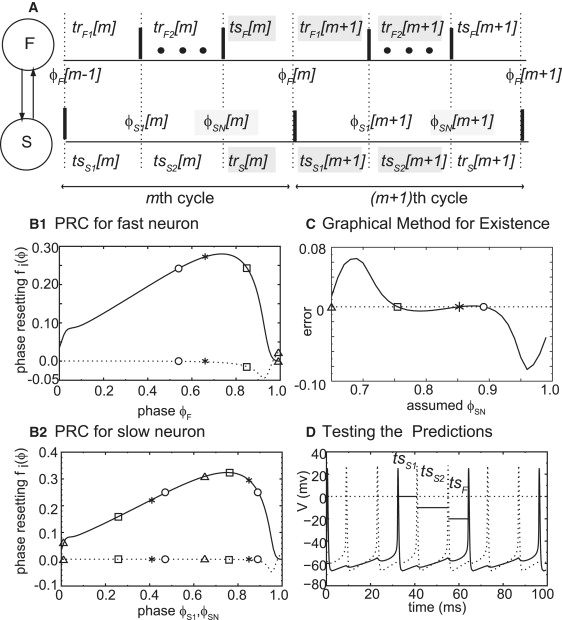
Mode prediction for pulsatile coupling. (A) Assumed firing pattern for N:1 locking. The faster neuron (F) fires N times for each time that the slower neuron (S) fires. Firing times are indicated by thick vertical bars. The input phases ϕ are defined on the upper and lower traces for dotted lines corresponding to a vertical bar on the partner trace indicating the time of a spike in the partner. Only the first and last spikes of the fast neuron within each cycle of the slow neuron are shown, the remaining spikes are indicated by the dots. The stimulus (ts) and recovery (tr) intervals are the time elapsed between vertical dotted lines. Both phases and intervals are subscripted by the neuron and indexed by the cycle. The second subscript on the phases of the slow neuron indicates the jth input during the current cycle of the slow neuron (cycles m and m+ 1 are shown). The intervals highlighted in gray are defined in the text and used to construct a discrete map from ϕSN[m] to ϕSN[m + 1], the phases highlighted in gray. (B–D) show an example prediction for 2:1 modes at Esyn = 0.75 mV, gsyn = 0.25 mS/cm2, Iapp = 1.0 μA/cm2, and ɛ = 0.241 μA/cm2. (B) PRCs for the faster neuron (B1) and the slower neuron (B2). The phases for four modes identified in C are shown. The open symbols correspond to unstable modes in C and the asterisks to stable modes. (C) Graphical method for existence. The error is the difference between assumed and predicted values of ϕSN and is plotted as a function of the assumed ϕSN. The open circles indicate unstable fixed points and the asterisk indicates a stable fixed point. (D) Testing the predictions. The full set of differential equations for two coupled neurons was integrated and produced a 2:1 mode with the membrane potential for the fast neuron (dotted curves) and slow neuron (solid curves) exhibiting the predicted intervals (labeled horizontal bars). Technical note: The open triangle in C is not exactly a zero crossing, but rather was detected by checking for a change in the sign of the error between the leftmost point on the error curve and the rightmost point on the error curve. The leftmost point corresponds to a ϕS1 > 0 and the rightmost to a ϕSN < 1, so any near synchronous solution must lie between these two points and the algorithm declares synchronous solution to be at the endpoint with the least error.
The central idea of this study is to use the phase resetting curves for the fast and slow neurons to predict which parameter values will give rise to N:1 lockings, and to predict the phasic relationships between the neurons during the lockings. This can be accomplished under the assumption of pulsatile coupling. If the phase resetting due to each input is assumed to be complete before the next input is received, then the PRCs can be used to update the phase when an input is received. This affects the phase at which subsequent inputs are received, and ultimately determines when each neuron will fire next. To be consistent with the assumption of pulsatile coupling, only the first order resetting for each input is considered unless the input is the last one received by a given neuron in a cycle. For the last input only, the second order resetting is added to the first stimulus interval in each neuron. In terms of the phase, each neuron reaches firing threshold when its phase reaches a value of 1, at which time its own phase is reset to 0 and the phase of its partner is updated by the appropriate amount of resetting. Under this assumption, each interval can be written in terms of the phases at which inputs are received (described below). The resetting at each phase is given by fiF where the first subscript indicates the order of the resetting and the second subscript denotes the neuron.
We will define the gray highlighted intervals in Fig. 4 A in terms of the phases. In this study, we use (…) to enclose the argument of a function, {…} to delimit quantities being multiplied, and […] for indices of a map. The stimulus interval for the fast neuron is the intrinsic period of the fast neuron (PF) times the phase at which the input is received (tsF[m] = PF ϕF[m]). The first recovery interval for the fast neuron is the first order phase resetting f1F(ϕF) plus the fraction (1 − ϕF) of the cycle that remains to be traversed at the time the input is received (trF1[m + 1] = PF {1 − ϕF [m] + f1F(ϕF[m])}). The second recovery interval for the fast neuron includes N-1 fast cycles plus the second order resetting due to the input received at ϕF [m], so trF2 [m + 1] = PF {N −1 + f2F (ϕF[m])}. The recovery interval in the slow neuron can be determined in the same way as the first recovery interval for the fast neuron (trS [m] = PS {1 − ϕSN [m] + f1S(ϕSN [m])}). The first stimulus interval for the slow neuron includes the second order resetting from the most recent input (tsS1 [m + 1] = PS {ϕS1 [m + 1] + f2S(ϕSN [m])}). The second stimulus interval in the slow neuron is the most difficult to calculate because it requires the knowledge of N phases ϕS1 through ϕSN associated with each of the N inputs received per cycle of the slow neuron. This interval is equal to the intrinsic period times the difference in phase between the last and first inputs plus the first order resetting due to the first N-1 inputs: . Taking advantage of the fact that the interval between successive inputs is equal to the intrinsic period of the fast neuron, each ϕSj [m + 1] can be iteratively calculated from the previous one. The first interval contains second order resetting from the sole input to the fast neuron, so the phase ϕS2 [m + 1] can be calculated from ϕS2 [m + 1] = ϕS1 [m + 1] − f1S(ϕS1[m + 1]) + PF/PS{1 + f2F(ϕF [m])} and subsequent ones as ϕSj[m + 1] = ϕS,j-1[m + 1] − f1S(ϕS1[m + 1]) + PF/PS. Using the description for each interval as described above, substituting the definition for each interval into the equalities, and rearranging we obtain the following equations:
| (1) |
| (2) |
| (3) |
In a steady N:1 locking, the stimulus and recovery intervals and all of the phases at which inputs are received do not change from cycle to cycle, and an asterisk is used instead to denote the N + 1 phases {ϕF∗,ϕS1∗…ϕSN∗} that constitute a fixed point of the map given in Eqs. 1–3. This fixed point corresponds to a periodic mode for the system of coupled neurons. We use the stability of the fixed point of the map to predict the stability of the periodic mode in the system of coupled neurons. The stability of the fixed points of the map was determined as follows. Assuming that the phases ϕij[m] (with index i indicating the neuron, F or S) converge to their steady state values ϕij as m → ∞, we look at a perturbation from steady state on each cycle m as ϕij[m] = ϕij∗ + Δϕij[m]. We linearize the PRCs about the steady state solution such that fki (ϕij [m]) = fki (ϕij∗) + fki′ (ϕij∗) Δϕij[m]. The full derivation is given in the Supporting Material, but the final result is that the linearized map can be rewritten in terms of a single perturbation variable ΔϕSN[m + 1] = λ ΔϕSN[m] where λ is the single eigenvalue and can be expressed in terms of the slopes of the appropriate PRCs. The perturbation is of the phase highlighted in blue in Fig. 4 A. The following eigenvalue λ must have an absolute value <1 for stability because the perturbation ΔϕSN[m] from the fixed point will then decay to zero:
| (4) |
To evaluate the above expression, we must first find the fixed points by finding the set of phases that satisfy the periodicity (existence) criteria in Eqs. 1–3. These were determined numerically as follows. If we assume a value of ϕSN, we can write down the equations for the other phases as follows, dropping the cycle indices because we are assuming steady state. Equation 1 can be rewritten in such a way that it gives a value for ϕF∗ in terms of an assumed ϕSN:
| (5) |
Equation 2 can be rewritten in such a way that it gives a value for ϕS1 in terms of ϕ∗F and the assumed ϕSN:
| (6) |
Equation 3 can be rewritten in such a way that it calculates ϕSN∗ from ϕS1∗ by calculating all the intervening values of ϕSj∗:
| (7) |
| (8) |
The zero crossings of the difference between the calculated value ϕSN∗ and the assumed value ϕSN correspond to the N:1 lockings that can exist because they satisfy the periodicity criteria. We illustrate this method with an example in Fig. 4, B–D. The first and second order PRCs for the fast and slow neurons respectively are shown in Fig. 4, B1 and B2. These PRCs were used to generate the error function (Fig. 4 C) for N = 2 (a different error function is generated for each N). The error function starts at ϕSN = 0.65 because it does not exist for all values of the assumed ϕSN. Only values that produced ϕS1 and ϕF between zero and one have their phase resetting defined and can be used to calculate ϕSN∗, otherwise they are ignored. There are four zero crossings in Fig. 4 C, corresponding to the four values of ϕSN∗ {0.65, 0.76, 0.85, and 0.89} in each of four possible 2:1 locking patterns between the fast and slow neurons. The same symbols were used to indicate the value of ϕF∗ on the fast neuron PRC in Fig. 4 B1 corresponding to each value of ϕSN∗ in Fig. 4 C, and to indicate the values of ϕS1∗ and ϕSN∗on the slow neuron PRC in Fig. 4 B2, where each ϕS1∗ < ϕSN∗. This was done to emphasize that the values of the PRC are required to compute the zero crossing in Fig. 4 C and the slopes are required to calculate stability per the eigenvalue given in Eq. 4. Only one mode is indicated by an asterisk because it was the only mode that was stable. The eigenvalue λ corresponding to the four values of ϕSN∗ are {−1.97, 1.40, 0.93, 1.22} respectively, so only the value for ϕSN∗ = 0.85 has an absolute value of <1 and is stable. The differential equations for fast and slow neurons coupled by reciprocal inhibition using the parameters used to generate the open loop PRCs in Fig. 4, B1 and B2, were integrated in a closed loop network, the predicted mode was indeed observed as indicated in Fig. 4 D. The stimulus intervals as defined above were calculated using the predicted steady state phases, and are indicated in Fig. 4 D. They correctly predict the actual stimulus intervals observed in the closed loop network simulations, using only the information contained in the open loop PRC.
Inhibitory lockings as conductance and heterogeneity are varied
To more rigorously test the existence and stability criteria that we developed, we ran parameter sweeps in a model system of two mutually inhibitory Wang and Buzsáki neurons. The intrinsic frequency of the model neuron increases with applied current, and the applied current to the faster neuron was (Iapp + ɛ) whereas that to the slower neuron was (Iapp − ɛ). First we explored a two-dimensional parameter space (Fig. 5) in which the x axis was the synaptic conductance, and the y axis was the spread in applied current indicated by ɛ. The heterogeneity variable, ɛ, was incremented in steps of 0.001 μA/cm2 and the synaptic conductance was incremented in steps of 0.01 mS/cm2. The red circles in Fig. 5 A indicate the parameter values that were predicted–using only the information from the PRCs–to support a stable 2:1 locking. Green indicates 3:1, blue indicates 4:1, and magenta indicates 5:1. Predictions were made as described in the previous section. If |λ| < 1, then the mode was predicted to be stable and indicated in Fig. 5 A. Fig. 5 B shows the parameter values in the full system of differential equations that supported the same phase locked modes indicated by the same colored symbols. The correspondence is qualitatively reasonable, although as the conductance strength is increased there are some discrepancies at the borders of stability and existence. These problems are exacerbated when the locking region is narrow as in some parts of Fig. 5 and not noticeable when the locking region is wide.
Figure 5.
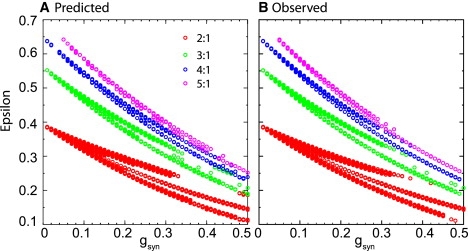
Qualitative comparison of predicted and observed modes for pulsatile coupling method as heterogeneity and conductance strength are varied. (A) The predictions were generated using the methodology described in Fig. 4. The circles indicate stable predicted modes at each locking ratio. (B) The observations were generated by numerically solving the full system of differential equations that describe the two coupled Wang and Buzsáki neurons. Iapp was held constant at 1 μA/cm2 as ɛ and gsyn were varied, and other parameters were as in the Methods.
At lower conductance values, there is a continuous transition as ɛ is varied between firing patterns in which the fast neuron leads the slow neuron spike, and patterns in which the slow neuron leads, but due to the steep region of initial slope in the Wang and Buszáki model PRC with inhibition, at stronger conductance values these bands separate and gaps appear in which complex firing patterns emerge in which the order often switches. This poses a challenge to our method that does not occur for more typical PRCs. At gsyn = 0.15 mS/cm2 in Fig. 5 A, the red band indicating 2:1 coupling splits into three bands. The upper and lower bands predict a 2:1 coupling regime in which the spike of the slower neuron is nearly synchronous with one of the faster neuron spikes. The order of the spikes is different in the two bands: in one the faster neuron leads whereas in the other it lags. In Fig. 6 A the upper trace shows the observed 2:1 mode at gsyn = 0.15 in which the slow neuron leads as predicted whereas the lowermost trace (Fig. 6 D) shows the observed mode in which the fast neuron leads. In between the two corresponding red bands complex, higher order locking patterns are observed but not indicated in Fig. 5, including some that exhibit leader switching, or leapfrog mode. The analytical prediction method cannot predict these leapfrog modes, one of which is illustrated in Fig. 6 C, because the firing order does not conform to the pattern assumed in Fig. 4 A, but instead switches on every firing cycle of the slow neuron. The existence of these modes is the result of the very steep initial portion of the first order PRC (Fig. 1 B) that allows leader switching at constant parameter values (24,25). The center band of red dots in Fig. 5, A and B, indicates a mode that is bistable with the higher order locking and can only be reached from a subset of initial conditions. In this mode, the spike of the slower neuron falls approximately midway between the two spikes from the fast neuron, as shown in Fig. 6 B. The predicted mode, in which the slow neuron spike is in near antiphase rather than in near synchrony with the closest fast neuron spike, was not observed initially, because the selected initial conditions led to the complex higher order locking instead. This mode was only observed after the initial conditions were set to values corresponding to points near the limit cycle attractor that map onto the phase determined by the predictions just before the spike in the slow neuron.
Figure 6.
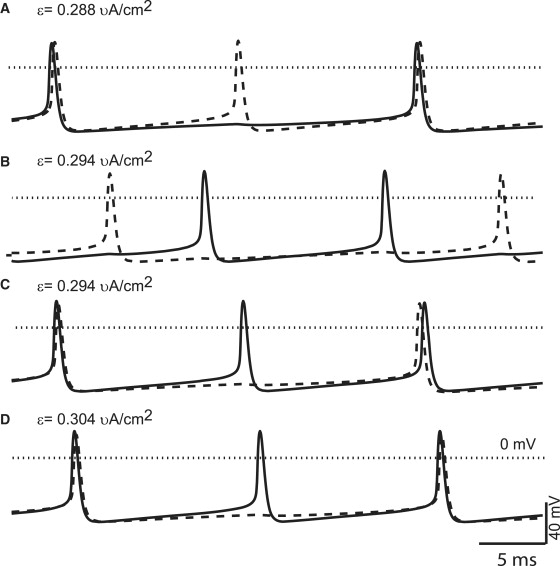
Different phasic relationships observed at 2:1 frequency ratios. (A) Near synchrony; 2:1 locking, near synchrony between the slow (solid line) neuron spike and one of the fast (dashed line) neuron spikes, slow neuron leads. (B) Near antiphase; 2:1 locking, slow neuron fires near the midpoint of two fast spikes in near antiphase. (C) Leapfrog. Complex locking (4:2) in which the firing order of the fast and slow neurons switches each time the slow neuron fires. (D) Near synchrony; 2:1 locking, near synchrony between the slow neuron spike and one of the fast neuron spikes, fast neuron leads. These points were sampled from the points in the previous figure at gsyn = 0.15 mS/cm2.
Fig. 7 A shows the stimulus and response intervals for the predictions and the observations to make a quantitative comparison. The intervals for a single conductance in Fig. 5 are shown as the heterogeneity parameter is varied for the 2:1 mode. As N increases, the likelihood of returning to the limit cycle between inputs decreases and the prediction is expected to deteriorate. There is an excellent match between the predictions (blue circles) and observations (red crosses). There is a dramatic drop in the tsF at ɛ = 0.359 μA/cm2, indicating that the slow neuron leads (long interval tsF between fast neuron firing and that of the slow neuron but short trF1 interval between the firing of the slow neuron and that of the fast neuron) to the left of this point and lags to the right.
Figure 7.
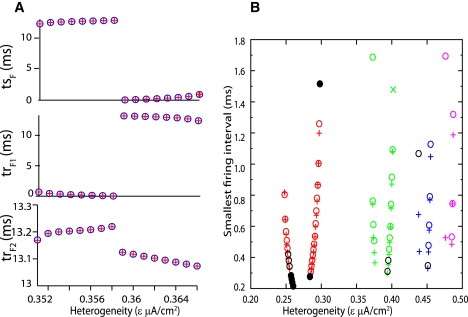
Quantitative comparison of predicted and observed intervals for pulsatile coupling method. (A) The values for the successive intervals tsF, trF1, and trF2 as defined in Fig. 2 are shown for selected parameter values from Fig. 5 (gsyn = 0.15 mS/cm2, Iapp = 1 μA/ cm2). Open circles indicate observations and crosses indicate predictions. (B) The smallest stimulus interval at gsyn = 0.2 mS/cm2 from Fig. 5 is plotted against epsilon. Circles indicate predictions and crosses and the X indicate observed. Colors indicate locking mode as in Fig. 5. Black circles indicate incorrect predictions as described in the text.
The prediction in Fig. 5 is quite good at the values illustrated in Fig. 7 A. However, after the swath of red circles in Fig. 5 indicating 2:1 locking splits into three bands, the uppermost band of red circles (2:1 lockings) in the prediction does not match the observed very well above conductance values of 0.32 mS/cm2. Similarly, the two bands (actually three, but the middle band is sparse) of green circles indicating 3:1 do not match well between predicted and observed above conductance values of 0.25 mS/cm2. The observed tend to follow the lower branch at high conductance values whereas the predicted follow the upper branch. Mismatches between the thin bands representing the 4:1 and 5:1 lockings start at even smaller values of conductances. The method begins to fail at very strong conductance values amid higher order lockings because the error in identifying the modes that exist becomes great enough that the existence criterion fails or is off enough to give incorrect stability results. When the parameter regime that supports locking becomes thin, the entire regime may fall in the boundary region in which errors can occur.
The prediction can fail because the assumptions of pulsatile coupling with the exact same form in the closed loop as the open loop and complete return to the limit cycle between inputs are not satisfied exactly, introducing error especially near the existence and stability boundaries. As the conductance is increased, the slopes of the resetting in some regions near ϕ = 0 and ϕ = 1 are changing more rapidly, thus near synchronous firing of the slow spike and one of the fast spikes the prediction is more sensitive to any small error due to slight deviations from the assumptions or to numeric errors. Fig. 7 B shows the ways in which the method can fail as deviations from perfect pulsatile coupling result in errors. The shortest predicted or observed stimulus interval was plotted versus ɛ at a fixed conductance of gsyn = 0.2 mS/cm2, constituting a vertical line in Fig. 5. In no case was the relative magnitude of the intervals predicted incorrectly, so the smallest interval was plotted as the most sensitive readout of the error. A short interval would cause an input to be received at a very early phase in one neuron and at a very late phase in its partner. The circles indicate predictions and the crosses (and one X) indicate observed modes. Red, green, blue, and magenta correspond to the 2:1, 3:1, 4:1, and 5:1 locking as in Fig. 5. The exception is that the black circles indicate incorrect predictions, and are not color coded by locking mode, although the locking mode is obvious from their location within a colored band. Open black circles indicate a prediction of a mode that was not observed. Either the predicted mode does not in fact exist, or it exists but is unstable. This type of error occurred at the highest and lowest values of the stimulus interval that fell on the boundaries of the locking mode. The solid black circles indicate an incorrect prediction of an unstable mode when a stable mode was actually observed. In some cases (for 2:1 locking) the eigenvalues were very close to 1. In others (4:1 locking mode, ɛ = 0.438–9 μA/cm2) the error in the interval could be relatively large. The largest error in the stimulus interval occurred at a 5:1 locking for an ɛ value of 0.476 μA/cm2 but curiously did not result in a stability error. The X at ɛ = 0.402 μA/cm2 indicates a different type of error; a 4:1 locking mode was observed but was predicted not to exist, a failure of the existence criterion. Sensitivity to error on the borders of existence and stability is not a major failure of the method but rather is to be expected from any mathematical method due to the inevitable inherent approximations.
Ranges of frequencies that support inhibitory lockings at two conductance values
We examined the range of frequencies that support N:1 locking; we parameterized the two heterogeneous neurons by their intrinsic, uncoupled frequencies and illustrated the bands in which locking is enabled. The symbols in Fig. 8 show the parameter values at which N:1 lockings were observed at a relatively strong conductance of gsyn = 0.15 mS/cm2 whereas the solid lines show the narrow regimes in which N:1 locking are observed at the relatively weak conductance of gsyn = 0.01 mS/cm2. The color scheme from Fig. 5 is retained, but the 1:1 lockings are shown for completeness (weak coupling, black line; strong coupling, gray circles). These were calculated using similar methods based on PRCs that have been published elsewhere (7,8). Clearly, stronger coupling broadens the range of ratios of intrinsic frequencies that allow locking because there is a greater range of frequencies for each neuron with greater phase resetting, thus more opportunity to reach an exact locking. The solid lines indicate the regions in which the intrinsic frequency of the fast neuron is essentially an integral multiple of the slow neuron, but the broad bands indicate that for strong coupling an integer ratio of intrinsic frequency is no longer necessary. Not only are the bands broadened, but additional bands such as those for 4:1 (Fig. 8, blue circles) and 5:1 (Fig. 8, magenta circles) lockings appear in this region of parameter space for strong but not weak coupling. The separation of the modes into distinct bands such as those seen in Fig. 5 is also evident here, becoming more prominent at lower frequencies. Initially, a few parameter values that were predicted to support phase locking did not support locking in the observations. This was determined to be a result of bistability. The same initial conditions were used for all simulations, and at some parameter values these led to complex modes. If initial conditions from phase locked modes located nearby in the parameter space were instead used as initial conditions, the predicted modes were observed. In general, one can see from Fig. 8 that the correspondence between predicted and observed was quite reasonable.
Figure 8.
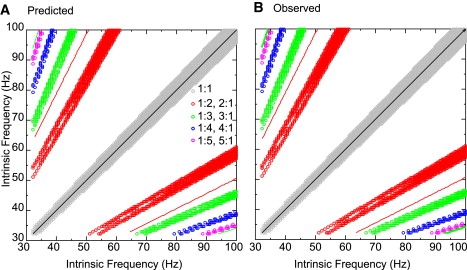
Qualitative comparison of predicted and observed modes for pulsatile coupling method as both intrinsic frequencies are varied. (A) The predictions were generated using the methodology described in Fig. 4. The circles indicate stable predicted modes at each locking ratio. (B) The observations were generated by numerically solving the full system of differential equations that describe the two coupled Wang and Buzsáki neurons. The colors indicate the value of N. The solid lines correspond to the very narrow bands predicted and observed at gsyn = 0.05 mS/cm2 whereas the bands composed of small open circles correspond to the broader bands predicted at gsyn = 0.15 mS/cm2. The stronger inhibitory coupling enabled the observation of 4:1 and 5:1 locking, which were not observed at the weaker coupling strength in the range of intrinsic frequencies shown.
The conductance was increased still further to gsyn = 0.25 mS/cm2 in Fig. 9, and the locking bands became even broader. The gaps between the bands of the same color indicate complex lockings similar to but not exactly N:1. The observations shown in Fig. 9 B are the result of parameter sweeps from two different initial conditions. In one sweep the next spikes of the fast and slow neuron were aligned closely, and in one sweep they were not. Using both sets of initial conditions was necessary to prevent large gaps in the observations (Fig. 9 B) compared to the predictions (Fig. 9 A) due to bistability. Some of the small remaining gaps in the observed versus predicted could likely be resolved by a more exhaustive search of the state space. However, as in the case of Fig. 5, some incorrect predictions were due to errors on the boundary of stability. In some of these cases, rather than predictions that were not observed, modes were observed but not predicted. For example at gsyn = 0.25, there was a very thin band of 3:1 solutions (Fig. 9 B, green open circles) that were often missed because the band was too narrow to be robustly detected in the parameter space in the presence of error. For example, a 3:1 solution is correctly predicted and observed at Iapp values of (0.78, 1.64), corresponding to frequencies of (20.6, 11.37 Hz). A 3:1 mode was also observed at Iapp values of (0.77, 1.62) or (20.9, 11.8 Hz), and its existence was predicted correctly. However, that mode was incorrectly predicted to be unstable because one of the predicted phases was near a region of rapidly changing slope of the PRC, causing it to be vulnerable to error. A similar phenomenon was observed in that several 4:1 modes (blue open circles) at gsyn = 0.15 (Fig. 8) in a similarly narrow band of solutions were also missed.
Figure 9.
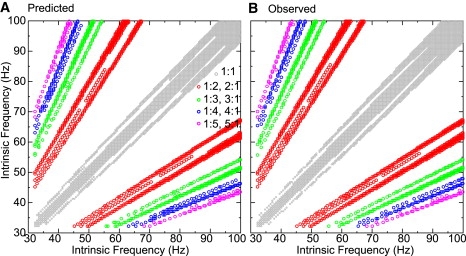
Qualitative comparison of predicted and observed modes for stronger pulsatile coupling as both intrinsic frequencies are varied. (A) The predictions were generated using the methodology described in Fig. 4. The circles indicate stable predicted modes at each locking ratio. (B) The observations were generated by numerically solving the full system of differential equations that describe the two coupled Wang and Buzsáki neurons. The colors indicate the value of N whereas the bands composed of small open circles correspond to the bands predicted at gsyn = 0.25 mS/cm2.
Our methods provide an improvement over weak coupling
In the weak coupling regime, our method and weak coupling methods gave similar results. For a weak coupling strength of gsyn = 0.01 mS/cm2, the predictions from the weak coupling method agreed with our predictions (Fig. 4). For this specific example, the upper and lower limits of the adjustment are Iadded,low = −0.026 μA/cm2 and Iadded, high = −0.0385 μA/cm2, which means that the original value of 1.842 μA/cm2 leads to a range of applied currents from 1.8035 to 1.816 μA/cm2, corresponding to the point at Iapp,F = 1.81 and Iapp,S = 0.77, which is in agreement with the point (freqF = 94.33 and freqS = 47.16) on the red line in Fig. 8 B. The shaded region in Fig. 4 displays all possibilities for a stable locked mode.
For the stronger coupling strengths, we see that the weak coupling method fails as expected. This is due to the assumptions of the method in calculating the coupling functions. In Fig. 10 we show the prediction from weak coupling method for gsyn = 0.25 mS/cm2, Iapp,F = 1.842 μA/cm2, and Iapp,S = 0.77 μA/cm2. The red curve illustrates the effective coupling function when coupling is turned on. There are no zero crossings indicating that 2:1 locking does not occur for these parameter values (initial frequencies are freqF = 95.8 Hz and freqS = 47.9 Hz), although Fig. 9 B clearly shows locking at these values. Further changing the value of Iapp,F in the regime predicted by our method does not improve the results. The weak averaged coupling method predicts the locking to occur in the range of frequency values freqF = [56.82, 80.32] Hz and freqS = [32.9, 36.76] Hz, which is clearly not the region where these modes are observed in Fig. 9 B. This shows that the weak coupling method fails for stronger coupling strengths.
Figure 10.
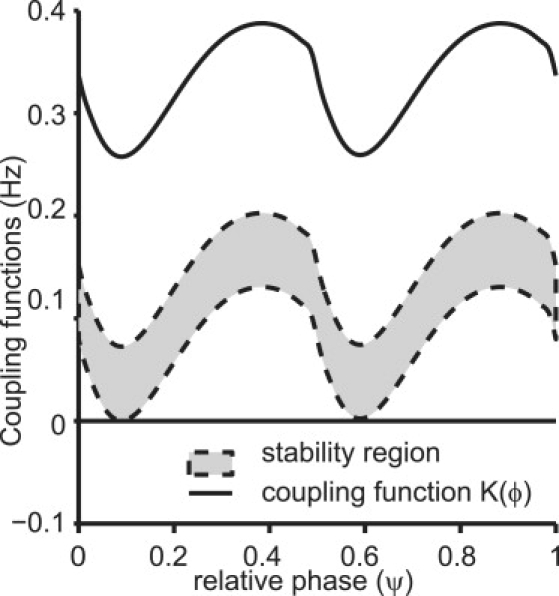
Weak coupling predictions compared to observations from our method. Shown are the effective coupling function (solid black curve) for the coupled system with gsyn = 0.25 mS/cm2. The system does not have a stable locking mode at the values of the applied current that give rise to a 2:1 mode in the uncoupled system. Changing the applied current value for the fast neuron shifts the coupling function down. For the range of values where there was a predicted and observed 2:1 locking in the system with our method (shaded region enclosed by the dashed curves), weak coupling method does not predict such a mode. This is due to a failure to satisfy the conditions required for the weak coupling method.
Ranges of frequencies that support excitatory lockings
To illustrate that our method is quite general, we also tested the predictions on a two neuron Wang and Buzsáki network identical to the one used in Figs. 8 and 9 except that Esyn was changed from −75 mV to 0 mV to represent an excitatory rather than inhibitory synapse. Because the membrane potential in a free-running model neuron spends much more time near −75 mV than near 0 mV, the driving force for excitation is much stronger than for inhibition. Therefore a smaller conductance value (gsyn = 0.04 mS/cm2) was chosen for this example. The use of excitation rather than inhibition prevents the appearance of the leapfrog modes in which the firing order switches (7,26), so the picture is simpler. Using the same range of intrinsic frequencies as in the inhibitory examples produced only 2:1 locking. The Wang and Buzsáki model neuron used in this study has Type I excitability (27), which produces Type I phase resetting (28) in which inhibition produces only delays and excitation produces only advances. The amount of advance that excitatory coupling can produce is limited by causality. That is, an input cannot cause a spike to occur before the input is presented, so the total advance cannot exceed Pi(1 − ϕ). The delays produced by inhibition are not limited; hence delays can produce larger changes in the period of the slower neuron that receives multiple inputs per cycle. These larger changes led to up to 5:1 lockings for inhibition but only 2:1 for excitation (Fig. 11).
Figure 11.

Accurate prediction of 2:1 locking band in two neuron network with excitation. The parameters were the same as in Figs. 8 and 9 except Esyn = 0 mV and gsyn = 0.04 mS/cm2. Two to one lockings are indicated in red. For completeness, 1:1 lockings are shown in gray. (A) Predicted. Modes were predicted directly from the PRCs using the existence and stability criteria. (B) Observed. The solution to the differential equations were run until the transients dissipated (1 s) and locked modes were identified by the periodic repetition of intervals. The agreement between predicted and observed is excellent.
Prediction of locking between populations
Harmonic N:1 locking in the nervous system is likely to be manifested in populations of oscillators. Achuthan and Canavier (29) suggested a method recently for applying phase resetting tools to predict clustering of oscillators. The basic idea was to treat interactions within a cluster separately from interactions between clusters. For an illustrative example, we examine one slow synchronous cluster of two neurons and one faster synchronous cluster of two neurons. Because the Wang and Buzsáki model neurons used in this study synchronize readily with inhibition (7), we chose inhibitory connections with gsyn = 0.025 mS/cm2 for the within-cluster synapses. We make the assumption that if two such neurons coupled by excitation would lock in an N:1 mode, so will the two clusters. Because each neuron receives two synaptic inputs from the other cluster (one from each neuron) the effective conductance that each neuron sees from the other cluster is twice the conductance of an individual between-cluster synapse. We set the individual between-cluster excitatory synapses to 0.02 mS/cm2 for a total between-cluster conductance of 0.04 mS/cm2, and picked the intrinsic frequencies for the two clusters by choosing a value in the center of the red 2:1 locking band in Fig. 11, with an intrinsic frequency of 35.3 Hz for the slower cluster and 94.3 Hz for the faster cluster, corresponding to Iapp values of 0.55 and 1.8 μA/cm2. We then used our PRC methods to predict a locking between one slow and one fast neuron coupled by the effective between-cluster conductance 0.04 mS/cm2 (see Fig. 12 A and Pervouchine et al. (30)), and applied that prediction to the network. The PRC-based prediction method identified a stable 2:1 mode in which the synchronous firing of the slow cluster occurred in the middle of a cycle of the fast cluster, followed 4.89 ms later by the synchronous firing of the fast cluster, by another firing of the fast cluster 10.64 ms later, followed by the next firing of the slow cluster 4.29 ms later. When the full system of differential equations was integrated (Fig. 12 B), a locking was observed with the corresponding intervals of 4.89, 10.64, and 4.25 ms, which is a very good match.
Figure 12.
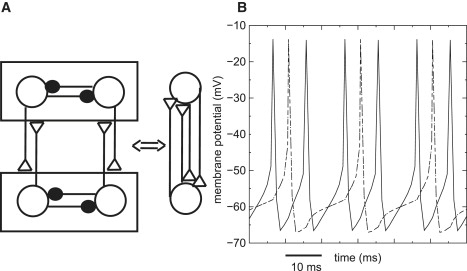
Prediction of population locking. (A) A four neuron network with two clusters of neurons with different intrinsic frequencies. Each cluster is indicated inside a box. The within cluster connections are inhibitory (solid circles) and the between cluster connections are excitatory (open triangles). Each cluster is collapsed into a single oscillator representing the cluster. (B) The example chosen shows 2:1 locking as predicted. The traces of the neurons in the fast (solid lines) and slow (dashed lines) cluster are indistinguishable.
This example is intended to capture the essentials of potential N:1 locking between networks of inhibitory interneurons coupled via excitatory pyramidal cells. The excitation between groups of interneurons is not mediated directly by interneurons, but rather relayed via pyramidal neurons. For simplicity, we ignored the delay between the firing of pyramidal and interneuronal cells and simply wired the network with the clusters of interneurons directly exciting each other. Delays can be incorporated if necessary; they simply shift the locking point (31). This approach is easily extended to larger and unequal cluster sizes.
Discussion
Relationship to previous work by others
N:1 phase-locked solutions in the case of forced oscillators, in which there is no feedback from the driven oscillator to the driving oscillator, have been studied extensively (32–35). Recently, Oprisan and Boutan (36) derived a criterion for 1:N forcing of pulse coupled oscillators using strong coupling PRC methods. Ermentrout (16) published existence and stability requirements for N:M modes in the case of weakly coupled oscillators, which also covered periodically forced oscillator systems for all values of N:M. In this study, we used the averaged weak coupling methods to identify 2:1 modes as described in Methods. This method is more computationally intensive and difficult to implement than the pulsatile coupling methods we developed in this study. Its strength is that the coupling is not required to be pulsatile, as it is possible to sum the contributions of the coupling to multiple cycles. However, the coupling is constrained to be quite weak to not violate the assumptions. Thus the methods presented in this study extend the regime in which the behavior of coupled oscillators is understood.
Palacios et al. (37) examined N:1 locking between arrays of mutually diffusively coupled van der Pol neurons, and found that mutual coupling was more effective than unidirectional coupling in establishing such lockings. Our results do not apply to diffusive coupling, but are novel in that similar results for pulse-coupled oscillators have not, to our knowledge, been derived previously. Grassman (38) used perturbation methods to study N:M locking of coupled oscillators assuming that the component oscillators were relaxation oscillators whose limit cycles were known and that the coupling simply changed the rate of travel along the trajectory on each branch by changing the rate of change of the slow variable. The method of Grassman is less general than the method presented herein. The strength of the method presented in this study is that it provides a simple way of predicting the locked modes for a system of coupled oscillators by only using their phase resetting curves, which are generated easily for biological neurons as well as for model neurons. The applicability is not limited to neural or biological systems; the results apply to any coupled limit cycle oscillators that can be characterized by their PRCs.
Applications
In a recent book entitled Rhythms of the Brain, Buzsáki (39) classifies the oscillatory rhythms observed in human EEG into 10 frequency bands, such as gamma and theta oscillations, that cover four orders of magnitude of frequencies. It was once thought that because the mean frequencies of these bands are not integer multiples of each other, they could not phase lock. Although this is true for weak coupling (16), we have shown in Figs. 8 and 9 that it is not true for strong coupling. Strong coupling produces greater changes in the intrinsic frequency, resulting in a larger range of frequencies from which the two oscillators can select to find a phasic relationship that allows exact locking. Evidence that at least some of these frequency bands are intrinsic oscillators that can be reset and entrained is provided by the observation that the occipital alpha rhythm can be entrained by subharmonic light flashes (25). Another example of a possible 2:1 locking in humans is given by the observation of Timmermann et al. (40) of an 8 ± 12 Hz motor cortical oscillatory activity in patients exhibiting Parkinsonian tremor at the first subharmonic frequency of 4 ± 6 Hz. This is consistent with recent physiological studies of 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine-treated monkeys, which showed that the maximal power of the synchronous oscillators in various regions of the basal ganglia was ∼10–12 Hz, which is double the Parkinsonian tremor frequency (24).
Whereas the preceding examples may reflect unidirectional driving rather than an emergent phenomenon arising from reciprocal coupling, there is data to suggest that N:1 dynamics as a result of mutual phase locking between rhythms in the nervous system can occur. Stein (41) produced a 2:1 locking between the swimming movements of the forelimb and the hindlimbs in a freely moving turtle with a partially transected spinal cord, which indicates the presence of separate oscillators for the control of each limb that can mutually reset each other's phase to produce a locking. Three to one locking has been observed in hippocampal slices between interneurons firing at gamma and pyramidal neurons firing at beta frequencies with missed gamma beats (42). Additionally, in a model network, 5:1 and 6:1 locking could be observed between gamma modules composed of basket cells and pyramidal cells and O-LM cells firing at theta frequency (43). Hence it may be important to understand under what circumstances such lockings can occur.
Limitations
In this study, we did not predict the complex lockings shown in Fig. 6 C and implied by the gaps between bands in Figs. 5, 8, and 9. It is theoretically possible to predict the leapfrog modes by following an approach similar to that given in Graves et al. (34) for 2:2 lockings, but because they were bracketed by predicted modes we did not find it necessary to predict these complex modes analytically. The inhibitory type I Wang and Buzsáki model neuron used in this study is a severe test of the method because most other simple networks (see Fig. 11 for excitatory coupling in the same network) do not exhibit such complex behavior (29). Not only the leapfrog modes but also higher order and aperiodic complex modes could be predicted (not shown) using an iterative map program that does not presume a particular firing order as described in Maran and Canavier (7) and Sieling et al. (44). This proves that the PRC also contained all information necessary to predict complex modes.
The main limitation of our method is that the underlying assumptions of pulsatile coupling must be approximately satisfied. The most stringent one is that the slower neuron must return to its limit cycle after it is perturbed by one input from the slower neuron before the next input is received, otherwise the phase is undefined and the phase resetting due to the second input cannot be calculated. Thus as N becomes large enough, eventually the approximation will break down. In practice, this means that only sufficiently nearby frequencies from the ten bands identified by Buzsaki could lock under pulsatile coupling. In the network we studied, as N gets larger the slow neuron is suppressed, which eliminates the observance of harmonic locking. If the synaptic time constant is small relative to the interval between inputs then the assumptions may be satisfied, but increasing the frequency or the synaptic time constant could cause a breakdown. Because the assumptions are not exactly satisfied, some error in the method can be expected at the boundaries where solutions lose existence or stability, and this is exactly where the errors in Figs. 5, 7, and 8 are observed. Another potential problem is adaptation, in which multiple pulses evoke a conductance that is not significantly activated by a single pulse. Other studies address the effects of adaptation (45) and these techniques could be incorporated into the methodology as necessary. Finally, the issue of robustness to noise is an area for future exploration.
Conclusions
This prediction method provides what we believe is an understanding of under which conditions N:1 locking can occur, and gives insight into how such locking could be facilitated or suppressed by adjusting the phase resetting curves until the conditions for existence and stability are met or not met. We also illustrate that strong coupling greatly increases the region of parameter space in which N:1 lockings can be observed. Our prediction method is generally applicable, including in cases of inhibitory and excitatory coupling, and can be extended to networks of multiple coupled oscillators.
Supporting Material
Twenty-five equations describing the full derivation of Eq. 4 in the text as well as notes on the use of the program XPPAUT are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00841-8.
Supporting Material
Acknowledgments
We thank Bard Ermentrout, Dr. Srisariam Achuthan, and members of the PRC research group for helpful discussions.
This work was supported by the National Institutes of Health grant NS54281 under the Collaborative Research in Computational Neuroscience program.
References
- 1.Betterman H., Amponsah D., Cysarz D., van Leeuwen P. Musical rhythms in heart period dynamics: a cross-cultural and interdisciplinary approach to cardiac rhythms. Am. J. Physiol. 1999;277:1762–1770. doi: 10.1152/ajpheart.1999.277.5.H1762. [DOI] [PubMed] [Google Scholar]
- 2.Bramble D.M., Carrier D.R. Running and breathing in mammals. Science. 1983;219:251–256. doi: 10.1126/science.6849136. [DOI] [PubMed] [Google Scholar]
- 3.Censi F., Calcagnini G., Lino S., Seydnejad S.R., Kitney R.I. Transient phase locking patterns among respiration, heart rate and blood pressure during cardiorespiratory synchronization in humans. Med. Biol. Eng. Comput. 2000;38:416–426. doi: 10.1007/BF02345011. [DOI] [PubMed] [Google Scholar]
- 4.Prokhorov M.D., Ponomarenko V.I., Gridnev V.I., Bodrov M.B., Bespyatov A.B. Synchronization between main rhythmic processes in the human cardiovascular system. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2003;68:041913. doi: 10.1103/PhysRevE.68.041913. [DOI] [PubMed] [Google Scholar]
- 5.Aschoff J. Naps as integral parts of the wake time within the human sleep-wake cycle. J. Biol. Rhythms. 1994;19:145–155. doi: 10.1177/074873049400900205. [DOI] [PubMed] [Google Scholar]
- 6.Canavier C.C., Achuthan S. Pulse coupled oscillators. Scholarpedia. 2007;2:1331. [Google Scholar]
- 7.Maran S.K., Canavier C.C. Using phase resetting to predict 1:1 and 2:2 phase locking in two neuron networks in which firing order is not always preserved. J. Comput. Neurosci. 2008;24:37–55. doi: 10.1007/s10827-007-0040-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oprisan S.A., Prinz A.A., Canavier C.C. Phase resetting and phase locking in hybrid circuits of one model and one biological neuron. Biophys. J. 2004;87:2283–2298. doi: 10.1529/biophysj.104.046193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Isler J.R., Grieve P.G., Czernochowski D., Stark R.I., Friedman D. Cross-frequency phase coupling of brain rhythms during the orienting response. Brain Res. 2008;1232:163–172. doi: 10.1016/j.brainres.2008.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sauseng P., Klimesch W., Gruber W.R., Birbaumer N. Cross-frequency phase synchronization: a brain mechanism of memory matching and attention. Neuroimage. 2008;40:308–317. doi: 10.1016/j.neuroimage.2007.11.032. [DOI] [PubMed] [Google Scholar]
- 11.Sauseng P., Klimesch W., Gruber W., Doppelmayr M., Stadler W. The interplay between theta and alpha oscillations in the human electroencephalogram reflects the transfer of information between memory systems. Neurosci. Lett. 2002;324:121–124. doi: 10.1016/s0304-3940(02)00225-2. [DOI] [PubMed] [Google Scholar]
- 12.Canavier C.C., Baxter D.A., Clark J.W., Byrne J.H. Control of multistability in ring circuits of oscillators. Biol. Cybern. 1999;80:87–102. doi: 10.1007/s004220050507. [DOI] [PubMed] [Google Scholar]
- 13.Canavier C.C., Butera R.J., Dror R.O., Baxter D.A., Clark J.W. Phase response characteristics of model neurons determine which patterns are expressed in a ring circuit model of gait generation. Biol. Cybern. 1997;77:367–380. doi: 10.1007/s004220050397. [DOI] [PubMed] [Google Scholar]
- 14.Luo C., Canavier C., Baxter D.A., Byrne J.H., Clark J.W. Multimodal behavior in a four neuron ring circuit: mode switching. IEEE Trans. Biomed. Eng. 2004;51:205–218. doi: 10.1109/TBME.2003.820380. [DOI] [PubMed] [Google Scholar]
- 15.Netoff T.I., Banks M.I., Dorval A.D., Acker C.A., Haas J.S. Synchronization in hybrid neuronal networks of the hippocampal formation. J. Neurophysiol. 2005;93:1197–1208. doi: 10.1152/jn.00982.2004. [DOI] [PubMed] [Google Scholar]
- 16.Ermentrout G.B. N:M phase-locking of weakly coupled oscillators. J. Math. Biol. 1981;12:327–342. [Google Scholar]
- 17.Wang X.J., Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Skinner F.K., Chung J.Y.J., Ncube I., Murray P.A., Campbell S.A. Using heterogeneity to predict inhibitory network model characteristics. J. Neurophysiol. 2005;93:1898–1907. doi: 10.1152/jn.00619.2004. [DOI] [PubMed] [Google Scholar]
- 19.Acker C.D., Kopell N., White J.A. Synchronization and strongly coupled excitatory neurons: relating network behavior to biophysics. J. Comput. Neurosci. 2003;15:71–90. doi: 10.1023/a:1024474819512. [DOI] [PubMed] [Google Scholar]
- 20.Canavier C.C. Phase response curve. Scholarpedia. 2006;1:1332. [Google Scholar]
- 21.Brown E., Moehlis J., Holmes P. On the phase reduction and response dynamics of neural oscillator populations. Neural Comput. 2004;16:673–715. doi: 10.1162/089976604322860668. [DOI] [PubMed] [Google Scholar]
- 22.Ermentrout B. SIAM; Philadelphia: 2002. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. [Google Scholar]
- 23.Ermentrout G.B., Kopell N. Multiple pulse interactions and averaging in coupled neural oscillators. J. Math. Biol. 1991;29:195–217. [Google Scholar]
- 24.Hammond C., Bergman H., Brown P. Pathological synchronization in Parkinson's disease: networks, models and treatments. Trends Neurosci. 2007;30:357–364. doi: 10.1016/j.tins.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 25.Moore N. A review of EEG biofeedback treatment of anxiety disorders. Clin. Electroencephalogr. 2000;31:1–6. doi: 10.1177/155005940003100105. [DOI] [PubMed] [Google Scholar]
- 26.Oh M., Matveev V. Loss of phase-locking in non-weakly coupled inhibitory networks of type-I model neurons. J. Comput. Neurosci. 2009;26:303–320. doi: 10.1007/s10827-008-0112-8. [DOI] [PubMed] [Google Scholar]
- 27.Hodgkin A.L. The local electric changes associated with repetitive action in a non-medullated axon. J. Physiol. 1948;107:165–181. doi: 10.1113/jphysiol.1948.sp004260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ermentrout G.B. Type I membranes, phase resetting curves and synchrony. Neural Comput. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- 29.Achuthan S., Canavier C.C. Phase resetting curves determine synchronization, phase-locking, and clustering in networks of neural oscillators. J. Neurosci. 2009;29:5218–5233. doi: 10.1523/JNEUROSCI.0426-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pervouchine D.D., Netoff T.I., Rotstein H.G., White J.A., Cunningham M.O. Low dimensional maps encoding dynamics in entorhinal cortex and hippocampus. Neural Comput. 2006;18:2617–2650. doi: 10.1162/neco.2006.18.11.2617. [DOI] [PubMed] [Google Scholar]
- 31.Canavier, C. C., and M. M. Woodman. 2008. A mechanism for synchronization in the presence of delays in which strong coupling compensates for deviations from symmetry. 2008 Society for Neuroscience Meeting, Poster: 376.3.
- 32.Glass L., Mackey M.C. A simple model for phase locking of biological oscillators. J. Math. Biol. 1979;7:339–352. doi: 10.1007/BF00275153. [DOI] [PubMed] [Google Scholar]
- 33.Glass L., Perez R. Fine structure of phase locking. Phys. Rev. Lett. 1982;48:1772–1775. [Google Scholar]
- 34.Graves C., Glass L., Laporta D., Meloche R., Grassino A. Respiratory phase locking during mechanical ventilation in anesthetized human subjects. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1986;250:902–909. doi: 10.1152/ajpregu.1986.250.5.R902. [DOI] [PubMed] [Google Scholar]
- 35.Pikovsky A., Rosenblum M., Kurths J. Phase synchronization in regular and chaotic systems: a tutorial. Int. J. Bifurcat. Chaos. 2000;10:2291–2305. [Google Scholar]
- 36.Oprisan S.A., Boutan C. Prediction of entrainment and 1:1 phase locked modes in two-neuron networks based on phase resetting curve method. Int. J. Neurosci. 2008;118:867–890. doi: 10.1080/00207450701750471. [DOI] [PubMed] [Google Scholar]
- 37.Palacios A., Carretero-Gonzalez R., Longhini P., Renz N., In V. Multifrequency synthesis using two coupled nonlinear oscillator arrays. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:026211. doi: 10.1103/PhysRevE.72.026211. [DOI] [PubMed] [Google Scholar]
- 38.Grassman J. The mathematical modeling of entrained biological oscillators. Bull. Math. Biol. 1984;46:407–422. doi: 10.1007/BF02462016. [DOI] [PubMed] [Google Scholar]
- 39.Buzsáki G. Oxford University Press; New York, NY: 2006. Rhythms of the Brain. [Google Scholar]
- 40.Timmermann L., Gross J., Dirks M., Volkmann J., Freund H. The cerebral oscillatory network of parkinsonian resting tremor. Brain. 2003;126:199–212. doi: 10.1093/brain/awg022. [DOI] [PubMed] [Google Scholar]
- 41.Stein P. Application of the mathematics of coupled oscillator systems to the analysis of the neural control of locomotion. Fed. Proc. 1977;36:2056–2059. [PubMed] [Google Scholar]
- 42.Whittington M., Traub R.D., Kopell N., Ermentrout B., Buhl E. Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int. J. Psychophysiol. 2000;38:315–336. doi: 10.1016/s0167-8760(00)00173-2. [DOI] [PubMed] [Google Scholar]
- 43.Tort A., Rotstein H., Dugladze T., Glovelli T., Kopell N. On the formation of gamma-coherent cell assemblies by oriens lacunosum-moleculare interneurons in the hippocampus. Proc. Natl. Acad. Sci. USA. 2007;104:13490–13495. doi: 10.1073/pnas.0705708104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sieling F.H., Canavier C.C., Prinz A.A. Predictions of phase-locking in excitatory hybrid networks: excitation does not promote phase-locking in pattern generating networks as reliably as inhibition. J. Neurophysiol. 2009 doi: 10.1152/jn.00091.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cui J., Canavier C.C., Butera R.J. Functional phase response curves: A method for understanding synchronization of adapting neurons. J. Neurophysiol. 2009 doi: 10.1152/jn.00037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


