Determining Protein-Induced DNA Bending in Force-Extension Experiments: Theoretical Analysis

Abstract

Computer simulations were used to investigate the possibility of determining protein-induced DNA bend angles by measuring the extension of a single DNA molecule. Analysis of the equilibrium sets of DNA conformations showed that shortening of DNA extension by a single protein-induced DNA bend can be as large as 35 nm. The shortening has a maximum value at the extending force of ∼0.1 pN. At this force, the DNA extension experiences very large fluctuations that dramatically complicate the measurement. Using Brownian dynamics simulation of a DNA molecule extended by force, we were able to estimate the observation time needed to obtain the desired accuracy of the extension measurement. Also, the simulation revealed large fluctuations of the force, acting on the attached magnetic bead from the stretched DNA molecule.

Introduction

Many DNA-binding proteins bend the double helix upon forming complexes. Such bends can contribute to DNA packing (1), regulate DNA functioning (2,3), and even affect the outcome of enzymatic transformations of the DNA topology (4,5). The bends are observed experimentally by x-ray analysis of cocrystals (6), by measuring the fluorescence resonance energy transfer (7), by shift of electrophoretic mobility of the DNA-protein complexes (8), by measuring the cyclization efficiency of short DNA fragments (5), by electron and cryoelectron microscopy (see (9–11), for example), and by the effect of protein binding on DNA extension (12). All these methods have certain advantages and limitations for quantitative analysis of protein-induced DNA bends, and none of them can address all types of DNA-protein complexes. It is especially difficult to investigate DNA bends induced by binding proteins with low specificity to DNA sequence. Thus, new experimental approaches are definitely needed for the quantitative analysis of the protein-induced DNA bends. One such potential approach based on single-molecule measurements of DNA stretching, was suggested recently (13). An alternative, more straightforward approach, based on the same measurements of DNA extension, is analyzed in this article.

Experimental methods based on DNA stretching are being developed at an amazing pace (see (14,15) for reviews). Researchers have learned how to measure increments of DNA extension corresponding to one basepair of the double helix (16). Still, the theoretical analysis shows that the problem of measuring protein-induced DNA bending brings new challenges that have not been solved. We hope that accurate simulation of the experiments can help to clarify and overcome any problems one might experience in applying this approach for bend-angle determination.

It is clear that the bending of stretched DNA by a bound protein should result in a certain decrease of DNA extension. Due to the high bending rigidity of the double helix, the protein-induced DNA deformation spreads beyond the protein binding site, so the shortening could be rather large. To obtain a quantitative estimate of this effect, we performed a computer simulation of the system based on the well-tested model of DNA. We calculated the reduction of DNA extension for various values of the bend angle and the force applied to the DNA ends. Although the effect obtained in the simulation exceeds the precision of the method substantially, it may be very difficult to measure this reduction of DNA extension. The problem is that the proteins are bound to DNA for restricted time intervals, and large fluctuations of the extension have to be well averaged over these intervals. We analyzed the problem quantitatively by Brownian dynamics (BD) simulation of the system. This method provides an accurate description of large-scale DNA dynamic properties (see (17) for review). It allowed us to investigate the fluctuations of the molecule extension directly over various time intervals, and to observe the longitudinal correlation of the extension fluctuations. We also studied fluctuations of the force acting from the stretched DNA on the bead attached to the chain end. We estimated the time intervals needed to measure DNA extension with the desired precision. The simulation results are compared with available experimental data.

Simulation Methods

The DNA model used for the BD simulation is based on the discrete wormlike chain and is similar to one developed originally by Allison et al. (18,19) and further elaborated on by Langowski and coworkers (20,21) and by our group (22,23).

A DNA molecule composed of n Kuhn statistical lengths is modeled as a chain of kn straight elastic segments of equilibrium length l₀. The chain energy consists of three terms:

• 1.
  The stretching energy is computed as

  $$E_{\text{s}}=\frac{k_{\text{B}}Th}{2}\sum _{i=1}^{nk}{(l_i-l_0)}^2,$$ (1)

  where l_i is the actual length of segment i, h is the stretching rigidity constant, and k_BT is the Boltzmann temperature factor. The energy (E_s) should be considered as a computational device rather than an attempt to account for the actual stretching elasticity of the double helix. Smaller values of h allow larger time steps, Δt, in the BD simulations, but also imply larger departures from l₀ (22). To allow larger values of Δt, we chose $h=100/l_0^2$, so that the variance of l_i was close to $l_0^2/100$. Although this value of h is smaller than the actual stretching rigidity of the double helix (24), it has been shown that such a choice does not affect the simulation results (22).
• 2.
  The bending energy (E_b) is specified by angular displacements, θ_i, between segments (i + 1) and i:

  $$E_{\text{b}}=\frac{k_{\text{B}}Tg}{2}\sum _{i=1}^{kn}{\mathrm{\theta }}_i^2\text{.}$$ (2)

  The bending rigidity constant, g, is defined in such a way that the Kuhn statistical length corresponds to k rigid segments of the model chain (25). It has been shown previously that the majority of DNA equilibrium properties do not change within the accuracy of the simulations if k ≥ 10 (26), although larger values of k are needed for the simulation of DNA extension by forces >1 pN (27). The value of k = 10 used here corresponds to g = 4.81 and l₀ = 10 nm when using 100 nm for the Kuhn length (28).
• 3.
  The energy of electrostatic intersegment interaction (E_e) is specified by the Debye-Hückel potential as a sum over all pairs of the point charges located on the chain segments. The number of point charges placed on each segment, λ, is chosen to approximate well continuous charges with the same linear density. The value of λ should increase as the Debye length, 1/κ, decreases. The simulation results presented here were obtained for [Na⁺] = 0.1 M, which requires that λ ≥ 5 (22). The E_e is specified as

  $$E_{\text{e}}=\frac{{\nu }^2{l}_{\text{o}}^2}{{\lambda }^{2}D}\sum _{i,j}^N\frac{\exp (-\kappa r_{ij})}{r_{ij}},$$ (3)

  where ν is the effective linear charge density of the double helix, D is the dielectric constant of water, N = knλ is the total number of point charges, and r_ij is the distance between point charges i and j. The value of ν is 6.08 e/nm for [Na⁺] = 0.1 M (29). This value of ν corresponds to the solution of the Poisson-Boltzmann equation for DNA modeled as a charged cylinder. It was found by Stigter (29) that this solution can be approximated well by the Debye-Hückel potential for the charged line. This approximation requires only a suitable definition of ν to match the potential-distance curve in the overlap region far from the cylindrical surface.

To account for hydrodynamic interactions of the DNA with the solvent, beads of radius a were placed at each vertex of the chain. These beads are used only to define the hydrodynamic interaction and thus do not affect equilibrium properties of the model chain. We used the Rotne-Prager diffusion tensor to specify the hydrodynamic interaction (30). The value of a was 2.24 nm. This value was chosen to provide experimentally measured values of the translational diffusion (sedimentation) coefficients of circular DNA molecules (31–33). In some simulations, a large bead, 1 μm in diameter, was attached to a DNA end. In this case, we assumed that the hydrodynamic interaction between the DNA chain and the bead does not affect the bead motion, so this interaction was ignored.

It was assumed that only one strand of DNA is attached to the bead (and the supporting pipette), so there is no torsional stress of the double helix in this setting.

For the majority of the simulation, the time step was 400 ps; for the simulation result shown in Fig. 5 A, the time step was 2 ps.

Figure 5.

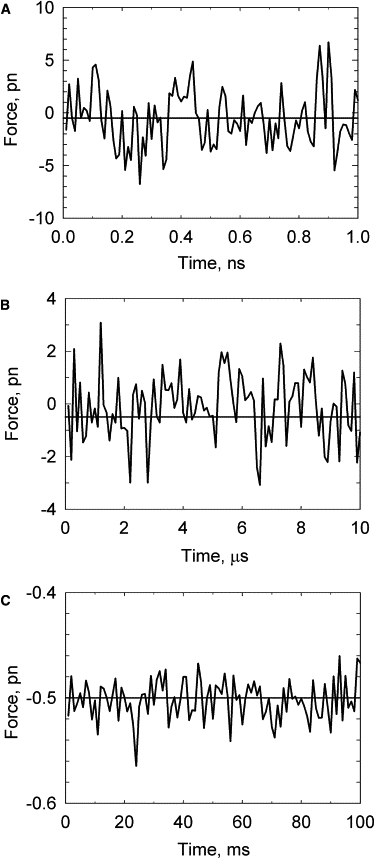
Fluctuations of the force, acting from the DNA on a very small bead attached to its end. The force was averaged over time intervals of 10 ps (A), 0.1 μs (B), and 1 ms (C). The average value of the force was 0.5 pN. The length of the model chain corresponds to 1.5 kb DNA.

Although all large-scale equilibrium properties of DNA could be estimated by BD simulation, it can be done much faster by Monte Carlo (MC) simulation, which was also used in this study (see (17) for a review of both kinds of simulation). The DNA model for the MC simulation is very similar to one described above, with two small distinctions. There is no need of the segment-stretching potential in the MC simulation, so the length of the chain segments is always l₀ in the model. Also, the Debye-Hückel potential is replaced by a hard-core potential: each segment is represented by an impenetrable cylinder of diameter d. The value of d, the DNA effective diameter (29), accounts for both the geometrical diameter of the double helix and the electrostatic repulsion between negatively charged DNA segments. Thus, the value of d is larger than the geometric diameter; for a [Na⁺] of 0.1 M, d = 5.6 nm (29). The concept of effective diameter is the simplest but sufficiently accurate way to account for the electrostatic interaction between DNA segments (34).

The BD and MC simulation procedures have been described in detail previously (22,27).

Results

Extension of DNA molecules with a protein-induced bend

We modeled the double helix by the discrete wormlike chain, which provides a very accurate description of DNA extension by the stretching force (27). The stretching force (F) is applied to a bead attached to one end of the chain, with the other end in a fixed position (Fig. 1). We consider a system where the value of F does not depend on the bead position, the case where the bead is placed in a uniform magnetic field (15). It was assumed that the protein binding site has length b, and the protein-induced bending by angle ϕ is uniformly distributed over the site. It was also assumed, for simplicity, that the binding site is absolutely rigid when the protein is bound to the site.

Figure 1.

Extension of DNA molecule with a protein-induced local bend. The bend is localized at a DNA segment of 6 nm in length (red/dark). The simulated DNA conformation corresponds to a DNA fragment of 100 nm in length (much longer model chains were used for the simulations reported here). The DNA conformation shown was obtained for a stretching force of 0.2 pN.

We simulated equilibrium sets of DNA conformations for the chain without any bound protein and calculated its average extension, 〈x₀(F)〉. Then we calculated the extension for the same DNA with a bound protein, 〈x(ϕ,F)〉. The change of the extension due to the protein binding, 〈Δx〉 = 〈x₀(F)〉 − 〈x(ϕ,F)〉, is plotted in Fig. 2 for various values of ϕ as a function of F. First, we see that for all angles 〈Δx〉 has a maximum near F = 0.1 pN. The reduction of the extension at this force is quite large: for ϕ = 120°, for example, it reaches 25 nm. The fact that 〈Δx〉 has a maximum is easy to understand. At very small forces, the extension is small regardless of the bend; therefore, 〈Δx〉 has to be small as well. At large forces, 〈Δx〉 is small, because DNA deformation produced by the protein binding has smaller spreading beyond the protein binding site.

Figure 2.

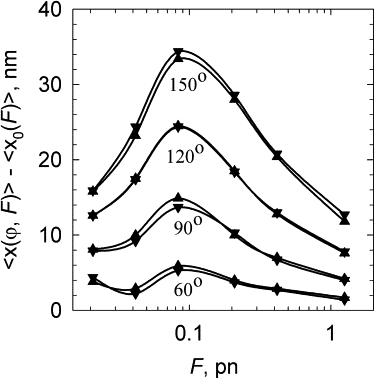
DNA extension change due to protein-induced DNA bending. The results of computer simulation were obtained for a discrete wormlike chain whose length corresponded to a 3000-bp DNA. The protein binding site was localized in the middle of the chain and its length corresponded to 6 nm (▴) and 10 nm (▾). The bend angle (ϕ) was uniformly distributed along the site. The values of ϕ used in the computations are shown near the corresponding data.

Our calculations also showed that changing the length of the DNA binding site in the range of 6–10 nm has no significant effect on the extension (Fig. 2). Nearly identical results were recently obtained for a different model of protein-induced DNA bend by a very different theoretical method (35). The authors of that study analyzed 〈Δx〉 caused by DNA bends localized at a single point of the double helix. The agreement between their results and ours gives additional confirmation that 〈Δx〉 depends on the value of ϕ only and not on the size of the binding site. We also observed that the simulation results do not depend on the length of the model chain if it is >1000 bp (data not shown). This definitely simplifies the angle determination, which can be done by comparing the experimental and theoretical values of 〈Δx〉.

A strong stretching force can disturb the structure of the DNA-protein complex and change the bend angle. Therefore, a maximum value of 〈Δx〉 corresponding to a small force is favored for angle determination. Additional extension of the DNA after dissociation of the protein from the binding site would reduce the binding free energy, ΔG_b, by the value F〈Δx〉. Since 〈Δx〉 does not exceed 35 nm (Fig. 2), we learn that for a force of 0.1 pN, F〈Δx〉 < k_BT, which is a small fraction of a typical ΔG_b value. Thus, a stretching force of 0.1 pN has little effect on the protein binding affinity and should not disturb the structure of the DNA-protein complex notably.

The values of 〈Δx〉 plotted in Fig. 2 are the average values that can be computed with any desirable accuracy. In the real experiment, the situation is more complicated, however, because the extension fluctuations are large, especially at small forces. We computed the amplitude of these fluctuations, ${\sigma }_x=\sqrt{\langle x^2\rangle -{\langle x\rangle }^2}$, for two different values of F (Fig. 3). These data show that σ_x increases sharply when the extending force decreases, and for a value of F = 0.1 pN and DNA length of 3000 bp, σ_x becomes much larger than 〈Δx〉 (Fig. 2). These large fluctuations impose a serious difficulty for the measurement of 〈Δx〉.

Figure 3.

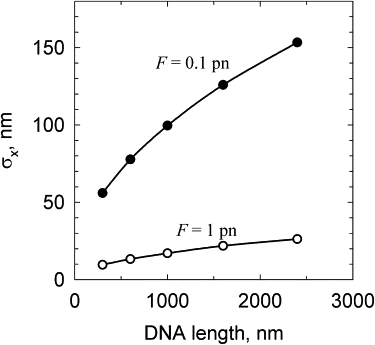
The average amplitude of the extension fluctuations (σ_x) as a function of DNA length (L). For chains of a few Kuhn statistical lengths or longer the value of ${\sigma }_x^2$ is proportional to L. The values of F used in the computation are shown near the corresponding data.

There is no problem measuring 〈x₀(F)〉 with sufficient accuracy, since the magnitude of the extension can be recorded and averaged over a sufficiently large time interval, Δt. The situation is more complex for DNA molecules with bound proteins. These proteins, dissolved in the surrounding solution, bind the DNA molecule and dissociate from it. We assume that the protein concentration in the solution is sufficiently low that the great majority of the time there are no bound protein molecules, or only one protein molecule is, bound to the stretched DNA. Under normal circumstances, the only way to detect the protein binding is to observe the reduction of the DNA extension. Therefore, the time interval Δt for the extension averaging should be sufficient to distinguish between the naked and the protein-bound states of DNA (Fig. 4). Clearly, large and slow fluctuations of the extension create an obstacle there, since larger Δt is required for the estimation of 〈x〉. On the other hand, Δt should be essentially smaller than the average lifetime of the bound state of the protein, 〈t_b〉. Thus, the condition Δt << 〈t_b〉 is a necessary condition for the successful measurement of 〈Δx〉. To analyze this condition in detail, we need to analyze the dynamics of the extension fluctuations in the stretched DNA molecules. Some problems addressed in our analysis were analyzed recently by Wallin et al. (36).

Figure 4.

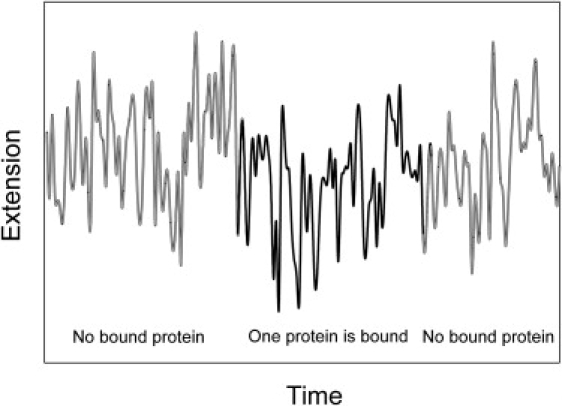
Diagram illustrating the fluctuations of DNA extension under a constant force as a function of time. The time intervals shown correspond to the DNA molecule without (gray) and with (black) bound proteins. Although the average extension is changed substantially by the protein-induced bend, there is no way to extract this shortening from the data shown, since the moments of the protein binding and dissociation are masked by the extension fluctuations. A much longer lifetime of the bound state is needed for quantitative analysis of the extension change.

Dynamics of the extension fluctuations

It seems clear that the fluctuations do not depend essentially on the presence of a single DNA bend, so we consider below the dynamic properties of intrinsically straight molecules in the absence of bound proteins. It is shown in Fig. 3 that fluctuations of DNA extension in this system are very large at the low-force regime. We investigated dynamic properties of the system by BD simulation of the stretched DNA molecule. It has been shown that the method provides an accurate description of large-scale DNA dynamics (37). The DNA model used in the BD simulations is similar to that used for the Monte Carlo simulations (see Methods), and the same DNA equilibrium properties can be obtained by BD simulations, although many times more computer time is needed for this (17). In the majority of the simulation results shown below, we did not account for the large magnetic bead attached to the chain end, although its effect will be considered at the end of this section.

The force acting on the bead from the polymer chain is entropic in nature, originating from the fact that there are many more compact, coiled chain conformations than extended ones. The chain, however, has no memory of this, and at each particular moment the value of the force is random, with very broad distribution. A constant force is observed only when its actual values are averaged over a substantial time interval. The simulated oscillations of the force acting on the chain end from the fluctuating polymer chain are shown in Fig. 5 (we assumed that a very small imaginary bead is attached to the chain end and that external force F is applied to this bead). The value of the force was averaged over various time intervals, Δt, which were in the range 10 ps to 1 ms. One can see from the figure that the force fluctuations for Δt of 10 ps are many times larger than the average value of the force, 0.5 pN. Only when the force is averaged over a 1 ms time interval do the fluctuations become relatively small. The oscillations of F only weakly depend on the average value of the force and do not depend on DNA length if it is >1 kb (Fig. 6). The latter observation means that the force fluctuations are determined by fluctuations of a relatively short part of the fluctuating chain close to the chain end.

Figure 6.

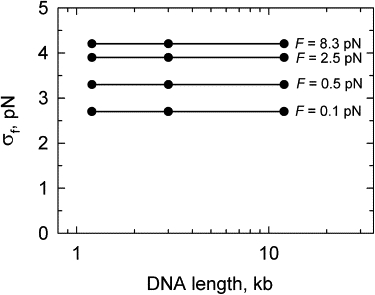
Fluctuations of the force, acting from the DNA on the bead attached to the molecule end. The amplitude of the fluctuations is plotted as a function of DNA length for different values of applied force. There was no preliminary averaging of the force values in this calculation. It was found that the results of BD simulations of the force fluctuations do not depend on the length of the model chain if it corresponds to DNA molecules >1 kb in length.

Fluctuations of DNA extension are different from force fluctuations. In general, to obtain the average value of the extension with good accuracy, a much longer observation time is required. Fig. 7 illustrates this issue for the simulated extension of 1.5 kb DNA under 0.1 pN force. One can see from the figure that the extension fluctuations averaged over a Δt of 0.4 ms remain very large, whereas the fluctuations of the averaged force are nearly negligible (Fig. 5). The extension fluctuations are reduced greatly for a Δt of 25 ms but remain large for this extending force, even for short DNA molecules (Fig. 7 B).

Figure 7.

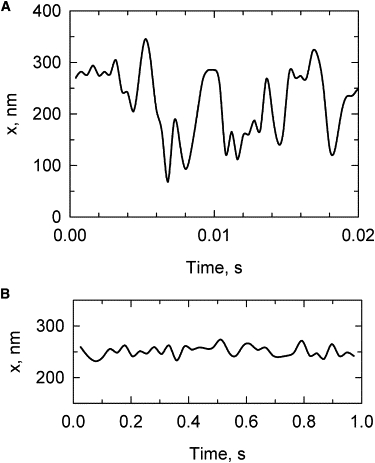
Fluctuations of DNA extension. The length of the model chain corresponds to 1.5 kb DNA. The extension was averaged over time intervals of 0.4 ms (A) and 25 ms (B). The stretching force was equal to 0.1 pN.

The simulation showed that the extension fluctuations strongly depend on the value of F when F < 0.5 pN. The amplitude of the extension fluctuations, averaged over a Δt of σ_x (Δt), is shown in Fig. 8. Again, this is sharply different from the force fluctuations (Fig. 6). It is clear that the fluctuations should increase with increasing DNA length. If the DNA length is larger than the correlation length for the extension fluctuations, σ_x (Δt) should be proportional to the square root of the DNA length, according to the central limit theorem (38).

Figure 8.

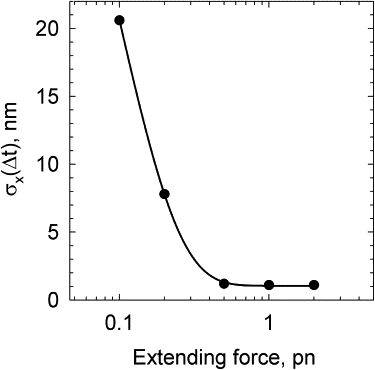
Fluctuations of DNA extension at different values of applied force. The length of the model chain corresponds to 1.5 kb DNA. The amplitudes of the extension fluctuations were calculated for the extension averaged over a time interval of 10 ms.

Using the BD simulation we investigated the correlation length for the extension fluctuations at different points of the chain contour,

$$C\left(s\right)=\langle \Delta x(L,\Delta t)\Delta x(L-s,\Delta t)\rangle /\sqrt{\mathrm{var}[\Delta x(L,\Delta t)]\mathrm{var}[\Delta x(L-s,\Delta t)]},$$ (4)

where Δx(L − s, Δt) is the displacement of the chain element with coordinate L − s along the contour over time interval Δt, and L refers to the free end of the chain. The correlation functions for different values of Δt are well described by an exponential decay (Fig. 9):

$$C\left(s\right)=\exp (-s/s_0),$$ (5)

where s₀ is the correlation length. We found that the value of s₀ increases when Δt increases, but even for the largest Δt accessible in the simulations, 50 μs, s₀ was only 1000 nm, or 10 Kuhn statistical segments of double-stranded DNA. We see that the greater the separation between extension fluctuations at different points of the chain, measured along the contour, the smaller the correlation between them. This result is consistent with the finding that force fluctuations do not depend on DNA length if the length exceeds 1 kb (Fig. 6).

Figure 9.

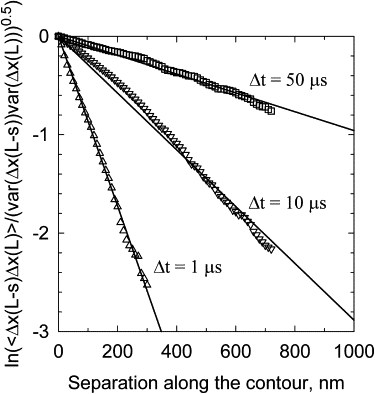
Correlation of the extension fluctuations between different points of the chain. The correlation function (Eq. 4) was calculated by BD simulation for DNA molecules 3 kb in length stretched by 1 pN force (Extension of the model chain was 0.85 of its contour length under this force.) The data were obtained for the displacements over different time intervals, Δt, shown in the plot.

The BD simulation makes it possible to determine the time interval for extension averaging, which is sufficient for reliable determination of the bend angle ϕ. To do this, we plotted σ_x (Δt) as a function of Δt (Fig. 10). If Δt is sufficiently large, the values of extension averaged over successive time intervals are not correlated, and σ_x (Δt) should be proportional to $1/\sqrt{\Delta t}$. One can see from the data shown in Fig. 10 that in the absence of the end magnetic bead such a critical value of Δt is close to 10 ms. The proportionality of σ_x (Δt) to $1/\sqrt{\Delta t}$ allows us to extrapolate the plot to very large values of Δt, which are not accessible by the simulation. In this way, we estimated the value of Δt that should give the desired accuracy of the extension measurement. To measure the bend angle introduced by a bound protein molecule with reasonable accuracy, we need σ_x (Δt) ≈ 2 nm. This condition is satisfied for Δt ≈ 1 s (Fig. 10).

Figure 10.

Fluctuations of DNA extension averaged over time interval Δt. The amplitudes of the extension fluctuations, σ_x (Δt), were obtained in the BD simulation for the model chain with attached bead of 1 μm in diameter (▾) and without any bead (▴). The stretching force was equal to 0.1 pN. For a sufficiently large value of Δt, the average values of extension for adjacent time intervals are not correlated, so the value of σ_x (Δt) has to be proportional to $1/\sqrt{\Delta t}$ (this dependence is shown by the dotted line). The simulated dependences satisfy this condition for Δt > 10 ms and Δt > 100 ms for the chains without and with the bead, respectively. This consideration allows extrapolation of the simulated results to larger values of Δt that are not accessible in the simulation directly.

The results of BD simulation on the extension fluctuations shown above do not account for the fact that a large bead is attached to one end of the DNA molecule in the experimental setting (15). The radius of this bead is 0.5–2 μm, so it corresponds to the contour length of 1.5–6 kb DNA. This bead strongly affects the timescale of the extension fluctuations. As a result, much larger values of Δt are required to obtain the average values of the extension with sufficient accuracy. We repeated the previous analysis of the required averaging interval for the model chain with the attached bead of 1 μm in diameter. The data (Fig. 10) show that the same standard deviation of 2 nm can be achieved for Δt ≈ 20 s for a DNA fragment of 1.5 kb in length. The averaged extension has to be recorded at least 20–30 times during a single experiment, so its total length, t_exp, cannot be <10 min. For DNA molecules of N bp in length, where the length exceeds 1.5 kb, the minimal t_exp in minutes can be estimated as

$$t_{\exp }\approx 10\sqrt{\frac{N}{1500}}\text{.}$$ (6)

Discussion

We found that a protein-induced bend can strongly affect DNA extension at low extending force. This result is in full quantitative agreement with theoretical calculations by Nelson and co-workers (35). The shortening has a maximum at a force of 0.08 pN, which is low enough to preserve the structure of the DNA-protein complex. However, the measurement of the extension change at such low force represents a great challenge due to very large fluctuations in the system in the low-force regime. We investigated this issue in detail by direct BD simulation of the system dynamics. Our analysis shows that even for a short DNA molecule 1500 bp in length, the extension has to be averaged over ∼1 min to obtain ∼1 nm precision in the measurement at a force of 0.1 pN. This can be a serious problem, since the averaging interval, Δt, should be much shorter than the lifetime of the DNA-protein complex. The majority of DNA-protein complexes do not have such long lifetimes.

The above estimation accounts for a large bead attached to the DNA end. The bead slows down the fluctuation dramatically. In the absence of such a bead, the averaging time can be reduced to 1 s for 1500-bp DNA. It is clear that a reduction in the bead size can help greatly in this situation.

The extension fluctuations strongly depend on the applied force. At a force of 1 pN, the value of Δt needed to obtain sufficient precision of the extension measurement is 10 times smaller than at a force of 0.1 pN (Fig. 8). However, this force can disturb the complex structure and increase the complex dissociation rate.

We also found very large fluctuations of the force acting from the extended DNA molecule on the attached bead (Figs. 5 and 6). The amplitude of these fluctuations grows slightly when the applied force increases. Although the force fluctuations are averaged well over a 1-ms time interval, they can be important in studies focusing on the response of a molecular system to applied force (16,39). One basepair translocation of a molecular complex along a DNA molecule (16) can occur on the microsecond timescale, and during this time the complex may experience substantially lower force than its average value.

Force fluctuations do not notably affect the fluctuations of DNA extension, however. The reason for this is simple: thermal motion of the solvent molecules that collide with the bead creates a much larger fluctuating force. Although there is no way to specify this force, we can estimate the average displacement of the end bead (〈Δr〉) by different forces over the time step in the BD integration procedure, which is 0.4 ns. For a bead of 1 μm in diameter, >99% of the total value of 〈Δr〉 is due to thermal motion of the solution molecules, and even for a very small bead of 5 nm in diameter the contribution of thermal motion to 〈Δr〉 remains close to 90%. At low force (when F is a few pN or less), these estimations do not depend on the external force acting on the bead.

It is interesting to compare our simulation results with published experimental data. To the best of our knowledge, there is only one study on DNA extension shortening due to binding with a single protein (40). The authors observed an 8-nm change in DNA extension due to binding of a single IHF protein, and a time interval needed for sufficiently accurate averaging of the extension consisted of a few seconds in their experiments. Unfortunately, a quantitative analysis of these data in terms of the bend-angle value is not possible because of the very short length of the DNA molecule used in that study (74 bp). In such a setting, the bead is located so close to the surface that there is substantial electrostatic and entropic repulsion between the surface and the bead, which depend on the distance between the bead and the surface. Also, unknown flexibility at a DNA attachment point becomes an important factor for such short fragments. We can only say that the experimental results are in semiquantitative agreement with the simulations described here. In general, too short a DNA tether complicates the analysis, so the tether length should not be <1 kb. On the other hand, the tether length should not be much larger than 1 kb since increasing the tether length increases the extension fluctuations.

We can also compare the simulated amplitude of the extension fluctuations with available experimental data. We analyzed the time course of the extension fluctuations published recently by Lia et al. (41). One can estimate from Fig. 1 d in that work that for 3.6 kb DNA, in the absence of any bound proteins, σ_x (Δt) ≈ 10 nm for a Δt of 1 s, a bead diameter of 2.4 mm, and a force of 0.9 pN. We performed simulations in exactly the same setting, and found that σ_x (Δt = 1 s) should be 1.5 nm. There are at least two possible reasons for the discrepancy. It is possible that DNA supercoiling, which was introduced into the stretched DNA in the experiment, increases the extension fluctuation. Also, the discrepancy between the simulated and experimental data may be due to low accuracy of the extension measurements at 1 pN force in the experimental setting used by Lia et al. ((41), and see (42)). The variance of row data, recorded without any preliminary averaging, was ∼50 nm in the experiment and also exceeded the theoretical value, which is only 20 nm. The latter value seems very reliable since it was obtained using three different methods: Monte Carlo and BD simulations, and the equipartition theorem combined with the force-extension equation for the wormlike chain (see (42,43)).

Another experimental study, related to the work presented here, describes the correlation between fluctuating forces applied to the ends of a long DNA molecule (44). In the experimental setting, the beads were attached to each end of phage λ DNA and stretched with a dual-beam optical tweezers. The authors reported a correlation between Brownian motion of the beads. The cross-correlation functions measured in their study had relaxation times in the millisecond timescale. The experimental results were obtained for bead displacements over 50 μs (44). We found that the longitudinal correlation length measured for the same time interval is ∼1000 nm (Fig. 9). Thus, the simulation results exclude any correlation between fluctuations of beads attached to the ends of a DNA molecule ∼15,000 nm in length. The reasons for this discrepancy between the simulation and the experimental data are not yet known.