Blind Source Separation Techniques for the Decomposition of Multiply Labeled Fluorescence Images

Abstract

Methods of blind source separation are used in many contexts to separate composite data sets according to their sources. Multiply labeled fluorescence microscopy images represent such sets, in which the sources are the individual labels. Their distributions are the quantities of interest and have to be extracted from the images. This is often challenging, since the recorded emission spectra of fluorescent dyes are environment- and instrument-specific. We have developed a nonnegative matrix factorization (NMF) algorithm to detect and separate spectrally distinct components of multiply labeled fluorescence images. It operates on spectrally resolved images and delivers both the emission spectra of the identified components and images of their abundance. We tested the proposed method using biological samples labeled with up to four spectrally overlapping fluorescent labels. In most cases, NMF accurately decomposed the images into contributions of individual dyes. However, the solutions are not unique when spectra overlap strongly or when images are diffuse in their structure. To arrive at satisfactory results in such cases, we extended NMF to incorporate preexisting qualitative knowledge about spectra and label distributions. We show how data acquired through excitations at two or three different wavelengths can be integrated and that multiple excitations greatly facilitate the decomposition. By allowing reliable decomposition in cases where the spectra of the individual labels are not known or are known only inaccurately, the proposed algorithms greatly extend the range of questions that can be addressed with quantitative microscopy.

Introduction

Multiple fluorescent labeling has become a key tool for the elucidation of signaling networks in cells and tissues (1,2). To understand a system's properties, it is essential to label and monitor simultaneously as many components as possible. Modern laser-scanning and wide-field microscopes allow rapid acquisition of spectrally resolved images, from which the separate contributions of simultaneously present labels can be obtained.

Traditionally, this task is solved by choosing narrow emission bands where only one dye contributes significantly, but this approach discards the majority of the photons and severely limits the choice of available dyes to those with well-separated emissions. If the emission spectra of the dyes are known, these drawbacks can be overcome by linear unmixing or spectral fingerprinting (3). However, the relevant emission spectra of the fluorophores depend on the instrumentation and the chemical environment, and therefore, their acquisition requires extensive calibration efforts. One way to overcome these difficulties is to use fluorescence lifetime information or modulated excitation schemes (4–6). On the other hand, several attempts have been made to use blind source separation (BSS) techniques that estimate spectra and concentrations simultaneously (7–10). However, the decompositions are often ambiguous. Furthermore, most algorithms do not account for the noise characteristics of fluorescence data and thereby put undue emphasis on some parts of the data. Here, we present an algorithm adapted to fluorescence microscopy and test it on various samples to systematically investigate its reliability. We discuss techniques for incorporating additional qualitative knowledge about spectra and spatial features of images to reduce ambiguity in the decomposition. We conclude with a method for integrating data acquired at different excitation wavelengths, which further facilitates the decomposition (8,11). Our benchmark examples include the separation of the most commonly used fluorescent proteins, including enhanced cyan (ECFP), green (EGFP), and yellow (EYFP) variants, as well as three or four subcellular structures labeled with the common Alexa Fluor dyes, fluorescein isothiocyanate (FITC), and ethidium bromide (EtBr).

Nonnegative matrix factorization for fluorescence microscopy

Modern laser-scanning and wide-field microscopes allow for rapid acquisition of the fluorescence emissions in several spectral channels at each pixel of an image. In the absence of nonlinear effects, the recorded signal y_ij at pixel j in channel i is the sum of the contributions of the different labels. The contribution of label k is proportional to its concentration x_kj at pixel j and the fraction a_ik of its emission that falls into channel i. This is summarized in the equation

$$y_{ij}=\sum _{k\text{=}1}^M{a}_{ik}{x}_{kj},$$ (1)

where the sum extends over all labels k = 1…M. Viewing y_ij, x_kj, and a_ik as matrices Y, X, and A, Eq. 1 can be written, apart from noise, as Y = AX. Typically, a researcher is interested in the concentration distributions, X, of the labels. If the spectra, A, are known, then X can be calculated from Y by “linear unmixing” (3,12). If A is not known, Y can be factorized into a pair of A^∗ and X^∗ in many different ways and additional assumptions have to be made to arrive at a unique solution. We will show that the trivial constraint, whereby all concentration and spectra have to be nonnegative, suffices in many cases to achieve a reliable decomposition of the image. Such a factorization into nonnegative A^∗ and X^∗ is efficiently achieved by an algorithm known as nonnegative matrix factorization (NMF) (13,14). NMF decomposes Y by an iterative minimization of a cost function, which reflects the deviation between the measured intensities and those predicted by the matrix product. The condition of nonnegativity is imposed by choosing nonnegative starting values and by choosing the update rules, such that no zero-crossings can occur. A detailed discussion of the estimation of matrices A^∗ and X^∗ from shot-noise-dominated microscopy data and a derivation of suitable update rules is presented in the Appendix.

Materials and Methods

Implementation and data processing

All algorithms were implemented as MATLAB functions (The MathWorks, Natick, MA). The image data were preprocessed by subtracting the constant background signal, which was measured from a dark region of the image or with the laser shut off. Subsequently, all pixels below a background threshold (typically 100 counts) and above a saturation threshold of 4000 counts (4096 is the maximal range of the analog-to-digital converter) were excluded from the analysis. The iterative algorithm was initialized by Gaussian spectra peaked at the wavelength of the reference spectra (Molecular Probes, Eugene, OR). The concentrations were initialized randomly and adjusted to the start spectra by 10 rounds of concentration updates only. The algorithm was run for 1000 iterations, which took ∼2 min for a typical data set in the case of NMF. Eventually, the concentrations at the excluded pixels were calculated by nonnegative linear unmixing using the estimated spectra and included in the image. A more complete account of our experience with different initial conditions, dependence on signal/noise ratio, and possible pitfalls is given in the Supporting Material.

Summary of sample preparation and microscopy

Reagents were obtained from Sigma Aldrich (St. Louis, MO) unless stated otherwise. Stress-fiber formation was facilitated by growing HeLa SS6 (kindly provided by Prof. Lührmann, Max Planck Institute for Biophysical Chemistry, Göttingen, Germany) and NIH-3T3 cells (DSMZ, Braunschweig, Germany) on fibronectin-coated coverslips. In the appropriate cases, cells were incubated with A555-conjugated transferrin (Invitrogen, Carlsbad, CA). The ensuing acrolein-paraformaldehyde fixation and Triton X-100 permeabilization allowed for simultaneous tubulin and F-actin (Sigma Aldrich and Invitrogen, respectively) stains. Finally, cells were mounted in EtBr-containing medium after RNase treatment.

Heterozygous, triple transgenic mice were generated by interbreeding the mouse lines TgN(Thy1-ECFP) (15), TgH(CX3CR1-EGFP) (16), and TgN(GFAP-EYFP) (15). These mice are characterized by selective expression of EGFP, EYFP, and ECFP, respectively, in microglia, subpopulations of neurons, and astroglia. Bright fluorescence can be detected in microglia, Bergmann glia, and mossy fiber terminals in the cerebellum. For imaging, transgenic mice (4 weeks old) were anesthetized and perfused transcardially with Hank's balanced salt solution (HBSS, Gibco, Gaithersburg, MD), followed by perfusion with 4% paraformaldehyde (PFA) in phosphate-buffered saline (PBS) for 15 min. The brain was removed and incubated in PFA overnight at 4°C. After washing twice in PBS, the cerebellum was dissected and 50-μm sagittal vibratome sections (VT 1000S, Leica Instruments, Nussloch, Germany) were prepared and mounted with Immu-Mount (Shandon, Pittsburgh, PA).

Images were acquired with an Axiovert 200M equipped with an LSM510-Meta confocal microscope (Carl Zeiss, Jena, Germany) using a 63×/1.2 NA water-immersion objective. The 458-, 477-, and 488-nm lines of a 40-mW argon laser were used at 100, 50, and 10% power, respectively. The HFT458 and HFT488 dichroic mirrors were used for the mouse tissue sections and cultured cell samples, respectively. Channel settings are different for the specific samples and are mentioned in the text and appropriate figure captions. Reasonable detector gains were used between 550 and 650 a.u. in the Zeiss AIM software. The raw data provided by the microscope software was used in the NMF algorithm, as described above.

Results

Single-exposure measurements

We first tested the NMF algorithm on an image stack generated from adherent NIH-3T3 fibroblast cells. Herein, nucleic acids (mainly ribosomal RNA and nuclear DNA) were labeled with EtBr (17,18); filamentous actin (F-actin) was stained with Alexa Fluor 532 (A532)-conjugated phalloidin, whereas tubulin was labeled with an Alexa Fluor 488 (A488)-linked antibody. The sample was imaged with a Zeiss LSM Meta 510 using eight evenly spaced spectral emission channels from 508 to 657 nm (width 21.4 nm) and excited with a 488-nm laser. Fig. 1 shows the measured images in the eight spectral channels on the left, and the estimated concentrations (X^∗) on the right. The label distributions, X^∗, of the three dyes were consistent with the known morphology of the sample. Closer inspection, however, shows that a faint replica of the tubulin structure is superimposed onto the image of F-actin stain, and similarly for the F-actin stain in the image of the DNA stain. This is a consequence of small deviations of the estimated spectra from the reference spectra, which we measured independently on singly stained samples (see Fig. 1, lower left). The spectrum of A488, for example, is too narrow. To compensate for this deviation, the algorithm assigns ∼10% of the photons originating from A488 to the F-actin image. The sum of 90% estimated A488 and 10% A532 yields precisely the true A488 spectrum.

Figure 1.

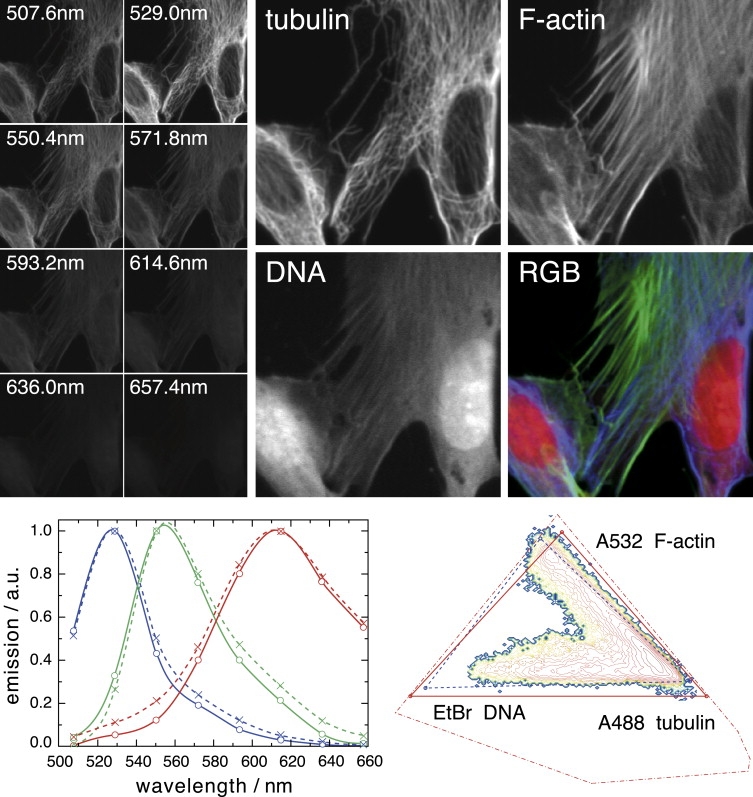
NMF estimation of spectra and label distributions of three spectrally and spatially overlapping labels; panel size 60 × 60 μm. (Left) The emission in eight spectral channels, ranging in wavelength from 508 to 657 nm, of NIH-3T3 fibroblasts, where tubulin is labeled with A488, F-actin with A532, and nucleic acids with EtBr. (Right) The estimated concentration maps for tubulin, F-actin, and nucleic acids. Images are rescaled by the inverse maximum, with relative scaling factors of 1, 0.51, and 0.18 for A488, A532, and EtBr, respectively. The F-actin image contains a faint replica of the tubulin structure, best visible in the lower-right nucleus region. Similarly, the nucleic acid stain was assigned a fraction of the emission of A532 (F-actin). The RGB false color representation of the individual concentration maps, with blue for tubulin, green for F-actin, and red for nucleic acids. (Lower left) Spectra plot from blue to red according to A488, A532, and EtBr. The estimated spectra (solid lines) are slightly narrower than the spectra measured in singly labeled specimens (dotted). (Lower right) The eight dimensional data vectors can be projected into a simplex plane (see text). The NMF run was initialized with Gaussian spectra with 524-, 558-, and 617-nm center positions and a full width at half-maximum (FWHM) of 75 nm.

Such problems in the decomposition are expected on theoretical grounds. They are due to the fact that any linear combination A^∗ = AB of the true spectra, A, such that A^∗ and X^∗ = B⁻¹X are nonnegative, is a valid solution of the matrix equation (Eq. 1) (B is a full rank M-by-M matrix). The cost functions for X and X^∗ are identical and therefore the minimization of the cost function may result in any such eligible linear combinations. This ambiguity is the basic problem of NMF. The main objective of our study is to explore its extent and to identify procedures for minimizing its consequences. To illustrate this issue in more detail, we consider a graphical representation of the fitting results. The high-dimensional vectors y_j representing the measured intensities at pixel j lie, up to fluctuations, in the three-dimensional subspace spanned by the three spectra of the dyes. In other words, y_j can be described by three scalars corresponding to the abundances of the labels, rather than by the intensities in each spectral channel. This subspace can be further reduced to two dimensions if absolute values are not relevant, as is the case for the ambiguity discussion. We therefore normalized all data points and spectra. A projection of this 2D space is shown in Fig. 1 (lower right) (see Supporting Material for details). We will refer to this representation henceforth as the “simplex”. The spectra returned by NMF are shown as red dots connected by red lines forming a triangle (the “NMF triangle”). As argued above, the NMF spectra are a linear combination of the reference spectra. The latter therefore can be represented in the same 2D subspace and are shown in blue as the reference triangle (Fig. 1, lower right). The density of the data points is represented in the diagram by color and contour lines. A pixel containing contributions from two of the three spectra will lie on the side of the reference triangle connecting the two dyes, whereas a pixel containing all three dyes will be located in the bulk of the triangle. Points outside the triangle correspond to negative contributions of one or several spectra. This observation highlights one central constraint to the possible decompositions: for all concentrations to be nonnegative, the NMF triangle has to include the cloud of data in the two-dimensional representations (apart from some scatter due to noise fluctuations). In the examples we studied, vertices of NMF triangles (representing the estimated spectra) often were located outside the reference triangle. NMF favors such decompositions, since they result in nonnegative coefficients even for many data points that lie outside the reference triangle. Spectra outside the reference triangle are narrower than the correct spectra and have reduced spectral overlap. Such spectra are allowed in NMF as long as all their individual values remain nonnegative. This restriction sets bounds to the decomposition errors. It also defines conditions under which the decomposition is unique. These are readily appreciated in the case of two overlapping dyes: subtracting fractions of one spectrum from another is only allowed if the spectrum to be subtracted vanishes at all wavelengths at which the other dye does not emit. This condition, termed condition 1 below, “protects” dyes emitting predominantly at long wavelengths (and not at short ones) against distortions by short-wavelength dyes.

In the more general case of several dyes, the domain of all nonnegative spectra can be defined algebraically (see Supporting Material). A mapping for the case of three dyes into the 2D diagram is shown by the dashed red polygon in Fig. 1 (lower right). Although these constraints strongly limit the set of possible solutions, it is obvious from the diagram that significant freedom remains and many solutions are equivalent from the NMF perspective. The outcome, therefore, can depend on initial conditions. The run in Fig. 1 was initialized with broad, heavily overlapping Gaussians centered at emission peaks of the respective dyes. Runs with narrow or random initial spectra are presented in the Supporting Material.

If the data points do not fill the reference triangle, NMF can also return spectra that lie inside the reference triangle. Such spectra are positive linear combinations of the reference spectra and therefore too broad. Deviations of this type are not possible if a sufficient number of data points lie on the boundary of the reference triangle. These data points represent pixels at which one dye is absent, whereas others are present. This condition will be termed condition 2 below. Note that this condition is much less restrictive than the requirement of singly labeled regions, which has to be fulfilled for the traditional acquisition of reference spectra.

Removing the ambiguity by applying constraints

The ambiguity of the NMF-decomposition can be removed by adding constraints or a bias that favors certain solutions (19). This is readily achieved during the iterative optimization procedure by adding a bias term to the cost function, derived from additional knowledge about spectra or label distributions. If it is known, for example, that labels are sufficiently segregated, i.e., condition 2 is fulfilled, the correct set of spectra is the one with the smallest possible triangle, which is equivalent to maximally overlapping spectra. To exploit this knowledge about the label distribution, we modified the NMF algorithm such that it returns the smallest possible triangle automatically. This can be achieved either by maximizing spectral overlap directly, or by favoring decompositions with segregated label distributions (20). For maximal label segregation, the data points have to be as close as possible to the boundary of the triangle, resulting in a bias toward small triangles. The latter strategy proved most robust, and we implemented this “segregation bias” by adding the ratio of the 1-norm to the 2-norm of the concentration vector at each pixel to the cost function. The implementation of these biases is detailed in the Appendix (Eqs. A6–A9).

As a test sample with segregated labels, we imaged vibratome sections of the cerebellum obtained from triple transgenic mice with cell-type-specific visible fluorescent protein expression (Bergmann glia, ECFP; microglia, EGFP; and neuronal mossy fibers, EYFP). Without the segregation bias, NMF estimated too narrow spectra, i.e., the NMF triangle was larger than the reference triangle, and the label distributions exhibited some cross talk (Fig. 2, upper row). When we increased the relative weight of the segregation bias, the spectra changed gradually and approached the actual spectra of the individual labels. At the same time, the three labels expressed in different cell types became perfectly separated (Fig. 2, middle row). One typically finds that spectra and concentrations change very little after λ exceeds a certain value, until eventually—upon further increase of λ—the additional term overwhelms the primary requirement to describe the data accurately. This is consistent with the interpretation that a variety of permissible solutions have almost identical cost functions and a small bias is sufficient to favor one over the others. Only a large bias will lead to spectra, which violate the nonnegativity requirement. Within an intermediate regime, the results are fairly independent of the choice of λ.

Figure 2.

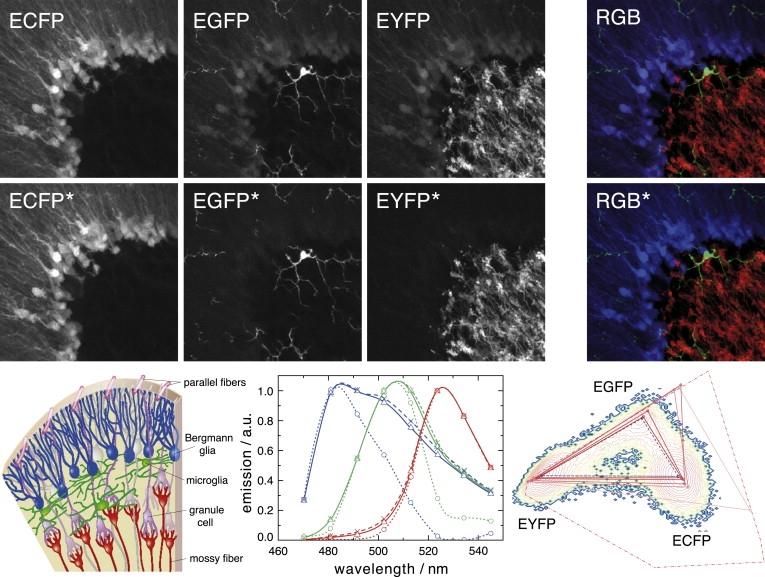
A segregation bias is necessary to find correct decomposition if spectra are overlapping strongly. A brain slice of a mouse expressing ECFP, EGFP, and EYFP in different cell types is imaged in eight spectral channels from 470 to 550 nm (z-stack image size 146 × 146 × 20 μm, z-projection presented). (Upper row) A bare NMF run returns concentration maps that exhibit some cross talk between the images. This corresponds to too-narrow spectra (dotted lines in spectra plot) and an NMF triangle much larger than the reference triangle (light red triangle in the simplex projection). (Middle row) When applying the segregation bias as described in the text, the NMF triangle gradually approaches the reference triangle (see Appendix, Segregation bias). For λ = 0.3, the different labels are well separated. The RGB panels show an overlay of ECFP (blue), (EGFP (green), and EYFP (red) (all channels are oversaturated by 1.5 for better visibility). (Lower row, left) Schematic drawing of the different cell types; (center) spectra plot of bare NMF (dotted lines), NMF with segregation bias (solid lines), and reference spectra from singly labeled specimens (dashed lines); (right) simplex projection with red triangles of resulting spectra with increasing segregation bias from light to dark red. The spectra change very little for λ > 0.2 and λ < 0.01, such that the result is independent of the precise value of λ. In all cases, the NMF run was initialized with Gaussian spectra with FWHM of 50 nm and centered between the half-maximum values of the literature spectra.

Although the segregation bias works well in many cases, it is not applicable if label distributions are not sufficiently segregated and the data leave large parts of the reference triangle empty, violating criterion 2. In this case, the bias will result in too small triangles and spectra that exhibit secondary peaks (see Supporting Material). However, even images with strongly overlapping label distribution often show sufficient signal modulation and fulfill criterion 2 approximately. The sample in Fig. 1 represents such a case. When we subjected it to a segregation bias, the tubulin pattern in the F-actin stain disappeared and the estimated spectra approached the true spectra. However, with such a bias, EtBr can develop a secondary peak at small wavelengths (see below and Supporting Material).

Furthermore, if colocalization versus segregation is the basis of the scientific question to be addressed, a segregation bias is certainly not an appropriate method, even if criterion 2 is fulfilled. In this case, a bias should be used that targets the spectral overlap directly.

Including prior knowledge about spectra

We have shown above that the ambiguity of NMF can be reduced by biases, based on qualitative knowledge about the distribution of labels (segregation). An alternative way of invoking prior knowledge is to determine the spectra of some of the components separately, estimating only the remaining spectra. This is especially valuable for dyes, which are faint and therefore hard to estimate. To explore this possibility, we labeled F-actin with FITC-conjugated phalloidin, tubulin with Alexa Fluor 514 (A514), allowed cells to import Alexa Fluor 555 (A555)-labeled transferrin, and stained for nucleic acids with EtBr in adherent HeLa SS6 cells. The transferrin stain was comparatively weak, and we fixed its spectrum to that provided by Molecular Probes (www.invitrogen.com). With a slight segregation bias as described above, NMF estimated the other three spectra with good accuracy and delivered satisfactory concentration maps for all four dyes (Fig. 3). In fact, the precise shape of the spectrum of a faint dye is not important, as long as it captures the peak. The remaining part of the emission is then assigned to other dyes, which does not make a big difference if such dyes are strong.

Figure 3.

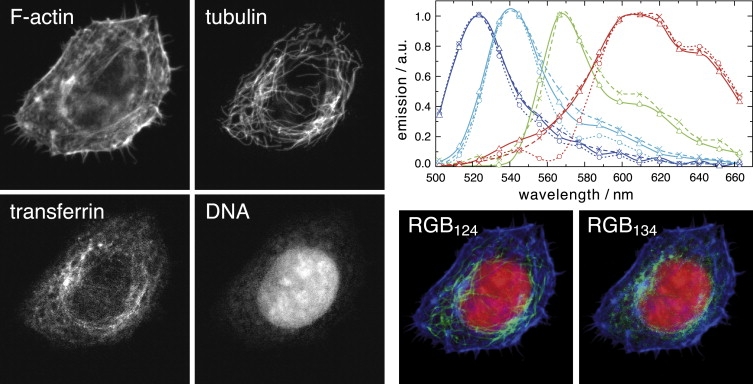
NMF is capable of separating four simultaneously present labels when the spectrum of one label is known. A HeLa SS6 cell labeled with FITC phalloidin F-actin, A514 tubulin, A555 transferrin, and EtBr DNA was excited at 488 nm and imaged over 16 spectral channels ranging from 503 to 663 nm (width 10.7 nm, image size 49 × 49 μm). A555 transferrin is the weakest label and its spectrum was fixed to the literature spectrum. Running NMF with a slight segregation bias yielded the label distributions and the spectra from blue to red according to FITC, A514, A555, and EtBr (dotted lines, bare NMF; solid lines, NMF with segregation bias; dashed lines, reference spectra from singly labeled specimens). Both the label distributions and spectra are estimated to high accuracy. The RGB panels show the false color overlay of F-actin (blue), tubulin (green), and nucleic acids (red) (RGB₁₂₄), and of F-actin (blue), transferrin (green), and nucleic acids (red) (RGB₁₃₄). The NMF run was initialized with Gaussian spectra with FWHM of 75 nm and 524-, 558-, and 617-nm center positions, which represent the FWHM centers of the literature spectra.

Post-NMF data processing

The strategies to reduce the ambiguity in NMF discussed so far involved the selection of a suitable bias, followed by an unsupervised run of the decomposition algorithm. For three dyes, there is an alternative strategy: The true spectra are (unknown) points in the 2D representation of the decomposition by NMF, and one can attempt to identify the appropriate spectra interactively. To this end, we created a software tool. After an initial NMF run, the tool presents the user with a 2D representation of the data density and the NMF triangle (similar to the simplex projections in Figs. 1 and 2). It also displays the NMF spectra and the label distributions. The user can now explore the set of possible spectra by moving the mouse cursor within the domain of nonnegative spectra. The tool calculates and displays the spectrum that corresponds to the position of the mouse cursor in real time. Once a satisfactory spectrum is found, the user can drag the corresponding vertex of the NMF triangle to the new location. The software then rapidly recalculates the label abundances. This way, secondary spectral peaks that may emerge as the consequence of a segregation bias (see above) can readily be removed. It is our experience that for two to three dyes, it is straightforward to arrive at a unique solution, which has neither unusual features in the spectra nor cross talk between images in the form of shadows of characteristic structures (see Supporting Material for an example). The successful application of this tool depends critically on a reasonable starting decomposition, such that each of the labels dominates one of the decomposed images. NMF almost always delivers appropriate starting values.

Multiple-exposure measurements

Commonly used dyes differ not only in their emission spectra but also in their excitation spectra. If the same sample is imaged with different excitation wavelengths, the relative strengths of the dyes will vary from excitation to excitation, whereas the spatial distributions and the emission spectra remain unchanged. These differences in excitation efficiency contain very valuable information for decomposing the image. Furthermore, it is much easier to collect a sufficiently large number of photons from each dye, since excitation wavelengths can be chosen such that each dye is strongly excited at least once. To handle such three-dimensional data (excitation wavelength, emission channel, and image pixels), NMF has to be generalized to what is known as nonnegative tensor factorization (NTF) (21) or parallel factor analysis (PARAFAC) (8,11). We derived update rules for NTF that account for the Poisson distribution of photon counts in fluorescence microscopy (see Appendix, Eq. A12).

We applied NTF to an image of the quadruply labeled cells of the previous section. The samples were imaged using the excitation wavelengths 458 nm, 477 nm, and 488 nm. The emission was recorded in 16 channels from 502 to 663 nm (width 10.7 nm). NTF, initialized with Gaussian spectra, estimated all four spectra and label distributions correctly, although the excitation efficiencies of the dyes chosen do not differ greatly (Fig. 4).

Figure 4.

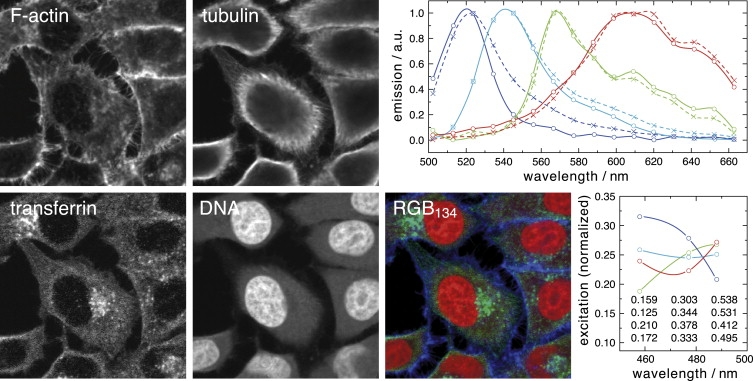
Multiple excitations allow the separation of greater numbers of labels. HeLa SS6 cells labeled like the sample in Fig. 3 were excited at 458, 477, and 488 nm while the emission was being recorded in 16 channels from 503 to 663 nm (image size 73 × 73 μm). NTF delivered the label distributions (FITC F-actin, A514 tubulin, A555 transferrin, and EtBr DNA); the RGB₁₃₄ panel shows the false color overlay of F-actin (blue), transferrin (green), and nucleic acids (red); the spectra (upper right) are colored from blue to red according to FITC, A514, A555, and EtBr (solid lines, NTF; dashed lines, reference spectra from singly labeled specimen) and the normalized excitation efficiencies of the four labels (absolute values in table) without invoking auxiliary assumptions are shown in the lower right corner. Only the spectrum of FITC (blue) shows a significant deviation, which is due to cross talk between FITC and A514. Their excitation efficiencies are exactly collinear, such that multiple excitations do not provide additional information. Hence, we encounter too-narrow spectra, as already discussed for a single excitation. For the run shown, we used Gaussian waveforms with the width and peak position obtained from literature spectra.

Another example with substantial variation in excitation efficiency is provided by the brain slice expressing ECFP, EGFP, and EYFP (see above). We used the same excitation wavelengths as above and recorded emissions in eight spectral channels ranging from 470 to 545 nm. Channels of wavelengths shorter than the respective excitation wavelengths were excluded from the analysis (NTF seamlessly integrates overlapping spectral ranges in different excitations (see Appendix)). The algorithm reliably separated the raw data into three components that corresponded to ECFP, EYFP, and EGFP, without invoking any of the additional constraints required for single-shot measurements.

Care has to be taken that neither the sample nor the apparatus drift between successive illuminations. NTF will fail in such cases, unless images are brought into register before processing. NTF is also prone to get stuck in local minima. The latter, however, is rarely a problem since good initial guesses for spectra are usually available from the literature.

Discussion

The conventional technique in fluorescence microscopy of separating fluorescent labels using optical filter cubes limits the choice of fluorophores to those with well-separated spectral bands. Newer methods to overcome this limitation include multiepitope-ligand cartography (22), methods using multiple excitations or fluorescence lifetime information (4–6), and methods of spectral fingerprinting (3,23). The latter method can be used on laser-scanning and wide-field microscopes, which provide spectrally resolved data. Data sets from such microscopes typically consist of image stacks of the emissions at up to 32 different wavelengths. We investigated the potential of BSS techniques to decompose such data into the contributions by the individual labels, when emission spectra are not, or are only approximately, known.

Different BSS algorithms use different criteria to determine the sources. Principal component analysis, for example, decomposes the data into eigenvectors of the covariance matrix of the data, yielding orthogonal sources. Independent component analysis tries to find a representation of the data in which different sources are as statistically independent as possible. However, typical spectra are not orthogonal, nor are the label distributions independent. On the other hand, both spectra and label concentrations are strictly nonnegative. This is why we suggest NMF and NTF as the methods of choice. Nonnegativity is a mild constraint and little prejudice is implicit in the algorithm. The flip side, however, is that the nonnegativity constraint provides a unique decomposition only if conditions 1 and 2, formulated above, are fulfilled. In that case, only one nonnegative solution is possible, for geometrical reasons. Condition 1 states that each label must not emit in at least one spectral channel where the other labels do, whereas condition 2 states that the image has to contain pixels in which one dye is absent and others are present in various concentration ratios. This ensures that the boundary of the simplex formed by the data is well defined. Both conditions are much less restrictive than those required for conventional techniques, where singly labeled regions of interest or spectral channels with emissions of only one dye are necessary. In other words, the conditions are relaxed from “all absent but one” to “one absent at a time”. If only one of the conditions is violated, we nevertheless can retrieve a unique (and correct) solution by biasing the algorithms toward well-segregated label distributions (if condition 2 is fulfilled) or else toward spectra with minimal or maximal overlap (if conditions 1 or 2, respectively, are fulfilled). Even when these conditions are only approximately fulfilled, the algorithm yields satisfactory results. However, it has to be stated clearly that the algorithm is not applicable to samples where both conditions are grossly violated, i.e., where label distributions are similar and spectra overlap strongly. As fluorescence microscopy data is often noisy, the two conditions are somewhat soft, and confidence intervals for the estimated spectra will depend on the degree to which the conditions are fulfilled. The problem of ambiguous solutions can be overcome by using multiple excitations and NTF.

We also created a tool that allows one to interactively correct for errors in the decomposition provided by the NMF algorithm. The best way to use this tool is to obtain an NMF run with a mild segregation bias. This usually provides decompositions in which the strongly represented labels are estimated quite accurately. Weakly represented labels may be contaminated by “ghost images” of the strong ones, whereas their spectra may show secondary peaks. The shape of the spectra and possible cross talk between images is then readily corrected by eliminating such obvious artifacts.

Alternatively, it is straightforward to fix the spectra of a subset of labels to predetermined ones. This is indicated for weak labels with broad spectra and also for handling autofluorescence. Such constrained optimization can also be used to test whether the spectrum of a dye deviates in a given region from a known spectrum. To this end, one spectrum can be fixed to the known spectrum in an NMF run with one additional free spectrum. If the sample contains regions where the spectrum deviates from the reference spectrum, NMF will yield a new spectrum localized to those regions, e.g., organelles. In this sense, NMF can be used as an analytical tool.

We have also shown that combining data from multiple excitations at different wavelengths greatly facilitates the decomposition. We anticipate that a large number of labels can be separated when patching together measurements, each one exciting a subset of the dyes. The full potential of NTF is still to be explored.

Appendix

The light y_ij recorded in a particular channel i at a given pixel j is a sum of the contributions of the labels present at the pixel. The contribution of dye k is proportional to its concentration, x_kj, at this pixel and to the contribution of its emission, a_ik, that falls into the spectral range of channel i. Hence, we have

$$y_{ij}=\sum _{k\text{=}1}^M{a}_{ik}{x}_{kj},$$ (A1)

where the sum runs over all dyes k = 1,…M. This model is conveniently written as the matrix equation Y = AX, which describes all pixels simultaneously. This equation, however, is not quite correct, since it equates the actual signal, y_ij, with the expected signal, $\sum _k{a}_{ik}{x}_{kj}$. This distinction is necessary, since light emission from fluorophores is not a deterministic process but the number of detected photons is distributed according to a Poisson distribution with mean AX, i.e., the recorded signal Y will scatter around AX. Our aim here is to estimate A and X from a noisy, spectrally resolved image Y. To this end, we determine matrices A^∗ and X^∗ that maximize the probability of measuring Y, assuming a Poisson distribution of the data, which implies minimizing the negative log-likelihood function

$$C({\mathbf{A}}^{\ast },{\mathbf{X}}^{\ast }|\mathbf{Y})=\sum _{i,j}\left[\sum _k{a}_{ik}{x}_{kj}-y_{ij}\ln \left(\sum _k{a}_{ik}{x}_{kj}\right)\right]+\text{const}\text{.},$$ (A2)

where i is the index of spectral channels, k that of labels, and j that of pixels of the image, and const. represents all terms that do not depend on A or X. To distinguish inferred quantities from the actual one, we mark them with an asterix (A^∗ and X^∗ versus A and X; for the lower case quantities this is omitted for clarity). Since spectra and concentrations are nonnegative quantities, the minimization has to be restricted to purely nonnegative values. This kind of minimization problem, where one matrix Y is approximated by a product of two nonnegative matrices A^∗ and X^∗, is known as nonnegative matrix factorization. Such a minimization is efficiently performed by iterative algorithms with multiplicative update rules that preserve the sign of the matrix entries (13,14). Following closely the derivation given in Lee and Seung (14), we derive multiplicative update rules for the cost function (Eq. A2). One begins by considering an ordinary gradient descent with step size η_rs

$$a_{rs}\leftarrow a_{rs}-{\eta }_{rs}\frac{\partial C}{\partial a_{rs}}=a_{rs}-{\eta }_{rs}\sum _j\left[x_{sj}-\frac{y_{rj}}{\sum _k{a}_{rk}{x}_{kj}}{x}_{sj}\right],$$ (A3)

as shown here for a_rs, with similar rules for x_rs. The step size can now be chosen to be ${\eta }_{rs}=\frac{a_{rs}}{{\sum }_j{x}_{sj}}$, in which case the update rule becomes multiplicative and preserves nonnegativity. The update rule for concentrations can be derived analogously, and when alternating the two update steps, we arrive at

$$\begin{array}{c}{a}_{rs}\leftarrow \frac{a_{rs}}{\sum _j{x}_{sj}}\sum _j\frac{y_{rj}}{\sum _k{a}_{rk}{x}_{kj}}{x}_{sj}\\ x_{rs}\leftarrow \frac{x_{rs}}{\sum _i{a}_{ir}}\sum _i\frac{y_{is}}{\sum _k{a}_{ik}{x}_{ks}}{a}_{ir}\end{array}\text{.}$$ (A4)

It can be shown that these update rules converge to a local minimum of the cost function using arguments similar to those of Lee and Seung (14).

In the main text, we discuss that the factorization of Y into A^∗ and X^∗ is not unique in many cases. For any invertible matrix B, an equally valid decomposition of the data is given by

$$\mathbf{Y}={\mathbf{A}}^{\ast }{\mathbf{X}}^{\ast }=\mathbf{A}\mathbf{B}{\mathbf{B}}^{-1}\mathbf{X}=\mathbf{A}\mathbf{X},$$ (A5)

provided ${\mathbf{A}}^{\ast }=\mathbf{A}\mathbf{B}$ and ${\mathbf{X}}^{\ast }={\mathbf{B}}^{-1}\mathbf{X}$ have nonnegative entries only. The range of permissible matrices B depends on the spectral and spatial overlap of the sources. To overcome this ambiguity, we suggest the use of several biases that favor some solution to others.

Segregation bias

When the label distributions are highly modulated, such that all possible combinations of label concentrations occur, the correct solution is the one with maximally overlapping spectra and segregated labels. To bias the NMF algorithm toward such solutions, we add the following term, E, to the cost function (Eq. A2)

$$E=-\lambda \sum _j\frac{\sum _k\left|x_{kj}\right|}{\sqrt{\sum _k{x}_{kj}^2}}\text{.}$$ (A6)

The first sum extends over all pixels, the fraction is the ratio of the 1-norm to the 2-norm of the concentration vector at pixel j, and λ is the weight of the additional term. The ratio of the 1-norm to the 2-norm is 1 if only one label is present at the respective pixel, whereas it is equal to $\sqrt{M}$ if M labels are present in equal amounts. Hence, the term is smaller the better segregated the labels are. The prefactor λ is used to adjust the importance of the bias relative to the original cost function. This additional term changes the update rules for the concentrations to

$$x_{rs}\leftarrow \frac{x_{rs}}{\sum _i{a}_{ir}}\left[\sum _i\frac{y_{is}}{\sum _k{a}_{ik}{x}_{ks}}{a}_{ir}-\lambda \left(\frac{1}{{\left(\sum _k{x}_{ks}^2\right)}^{0.5}}-\frac{x_{rs}\sum _k{x}_{ks}}{{\left(\sum _k{x}_{ks}^2\right)}^{1.5}}\right)\right]\text{.}$$ (A7)

Biasing spectral overlap

To control the overlap of the spectra, we propose to maximize or minimize the overlap between pairs of spectra in certain circumstances. This can be achieved by adding the term

$$F=\sum _{v<w}{m}_{vw}\sum _i{a}_{iv}{a}_{iw}$$ (A8)

to the cost function. The matrix elements, m_vw, specify the weight of the bias for each pair of dyes v,w, whereas the second sum over i is simply the scalar product between the spectra of dyes v and w. With this addition, the update rule for the spectra changes to

$$a_{rs}\leftarrow \frac{a_{rs}}{\sum _j{x}_{sj}}\left[\sum _j\frac{y_{rj}}{\sum _k{a}_{rk}{x}_{kj}}{x}_{sj}-\sum _v{m}_{vs}{a}_{rv}\right]\text{.}$$ (A9)

This shows that during one update, a small fraction of the spectrum of one dye is subtracted or added (depending on the sign of m_vw) from another dye.

The update rules including biases can lead to negative values. However, for reasonably small biases this is rarely the case. If some concentrations or spectra do become negative during the update, they should be set to small positive values.

Multiple excitations

The excitation efficiencies of most labels depend on the wavelength of the excitation light. Hence, the different labels contribute with different intensities when the same sample is imaged at different wavelengths. This can be incorporated into our data model by assigning an excitation efficiency q_kl to dye k at excitation wavelength l. The signal expected at the pixel k in the emission channel i and excitation wavelength l is given by

$$y_{ijl}=\sum _k{a}_{ik}{x}_{kj}{q}_{kl},$$ (A10)

where the sum extends over the labels in the sample. The cost function for a Poisson distribution of light intensities is essentially unchanged and given by

$$C({\mathbf{A}}^{\ast },{\mathbf{X}}^{\ast },{\mathbf{Q}}^{\ast }|\mathbf{Y})=\sum _{i,j,l}\left[\sum _k{a}_{ik}{x}_{kj}{q}_{kl}-y_{ijl}\ln \left(\sum _k{a}_{ik}{x}_{kj}{q}_{kl}\right)\right]\text{.}$$ (A11)

Methods to infer the three matrices A^∗, X^∗, and Q^∗ from the three dimensional data, y_ijl, are known as PARAFAC (11) or nonnegative tensor factorization (21). While PARAFAC often resorts to alternating least-square updates, NTF algorithms are a direct generalization of NMF that naturally preserves positivity. For the above cost function, we derived the update rules

$$\begin{array}{c}{a}_{rs}\leftarrow \frac{a_{rs}}{\sum _{j,l}{x}_{sj}{q}_{sl}}\sum _{j,l}\frac{y_{rjl}}{\sum _k{a}_{rk}{x}_{kj}{q}_{kl}}{x}_{sj}{q}_{sl}\\ x_{rs}\leftarrow \frac{x_{rs}}{\sum _{i,l}{a}_{ir}{q}_{sl}}\sum _{i,l}\frac{y_{isl}}{\sum _k{a}_{ik}{x}_{ks}{q}_{kl}}{a}_{ir}{q}_{lr}\\ q_{rs}\leftarrow \frac{q_{rs}}{\sum _{i,j}{a}_{ir}{x}_{sj}}\sum _{i,j}\frac{y_{ijs}}{\sum _k{a}_{ik}{x}_{ks}{q}_{kl}}{a}_{ir}{x}_{rj}\end{array}\text{.}$$ (A12)

The update rules can be derived in very much the same way as those described for NMF above. If the spectral channels recorded differ for different excitations, the summations on the righthand side of Eq. A12 have to be restricted to the relevant channels for each excitation.

It can be shown that the decomposition into A^∗, X^∗, and Q^∗ is unique if the sources differ sufficiently in their spectra, A, their concentration distribution, X, and their excitation spectra, Q. More specifically, the decomposition is unique if (11,24)

$$\mathrm{k}\left(\mathbf{A}\right)+\mathrm{k}\left(\mathbf{X}\right)+\mathrm{k}\left(\mathbf{Q}\right)\ge 2M+2,$$ (A13)

where k(A) is the k-rank of matrix A and M is the number of dyes. The k-rank is the maximal k such that any combination of k columns of A has full rank.

An implementation of the NMF algorithm as an ImageJ plugin can be obtained at http://www.mh-hannover.de/cellneurophys/poissonNMF.