Abstract
Long timescale (>1 μs) molecular dynamics simulations of protein folding offer a powerful tool for understanding the atomic-scale interactions that determine a protein's folding pathway and stabilize its native state. Unfortunately, when the simulated protein fails to fold, it is often unclear whether the failure is due to a deficiency in the underlying force fields or simply a lack of sufficient simulation time. We examine one such case, the human Pin1 WW domain, using the recently developed deactivated morphing method to calculate free energy differences between misfolded and folded states. We find that the force field we used favors the misfolded states, explaining the failure of the folding simulations. Possible further applications of deactivated morphing and implications for force field development are discussed.
Introduction
Computational efforts to study the folding process of proteins have long accompanied experimental studies of protein folding pathways and kinetics, beginning with lattice models (reviewed in (1)) and more recently progressing to atomistic or coarse-grained simulations of protein folding trajectories or folding-unfolding equilibria (e.g., (2–6)). Such simulations have always faced multiple technical and practical challenges, chief among them problems of timescale and accuracy. The fastest folding full-length proteins currently known require 0.7–1.0 μs to fold (7,8) with a hypothesized limit at approximately (N/100) μs for an N residue protein (9); only recently have atomistic molecular dynamics (MD) simulations with explicit solvent on microsecond timescales become feasible (10–12). At the same time, all MD simulations are reliant on the force field used to both correctly identify the native state of the protein as lowest in free energy and to provide a realistic description of the intermediate structures encountered during folding and the transitions between them (13). While numerous successes of all-atom MD in folding proteins to near-native or native states illustrate that in many cases an accurate treatment is possible, recent studies have also found hurdles such as a preference for helical structures in many force fields (14–16) and failures to consistently rank folded structures of proteins as free energy minima (17,18). Additional concerns have been noted for implicit-solvent folding simulations, which may yield free energies for folding intermediates that are different from those obtained through explicit solvent MD (18,19).
The combination of recent research into identifying fast folding proteins (8,20,21), improving performance of molecular dynamics software, and ever-increasing scientific computing resources has made it possible to perform the multiple microsecond, explicit solvent MD simulations necessary to observe complete protein folding events. Using a selected subset of the machines available to their Foldinghome effort, Ensign et al. recently presented a large ensemble of folding trajectories for a fast folding villin mutant (11). We recently reported a 10-μs trajectory of the fast-folding human Pin1 WW domain mutant Fip35 beginning from an unfolded state; however, an array of helical structures was observed instead of the expected β-sheet structure (12).
WW domains are small, antiparallel three-strand β-sheet proteins; we focus on the human Pin1 WW domain, which has a well-characterized folding mechanism in which formation of the first turn is the rate-limiting step (22). More recent experimental studies on a variety of Pin1 WW domain mutants showed that mutants with increased melting temperatures tended toward incipient downhill or downhill folding behavior (23). Simulations of Pin1 WW domain folding using Gō-like models have yielded a variety of hypotheses for the order of folding, either with the hydrophobic core forming first (24) or last (25), and with the potential for different orders of β-sheet assembly at different temperatures (26).
All-atom molecular dynamics simulations using physics-based potentials could provide valuable additional information on the folding process of the Pin1 WW domain and aid in distinguishing between proposals from previous simulations, allowing for greater understanding of the role of factors such as nonnative interactions and solvent effects. However, the failure of a 10-μs trajectory starting from a fully denatured Pin1 WW domain mutant to show any progress toward a nativelike structure (12) raises the specter of the challenges to molecular dynamics discussed earlier. Clearly the simulation failed to properly treat WW domain folding, but whether this failure is due to kinetic trapping, a fundamental thermodynamic problem in the force field, or some other issue, is unclear. To distinguish between these possibilities, we performed three additional multiple-microsecond folding simulations of the WW domain from different starting conditions. In addition, the recently developed deactivated morphing (DM) method (27) was used to calculate free energy differences between the native state and three commonly observed helical states in the folding trajectories. We find that under the simulation conditions used, all three helical states are favored over the native state by 4.4–8.1 kcal/mol. In addition, with defined free-energy differences between chosen reference structures, the effects of perturbations to the bonded and nonbonded parameters on the overall free energy differences between conformations can be studied. The DM procedure can thus be used in establishing a foundation for other free energy calculations where more than one conformational state of a protein must be studied, and in testing the effects of alterations to the potential energy functions used for MD simulations.
Methods
Molecular dynamics
All simulations were carried out using the development version of NAMD 2.7 (28). As in Freddolino et al. (12), appropriate mutations were applied to a Pin1 WW domain crystal structure (PDB code 2F21 (29)) to yield the sequence described in variant 23 from Liu et al. (23), which is referred to as Fip35. The protein was solvated in a cubic box of 10,014 TIP3P water molecules and neutralized with 30 mM NaCl using VMD (30). Starting structures for folding simulations were generated either by setting all (ϕ, ψ) angle pairs to (−135,135) for SimFold1 and SimFold2, or for SimFold3 and SimFold4 by generating two separate thermally denatured states through simulation at 490 K for 100 ns, in both cases yielding structures with no sheet or helix structure (as calculated by STRIDE (31)). The denatured starting structures for SimFold3 (SimFold4) had Qres (32) of 0.139 (0.183), Cα-RMSDs to the folded structure of 13.1 Å (10.2 Å), and radii of gyration of 14.0 Å (12.8 Å) (compare to 9.7 in the folded structure), respectively. The starting structures were subjected to 3000 steps of minimization and 100 ps of NVT equilibration before production runs, using a periodic cell size obtained from a 100-ps NPT equilibration of the wild-type Pin1 WW domain structure. For SimFold1 and SimFold2 different initial velocities (and a different series of random number seeds for the thermostat) were used, although the initial protein conformations were identical.
Except where otherwise noted, the CHARMM22 force field with CMAP corrections (33) was used for the protein. Short-range nonbonded interactions were cut off at 8.0 Å with switching beginning at 7.0 Å; long-range electrostatics was treated using the particle-mesh Ewald method. All bonds involving hydrogens in the protein were constrained using the RATTLE algorithm (34) with water geometry maintained using SETTLE (35). An integration timestep of 2.0 fs was used, with bonded and short-range interactions evaluated every timestep and long-range electrostatics once every three timesteps. A temperature of 337 K was maintained using a Langevin thermostat with a damping constant of 0.1 ps−1. Cluster analysis used the g_cluster module of GROMACS 3.3 (36) with the GROMOS clustering method (37); further details are provided in Cluster Analysis of Folding Trajectories in Supporting Material. Free energy calculations (see below) were performed in the NPT ensemble using a Nosé-Hoover Langevin piston barostat (28) with a period of 200.0 fs and damping timescale of 100.0 fs. For the free energy calculations, a Langevin damping constant of 1.0 fs−1 was used, and coordinates and other data were saved once every 100 fs.
Free energy calculations
Deactivated morphing (DM) between sheet and each of helixU, helixL, and helixV was performed as described in Park et al. (27), with the details of all calculations and modifications of the original DM procedure described in The Deactivated Morphing Process in Supporting Material. In brief, the calculation of the conformational free energy difference between any two reference conformations is divided into a series of steps between intermediates. We refer to the unrestrained ensemble of structures within a specified protein RMSD cutoff of a reference conformation as E; the state with harmonic restraints applied to all protein atoms restraining it to the reference conformation with κ = 1000 kcal/mol Å as K1; the deactivated state with all protein atoms restrained to their coordinates in reference state as Q; and a “dummy” state with a uniform set of van der Waals parameters and charges applied as D (see The Deactivated Morphing Process in Supporting Material). Calculation of the free energy difference between the unrestrained ensembles E(A) and E(B) for reference conformations A and B is thus performed by following a path from E(A) through the increasingly restrained states to D(A), then morphing D(A) to D(B) along the least-squares path (38), and finally following a path of decreasing restraints to E(B); this process is shown schematically (see Fig. 3). Each of the transitions is further subdivided to provide sufficient overlaps between adjacent states, as detailed in the Supporting Material. For the case of morphs involving helixU or helixV, an additional step needed to be taken to account for the effects of a site-bound water in the reference structure (see Site-bound waters, in The Deactivated Morphing Process, Supporting Material); the free energy difference from this added step is included in the morphing step (see Fig. 3) and in the discussion below.
Figure 3.
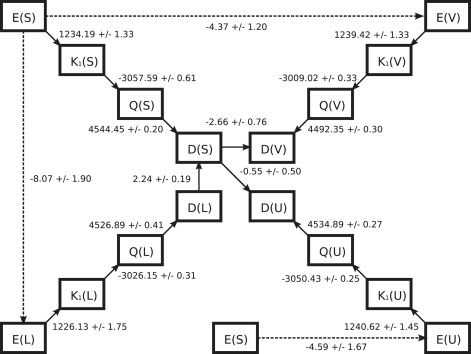
Schematic of deactivated morphing between sheet (S) and three helical conformations (L, U, and V for helixL, helixU, and helixV). Solid arrows represent transitions, which were calculated using deactivated morphing, with the dashed arrows showing the sum over the path of calculated transitions between two unrestrained states. All energies given in kcal/mol.
Error analysis for all free energy calculations was performed using block averaging; all data were split into 10 blocks, the first block was discarded, and then free energy calculations were performed independently for the data in each of the nine remaining blocks, with the mean of these block estimates corresponding to the reported value and error bars given as ±2σ /, with σ the standard deviation of the block estimates.
Results
To aid in ruling out kinetic trapping or a single pathological trajectory in the failure of WW domain folding in previous simulations, three long-timescale folding trajectories were run, one (SimFold2) starting from the same fully extended conformation as in the previous work (12) and run for 3.4 μs, and two (SimFold3 and SimFold4) starting from heat-denatured structures (see Materials and Methods) and run for 4.1 and 4.4 μs, respectively. For reference, the 200-ns native state simulation and 10.0-μs folding trajectory from our previous work are denoted SimCryst and SimFold1, respectively.
The secondary structure, fraction of native contacts Qres (32), exposed hydrophobic surface area, and Cα-RMSD observed in SimFold2, SimFold3, and SimFold4 are plotted in Fig. 1. A similar pattern to SimFold1 is observed in SimFold2 and SimFold3: the trajectories show rapid hydrophobic collapse, followed by the formation of mostly helical structure, which persists throughout the simulation. SimFold4 takes longer to reach helical conformations, as it spends most of the duration of the trajectory after its initial collapse in a coil state stabilized by an intricate network of salt bridges; however, even in this trajectory, stable helical structure forms after 2.5 μs. In no case is significant progress toward the native state observed, nor is any persistent β-structure formed. For reference, as reported previously, SimCryst showed that Fip35 is remarkably stable in a crystal-structure-like conformation over the 200-ns simulation, with no structures showing a Cα-RMSD >2.0 Å, and only one frame (at ∼61 ns) with an all-protein atom RMSD >4.0 Å, relative to the crystal structure.
Figure 1.
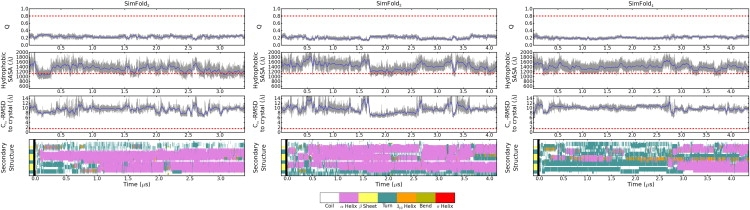
Properties of the WW domain in simulations SimFold2, SimFold3, and SimFold4. For Qres, solvent-accessible surface area of hydrophobic groups, and Cα-RMSD to the crystal structure, mean values from SimCryst for the native state are shown as dashed lines. Secondary structure throughout the simulations is plotted using the color scale shown below the figure.
As was the case for SimFold1, clustering analysis (see Cluster Analysis of Folding Trajectories, Supporting Material) illustrates that there is no one stable helical conformation being formed in any of the new folding trajectories; instead, a series of interconverting helical states are observed. While suggesting that the previous finding of mostly helical structure in SimFold1 was not a statistical anomaly, however, these additional simulations still cannot rule out the possibility that what is observed in the WW domain simulations is simply a case of conformational trapping, and that given a sufficiently long simulation (beyond the experimental folding timescale of the WW domain), the proper β-sheet structure would form.
To decisively distinguish between kinetic and thermodynamic problems in WW domain folding simulations, deactivated morphing calculations (27) were performed to calculate conformational free energy differences between the folded state and a set of three commonly occurring helical structures observed in the folding simulations.
Selection of reference structures
Deactivated morphing requires both the definition of reference structures for all endpoints being used, and choice of a criterion to define the conformational ensemble which will be included as part of that endpoint. Here we use the all-atom RMSD relative to the pertinent reference state to define the conformational ensembles; based on the observed fluctuations in SimCryst, a 4.0 Å cutoff is assumed unless otherwise noted.
In the absence of any obvious reference structure for the misfolded helical states, clustering analysis was performed using a 4.0 Å all-atom RMSD cutoff on each of SimFold1, SimFold2, and SimFold3 to identify candidate reference structures. For each identified cluster, the structure from that cluster with the lowest pairwise RMSD to all structures in the same cluster was taken as a representative, and the number of structures in SimFold1, SimFold2, and SimFold3 within 4.0 Å of this reference structure was calculated. For each simulation, the structure that included the largest total number of frames from the folding simulations in its defined conformational ensemble was taken as a helical reference conformation and further refined (see The Deactivated Morphing Process in the Supporting Material) to yield helixU (from SimFold1), helixV (from SimFold2), and helixL (from SimFold3); in the case of SimFold1 the second-highest occupancy cluster was used since the highest occupancy cluster was nearly identical to helixL. These reference conformations, along with the sheet state from SimCryst, are shown in Fig. 2. The fraction of frames from each folding simulation within 4.0 Å of the DM reference states is shown in Table 1; we note that while these populations may seem rather small, no more inclusive set of reference states could be identified, a fact attributable to the wide variety of different helical conformations observed in the folding simulations. The predominant helical structure formed during the latter half of SimFold4 is distinct from the common helical structures in the other three trajectories, and is not considered in the deactivated morphing calculations. While the use of other distance metrics such as dRMSD (39,40) for clustering might allow the identification of more consolidated clusters, RMSDs were used to maintain compatibility with the definitions of end states for deactivated morphing. It must be noted that SimFold3, and thus the structure chosen for helixL, contains a cis-peptide bond at PRO3. As seen in the clustering results, the structures occurring in SimFold3 were very similar to those in SimFold1 and SimFold2, likely because the N-terminus is part of an N-terminal coil in all major conformations observed, but the DM results for helixL sample only conformations with a cis bond at residue 3, and it is not clear exactly how similar the free energy of helixL-like conformations (such as those observed in SimFold1 and SimFold2) with a trans bond at PRO3 would be.
Figure 2.
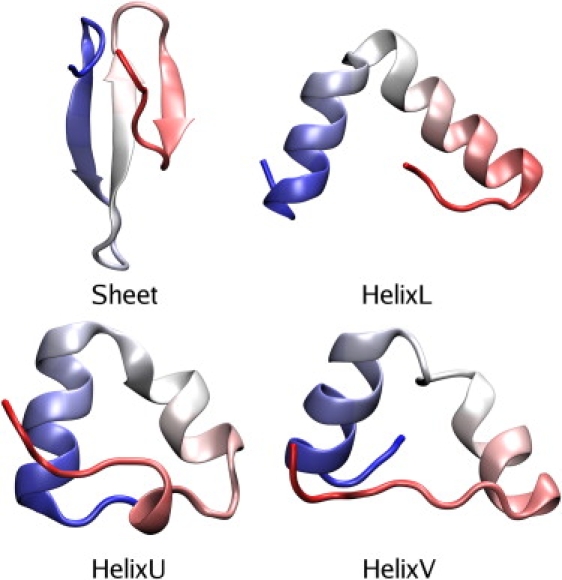
Cartoon representations of the reference structures used as endpoints for deactivated morphing simulations. Color scale runs blue to red from N-terminus to C-terminus.
Table 1.
Durations of all trajectories in this study, and the fraction of timesteps from each trajectory within 4.0 Å of each of the DM reference states
| Simulation | Duration (ns) | Fraction of timesteps within 4.0 Å of |
|||
|---|---|---|---|---|---|
| sheet | helixL | helixU | helixV | ||
| SimCryst | (200) | 1.000 | 0.000 | 0.000 | 0.000 |
| SimFold1 | (10000) | 0.000 | 0.053 | 0.042 | 0.025 |
| SimFold2 | 3384 | 0.000 | 0.000 | 0.014 | 0.048 |
| SimFold3 | 4139 | 0.000 | 0.068 | 0.000 | 0.000 |
| SimFold4 | 4357 | 0.000 | 0.000 | 0.000 | 0.000 |
Durations in parentheses indicate trajectories that were originally reported in Freddolino et al. (12). The total simulation time shown is 22 μs.
Conformational free energy differences between states
A schematic showing the free energy differences associated with each DM step is given in Fig. 3, with all pairwise free energy differences for the four reference structures shown in Table 2. All three helical states are significantly lower in free energy than the native state, and the free energy gap is observed to widen for larger ensemble cutoffs, likely reflecting the significant conformational freedom observed in the misfolded helical states during folding simulations. Given the presence of at least three local free energy minima corresponding to helical states which are several kBT below the free energy of the native state, it is not surprising that the WW domain did not fold in our simulations, and even longer simulations using the same parameters should not significantly occupy the folded state. The cis-proline containing helixL conformation is notably lower in free energy than any of the all-trans cases; it appears that this conformation is stabilized by the cis-PRO3, since trajectory SimFold3 showed little population of helixU and helixV-like conformations, whereas SimFold1 and SimFold2 show more even population of conformations resembling the DM reference structures (likely indicating that helixL-like conformations with trans-PRO3 are similar to helixU and helixV in stability).
Table 2.
Conformational free energy changes calculated via deactivated morphing for a transition from the state shown on top to the state shown at left
| State-state free energy differences (kcal/mol) | ||||
|---|---|---|---|---|
| State | sheet | helixL | helixU | helixV |
| sheet | ||||
| 2.0 | — | 7.28 ± 1.84 | 1.37 ± 1.65 | 0.08 ± 1.59 |
| 3.0 | — | 7.99 ± 1.84 | 3.75 ± 1.64 | 2.53 ± 1.37 |
| 4.0 | — | 8.07 ± 1.90 | 4.59 ± 1.67 | 4.37 ± 1.20 |
| helixL | ||||
| 2.0 | −7.28 ± 1.84 | — | −5.76 ± 1.73 | −6.76 ± 1.26 |
| 3.0 | −7.99 ± 1.84 | — | −4.08 ± 2.00 | −5.02 ± 1.13 |
| 4.0 | −8.07 ± 1.90 | — | −3.33 ± 2.16 | −3.26 ± 1.16 |
| helixU | ||||
| 2.0 | −1.37 ± 1.65 | 5.76 ± 1.73 | — | −1.65 ± 1.26 |
| 3.0 | −3.75 ± 1.64 | 4.08 ± 2.00 | — | −1.59 ± 1.18 |
| 4.0 | −4.59 ± 1.67 | 3.33 ± 2.16 | — | −0.58 ± 1.31 |
| helixV | ||||
| 2.0 | −0.08 ± 1.59 | 6.76 ± 1.25 | 1.65 ± 1.26 | — |
| 3.0 | −2.53 ± 1.37 | 5.02 ± 1.13 | 1.59 ± 1.18 | — |
| 4.0 | −4.37 ± 1.20 | 3.26 ± 1.16 | 0.58 ± 1.31 | — |
The numbering included with the destination states refers to the cutoff (in Å) used to define the unrestrained ensembles at both endpoints.
Decomposition of the conformational free energy difference into the changes associated with different DM steps (see Methods) can yield qualitative insight into factors contributing to the observed free energy difference. To a first approximation, the restraint step (E → K1) primarily represents the conformational and vibrational entropy of the protein in a given conformational well, the deactivation step (K1 → Q) represents the internal enthalpic interactions of the reference structure, and the combination of dummying (Q → D) and morphing (D → D) steps yields the difference in interactions with water between the two structures. The calculated free energy differences may be further understood through comparison with a number of characteristics of the reference states shown in Table 3.
Table 3.
Energetic and qualitative contributions for the DM reference conformations; ΔGsolv is the Poisson-Boltzmann solvation free energy
| Properties of DM reference conformations |
||||
|---|---|---|---|---|
| sheet | helixL | helixU | helixV | |
| UP, short (kcal/mol) | 2902.05 | 2870.45 | 2893.96 | 2852.60 |
| ΔGsolv (kcal/mol) | −403.82 | −526.58 | −350.23 | −268.28 |
| Hydrogen bonds | 21 | 27 | 21 | 24 |
| Backbone H-bonds | 11 | 19 | 13 | 13 |
| Salt bridges | 3 | 3 | 5 | 6 |
| SASA (Å2) | 2972.7 | 3071.1 | 3143.7 | 3019.7 |
| Hydrophobic SASA (Å2) | 1071.7 | 1301.2 | 1137.2 | 1319.5 |
Hydrogen bonds were calculated using a 3.5 Å heavy atom distance cutoff and 35° donor-hydrogen-acceptor angle cutoff.
Based on the rough breakdown of free energy contributions above, the free energies from the restraining step suggest that helixU and helixV have similar levels of conformational entropy, both greater than sheet, and helixL is significantly more constrained than three of the other states. While one might expect, based on AFM data, that all three helical states would be lower in conformational entropy than the sheet (41), both helixU and helixV have a relatively free C-terminal coil that likely contributes to their conformational freedom; it should also be noted that the free energy differences between these structures and sheet drops significantly for lower RMSD cutoffs defining the unrestrained ensemble E(A) (see Methods). Given the increasing favorability of helixU and helixV throughout the range of RMSD cutoffs that we included, it is likely that the helical states would be even more heavily favored for cutoffs above 4.0 Å, due to the wide variety of accessible helical conformations present in the trajectories; however, obtaining converged results for the restraining step becomes increasingly more difficult for larger cutoff values, and thus we restrict ourselves to a maximum of 4.0 Å all-atom RMSD.
Based on the energies from the deactivation step, all three helical states appear to have more favorable protein-protein interactions than sheet, which is also apparent in the total energy of internal interactions, UP,short (defined as all short-range interactions between protein atoms). Inspection of polar interactions in the reference states (see Table 3) illustrates that two of the three helical states contain more protein-protein hydrogen bonds than sheet, and that all three contain more backbone-backbone hydrogen bonds. In addition, helixU has two more protein-protein salt bridges, and helixV three more than sheet and helixL.
One particular concern that has been commonly raised in recent discussions of classical MD force fields is the treatment of hydrogen bonding primarily as a dipole-dipole interaction, which is known in some cases to lead to deviation from experimental and high-level theory data (42,43) and, for proteins, from the expected distribution of geometries from high-resolution crystal structures (44). To analyze the protein-protein hydrogen bonding geometries of the conformations in this study, the hydrogen-acceptor distance δHA, angle at the hydrogen Θ, angle at the acceptor Ψ, and acceptor antecedent dihedral angle X were plotted for a set of frames from the most weakly restrained states of the DM calculations (here we use the notation and definitions from (45)). These data are shown in Hydrogen Bonding Analysis in the Supplementary Material. The distributions of δHA, Θ, and X for backbone-backbone and sidechain-sidechain hydrogen bonds follow the general patterns observed in a survey of x-ray crystal structures (in (45)). In the case of Ψ angles, the backbone hydrogen bonds of the helical state follow the expected distribution, with a maximum occurring at ∼155°, likely due to other constraints imposed by this secondary structure (45); however, the distribution for backbone hydrogen bonds in sheet shows that the backbone-backbone hydrogen bonds here are mostly linear, and in both helixL and helixV the sidechain-sidechain hydrogen bonding also showed overpopulation of near-linear conformations. It is, however, somewhat remarkable that the Ψ angle distributions for side-chain hydrogen bonds were in all cases peaked near 120° rather than 180°.
The combined free energies for dummying and morphing steps (i.e., the path Q(S) → D(S) D(H) → Q(H)) for going from sheet to the helical states helixL, helixU, and helixV yield ΔG values of 15.32, 9.01, and 49.44 kcal/mol, respectively, suggesting that water interacts more favorably with sheet than any of the helical states. It should be noted that the favorability of sheet likely comes from specific polar interactions with water, since D(S) is less stable than the dummied helical conformations. As seen in Table 3, both the overall solvent-exposed surface area (SASA) and hydrophobic SASA are lower for sheet than the helical states. Of these, the overall protein SASA is expected to be approximately proportional to the entropy of solvation for a large hydrophobic or heterogeneous solute, although corrections are required for factors such as excluded volume, attractive solvent-solute interactions, and deviations from ideal behavior due to exposure of portions of solute too small for the SASA-based approximation to hold (46–50); the hydrophobic SASA simply provides a qualitative measure of how well packed the conformations are and how favorable the total free energy of solvation may be.
Effects of changes in the potential
The presence of calculated conformational free energy differences between the native state and multiple nonnative states that are favored by the force field allows the testing of changes to the potential which might be expected to change the ranking of these states, simply by calculating the effect of a proposed change on the free energy of each of the structural ensembles used in DM. Given that a relatively short real-space nonbonded interaction cutoff of 8 Å was used in the folding simulations, one can determine whether using a larger cutoff of 12 Å would stabilize the native state. Inspired by previous calculations on a WW domain in which backbone electrostatics and torsional terms were investigated to determine their effects on structure (14), we also calculated the internal energy change ΔUP,short of the protein in each reference conformation in the presence of increased and decreased backbone polarization, and with the CMAP correction removed (i.e., using the CHARMM22 backbone potential), in an effort to identify modifications that might favor the native state (data not shown). Only the removal of CMAP favored sheet relative to all three helical states, and thus the free energy change associated with removing CMAP corrections was also calculated for all four conformations. The complete set of intermediates simulated to investigate the effects of these changes to the potential is shown in Fig. S13 in the Supporting Material, with the calculated energies shown in Table 4.
Table 4.
Free energy changes for perturbing the potential in each of the four reference states
| Free energy differences for perturbations (kcal/mol) |
||||
|---|---|---|---|---|
| sheet | helixL | helixU | helixV | |
| A → B | 28.79 ± 0.84 | 24.58 ± 1.70 | 27.23 ± 1.86 | 29.01 ± 1.51 |
| A → C | −716.49 ± 0.48 | −716.37 ± 0.51 | −717.04 ± 0.63 | −716.43 ± 0.82 |
Endpoints are shown in Fig. S13; A, B, and C refer to states with the original simulation parameters, no CMAP correction, and 12 Å cutoffs, respectively.
As expected given the use of long-range electrostatics, expanding the short-range nonbonded cutoff from 8.0 Å to 12.0 Å does not significantly alter the free energy differences between states. Likewise, the removal of CMAP corrections does not stabilize sheet relative to helixU or helixV, and actually makes it less favorable relative to helixL. Thus, neither of the simple perturbations to the potential tested here significantly alters the helix-sheet equilibrium from the values obtained via deactivated morphing; the DM results do, however, provide a convenient scaffold for testing other modifications of the potential through a similar mechanism without needing to redo the complete DM calculations. It must be noted that the nonnative reference states chosen using the original potential will not necessarily represent local free energy minima in the new potential, and thus for some applications (for example, if alterations to the potential caused the native state to become more favorable than the misfolded states in this study) it may be necessary to perform further conformational sampling in the new potential to identify appropriate reference states.
Discussion
After consistent failure of the WW domain to fold into a native or near-native state over microsecond timescales in silico, one was left with the question of whether this failure was due to kinetic or thermodynamic inaccuracies. The deactivated morphing calculations presented here firmly indicate the latter; three helical misfolded states observed in folding simulations were all found to be >6 kBT lower in free energy than the native state. A set of related questions now arises; among them, questions of what energetic factors lead to this free energy gap, how the force field and simulation conditions might be modified to yield proper relative stabilities for different conformations of the WW domain, and whether the failure for this protein reflects a more systematic problem that would also occur for other, similar proteins.
A number of recent studies have indicated that modern MD force fields, including the CHARMM force field, slightly overestimate the presence of helical structure in small peptides (15,51). This may be associated with systematic errors in the protein backbone potential (investigated in (52)) along with inherent limitations in the simplified energy function used in protein force fields. Comparison of backbone-backbone hydrogen bonding patterns in the DM reference states to data from a survey of crystallographic structures (45) illustrated irregularities in the distribution of angles centered on the hydrogen and acceptor atoms, which might significantly affect the relative stability of the studied structures. Further calculations using a potential with explicit hydrogen bonding terms or other features designed to refine the treatment of hydrogen bonds (such as inclusion of virtual sites (53)) would be required to assess the effects of improved descriptions of hydrogen bonding on the structure of Fip35. The helical states of the WW domain in our simulations are also likely stabilized by the presence of additional protein-protein hydrogen bonds and salt bridges in all cases. Any inaccuracy in backbone hydrogen-bonding treatment, such as those discussed above, could also extend to sidechain-sidechain and sidechain-backbone hydrogen bonds and salt bridges.
Another possible cause for the overstabilization of helical states observed here is an artifact related to the system's periodicity. In a series of comparisons between MD simulations using Ewald electrostatics and continuum electrostatics calculations, it was found that unduly small periodic cells could overstabilize helical conformations of short polypeptides (54) or other compact conformations (55), and lead to biases on the order of a few kBT between different conformations in a nanosecond timescale MD trajectory of a 66-residue protein (56). While such periodicity artifacts cannot be ruled out in this study, a number of factors suggest that any such effects do not, on their own, lead to the free energy differences observed between WW domain conformations: the WW domain is smaller and less heavily charged than the solutes characterized in Kastenholz and Hunenberger (56), and is simulated in dilute NaCl in a large periodic cell (6.8 nm cube) given the size of the solute relative to the simulations in that study (56). In addition, the reference conformations being considered are similarly compact relative to each other, and the free energy differences between states are significantly larger than the maximum biases reported in Kastenholz and Hunenberger (56).
While the calculations presented here cannot firmly establish what factor or combination of factors in the force field leads to overstabilization of helical conformations of the WW domain, the decomposition of the free energy differences into differences between a series of intermediates indicates that internal protein-protein interactions favor the helical states, interactions with water (polar and apolar) favor the sheet state, and that helixU and helixV both have significant contributions to their conformational entropy from the wide variety of accessible conformations near the reference state. These contributors, of course, cannot be fully separated, as (for example) a refinement of the potential governing protein-protein interactions would also significantly affect the conformational entropy of the different states. The overpopulation of near-linear hydrogen bonding geometries in several of the simulations suggests one possible point of improvement for the potential, which could also significantly affect the overall helix/sheet ratio observed using CHARMM22 and other modern force fields. Sources of error other than the treatment of hydrogen bonding are of course also possible, such as failure to accurately treat the solvation free energy (which favors sheet); further simulations with water models other than TIP3P might help to address this possibility.
The effects of two simple and general perturbations to the potential, namely the removal of CMAP corrections and extension of the short-range nonbonded cutoff, were considered in this study. While those perturbations failed to significantly alter the observed difference in free energies between sheet and the helical states, they do illustrate how the results from DM can be used to test possible changes to the force field. Since the free energy difference between the native state and multiple decoy conformations can be calculated using the full potential in explicit solvent assuming some reference potential energy function, the free energy change for each of the reference states associated with perturbing the potential can then be used to determine whether that change favors the native state. If, as in the case of the WW domain, the native state is initially higher in free energy than some or all of the decoys, alterations to the potential to make it more stable than the other conformations would constitute a necessary (but not sufficient) modification to appropriately treat the folding and conformational equilibrium of the target protein. For example, approximations to the change in free energy in each reference conformation (see Corrective Perturbations to the Force Field in Supporting Material) show that altering the relative potential energy of the α- and β-region of the ϕ-ψ Ramachandran map by <0.45 kcal/mol would be enough to shift the balance between properly and improperly folded protein. Altering the hydration energy of amino acids by 13 kcal/mol would achieve a similar outcome, although in the latter case the magnitude of the needed perturbation appears to fall far beyond the acceptable range, based on previous studies indicating that current atomistic force fields (CHARMM, AMBER) are within 1–2 kcal/mol of experimental values (57,58). Additionally, such ad hoc corrections to the carefully parameterized CMAP and Lennard-Jones terms are unlikely to be generally applicable to systems other than the WW domain.
Improvement of a physics-based potential with implicit solvent to stabilize the native state of a protein has recently been used in tuning AMBER ff03 for use in structural refinement (17,59); similar tuning of the free energy differences between states using explicit solvent simulations based on deactivated morphing may also be useful for the refinement or testing of force fields for use in molecular-dynamics simulations. We must emphasize, however, that while the qualitative analysis of different components of the stability of the various conformations presented here can suggest factors that may be involved in the overstabilization of the helical states, it is not possible to unambiguously identify which of the competing physical effects involved is primarily responsible. It would, furthermore, be unrealistic to simply perturb single terms in the force field and attempt to identify one term to be corrected (for an example, see Corrective Perturbations to the Force Field in Supporting Material), because it is impossible to determine whether an altered term actually corrects an underlying physical defect in the force field or simply compensates for it sufficiently to stabilize the native state relative to misfolded states in the case of the WW domain. Such an effort would be physically meaningful only in the context of testing a complete, systematically parameterized force field with changes expected to correct factors such as the hydrogen bonding geometry noted here, and would preferably be performed on a variety of different proteins. The lack of directionality in hydrogen bonding has also recently been suggested as a possible cause for the failure of modern MD force fields to yield appropriate thermodynamics for helix/coil equilibria in primarily helical peptides (R.B. Best and G. Hummer, unpublished).
The deactivated morphing procedure presented in Park et al. (27) and applied here provides a rigorous method for determining the free energy difference between two defined conformational ensembles of a biomolecule in explicit solvent. As detailed in The Deactivated Morphing Process in Supporting Material, ∼300 ns of simulation were required for the transformation from E(A) to D(A) for each conformation A (see Methods), with an additional 50 ns of simulation for each morph between two conformations. While these computational costs are considerable, they are orders-of-magnitude less than the time that would be required to adequately sample both the helix and sheet structures in an equilibrium simulation (where sheet was never observed in 21.9 μs of simulation). Of the steps in DM, the restraining portion is by far the most expensive and carries the highest statistical uncertainty, so refinements to this portion of the procedure would be particularly useful. As in previous tests (27), it was found here that the relative free energy difference between two conformations due to the deactivation step can be approximated by the total internal potential energy of the protein, but unlike the case for decaalanine, the morphing component could not be adequately approximated by continuum electrostatics calculations for the WW domain.
In summary, to follow up on previous attempts to fold a fast-folding mutant of the human Pin1 WW domain in silico, we obtained three additional ∼4 μs MD trajectories of this protein, all of which formed similar distributions of misfolded helical states. Free energy calculations using deactivated morphing were then performed to determine the conformational free energy difference between the crystal structure and several commonly observed helical states, and indicated that the helical states are 4–8 kcal/mol more stable under these simulation conditions. Folding simulations of Fip35 will thus not be possible without alteration of the force field being used. As protein folding simulations and other long timescale MD simulations studying large conformational changes become increasingly common, force field parameterization or testing based on the establishment of proper free energy differences between chosen conformations of biomolecules become increasingly essential.
Acknowledgments
This work was supported by National Institutes of Health grant No. P41-RR05969 and National Science Foundation grant No. PHY0822613. Computer time was provided by the National Center for Supercomputing Applications through grant MCA93S028. P.L.F. has been supported by an National Science Foundation Graduate Research Fellowship.
The authors thank Dr. Chris Harrison for many useful discussions.
Supporting Material
References
- 1.Onuchic J.N., Wolynes P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 2.Lei H., Duan Y. Ab initio folding of albumin binding domain from all-atom molecular dynamics simulation. J. Phys. Chem. B. 2007;111:5458–5463. doi: 10.1021/jp0704867. [DOI] [PubMed] [Google Scholar]
- 3.Duan Y., Kollman P. Pathways to a protein folding intermediate observed in a 1 microsecond simulation in aqueous solution. Science. 1998;282:740–744. doi: 10.1126/science.282.5389.740. [DOI] [PubMed] [Google Scholar]
- 4.Simmerling C., Strockbine B., Roitberg A.E. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc. 2002;124:11258–11259. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 5.Chowdhury S., Lee M.C., Xiong G., Duan Y. Ab initio folding simulation of the Trp-cage mini-protein approaches NMR resolution. J. Mol. Biol. 2003;327:711–717. doi: 10.1016/s0022-2836(03)00177-3. [DOI] [PubMed] [Google Scholar]
- 6.Sanbonmatsu K.Y., Garca A.E. Structure of Met-encephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins. 2002;46:225–234. doi: 10.1002/prot.1167. [DOI] [PubMed] [Google Scholar]
- 7.Yang W.Y., Gruebele M. Folding λ-repressor at its speed limit. Biophys. J. 2004;87:596–608. doi: 10.1529/biophysj.103.039040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kubelka J., Chiu T.K., Davies D.R., Eaton W.A., Hofrichter J. Sub-microsecond protein folding. J. Mol. Biol. 2006;359:546–553. doi: 10.1016/j.jmb.2006.03.034. [DOI] [PubMed] [Google Scholar]
- 9.Kubelka J., Hofrichter J., Eaton W.A. The protein folding “speed limit”. Curr. Opin. Struct. Biol. 2004;14:76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 10.Maragakis P., Lindorff-Larsen K., Eastwood M.P., Dror R.O., Klepeis J.L. Microsecond molecular dynamics simulation shows effect of slow loop dynamics on backbone amide order parameters of proteins. J. Phys. Chem. B. 2008;112:6155–6158. doi: 10.1021/jp077018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ensign D.L., Kasson P.M., Pande V.S. Heterogeneity even at the speed limit of folding: large-scale molecular dynamics study of a fast-folding variant of the villin headpiece. J. Mol. Biol. 2007;374:806–816. doi: 10.1016/j.jmb.2007.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Freddolino P.L., Liu F., Gruebele M., Schulten K. Ten-microsecond MD simulation of a fast-folding WW domain. Biophys. J. 2008;94:L75–L77. doi: 10.1529/biophysj.108.131565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.MacKerell A.D. Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 14.Wang T., Wade R. Force field effects on a β-sheet protein domain structure in thermal unfolding simulations. J. Chem. Theory Comput. 2006;2:140–148. doi: 10.1021/ct0501607. [DOI] [PubMed] [Google Scholar]
- 15.Best R.B., Buchete N.-V., Hummer G. Are current molecular dynamics force fields too helical? Biophys. J. 2008;95:L07–L09. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yoda T., Sugita Y., Okamoto Y. Secondary-structure preferences of force fields for proteins evaluated by generalized-ensemble simulations. Chem. Phys. 2004;307:269–283. [Google Scholar]
- 17.Wroblewska L., Skolnick J. Can a physics-based, all-atom potential find a protein's native structure among misfolded structures? I. Large scale AMBER benchmarking. J. Comput. Chem. 2007;28:2059–2066. doi: 10.1002/jcc.20720. [DOI] [PubMed] [Google Scholar]
- 18.Zhou R. Free energy landscape of protein folding in water: explicit vs. implicit solvent. Proteins. 2003;53:148–161. doi: 10.1002/prot.10483. [DOI] [PubMed] [Google Scholar]
- 19.Zhou R., Berne B.J. Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water? Proc. Natl. Acad. Sci. USA. 2002;99:12777–12782. doi: 10.1073/pnas.142430099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu F., Gruebele M. Tuning λ6–85 towards downhill folding at its melting temperature. J. Mol. Biol. 2007;370:574–584. doi: 10.1016/j.jmb.2007.04.036. [DOI] [PubMed] [Google Scholar]
- 21.Nguyen H., Jäger M., Kelly J.W., Gruebele M. Engineering a β-sheet protein toward the folding speed limit. J. Phys. Chem. B. 2005;109:15182–15186. doi: 10.1021/jp052373y. [DOI] [PubMed] [Google Scholar]
- 22.Jäger M., Nguyen H., Crane J.C., Kelly J.W., Gruebele M. The folding mechanism of a β-sheet: the WW domain. J. Mol. Biol. 2001;311:373–393. doi: 10.1006/jmbi.2001.4873. [DOI] [PubMed] [Google Scholar]
- 23.Liu F., Du D., Fuller A.A., Davoren J.E., Wipf P. An experimental survey of the transition between two-state and downhill protein folding scenarios. Proc. Natl. Acad. Sci. USA. 2008;105:2369–2374. doi: 10.1073/pnas.0711908105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cecconi F., Guardiani C., Livi R. Testing simplified proteins models of the hPin1 WW domain. Biophys. J. 2006;91:694–704. doi: 10.1529/biophysj.105.069138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Karanicolas J., Brooks C.L. Improved Gō-like models demonstrate the robustness of protein folding mechanisms to non-native interactions. J. Mol. Biol. 2003;334:309–325. doi: 10.1016/j.jmb.2003.09.047. [DOI] [PubMed] [Google Scholar]
- 26.Luo Z., Ding J., Zhou Y. Temperature-dependent folding pathways of Pin1 WW domain: an all-atom molecular dynamics simulation of a Gō model. Biophys. J. 2007;93:2152–2161. doi: 10.1529/biophysj.106.102095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park S., Lau A.Y., Roux B. Computing conformational free energy by deactivated morphing. J. Chem. Phys. 2008;129:134102. doi: 10.1063/1.2982170. [DOI] [PubMed] [Google Scholar]
- 28.Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jäger M., Zhang Y., Bieschke J., Nguyen H., Dendle M. Structure-function-folding relationship in a WW domain. Proc. Natl. Acad. Sci. USA. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Humphrey W., Dalke A., Schulten K. VMD—visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 31.Frishman D., Argos P. Knowledge-based secondary structure assignment. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 32.Roberts E., Eargle J., Wright D., Luthey-Schulten Z. MultiSeq: unifying sequence and structure data for evolutionary analysis. BMC Bioinformatics. 2006;7:382. doi: 10.1186/1471-2105-7-382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.MacKerell A.D., Jr., Feig M., Brooks C.L., III Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 34.Andersen H.C. RATTLE: a “velocity” version of the SHAKE algorithm for molecular dynamics calculations. J. Chem. Phys. 1983;52:24–34. [Google Scholar]
- 35.Miyamoto S., Kollman P.A. Absolute and relative binding free energy calculations of the interaction of biotin and its analogs with streptavidin using molecular dynamics/free energy perturbation approaches. Proteins Struct. Funct. Gen. 1993;16:226–245. doi: 10.1002/prot.340160303. [DOI] [PubMed] [Google Scholar]
- 36.van der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A.E. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 37.Daura X., Gademann K., Jaun B., Seebach D., van Gunsteren W.F. Peptide folding: when simulation meets experiment. Angew. Chem. Int. Ed. 1999;38:236–240. [Google Scholar]
- 38.Anitescu M., Park S. A linear programming approach for the least-squares protein morphing problem. Math. Program. 2009 In press. [Google Scholar]
- 39.Singhal N., Snow C.D., Pande V.S. Using path sampling to build better Markovian state models: predicting the folding rate and mechanism of a tryptophan zipper β-hairpin. J. Chem. Phys. 2004;121:415–425. doi: 10.1063/1.1738647. [DOI] [PubMed] [Google Scholar]
- 40.Jayachandran G., Vishal V., Pande V.S. Using massively parallel simulation and Markovian models to study protein folding: examining the dynamics of the villin headpiece. J. Chem. Phys. 2006;124:164902. doi: 10.1063/1.2186317. [DOI] [PubMed] [Google Scholar]
- 41.Thompson J.B., Hansma H.G., Hansma P.K., Plaxco K.W. The backbone conformational entropy of protein folding: experimental measures from atomic force microscopy. J. Mol. Biol. 2002;322:645–652. doi: 10.1016/s0022-2836(02)00801-x. [DOI] [PubMed] [Google Scholar]
- 42.Lii J.-H., Allinger N.L. Directional hydrogen bonding in the MM3 force field: II. J. Comput. Chem. 1998;19:1001–1016. [Google Scholar]
- 43.Fabiola F., Bertram R., Korostelev A., Chapman M.S. An improved hydrogen bond potential: impact on medium resolution protein structures. Protein Sci. 2002;11:1415–1423. doi: 10.1110/ps.4890102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Morozov A.V., Kortemme T., Tsemekhman K., Baker D. Close agreement between the orientation dependence of hydrogen bonds observed in protein structures and quantum mechanical calculations. Proc. Natl. Acad. Sci. USA. 2004;101:6946–6951. doi: 10.1073/pnas.0307578101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kortemme T., Morozov A.V., Baker D. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein-protein complexes. J. Mol. Biol. 2003;326:1239–1259. doi: 10.1016/s0022-2836(03)00021-4. [DOI] [PubMed] [Google Scholar]
- 46.Cramer C., Truhlar D. Implicit solvation models: equilibria, structure, spectra, and dynamics. Chem. Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 47.Lum K., Chandler D., Weeks J. Hydrophobicity at small and large length scales. J. Phys. Chem. B. 1999;103:4570–4577. [Google Scholar]
- 48.Huang D.M., Chandler D. Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding. Proc. Natl. Acad. Sci. USA. 2000;97:8324–8327. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wagoner J.A., Baker N.A. Assessing implicit models for nonpolar mean solvation forces: the importance of dispersion and volume terms. Proc. Natl. Acad. Sci. USA. 2006;103:8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chen J., Brooks C.L. Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys. Chem. Chem. Phys. 2008;10:471–481. doi: 10.1039/b714141f. [DOI] [PubMed] [Google Scholar]
- 51.Tanizaki S., Clifford J., Connelly B.D., Feig M. Conformational sampling of peptides in cellular environments. Biophys. J. 2008;94:747–759. doi: 10.1529/biophysj.107.116236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Feig M. Is alanine dipeptide a good model for representing the torsional preferences of protein backbones? J. Chem. Theory Comput. 2008;4:1555–1564. doi: 10.1021/ct800153n. [DOI] [PubMed] [Google Scholar]
- 53.Harder E., Anisimov V., Vorobyov I., Lopes P., Noskov S. Atomic level anisotropy in the electrostatic modeling of lone pairs for a polarizable force field based on the classical Drude oscillator. J. Chem. Theory Comput. 2006;2:1587–1597. doi: 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- 54.Weber W., Hünenberger P., McCammon J. Molecular dynamics simulations of a polyalanine octapeptide under Ewald boundary conditions: influence of artificial periodicity on peptide conformation. J. Phys. Chem. B. 2000;104:3668–3675. [Google Scholar]
- 55.Hünenberger P.H., McCammon J.A. Effect of artificial periodicity in simulations of biomolecules under Ewald boundary conditions: a continuum electrostatics study. Biophys. Chem. 1999;78:69–88. doi: 10.1016/s0301-4622(99)00007-1. [DOI] [PubMed] [Google Scholar]
- 56.Kastenholz M., Hünenberger P. Influence of artificial periodicity and ionic strength in molecular dynamics simulations of charged biomolecules employing lattice-sum methods. J. Phys. Chem. B. 2004;108:774–788. [Google Scholar]
- 57.Shirts M.R., Pande V.S. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys. 2005;122:134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 58.Deng Y., Roux B. Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B. 2009 doi: 10.1021/jp807701h. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jagielska A., Wroblewska L., Skolnick J. Protein model refinement using an optimized physics-based all-atom force field. Proc. Natl. Acad. Sci. USA. 2008;105:8268–8273. doi: 10.1073/pnas.0800054105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


