Reconstruction and Stability of Secondary Structure Elements in the Context of Protein Structure Prediction

Abstract

Efficient and accurate reconstruction of secondary structure elements in the context of protein structure prediction is the major focus of this work. We present a novel approach capable of reconstructing α-helices and β-sheets in atomic detail. The method is based on Metropolis Monte Carlo simulations in a force field of empirical potentials that are designed to stabilize secondary structure elements in room-temperature simulations. Particular attention is paid to lateral side-chain interactions in β-sheets and between the turns of α-helices, as well as backbone hydrogen bonding. The force constants are optimized using contrastive divergence, a novel machine learning technique, from a data set of known structures. Using this approach, we demonstrate the applicability of the framework to the problem of reconstructing the overall protein fold for a number of commonly studied small proteins, based on only predicted secondary structure and contact map. For protein G and chymotrypsin inhibitor 2, we are able to reconstruct the secondary structure elements in atomic detail and the overall protein folds with a root mean-square deviation of <10 Å. For cold-shock protein and the SH3 domain, we accurately reproduce the secondary structure elements and the topology of the 5-stranded β-sheets, but not the barrel structure. The importance of high-quality secondary structure and contact map prediction is discussed.

Introduction

One of the central problems of computational biophysics is the difficulty of predicting and reconstructing protein structure from sequence (1,2). There are three main paradigms that are employed to address this problem. The first paradigm is ab initio molecular dynamics or Markov chain Monte Carlo simulations guided by physical forces (3,4). The second is fold-recognition or threading using sequence-structure compatibility between the sequence of interest and proteins with known 3D structures (5,6). The third approach is homology or comparative modeling, based on sequence alignment to a template of known 3D structure with high sequence similarity to the sequence (7,8).

In this work we explore an alternative approach that involves reconstruction of secondary structure elements and an overall 3D fold based on preliminary prediction of secondary structure and a contact map. Reconstruction of the 3D structure can then be achieved with the use of distance geometry optimization (9,10) or a Metropolis Monte Carlo scheme with annealing (11,12) in the field of Go-type potentials (13,14) specified by the contact map. Recognizing the fundamental importance of secondary structure, along with long-range contacts in β-sheets, we extend the hierarchical folding theory of Baldwin and Rose (15,16) in this work. We hypothesize that lateral contacts between β-strands and between the turns of an α-helix are most important for stabilizing secondary structural elements. Therefore, in our reconstruction procedure we only consider residue contacts in the context of secondary structure, in contrast to other procedures (9–12) that identify contacts purely by distance.

In this study we reconstructed the protein backbone conformation by using a highly efficient Metropolis Monte Carlo procedure that we described in an earlier work (17). Our backbone model features an all-atom representation in continuous space, including the positions of β-carbon atoms (C_β), whereas the majority of previously published methods rely on α-carbon (C_α) trace reconstruction (9,11,12). Therefore, one clear advantage of our methodology is that it provides a more detailed atomistic description of the protein backbone during reconstruction, which ensures, for example, the correct chirality of α-helices and appropriate dihedral angles for the entire backbone. We are particularly interested in faithful reconstruction of secondary structural elements, including hydrogen-bonding patterns in α-helices and β-sheets. Our approach, therefore, also recognizes the fundamental principles of the backbone-based theory of protein folding (18).

The reconstruction of tertiary structure usually utilizes residue-independent empirical potentials in the course of a simulated annealing or energy minimization protocol (10–12). In contrast, our Metropolis Monte Carlo procedure does not rely on annealing. It is, therefore, important to estimate the strength of the contacts in α-helices and β-sheets and their stability at room temperature before employing the contact potentials in a reconstruction. Specifically, we draw on a novel statistical machine learning technique, known as contrastive divergence learning (19,20), to determine the average strength of side-chain interactions, the strength of hydrogen bonding, and other force-field parameters in a simultaneous optimization scheme. The estimates obtained from a data set of 466 protein domains with known structure are used in conformational reconstruction simulations in the framework of our polypeptide model.

The contact map, a matrix that indicates which amino acids are in close proximity (21), can be moderately predicted by correlated mutation analysis (22) and neural network methods (23). In this work we rely on an alternative approach that uses a segmental semi-Markov model (SSMM) (24) to simultaneously predict the contact map and secondary structure of a protein. This procedure enables reasonably accurate contact map prediction for the β-strand residues involved in β-sheet formation, and we briefly recapitulate its details below. In summary, the first goal of this work is to evaluate the stability of secondary structure elements that are formed early in the folding process. The second goal is to investigate the possibility of overall 3D fold reconstruction based only on predicted secondary structure and β-sheet contacts. We tested the procedure using protein G, chymotrypsin inhibitor 2, the SH3 domain, and the major cold-shock protein, all of which are rich in β-strands.

Methods

Protein model

The probability P(R, Ω) that a protein sequence R will adopt a conformation Ω is governed by the Boltzmann distribution. It is convenient to factorize this probability into the product of the probability of the sequence given the conformation (likelihood) and the prior distribution of conformations P(R, Ω) = P(R|Ω)P(Ω). In energetic terms, this can be rewritten as

$$E(R,\Omega )=-\ln P\left(R\right|\Omega )+E(\Omega ),$$ (1)

where sequence-dependent and sequence-independent contributions to the energy are separated. We assume that the sequence-independent term, E(Ω), is defined by short-range interactions between the polypeptide backbone atoms as well as C_β atoms:

$$E(\Omega )=\sum _{i=1}^N{E}_i^{\text{B}}+\sum _{i=1}^N\sum _{j=1}^i\left(E_{ij}^{\text{vdW}}+E_{ij}^{\text{HB}}\right),$$ (2)

where we consider valence elasticity, E_i^B; van der Waals repulsions, E_ij^vdW; and hydrogen bonding, E_ij^HB (which represents the main contribution from polar interactions). As such, our treatment of the sequence-independent part of energy is similar to the traditional ab initio modeling approaches. A detailed description of the backbone model and the interactions can be found in our previous work (17).

The sequence-dependent part of the potential (the negative log-likelihood) was approximated in our model by pairwise interactions between side chains. Our main focus was on the resulting effect of these interactions and how they stabilize secondary structural elements. We did not consider the detailed physical nature of these forces or how they depend on the amino acid types. We introduced these interactions between the polypeptide side chains as an effective Go-type potential dependent on the distance between C_β atoms:

$$E_{ij}^{\text{SC}}=\kappa C_{ij}{r}_{ij}^2,$$ (3)

where r_ij is a distance between nonadjacent, |i − j| > 1, C_β atoms, and κ is a force constant. In this work we introduce a “regularized contact map”, C_ij. In this binary matrix, two types of contacts are defined in the context of protein secondary structure. First, only lateral contacts in the parallel and antiparallel β-sheets are indicated by ones. Second, the contacts between amino acids i and i+3 in α-helices are also represented by ones. The contacts of the first and second types typically have the closest C_β–C_β distance among nonadjacent contacts in native proteins. The force constants depend on the secondary structure type, introducing positive κ_α and κ_β. Nonadjacent contacts in secondary structural elements are therefore stabilized by attracting potentials.

We also modeled interactions between sequential residues. This interaction is defined by the mutual orientation of adjacent residues that are involved in secondary structural elements:

$$E_{i,i+1}^{\text{SC}}=\eta \cos {\gamma }_{i,i+1},$$ (4)

where γ_i,_i+1 is the dihedral angle C_β–C_α–C_α–C_β between the adjacent residues. The purpose of this interaction is to bias the conformation toward the naturally occurring orientations of residues in secondary structural elements. In α-helices, adjacent residues adopt a conformation with cosγ positive. In β-sheets, cosγ is, in contrast, negative. We therefore used two values of the force constant: negative η_α and positive η_β.

To summarize, the total energy of a polypeptide chain with conformation Ω was calculated as follows:

$$E(R,\Omega )=\sum _{i=1}^N{E}_i^{\text{B}}+\sum _{i=1}^N\sum _{j=1}^i\left(E_{ij}^{\text{vdW}}+E_{ij}^{\text{HB}}+E_{ij}^{\text{SC}}\right)\text{.}$$ (5)

The valence elasticity, van der Waals repulsions, and hydrogen bonding that contribute to this potential have a clear physical meaning and are analogous to traditional ab initio approaches. The side-chain interactions, E_ij^SC, in this model were introduced as a long-range quadratic Go-type potential based on the contact map and secondary structure assignment. This pseudo-potential had two purposes: to stabilize the secondary structural elements, and to provide a biasing force that allows reconstruction of the backbone conformation in the course of our Metropolis Monte Carlo simulations (17,20).

Model tuning and training data set

Since our procedure does not involve simulated annealing, we carefully optimized the force-field parameters of our model. The values of many parameters of our protein model (i.e., lengths and angles (25,26) and atomic radii (27)) are fairly well established. We used these parameters to model protein backbone structure and introduce hard-sphere repulsion between the backbone atoms as well as β-carbons, the only side-chain atom that we used in our model. Other model interactions necessitated calibration of their parameters. Our model featured an interpeptide hydrogen bonding specified by a square-well potential. Four parameters of hydrogen-bonding interactions were optimized in the procedure: hydrogen bond strength, H; the maximum allowed H···O distance, δ; and the minimum allowed angles ∠COH and ∠OHN, Θ and Ψ. Our model also featured interactions between side chains that were parts of secondary structural elements. Four force constants—κ_α, κ_β, η_α, and η_β—corresponding to different types of side-chain interactions were also optimized.

We used a novel machine learning procedure known as contrastive divergence (19) to calibrate the aforementioned eight parameters: θ = {H, δ, Θ, Ψ, κ_α, κ_β, η_α, η_β}. Contrastive divergence is a fast approximate gradient-ascent maximum likelihood method for estimating force constants and other energy parameters from a training set of known structures. The gradient of log-likelihood with respect to the model parameters was evaluated as follows:

$$\frac{\partial \ln P(R,{\Omega }_0|\theta )}{\partial \theta }\approx \frac{\partial E(R,{\Omega }_K)}{\partial \theta }-\frac{\partial E(R,{\Omega }_0)}{\partial \theta },$$ (6)

where Ω₀ corresponds to initial conformations in the training data set, and Ω_K corresponds to conformations after K = 4096 Metropolis steps. For details of the procedure, see our previous work (20).

To prepare a training set of proteins of known structure, we used ASTRAL 1.69 (28,29). We initially downloaded the 945 highest Summary PDB Astral Check Index (SPACI) scoring Protein Data Bank (PDB)-style structures that represent different folds according to the Structural Classification of Proteins (SCOP) database. SPACI is an approximate measure of structure quality that incorporates resolution, R-factor, and stereochemical checks (29). A large portion of these structures was eliminated from this data set. We kept only representatives of the α, β, α/β, and α+β classes. We dropped all structures with missing residues. Finally, we removed the structures with SPACI scores of <0.4 and NMR structures. This left us with 466 high-quality diverse x-ray structures containing 79,918 residues. The chain lengths ranged from 31 to 759 residues, with the median length of 145 residues. In our modeling procedure, the chains are regularized so that the peptide bonds are absolutely flat and the C_α–C_α distances are fixed. The root mean-square error of the regularization was, on average, equal to 0.037 Å and never exceeded 0.104 Å. The structures in the training set are listed in the Supporting Material, along with the corresponding number of residues, the SPACI score, and the root mean-square error of the regularization.

Secondary structure and contact map prediction

The secondary structure and the contact map were predicted based on a given sequence of amino acids and its multiple sequence alignment profile (30). The prediction procedure is based on the concept of proteins as collections of local secondary structure segments, which may be shared by unrelated proteins. We adopted the framework of the SSMM (31,32), a generalization of hidden Markov models that allows each hidden state to generate a variable length sequence of the observations. The observation sequence, O, included both a residue sequence and a multiple alignment profile. The associated secondary structure, T, was fully specified in terms of segment locations and segment types. The contacts between β-strand residues are specified by nonzero elements in the binary contact map, C.

The secondary structure prediction for a given observation sequence, or the posterior distribution P(T|O), was derived using a Bayesian approach from the distribution of observations for a given secondary structure, P(O|T), in the training data set. The training data set consisted of ∼2000 proteins from the PDB (33) with a low pairwise sequence identity. The contact map prediction, P(C|O), was derived using a Markov Chain Monte Carlo approach, drawing samples from the distributions of P(C|T) and P(T|O). When samples were drawn from the former distribution, any β-strand was allowed to form one or two contacts with other β-strands. For more details on the procedure, see our previous publication (24) (for web server implementation see http://wsbc.warwick.ac.uk/www/eva/contacteva.html).

We further used the prediction results for the reconstruction of tertiary structure in the framework of our protein model. Specifically, the most likely secondary structure was assigned to each residue based on P(T|O), the interaction between two adjacent residues that belong to the same secondary structure element. These were, in turn, defined according to Eq. 4, and, in the case of α-helix, the interactions between side-chains i and i+3 were defined according to Eq. 3. The contact map prediction, P(C|O), was regularized to define off-diagonal bands in the C_ij matrix that defined the specific β-sheet lateral interactions according to Eq. 3.

Results

Learning model parameters

Secondary structure elements that are formed early in protein folding (15,16) are stabilized by both sequence-dependent side-chain interactions and sequence-independent backbone interactions (particularly hydrogen bonding). A careful balance between the two contributions is crucial for faithful reconstruction of secondary structure elements in the course of room-temperature simulations. In the context of our protein model, this balance requires careful optimization of hydrogen-bonding parameters and interactions between side chains as mimicked by Go-type interactions between C_β atoms (see “Protein Model” in Methods). The contrastive divergence technique (19) provides an efficient tool to estimate these parameters from the data set of known structures as they are observed in the PDB, by relying on short Metropolis simulations (20). Contrastive divergence is a better alternative to statistical potentials (34) for evaluating interactions from the PDB.

Overall, eight model parameters were simultaneously optimized with the use of contrastive divergence. Fig. 1 shows the parameter learning curves produced by the iterative procedure. We found that hydrogen bonding is characterized by the strength, H/RT = 1.85; the H···O distance cutoff, δ = 2.14 Å; and the minimum allowed angles ∠COH and ∠OHN, Θ = 140° and Ψ = 150°, respectively. Our estimation of hydrogen-bonding parameters is in perfect agreement with our previous work, in which we used a smaller data set (20), and in good agreement with experimental evidence (H = 1…2 kcal/mol) (35). We also found the value of the force constant for the attracting potential between amino acids in secondary structural elements to be equal to κ_α/RT = 0.10 Å⁻² and κ_β/RT = 0.09 Å⁻². The two values are very close to each other, indicating that these interactions are indeed similar in both helices and sheets. This is an expected result because the separation between the C_β atoms in both α-helices and β-sheets is ∼5.4 Å. The effective force constants for the interactions between adjacent residues were determined to be η_α/RT = −0.6 and η_β/RT = 4.5. In agreement with our expectations, these force constants have opposite signs, stabilizing alternative mutual orientations of adjacent residues in α-helices and β-strands.

Figure 1.

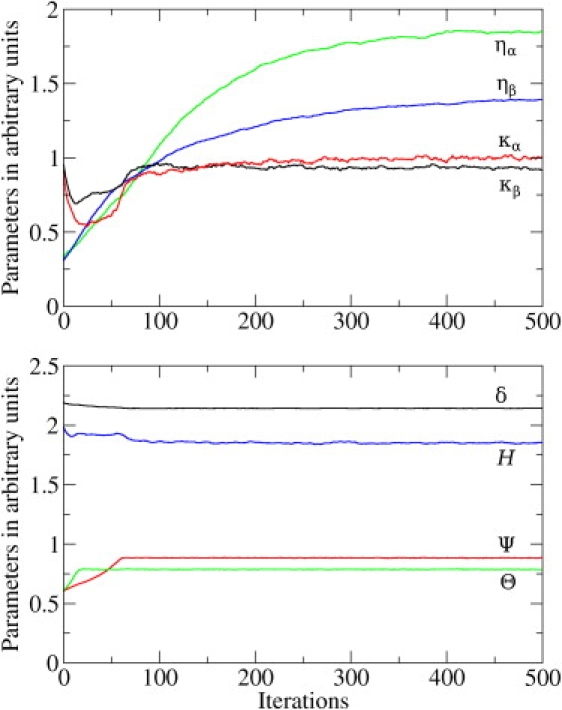
Contrastive divergence optimization of the model parameters. The top panel shows iterative convergence of four parameters of side-chain interactions: κ_α in red, κ_β in black, η_α in green, and η_β in blue. The bottom panel shows the convergence of hydrogen-bond parameters: H in blue, δ in black, Θ in green, and Ψ in red.

Isolated α-helix and β-hairpin reconstruction

Experimental evidence suggests that the polyalanine conformation in solution can be either an α-helix or a 3₁₀-helix (36). Our previous simulations of a model polyalanine without side-chain interactions also demonstrated that hydrogen bonding alone stabilized an α-helix or a 3₁₀-helix equally well. Yet, the overwhelming majority of helical conformations in proteins are α-helices. We believe that attracting interactions between side chains can explain the preference for α-helices in proteins. Such forces should constrict the helix toward a smaller pitch in α-helices. We reliably observed formation of stable α-helices from an extended conformation in specially designed simulations. The simulations were initiated from a β-hairpin conformation of a 16-residue polypeptide. The side-chain interactions were specified between C_β atoms i and i+3, as well as adjacent residues (see Methods). The formation of stable α-helix was usually complete within 5 million steps of our simulations. Fig. 2 A shows a representative resultant α-helix.

Figure 2.

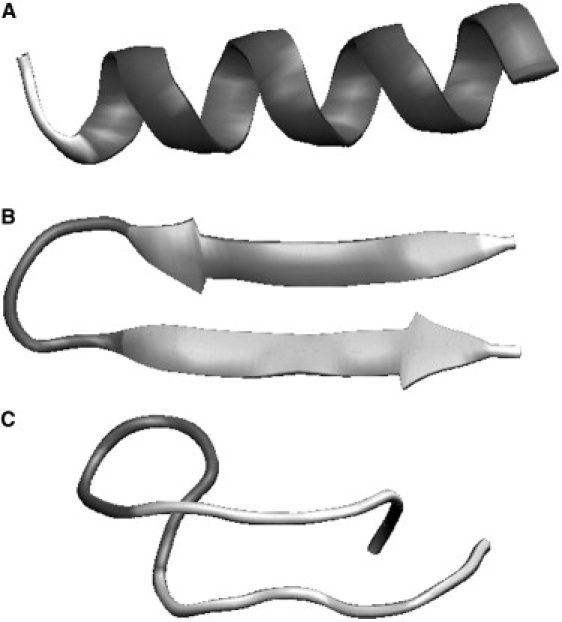
Examples of reconstructed secondary structural elements. The chains of 16 residues were modeled. The visualization is done in VMD (54). The secondary structure is automatically assigned by STRIDE (55) and reflects the backbone hydrogen-bonding criteria that are spontaneously satisfied in the course of simulations.

Although spontaneous folding of helical structures is possible under the influence of hydrogen bonds alone, the folding of isolated β-hairpins seems extremely unlikely (and was not actually observed) (17). In this work, we added two types of biasing interactions between side chains to facilitate the formation of β-hairpins in special simulations: 1), an attracting potential between the C_β atoms of amino acids that form lateral contacts in the β-hairpin; and 2), repulsion between sequential residues (see Methods) that favored alternating orientations of side chains. Starting from a helical conformation of a 16-residue polypeptide, the formation of a stable β-hairpin was usually complete within 30 million steps of our Metropolis procedure. Fig. 2 B shows a representative resultant β-hairpin. Of interest, without repulsion between adjacent residues, β-hairpins routinely bent on themselves and formed stable structures, such as those shown in Fig. 2 C. Therefore, the interactions between the lateral neighbors alone were not sufficient to produce long, straight β-hairpins.

To improve the stability of α-helices and β-sheets in these and further simulations, we moderately adjusted some force constants (κ_α/RT = 0.12 Å⁻², κ_β/RT = 0.11 Å⁻²) and hydrogen-bonding parameters (H/RT = 2.5, δ = 2.19 Å, Θ = 130°, and Ψ = 140°). The difference between these values and those determined in the contrastive divergence procedure is <30%. Unfortunately, without this modest modification, the formation of persistent and hydrogen-bonded α-helices and β-sheets became unlikely in our simulations, with lateral C_β–C_β distances noticeably exceeding native 5.4 Å. Unavoidable systematic errors in the data set may explain the underestimation of force parameters in a contrastive divergence procedure that assumes a correct representation of thermal fluctuations in the data set. Another justification for the small adjustment is the necessity to compensate for other interactions that were not considered in our model.

To summarize, we developed biasing potentials and determined the force constants that are sufficient to fold and stabilize both α-helices and β-hairpins. Our biasing potentials do not involve artificial constraints on dihedral angles. We believe that values of dihedral angles pertaining to different secondary structural elements are the result of the adopted conformation, rather than its cause. In our model, to assemble a secondary structure, side chains are first properly arranged by long-range specific interactions and then short-range, nonspecific hydrogen bonds are spontaneously formed.

Protein G modeling from an ideal contact map

Protein G (e.g., PDB code 1PGA) is a widely used model system for testing protein-folding procedures (37–39). Protein G is a 56-residue-long protein that contains all the important structural motifs: parallel and antiparallel β-sheets and an α-helix. As a benchmark for a “best possible case” reconstruction, we first simulated protein G folding by introducing attractive interactions between lateral neighboring C_β atoms as they appear in the native β-sheets and the helix (see Methods), rather than relying on prediction results. We also used interactions between adjacent C_β atoms as appropriate for the native secondary structure. C_β atoms in the coil conformation were not included in any interaction. The regularized contact map that corresponds to these interactions is shown in Fig. 3 A. This is an ideal case with Go-type potentials specified by native interactions. The simulations were started from an overall extended conformation, where the residue initial conformations had dihedral angles corresponding to their native secondary structures. None of the β-sheet contacts were formed in the initial conformation. We continued protein G simulations for 65 million steps. Folds resembling the native fold started to appear after ∼30 million steps. To analyze the folding pathway, we followed the microscopic energy and the fraction of native contacts specified in the regularized contact map among all contacts formed (40). Fig. 4 demonstrates the relaxation of the total microscopic energy and evolution of the fraction of native contacts during this simulation. The conformation corresponding to a relatively low energy and maximal fraction is also shown in Fig. 3 B. These simulations were completed within 10 h on a Sun Netra X1 Cluster Grid (Sun Microsystems, Santa Clara, CA).

Figure 3.

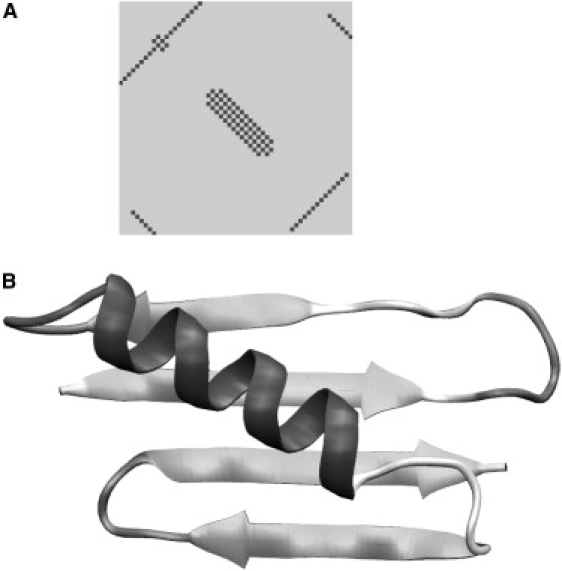
Reconstruction of the protein G fold by specifying native interactions. The top-left panel shows the regularized contact map with native interactions in α-helix and β-sheets. The best structure corresponding to the maximum fraction of native contacts at relatively low energy is shown in the top-right corner.

Figure 4.

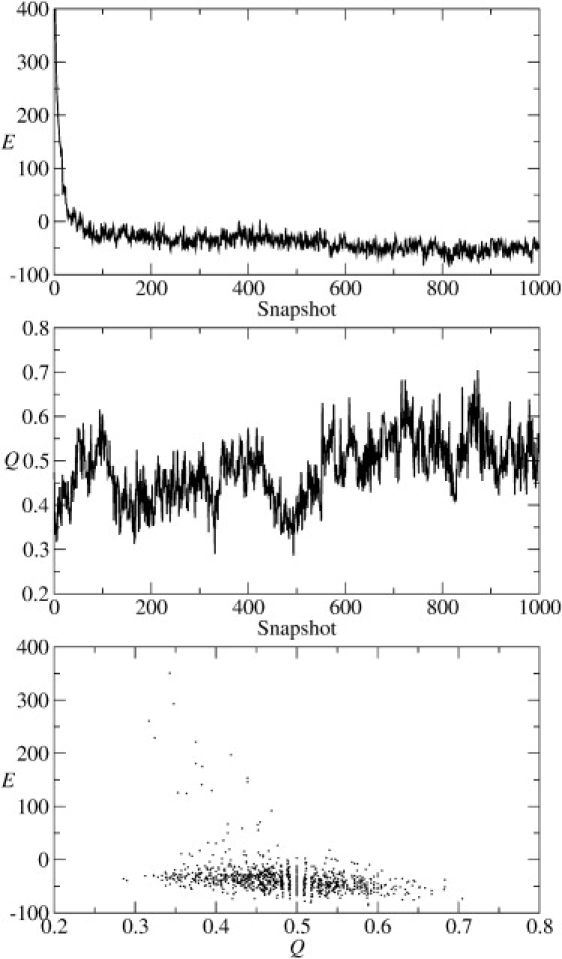
Protein G modeling from the ideal regularized contact map. The graphs demonstrate the evolution of the microscopic energy, E, and fraction of the native contacts, Q, during the simulation run in the top and middle panel, respectively. The bottom panel demonstrates the relationship between Q and E.

This simulation demonstrates that, in the case of protein G, our framework is capable of reconstructing the overall fold of the protein if a detailed description of secondary structure and β-sheet contacts is available. The structure shown in Fig. 3 B contains the correct α-helix and β-sheets with correct interpeptide hydrogen bonding and topology, although the root mean-square deviation (RMSD) between this structure and the native structure is 8.6 Å. Hypothetically, the more compact native structure may be stabilized by interactions that are omitted from our model, e.g., by packing of the hydrophobic core of the protein in the later stages of folding.

Protein G modeling from a predicted contact map

In the second experiment, we attempted to reconstruct the protein G conformation by relying on a predicted secondary structure and contact map. The prediction was provided by the SSMM procedure (24) and required some manual interpretation of the results to resolve ambiguities and enable its use for the reconstruction of 3D structure. Fig. 5 A illustrates the three-step interpretation of the prediction results. First, the predicted helical region in the middle of the protein specified helical contacts and corresponding Go-type potentials in our protein model. Second, the pairing between central β-strand residues was specified based on the position of a local maximum on the predicted contact map. Third, the corresponding regularized contacts were diagonally extended in a parallel or antiparallel direction to the boundaries of the reliable prediction, where the predicted probability dropped to the background level.

Figure 5.

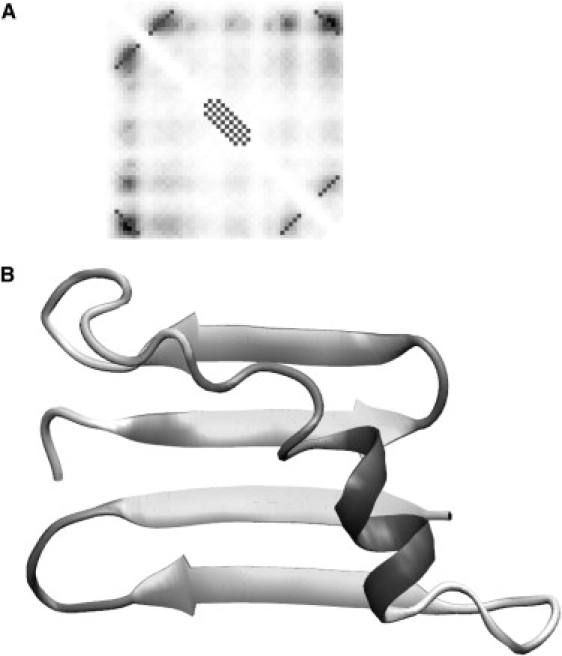
Reconstruction of the protein G fold by specifying predicted interactions. Panel A shows the regularized contact map with predicted interactions in α-helix and β-sheets, with the predicted contact map in the background. The gray levels in the predicted contact map represent the predicted probability of a particular contact. The regularized diagonal contacts pass through the local maxima on the predicted contact map and extend until the predicted contact probability levels off. The best structure corresponding to the maximum fraction of predicted contacts at relatively low energy is shown in panel B.

For protein G, the predicted α-helix was slightly shorter than the native one. The ambiguity in predicted positions corresponded to a plausible two- or four-residue shift between the β-strands. The orientation of the contacts that appeared close to the main diagonal necessarily corresponded to antiparallel β-hairpins. The predicted contact between N- and C-termini could be both parallel (as in the native protein structure) or antiparallel. We separately simulated both the parallel and antiparallel orientations as represented in Figs. 5 and 6, respectively. The evolution of the total energy and the fraction of predicted contacts specified in the regularized contact map during the simulations can be found in the Supporting Material. These simulations of ∼100 million Metropolis steps were completed within 5 h on a Sun Netra X1 Cluster Grid.

Figure 6.

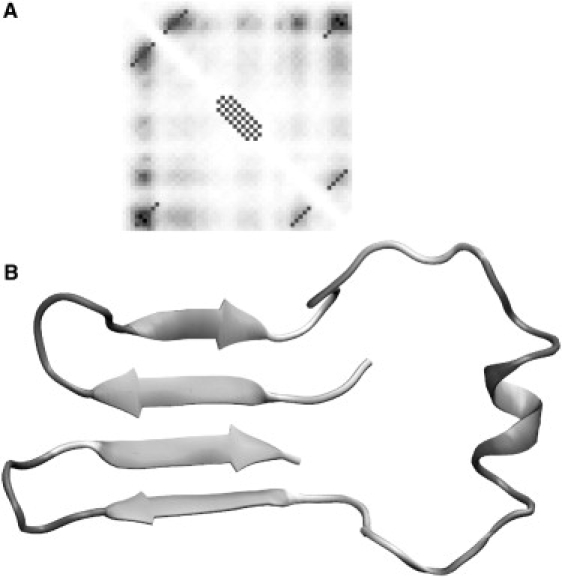
Reconstruction of the protein G fold by specifying predicted interactions. Panel A shows the regularized contact map (alternative to Fig. 5) with the predicted contact map in the background. The regularized diagonal contacts pass through the local maxima on the predicted contact map and extend until the predicted contact probability levels off. The best structure corresponding to the maximum fraction of predicted contacts at relatively low energy is shown in panel B.

Figs. 5 B and 6 B show the structures that correspond to the maximum fraction of predicted contacts at relatively low total energy. The fold of the structure shown in Fig. 5 B corresponds to the native fold of the protein G, although the RMSD with the native structure is 10 Å. Because of the underprediction of the length of both the α-helix and β-sheets, larger portions on the chain were left as coils in comparison to the native structure. This can partly explain why the α-helix does not pack against the β-sheets in our simulated structures. Both the antiparallel and parallel β-sheets between the termini of the chain were able to form in our simulations. It is, therefore, impossible to rule out the antiparallel conformation based on the contact map prediction alone. Our results indicate that it is crucial to obtain a good-quality predicted contact map and secondary structure to faithfully reconstruct the 3D fold of a protein.

Other examples of protein modeling from a predicted contact map

We demonstrated the general applicability of the modeling procedure described above by modeling three other proteins: chymotrypsin inhibitor 2 (CI2, PDB code 2CI2) (41), Src tyrosine kinase SH3 domain (SH3, PDB code 1SRL) (42), and the major cold-shock protein of Escherichia coli (CspA, PDB code 1MJC) (43). These peptides are often used as folding model and simulation systems (44,45). The native 65-residue CI2 fold contains a four-stranded β-sheet and an α-helix, and differs in topology from protein G. Both native 56-residue SH3 and 69-residue CspA have five-stranded β-barrel structures, with slightly different topologies. We again modeled these proteins by relying on secondary structure and contact map prediction, in a similar fashion to the protein G modeling described above. These simulations required ∼100 million Metropolis steps (20). The secondary structure and contact map prediction were again produced using the SSMM procedure (24).

The simulation results for proteins CI2, SH3, and CspA are shown in Figs. 7–9, respectively. For all considered proteins, the quality of the secondary structure prediction was comparable to that of protein G: β-strand locations in the sequence were correctly predicted, whereas their length was slightly underpredicted. The contact map prediction (shown in panel A of each figure) presented a challenge for our further modeling because all possible combinations between the β-strands were predicted with comparable probability. The correctly predicted β-hairpin contacts allowed unambiguous interpretation in terms of residue contacts and Go-type potentials in our protein model (see protein G modeling above). In contrast, the other predicted contacts were mostly false positives. For further simulations, we used three β-hairpin contacts and one longer-range contact between N- and C-termini that were reliably predicted and corresponded to the native structure. The plots for the evolution of the total energy and the fraction of predicted contacts specified in the regularized contact map during the simulations can be found in the Supporting Material.

Figure 7.

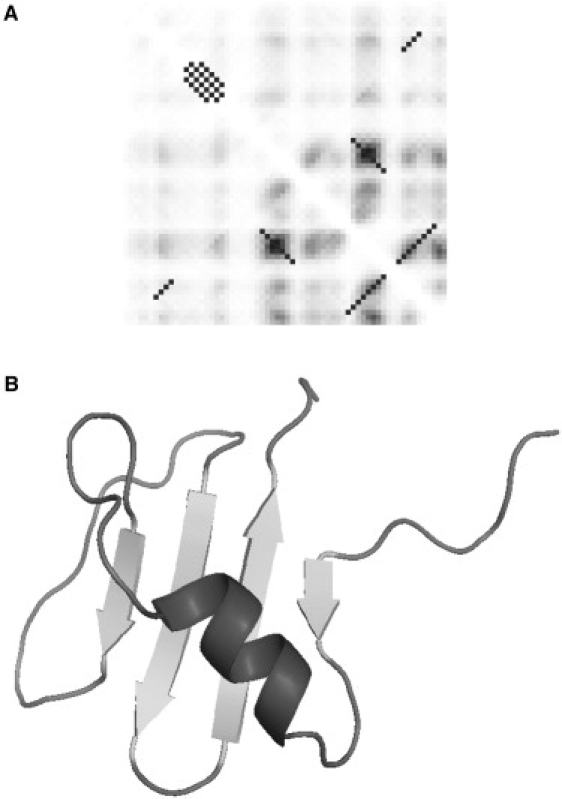
Reconstruction of chymotrypsin inhibitor 2 CI2. Panel A shows the regularized contact map with the predicted contact map in the background. The regularized diagonal contacts pass through the local maxima on the predicted contact map and extend until the predicted contact probability levels off. The selected regularized contacts correspond to the native fold of CI2. False-positive predictions are not included in the reconstruction. The best structure corresponding to the maximum fraction of predicted contacts at relatively low energy is shown in panel B.

Figure 8.

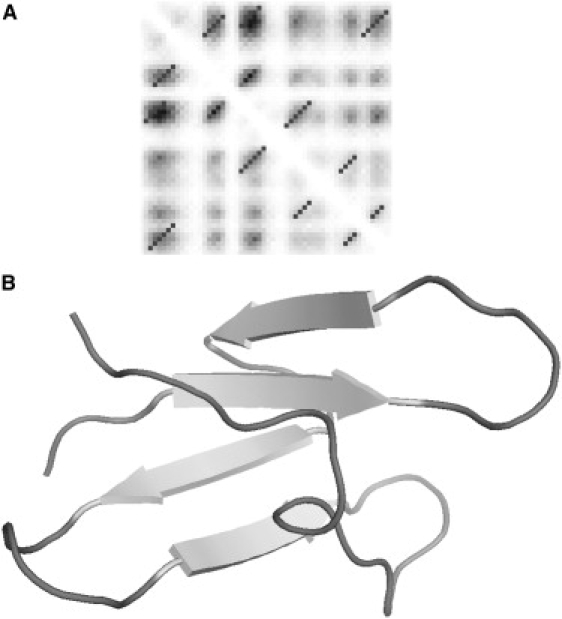
Reconstruction of the Src tyrosine kinase SH3 domain. Panel A shows the regularized contact map with the predicted contact map in the background. The regularized diagonal contacts pass through the local maxima on the predicted contact map and extend until the predicted contact probability levels off. The selected regularized contacts correspond to the native fold of SH3. False-positive predictions are not included in the reconstruction. The best structure corresponding to the maximum fraction of predicted contacts at relatively low energy is shown in panel B.

Figure 9.

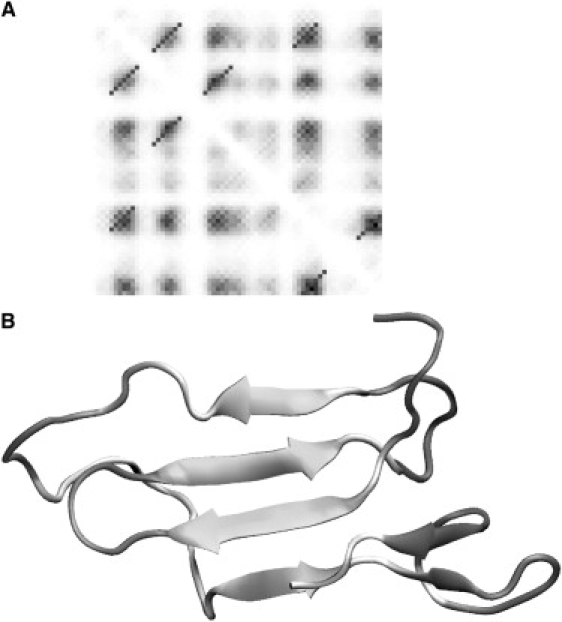
Reconstruction of the major cold-shock protein CspA. Panel A shows the regularized contact map with the predicted contact map in the background. The regularized diagonal contacts pass through the local maxima on the predicted contact map and extend until the predicted contact probability levels off. The selected regularized contacts correspond to the native fold of CspA. False-positive predictions are not included in the reconstruction. The best structure corresponding to the maximum fraction of predicted contacts at relatively low energy is shown in panel B.

The structures shown in Figs. 7–9 B were selected based on the maximum fraction of predicted contacts at relatively low total energy. The quality of reconstruction of CI2 (Fig. 7 B) was comparable to the case of the protein G described above. The resulting structure features a correctly folded β-sheet with an α-helix. The RMSD of the structure with the native fold was 6.8 Å. In the case of the SH3 domain (Fig. 8 B), four out of five strands correctly packed in the β-sheet with small misalignments of up to two residues. The C-terminus was correctly packed against the rest of the structure, but the hydrogen bonds did not completely form to complete the barrel. The RMSD of the shown structure with the native fold was equal to 5.8 Å. In the case of CspA (Fig. 9 B), instead of the barrel-like native structure, this structure resembles a flattened five-stranded β-sheet. The contacts between the strands were in good agreement with the native structure except for some small misalignments by up to three residues. The reason for the flattened, rather than barrel-like, structure is the missing contact between the edges. Indeed, the native structure contains one additional contact between the β-strands that involves only three pairs of residues near residues 30 and 62. This contact was not reliably predicted (see Fig. 7 A) and was omitted from the 3D reconstruction procedure. The overall RMSD of the native and predicted structure is 10.8 Å. In all of these cases, we can speculate that the resulting structures are stable folding intermediates, with the native structure being adopted as a result of the formation of the final contacts and small adjustments in alignment between the β-strands.

Discussion

We have presented a framework for reconstructing protein backbone conformation from the primary sequence with a focus on secondary structural elements. This work represents a further development of the simulation techniques we described in earlier works (17,20). Our model features an all-atom backbone representation with standard bond lengths and angles as well as atomic radii (25–27). We introduced two types of sequence-independent short-range interactions: van der Waals repulsions and hydrogen bonding. The sequence-dependent part of the potential was mimicked by means of special Go-type potentials between C_β atoms. We only specified these interactions between lateral neighbors in β-sheets and across the turns of α-helices. To sample the conformations, we used an efficient Metropolis Monte Carlo sampler that is capable of performing simulations in reasonable time.

To calibrate the magnitude of the model interactions, we used a modern machine learning technique called contrastive divergence (20). In this work, we performed combined optimization of hydrogen-bonding parameters along with Go-type side-chain interactions. The estimates of the hydrogen-bonding interactions are in full agreement with our previous work, in which hydrogen bonding interactions were optimized regardless of side-chain interactions. They are also in agreement with some experimental observations (35).

We identified and estimated the magnitude of the model side-chain interactions that are capable of stabilizing secondary structural elements in our simulations. We observed that α-helices were sufficiently stabilized by attractions between side chains at positions i and i+3. (In this study we did not consider the important interactions between side chains i and i+4 (46,47).) It turned out that, besides lateral attractions between β-strands, a special interaction that favored alternating orientations of adjacent residues was necessary to form flattened β-sheets. This observation is in agreement with numerous experimental observations (48). These interactions can be conveniently specified on the regularized contact map. We did not consider the dependence of these potentials on amino acid types because such potentials can only be optimized to stabilize the tertiary structure of a finite number of proteins, and thus cannot be universally optimized (49,50).

In the framework of our model, we were able to successfully reconstruct the general fold of protein G by precisely specifying native interactions in its α-helix and β-sheets. We reconstructed secondary structural elements in atomic detail, including hydrogen-bonding patterns. Despite the fact that our model did not include interactions between the α-helix and the β-sheets, we obtained reasonable packing between the secondary structural elements. We also successfully reconstructed the overall folds of proteins G and CI2 from predicted contact maps, although the orientation of one out of three predicted β-sheet contacts was ambiguous in both cases. In addition, the specific location of some contacts disagreed with the specific pairing in native folds by a two-residue shift. The attempt to reconstruct the overall folds of CspA and SH3 domain turned out to be more challenging because of a large number of false-positively predicted β-sheet contacts. Most of the β-strand packing into a β-sheet was, however, reconstructed successfully. We concluded that ambiguities in the predicted contact map presented the major obstacle to successful reconstruction of the 3D fold.

In our current model, the side-chain interactions were specified according to the secondary structure regardless of a particular residue position. This is a significant simplification considering that interactions in α-helix caps and on β-sheet edges are believed to be stronger to compensate for the lack of backbone hydrogen bonding (51,52). In addition, our model lacks any interactions between secondary structure elements and therefore is not suitable for pure α-proteins. This also resulted in rather loose agreements between the modeled structures and native folds with RMSDs up to 10 Å. Our goal in this work was to identify a minimal set of interactions that are sufficient to stabilize secondary structure elements, rather than produce a precise tertiary structure. Smaller RMSDs have been achieved by specifying a more complete set of interactions, albeit in C_α-only models (11,12). The discrepancy can therefore be attributed to the lack of side-chain interactions other than the direct secondary-structure interactions (53). The introduction of special interactions between the side chains near the edges and between secondary structure elements would be a significant advancement of our model, and will be the focus of future work.