Abstract
By exploring a recent model in which DNA bending elasticity, described by the wormlike chain model, is coupled to basepair denaturation, we demonstrate that small denaturation bubbles lead to anomalies in the flexibility of DNA at the nanometric scale, when confined in two dimensions (2D), as reported in atomic-force microscopy experiments. Our model yields very good fits to experimental data and quantitative predictions that can be tested experimentally. Although such anomalies exist when DNA fluctuates freely in three dimensions (3D), they are too weak to be detected. Interactions between bases in the helical double-stranded DNA are modified by electrostatic adsorption on a 2D substrate, which facilitates local denaturation. This work reconciles the apparent discrepancy between observed 2D and 3D DNA elastic properties and points out that conclusions about the 3D properties of DNA (and its companion proteins and enzymes) do not directly follow from 2D experiments by atomic-force microscopy.
Introduction
Whereas traditional bulk experiments provide average behaviors of dominant subpopulations, new methods exist that address DNA mechanical properties at the single-molecule level (1–3). Observations by atomic force microscopy (AFM) of double-stranded DNA (dsDNA) adsorbed on a two-dimensional (2D) substrate (4,5) have recently allowed a direct quantification of the distribution, p(θ), of bending angles θ (6,7). This led to the unexpected observation of an overabundance of large θ (8), with respect to the wormlike chain (WLC) model, at very short range (≈5 nm, much less than the persistence length ≈50 nm). These observations suggest that, even in the absence of any bending constraints, nonlinearities, such as kinks where DNA is locally unstacked (9) or small denaturation bubbles, are excited solely by thermal fluctuations with a high enough probability to be observable at room temperature (T R = 298.15 K). These findings cast some doubt upon the adequacy of the WLC model traditionally adopted in three dimensions (3D) (10). In this respect, Cloutier and Widom (11) have observed that short dsDNA, ∼100 basepairs (bp) long, formed looped complexes in 3D with a much higher probability than expected, which was attributed to partial denaturation (12). However, these findings have been questioned by new experiments that pointed out a flaw in the experimental procedure (13) and showed that short-DNA cyclization data were accurately fitted by the WLC model, without invoking kinks. A recent study based on flow experiments draws similar conclusions (14). These converging elements are supported by all-atom numerical simulations (9,15) suggesting that kinks are not excited by thermal fluctuations with any measurable probability in unconstrained DNA fluctuating freely in solution.
Apart from 2D confinement, what is the difference between both types of experiments? Fig. 1 shows a sketch of DNA fluctuating in solution or adsorbed on a mica surface as in AFM experiments (5–7). These experiments are carried out in air (the solvent is dried) and DNA is electrostatically adsorbed using magnesium ions, forming an ionic crystal with the charged substrate. DNA electrostatics are thus expected to be strongly affected as compared with DNA in water, hence hydrogen-bonding energies between two complementary bps and stacking energies between adjacent base aromatic rings are substantially modified.
Figure 1.
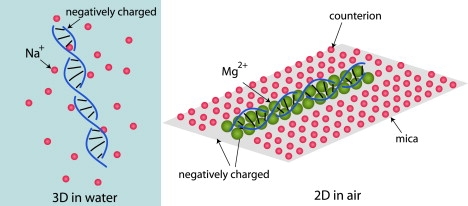
Sketch of a dsDNA segment solvated in water (left) with its sodium counterion cloud (the phosphate groups of the DNA backbone are negatively charged); and in air (right), electrostatically adsorbed on a mica substrate forming an ionic crystal via magnesium ion bridges between the DNA and the negatively charged substrate. Therefore, the parameters associated with the hydrogen bonding of bps and the stacking of adjacent bases are significantly modified.
Recently, we have proposed a solvable model where bending elasticity is intrinsically coupled to bp melting (16,17) in contrast to older approaches for which bending is not explicitly included (18,19). Single-stranded DNA being two orders-of-magnitude more flexible than dsDNA, this coupling must be taken into account because local denaturation strongly increases flexibility. Here, we argue that in 2D the modification of the above denaturation parameters (bonding and stacking energies), due to adsorption, increases the probability of bp opening, which lowers, in turn, the bending rigidity. This explanation reconciles the apparent discrepancy between 3D and 2D experiments.
Theory
Model background
We model dsDNA as a chain of N bps i (1 ≤ i ≤ N) possessing two degrees of freedom (16,17): an Ising variable, σ i, set to +1when the bp is unbroken (U) or set to −1 when the bp is broken (B). In addition to this internal variable, an external one, the unit vector t i, sets the spatial orientation of the monomer. The Hamiltonian couples explicitly the σ i and t i:
| (1) |
The bending rigidity of the joint between bps i and i + 1, κ(σ i, σ i+1), takes different values according to the internal state of the two neighboring bps. We denote κ U ≡ κ(1, 1), κ B ≡ κ(−1, −1), and κ UB ≡ κ(1, −1) = κ(−1, 1). The Ising parameters J and μ have the following physical meanings: J is the destacking energy (energetic cost to unstack two consecutive aromatic rings); and 2μ is the energy difference per bp between open and closed states.
This discrete WLC model coupled to an Ising model can be completely solved using a transfer matrix approach (16,17). Calculating the partition function amounts to solving a spinor eigenvalue problem (formally equivalent to a quantum rigid rotator). In 3D, the orthogonal eigenstates, denoted by , are indexed by three quantum numbers: l = 0, 1, …, ∞; and m = −l, …, l are the usual azimuthal and magnetic quantum numbers associated with the spatial orientation of t i and τ = ± is related to the bonding and antibonding bp states (as for the one-dimensional Ising model or the H 2 + covalent bond). When projecting the eigenstates onto the real space basis |σΩ〉, with σ a bp state and (θ, φ) ≡ Ω, the two spherical angles defining t, one gets . The , proportional to the spherical harmonics, are the eigenvectors of the pure chain model (i.e., when all κ are set equal). The eigenvalues λ l, τ are degenerate in m and can be expressed in terms of modified Bessel functions of the first kind Iν () (20) (see (17) for the expressions for the |l, τ〉). We have 〈l, τ′|l, τ〉 = δττ ′, but 〈l′, τ′|l, τ〉 ≠ δ ll′ δττ ′, because if l ≠ l′, the matrix element is between states of different rotational symmetry. This is why our coupled model is not the trivial direct product of both the Ising and discrete WLC models.
The previous exact solution can also be found when the chain is confined to 2D, as already stated by one of us in Palmeri and Leibler (21); for example, when DNA is adsorbed on a substrate at thermodynamical equilibrium (7). The spherical angles (θ, φ) become a single polar angle θ ∈ (−π, π]; the spherical harmonics ψ l, m(θ, φ) become the simpler ψn(θ) = e inθ, with n integer; the 2D analogs of the eigenvalues are denoted by λn, τ and the eigenvectors by |n, τ〉 (21).
In the model as presented here, we do not take into account additional DNA degrees of freedom, such as torsion or stretching. Although we have recently demonstrated that it is possible to do so in the context of thermal denaturation (22), the additional mathematical complications of taking them into account in the bending-angle distribution calculation would tend to obscure the basic physical mechanism leading to the onset of nonlinear effective bending elasticity, and is therefore not warranted here.
Short-distance chain statistics in 3D and 2D
To compute the probability distribution p(t i·t i+r) of finding the polymer with a given relative orientation between bps i and i + r, we introduce the partial partition function, Z(z i, z i+r), where all degrees of freedom are integrated out except the projections on the z axis of t i and t i+r, which are set to z i and z i+r (both ∈ [−1, 1]),
| (2) |
where is the transfer matrix and |V〉 the boundary vector (16). The complete calculation from Eq. 2 of p(s) = 4πZ(1, s)/Z, where s ≡ t i·t i+r ≡ cos θ, θ is the bending angle between two monomers separated by a distance r, and Z is the full partition function, is given in the section B in Supporting Material. It uses the decomposition of on the eigenbasis . We have checked that boundary effects are negligible at T R as soon as i is larger than a few unities. We thus give the final result for p(s) in the limit of long DNA when the internal segment [i, i + r] is far from both chain ends (i.e., for N → ∞ and i → ∞),
| (3) |
where P l(s) is a Legendre polynomial (20). Equation 3 is a sufficient approximation of Eq. S12 (in Supporting Material) for fitting purposes. This expression reveals the role of infinitely many tangent-tangent correlation lengths, = 1/ln(λ 0, +/λ l, τ). At T R, the persistence length, ξ p = 150 bp, coincides with the dominant correlation length ξ p 1, + (17).
The same calculation holds in 2D. We find the probability distribution (section C in Supporting Material)
| (4) |
where = 1/ ln(λ 0, +/λn, τ) are also the tangent-tangent correlation lengths associated with 2D eigenmodes |n, τ〉 with eigenvalues λn, τ. For the numerical calculation of infinite series such as Eq. 3 or Eq. 4, the sum is performed up to order 100 (a higher cutoff has been checked not to change numerical values).
At room temperature, T R, one observes below (see also Fig. 2, a and c) that, for θ smaller than a threshold θ c, p(s) and p(θ) coincide with the discrete WLC model probability distribution, p DWLC, which is the simplified version of Eq. 3 or Eq. 4 when no denaturation bubbles appear (formally all κ equal to κ U),
| (5) |
| (6) |
in 3D and 2D, respectively (dotted lines in Fig. 2, a and c), with β = (k B T)−1. In the Gaussian spin-wave approximation, βκ >> 1, valid here, the discrete WLC model leads to a quadratic dependence in θ. Indeed, in this case, . One ends up with the probability distribution for a single joint of effective bending modulus κ/r, and in 2D (section E in Supporting Material). This implies that the free energy required to bend the polymer by an angle θ is quadratic, F(θ, r) = κθ 2/(2r). In this approximation, the bending rigidity κ and the persistence length ξ p are related through ξ p = 2βκ in 2D and ξ p = βκ in 3D (23).
Figure 2.
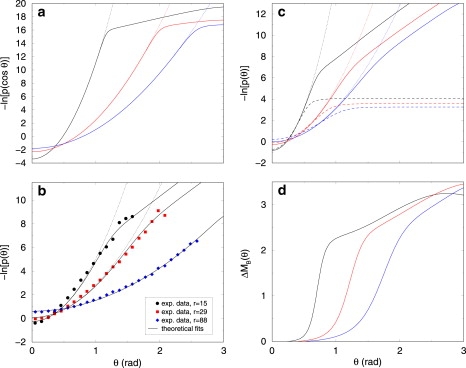
Theoretical predictions of DNA elastic properties in two and three dimensions. (a) Logarithm of the probability distribution p(cos θ) = p(s) in 3D (Eq. 3, solid lines) for different values of r = 5, 15, and 25 bp (from left to right) compared with the WLC model (dotted lines). One bp length is a = 0.34 nm. The Ising and elastic parameter values (in units of kBTR) come from fits to earlier experiments (16): κU = κUB = 147; κB = 5.54; μ = 1.7977; and J = 3.6674. The probability distribution is given by , because ds = sin θ dθ. (b) Logarithm of the probability distributions p(θ) in 2D. Symbols represent experimental data taken from Wiggins et al. (7), whereas the curves are now our best fits, from Eq. 4. The curvilinear distances between monomers in Wiggins et al. (7), namely 5, 10, and 30 nm, correspond, respectively, to r = 15, 29, and 88 bp. The value κB = 5.54 (in units of kBTR) comes from Palmeri et al. (16) and κU = 160.82 comes from fitting the r = 88 bp set of data by a pure WLC model, as in Wiggins et al. (7) (because for such large r, the Gaussian character is restored). The remaining parameters (κUB, J, and μ) are fitted. One possible parameter set is (κUB, J, and μ) = (20.97,1.3173,and 1.6685) (section D in Supporting Material). Dotted lines show the predictions of the WLC model, for comparison. (c) Logarithm of the probability distribution p(θ) in 2D. Parameter values are coming from fits (see panel b), and r = 5, 15, and 25 bp (from top to bottom, solid lines). Dotted line shown the predictions of the WLC model and dashed lines show the same profiles when κB = 0. (d) Average excess chain melting ΔMB(θ) in 2D. Same parameter values as in panel b. From left to right, r = 5, 15, and 25 bp. The elasticity is linear until a threshold , where excessive bending induces bp melting.
Results
We first examine the distribution p(s) ≡ p(t i·t i+r) in 3D. Whereas it is dominated at large r by the largest persistence length ξ p = 150 bp and is well described by the WLC model, this is not true at short r and large θ.
Fig. 2 a displays the probability density p(s), s = t i·t i+r ≡ cos θ, for realistic parameters (16,17). At T R, for θ smaller than a threshold θ c, p(s) coincides with the discrete WLC model distribution, p WLC(s) (Eq. 5), the simplified version of Eq. 3 when no denaturation bubbles appear. For θ > θ c, the plot becomes nonquadratic because of partial DNA denaturation. The threshold θ c is estimated by equating the energetic cost of bending the polymer by an angle θ in its unmelted state, F(θ, r) = κ U θ c 2/(2r), with the free-energy cost of nucleating a single denaturation bubble (of one bp), denoted by ΔG B, which is ΔG B ≃ 17 k B T in 3D (17). Using this scaling argument, we find
| (7) |
which gives a good estimate of the observed thresholds (Fig. 2 a). The anomalies (or nonlinearities) appear for larger and larger values of θ when r grows, and are nonexistent in the plots of p(s) as soon as r > 50 bp, i.e., at length-scales larger than 15 nm, thus recovering standard Gaussian behavior. Indeed, setting θ c = π in Eq. 7 yields the upper limit, r max ≃ 50 bp, as observed in the plots. This also explains why cyclization experiments with r > 50 bp are correctly described by the WLC model (13). For r < 50 bp, this local melting effect is extremely weak, occurring with a probability for r ≥ 5.
The situation is very different when DNA is confined in 2D. It has been demonstrated in experiments that DNA is in 2D thermodynamical equilibrium (5,7). This is the reason why our statistical mechanical model applies and in the large N limit, the probability distribution p(θ) is given by Eq. 4. Plots are provided in Fig. 2, b and c, for realistic parameter values. At large enough angles, one also sees deviations from the WLC behavior, appearing as soon as p(θ) ≈ 0.01 rad−1, a now measurable value (7).
We fit 2D experimental data (7) in Fig. 2 b, using Eq. 4 with κ UB, J, and μ as fitting parameters (section D in Supporting Material). The fits are good over the whole θ-range. For the best-fit parameter sets, the fraction of melted bps for unconstrained DNA is then >0.1% at T R, two orders-of-magnitude higher than in 3D (16). The predicted melting temperature, T m, and transition width, both ∼600 K, are also much higher than their 3D analogs. Despite the high value for T m in 2D, the large transition width leads, with respect to 3D, to nonnegligible bubble nucleation, even at T R. In other words, the loop initiation factor (18), where J 0 is the renormalized destacking parameter (17), is increased by several orders of magnitude with respect to 3D (24). The same argument as in 3D leads to r max ≃ 120 bp in 2D, after modifying ΔG B = 6.6 k B T according to our fitted parameters. Furthermore, we display in Fig. 2 d the average excess of melted bps when t i·t i+r = cos θ is fixed, as compared with an unconstrained DNA (see Appendix). As anticipated, the deviation from the WLC behavior at θ c coincides with the appearance of melted bps making the polymer more flexible.
Discussion
How can the apparent discrepancy between 2D and 3D parameter values be explained? Not by the fact that the DNA used in 2D experiments are heteropolymers, whereas the values derived in 3D come from poly(dA)-poly(dT) homopolymers (16). Indeed, even for the most robust poly(dG)-poly(dC), T m = 360 K in solution. A simple and straightforward explanation for the discrepancy in parameter values is related to the change in the DNA electrostatic energy when it is solvated in water (3D) or adsorbed through magnesium (Mg2+) bridges on the mica in a dry environment. Indeed, it is known that slightly modifying electrostatic interactions (such as by varying the salt concentration) changes dramatically the denaturation profile of DNA in solution (see, e.g., (25)). The energy required to break a bp, 2μ, and the energy to destack consecutive bps, 2J, should also be sensitive to the change in the direct adsorption energy between mica and ds or single-stranded DNA. Strong support for this mechanism comes from the experimental results of Wiggins et al. themselves (7). In their Fig. S3, they present the angle distribution and end-to-end distance statistics for DNA adsorbed on a different-quality mica. Even though the data match to a good approximation those of their Fig. 3, a detailed analysis of the plots for r = 5 and 7.5 nm leads to the conclusion that the two data sets do not coincide, even taking into account error bars. This is an experimental indication that the substrate on which DNA molecules are adsorbed does indeed influence its microscopic parameters. Recent AFM experiments also testified to a DNA structural modification after adsorption on mica and drying (26): poly(dG)-poly(dC) proves to shorten its contour length, supposedly by taking an A-DNA conformation, in contrast to poly(dA)-poly(dT) or plasmid DNA, both of which keep their B-DNA conformations.
Figsure 3.
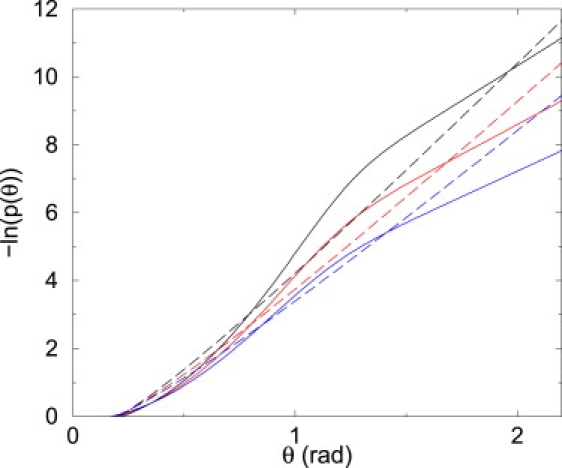
Logarithm of the probability distributions p(θ) in 2D (r = 15 bp), for both the LSEC model (with Λ = 27.2 pN.nm (7), dashed lines) and our theory (solid lines), for increasing temperature T. From top to bottom, T = 298.15 K, 330 K, and 360 K. Our model predicts that increasing T enhances flexibility in a pronounced manner (note the logarithmic scale) thanks to the opening of bps. At θ = 1.5 rad, an experimentally accessible value (7), the decrease of –ln p(θ) with increasing T is twice that found with the LSEC model.
As a result, inferring the parameters μ and J from their 3D analogs is a challenging task. At the time of the writing of this article, the best strategy is certainly to fit them to experimental data. The above results are confirmed by recent accurate all-atom molecular dynamics simulations: Mazur has investigated in detail the short-distance angle distribution of 3D DNA and did not find any evidence for the strong deviations from a WLC distribution found experimentally in 2D (15).
Now we discuss in greater detail the role of bubble flexibility, κ B, and of cooperativity, J, by comparing our model with earlier ones. In the kinkable WLC model (27), kinks of vanishing rigidity can be activated by thermal fluctuations. This model and ours become physically equivalent in the κ B → 0 limit: a 2-bp denaturation bubble plays the role of a kink, in the sense of a thermally activated local defect without rigidity. Our microscopic vision of a kink thus differs from Lankas et al.'s local unstacking one (9), but yields the same short-range mechanical properties. When κ B = 0, the interesting behavior of p(θ) in the denatured region is destroyed: p(θ) becomes flat (Fig. 2 c), as in Wiggins et al. (27), and is practically insensitive to r once a kink is nucleated, because a chain segment including a kink has vanishing rigidity. This is the reason why Wiggins et al. appeal to a different linear subelastic chain (LSEC) model, with a phenomenological bending energy E LSEC = Λ|θ|, which enables them to satisfactorily fit their experimental data (7,28). In contrast to this LSEC model, our approach proposes a microscopic explanation associated with bubble nucleation for the subharmonic behavior of p(θ). Due to excess bubble formation, our model predicts deviations from WLC (or Gaussian) behavior as soon as r < r max with r max ≡ π 2 κ U/(2ΔG B) (from Eq. 7). This expression differs from the LSEC model one, for which r max ≈ βκ U.
Setting J = 0 with κ B finite also affects the profiles by softening the transition and increasing significantly the large angle probabilities, by a factor >10 (data not shown), which confirms the importance of cooperativity (when in addition κ UB = 0, we find again the model proposed in Yan and Marko (12) in the context of cyclization). Neglecting J or κ UB would require the use of unphysically large κ B values when fitting experimental data, while worsening the fit quality.
Our model is restricted to homopolymer DNA. However, a more accurate treatment should incorporate sequence effects by using bp-dependent model parameters (29). Considering that the heteropolymer case is difficult to treat theoretically, and experiments provide only an average description of bending angle probability distribution, we limit ourselves here to describing the anomalous behavior using an averaged approach. If more detailed experimental results become available, it would be worthwhile to extend our model to treat the heterogeneous case.
Currently, many AFM experiments explore DNA conformations and complexation between nucleic acids and proteins (see reviews (4,30,31)). When AFM imaging is carried out on DNA (6,7,32,33) or DNA/histone complexes (34) to access their statistical and dynamical properties, effects of surface interactions on DNA structure are likely to modify sensibly these properties. More generally, our work suggests that studying DNA/companion proteins interactions by AFM (35–38) does not provide any quantitative clue to 3D complexation.
In the cell, packaging involves wrapping DNA around positively charged histones (39). It has been shown that this adsorption is mainly driven by electrostatics (40). Our results suggest that in this case, DNA adsorption on a curved charged surface (such as the histone) is likely to modify profoundly local elastic and denaturation properties of dsDNA. Enhanced flexibility due to denaturation is then likely to facilitate wrapping. This mechanism might also be important for improving the accessibility of enzymes to the single strands in local bubbles (41,42) when DNA is wrapped.
One way of validating this model at the experimental level would be to quantify the effects of temperature, which can be predicted for both our coupled model and the LSEC one (28) ( Fig. 3; see section E in Supporting Material for LSEC formula). Our model predicts that increasing temperature enhances flexibility in a more pronounced manner, thanks to the opening of bps. We believe that such a deviation between the predictions of both models would be a credible experimental test of their respective validities. Additional tests of the quantitative difference between DNA properties in 3D and 2D would be to compare cyclization rates by AFM in both situations for the same dsDNA strands, or to check that denaturation remains weak in 2D when approaching the 3D melting temperature, as predicted by our results.
Acknowledgments
We thank Roland R. Netz and Catherine Tardin for enlightening discussions.
This work was supported in part by the French Research Program ANR-07-NANO-055, Project SIMONANOMEM.
Appendix: Bending-Induced Melting In 2d
Following a calculation as in Wiggins et al. (27), we derive the excess chain melting ΔM B as a function of θ. It measures the average excess of melted bps in the bended chain as compared with the free, unconstrained one and is given by (section F in Supporting Material). The comparison of Fig. 2, c and d, confirms that the deviation from the WLC model corresponds to the appearance of melted bps that make the polymer more flexible at short range. An interesting feature of these calculations is the saturation of ΔM B at a finite value, even when r < rmax increases. In Fig. 2 d, this value is close to 3, which means that the total excess number of denatured bps does not exceed 3 on average. In other words, even if r bps, or more, can in principle be melted to relax the constraint t i·t i+r = cos(θ), only a few of them actually do, since it costs more energy to melt more bases, whereas, owing to the small value of κ B, a small denaturation bubble suffices to give the whole molecule a very small resistance to torque.
Supporting Material
References
- 1.Bustamante C., Bryant Z., Smith S.B. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 2.Finzi L., Gelles J. Measurement of lactose repressor-mediated loop formation and breakdown in single DNA molecules. Science. 1995;267:378–380. doi: 10.1126/science.7824935. [DOI] [PubMed] [Google Scholar]
- 3.Pouget N., Turlan C., Destainville N., Salomé L., Chandler M. IS911 transpososome assembly as analyzed by tethered particle motion. Nucleic Acids Res. 2006;34:4313–4323. doi: 10.1093/nar/gkl420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hansma H.G. Surface biology of DNA by atomic force microscopy. Annu. Rev. Phys. Chem. 2001;52:71–92. doi: 10.1146/annurev.physchem.52.1.71. [DOI] [PubMed] [Google Scholar]
- 5.Rivetti C., Guthold M., Bustamante C. Scanning force microscopy of DNA deposited onto mica: equilibration versus kinetic trapping studied by statistical polymer chain analysis. J. Mol. Biol. 1996;264:919–932. doi: 10.1006/jmbi.1996.0687. [DOI] [PubMed] [Google Scholar]
- 6.van Noort J., van der Heijden T., de Jager M., Wyman C., Kanaar R. The coiled-coil of the human Rad50 DNA repair protein contains specific segments of increased flexibility. Proc. Natl. Acad. Sci. USA. 2003;100:7581–7586. doi: 10.1073/pnas.1330706100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wiggins P.A., van der Heijden T., Moreno-Herrero F., Spakowitz A., Phillips R. High flexibility of DNA on short length scales probed by atomic force microscopy. Nature Nanotech. 2006;1:137–141. doi: 10.1038/nnano.2006.63. [DOI] [PubMed] [Google Scholar]
- 8.Podgornik R. DNA off the hook. Nature Nanotech. 2006;1:100–101. doi: 10.1038/nnano.2006.114. [DOI] [PubMed] [Google Scholar]
- 9.Lankas F., Lavery R., Maddocks J.H. Kinking occurs during molecular dynamics simulations of small DNA minicircles. Structure. 2006;14:1527–1534. doi: 10.1016/j.str.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 10.Kratky O., Porod G. X-ray study of coiled polymers in solution. Rec. Trav. Chem. 1949;68:1106–1123. [Google Scholar]
- 11.Cloutier T.E., Widom J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes. Proc. Natl. Acad. Sci. USA. 2005;102:3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yan J., Marko J.F. Localized single-stranded bubble mechanism for cyclization of short double helix DNA. Phys. Rev. Lett. 2004;93:108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
- 13.Du Q., Smith C., Shiffeldrim N., Vologodskaia M., Vologodskii A. Cyclization of short DNA fragments and bending fluctuations of the double helix. Proc. Natl. Acad. Sci. USA. 2005;102:5397–5402. doi: 10.1073/pnas.0500983102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Linna R.P., Kaski K. Analysis of DNA elasticity. Phys. Rev. Lett. 2008;100:168104. doi: 10.1103/PhysRevLett.100.168104. [DOI] [PubMed] [Google Scholar]
- 15.Mazur A.K. Wormlike chain theory and bending of short DNA. Phys. Rev. Lett. 2007;98:218102. doi: 10.1103/PhysRevLett.98.218102. [DOI] [PubMed] [Google Scholar]
- 16.Palmeri J., Manghi M., Destainville N. Thermal denaturation of fluctuating DNA driven by bending entropy. Phys. Rev. Lett. 2007;99:088103. doi: 10.1103/PhysRevLett.99.088103. [DOI] [PubMed] [Google Scholar]
- 17.Palmeri J., Manghi M., Destainville N. Thermal denaturation of fluctuating finite DNA chains: the role of bending rigidity in bubble nucleation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;77:011913. doi: 10.1103/PhysRevE.77.011913. [DOI] [PubMed] [Google Scholar]
- 18.Poland D., Scheraga H.A. Academic Press; New York: 1970. Theory of Helix Coil Transition in Biopolymers. [Google Scholar]
- 19.Wartell R.M., Benight A.S. Thermal denaturation of DNA molecules: a comparison of theory with experiment. Phys. Rep. 1985;126:67–107. [Google Scholar]
- 20.Abramowitch M., Stegun I.A. Wiley; New York: 1964. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. [Google Scholar]
- 21.Palmeri J., Leibler S. Fluctuating chains with internal degrees of freedom. In: Beysens D., Boccara N., Forgacs G., editors. Dynamical Phenomena at Interfaces Surfaces and Membranes. Nova Science Publishers; New York: 1993. [Google Scholar]
- 22.Manghi M., Palmeri J., Destainville N. Coupling between denaturation and chain conformations in DNA: stretching, bending, torsion and finite size effects. J. Phys. Condens. Matter. 2009;21:034104. doi: 10.1088/0953-8984/21/3/034104. [DOI] [PubMed] [Google Scholar]
- 23.des Cloiseaux J., Jannink J. Les Editions de Physique; Les Ulis, France: 1987. Polymers in Solution: Their Modeling and their Structure. [Google Scholar]
- 24.Amirikyan B.R., Vologodskii A.V., Lyubchenko Y.L. Determination of DNA cooperativity factor. Nucleic Acids Res. 1981;9:5469–5482. doi: 10.1093/nar/9.20.5469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Korolev N., Lyubartsev A.P., Nordenskiöld L. Application of polyelectrolyte theories for analysis of DNA melting in the presence of Na+ and Mg2+ ions. Biophys. J. 1998;75:3041–3056. doi: 10.1016/S0006-3495(98)77745-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Borovok N., Molotsky T., Ghabboun J., Cohen H., Porath D. Poly(dG)-poly(dC) DNA appears shorter than poly(dA)-poly(dT) and possibly adopts an A-related conformation on a mica surface under ambient conditions. FEBS Lett. 2007;581:5843–5846. doi: 10.1016/j.febslet.2007.11.058. [DOI] [PubMed] [Google Scholar]
- 27.Wiggins P.A., Phillips R., Nelson P.C. Exact theory of kinkable elastic polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:021909. doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wiggins P.A., Nelson P.C. Generalized theory of semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:031906. doi: 10.1103/PhysRevE.73.031906. [DOI] [PubMed] [Google Scholar]
- 29.Krueger A., Protozanova E., Frank-Kamenetskii M.D. Sequence-dependent basepair opening in DNA double helix. Biophys. J. 2006;90:3091–3099. doi: 10.1529/biophysj.105.078774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hansma H.G., Kasuya K., Oroudjev E. Atomic force microscopy imaging and pulling of nucleic acids. Curr. Opin. Struct. Biol. 2004;14:380–385. doi: 10.1016/j.sbi.2004.05.005. [DOI] [PubMed] [Google Scholar]
- 31.Cohen S.R., Bitler A. Use of AFM in bio-related systems. Curr. Opin. Colloid Interface Sci. 2008;13:316–325. [Google Scholar]
- 32.Liu W.Y., Wang X., Wang T., Sha R.J., Seeman N.C. PX DNA triangle oligomerized using a novel three-domain motif. Nano Lett. 2008;8:317–322. doi: 10.1021/nl072803r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dahlgren P.R., Lyubchenko Y.L. Atomic force microscopy study of the effects of Mg2+ and other divalent cations on the end-to-end DNA interactions. Biochemistry. 2002;41:11372–11378. doi: 10.1021/bi026102e. [DOI] [PubMed] [Google Scholar]
- 34.Montel F., Fontaine E., St. Jean P., Castelnovo M., Faivre-Moskalenko C. Atomic force microscopy imaging of SWI/SNF action: mapping the nucleosome remodeling and sliding. Biophys. J. 2007;93:566–578. doi: 10.1529/biophysj.107.105569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sorel I., Pietrement O., Hamon L., Baconnais S., Le Cam E. The EcoRI-DNA complex as a model for investigating protein-DNA interactions by atomic force microscopy. Biochemistry. 2006;45:14675–14682. doi: 10.1021/bi060293u. [DOI] [PubMed] [Google Scholar]
- 36.Henn A., Medalia O., Shi S.P., Steinberg M., Francheschi F. Visualization of unwinding activity of duplex RNA by DbpA, a DEAD box helicase, at single-molecule resolution by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 2001;98:5007–5012. doi: 10.1073/pnas.071372498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang H., Tessmer I., Croteau D.L., Erie D.A., Van Houten B. Functional characterization and atomic force microscopy of a DNA repair protein conjugated to a quantum dot. Nano Lett. 2008;8:1631–1637. doi: 10.1021/nl080316l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Guo C., Song Y., Wang L., Sun L., Sun Y. Atomic force microscopic study of low temperature induced disassembly of RecA-dsDNA filaments. J. Phys. Chem. B. 2008;112:1022–1027. doi: 10.1021/jp077233y. [DOI] [PubMed] [Google Scholar]
- 39.Alberts B., Johnson A., Lewis J., Raff M., Roberts K. Garland Publishing; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 40.Oohara I., Wada A. Spectroscopic studies on histone-DNA interactions. II: Three transitions in nucleosomes resolved by salt-titration. J. Mol. Biol. 1987;196:399–411. doi: 10.1016/0022-2836(87)90700-5. [DOI] [PubMed] [Google Scholar]
- 41.Pant K., Karpel R.L., Rouzina I., Williams M.C. Mechanical measurement of single-molecule binding rates: kinetics of DNA helix-destabilization by T4 gene 32 protein. J. Mol. Biol. 2004;336:861–870. doi: 10.1016/j.jmb.2003.12.025. [DOI] [PubMed] [Google Scholar]
- 42.Sokolov I.M., Metzler R., Pant K., Williams M.C. Target search of N sliding proteins on a DNA. Biophys. J. 2005;89:895–902. doi: 10.1529/biophysj.104.057612. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


