Abstract
Spontaneously rhythmic pacemaker activity produced by interstitial cells of Cajal (ICC) is the result of the entrainment of unitary potential depolarizations generated at intracellular sites termed pacemaker units. In this study, we present a mathematical modeling framework that quantitatively represents the transmembrane ion flows and intracellular Ca2+ dynamics from a single ICC operating over the physiological membrane potential range. The mathematical model presented here extends our recently developed biophysically based pacemaker unit modeling framework by including mechanisms necessary for coordinating unitary potential events, such as a T-Type Ca2+ current, Vm-dependent K+ currents, and global Ca2+ diffusion. Model simulations produce spontaneously rhythmic slow wave depolarizations with an amplitude of 65 mV at a frequency of 17.4 cpm. Our model predicts that activity at the spatial scale of the pacemaker unit is fundamental for ICC slow wave generation, and Ca2+ influx from activation of the T-Type Ca2+ current is required for unitary potential entrainment. These results suggest that intracellular Ca2+ levels, particularly in the region local to the mitochondria and endoplasmic reticulum, significantly influence pacing frequency and synchronization of pacemaker unit discharge. Moreover, numerical investigations show that our ICC model is capable of qualitatively replicating a wide range of experimental observations.
Introduction
The interstitial cells of Cajal (ICC) are a specialized group of pacemaker cells located within the gastrointestinal (GI) tract (1); they generate spontaneous, rhythmic electrical activity without obligatory input from the enteric nervous system (2). The coordinated electrical activity produced by ICC, termed slow waves, is conducted to electrically coupled smooth muscle cells (3). Some authors have distinguished slow wave events recorded from ICC versus the events recorded from smooth muscle cells with different terms. For instance, slow waves in ICC have also been called pacemaker or driving potentials and the same events in smooth muscle cells have been referred to as slow waves (4,5). Since it is now recognized that both events are of common origin, we will refer to these events simply as slow waves throughout this article. Over the last 25 years, experimental studies have been performed on GI tissue to determine the biophysical mechanisms underlying slow waves. Such studies have yielded several possible mechanisms for pacemaker activity (6–9), the most extensive, and experimentally supported, being the Sanders' Hypothesis (10–12).
The Sanders' Hypothesis proposes that fundamental GI pacemaker activity is generated within structures, termed pacemaker units, which are formed by the endoplasmic reticulum (ER), mitochondria, and plasma membrane. Cycling of Ca2+ within these structures activates the primary pacemaker conductance, a Ca2+-inhibited nonselective cation conductance (NSCC), resulting in small amplitude depolarizations known as unitary potentials. Transient unitary potentials (Fig. 1 A) activate voltage-dependent Ca2+ channels, specifically the dihydropyridine-resistant T-Type (ICa(T)) Ca2+ current, which accounts for the slow wave upstroke phase (Fig. 1 B). Ca2+ entry through these channels diffuses into the domain local to the IP3 receptors (IP3R) of pacemaker units, which did not discharge before the initial event. This increases the probability of the IP3R being in the open configuration/state, which effectively phase-advances the pacemaker unit from its natural (unforced) oscillatory cycle. Synchronization of pacemaker unit discharge via this mechanism is responsible for the slow wave plateau phase (Fig. 1 C). The subsequent activation of K+ currents and other restitution mechanisms return the cell to a susceptible state (Fig. 1 D), and the pacemaker cycle continues ad infinitum. For a full description of the Sanders' Hypothesis, the reader is directed to the comprehensive review of Sanders et al. (12).
Figure 1.
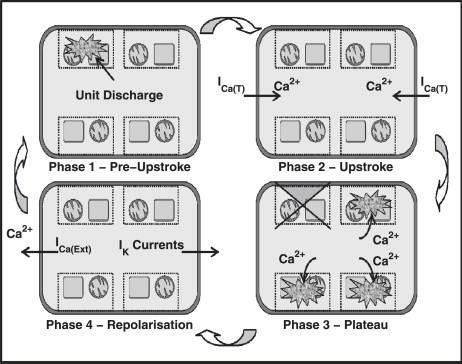
Schematic diagram showing the important phases of the ICC pacemaker cycle as described by the Sanders' Hypothesis. (Phase 1) Discharge of pacemaker units operating at the dominant pacing frequency. (Phase 2) Transient unitary potential depolarizations from the dominant pacemaker unit discharge activates the Vm-dependent Ca2+ currents; specifically the dihydropyridine-resistant T-Type Ca2+ current (ICa(T)). (Phase 3) Ca2+ diffuses throughout the cell into pacemaker units that are not discharged during the upstroke phase, resulting in advancement of their oscillatory cycle. The staggered firing of these pacemaker units forms the slow wave's plateau phase. (Phase 4) Cellular repolarization, which has been suggested to occur via activation of the K+ currents, from the plasma membrane and intracellular Ca2+ handling mechanisms, such as the Ca2+ extrusion pumps (I(Ca(Ext)), restores the cell to its original resting state allowing for repetition of the pacemaker cycle.
Over the last decade, there have been several attempts to mathematically model ICC pacemaker activity, each of which is detailed in Table 1. From the list given in Table 1, the two ICC slow wave models that are most compatible with the Sanders' Hypothesis are that of Edwards and Hirst (EH) (7) and Corrias and Buist (CB) (13). The EH model assumes that slow waves are generated by the summation of discrete unitary conductances, which are representative of pacemaker unit discharge. This model proves the feasibility of pacemaker unit activity being responsible for 1), the upstroke phase, by activating a membrane potential (Vm) dependent conductance; and 2), the plateau phase, with entrainment of pacemaker unit discharge. However, the EH model is largely phenomenological and therefore is incapable of representing the underlying intracellular processes. Furthermore, the EH model assumes that pacemaker unit entrainment occurs in response to Vm-dependent IP3 synthesis, as opposed to the Sanders' Hypothesis which suggests that this phenomenon is primarily attributed to intracellular Ca2+ dynamics. The relatively more complex CB model is the only established ICC modeling framework that, to our knowledge, is both biophysically based and generates pacemaker activity from a unitary potential basis. This model is also the only framework to incorporate mitochondrial Ca2+ handling mechanisms, and an NSCC as the primary pacemaker conductance. However, the pacemaker unit subspace model used in the CB model is representative of the aggregate pacemaker unit response. As a result, the CB model is incapable of simulating unitary potential entrainment as it is does not differentiate between the responses from individual pacemaker units. In summary, there are no biophysically based quantitative ICC modeling frameworks in existence that strictly reproduce the mechanisms detailed by the Sanders' Hypothesis.
Table 1.
Properties of established ICC mathematical models
| Ref. | Model type | Behavior | UP basis | Tracks ionic species | UP representation | Spatial scale |
|---|---|---|---|---|---|---|
| (53) | P | D | No | No | N/A | SC/MC |
| (54) | P | D | No | Yes | N/A | SC/MC |
| (55) | P | S | Yes | No | P | MC |
| (42) | BB | D | No | Yes | N/A | SC |
| (13) | BB | D | Yes | Yes | BB | SC |
P is phenomenological; BB is biophysically based; D is deterministic; S is stochastic; SC is single cell; MC is multiple cell; UP is unitary potential.
Recently, we developed a biophysically based mathematical modeling framework that quantitatively describes the activity from a single isolated pacemaker unit (14). This pacemaker unit model was developed with the intention of being implemented within a whole-cell modeling framework. The question then naturally arises as to how these pacemaker unit representations can be combined to quantitatively describe cellular slow wave activity. This is because the pacemaker unit model, in its current form, does not include any mechanisms by which to synchronize pacemaker unit discharge.
In this study, we present the first biophysically based computational modeling framework that simulates whole-cell ICC pacemaker activity generated from a discrete pacemaker unit population in accordance with the Sanders' Hypothesis. This model is specifically designed to reproduce slow wave activity from a single isolated myenteric ICC cell operating over the entire physiological Vm range. The whole-cell model framework is comprised of the following two separate components, which we will introduce in turn: 1), the pacemaker unit population; and 2), the bulk cytoplasmic subspace. A schematic diagram of the ionic conductances, pacemaker unit population, and other compartmental volumes that comprise the slow wave model is given in Fig. 2.
Figure 2.
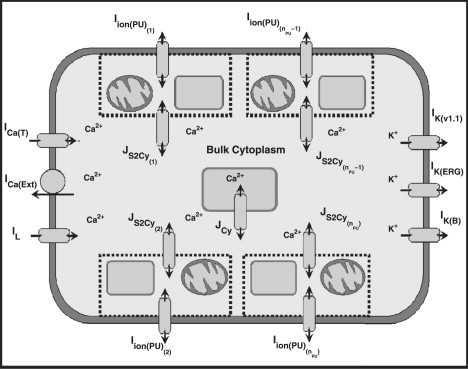
Schematic diagram illustrating the components involved in the whole-cell model framework. Displayed are the ionic conductances and their respective interactions with the pacemaker units and the bulk cytoplasm. Included are a population of nPU pacemaker units, each of which has a transmembrane ionic flux contribution denoted by Iion(PU). The two types of intracellular Ca2+ fluxes responsible for Ca2+ movements throughout the bulk cytoplasm are 1), the intercytoplasmic/pacemaker unit Ca2+ flux from each pacemaker unit (JS2Cy), and 2), the bulk cytoplasm intracellular Ca2+ flux (JCy). Also included are six plasma conductances that regulate cellular electrophysiology: 1), the T-Type Ca2+ current (ICa(T)); 2), the Ca2+ extrusion pump (ICa(Ext)); 3), the K(v1.1) K+ current (IK(v1.1)); 4), Ether-a-go-go (ERG) K+ current (IK(ERG)); 5), a background K+ leakage current (IK(B)); and 6), a nonselective inward leakage current (IL).
Pacemaker Unit Model Modifications
The model of Faville et al. (14) is a generic representation of biophysical activity from a single pacemaker unit. However, the original framework is only representative of an isolated pacemaker unit operating near minimum diastolic potential (MDP), which is ∼−70 mV (5,15,16). To accommodate physiological function within a whole-cell environment over the entire physiological Vm range, several minor modifications to the model framework were required. Below we discuss and justify each of these modifications.
A schematic diagram of the modified pacemaker unit model is illustrated in Fig. 3. The full set of equations and corresponding parameter values that comprise the pacemaker unit model have been included within the Supporting Material (see Pacemaker Unit Model Equations and Table S1, Table S3, and Table S4).
Figure 3.
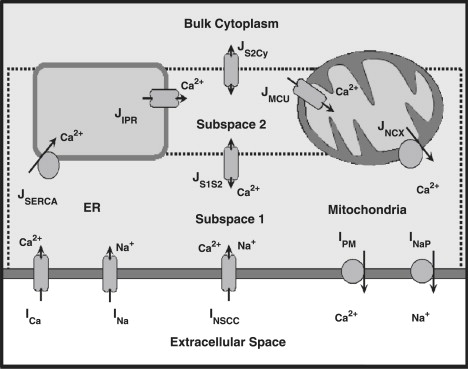
Schematic diagram illustrating the modified pacemaker unit modeling framework. Modifications to the original pacemaker unit model, detailed in Faville et al. (14), include the introduction of the inward Na+ current, INa (note that the outward Na+ pump is now denoted by INaP). The full set of pacemaker unit model equations and parameter values are given in the Supporting Material.
The inward Na+ current
To augment the influx of Na+ into the pacemaker unit from INSCC, we have included an additional Na+ inward current, denoted by INa. Note that, for the sake of convention, the outward Na+ pump (which was represented by INa in the original pacemaker unit model) is now represented henceforth by INaP. INa represents the passive leakage of Na+ into the pacemaker unit, and is modeled by
| (1) |
The maximum conductance rate, gNa, was fitted to a value of 13.5 pS to ensure that baseline Subspace 1 [Na+] (NS1) was Vm-independent (see also Plasma Membrane Conductance Voltage Dependency below). The Na+ Nernst potential, ENa, is given by
| (2) |
where NO is extracellular [Na+] of 140 × 103 μM, T is body temperature of 310.16 K, R is the universal gas constant, and F is Faraday's constant.
Plasma membrane conductance voltage dependency
As mentioned previously, the original pacemaker unit model only considered pacemaker activity generated near MDP. However, analysis of the model under depolarized conditions (Vm > −60 mV) demonstrates there is a significant reduction in the magnitude of the primary pacemaker conductance, INSCC (results not shown). This has the effect of reducing both [Ca2+] and [Na+] within the subplasma membrane compartment, denoted by Subspace 1 (S1). The reduction in baseline S1 [Ca2+] (CS1) is of particular importance, as pacemaker unit discharge has been observed by multiple investigators to be highly dependent on [Ca2+] (6,17,18). This phenomenon has also been previously demonstrated by our pacemaker unit model (14). However, multiple investigators have also observed that the frequency of the spontaneously rhythmic inward currents generated by voltage-clamped ICC is Vm-independent (15,19–22). Taken altogether, this suggests that baseline CS1 levels must also be Vm-independent. Note that in the absence of any physiological data detailing ICC intracellular [Na+], we have conservatively assumed that baseline NS1 levels are also Vm-independent.
For baseline S1 ion concentrations to remain constant during cellular depolarization, there must be either 1), an increase in the magnitude of the inward conductances; or 2), a decrease in the magnitude of the outward conductances. In considering the Ca2+ plasma membrane conductances, we can discount the Ca2+-ATPase pump, IPM, because experimental evidence suggests that this conductance is not Vm-dependent (23,24). Consequently, the conductance rate of the remaining Ca2+ conductance, ICa, must increase with depolarization. We model the Vm-dependent increase in the conductance rate of ICa by
| (3) |
The parameter values of ˜gCa = 0.148 pS and kCa = 0.013 mV−1 were fitted such that baseline CS1 levels remained constant during depolarization.
With regard to the Na+ conductances, the most likely candidate Vm-dependent conductance is INaP. This is because experimental observations suggest that the magnitude of Na+ extrusion pumps, such as the sodium-potassium exchanger (25) or the reverse Na+ pump (26), are highly Vm-dependent. We model the decrease in the INa conductance rate with a linear relationship as
| (4) |
The value of the reversal potential, ENaP, was set to 10 mV, which is similar to values quoted for the reverse Na+ pump (26). The maximum conductance rate, ˜gNaP, of 187.5 pS, was calculated from the original value (1.5 × 104 fA) by correcting for the electrical gradient at Vm = −70 mV (i.e., ˜gNaP = (1.5 × 104)/(10 + 70) = 187.5).
IP3R model
From the original pacemaker unit model, the rate at which the IP3R returns to a susceptible state, denoted by ϕ3, was modeled by a Hodgkin-Huxley (HH) style time-dependent variable (27). The purpose of modeling ϕ3 as a time-dependent variable was to prevent the IP3R from rapidly recovering to an active state. However, the kinetic equations used to describe ϕ3 meant that it was not possible for the IP3R to respond properly to local sudden changes in [Ca2+] while simultaneously retaining the receptor's refractory properties. To overcome this issue, the functional representation of ϕ3 was separated into two independent components as
| (5) |
where CS2 is the [Ca2+] local to the IP3R, ϕ3(CS2) is an instantaneous function of CS2, and ζ(t) is a time-dependent recovery variable that takes values between 0 and 1 inclusively. Note that ζ(t) represents the instantaneous state of the IP3R, whereby ζ(t) = 1 denotes a fully susceptible state, but will approach a value of 0 during ER Ca2+ release. To highlight the functionality of ζ(t) within the new ϕ3 formulation, consider the following two scenarios: 1), the IP3R in a fully susceptible state (ζ(t) = 1); and 2), the IP3R directly after ER Ca2+ release (ζ(t) → 0). Under the first scenario, ϕ3 ≈ ϕ3(CS2), meaning the IP3R will respond instantly to changes in local [Ca2+]. However, under the second scenario, as ζ(t) is much less than unity, the value of ϕ3 is significantly decreased which, in turn, reduces the IP3R's ability to respond to CS2. Therefore, conditions that would be sufficient for the activation of a fully susceptible IP3R may not necessarily be sufficient for an IP3R directly after ER Ca2+ release. We model the instantaneous component of ϕ3 by
| (6) |
where and are the half-concentration and Hill coefficient, respectively, and X is either activation (act) or inhibition (inh). The biphasic functional form of ϕ3(CS2) is a phenomenological representation of IP3R inhibition in the presence of either very high or very low [Ca2+]. Such a phenomenon has been observed experimentally for the Type-1 IP3R (28), which is the dominant IP3R isoform present in ICC (29). We model ζ(t) as a HH-style gating variable whose kinetics are governed by the ordinary differential equation (ODE)
| (7) |
where αζ and βζ are the forward and reverse rates, respectively. The functional forms, and corresponding parameter values, of these rate equations were chosen such that ζ(t) would approach zero in response to elevated CS2 levels (CS2 ≥ 0.5 μM) caused by ER Ca2+ release, but would otherwise approach a value of unity.
Increased pacing frequency
Due to the availability of species-specific experimental data, the pacemaker unit model was reparameterized specifically to represent murine small intestinal (SI) ICC pacemaker activity. This is because slow waves recorded from the SI ICC have the shortest duration of all GI organs, and thus require the least number of pacemaker units to represent the plateau phase. Note that despite the difference in pacing frequency and slow wave duration, we assume that the pacemaker mechanisms are the same between cell types.
The model pacing frequency was increased, from 3 cpm, to specifically represent that from murine SI ICC, which is ∼16–26 cpm (15,5,16). This increase in pacing frequency was achieved by increasing the intersubspace Ca2+ diffusion rate, μS1S2, from 0.04 s−1 to 0.30 s−1 and the IP3R activation rate parameter, r2, from 200 s−1 to 250 s−1. A comparison of the unitary potentials generated by the original and modified pacemaker unit models is illustrated in Fig. 4 A.
Figure 4.
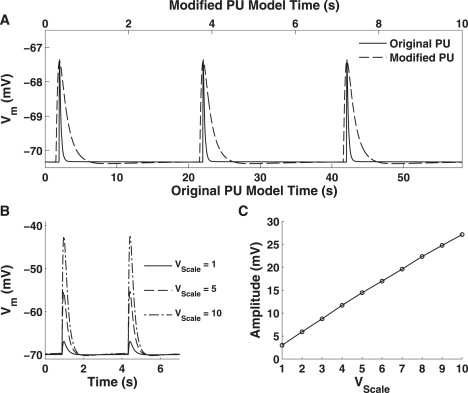
(A) Comparison of the unitary potentials generated by the original (solid) and modified (dashed) pacemaker unit models. Note the differing timescales for each scale with the bottom timescale representing the original model, and the top timescale the modified framework. (B) Simulated unitary potentials depolarizations for VScale = 1, 5, and 10. (C) Relationship between unitary potential amplitude and VScale.
Pacemaker unit volume scaling
Analyses of electrical recordings from guinea-pig gastric antrum tissue (18) observe that unitary potential depolarizations are produced with mean amplitude of ∼3 mV. However, the amplitude of these depolarizations is relatively small when compared to the amplitude of full slow waves (∼40–70 mV) from guinea-pig gastric antrum (4,30,31) and murine SI tissue samples (5,15,16). If unitary potentials are responsible for 1), depolarizing the cell into the ICa(T) Vm-activation window and 2), maintaining the slow wave plateau phase, then potentially tens to hundreds of pacemaker units would be required to represent slow wave activity. The computational expense of simulating such a large number of pacemaker units would reduce the model framework's tractability.
To overcome this issue, we have introduced a scale factor, denoted by VScale, which controls S1 volume. If we assume that 1), S1 thickness is very small relative to the cell membrane surface area and 2), the pacemaker unit ion channel density is constant, then the pacemaker unit plasma membrane conductance rates should approximately increase proportional to VScale:
| (8) |
| (9) |
In other words, by increasing the volume of S1 we also increase the individual transmembrane ion contribution from each individual unit. As a result, we require fewer pacemaker units overall to generate the same activity. However, a consequence of this model construct is that pacemaker unit activity is now representative of the equivalent pacemaker activity generated by multiple units.
It should be noted that as the current/flux ratio (δS(PU)) is inversely proportional to pacemaker unit volume, then the value of δS(PU) should also be reduced by a factor of VScale. This has also been incorporated into the differential equations governing Subspace 1 [Ca2+] and [Na+] (see Eq. S30 and Eq. S34). The value of VScale is related to the pacemaker population size, nPU, by the relationship
| (10) |
where nPU(Base) was set to 50 pacemaker units. Analysis of the effects of VScale on the pacemaker unit model (Fig. 4B) demonstrates that there is a linear relationship between unitary potential amplitude and VScale (Fig. 4 C). It should be noted that there is a lower limit to nPU, because if VScale is too large then the approximation of S1 cell membrane surface area scaling with S1 volume is no longer realistic. A consequence of this is that it would be unrealistic to scale the plasma membrane conductance rates proportionately with VScale. From analysis of Fig. 4 C, we suggest a lower limit of nPU = 5, because smaller population sizes would produce unitary potentials that were greater than half the amplitude of full slow waves (which is ∼50–70 mV; see Table 2).
Table 2.
Pacemaker potential characteristic values comparison
| Ref. | n | MDP (mV) | Frequency (cpm) | Amplitude (mV) | Half-width (s) | dVm/dtmax (V s−1) |
|---|---|---|---|---|---|---|
| (5) | 39 | −69.6 ± 4.5 | 26.1 ± 2.4 | 56.3 ± 5.3 | 1.00 ± 0.16 | 1.51 ± 0.30 |
| (16) | 12 | −68.7 ± 2.5 | 24.2 ± 1.5 | 58.9 ± 3.0 | 0.91 ± 0.09 | 1.85 ± 0.29 |
| (15) | 5 | −70.0 | 16.2 | 73.1 | 0.49 ± 0.03 | 6.40 ± 0.60 |
| Range | (−74.1)–(−65.1) | 16.2–28.5 | 51.0–73.1 | 0.46–1.16 | 1.21–7.00 | |
| Youm et al. (42) | −78.0 | 20 | 79.2 | 0.64 | 7.10 | |
| Model simulations | −69.8 ± 0.14 | 17.4 ± 0.03 | 64.5 ± 0.16 | 0.72 ± 0.02 | 1.32 ± 0.05 | |
Here, n denotes the number of observations made from separate tissue preparations.
The Bulk Cytoplasmic Subspace
Parameter estimation
Where possible, model parameters were obtained either by fitting to appropriate ICC experimental data or were based on values quoted from other biophysically based ICC electrophysiological models (7,13). All model parameters determined by this process are explicitly stated below. The remaining parameters, for which there was no suitable data or appropriate alternatives, were fitted using nonlinear optimization techniques. The fitting procedure optimized these parameter values such that the whole-cell model reproduced experimentally observed slow wave metrics. These metrics were:
-
1.
Amplitude (YA).
-
2.
Frequency (YF).
-
3.
Half-width (YHW).
-
4.
MDP (YMDP).
-
5.
Maximum Vm rate change, dVm/dtmax (YdVm).
Note that the YHW is defined as the duration where Vm > 50% × YA, and YdVm is the maximum Vm rate change during the slow wave upstroke phase. The values for these metrics were obtained from slow waves recorded from murine SI tissue (5,15,16), and are summarized in Table 2.
To fit the parameter values so that the model response falls within the physiological range of experimentally observed slow wave characteristic values, the cost function was calculated for each metric,
| (11) |
where X = A, F, HW, MDP, or dVm, and YX(LB) and YX(UB) denote the lower and upper bounding values, respectively, for a given metric (see Table 2). The form of the cost function was chosen such that if YX was within the physiological bounds, then the function value would be zero. For YX outside of the bounds, the value of the cost function was calculated as the absolute difference between the metric and the closest bounding value. The total optimization objective function, FCost, was calculated as the sum of the individual metric cost function values:
| (12) |
To obtain a feasible solution such that all metrics were within physiological bounds, which is denoted by FCost = 0, we employed a Monte Carlo minimization algorithm (32).
Intracellular Ca2+ fluxes
The intracellular Ca2+ fluxes represent the intracellular Ca2+ handling mechanisms responsible for unitary potential entrainment. Furthermore, these conductances contribute to shaping the Ca2+ spatio-temporal response within the bulk cytoplasm. Our model includes two intracellular Ca2+ fluxes, which are 1), the intercytoplasmic/pacemaker unit Ca2+ flux, JS2Cy; and 2), the bulk cytoplasm intracellular Ca2+ flux, JCy.
The intercytoplasmic/pacemaker unit Ca2+ flux represents Ca2+ diffusion between the bulk cytoplasm and the pacemaker units. It is via this mechanism that individual pacemaker units are entrained to maintain the slow wave plateau phase. The equation describing Ca2+ diffusion between the bulk cytoplasm and the ith pacemaker unit is given as
| (13) |
where CCy is bulk cytoplasmic [Ca2+], and CS2(i) and μS2Cy(i) are the Subspace 2 (S2) [Ca2+] and Ca2+ diffusion rates, respectively, for the ith pacemaker unit. The distribution of μS2Cy values that were used for the entire ICC model is discussed in detail below (see Ca2+ Diffusion Rates). Note that Ca2+ diffusion is only permitted to occur between the bulk cytoplasm and S2, and not between the bulk cytoplasm and the pacemaker unit's subplasma membrane subspace (denoted by S1). This is because Ca2+ diffusion directly into S1 would inactivate the Ca2+-inhibited INSCC, thereby abolishing unitary potential depolarizations.
For Ca2+ to be conserved within the pacemaker unit model, the ODE describing S2 [Ca2+] (CS2) must be updated to include JS2Cy. Therefore, with reference to Faville et al. (14), the new ODE governing S2 [Ca2+] for the ith pacemaker unit is given by
| (14) |
Via this biophysical structure, it becomes evident how pacemaker unit entrainment occurs in response to elevated CCy levels from ICa(T) activation. As CCy increases, there is a positive increase in the magnitude of JS2Cy (Eq. 13) resulting in Ca2+ preferentially diffusing from the bulk cytoplasm into S2. The consequential elevation in S2 [Ca2+] (Eq. 14) causes an increase in IP3R open probability, hence phase-advancing the rate at which the receptor would otherwise normally fire. By varying the value of μS2Cy for a given pacemaker unit, we can effectively control the rate at which the IP3R will fire, and thus control pacemaker unit entrainment. Note that this model construct also quantifies the effect of pacemaker unit dominance, whereby units with the highest μS2Cy will fire at a faster rate than those with lower Ca2+ diffusion rates.
Also included in the model is the bulk cytoplasmic intracellular Ca2+ flux, which provides an intracellular mechanism to remove Ca2+ from the bulk cytoplasm. Moreover, JCy is a phenomenological representation of the intracellular Ca2+ handling mechanisms (such as ER/mitochondrial Ca2+ uptake) that are not directly involved with pacemaker unit activity. We model JCy by the diffusion equation
| (15) |
We use values of μCy = 1.3 s−1 and C∞ = 0.12 μM to shape the restitution phase of the bulk cytoplasmic [Ca2+] signal and maintain resting Ca2+ levels.
Plasma Membrane Conductances
Ca2+ conductances and transporters
The Ca2+ conductances play a dual role in ICC pacemaker activity. Firstly, the net Ca2+ influx from the activation of the inward ionic currents causes cellular depolarization (16). Secondly, Ca2+ diffusion between the bulk cytoplasm and the neighboring pacemaker units coordinates unitary potential discharge (12). The two Ca2+ plasma membrane conductances which have been included in the whole-cell model are the 1), T-Type Ca2+ current (ICa(T)); and the 2), Ca2+ extrusion pump (ICa(Ext)).
The T-Type Ca2+ current is suggested to be the conductance responsible for the upstroke phase of slow wave depolarizations (16,33,34). The ICa(T) was resolved via voltage-clamp experiments performed on murine SI and colon ICC (33). We model ICa(T) using the Vm-dependent primary current as described by the EH model, which has the functional form
| (16) |
where OCa(T) is the conductance open probability, the fitted value of gCa(T) was 800 pS, and ECa(T) = 17 mV was derived from voltage-clamp experiments performed on rat CaV3.2 channel isoforms at 37°C (35).
Several Ca2+ extrusion mechanisms have been identified in ICC, specifically the Ca2+-ATPase pump and plasma membrane Na-Ca exchange pump proteins (36). These conductances regulate intracellular [Ca2+] by extruding Ca2+ across the cell membrane. However, as the kinetics of these conductances have not been fully characterized in ICCs, we model the action of these conductances phenomenologically using the following Ca2+-activated Hill equation:
| (17) |
We set gCa(Ext) = 100 fA and KCa(Ext) = 1 μM to ensure the resting bulk cytoplasmic [Ca2+] was maintained over multiple pacemaker cycles at a physiological intracellular [Ca2+] of 0.12 μM.
Note that the L-Type Ca2+ current (ICa(L)) has also been identified via voltage-clamp experiments performed on murine SI and colonic ICCs (33). However, the exact role that ICa(L) plays in ICC pacemaker activity is unknown. This is because experimental investigators have observed that dihydropyridines, known ICa(L) blockers, have little-to-no effect on ICC pacemaker activity (12). Therefore, as ICa(L) is apparently superfluous to pacemaker activity, we have omitted this conductance from our modeling framework.
K+ conductances
The K+ plasma membrane conductances contribute to pacemaker activity by repolarizing the membrane potential and maintaining the resting membrane potential during the pacemaker cycle's quiescent phase. We include in our slow wave model three whole-cell K+ currents, which are the 1), voltage-dependent KV1.1 current, IK(v1.1); 2), Ether-a-go-go (ERG) K+ current, IK(ERG); and 3), background K+ leakage current, IK(B).
The functional form of the equations used to model all the bulk cytoplasmic K+ conductances have been adapted from Corrias and Buist (13). It should be noted that we have assumed a constant physiological intracellular (Ki) and extracellular (KO) [K+] of 5.4 × 103 μM and 145 × 103 μM, respectively. This is because all the whole-cell plasma membrane conductances are either dependent on Vm and/or CCy. A consequence of this assumption is that all K+ currents (except IK(B); see below) flow against a constant K+ reversal potential, denoted by EK, and are calculated by
| (18) |
The ERG K+ channels have been identified in murine SI ICC by multiple investigators (37,38) and are suggested to regulate ICC excitability and pacemaker activity. The model for IK(ERG) is characterized using
| (19) |
where dERG is the activation gating variable, and the maximum conductance rate, gK(ERG), was fitted giving a value of 6 pS.
The voltage-dependent K+ channel (KV1.1) was identified in canine, murine, and guinea-pig ICC through immunohistochemical colocalization (39). We model IK(v1.1) using
| (20) |
where dv1.1 and fv1.1 are the activation and inactivation gating variables, and the fitted value for the maximum conductance rate, gK(v1.1), was 10 pS.
Finally, a background K+ leakage current was included to represent the passive K+ efflux, and is described by
| (21) |
where gK(B) is the maximum conductance rate and was fitted giving a value of 13.5 pS, and EK(B) is the reversal potential which was set to −70 mV to ensure slow wave MDP was approximately equal to this value.
Other conductances
The nonselective inward leakage current represents the aggregate background inward leakage currents. This current shapes the slope of Vm during the quiescent phase of the pacemaker cycle by balancing passive outward ion flows. The equation describing IL is given as
| (22) |
The maximum conductance rate, gL, was fitted to a value of 0.8 pS and the reversal potential, EL, was set to a value of 0 mV, which is characteristic of nonselective cation channels (20).
Gating variables
To model the time-dependent features of the whole-cell ionic conductances, we have employed HH-style gating kinetic variables. A list of all the whole-cell conductance gating variables that were implemented within our modeling framework are given in Table 3. The equations, and the corresponding parameter values, which describe the ODE rates parameters for all gating variables, are given in the Supporting Material (see Bulk Cytoplasmic Subspace Model Equations and Table S2, Table S3, and Table S4).
Table 3.
Whole-cell gating variables
State variable derivatives
Combining the response from all the bulk cytoplasmic conductances determines the ODEs governing Vm and CCy dynamics. Referring to Fig. 2, the conservation ODE for bulk cytoplasmic [Ca2+] is given by
| (23) |
where δS(Cy) is the bulk cytoplasm current-to-flux scale factor (2 × 10−3 μM C−1), and μS2Cy is the S2/bulk cytoplasm volume ratio. Note that we assumed that the bulk cytoplasm volume is significantly larger than that occupied by S2. However, due to the lack of morphological data describing the domains of the pacemaker units and bulk cytoplasm, it is not possible to quantify the volume of these compartments. Therefore, we set λS2Cy = 1 × 10−3, which is similar to the ratio of the compartmental volumes as quoted from Corrias and Buist (13). The equation governing cellular membrane potential is
| (24) |
where Cm is cellular membrane capacitance (20 pF), is the sum of the plasma membrane conductances from the ith pacemaker unit (see reference (14)), and Iion(Cy) is the sum of all the bulk cytoplasmic plasma membrane conductances:
| (25) |
Note that we have assumed that the cellular membrane is isopotential, with electrophysiological investigations performed on gastric antrum ICC suggesting that this assumption is valid (6). A consequence of this assumption is that the bulk cytoplasm and pacemaker units are exposed to the same Vm, meaning we only need to dynamically track a single Vm state variable.
Ensemble Slow Wave Model
Ca2+ diffusion rates
Due to the nonexistence of any physiological data by which to describe pacemaker unit entrainment, we quantify the μS1S2/μS2Cy distributions based on assumptions that are consistent with the Sanders' Hypothesis. Firstly, we assume that the intrinsic pacemaker unit discharge frequency (i.e., the discharge frequency independent of global [Ca2+]) must vary among the pacemaker units. This is because pacemaker units discharging at the dominant pacing frequency will be responsible for the slow wave upstroke phase, whereas the remaining subdominant pacemaker units are entrained by ICa(T) activation. We quantify this phenomenon by using the distribution to describe the pacemaker unit population μS1S2 values
| (26) |
where i denotes the pacemaker unit number, and μA and μB are the μS1S2 values for the fastest and slowest discharging units, respectively. We set μA = 0.30 s−1 and μB = 0.24 s−1, which translates into intrinsic pacing frequencies of 17.4 and 13.0 cpm, respectively, meaning the dominant pacemaker unit discharges 33% faster than the slowest firing unit.
To determine the population μS2Cy values, we assume that the proportion of the pacemaker unit population that has fired after time, t, can be described by a cumulative distribution function, denoted by ψ(t). This model construct is effectively a first-order approximation of the pacemaker unit spatial distribution, given that our model is a zero-dimensional (spatially independent) framework. The functional form that we use to represent ψ(t) is the two-parameter Boltzmann function, which is given as
| (27) |
where kψ is the slope factor and Tψ is the half-activation time. This functional form is based on the relationship between slow wave initiation and diastolic interval, which was determined from experimental observations made from guinea-pig antrum ICC (4). Care must be taken with this result, however, because this relationship does not strictly represent the distribution of pacemaker unit discharge. However, analysis of pacemaker unit discharge from the EH model demonstrates that ψ(t) is well approximated by Eq. 27 (data not shown).
By inverting Eq. 27 and fixing t = 0 as the time at which the first (dominant) pacemaker unit fires, then the time at which the ith pacemaker unit discharges, t(i), is given by the following equation (see Pacemaker Unit Firing Times in the Supporting Material for derivation):
| (28) |
The value of μS2Cy(i) was optimized such that τFire(i) – τFire(1) = t(i) (where τFire(j) is the firing time of the jth simulated pacemaker unit) using a Newton-Raphson root-finding method for kψ = 11 s−1. This value of kψ is based on that quoted from Hirst and Edwards (4) (kψ = 1.1 s−1), but was scaled by a factor of 10 to compensate for the decreased SI slow wave duration and pacing cycle period. The distribution of μS2Cy values fitted for nPU = 5–10, 15, 20, and 25 are given in Table S5.
Model simulations
Numerical simulations of the slow wave model were conducted on a 3.0 GHz Intel Pentium 4 desktop computer using the C programming language. The model ODEs were integrated using the CVODE integration package (40). All simulated pacemaker activity presented in Results were generated for nPU = 10, unless specifically stated otherwise. It should also be noted that the state variable initial conditions do not represent a stable point in the pacemaker oscillatory cycle. Therefore, all the model simulations discussed below were run for 20 s of simulated pacemaker activity to achieve a stable oscillatory cycle.
Model translation
To facilitate accurate dissemination of our modeling framework for purposes of numerical simulation, we have made the model equations available in CellML, an XML-based modeling language (41). CellML has been developed as a potential solution to the problems associated with publishing and implementing a mathematical model, the idea being that the journal article is published concurrent with the CellML model code. Furthermore, reviewers can test a prospective model during the peer-review process to check the validity of the results being published.
The pacemaker unit model and whole-cell model framework has been translated into CellML and the code is freely available for download (http://www.cellml.org/cellml/models/faville_pullan_lloyd_koh_sanders_smith_2008_version01_variant01) (http://www.cellml.org/models/faville_pullan_lloyd_koh_sanders_smith_2008_version01) and can be run using the open source tool Physiome CellML Environment (http://www.cellml.org/downloads/pcenv). In addition, the original pacemaker unit model (14) has also been translated into CellML (http://www.cellml.org/models/faville_pullan_sanders_smith_2008_version02).
Results
Slow wave depolarizations
Integration of the model equations produced slow waves with an amplitude of 64.5 mV and half-width duration of 0.72 s from a MDP of −69.8 mV (Fig. 5 A). These slow waves were produced at a rate of 17.4 cpm with dVm/dtmax of 1.32 V s−1, which occurs at roughly −35.8 mV. Depolarizations were generated with spontaneous rhythmicity and were stable for >5 min of simulated pacemaker activity (data not shown). The pacemaker unit rastergram, which indicates the temporal firing of the IP3R's over the pacemaker unit population, demonstrates that each unit fires only once during each slow wave (Fig. 5 B).
Figure 5.
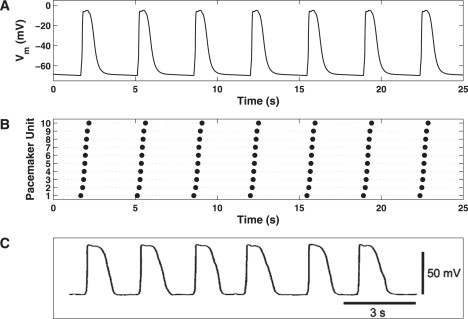
(A) Slow wave depolarizations generated over multiple pacemaker cycles for nPU = 10. (B) Pacemaker unit rastergram, which indicates the temporal discharge of the pacemaker units over the entire population. Each dot, for a given pacemaker unit, represents the time at which peak subspace 2 [Ca2+] occurs (for transients >1.0 μM). (C) Slow waves recorded from murine SI ICC (trace reprinted from Fig. 2Aa of Kito et al. (16), with permission).
We compare the results of these model simulations to slow waves, which were recorded experimentally from murine SI ICC (16) in Fig. 5 C. Table 2 summarizes the aforementioned slow wave characteristic values and compares them to analogous values recorded experimentally from murine SI ICC. In the same table, we also compare these results to those generated by the Youm et al. (42) slow wave (YSW) model, the only other established slow wave model that is representative of SI pacemaker activity.
Intracellular Ca2+ dynamics
Underlying cellular electrophysiological effects are the intracellular Ca2+ handling mechanisms of the bulk cytoplasm and pacemaker units. The bulk cytoplasmic [Ca2+] and membrane potential are shown together in Fig. 6 A, illustrating the one-to-one relationship between membrane potential and Ca2+ oscillations. This direct correlation has been noted by multiple investigators who have studied ICC intracellular Ca2+ dynamics (21,43–46). Further to this, we calculate the spatially averaged cytosolic [Ca2+], [Ca2+]avg as
| (29) |
where
Figure 6.
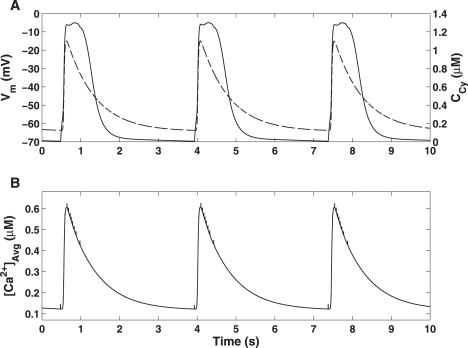
Simulated intracellular Ca2+ oscillations generated by the slow wave model. (A) Vm (solid) and CCy (dashed) traces showing a phase-locked correlation between slow wave activity and Ca2+ oscillations. (B) Spatially averaged [Ca2+] calculated over all cytoplasmic compartmental volumes. Note the spiking activity indicating the Ca2+ hotspots that are generated from ER Ca2+ release.
The values of γS1 and γS2, as quoted in Faville et al. (14), are 100 and 1, respectively. The [Ca2+]avg trace produced from model simulations (Fig. 6 B) is similar in shape to, but approximately half the magnitude of, the bulk cytoplasmic [Ca2+] trace. This indicates that the majority of the model's intracellular Ca2+ activity that is observable on a global scale is taking place in the bulk cytoplasm. The spiking activity from the [Ca2+]avg trace indicates the firing of an individual pacemaker, due to the extremely high local [Ca2+] hotspots generated from ER Ca2+ release.
Effects of population size
To test the effects of pacemaker unit population size on simulated slow wave activity, we fitted parameters for nPU = 5–10, 15, 20, and 25 (see Ca2+ Diffusion Rates above). The fitted μS2Cy values for these populations are given in Table S5. Fig. 7 A illustrates that the macroscopic properties of slow wave activity such as frequency, amplitude, and half-width are not significantly affected by nPU.
Figure 7.
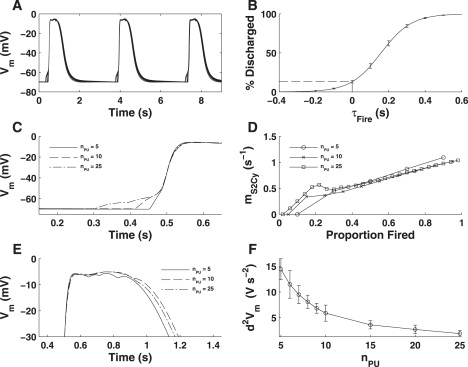
(A) Simulated pacemaker activity for various population sizes (nPU = 5–10, 15, 20, and 25) demonstrating that there is little difference in the slow wave macroscopic properties. (B) Pacemaker unit discharge cumulative distribution function (ψ(t)) calculated with respect to dVm/dtmax. The dashed line indicates that ∼14% of the pacemaker unit population discharges before dVm/dtmax. (C) Slow wave upstroke phase for nPU = 5, 10, and 25. Note that larger nPU (nPU ≥ 10) requires multiple pacemaker units to activate ICa(T). This is reflected in the fitted μS2Cy values for each population (D), which shows a discontinuity in the gradient of this distribution for pacemaker units firing around the upstroke phase (∼10–30% of population). (E) Slow wave plateau phase for nPU = 5, 10, and 25. Note that increasing nPU results in a smoothing of the plateau phase, as indicated by a reduction in the curvature of the Vm signal (F).
The pacemaker unit firing distributions that were fitted for each population, with t = 0 denoting t(dVm/dtmax), shows that ∼14% of the pacemaker unit population discharges before dVm/dtmax (Fig. 7 B). A consequence of this is that for nPU ≥ 10, more than one pacemaker unit must discharge to reach the ICa(T) activation threshold (Fig. 7 C). Interestingly, the μS2Cy distributions for nPU ≥ 10 show that there is a discontinuity in the gradient of the Ca2+ diffusion rates around the slow wave upstroke (i.e., 10% < Px < 30%; Fig. 7 D). This result suggests the possibility of two different types of pacemaker unit populations, either of which is specifically responsible for the slow wave upstroke and plateau phases. Such a concept is consistent with experimental observations made from guinea-pig gastric antrum ICC, suggesting that the slow wave upstroke and plateau phases are generated separately (4).
Closer inspection of the slow wave plateau phase demonstrates that increasing nPU produces a smoother plateau (Fig. 7 E). This phenomenon is also exemplified by the Vm curvature (d2Vm/dt2) calculated during the slow wave plateau (Fig. 7 E). This is primarily because reducing population size causes an increased resolution in the unitary potential depolarizations, which produces a corrugated effect. Such a result shows that there is a lower limit on nPU for which slow waves can be feasibly represented.
Voltage-clamp
Simulations of voltage-clamp experiments were performed to determine the effect that membrane potential has on pacemaker activity. These simulations were run in two phases:
Phase 1. Control conditions (t = 0–30 s).
Phase 2. Vm-clamp conditions (t = 30–60 s) (Eq. 24 set to zero and Vm fixed at the clamp potential).
Simulations for Vh = −70 mV (Fig. 8 A) and −40 mV (Fig. 8C) show that pacemaker activity persists under voltage-clamp, as signified by the production of spontaneous unitary membrane currents (Fig. 8, B and D). Comparison of the membrane currents between clamp potentials shows a reduction in magnitude with depolarization as regular peak inward currents decreased from ∼15 pA at Vh = −70 mV (Fig. 8 B) down to ∼10 pA at Vh = −40 mV (Fig. 8 D).
Figure 8.
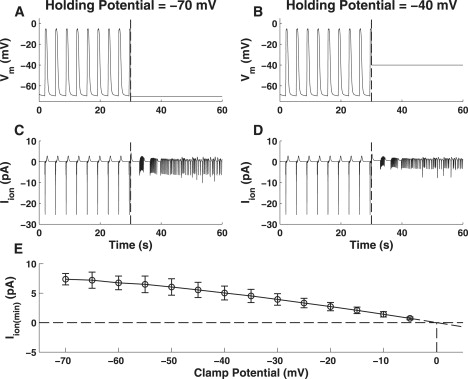
Pacemaker activity produced under simulated voltage-clamp conditions. Illustrated are the Vm (row 1) and clamped membrane currents (row 2) produced for holding potentials of −70 mV (A and B) and −40 mV (C and D). The vertical dashed line at t = 30 s indicates the point where simulated voltage-clamp commences. Note the persistence of pacemaker activity under voltage-clamp, as illustrated by the generation of unitary currents (row 2; t > 30 s). Note also that the magnitude of these unitary currents decreases with depolarization from a holding potential of −70 mV (B) to −40 mV (D). (E) Magnitude of the unitary currents generated under voltage clamp (bars indicated mean ± SD). Extrapolation of this relationship indicates that the unitary currents reverse around 0 mV.
Idealized conductance block
Numerical experiments were performed on the slow wave model to determine the response to the simulated pharmacological inhibition of important conductances, namely the SERCA pump proteins (JSERCA), the IP3R (JIPR), and the mitochondrial Ca2+ uniporter (JMCU). These simulations were conducted to determine whether the slow wave model was capable of qualitatively reproducing experimental investigations that specifically targeted these conductances (see Table 4).
Table 4.
Conductance block experiments
For these simulations, it was assumed that the effects of the simulated pharmacological agents acted specifically, reversibly, instantaneously, and were applied in supermaximal doses sufficient to completely block the targeted conductance (i.e., flow rate of targeted conductance set to zero). The idealized conductance block simulations were run in three phases:
Phase 1. Control condition (t = 0–40 s).
Phase 2. Conductance blockage (t = 40–80s).
Phase 3. Wash-out of the inhibiting pharmacological agent (t = 80–120 s).
Fig. 9 illustrates the membrane potential traces (Fig. 9, column 1) and pacemaker unit discharge rastergram (Fig. 9, column 2) for JSERCA (row 1), JMCU (row 2), and JIPR (row 3). In all cases, global pacemaker activity was completely abolished during the conductance block simulation phase. This abolishment of global pacemaker activity appears to be due to the cessation of pacemaker activity on the pacemaker unit spatial scale, as exemplified by the S2 [Ca2+] traces.
Figure 9.
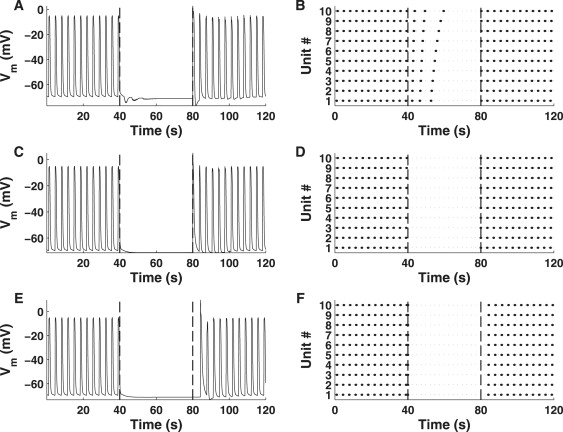
Simulated slow wave activity produced from the complete inhibition of JSERCA (row 1), JMCU (row 2), and JIPR (row 3). Displayed are the simulated Vm (column 1) and pacemaker unit discharge rastergrams (column 2) to illustrate global and local pacemaker activity, respectively. The vertical dashed lines denotes the starts of the conductance block (t = 40 s) and wash-out (t = 80 s) phases. For all scenarios, conductance block abolishes pacemaker activity on all levels. This effect is reversed during the wash-out phase whereby spontaneous pacemaker activity is restored.
Further to this, it can be seen that there is a reversal in pacemaker activity cessation during the simulated wash-out phase. This reversal in pacemaker activity cessation has also been observed experimentally for all the conductances studied in these simulations. This phenomenon is due to the reactivation of pacemaker unit activity, thus highlighting the importance of the pacemaker units in generating global ICC pacemaker activity.
Dose-response simulations
In addition to the conductance block simulations, we investigated the qualitative dose-response that certain experimental conditions have on simulated model pacemaker activity. These simulations were run to validate the model's response to the partial inhibition/reduction of physiological parameters. In this study, we present results from numerical investigations into the dose-response effects of mibefradil/NiCl2, both of which are inhibitors of ICa(T), and BAPTA, a Ca2+ chelator that reduces intracellular [Ca2+]. Note that further simulations of this type were conducted but, due to reasons of brevity, have instead been included in the Supporting Material (see that source's Dose-Response Simulations). The results of all dose-response simulations, compared to their corresponding experimental observations, are summarized in Table 5.
Table 5.
Dose-response experiments
| MDP |
Frequency |
Amplitude |
dVm/dtmax |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Drug | Parameter | Ref. | E | MS | E | MS | E | MS | E | MS |
| Mibefradil NiCl2 | gCa(T) | (5,16)∗ | NS | Dec | Dec | Dec | Dec | Dec | Dec | Dec |
| BAPTA | μS1S2/μS2Cy | (5,47)† | Inc | NC | Dec | Dec | Dec | Dec | Dec | Dec |
| Low [Ca2+]o | CO | (5)∗ | Dec | Dec | Dec | Dec | Dec | Dec | Dec | Dec |
| Low [Na+]o | NO | (5)∗ | Inc | Inc | Dec | Dec | Dec | Dec | Dec | Dec |
| High [K+]o | KO | (5) | Inc | Inc | Dec | Dec | Dec | Dec | Dec | Dec |
| Norepinephrine phenylephrine | P | (47) | NS | Dec | Inc | Inc | NS | Inc | NS | Inc |
| CGP37157 clonazepam | VNCX‡ | (57) | Inc | NC | Dec | Dec§ | Dec | Dec | Dec | Dec |
| E-4031 | gK(ERG) | (58) | Inc | Inc | Dec | Dec | Inc | Dec | NS | Dec |
E is experimental observation; MS is model simulation; NS is not specified; Inc is increased; Dec is decreased.
Loss of coordinated pacemaker activity.
Loss of all pacemaker activity.
Na-Ca exchange pump proteins.
Decrease in slow wave frequency but an increase in rate of pacemaker unit discharge.
To simulate the effects of experimental conditions, specific model parameters (see list of targeted parameters in Table 5) were set to a fixed proportion of their original value. The slow wave model was then run until a steady oscillatory cycle had been reached which, provided coordinated pacemaker activity had not been lost, was usually achieved after ∼30 s of simulation time.
Simulated inhibition of ICa(T) resulted in a reduction of both slow wave frequency and amplitude and an increase in half-width duration compared with control conditions (Fig. 10, A and B). Further inhibition of ICa(T) resulted in an increased resolution of unitary potential depolarizations (Fig. 10 C) and loss of coordinated global pacemaker activity (Fig. 10 D). Moreover, increased inhibition of ICa(T) results in a reduction of dVm/dtmax (Fig. 10 I). Note that despite this, activity on the pacemaker unit spatial scale remained regular (Fig. 10, column 2). This would suggest that the T-Type Ca2+ conductance is essential for coordinating pacemaker unit discharge, but is not required for generating activity on the pacemaker unit spatial scale.
Figure 10.
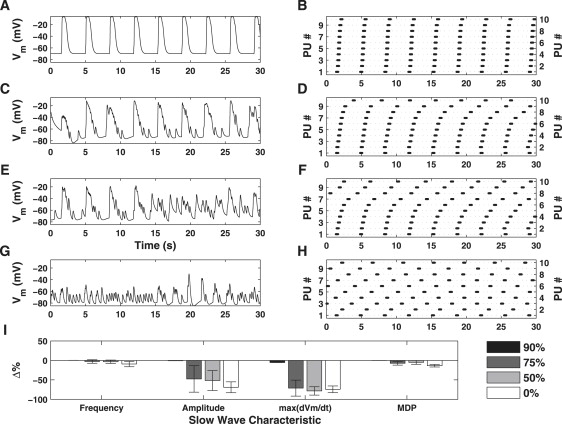
Simulated dose-response effects of ICa(T) inhibition on Vm (column 1) and pacemaker unit discharge (column 2). The slow wave characteristic metrics are summarized in the bar plot given in panel I (bars indicate mean value ± SD). Shown are the simulated results for 90% (row 1), 75% (row 2), 50% (row 3), and 0% (row 4) of the original value for gCa(T). Partial inhibition of ICa(T) (row 2) causes a reduction in pacing frequency and amplitude relative to control conditions. Further inhibition of ICa(T) results in increased resolution of unitary potential depolarizations (row 3) and a loss of coordinated pacemaker activity (row 4). Moreover, ICa(T) inhibition causes a significant decrease in dVm/dtmax (I). Note, however, that activity on the pacemaker unit level, although uncoordinated, is generated in a regular manner (column 2). This result is important as it shows Ca2+ entry from ICa(T) is required for coordinated pacemaker activity.
The simulated effects of BAPTA caused a significant reduction in pacing frequency and amplitude relative to the control conditions (Fig. 11, A and B). Increased concentrations of BAPTA results in the loss of coordinated pacemaker activity (Fig. 11, C and E), reduction in dVm/dtmax (Fig. 11 I), and pacemaker unit discharge becomes increasingly irregular (Fig. 11, D and F). Further increases in BAPTA concentration resulted in a complete loss of all pacemaker activity on both the global (Fig. 11 G) and pacemaker unit (Fig. 11 H) spatial scales.
Figure 11.
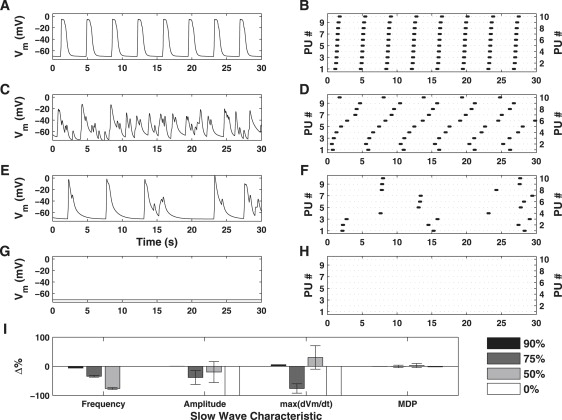
Simulated dose-response effects of BAPTA on Vm (column 1) and pacemaker unit discharge (column 2). The slow wave characteristic metrics are summarized in the bar plot are given in panel I (bars indicate mean value ± SD). Shown are the simulated results for 90% (row 1), 75% (row 2), 25% (row 3), and 0% (row 4) of the original values for μS1S2 and μS2Cy (for all pacemaker units). Low doses of BAPTA cause a significant decrease in pacing frequency and amplitude (row 2), relative to control conditions. Higher concentrations results in uncoordinated pacemaker activity and irregular pacemaker unit discharge (row 3) and abolishment of all pacemaker activity (row 4). Note that low doses of BAPTA have little effect on dVm/dtmax, but increased doses lead to a reduction in the value of this metric (I). This result is extremely important, as it shows pacemaker unit activity is a necessary precursor for slow wave generation.
Discussion
Physiological simulations
Integration of the model equations, under normal conditions, shows that the fundamental aspects of ICC pacemaker activity are represented correctly. Slow waves produced by the model display spontaneous rhythmicity (Fig. 5 B), and have characteristics that are consistent with experimental recordings of slow wave activity (Fig. 5 A and Table 2). The physiological basis of our modeling framework was the Sanders' Hypothesis (12). The mechanisms described by Sanders et al. that have been included within the model framework are:
-
1.
The discrete biophysical representations of pacemaker unit activity.
-
2.
Inclusion of a dihydropyridine-resistant T-Type Ca2+ current.
-
3.
Pacemaker unit entrainment in response to elevated intracellular [Ca2+].
-
4.
K+ conductances to account for cellular repolarization.
These mechanisms are combined to represent ICC slow wave activity as the coordinated discharge of discrete unitary potentials generated from a population of pacemaker units. This property is fundamental to the Sanders' Hypothesis and, to the best of our knowledge, none of the established ICC mathematical models is capable of representing such behavior.
The only other established model of SI ICC slow wave activity is that of the YSW model (42), the properties of which are given in comparison to our model in Table 2. Both slow wave models are similar in that they are biophysically based and are dependent on cyclical [Ca2+] oscillations. However, our model assumes that fundamental slow wave activity occurs on the pacemaker unit spatial scale, a phenomenon that is not considered by the YSW model. Furthermore, pacemaker activity generated by the YSW model incorporates Vm-dependent IP3 synthesis, whereas we have assumed a constant [IP3] (see Vm-Dependent IP3 Synthesis below for justification). Finally, the YSW model includes a Ca2+-activated autonomous inward current, based on experimental observations performed on murine SI ICC (15), as the primary pacemaker conductance. This is opposed to our model framework, which utilizes the Ca2+-inhibited INSCC. Note, however, that despite their apparent dichotomous Ca2+-dependencies, parallels can be drawn between these two conductances for the reason that both are activated by increases in global intracellular [Ca2+]. This is because our modeling framework predicts that entrained pacemaker unit discharge, and hence INSCC activation, occurs in response to increased global [Ca2+].
Results of simulated pacemaker activity generated from varying pacemaker population sizes shows that nPU has little effect on the macroscopic slow wave properties. However, closer inspection of the slow wave plateau phase reveals that increasing nPU reduces unitary potential resolution, resulting in a more continuous response. Of greater interest though is the effect that nPU has on the slow wave upstroke, with pacemaker activity generated for nPU ≥ 10 requiring more than one pacemaker unit to activate ICa(T) (Fig. 7, B and C). Moreover, the distribution of μS2Cy values for nPU ≥ 10 suggests that there are possibly two different populations of pacemaker units (Fig. 7 D), which have differing sensitivities, responsible for the slow wave upstroke and plateau. However, as the μS2Cy distribution was fitted to produce a particular response, it is not possible to definitively say what biophysical mechanisms are actually responsible for these differing sensitivities.
Validation simulations
Validation simulations were performed to test and qualitatively compare the model's response to specific experimental perturbations. The differing types of numerical simulations we performed on the modeling framework were 1), voltage-clamp; 2), blocking of key ion transport pathways; 3), dose-response effects of reducing Ca2+ availability; and 4), buffering of intracellular Ca2+. The results from each of these simulations are discussed in turn below.
Voltage-clamp
Voltage-clamp numerical simulations were undertaken to determine the influence of membrane potential on pacemaker activity. If slow wave activity requires a voltage-dependent step, such as activation of ICa(T), then spontaneous slow wave activity should cease when membrane potential is held constant. Results of this numerical simulation demonstrate that pacemaker activity persisted under voltage-clamp, exemplified by the generation of spontaneous membrane currents that underlie unitary potentials (Fig. 8, row 2), but these events failed to be entrained into slow waves. This result is consistent with observations made by multiple investigators studying voltage-clamped ICC (15,19–22) and shows that the pacemaker unit oscillatory cycle is voltage-independent, but entrainment of pacemaker unit currents or active propagation of slow waves in a network necessitates a voltage-dependent mechanism.
Further analysis of the ionic currents produced under voltage-clamp demonstrates a reduction in the magnitude of these currents with depolarization from a holding potential of −70 mV (Fig. 8 B) to −40 mV (Fig. 8 D). However, it should be appreciated that the magnitude of the unitary currents in an actual cell would be less than that from the simulated pacemaker units. This is because we have used nPU = 10 for this investigation, whereas in an actual ICC there are potentially tens to hundreds of pacemaker units sites. The model predicts that this is due to a reduction in the magnitude of the primary pacemaker conductance and a Ca2+-inhibited NSCC, and is consistent with experimental observations made from voltage-clamped murine SI ICC (15).
Blocking of key ion-transport pathways
There are several ion-transport pathways that are integral to the ICC pacemaker cycle (12). Numerical simulations were performed under conditions in which the SERCA pump, IP3 receptors, and mitochondrial Ca2+ uptake were individually blocked to determine the effects on pacemaker activity. Results from these numerical investigations predict that conductance blockage, for each scenario, causes abolishment of all pacemaker activity (Fig. 9). Furthermore, simulated washout of the pharmacological agents results in a resumption of pacemaker activity. These results are qualitatively similar to experimental observations and reinforce the fact that ER/mitochondrial Ca2+ handling is essential in generating ICC pacemaker activity (see references in Table 4).
Dose-response effects of reducing Ca2+ availability
Dose-response simulations were performed in which the availability of the channels responsible for ICa(T) was reduced by simulating the effects of mibefradil or Ni2+. Simulations of ICa(T) inhibition caused degradation of slow wave activity (e.g., reduction in spontaneous frequency, reduced upstroke velocity, dVm/dtmax, and eventual block of slow waves) in a dose-dependent manner (Fig. 10, C and E). As slow waves were blocked, we noted greater resolution of unitary potential depolarizations (Fig. 10 D). ICa(T) inhibition leads to reduced dVm/dtmax during the upstroke phase of the pacemaker cycle (Fig. 10 I). These results mimic the effects of NiCl2 (5) and mibefradil (16) on slow wave activity recorded from ICC in situ in the murine SI. The model predicts that the observed weakening in pacemaker unit synchronization is due to decreased CCy levels caused by a reduction in ICa(T)Ca2+ influx. From Eqs. 13 and 14, we see that a reduction in CCy directly correlates with decreased CS2 levels which, in turn, reduce the rate at which the IP3R reaches its threshold open probability. This phenomenon is exemplified by the pacemaker unit discharge rastergram (Fig. 10, column 2), which shows a decrease in pacing frequency, and hence entrainment, with increased ICa(T) inhibition. These results are consistent with the concept that ICa(T) activation is required to entrain pacemaker unit discharge to produce a coordinated response (12).
Buffering of intracellular Ca2+
The simulated effects of BAPTA show that, similar to ICa(T) inhibition, there is a reduction in pacemaker unit entrainment causing a discordant membrane potential response (Fig. 11). However, with further increases in BAPTA concentration we observe a complete abolishment of all pacemaker activity (Fig. 11, row 4). These results are consistent with observations from multiple investigations whereby exposure of GI tissue to BAPTA resulted in a transient reduction in pacing frequency and amplitude, followed by cessation of slow wave activity (5,6,17,18,47). Loss of entrained pacemaker unit activity is due to reduced [Ca2+] in pacemaker units containing IP3R. If Ca2+ buildup in pacemaker units is restricted by buffering, then IP3R will not reach firing threshold, causing the observed cessation of pacemaker activity. This result, coupled with the conductance block simulations mentioned above, is consistent with the Sanders' Hypothesis in that activity on the pacemaker unit spatial scale is essential for generating ICC slow waves (12).
The results of other simulated dose-response numerical investigations demonstrate that this modeling framework is capable of reproducing a wide range of experimentally observed phenomena (Table 5). However, we note that the slow wave model framework fails to produce the MDP that is consistent with experimental observations for BAPTA, reduced extracellular [Ca2+], and CGP37157/clonazepam. As MDP is maintained by the K+ conductances (48), this would suggest that further investigation is required to properly characterize the role of K+ conductances within the modeling framework. Despite this, as all the other simulation results are consistent with experimental observations, the modeling framework presented seems capable of successfully replicating the biophysical mechanisms underlying the slow wave upstroke and plateau phases.
Competing theories
As previously mentioned, our mathematical modeling framework utilizes the Sanders' Hypothesis as a physiological basis. However, there are several other competing theories that, although not included in our model, have been suggested to contribute to ICC pacemaker activity.
Ca2+-activated Cl− conductance
Numerous studies have suggested that a Ca2+-activated Cl− conductance contributes to ICC slow waves either by acting as the primary pacemaker conductance instead of INSCC (30,18) or by acting in combination with unitary potential depolarizations to maintain the slow wave plateau phase (13). The main experimental evidence supporting the presence of a Ca2+-activated Cl− conductance was drawn from pharmacological investigations involving Cl− conductance blockers (49). However, the concentration of the pharmacological agents used in this investigation brings into question the specificity of these drugs (12). Furthermore, several investigations have noted the absence of Ca2+-activated conductances contributing to cellular depolarization (20,33,50). Finally, observations from pharmacological investigations involving caffeine, an antagonist of ER Ca2+ release which should theoretically activate a Ca2+-activated Cl− conductance, demonstrate a complete abolishment of all ICC pacemaker activity (4,6,18). Therefore, based on measurements of conductances in ICC, a role for Ca2+-activated Cl− channels in pacemaker activity remains unclear.
Tetrodotoxin-resistant Na+ current
A tetrodotoxin-resistant Na+ conductance, encoded by the SCN5A gene, was identified in human intestinal ICC (51,52). This conductance, working in combination with ICa(T), has been suggested to influence the slow wave upstroke phase. However, the existence of such a Na+ current has not been identified in any other species and/or tissue type. As a result, it is not possible to definitely say that this conductance is involved with pacemaker activity, hence this conductance was not considered necessary for the current modeling framework.
Vm-dependent IP3 synthesis
Despite the overwhelming consensus that Ca2+ release from IP3R-operated ER stores is an essential component of the pacemaker cycle (9,10,22,29), controversy remains over the exact mechanism by which Ca2+ release is initiated. Several investigators have suggested that Vm-dependent IP3 synthesis is responsible for regulating ER Ca2+ release (9), as opposed to the Ca2+ entry method used within our modeling framework. These conclusions were drawn from experiments performed on guinea-pig muscle tissue whereby membrane depolarization evoked slow waves, suggesting that voltage-dependent synthesis of IP3 was responsible for this event. However, the issue with this mechanism is that [IP3] oscillations, which are phase-locked to ICC pacemaker activity, have not been demonstrated experimentally in ICC (12). This is juxtaposed with the fact that numerous investigators have observed a one-to-one relationship between intracellular [Ca2+] oscillations and pacemaker activity (21,43–46). Furthermore, the predominant IP3R isoform found in ICC is the Type-1 isoform (29). This IP3R isoform is characterized by a high Ca2+-gain, low IP3-gain response (28), meaning the receptor will be more sensitive to changes in [Ca2+] relative to changes in [IP3].
Ryanodine receptors
Some investigators have suggested the involvement of ryanodine receptors (RyRs) in ICC pacemaker activity (21,43). A role for RyR was suggested from experiments performed on cell clusters in which the application of ryanodine abolished pacemaker activity. Immunohistochemical staining revealed the existence of the Type-3 RyR isoform (21). The suitability of cell cluster preparations for the study of ICC is questionable, since all pharmacological responses would represent contributions from multiple cell types. The role of RyRs in pacemaker activity is also doubtful, since several studies have noted little or no effect of ryanodine pacemaker activity in ICC (22), or in intact strips of GI muscles (9). Therefore, although RyRs may be present in ICC, they do not appear to be directly involved in pacemaker activity.
In spite of the omission of the several mechanisms proposed by others from the current modeling framework, the biophysical nature of our model readily allows expansion to account for additional features. Therefore, if future experimental observations necessitate inclusion of these or additional mechanisms, then the modeling framework we have developed can be expanded to include descriptions of this behavior.
Limitations
The model's main limiting factor is the lack of usable experimental data with which to characterize ionic conductances kinetics, metabolic pathways, and intracellular ion dynamics. Despite our best attempts to characterize model parameters using data from ICC, or appropriate alternative cell types, there are parameters remaining that are poorly defined in the literature. The values of these parameters were fitted using nonlinear optimization techniques so that the model reproduced characteristic features from experimentally recorded slow waves. However, the number of fitted parameters was greater than the number of characteristic features used to constrain the optimization objective function, meaning the model's parameter set may not necessarily represent a unique solution. Despite this, the biophysical structure of the modeling framework means that data from future experimentation can be utilized to constrain the values of these fitted parameter values.
Another limitation of the model is the inability to reproduce all observations made from pharmacological investigations; specifically the dose-response numerical experiments (see Table 5 for the results of these simulations). Although such inconsistencies are rare, the results from the dose-response simulations suggest that further investigation into the contribution of K+, and hence, the K+ plasma membrane conductance, on pacemaker activity, is required. Despite this, the results from the validation simulations suggest that the major phases of pacemaker activity, including the slow wave upstroke/plateau phases and pacemaker unit entrainment, are represented well by our model.
Finally, our slow wave modeling framework does not incorporate any mechanisms by which pacemaker units can directly influence each other. This is because we have assumed that 1), the cellular membrane is isopotential; and 2), Ca2+ is only permitted to diffuse into the pacemaker unit via the bulk cytoplasm, and not from the other pacemaker units. Although investigating inter-pacemaker unit activity would be interesting, we would first need to determine the relative spatial orientation of the pacemaker unit domains. However, given the lack of usable morphometric data, we can only speculate as to the relative orientations of the pacemaker units within the cell. Therefore, such a model construct was deemed to add unjustified complexity, and hence was not considered for our modeling framework.
Summary
In this study, we introduced a biophysically based, mathematical model that represented whole-cell small intestinal ICC slow wave activity generated from a discrete unitary potential basis. This model expanded on the recently developed pacemaker unit modeling framework of Faville et al. (14) by incorporating mechanisms that are required for producing a coordinated global response. Numerical simulation of our model demonstrated that the framework is capable of reproducing a wide range of experimentally observed phenomena. Ultimately, our goal is to evolve this research effort to produce a multiscale model by embedding the zero-dimensional framework within anatomically topologies of GI organs.
Supporting Material
All model equations and parameter values are given in the Supporting Material, which is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00794-2. Also provided within the Supporting Material are the results of the other dose-response simulations that were not displayed in this document (see Table 5).
Supporting Material
Acknowledgments
The authors thank Prof. Sean Ward (Physiology and Cell Biology Department, University of Nevada, Reno, NV) for his assistance with ICC physiology.
R.A.F. was supported by the University of Auckland, the Auckland Bioengineering Institute, the New Zealand Institute of Mathematics and its Applications, the Royal Society of New Zealand, the National Institute of Health (grant No. R01 DK64775), and the Todd Foundation. C.M.L. was funded by the Maurice Wilkins Centre for Molecular Biodiscovery. N.P.S. acknowledges the support of Marsden Fund (grant No. 04-UOA-177) and Biotechnology and Biological Sciences Research Council (grant No. BB/F01080X/1). K.M.S. and S.D.K. were supported by National Institutes of Health grants No. P01 DK41315 and No. R37 DK40569.
References
- 1.Thuneberg L. Interstitial cells of Cajal: intestinal pacemaker cells? Adv. Anat. Embryol. Cell Biol. 1982;71:1–130. [PubMed] [Google Scholar]
- 2.Szurszewski J.H. Physiology of the Gastrointestinal Tract. 2nd Ed. Raven Press; New York: 1987. Electrical basis for gastrointestinal motility. [Google Scholar]
- 3.Cousins H., Edwards F., Hickey H., Hill C., Hirst G. Electrical coupling between the myenteric interstitial cells of Cajal and adjacent muscle layers in the guinea-pig gastric antrum. J. Physiol. 2003;550:829–844. doi: 10.1113/jphysiol.2003.042176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hirst G., Edwards F. Generation of slow waves in the antral region of guinea-pig stomach—a stochastic process. J. Physiol. 2001;535:165–180. doi: 10.1111/j.1469-7793.2001.00165.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kito Y., Suzuki H. Properties of pacemaker potentials recorded from myenteric interstitial cells of Cajal distributed in the mouse small intestine. J. Physiol. 2003;553:803–818. doi: 10.1113/jphysiol.2003.051334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Edwards F., Hirst G., Suzuki H. Unitary nature of regenerative potentials recorded from circular smooth muscle of guinea-pig antrum. J. Physiol. 1999;519:235–250. doi: 10.1111/j.1469-7793.1999.0235o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Edwards F., Hirst G. An electrical description of the generation of slow waves in the antrum of the guinea-pig. J. Physiol. 2005;564:213–232. doi: 10.1113/jphysiol.2004.077123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Imtiaz M., Smith D., van Helden D. A theoretical model of slow wave regulation using voltage-dependent synthesis of inositol 1,4,5-trisphosphate. Biophys. J. 2002;83:1877–1890. doi: 10.1016/S0006-3495(02)73952-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.van Helden D., Imtiaz M., Nurgaliyeva K., von der Weid P., Dosen P. Role of calcium stores and membrane voltage in the generation of slow wave action potentials in guinea-pig gastric pylorus. J. Physiol. 2000;524:245–265. doi: 10.1111/j.1469-7793.2000.00245.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sanders K., Ördög T., Koh S., Ward S. A novel pacemaker mechanism drives gastrointestinal rhythmicity. News Physiol. Sci. 2000;15:291–298. doi: 10.1152/physiologyonline.2000.15.6.291. [DOI] [PubMed] [Google Scholar]
- 11.Sanders K., Koh S., Ordög T., Ward S. Ionic conductances involved in generation and propagation of electrical slow waves in phasic gastrointestinal muscles. Neurogastroenterol. Motil. 2004;16(Suppl 1):100–105. doi: 10.1111/j.1743-3150.2004.00483.x. [DOI] [PubMed] [Google Scholar]
- 12.Sanders K., Koh S., Ward S. Interstitial cells of Cajal as pacemakers in the gastrointestinal tract. Annu. Rev. Physiol. 2006;68:307–343. doi: 10.1146/annurev.physiol.68.040504.094718. [DOI] [PubMed] [Google Scholar]
- 13.Corrias A., Buist M. Quantitative cellular description of gastric slow wave activity. Am. J. Physiol. Gastrointest. Liver Physiol. 2008;294:G989–G995. doi: 10.1152/ajpgi.00528.2007. [DOI] [PubMed] [Google Scholar]
- 14.Faville R., Pullan A., Sanders K., Smith N. A biophysically based mathematical model of unitary potential activity in interstitial cells of Cajal. Biophys. J. 2008;95:88–104. doi: 10.1529/biophysj.107.122507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goto K., Matsuoka S., Noma A. Two types of spontaneous depolarizations in the interstitial cells freshly prepared from the murine small intestine. J. Physiol. 2004;559:411–422. doi: 10.1113/jphysiol.2004.063875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kito Y., Ward S., Sanders K. Pacemaker potentials generated by interstitial cells of Cajal in the murine intestine. Am. J. Physiol. Cell Physiol. 2005;288:C710–C720. doi: 10.1152/ajpcell.00361.2004. [DOI] [PubMed] [Google Scholar]
- 17.Beckett E., Bayguinov Y., Sanders K., Ward S., Hirst G. Properties of unitary potentials generated by intramuscular interstitial cells of Cajal in the murine and guinea-pig gastric fundus. J. Physiol. 2004;559:259–269. doi: 10.1113/jphysiol.2004.063016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kito Y., Suzuki H., Edwards F. Properties of unitary potentials recorded from myenteric interstitial cells of Cajal distributed in the guinea-pig gastric antrum. J. Smooth Muscle Res. 2002;38:165–179. doi: 10.1540/jsmr.38.165. [DOI] [PubMed] [Google Scholar]
- 19.Koh S., Sanders K., Ward S. Spontaneous electrical rhythmicity in cultured interstitial cells of Cajal from the murine small intestine. J. Physiol. 1998;513:203–213. doi: 10.1111/j.1469-7793.1998.203by.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Koh S., Jun J., Kim T., Sanders K. A Ca2+-inhibited non-selective cation conductance contributes to pacemaker currents in mouse interstitial cell of Cajal. J. Physiol. 2002;540:803–814. doi: 10.1113/jphysiol.2001.014639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu H., Ohya S., Furuzono S., Wang J., Imaizumi Y. Co-contribution of IP3R and Ca2+ influx pathways to pacemaker Ca2+ activity in stomach ICC. J. Biol. Rhythms. 2005;20:15–26. doi: 10.1177/0748730404269572. [DOI] [PubMed] [Google Scholar]
- 22.Ward S., Ordog T., Koh S., Baker S., Jun J. Pacemaking in interstitial cells of Cajal depends upon calcium handling by endoplasmic reticulum and mitochondria. J. Physiol. 2000;525:355–361. doi: 10.1111/j.1469-7793.2000.t01-1-00355.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Carafoli E. The calcium pumping ATPase of the plasma membrane. Annu. Rev. Physiol. 1991;53:531–547. doi: 10.1146/annurev.ph.53.030191.002531. [DOI] [PubMed] [Google Scholar]
- 24.Carafoli E., Stauffer T. The plasma membrane calcium pump: functional domains, regulation of the activity, and tissue specificity of isoform expression. J. Neurobiol. 1994;25:312–324. doi: 10.1002/neu.480250311. [DOI] [PubMed] [Google Scholar]
- 25.Gadsby D., Kimura J., Noma A. Voltage dependence of Na/K pump current in isolated heart cells. Nature. 1985;315:63–65. doi: 10.1038/315063a0. [DOI] [PubMed] [Google Scholar]
- 26.De Weer P., Gadsby D., Rakowski R. Voltage dependence of the apparent affinity for external Na+ of the backward-running sodium pump. J. Gen. Physiol. 2001;117:315–328. doi: 10.1085/jgp.117.4.315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hodgkin A., Huxley A. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mak D., McBride S., Foskett J. Regulation by Ca2+ and inositol 1,4,5-trisphosphate (InsP3) of single recombinant type 3 InsP3 receptor channels. Ca2+ activation uniquely distinguishes types 1 and 3 InsP3 receptors. J. Gen. Physiol. 2001;117:435–446. doi: 10.1085/jgp.117.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Suzuki H., Takano H., Yamamoto Y., Komuro T., Saito M. Properties of gastric smooth muscles obtained from mice which lack inositol trisphosphate receptor. J. Physiol. 2000;525:105–111. doi: 10.1111/j.1469-7793.2000.00105.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hirst G., Bramich N., Teramoto N., Suzuki H., Edwards F. Regenerative component of slow waves in the guinea-pig gastric antrum involves a delayed increase in [Ca2+]i and Cl− channels. J. Physiol. 2002;540:907–919. doi: 10.1113/jphysiol.2001.014803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kito Y., Fukuta H., Suzuki H. Components of pacemaker potentials recorded from the guinea pig stomach antrum. Pflugers Arch. 2002;445:202–217. doi: 10.1007/s00424-002-0884-z. [DOI] [PubMed] [Google Scholar]
- 32.Kirkpatrick S., Gelatt C., Vecchi M. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 33.Kim Y., Koh S., Sanders K. Voltage-dependent inward currents of interstitial cells of Cajal from murine colon and small intestine. J. Physiol. 2002;541:797–810. doi: 10.1113/jphysiol.2002.018796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ward S., Dixon R., de Faoite A., Sanders K. Voltage-dependent calcium entry underlies propagation of slow waves in canine gastric antrum. J. Physiol. 2004;561:793–810. doi: 10.1113/jphysiol.2004.076067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Iftinca M., McKay B., Snutch T., McRory J., Turner R. Temperature dependence of T-type calcium channel gating. Neuroscience. 2006;142:1031–1042. doi: 10.1016/j.neuroscience.2006.07.010. [DOI] [PubMed] [Google Scholar]
- 36.Cho W., Daniel E. Proteins of interstitial cells of Cajal and intestinal smooth muscle, colocalized with caveolin-1. Am. J. Physiol. Gastrointest. Liver Physiol. 2005;288:G571–G585. doi: 10.1152/ajpgi.00222.2004. [DOI] [PubMed] [Google Scholar]
- 37.McKay C., Ye J., Huizinga J. Characterization of depolarization-evoked ERG K currents in interstitial cells of Cajal. Neurogastroenterol. Motil. 2006;18:324–333. doi: 10.1111/j.1365-2982.2006.00764.x. [DOI] [PubMed] [Google Scholar]
- 38.Zhu Y., Golden C., Ye J., Wang X., Akbarali H. ERG K+ currents regulate pacemaker activity in ICC. Am. J. Physiol. Gastrointest. Liver Physiol. 2003;285:G1249–G1258. doi: 10.1152/ajpgi.00149.2003. [DOI] [PubMed] [Google Scholar]
- 39.Hatton W., Mason H., Carl A., Doherty P., Latten M. Functional and molecular expression of a voltage-dependent K+ channel (Kv1.1) in interstitial cells of Cajal. J. Physiol. 2001;533:315–327. doi: 10.1111/j.1469-7793.2001.0315a.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cohen S., Hindmarsh A. CVODE, a stiff/nonstiff ODE solver. Comput. Phys. 1996;10:138–143. [Google Scholar]
- 41.Lloyd C., Halstead M., Nielsen P. CellML: its future, present and past. Prog. Biophys. Mol. Biol. 2004;85:433–450. doi: 10.1016/j.pbiomolbio.2004.01.004. [DOI] [PubMed] [Google Scholar]
- 42.Youm J., Kim N., Han J., Kim E., Joo H. A mathematical model of pacemaker activity recorded from mouse small intestine. Philos. Trans. A Math. Phys. Eng. Sci. 2006;364:1135–1154. doi: 10.1098/rsta.2006.1759. [DOI] [PubMed] [Google Scholar]
- 43.Aoyama M., Yamada A., Wang J., Ohya S., Furuzono S. Requirement of ryanodine receptors for pacemaker Ca2+ activity in ICC and HEK293 cells. J. Cell Sci. 2004;117:2813–2825. doi: 10.1242/jcs.01136. [DOI] [PubMed] [Google Scholar]
- 44.Lee H., Hennig G., Fleming N., Keef K., Spencer N. Septal interstitial cells of Cajal conduct pacemaker activity to excite muscle bundles in human jejunum. Gastroenterology. 2007;133:907–917. doi: 10.1053/j.gastro.2007.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Park K., Hennig G., Lee H., Spencer N., Ward S. Spatial and temporal mapping of pacemaker activity in interstitial cells of Cajal in mouse ileum in situ. Am. J. Physiol. Cell Physiol. 2006;290:C1411–C1427. doi: 10.1152/ajpcell.00447.2005. [DOI] [PubMed] [Google Scholar]
- 46.Torihashi S., Fujimoto T., Trost C., Nakayama S. Calcium oscillation linked to pacemaking of interstitial cells of Cajal: requirement of calcium influx and localization of Trp4 in caveolae. J. Biol. Chem. 2002;277:19191–19197. doi: 10.1074/jbc.M201728200. [DOI] [PubMed] [Google Scholar]
- 47.Malysz J., Donnelly G., Huizinga J. Regulation of slow wave frequency by IP3-sensitive calcium release in the murine small intestine. Am. J. Physiol. Gastrointest. Liver Physiol. 2001;280:G439–G448. doi: 10.1152/ajpgi.2001.280.3.G439. [DOI] [PubMed] [Google Scholar]
- 48.Hille B. 3rd Ed. Sinauer; Sunderland, MA: 2001. Ion Channels of Excitable Membranes. [Google Scholar]
- 49.Tokutomi N., Maeda H., Tokutomi Y., Sato D., Sugita M. Rhythmic Cl− current and physiological roles of the intestinal c-kit-positive cells. Pflugers Arch. 1995;431:169–177. doi: 10.1007/BF00410188. [DOI] [PubMed] [Google Scholar]
- 50.Lee H., Sanders K. Comparison of ionic currents from interstitial cells and smooth muscle cells of canine colon. J. Physiol. 1993;460:135–152. doi: 10.1113/jphysiol.1993.sp019463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Strege P., Ou Y., Sha L., Rich A., Gibbons S. Sodium current in human intestinal interstitial cells of Cajal. Am. J. Physiol. Gastrointest. Liver Physiol. 2003;285:G1111–G1121. doi: 10.1152/ajpgi.00152.2003. [DOI] [PubMed] [Google Scholar]
- 52.Strege P., Bernard C., Ou Y., Gibbons S., Farrugia G. Effect of mibefradil on sodium and calcium currents. Am. J. Physiol. Gastrointest. Liver Physiol. 2005;289:G249–G253. doi: 10.1152/ajpgi.00022.2005. [DOI] [PubMed] [Google Scholar]
- 53.Aliev R., Richards W., Wikswo J. A simple nonlinear model of electrical activity in the intestine. J. Theor. Biol. 2000;204:21–28. doi: 10.1006/jtbi.2000.1069. [DOI] [PubMed] [Google Scholar]
- 54.Imtiaz M., Katnik C., Smith D., van Helden D. Role of voltage-dependent modulation of store Ca2+ release in synchronization of Ca2+ oscillations. Biophys. J. 2006;90:1–23. doi: 10.1529/biophysj.104.058743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Edwards F., Hirst G. Mathematical description of regenerative potentials recorded from circular smooth muscle of guinea pig antrum. Am. J. Physiol. Gastrointest. Liver Physiol. 2003;285:G661–G670. doi: 10.1152/ajpgi.00145.2003. [DOI] [PubMed] [Google Scholar]
- 56.Fukuta H., Kito Y., Suzuki H. Spontaneous electrical activity and associated changes in calcium concentration in guinea-pig gastric smooth muscle. J. Physiol. 2002;540:249–260. doi: 10.1113/jphysiol.2001.013306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kim B., Jun J., So I., Kim K. Involvement of mitochondrial Na+-Ca2+ exchange in intestinal pacemaking activity. World J. Gastroenterol. 2006;12:796–799. doi: 10.3748/wjg.v12.i5.796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhu Y., Ye J., Huizinga J. Clotrimazole-sensitive K+ currents regulate pacemaker activity in interstitial cells of Cajal. Am. J. Physiol. Gastrointest. Liver Physiol. 2007;292:G1715–G1725. doi: 10.1152/ajpgi.00524.2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


