Electrohydrodynamic Model of Vesicle Deformation in Alternating Electric Fields

Abstract

We develop an analytical theory to explain the experimentally observed morphological transitions of quasispherical giant vesicles induced by alternating electric fields. The model treats the inner and suspending media as lossy dielectrics, and the membrane as an impermeable flexible incompressible–fluid sheet. The vesicle shape is obtained by balancing electric, hydrodynamic, bending, and tension stresses exerted on the membrane. Our approach, which is based on force balance, also allows us to describe the time evolution of the vesicle deformation, in contrast to earlier works based on energy minimization, which are able to predict only stationary shapes. Our theoretical predictions for vesicle deformation are consistent with experiment. If the inner fluid is more conducting than the suspending medium, the vesicle always adopts a prolate shape. In the opposite case, the vesicle undergoes a transition from a prolate to oblate ellipsoid at a critical frequency, which the theory identifies with the inverse membrane charging time. At frequencies higher than the inverse Maxwell-Wagner polarization time, the electrohydrodynamic stresses become too small to alter the vesicle's quasispherical rest shape. The model can be used to rationalize the transient and steady deformation of biological cells in electric fields.

Introduction

Electric fields are widely used for cell manipulation. Weak fields influence cell signaling, wound healing, and cell growth (1–4). Strong pulsed fields can induce transient perforation of the cell membrane, which enables the delivery of exogenous molecules (drugs, proteins, and plasmids) into living cells (4,5).

Biological cells exhibit various frequency-dependent behaviors in alternating current (AC) electric fields: orientation, translation (dielectrophoresis), and rotation. These phenomena have stimulated considerable modeling effort aimed at understanding of the physical mechanisms of the interaction of electric fields with cells and tissues. A common theme among different theoretical models is the assumption that the cell is a lossy dielectric particle of fixed shape (a sphere (6,9) or an ellipsoid (10,11)). For example, the orientation of cells can be predicted by considering the torque on an ellipsoid due to the effective dipole moment induced by the electric field (12,13); the dipole-based theory has been successfully applied to interpret electro-orientation of erythrocytes (14).

Cells, however, are soft objects, which deform when subjected to electric fields. The cell membrane plays a critical role in this process. For example, the shear elasticity of the red blood cell membrane controls the cell electrodeformation (15–17). The lipid bilayer is the main structural component of the cell membrane, yet, the electrodeformation of closed pure lipid bilayer membranes (vesicles) has been considered only to a limited extent (18–20). There is increasing interest in this problem, particularly in relation to electropermeabilization (21–27). Recent experiments have shown that vesicle behavior in electric fields exhibits peculiar features. Vesicles subjected to a direct-current electric pulse can deform into elliptical (28) or cylindrical shapes (29). Alternating-current electric fields deform vesicles into prolate or oblate ellipsoids depending on the frequency and the conductivities of the interior and suspending fluids (30–32).

The physical mechanisms responsible for vesicle electrodeformations are not fully understood at this time. It is generally agreed that the prolate shape results from electrostatic pressure that pulls the vesicle at the poles, where the electric field is maximal. However, the oblate deformation, and in particular the fact that it is observed only when the enclosed fluid is less conducting than the suspending medium, has eluded adequate explanation. It has been proposed that anisotropy in the dielectric constant of the membrane is responsible for the oblate shapes (33), but this model cannot explain the experimentally observed dependence on the conductivity ratio (30). Available theories do not account for the asymmetry in the fluid conductivities, and predict only prolate shapes (18–20). Moreover, these models employ an energy approach, according to which stationary shapes are computed by minimizing the sum of the membrane and electrostatic energies. Recently, unusual transient shapes of vesicles subjected to strong electric pulses have been observed (29). Explaining their existence goes beyond the scope of the equilibrium energy models. These transient features can be accounted for only by means of a truly nonequilibrium mechanical approach, which is based on force balance. To the authors' knowledge, there is only one attempt to describe vesicle dynamics in electric fields (34). However, the model provides little physical insight because membrane deformation is described by a postulated ad hoc kinematic equation instead of the actual force balance.

In this article, we develop a theoretical explanation of the observed effects of AC electric fields on vesicle shapes. The transient vesicle deformation is determined by evaluating all forces (electric, hydrodynamic, bending, and tension) exerted on the membrane (35). Our model is motivated by the possibility for fluid flow driven by the electric field. Free charges, e.g., ions, tend to accumulate at interfaces separating media with different electric properties. The electric field acting on these free charges gives rise to fluid flow relative to the interface (36,37). Electrohydrodynamic (EHD) flows have been observed long ago with drops (38,39), and only recently reported for vesicles (40). Drops adopt oblate shapes solely due to the EHD flow, as illustrated in Fig. 1. We propose that the EHD flow is also responsible for the oblate vesicle shapes.

Figure 1.

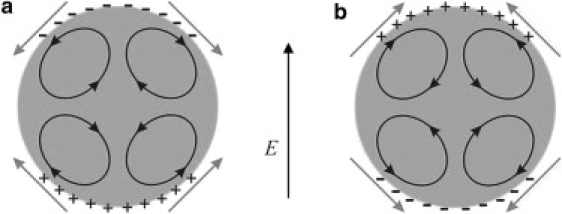
Illustration of the surface charge distribution and the streamlines of the electrohydrodynamic flow inside a drop (38,70) or a vesicle. The corresponding direction of the tangential electric traction is denoted by arrows. (a) Interior fluid less conducting than the exterior one, Λ/S < 1. The resulting shape is oblate because the EHD flow pushes fluid toward the equator; (b) interior fluid more conducting than the exterior one, Λ/S > 1.

Notwithstanding the qualitative similarity between drops and vesicles, the extension of the EHD model from drops to vesicles is not a straightforward task because the mechanics of lipid membranes is far more complex than the mechanics of fluid-fluid interfaces. There are three major challenges.

First, the lipid membrane is essentially an insulating shell impermeable to ions. When an electric field is applied, charges accumulate on both sides of the bilayer and the vesicle acts as a charging capacitor.

Second, since the lipid bilayer contains a fixed number of molecules the vesicle area is constant and the membrane is area-incompressible. Under stress, the membrane develops nonuniform tension, which adapts itself to the forces exerted on the membrane in order to keep the local area constant. At steady state, the gradients in tension counteract the flow-inducing tangential electric force and the electrohydrodynamic flow stops.

Third, lipid membranes are extremely soft and can be easily bent by thermal noise. The area constraint implies an effective or entropic tension for fluctuations (41). Deformation of quasispherical vesicles in electric field results from flattening of the shape undulations, which increases the membrane tension (42). In strong electric fields, vesicle deformation is in fact limited by the large membrane tension. The theories based on the energy approach (20,33) omit the tension and thereby exaggerate vesicle deformations (see the supporting material in Aranda et al. (30). Our approach rigorously accounts for these effects, and thus it is able to predict vesicle deformations consistent with experiment.

The article is organized as follows: The Model describes the physical model and formulates the governing equations; Solution for Small Deformations outlines the solution and discusses the frequency dependence of the electric stresses; and Results shows the theory predictions and comparison with experiment for the vesicle shape as a function of frequency and conductivity ratio.

The Model

The physical picture and characteristic timescales

Let us consider a giant vesicle with no net charge formed by a membrane with conductivity λ_mm and dielectric constant ɛ_mm. The bilayer thickness is h ∼ 5 nm, thus on the length scale of a cell-size vesicle (radius a ∼ 10 μm) the bilayer membrane can be regarded as a two-dimensional surface with capacitance C_m = ɛ_mm/h and conductivity G_m = λ_mm/h. The vesicle is filled with a fluid of viscosity η_in, conductivity λ_in, and dielectric constant ɛ_in, and suspended in a different fluid characterized by η_ex, λ_ex, and ɛ_ex. The physical properties of the fluids and the membrane are assumed to be frequency-independent.

The vesicle is subjected to a uniform AC electric field with an amplitude E₀,

$$E^{\mathrm{\infty }}=E_0\cos \left(\omega t\right),$$ (1)

where ω is the angular field frequency and t is the time. When an electric field E(t) is applied to an electrolyte solution, the free ions move parallel to the field. The ion redistribution leads to inhomogeneities in the bulk charge density, which decay on a timescale (36,39)

$$t_{\mathrm{c},i}=\frac{{\varepsilon }_i}{{\lambda }_i}\equiv \frac{l_{\mathrm{D},i}^2}{D},i=\text{in},\text{ex},$$ (2)

where ɛ and λ denote the absolute permittivity and conductivity of the fluid; l_D² = ɛk_BT/2e²C is the Debye length (for a symmetric 1:1 electrolyte) and D is the electrolyte ions diffusivity (43). Here C is the salt concentration, e is the electronic charge, k_B is the Boltzmann constant, and T is temperature. Hence, for frequencies ω < 2πt_c⁻¹, the bulk solution is electroneutral and free charges are present only at boundaries that separate media with different electric properties. The rate of accumulation of charges at the interface of a macroscopic object, e.g., a sphere, is given by the Maxwell-Wagner polarization time (10)

$$t_{\text{MW}}=\frac{{\varepsilon }_{\text{in}}+2{\varepsilon }_{\text{ex}}}{{\lambda }_{\text{in}}+2{\lambda }_{\text{ex}}}\text{.}$$ (3)

The electric field acts on the free charges at the interface and gives rise to a force, which is tangential to the interface. In the case of a simple fluid-fluid interface, e.g., a drop, only a hydrodynamic force can balance the shearing electric force. As a result, the fluids are set in continuous motion, the so-called electrohydrodynamic (EHD) flow (38). The EHD flow is characterized by a timescale, which corresponds to the inverse of the shear rate imposed by the tangential electric stress

$$t_{\text{el}}=\frac{{\eta }_{\text{ex}}}{{\varepsilon }_{\text{ex}}{E}_0^2}\text{.}$$ (4)

In the case of drops and quasispherical vesicles, the flow inside is toroidal, with a direction either from or toward the poles, depending on the surface charge distribution as illustrated in Fig. 1.

The membrane represents a more complex boundary compared to fluid-fluid interfaces.

First, it is an insulating shell and charges accumulate on both the inner and outer surfaces, as illustrated in Fig. 2. Hence, a vesicle of radius a acts as spherical capacitor that charges on a timescale given by (44,45)

$$t_{\text{cap}}=a{C}_{\mathrm{m}}\left(\frac{1}{{\lambda }_{\text{in}}}+\frac{1}{2{\lambda }_{\text{ex}}}\right)\text{.}$$ (5)

Figure 2.

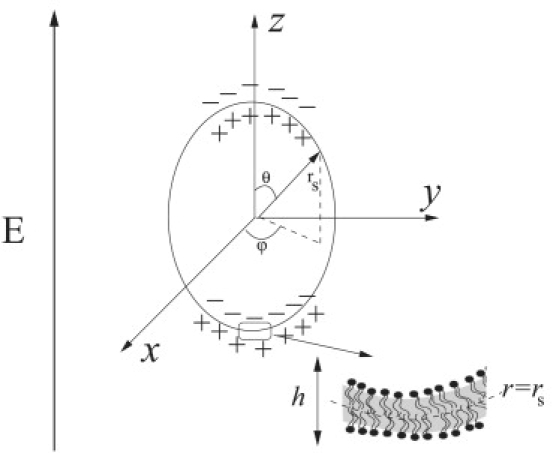
Sketch of a vesicle in a uniform electric field. The zoomed region of the interface illustrates the lipid bilayer structure of the membrane.

Second, the membrane mechanics is governed by resistance to bending. A distortion of the membrane shape relaxes on a timescale

$$t_{\kappa }=\frac{{\mathit{\eta }}_{\text{ex}}{a}^3}{\kappa },$$ (6)

where κ is the bending modulus. The curvature relaxation is controlled by the viscosity of the suspending fluid. In general, viscous dissipation takes place both in the embedding liquid and in the membrane (46). The relative importance of the bulk and membrane dissipation mechanisms is further discussed in Membrane Mechanics.

It is instructive to estimate the magnitude of the characteristic timescales involved in vesicle electrodeformation. Typical experimental conditions involve fluids with conductivities in the range λ ∼ 10⁻³–10⁻⁴ S/m and electric fields of E ∼ 1 kV/cm (19,29,30,47). In physiological conditions, e.g., blood, the internal conductivity of an erythrocyte is much higher, at ∼0.5 S/m (14). The typical size of a vesicle or cell is a ∼ 10 μm. The inner and outer fluids are essentially water: viscosity η ∼ 10⁻³ Pa.s, and density ρ ∼ 1000 kg/m³. The membrane capacitance is C_m ∼ 10⁻² F/m² (48) and bending rigidity κ ∼ 10⁻¹⁹ J. Therefore, for vesicles, we estimate the basic charging time and the Maxwell-Wagner polarization time t_c ∼ t_MW ∼ 10⁻⁷ s, the membrane charging time t_cap ∼ 10⁻³ s, the electrohydrodynamic time t_el ∼ 10⁻³ s, and the bending relaxation time t_κ ∼ 10 s.

We see that vesicle dynamics in electric fields involves processes that occur on very different timescales. Vesicle deformation takes place concurrently with fluid motion. The electric field adjusts to a new boundary configuration much faster than the fluid moves, because conduction (and hence charge redistribution) is fast, t_MW << t_el. Based on the timescale separation, we can assume the electric field to be quasistatic and dependent only on the instantaneous vesicle shape. The flow timescale is comparable to the capacitor charging time, t_el ∼ t_cap. The interplay between these two timescales is responsible for the observed dynamics of vesicles in electric fields (30).

Governing equations

In essence, our model consists of conservation of current, which obeys Ohm's law, and the Stokes equations to describe fluid motion (36). Charges carried by conduction accumulate at interfaces, and bulk phases become electroneutral on a very fast timescale given by t_c (Eq. 2). Accordingly, the equations of bulk fluid motion have no electric terms and the electromechanical coupling occurs only at boundaries.

Electrohydrodynamic problem

Electric field. The electric potential, Φ, for a quasistatic electromagnetic field is the solution of the Laplace equation

$${\nabla }^2\mathrm{\Phi }=0,\mathbf{E}=-\nabla \mathrm{\Phi }\text{.}$$ (7)

The membrane acts as a capacitor. Accordingly, the potential undergoes a jump across the interface of

$${\mathrm{\Phi }}^{\text{in}}-{\mathrm{\Phi }}^{\text{ex}}=\Delta \mathrm{\Phi }\left(\omega ,\mathrm{t}\right)\text{at}\mathrm{r}={\mathrm{r}}_{\mathrm{s}},$$ (8)

where r = r_s denotes the position of the interface in a coordinate system centered in the vesicle (see Fig. 2). The relation between the transmembrane potential and the membrane capacitance depends on geometry. The spherical shell is a widely used model for cells and vesicles (8,44), although a spheroidal geometry has also been considered (10).

Free charges at the interface cause a discontinuity in the normal component of the displacement vector

$$\mathbf{n}\cdot \left[{\varepsilon }_{\text{ex}}{\mathbf{E}}^{\text{ex}}-{\varepsilon }_{\text{in}}{\mathbf{E}}^{\text{in}}\right]=Q\left(\omega ,t\right)\text{at}r=r_{\mathrm{s}},$$ (9)

where n is the outward unit normal vector and Q is the free charge density. Neglecting effects of charge convection along the surface by fluid motion, the conservation of electric currents at the interface requires that

$$\mathbf{n}\cdot \left[{\lambda }_{\text{ex}}{\mathbf{E}}^{\text{ex}}-{\lambda }_{\text{in}}{\mathbf{E}}^{\text{in}}\right]=-\frac{\partial Q}{\partial t}\text{at}r=r_{\mathrm{s}}\text{.}$$ (10)

The forces due to an electric field E are calculated from the Maxwell stress tensor

$${\mathbf{T}}^{\text{el}}=\varepsilon \left(\mathbf{EE}-\frac{1}{2}{\mathbf{E}}^2\mathbf{I}\right),$$ (11)

where I denotes the unit tensor. A harmonic electric field can be written as

$$\mathbf{E}\cos \left(\mathit{\omega }t\right)=\frac{1}{2}\left(\mathbf{E}+{\mathbf{E}}^{\ast }\right),$$ (12)

where the superscript ^∗ denotes a complex conjugate. It gives rise to a nonzero time-averaged component of the Maxwell stress tensor

$${\mathbf{T}}^{\text{el}}\left(\mathit{\omega }\right)=\frac{1}{4}\left[{\mathbf{EE}}^{\ast }+{\mathbf{E}}^{\ast }\mathbf{E}-|E{|}^2\mathbf{I}\right],$$ (13)

which is responsible for the steady deformation of the vesicle.

All electric variables (electric field, potential, charge density) vary harmonically with time $u(\mathbf{r},t,\mathit{\omega })=\overline{u}(\mathbf{r},\mathit{\omega })\exp \left(i\mathit{\omega }t\right)$. Hence, hereafter unless specifically stated, we will always refer to the amplitude of an electric variable, $\overline{u}(\mathbf{r},\mathit{\omega })$, and we will omit the bar for convenience.

Hydrodynamic field. Vesicle deformation is accompanied by motion in the surrounding fluids. The fluid velocity, v, and pressure, p, inside and outside the vesicle are described by the Stokes equations (49,50)

$$\rho \frac{\partial \mathbf{v}}{\partial t}=\nabla \cdot {\mathbf{T}}^{\text{hd}},\nabla \cdot \mathbf{v}=0.$$ (14)

The bulk hydrodynamic stress is

$${\mathbf{T}}^{\text{hd}}=-\mathrm{p}\mathbf{I}+\eta \left[\nabla \mathbf{v}+{\left(\nabla \mathbf{v}\right)}^{†}\right],$$ (15)

where the superscript † denotes transpose.

Equation 14 is a simplified version of the more general Navier-Stokes equations. First, inertial effects are neglected because at the length-scale of the cell water is effectively very viscous. Second, the bulk stress has no contribution from the electric field because there are no excess free bulk charges. The unsteady term ∂v/∂t can be neglected provided that the viscous relaxation time, t_v = a²ρ/η, is faster than the changes in the electric field, i.e., ω < t⁻¹_v (51). The linearity and quasisteadiness of the Stokes equations, and the decoupling of the electric and hydrodynamic equations in the bulk, greatly simplify the solution of the problem.

Far away from the vesicle, the fluid is at rest and the flow field vanishes, v^ex → 0. In the absence of bilayer slip and membrane permeability, the velocity is continuous across the interface

$${\mathbf{v}}^{\text{in}}={\mathbf{v}}^{\text{ex}}\equiv {\mathbf{v}}_{\mathrm{s}}\text{at}\mathrm{r}={\mathrm{r}}_{\mathrm{s}}\text{.}$$ (16)

The interface moves with the normal component of the velocity of the adjacent fluid (52)

$$\frac{\partial r_{\mathrm{s}}}{\partial t}={\mathbf{v}}_{\mathrm{s}}\cdot \mathbf{n}\text{.}$$ (17)

Membrane permeability can be neglected in the case of osmotically stabilized vesicles and pore-free membranes, i.e., membranes in which the electric-field induced tension does not exceed the poration threshold.

Electromechanical coupling. The vesicle shape is determined by the balance of electric, hydrodynamic, and membrane tractions (surface force densities) at the interface r = r_s,

$$\mathbf{n}\cdot \left[\left({\mathit{\eta }}_{\text{ex}}{\mathbf{T}}^{\text{hd},\text{ex}}-{\mathit{\eta }}_{\text{in}}{\mathbf{T}}^{\text{hd},\text{in}}\right)+\left({\varepsilon }_{\text{ex}}{\mathbf{T}}^{\text{el},\text{ex}}-{\varepsilon }_{\text{in}}{\mathbf{T}}^{\text{el},\text{in}}\right)\right]={\mathit{\tau }}^{\text{mem}},$$ (18)

where flexoelectric bending of the lipid bilayer is neglected (53,54). For example, at rest, when the electric field is off, Eq. 18 reduces to the familiar Euler-Lagrange equation (46), which states that there can be a jump in the hydrostatic pressure across a membrane due to membrane tractions

$$p^{\text{in}}-p^{\text{ex}}=2\mathit{\sigma }H-\kappa \left[4H^3-4\mathit{KH}+2{\nabla }_{\mathrm{s}}^{2}H\right],$$ (19)

where κ is the bending rigidity, and H and K are the mean and Gaussian curvatures. In the next section, we discuss the membrane stresses in more detail.

Membrane mechanics

The pure lipid membrane consists of two sheets of lipid molecules. It stores elastic energy in bending, and dissipates energy by membrane surface viscosity and intermonolayer friction.

Within the framework of the minimal model (55), the bending resistance gives rise to a surface force density

$${\mathit{\tau }}^{\kappa }=-\kappa \left(4H^3-4\mathit{KH}+2{\nabla }_{\mathrm{s}}^{2}H\right)\mathbf{n}\text{.}$$ (20)

The surface gradient operator is defined as ∇_s = I_s·∇, where the matrix I_s = I – nn represents a surface projection.

The membrane leaflets consist of fixed number of lipids, which are optimally packed with a fixed area per lipid (under moderate stresses). As a result, a membrane element only deforms but cannot change its area. Under stress, the membrane develops tension, which adapts itself to the forces exerted on the membrane to keep the local and total area constant. Hence, the tension is nonuniform along the interface and varies with forcing. The membrane tension gives rise to surface force density

$${\mathit{\tau }}^{\sigma }=2\sigma H\mathbf{n}-{\nabla }_{\mathrm{s}}\mathit{\sigma ,}$$ (21)

where σ denotes the local membrane tension.

For lipid bilayers in the fluid phase, the lipids are free to move within the monolayer. Therefore, in contrast to gel-phase lipid membranes, a fluid bilayer membrane has no shear-elastic modulus (31). Moreover, the surface viscosity of lipid bilayers in the fluid phase is relatively low, η_mm ∼ 10⁻⁹ Ns/m, and its effects are usually negligible.

In addition to surface viscosity, other dissipation mechanisms are drag between the two monolayers (56) and permeation through the membrane. Dissipation by intermonolayer friction becomes important if bilayer shape changes occur on a timescale comparable to the lateral lipid redistribution within the bilayer (56–58). Vesicle deformation occurs on the electrohydrodynamic timescale, t_el ∼ 10⁻³ s (for the experiments of Aranda et al. (30)). The bilayer slip timescale is t_slip = ba²/K_A ∼ 0.1 s, where K_A ∼ 0.1 N/m is the bilayer stretch modulus and b ∼ 10⁸ N.s/m³ is the bilayer slip coefficient (31,59). Based on large separation of timescales, t_slip >> t_el, the bilayer slip was not included in the current model.

Membranes become permeable when subjected to submillisecond strong direct current pulses that cause poration (29,48,60,61); electropermeabilization in AC fields is less likely (62,63). Pores form when the transmembrane potential exceeds a critical value, which for a tension-free membrane is V_c ∼ 1 V and decreases with initial tension (28,48). Thus, in principle, it is possible to reach V_c in a low-frequency AC field, where V_c ∼ 3/2E₀a, provided that the electric field strength is higher than 10⁵ V/m. In the experiments of Aranda et al. (30), the electric field strengths were lower, 2 × 10⁴ V/m, and vesicles were fluctuating, which implies very low initial tensions. Hence, in this case, membrane permeation appears unlikely and we have neglected it in this study. In addition, the vesicle volume as observed in experiments remained constant, indicating no leakage through the membrane.

In summary, the external electric energy is stored in the membrane due to developing tension and bending moments, and dissipated by viscous friction in the bulk fluid. The bulk hydrodynamic dissipation prevails because the viscous relaxation time of the embedding fluids, t_v = a²ρ/η ∼ 1 μs, is much shorter than the timescales associated with dissipation in the membrane.

Dimensionless parameters

It is more convenient to describe the problem in terms of nondimensional parameters. Casting equations in dimensionless form helps show the generality of application to a broad class of situations rather than just one set of dimensional parameters.

Henceforth, bending stresses and tension are normalized by κ/a²; all other quantities are rescaled using η_ex, ɛ_ex, λ_ex, a, and E₀. The fluid velocity scale is v₀ = ɛ_exE₀²a/η_ex. The electric and viscous stresses are rescaled by ɛ_exE₀². Time and frequency are nondimensionalized with the basic charging time t_c = ɛ_ex/λ_ex.

The electric capillary number compares the shape-preserving bending stresses to the shape-distorting electric stresses,

$$Ca=\frac{t_{\kappa }}{t_{\text{el}}}=\frac{{\varepsilon }_{\text{ex}}{E}_0^2{a}^3}{\kappa }\text{.}$$ (22)

The other relevant parameters are the ratios of the electric properties of inner and outer fluid

$$\mathrm{\Lambda }=\frac{{\lambda }_{\text{in}}}{{\lambda }_{\text{ex}}},S=\frac{{\varepsilon }_{\text{in}}}{{\varepsilon }_{\text{ex}}}$$ (23)

and the viscosity ratio

$$\chi =\frac{{\mathit{\eta }}_{\text{in}}}{{\mathit{\eta }}_{\text{ex}}}\text{.}$$ (24)

The dimensionless membrane conductivity and capacitance per unit area are

$$G_{\text{m}}=\frac{{\lambda }_{\text{mm}}}{x{\lambda }_{\text{ex}}},C_{\mathrm{m}}=\frac{{\varepsilon }_{\text{mm}}}{x{\varepsilon }_{\text{ex}}},$$ (25)

where the dimensionless membrane thickness is x = h/a.

We estimate that Ca ∼ 10³ >> 1, from the typical values discussed at the end of The Physical Picture and Characteristic Timescales, which correspond to the experiments of Aranda et al. (30); the dielectric constants and viscosity ratios are S, χ ∼1, but the conductivity ratio vary between 10⁻³ and 100.

Solution for Small Deformations

In a coordinate system centered at the vesicle, the radial position r_s of the vesicle interface is described by

$$r_{\mathrm{s}}=1+f\left(\theta ,\mathrm{\varphi }\right),$$ (26)

where f is the deviation of vesicle shape from a sphere. For a nearly spherical vesicle, f << 1. In this case, the exact position of the interface is replaced by the surface of a sphere of equivalent volume, and all quantities that are to be evaluated at the interface of the deformed vesicle are approximated using a Taylor series expansion. The solution for electric and flow fields is derived as a regular perturbation expansion in some small parameter, e.g., the excess area.

In this study, we perform the leading order analysis. Accordingly, the electric and hydrodynamic fields are evaluated about a sphere. First, we determine the electric field and the electric tractions (surface force density) exerted on the membrane. Second, we determine the hydrodynamic tractions needed to satisfy the force balance Eq. 18 and the corresponding velocity field. Finally, we use the kinematic condition Eq. 17 to find the shape evolution.

In Eq. 26, the function f representing the perturbation of the vesicle shape depends only on angular coordinates. Thus, it is expanded into series of scalar spherical harmonics Y_jm given by Eq. 46:

$$f=\sum _{\text{j}=2}^{\mathrm{\infty }}\sum _{\mathrm{m}=-\text{j}}^{\text{j}}{f}_{\text{jm}}{Y}_{\text{jm}}\text{.}$$ (27)

Solutions for the electric field are growing and decaying harmonics, which derive from ∇(r^jY_jm) and ∇(r^−j−1Y_jm). The uniform applied electric field along the z direction, defined by Eq. 1, is described by the j = 1 harmonic

$${\mathbf{E}}^{\mathrm{\infty }}=d^{\mathrm{\infty }}\nabla \left(r{Y}_{10}\right),d^{\mathrm{\infty }}=\sqrt{\frac{4\pi }{3}}\text{.}$$ (28)

Accordingly, the induced electric field has j = 1, m = 0 symmetry.

Electrostatic field and stresses

The model for the electric field is based on the classic work by Schwan (44), in which it is shown that an external AC electric field induces a potential across the membrane of a spherical shell (64),

$$\Delta \mathrm{\Phi }={\mathrm{V}}_{\mathrm{m}}\left(\omega \right)\text{cos}\mathrm{\theta },$$ (29)

where

$$V_{\mathrm{m}}\left(\mathit{\omega }\right)=\frac{3}{2}\frac{1}{1+\left(G_{\mathrm{m}}+\mathrm{i}\mathit{\omega }{C}_{\mathrm{m}}\right)\left(1/\mathrm{\Lambda }+1/2\right)}\text{.}$$ (30)

The transmembrane potential is very sensitive to the membrane thickness. Fig. 3 a illustrates the variation of the transmembrane potential with frequency for a vesicle with a fixed size and two values of the membrane thickness, corresponding to a giant unilamellar lipid vesicle and a polymersome. For a simple fluid-fluid interface (a drop, i.e., x = 0), the transmembrane potential is zero.

Figure 3.

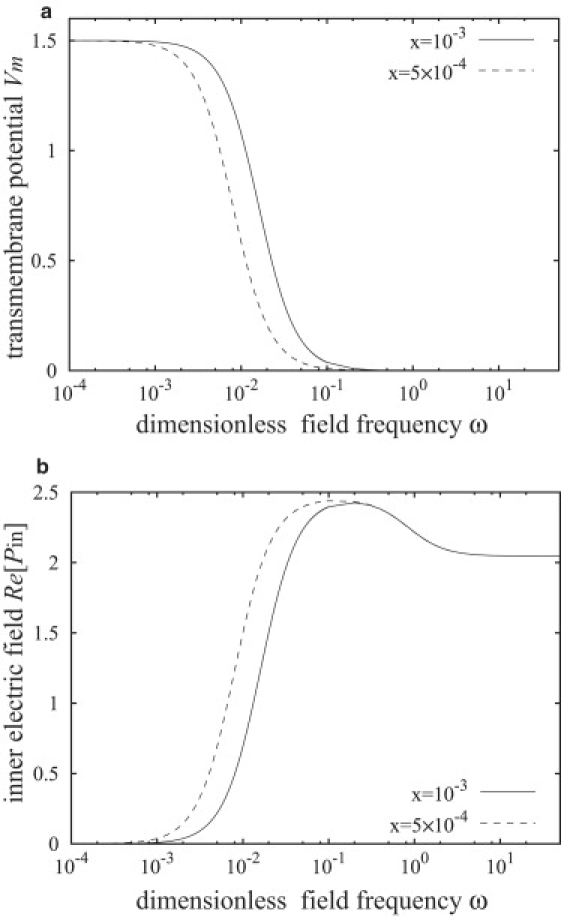
(a) Transmembrane potential at the poles θ = 0, π calculated from Eq. 30, and (b) interior electric field calculated from Eq. 49 for a spherical shell with different membrane thickness, x = 5 × 10⁻⁴ and x = 10⁻³, in a uniform AC electric field. Λ = 0.5, S = 1.001, C_m = 0.025/x, G_m = 0.

The electric tractions exerted on the membrane have radial and tangential components,

$${\mathit{\tau }}^{\text{el}}={\tau }_{\mathrm{r}}^{\text{el}}\left[1+3\cos \left(2\theta \right)\right]\widehat{\mathbf{r}}+{\tau }_{\theta }^{\text{el}}\sin \left(2\theta \right)\widehat{\mathit{\theta }}\text{.}$$ (31)

In terms of the electric field, the electric pressure can be written as

$${\tau }_{\mathrm{r}}^{\text{el}}=\frac{1}{2}\left[{\left(E_{\mathrm{r}}^{\text{ex}}\right)}^2-{\left(E_{\theta }^{\text{ex}}\right)}^2-S\left({\left(E_{\mathrm{r}}^{\text{in}}\right)}^2-{\left(E_{\theta }^{\text{in}}\right)}^2\right)\right],$$ (32)

and the tangential electric force is

$${\tau }_{\theta }^{\text{el}}=E_{\theta }^{\text{ex}}Q+{SE}_{\mathrm{r}}^{\text{in}}{\mathrm{V}}_{\mathrm{m}}\left(\omega \right)\text{sin}\theta ,$$ (33)

where we have used the definition of surface charge Q given by Eq. 9. The amplitudes of the electric tractions, τ_r^el and τ_θ^el, depend only on the electric properties of the media. Their expressions are given by Eqs. 51 and 52.

The electric stresses are complicated functions of the frequency ω as illustrated in Fig. 4, a and b. We can distinguish three regimes:

Figure 4.

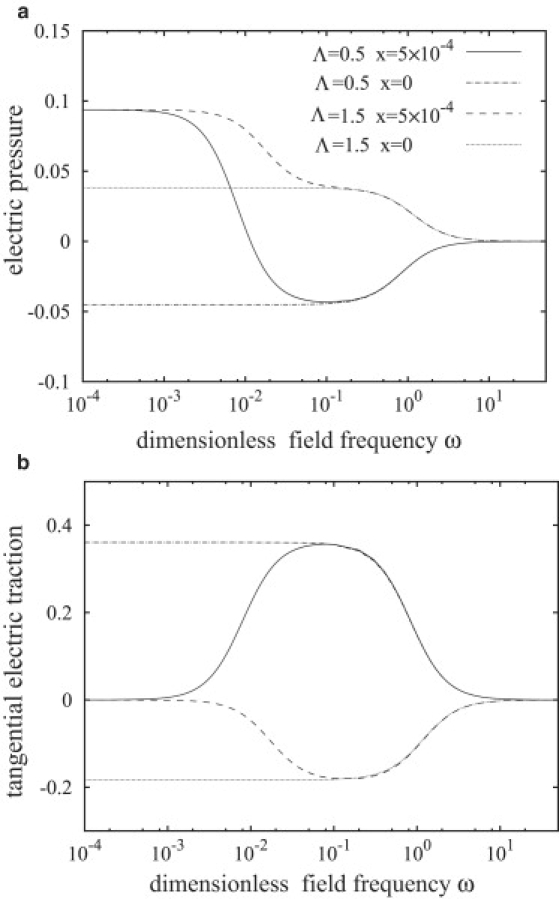
Electric tractions on the membrane as a function of the frequency for two conductivity ratios, Λ = 0.5 and Λ = 1.5. (a) Electric pressure calculated from Eq. 51; (b) tangential electric force calculated from Eq. 52. The values of the other physical parameters are S = 1.001, C_m = 0.025/x, and G_m = 0. The electric tractions in the case of a droplet (the zero-membrane-thickness limit x = 0) are also shown for comparison.

Low frequencies, ω < ω₁

In this case, the membrane shields the vesicle interior and the electric field inside zero, as seen from Fig. 3 b. The electric pressure is positive at the poles, and negative at the equator, thus pulling the vesicle into a prolate shape. The tangential electric stress is zero everywhere on the surface, because both induced charge and internal electric field are zero. In contrast, the tangential electric stress at a simple fluid-fluid interface, i.e., zero-membrane-thickness, is nonzero even at low frequencies (see Eq. 54). For conductivity ratio Λ < 1, the electric pressure changes its sign and the tangential electric traction becomes significant above a frequency ω₁ given by (8,44)

$${\omega }_1=\frac{G_{\mathrm{m}}}{C_{\mathrm{m}}}+\frac{2\mathrm{\Lambda }}{C_{\mathrm{m}}\left(\mathrm{\Lambda }+2\right)},$$ (34)

which reduces to 1/t_cap (Eq. 5), if the membrane is nonconducting.

Intermediate frequencies, ω₁ < ω < ω₂

In this frequency window, the membrane capacitor becomes short-circuited and the vesicle interior participates in the conduction process. The onset of decrease in the transmembrane potential and increase in the interior electric field coincides with the appearance of tangential electric tractions, as seen in Figs. 3 and 4. The tangential electric stress is mainly due to the free charges on the membrane (38) (see Eq. 33). Because of the different conductivities of the inner and outer fluids, charges accumulate at different rates on the membrane physical surfaces. As a result, charge densities on the inner and outer membrane surfaces can become imbalanced, which gives rise to a nonzero effective interfacial charge density as shown in Fig. 5. The effective charge is zero at low frequencies because the membrane capacitor is fully charged, having equal charge densities on the inner and outer membrane surface, and at high frequencies because of insufficient time for interface charging.

Figure 5.

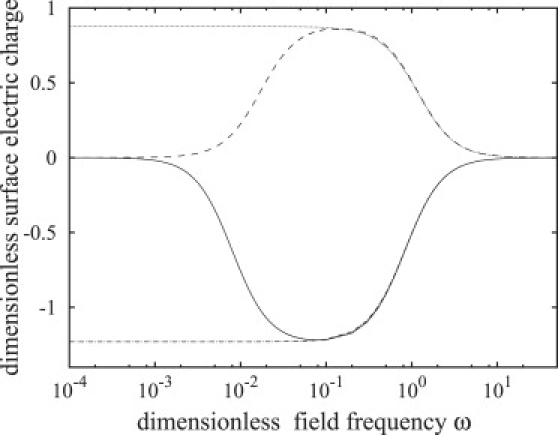
Absolute value of the amplitude of the interfacial charge density at the poles θ = 0, π. Notation and parameter values are the same as in Fig. 4.

High frequencies, ω > ω₂

The inverse Maxwell-Wagner polarization time, Eq. 3, defines a critical frequency

$${\omega }_2=\frac{\mathrm{\Lambda }+2}{S+2},$$ (35)

above which tangential stress starts to decrease. It vanishes at very high frequencies, where all media behave as perfect dielectrics. In this frequency regime, the electric pressure is small, but positive with magnitude ∼(S − 1)²/(S + 2)², which leads to small prolate deformation.

Hydrodynamic field and vesicle deformation

The stress balance at the interface Eq. 18 shows that the electric tractions need to be compensated by membrane and hydrodynamic forces. The latter can be found using the general solution for a nearly spherical vesicle subject to an external field (46,65–67). Details of the solution are presented in the Supporting Material.

The vesicle area, A, exceeds the area needed to enclose the volume of the interior fluid, 4πa². At rest, the excess area is redistributed among all shape modes

$$\Delta =A/a^2-4\pi =\sum _{\mathrm{j}=2}^{\mathrm{\infty }}\sum _{\mathrm{m}=-\mathrm{j}}^{\text{j}}\frac{{\left(-1\right)}^{\mathrm{m}}}{2}\left(j-1\right)\left(j+2\right)f_{\text{jm}}{f}_{\mathrm{j}-\mathrm{m}}\text{.}$$ (36)

Therefore, to accurately describe vesicle deformation, in general, we need the evolution equations for all shape modes. These are derived in Vlahovska and Gracià (65) (see also the Supporting Material) and have the general form of

$$\frac{\partial f_{\text{jm}}}{\partial t}=C_{\text{jm}}+\mathit{C}{\mathit{a}}^{-1}\left({\mathrm{\Gamma }}_1+{\mathit{\sigma }}_{\mathrm{h}}{\mathrm{\Gamma }}_2\right)f_{\text{jm}}+O\left(f^2\right)\text{.}$$ (37)

The first term describes the distortion of the vesicle shape by the electrohydrodynamic flow. The term including Ca is associated with shape relaxation driven by the membrane stresses. The coefficients C_jm, Γ₁, and Γ₂ are listed in the Supporting Material. The effective tension σ_h depends on the vesicle shape, which in turns depends on the applied electric field.

In general, the apparent area of a vesicle, $\overline{A}$, is lower than its true area, A, because of suboptical fluctuations in the shape modes. For example, a quasispherical vesicle at equilibrium is characterized by a zero apparent area, i.e., $\overline{\Delta }=0$. However, even though the membrane in inextensible, the vesicle can deform and increase its apparent area due to flattening of the shape undulations. This leads to an increase in the membrane tension (42)

$${\mathit{\sigma }}_{\mathrm{h}}={\mathit{\sigma }}_0\text{exp}\left[\frac{8\mathit{\pi \kappa }}{k_{\mathrm{B}}T}\left(\frac{\overline{A}\left(t\right)}{4\pi a^2}-1\right)\right]={\mathit{\sigma }}_0\text{exp}\left(\frac{2\kappa \overline{\Delta }}{k_{\mathrm{B}}T}\right),$$ (38)

where σ₀ is the initial tension in the membrane.

In the next section, we simplify the theory for the case of vesicle electrodeformation induced by a uniform AC electric field.

Results

Deformation of a quasispherical vesicle

When the electric field is turned on, it generates electrohydrodynamic flow with the same symmetry as the electric stresses. The corresponding fluid velocity, which is responsible for the vesicle deformation, is given by

$$C^{\text{el}}\equiv C_{20}=8\sqrt{\frac{\pi }{5}}\frac{6{\tau }_{\mathrm{r}}^{\text{el}}-{\tau }_{\theta }^{\text{el}}}{23\chi +32},$$ (39)

where the electric stresses are given by Eqs. 51 and 52, and the viscosity parameter χ is defined by Eq. 24. Since electric stresses directly affect only the ellipsoidal j = 2, m = 0 mode, the most important contribution to the vesicle deformation comes from the “elongational” f₂₀ mode. Moreover, because the shape modes are coupled through the area constraint Eq. 36, the area stored in the j ≠ 2 modes is transferred into the ellipsoidal f₂₀ mode. The maximum possible vesicle deformation corresponds to elongation where all excess area is stored in the f₂₀ mode

$$f_{20}^{\text{max}}=\pm \sqrt{\frac{\Delta }{2}},$$ (40)

where a positive sign corresponds to a prolate deformation.

The shape evolution strongly depends on the effective tension σ_h. For a quasispherical vesicle, using the relation between excess area and shape modes (Eq. 36), and including only the dominant contribution from the f₂₀ mode, we can rewrite Eq. 38 as

$${\mathit{\sigma }}_{\mathrm{h}}={\mathit{\sigma }}_0\text{exp}\left(\frac{4\kappa }{k_{\mathrm{B}}T}{f}_{20}^2\right)\text{.}$$ (41)

Inserting into Eq. 37, we obtain that the shape evolution of a vesicle in AC electric field is described by the nonlinear equation:

$$\frac{\partial f_{20}}{\partial t}=C^{\text{el}}-\mathit{C}{\mathit{a}}^{-1}\frac{24\left[6+\text{exp}\left(\frac{4\kappa }{k_{\mathrm{B}}T}{f}_{20}^2\left(t\right)\right)\right]}{23\chi +32}{f}_{20}\left(t\right)\text{.}$$ (42)

At steady state ∂f₂₀/∂t = 0, and the stationary vesicle shape is given by

$$f_{20}=\sqrt{\frac{\pi }{5}}\frac{6{\tau }_{\mathrm{r}}^{\text{el}}-{\tau }_{\theta }^{\text{el}}}{3\left(6+{\mathit{\sigma }}_{\mathrm{h}}\right)}\text{.}$$ (43)

The above equation is a generalization of the relation derived by Kummrow and Helfrich (19). Their model is valid only for frequencies <ω₁.

Discussion

The shape evolution obtained from Eq. 42 for several frequencies is illustrated in Fig. 6 a. We observe that a vesicle deforms on a hydrodynamic timescale approximated by t_d = 1/C^el. The final steady deformation depends on the strength of the deforming electric stresses, which decrease with frequency. The time needed to reach stationary shape depends strongly on the viscosity contrast between the inner and outer fluid. Fig. 6 b shows that increasing the viscosity of the inner fluid slows down the shape evolution. The viscosity effect may become important in the electrodeformation of red blood cells, which are characterized by χ ∼ 10.

Figure 6.

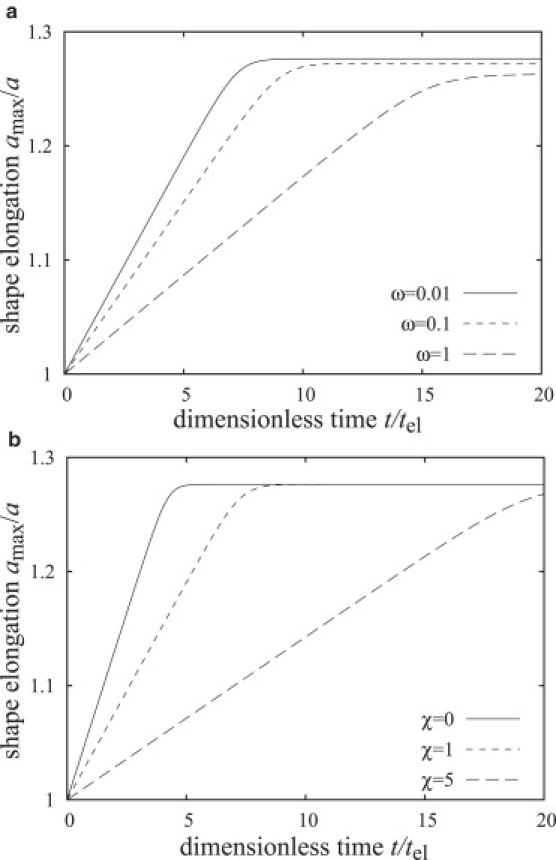
Evolution of the ellipsoidal deformation a_max/a, calculated from Eq. 42, of a quasispherical vesicle upon application of a uniform AC electric field. (a) For frequencies ω = 0.01, 0.1, 1, and same viscosity ratio χ = 1. (b) For viscosity ratios χ = 0, 1, 5, and the same AC field frequency ω = 0.01. The values of the physical parameters are Λ = 1.5, x = 5 × 10⁻⁴, S = 1.001, G_m = 0, and C_m = 50. Ca = 6837 corresponds to E₀ = 2 × 10⁴V/m, η_ex = 10⁻³Pa.s, κ = 10 k_BT, and a = 10 μm.

The steady shape of a vesicle in AC electric field is calculated by evaluating Eq. 43. Fig. 7 illustrates the steady shapes of vesicles in the AC field as a function of frequency for different conductivity ratios. The theory predicts that the type of deformation, prolate or oblate, is determined primarily by the frequency and the conductivity ratio. At low frequencies ω < ω₁, the deformation is prolate. For frequencies ω > ω₁, vesicles are prolate or oblate, depending on the conductivity ratio. At even higher frequencies, the deformation becomes again prolate but very small and the vesicle appears spherical.

Figure 7.

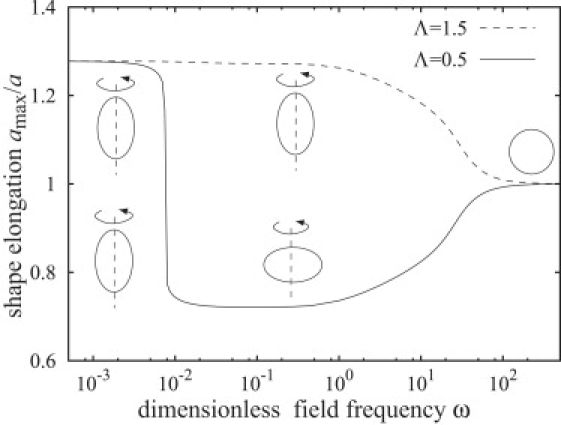
Ellipsoidal deformation a_max/a of vesicles in uniform AC electric field as a function of the dimensionless frequency for two conductivity ratios Λ = 0.5 and Λ = 1.5. Other parameters are the same as in Fig. 6.

Next, we analyze these morphological transitions in more detail.

Prolate-oblate transition for Λ < 1 at low frequencies

The transition frequency ω₁ corresponds to the capacitor charging time (Eq. 34).

At low frequencies, ω < ω₁, vesicle deformation is due solely to the positive electric pressure. It is maximal at the poles (see Eq. 51). The vesicle is pulled apart, and thus, adopts a prolate ellipsoidal shape.

At ω > ω₁, the tangential electric traction becomes significant and the electric pressure is negative, as seen from Fig. 4. The shearing tangential force induces electrohydrodynamic flow, similar to the one observed with drops (Fig. 1). If Λ/S < 1, the flow is directed from the poles to the equator and the resulting deformation is oblate; if Λ/S > 1, the flow is directed from the equator to the poles and the resulting deformation is prolate. Therefore, prolate-oblate transition is possible only if Λ/S < 1. In experiments with vesicles (30,32), the inner and outer fluids are sucrose and glucose, which have a similar dielectric constant, S ∼ 1. Oblate shapes were reported for conductivity ratio < 1, in agreement with the condition Λ/S < 1. In the case of biological cells, the difference between the dielectric constants of the cytosol and the cell environment is also small, and therefore similar deformation behavior is expected. In the case of drops, the electrohydrodynamic flow persists for as long as the electric field is applied because only viscous stresses can balance the tangential electric surface force. In contrast to drops, the electrohydrodynamic flow in vesicles is not sustained. It stops when the vesicle reaches steady deformation because the membrane tension counteracts the electric tangential force.

The capacitor charging time decreases with the size of the vesicle. Therefore, the smaller the vesicle, the higher the transition frequency. For a nanometer-size vesicle, this frequency is in the MHz range. Thus, nanovesicles are expected to deform only into prolate ellipsoids when subjected to AC fields with frequency less than a MHz, or for direct current pulses with length longer than 1 μs, which is in agreement with experimental observations (68).

Comparison with experiment

Figs. 8 and 9 demonstrate that our theory is consistent with the experiment. Our model captures the morphological transitions of vesicles in AC fields, in particular, the prolate-oblate one at low frequencies. The theory also shows that vesicles should be spherical at high frequencies as experimentally observed. In addition, it correctly predicts the effect of conductivity on the type of deformation, which has not been reported by other models.

Figure 8.

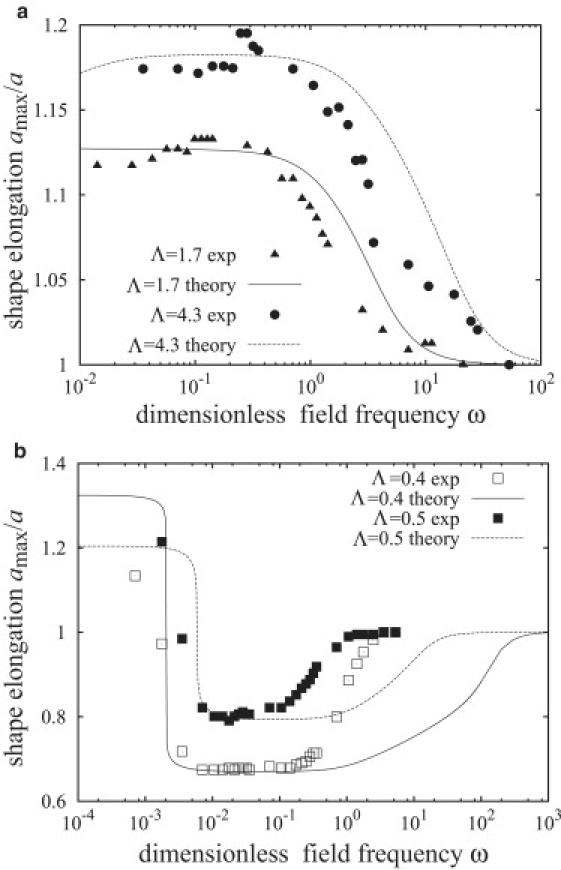
Comparison between theory and the experimental data of Aranda et al. (30). (a) Prolate deformations. The fitted initial tensions are σ₀ = 20,000 (corresponding to 1.1 × 10⁻³ mN/m) for Λ = 1.7 and σ₀ = 3000 (1.6 × 10⁻⁴ mN/m) for Λ = 4.3. (b) Oblate deformations. The fitted initial tensions are σ₀ = 1 (5.6 × 10⁻⁸ mN/m) for Λ = 0.4 and σ₀ = 100 (2.5 × 10⁻⁵ mN/m) for Λ = 0.5.

Figure 9.

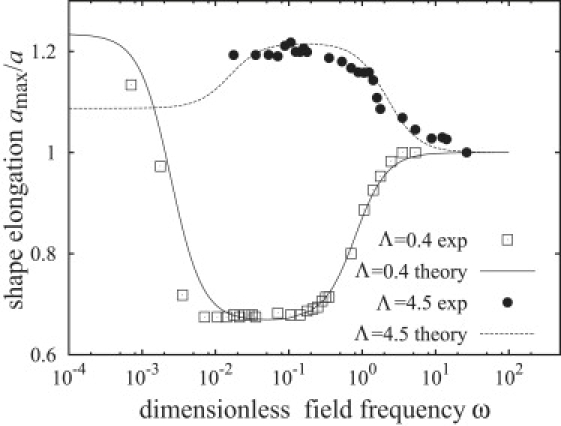
Comparison between theory (line) and the experimental data (symbols) of Aranda et al. (30) assuming constant tension. The theoretical line is calculated from Eq. 43 for Λ = 4.5 with σ_h = 40,000 (corresponding to 5.3 × 10⁻³ mN/m), and for Λ = 0.4 with σ_h = 55,000 (σ_h = 3 × 10⁻³ mN/m).

Fig. 8 shows the dependence of the vesicle deformation on the field frequency and conductivity ratio. We have calculated the vesicle half-length along the field direction $a_{\text{max}}/a=1+\sqrt{5/4\pi }{f}_{20}$ from Eq. 43, using the initial membrane tension σ₀ as the only fitting parameter. The choice of σ₀ as an adjustable variable is reasonable, considering that the equilibrium membrane tension cannot be controlled experimentally and it is not known a priori. The theoretical vesicle shapes are in a good agreement with the experimental data, albeit the onset of the decrease in the vesicle deformation is overestimated. The fitted values for the initial tensions are of the same order of magnitude as in earlier work (19).

Some of the discrepancy between theory and experiment in the MHz frequency range could be ascribed to the omission of unsteady fluid motion, conductivity dispersion in the bulk electrolyte, or effects due to electric double layers.

We have used a quasisteady approximation, tantamount to ignoring ρ∂v/∂t in the equations of motion(Eq. 14). Unsteady fluid motion is slower than a fully developed quasi-steady flow, resulting in weaker deforming stresses. Accordingly, vesicle deformation under unsteady flow conditions would be smaller. A quick estimate shows that temporal fluid acceleration becomes important at frequencies ω >> η/ρa² ∼ 10 kHz (51).

The frequency at which vesicle deformation begins to decrease is also comparable to the inverse of the shortest of the interior and exterior fluid bulk charging times, t_c = min{t_{c, in}, t_{c, ex}}. The charging time t_c is also interpreted as the time for the polarization of the screening cloud around an ion (43). If ω > 2π/t_c, the ion atmosphere becomes distorted, which leads to increase in the conductivity (Debye-Falkenhagen effect). If t_c = t_{c, in}, the increase of inner fluid conductivity could possibly decrease the tendency for oblate deformations.

Another possible explanation for the fact that at high frequencies the observed vesicle deformation is smaller than the theoretically predicted one is that the theoretical membrane tension is underestimated.

First, in the current model, the membrane tension increases solely due to flattening of the shape fluctuations by the electric forces. We have included only the contribution from the f₂₀ mode in the apparent excess area. However, due to the area constraint (see Eq. 36), a decrease of f₂₀ should be compensated by an increase in the amplitudes of the other shape modes. If all modes are accounted for, the apparent excess area would be larger and hence the tension would be higher (see Eq. 38).

Second, electric double layers (EDLs) give rise to an additional increase of the membrane tension (25,69). The electric field acting on the charges in the Debye layers on the interior and exterior sides of the membrane creates extensional stresses near the membrane that act to reduce membrane area, which is equivalent to increasing the tension (69). The calculation of the EDL contribution to the membrane tension is a complicated problem that has been solved only for a planar membrane (26,69). Accounting for this effect in the case of a vesicle is a challenging task that we postpone to future study. At this time we assume that the EDL tension is constant. Fig. 9 illustrates the frequency dependence of vesicle shape for Λ = 4.5 and Λ = 0.4 computed from Eq. 43 with σ_h as an adjustable parameter corresponding to the EDL tension. The somewhat surprising agreement between theory and experiment prompts further investigation.

Third, we focus on the prolate-oblate transition at lower frequencies, which previously eluded theoretical interpretation but is correctly captured by our theoretical model. Fig. 10 shows the experimentally measured transition frequency ω₁ for 28 vesicles with different sizes and conductivity conditions. The theoretically predicted dependence of the transition frequency on the conductivity ratio agrees very well with the experimental data. Note that the scatter in the data is due to variations in vesicle sizes and conductivity conditions. Differences in the vesicle size affect the dimensionless membrane thickness x, and therefore we have plotted ω₁(Λ) for three values of x corresponding to the average, the smallest, and the largest vesicle radii.

Figure 10.

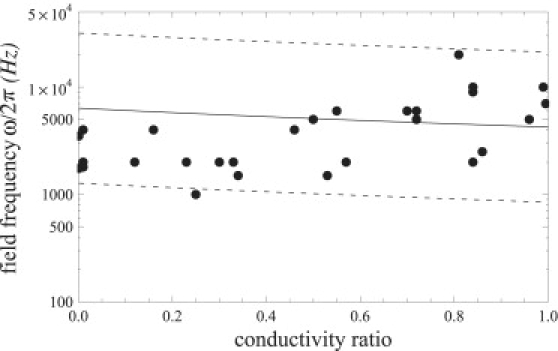
Prolate-oblate transition frequency for different conductivity ratios Λ. The points are experimental data (30,32) for 28 vesicles with different size; the fluids conductivities are ∼10⁻⁴ S/m. The solid line is the theoretical prediction using x = 10⁻⁴ corresponding to vesicle radius a = 50 μm. The bottom dashed line is calculated using x = 2 × 10⁻⁵ and the top dashed line is calculated using x = 5 × 10⁻⁴. The basic charging time is estimated to be t_c = 10⁻⁷ s.

Oblate-prolate transition for Λ < 1 at high frequencies

At high frequencies ω >> ω₁, the transmembrane potential vanishes, as seen in Fig. 3. The electric tractions are given by the zero-thickness results from Eqs. 53 and 54. The forcing term C^el in the shape evolution Eq. 42 changes sign at a frequency

$${\mathrm{\Omega }}_2={\left[\frac{4S-{\left(\mathrm{\Lambda }+1\right)}^2}{{\left(S-1\right)}^2}\right]}^{\frac{1}{2}}\text{.}$$ (44)

Correspondingly, the vesicle deformation changes from oblate to prolate at this frequency. The transition frequency Ω₂ becomes very large when the dielectric constants of the fluids are comparable. For vesicles filled with sucrose and suspended in glucose solutions, this frequency is ∼1 GHz, which is in the frequency range where electric tractions have already become too small to deform the vesicle. Thus, this oblate-prolate transition was not observed in the experiments of Aranda et al. (30); instead, the vesicles become spherical. Thus far, the prolate-oblate transition has been reported only for drops (70).

If Ω₂ < ω₁, the oblate deformation would be impossible. This situation arises if the membrane becomes highly conducting, e.g., because of poration. Another possibility is a thick membrane or small vesicle with

$$\frac{h}{a}>\frac{{\left(\mathrm{\Lambda }+2\right)}^2{S}_{\mathrm{m}}}{\left(S+2\right)\left(2\mathrm{\Lambda }+G_{\mathrm{m}}\left(\mathrm{\Lambda }+2\right)\right)},$$ (45)

where S_m = ɛ_mm/ɛ_ex. For a typical bilayer thickness of 5 nm, this condition holds for vesicle size below 100 nm. This prediction is in agreement with experimental studies of nanosized vesicles (68) that have reported only prolate deformations.

The oblate-prolate transition is independent of membrane properties; it is analogous to the one observed with drops (70,71). It is also independent of the viscosity ratio because the electrohydrodynamic flow stops at steady state due to the interface immobilization by gradients in the membrane tension.

The effective dipole theory does not predict the prolate-oblate transition

The effective dipole theory, summarized in Appendix C, models the cell as a sphere with effective permittivity. The theory successfully explains the dielectrophoresis and electrorotation of cells, because it correctly describes the perturbation due to the cell in the exterior electric field. However, the internal electric field is not physical, which leads to incorrect interior Maxwell stress and electric force distribution on the membrane. Accordingly, the predicted deformation is oblate at low frequencies (22), which is at odds with the experimental observations with vesicles (30).

Fig. 11 compares the predictions of our model and the effective dipole theory for the electric tractions. It shows that the two models agree at frequencies ω > ω₁, where the transmembrane potential has vanished. At low frequencies, where the field inside the vesicle is zero, the effective dipole theory would correctly predict the electric tractions if only the contribution from the exterior electric field is taken into account. However, at intermediate frequencies, where the vesicle interior participates in the conduction process and the transmembrane potential is still significant, i.e., ω ∼ ω₁, the effective dipole theory diverges from our model as well as experimental observations (30).

Figure 11.

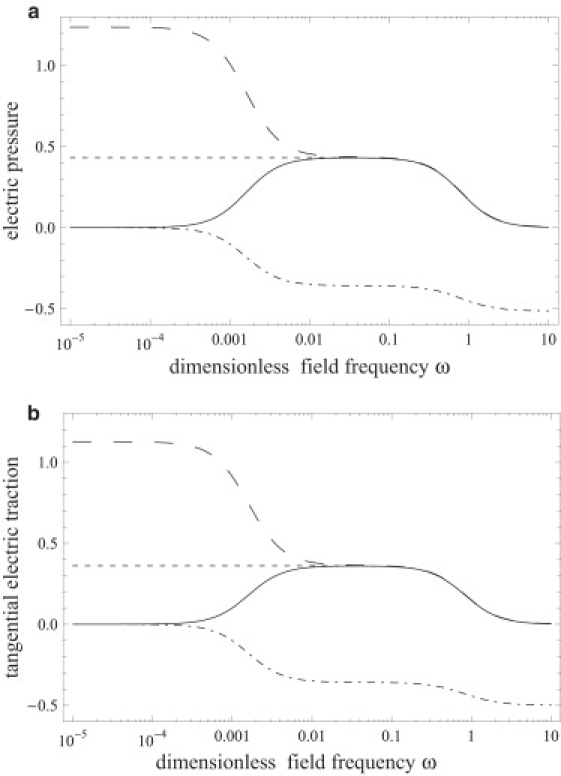
Electric tractions according to our model (solid line), the drop model (short-dashed line), the effective dipole theory (long-dashed line), and the only exterior field contribution in the effective dipole theory (dot-dashed line). (a) Electric pressure; (b) tangential traction component directed to the pole. Parameters are: Δ = 0.5, Λ = 1.5, x = 5 × 10⁻⁴, G_m = 0, C_m = 50, and Ca = 684.

Conclusions and Outlook

We have developed a theory that explains the observed morphological transitions of vesicles in a uniform AC electric field, in particular, the shape dependence on the field frequency and conductivity ratio between the inner and outer fluids. Prolate deformations at low frequencies have purely dielectric origin and result from electric pressure due to polarization charges pulling the vesicle at the poles. Oblate deformations, however, result from induced free surface charges, which cause negative pressure and transient electrohydrodynamic flow.

The prolate-oblate transition at low frequencies depends on the membrane capacitance and conductance. At high frequencies, electric stresses become negligible and do not affect the vesicle equilibrium quasispherical shape. The theory also predicts a high-frequency oblate-prolate transition, which is analogous to the one observed with drops: it is independent of the membrane electric properties and depends only on the conductivities of inner and outer fluids. The transition frequency, however, is not given by the Maxwell-Wagner polarization time, but is determined by electrohydrodynamics.

We have considered the problem of vesicle electrodeformation from a mechanical point of view. In this approach, vesicle shape is determined by balancing forces exerted on the interface, not by minimizing the bending and electrostatic energies as in earlier work. Thus, our formalism can be applied to study transient vesicle electrodeformation. Furthermore, it can be easily extended to electric fields of arbitrary symmetry as well as to situations in which both external electric and flow fields are present.

Our current theory is a first step in a systematic study of the electrohydrodynamics of deformable cells and, as such, some potentially important effects are neglected.

First, our treatment assumes that all media are electrically homogeneous and is based on solutions of Laplace's equation. This approach requires that the Debye length of the media is small compared to the radius of the vesicle or the thickness of the membrane. Thus, our theory might break down at low conductivities and frequencies. Electric double layers may also increase the membrane tension (25).

Second, the model does not include shear elasticity of the membrane, which is essential in the mechanics of the red blood cell (15).

Third, the membrane is assumed to be nonpermeable to ions. However, at low frequencies, the duration of the application of the electric field may be sufficient to porate the membrane (62). An electric current due to ion movement through field-induced pores would affect the electric field (27), and therefore vesicle shapes.

Last, but not least, the conductivity of the electrolyte solutions may exhibit frequency dispersion. Electrokinetic effects, the role of shear elasticity, membrane poration, and membrane charge represent interesting and challenging problems. We hope that our work will stimulate future research on these topics.

Appendix A: List of Symbols

Symbol	Description
Subscript r	Radial
Subscript θ	Tangential
Sub/superscript “el”	Electric
Sub/superscript “hd”	Hydrodynamic
Sub/superscript “mm”	Membrane
Sub/superscript “in”	Interior
Sub/superscript “ex”	Exterior
Superscript ∗	Complex conjugate
Re[…]	Real part of […]
Im[…]	Imaginary part of […]
a	Vesicle radius
Cm	Membrane capacitance
Ca	Capillary number
E	Electric field
fjm	Shape deformation parameter
Gm	Membrane conductivity
h	Membrane thickness
H	Mean curvature
p	Pressure
S	Permittivity ratio
t	Time
T	Bulk stress
v	Fluid velocity
Vm	Transmembrane potential
x = h/a	Dimensionless membrane thickness
Yjm	Spherical harmonic
η	Viscosity
ρ	Density
λ	Conductivity
ɛ	Permittivity
Λ	Conductivity ratio
χ	Viscosity ratio
ω1	Frequency of the prolate-oblate transition
ω2	Frequency corresponding to the inverse Maxwell-Wagner polarization time
Ω2	Frequency of the oblate-prolate transition
Φ	Electric potential
τ	Tractions
σ	Membrane tension
κ	Bending rigidity
Δ	Excess area

Appendix B: Spherical Harmonics

The normalized spherical scalar harmonics are defined as (72)

$$Y_{\text{jm}}\left(\theta ,\varphi \right)={\left[\frac{2j+1}{4\pi }\frac{\left(j-m\right)!}{\left(j+m\right))!}\right]}^{\frac{1}{2}}{\left(-1\right)}^{\mathrm{m}}{P}_{\mathrm{j}}^{\mathrm{m}}\left(\cos \theta \right)e^{\text{im}\varphi },$$ (46)

where (r, θ, ϕ) are the spherical coordinates, and P_j^m(cos θ) are the Legendre polynomials. For example,

$$Y_{10}=\frac{3}{\sqrt{4\pi }}\cos \theta \text{.}$$ (47)

Appendix C: Electrostatic Field and Stresses for a Spherical Shell

Our model: a sphere with interfacial capacitance and conductivity

Schwan (44) and Grosse and Schwan (64) have solved the problem for the electric field about a spherical shell with radius a and shell thickness h to obtain Eq. 8 for the potential difference between the inner and outer shell surfaces. Assuming a very thin shell h/a << 1, we can approximate the membrane with a two-dimensional interface that possesses capacitance. Accordingly, the spherical shell is approximated by a sphere with a discontinuous potential at the interface.

Solving Eq. 7 with the boundary conditions from Eqs. 8–10 leads to

$$\begin{array}{l}{\mathrm{\Phi }}^{\text{ex}}=-\left[r+P^{\text{ex}}{r}^{-2}\right]\text{exp}\left(\mathrm{i}\mathit{\omega }t\right)\cos \theta ,\hfill \\ {\mathrm{\Phi }}^{\text{in}}=-P^{\text{in}}r\text{exp}\left(\mathrm{i}\mathit{\omega }t\right)\cos \theta \text{.}\hfill \end{array}$$ (48)

where

$$\begin{array}{l}{P}^{\text{ex}}=d^{\mathrm{\infty }}\frac{\left(-k_{\text{in}}+k_{\text{ex}}\right)+k_{\text{in}}{V}_{\mathrm{m}}}{k_{\text{in}}+2k_{\text{ex}}},\hfill \\ P^{\text{in}}=d^{\mathrm{\infty }}{k}_{\text{ex}}\frac{3-2V_{\mathrm{m}}}{k_{\text{in}}+2k_{\text{ex}}},\hfill \end{array}$$ (49)

and k denote the dimensionless complex conductivities of the inner and outer fluids

$${\mathrm{k}}_{\text{in}}=\mathrm{\Lambda }+\mathrm{i}\omega \mathrm{S},{\mathrm{k}}_{\text{ex}}=1+\mathrm{i}\omega \text{.}$$ (50)

The tractions are computed from the Maxwell stress tensor. The radial (pressure) component is given by

$${\tau }_{\mathrm{r}}^{\text{el}}=\frac{1}{32\pi }\left[-2\left({\tau }_1^2+{\tau }_2^2\right)S+5{\tau }_3^2-2d^{\mathrm{\infty }}{\tau }_3+5{\tau }_4^2+2{\left(d^{\mathrm{\infty }}\right)}^2\right],$$ (51)

and the tangential (shearing) component is

$${\tau }_{\theta }^{\text{el}}=\frac{3}{8\pi }\left[\left({\tau }_1^2+{\tau }_2^2\right)S+2{\tau }_3^2+\left(d^{\mathrm{\infty }}\right){\tau }_3+2{\tau }_4^2-{\left(d^{\mathrm{\infty }}\right)}^2\right],$$ (52)

where τ₁ = Re[Pⁱⁿ], τ₂ = Im[Pⁱⁿ], τ₃ = Re[P^ex], and τ₄ = Im[P^ex]. Re[ ] and Im[ ] denote real and imaginary part. Taking the zero-thickness limit, x = 0, our solution reduces to the result for a spherical drop (70):

$${\tau }_{\mathrm{r}}^{\text{el},\text{drop}}=\frac{3}{8}\left(1+{\mathrm{\Lambda }}^2-2S+{\left(S-1\right)}^{2}S{\omega }^2\right){\left(2+S\right)}^2{\left({\omega }^2+{\mathit{\omega }}_2^2\right)}^{-1},$$ (53)

$${\tau }_{\theta }^{\text{el},\text{drop}}=-\frac{9}{2}\left(\mathrm{\Lambda }-S\right){\left(2+S\right)}^2{\left({\mathit{\omega }}^2+{\mathit{\omega }}_2^2\right)}^{-1},$$ (54)

where ω₂ is given by Eq. 35

The effective charge density is calculated from Eq. 9 as

$$\mathrm{Q}\left(\omega ,t\right)={\mathrm{q}}_{\mathrm{c}}\left(\omega \right)\text{cos}\left(\omega t\right)+{\mathrm{q}}_{\mathrm{s}}\left(\omega \right)\text{sin}\left(\omega t\right),$$ (55)

where

$${\mathrm{q}}_{\mathrm{s}}\left(\omega \right)=2{\tau }_4+\mathrm{S}{\tau }_2,{\mathrm{q}}_{\mathrm{s}}\left(\omega \right)={\mathrm{d}}^{\mathrm{\infty }}-2{\tau }_3-\mathrm{S}{\tau }_1\text{.}$$ (56)

The frequency dependence of the charge density can be cast into the form

$$Q\left(\mathit{\omega },t\right)=\overline{Q}\left(\mathit{\omega }\right)\cos (\mathit{\omega }t+\psi ),$$ (57)

where the amplitude is $\overline{Q}\left(\mathit{\omega }\right)={\left[q_{\mathrm{s}}+q_{\mathrm{c}}\right]}^{\frac{1}{2}}$, and the phase shift is ψ = q_s/q_c.

The effective sphere model

The dipole theory models the cell as a sphere with an effective permittivity (12,13)

$$k_{\text{in}}^{\text{eff}}=k_{\text{in}}\left[{\left(1-x\right)}^{-3}+2\frac{k_{\text{in}}-k_{\text{mm}}}{k_{\text{in}}+2k_{\text{mm}}}\right]{\left[{\left(1-x\right)}^{-3}-\frac{k_{\text{in}}-k_{\text{mm}}}{k_{\text{in}}+2k_{\text{mm}}}\right]}^{-1},$$ (58)

where

$${\mathrm{k}}_{\text{in}}=\mathrm{\Lambda }+\mathrm{i}\omega \mathrm{S},{\mathrm{k}}_{\text{mm}}={\mathrm{\Lambda }}_{\text{mm}}+\mathrm{i}\omega {\mathrm{S}}_{\text{mm}}\text{.}$$ (59)

The electric field is described by an electric potential

$${\mathrm{\Phi }}^{\text{ex}}=-d^{\mathrm{\infty }}\left[r+r^{-2}\frac{\left(-k_{\text{in}}^{\text{eff}}+k_{\text{ex}}\right)}{k_{\text{in}}^{\text{eff}}+2k_{\text{ex}}}\right]\cos \theta ,{\mathrm{\Phi }}^{\text{in}}=-r{d}^{\mathrm{\infty }}{k}_{\text{ex}}\frac{3}{k_{\text{in}}^{\text{eff}}+2k_{\text{ex}}}\cos \mathit{\theta ,}$$ (60)

where a continuity of the potential across the interface is assumed.

Supporting Material

Supporting text, equations, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00785-1.