Abstract
In the last decades, it has been demonstrated that many animal species orient in the Earth magnetic field. One of the best-studied examples is the use of the geomagnetic field by migratory birds for orientation and navigation. However, the biophysical mechanism underlying animal magnetoreception is still not understood. One theory for magnetoreception in birds invokes the so-called radical-pair model. This mechanism involves a pair of reactive radicals, whose chemical fate can be influenced by the orientation with respect to the magnetic field of the Earth through Zeeman and hyperfine interactions. The fact that the geomagnetic field is weak, i.e., ∼0.5 G, puts a severe constraint on the radical pair that can establish the magnetic compass sense. For a noticeable change of the reaction yield in a redirected geomagnetic field, the hyperfine interaction has to be as weak as the Earth field Zeeman interaction, i.e., unusually weak for an organic compound. Such weak hyperfine interaction can be achieved if one of the radicals is completely devoid of this interaction as realized in a radical pair containing an oxygen molecule as one of the radicals. Accordingly, we investigate here a possible radical pair-based reaction in the photoreceptor cryptochrome that reduces the protein's flavin group from its signaling state FADH• to the inactive state FADH– (which reacts to the likewise inactive FAD) by means of the superoxide radical, O2•–. We argue that the spin dynamics in the suggested reaction can act as a geomagnetic compass and that the very low physiological concentration (nM-μM) of otherwise toxic O2•– is sufficient, even favorable, for the biological function.
Introduction
Many animal and even plant species have been shown to react to magnetic fields (for reviews, see (1–8)). Birds, for instance, seem to use the geomagnetic field for navigation during migration (2). The typical strength of the geomagnetic field is 0.5 G or 50 μT, putting constraints on possible physical mechanisms of magnetoreception. Two models have attracted much attention, one involving magnetic particles (8–14) in a bird's beak, the other a magnetosensitive radical-pair reaction (7,15–20) in a bird's eye. The idea behind the latter mechanism, referred to as the radical pair mechanism (7,18–21), is that, in the course of a photochemical reaction in the retina, a pair of reactive radicals is produced, the reaction yield of which is influenced by the orientation of the bird with respect to the geomagnetic field and which, in turn, modulates visual perception.
Experimental observations speak strongly for the involvement of the radical pair mechanism in the magnetic compass sense of birds. For example, it was shown that the avian compass is an inclination one, i.e., sensitive only to the inclination of the Earth's magnetic field lines and not to their polarity (13,22–24). The avian compass is also known to be highly sensitive to the strength of the ambient magnetic field, requiring a period of acclimation before orientation can occur at intensities differing from those of the natural geomagnetic field (25). Furthermore, the avian compass is light-dependent, as first suggested by theory (15,17), normally requiring light in the blue-green range to function properly (26,27). The avian compass is supposedly localized in the right eye of migratory birds (28). A radical pair model in which a light-driven, magnetic-field-dependent chemical reaction in the eye of a bird modulates the visual sense indeed predicts these properties (7,15–18,20,21,29–31).
The radical-pair mechanism has been studied for a variety of model systems (7,15,16,18,30,32–36) and it was demonstrated that hyperfine, exchange, dipole-dipole, and Zeeman interactions acting on the electron spins can induce magnetic field effects in the reaction yields. The hyperfine interaction in a radical pair is determined by contributions from both radical partners, and the typical values of the individual coupling constants in organic radical pairs are ∼1–10 G (37–40). The effect of weak magnetic fields of ∼0.5 G, also known as the low-field effect, has been extensively discussed (16,31). It was shown that, to elicit a noticeable change in the reaction yield in the geomagnetic field, the hyperfine coupling interaction in the radical pair should be comparable with the Zeeman interaction (7,18,38). This puts a severe constraint on the radical pair involved in the magnetic compass sense of a bird as overall hyperfine coupling for organic radicals is typically in the 10–100 G range. The hyperfine interaction in the radical pair can be decreased, of course, if one of the radical partners is devoid of this interaction. This can be realized in a radical pair containing an oxygen molecule as one of the radicals, because oxygen atoms possess zero nuclear spin and, hence, no hyperfine coupling.
The search for the radical pair involved in the magnetic sense of birds as well as the underlying chemical reaction started three decades ago, after the radical pair mechanism was suggested as a candidate explaining this sensory capability (15,16). The most promising idea, widely discussed at present, is that the radical pair mechanism linked to the avian compass arises in the protein cryptochrome (7,18,19,38,41–43). Cryptochrome is a signaling protein found in a wide variety of plants and animals (44–47). Its role varies among organisms, from the entrainment of circadian rhythms in vertebrates to the regulation of hypocotyl elongation and anthocyanin production in plants (48–50). It was demonstrated that cryptochrome harbors blue-light-dependent radical pair formation and that it is localized in the retinas of some migratory birds (42,43) where its effects could intercept the visual pathway. There is strong evidence showing that retinal cryptochrome-expressing neurons and a forebrain region called “Cluster N” are highly active during magnetic compass orientation and require light for function. The differences in activation between migratory and nonmigratory birds have been documented (51–53), strongly supporting the idea that cryptochrome is involved in avian magnetoreception.
Cryptochrome binds the chromophore flavin adenine dinucleotide (FAD) (44,46,54). The protein is activated and performs its function when the fully oxidized FAD form is converted to the semireduced FADH• form (41,47,55–57). The conversion happens in the course of light-induced electron transfers involving a chain of three tryptophans that bridge the space between FAD and the protein surface (41,58,59).
The photoexcitation cycle of cryptochrome can be depicted as shown in Fig. 1. The flavin cofactor was observed in Arabidopsis thaliana cryptochrome (54) in three interconvertible redox forms, FAD, FADH•, and FADH– (56,57,59–61). It was demonstrated that the FAD form is inactive (nonsignaling) and accumulates to high levels in the dark. Blue light triggers photoreduction of FAD to establish a photoequilibrium that favors FADH• over FAD or FADH–. In plant cryptochromes, the biologically active signaling state FADH• can absorb a second, green light, photon, and be then converted to a fully reduced, inactive form, which reoxidizes in the dark to the original FAD resting state (56,60–62). The described photocycle was generalized for animal and human cryptochromes (60).
Figure 1.
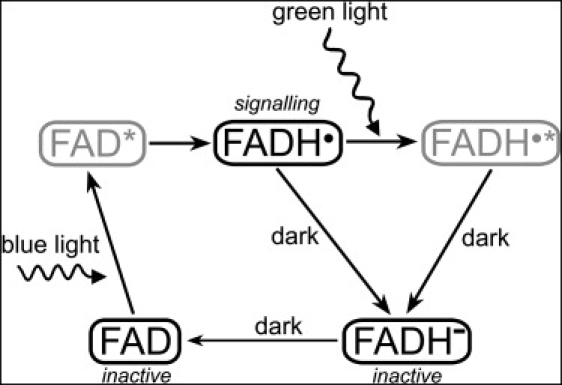
Light-induced photocycle in cryptochrome. The signaling state of cryptochrome is controlled by the oxidation state of its flavin cofactor FAD, which exists in three interconvertible redox forms, FAD, FADH•, and FADH– (56,60,61). The FAD form is inactive (nonsignaling) and accumulates to high levels in the dark. Blue light triggers photoreduction of FAD to establish a photoequilibrium that favors FADH• over FAD or FADH–. The semiquinone FADH• state corresponds to the signaling state of the protein. Green light photons can further be absorbed by the radical FADH• and shift the photoequilibrium to the fully reduced form (FADH–), which is inactive (nonsignaling). The FAD → FADH• and FADH• → FADH– reactions involve an active FADH• radical and, therefore, can be affected by an external magnetic field. The excited states of the flavin cofactor, FAD∗ and FADH•∗, colored gray, arise as short-lived intermediate stages of the cryptochrome photocycle.
The FAD → FADH• and FADH• → FADH– reactions in Fig. 1 involve an active FADH• radical and, therefore, can be manipulated by an external magnetic field. We have recently studied computationally the forward electron transfer process, i.e., FAD → FAD∗ → FADH•, in cryptochrome, and demonstrated that magnetic fields of ∼5 G can significantly influence its signaling state, although requiring suitable electron transfer rates to do so (7). Here we want to argue that the dark backreaction is better suited to endow cryptochrome with magnetotactic capabilities.
Under aerobic conditions, the stable FADH• molecule slowly reverts to the initial FAD state (41,55,56,60) (see Fig. 1). This process is not well understood and occurs on the millisecond timescale (41,55,56). The cryptochrome backreaction attracted considerable attention recently, due to indications that it is linked to avian magnetoreception. It was proposed that, during the backreaction, a radical pair is formed between flavin and an oxygen molecule and that the radical pair reaction responds significantly to reorientation in the Earth magnetic field (19,20,63). Moreover, the presence of molecular oxygen in the backreaction of cryptochrome was demonstrated in vitro (56). It was also suggested that reoxidation of the photochemically reduced flavin cofactor in flavoproteins is mediated by molecular oxygen (64).
The hypothesis that an oxygen molecule is involved in magnetoreception still needs to be verified experimentally. However, this idea is clearly promising because the oxygen radical is devoid of hyperfine coupling, which leads to an enhancement of magnetic field effects. In addition, such a radical pair (where one radical has no hyperfine coupling) would be consistent with studies on the effects of weak radio-frequency oscillating magnetic fields on migratory bird orientation. Ritz and co-workers not only found that appropriate orientation behavior depends on the strength and angle of the oscillating field, but also that the minimum field strength necessary to disrupt orientation depends on the frequency of the oscillating field in a resonancelike behavior that would be predicted by such a radical pair (63,65–67).
In this article, we are suggesting that the reaction with FADH• actually involves the superoxide radical O2•–. The superoxide radical O2•– occurs widely in nature (64,68,69) and can be obtained as the product of the one-electron reduction of dioxygen. O2•– is toxic to cells and under physiological conditions is available only in nM-μM concentrations (70,71). The reaction of the semiquinone FADH• state of the flavin cofactor in cryptochrome with O2•– is schematically shown in Fig. 2. The molecular oxygen radical O2•– enters the molecular pocket in cryptochrome, depicted in Fig. S1 in Supporting Material, with a rate constant kox, creating a radical pair [FADH• + O2•–], which can be either in a singlet or a triplet state, as denoted by 1[ ⋯ ] or 3[ ⋯ ], respectively. The rate constant kox corresponds to the rate of random encounters of FADH• and O2•–, which is expected to occur on a timescale significantly longer than that for geminate processes in the radical pair (72). If the radical pair is found in its singlet state, the electron from the O2•– radical should transfer to the FADH• radical, since the energy of the 1[FADH– + O2] state is lower than the energy of the 1[FADH• + O2•–] state. The energy difference between the two states is ΔE = 0.37127 eV, according to an ab initio density functional theory calculation (73,74) performed by us. In Supporting Material, we provide details of this calculation. The electron transfer is only possible from the singlet state of the radical pair, the corresponding rate constant being depicted in Fig. 2 as ket. The triplet state 3[FADH– + O2] can only produce FADH– after it is converted to the singlet state 1[FADH– + O2].
Figure 2.
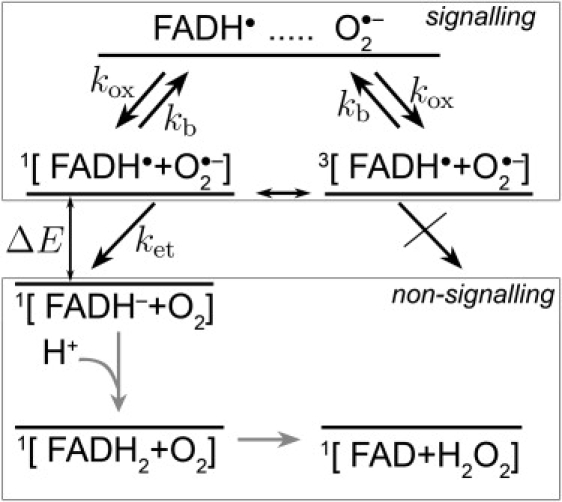
Schematic presentation of the postulated reaction scheme involving the flavin cofactor FADH• in cryptochrome and a molecular oxygen radical (superoxide) O2•–. Superoxide enters the molecular pocket of cryptochrome (see Fig. S1) with a rate constant kox, forming a radical pair [FADH• + O2•–], which is found in a singlet (25%) or a triplet (75%) state, denoted by 1[ ⋯ ] or 3[ ⋯ ], respectively. An external magnetic field as well as the hyperfine coupling interaction brings about an interconversion between the singlet and the triplet states of the radical pair. If the radical pair is in its singlet state, the electron from the O2•– radical can transfer to the FADH• radical, forming the singlet 1[FADH– + O2] state, which has lower (by ΔE = 0.37127 eV) energy than the initial 1[FADH• + O2•–] state; the corresponding electron transfer rate constant is ket. The electron transfer is not possible from the triplet state of the radical pair, due to spin conservation during the transfer. The radical pair can separate, i.e., the O2•– radical escapes (with a rate constant kb) from the molecular pocket before electron transfer occurs, leaving cryptochrome then in its signaling state. The nonsignaling FADH– state is transformed to the FAD resting state, possibly by subsequent protonation and release of a hydrogen peroxide molecule as suggested in Prabhakar et al. (64).
The external magnetic field and the hyperfine interaction affect the interconversion between the singlet and the triplet states of the radical pair in a manner that depends on the orientation in the Earth magnetic field. Once the FAD cofactor is reduced to the FADH– state, cryptochrome stops signaling, because the reaction FADH• + → FADH– + O2 is considered irreversible. However, before this reaction occurs, the radical pair may separate, namely, if the O2•– radical escapes from cryptochrome's molecular pocket, leaving cryptochrome then still in its signaling state. The escape reaction is governed by the rate constant kb and can occur equally likely from either the singlet or the triplet state of the radical pair, as depicted in Fig. 2. Thus, cryptochrome remains in its signaling state until another O2•– radical arrives, and the FADH• radical can be reduced again. The separation and reencounter of O2•– delay the magnetic field-dependent reaction, shifting it to the millisecond timescale, i.e., the timescale relevant for biological signaling.
The FADH– molecule in the reaction FADH• + → FADH– + O2 (see Fig. 2) is an intermediate of the FADH• → FAD reaction depicted in Fig. 1. Although the reaction shown in Fig. 2 looks similar to the FADH•∗ → FADH– photoinduced reaction in Fig. 1, the two reactions are different since the FADH•∗ → FADH– reaction involves the excited state FADH•∗, which is brought about by absorption of green light (see Fig. 1).
Here we focus on the influence of the applied magnetic field on the FADH• + → FADH– + O2 reaction depicted in Fig. 2. In Fig. 2, we also show how the nonsignaling FADH– state can be transformed to the original FAD resting state. The FADH– → FAD reaction does not involve a radical pair and, therefore, is not expected to be magnetic-field-dependent. The latter reaction is consistent with a theoretical study on glucose oxidase, where the reaction O2 + FADH2 → H2O2 + FAD has been suggested to arise (64).
In this article, we seek to investigate the suggested radical pair scenario (see Fig. 2) in cryptochrome involving superoxide. The goal is to provide a proof of principle that the FADH• + → FADH– + O2 reaction can act as a geomagnetic compass. Indeed, we demonstrate that a field of 0.5 G can produce effects that depend significantly on the orientation of the radical pair in the Earth magnetic field.
Theory
In this section, the computational description of the magnetic field dependence in the cryptochrome [FADH• + O2•–] radical pair reaction is outlined.
Density matrix
Once the radical pair is generated as depicted in Fig. 2, one can describe its spin state by a density matrix ρ(t), the time evolution of which is governed by the stochastic Liouville equation (7,18,75):
| (1) |
Here, denotes the spin Hamiltonian of the radical pair, and kb and ket are the rate constants for the O2•– escape process and for the electron transfer process as shown in Fig. 2. [A, B]± = AB ± BA denotes the commutator and anticommutator, respectively.
and in Eq. 1 are the projection operators onto the singlet and triplet states of the electron spin pair,
| (2) |
| (3) |
where and denote the electron spin operators of the FADH• and O2•– radicals, respectively. Using the relation , Eq. 1 can be rewritten
| (4) |
which allows one to express the density matrix in the form
| (5) |
Here ρ(0) is the density matrix describing the radical pair at the time of encounter. At the initial stage of the FADH• reduction reaction, the probability to find the FAD cofactor in its semiquinone FADH• state equals unity. Therefore, when [FADH• + O2•–] radical-pair partners encounter for the first time, the initial density of the radical pair is
| (6) |
Here Tr[A] denotes the trace of matrix A, N is the number of spin states in the system, and EN is the unity matrix of dimension N. The superscript “(1)” indicates that the initial condition given in Eq. 6 corresponds to the first encounter of the FADH• and O2•– radicals. Substituting Eq. 6 into Eq. 5, one can numerically calculate the time evolution of the density matrix.
Radical-pair Hamiltonian
The Hamiltonian for the radical pair, , in Eq. 5 is the sum of two Hamiltonians, one for each radical, e.g., a Hamiltonian for FADH• and a Hamiltonian for O2•–. In addition, a Hamiltonian arises that accounts for the exchange and dipolar interactions within the radical pair. Accordingly, the total Hamiltonian is partitioned
| (7) |
As explained in the literature (7,16,18), the Hamiltonians and are composed of Zeeman interaction and hyperfine coupling interaction terms and can be written
| (8) |
| (9) |
where is the spin operator of nucleus i, are the electron spin operators defined as
| (10) |
| (11) |
where are the Pauli spin matrices (76) acting on the electron spins of FADH• and O2•–, and E2 is the 2 × 2 identity matrix. The first tensor factor in Eq. 10 acts on the electron spin of FADH• and the second factor on the nuclear spin of FADH•; the operators in Eq. 11 act on the electron spin of O2•–.
In Eq. 8, is the hyperfine coupling tensor for nucleus i, μB = 5.78843 × 10−9 eV/Gauss is the Bohr magneton, and
| (12) |
is the external magnetic field. The operator in Eqs. 8 and 9 is the so-called g-tensor, which can be brought to diagonal form in an appropriate coordinate frame (7). The diagonal values of the g-tensor are chosen to be gii ≡ g = 2 for both radicals. Note that since both oxygen atoms in the O2•– radical have nuclear spin 0, the O2•– radical is devoid of hyperfine coupling and, therefore, interacts through its unpaired electron spin only with the external magnetic field (see Eq. 9).
For the radical-pair spin dynamics to be sensitive to different alignments with respect to the magnetic field, it is necessary that the hyperfine coupling tensor is anisotropic (18,38). The choice of the hyperfine coupling tensor in our model is explained in the Supporting Material.
In addition to the Zeeman and hyperfine interactions, one needs to account also for electron-electron exchange and dipolar interactions in the radical pair, which is done through the term in Eq. 7. The interaction in plays an important role when the distances between the radicals are small. In the Supporting Material, we argue that the term in the [FADH•+O2–] radical-pair Hamiltonian can be neglected.
Duration of the FADH• + →FADH– + O2 reaction
The radical pair evolves with time and decays either into the 1[FADH– + O2] state or to the initial, i.e., separated, FADH•…O2•–, state as indicated in Fig. 2. The probability of one or the other decay is influenced by the magnetic field as detailed below. If the FAD cofactor is reduced to the FADH– state then the protein stops signaling and the FADH• + →FADH–+O2 reaction is completed. However, if the radical pair is terminated through escape of the O2•– radical from the cryptochrome pocket (see Fig. S1) before the electron transfer process occurs, cryptochrome is left in its signaling state. The cryptochrome remains in the signaling state, until another O2•– radical arrives, and the FADH• radical can be reduced again.
The expected value of the reaction duration time 〈τ〉 can be calculated as
| (13) |
where α is the probability that an FADH• + O2•– encounter actually leads to reduction of FADH• and to an end of cryptochrome signaling and is magnetic-field-dependent. Equation 13 is derived in the Supporting Material. The analysis of 〈τ〉 at different magnetic field strengths and different orientations of the magnetic field vector is the primary goal of this article, and is discussed in the following section.
Results and Discussion
Theory and methods described above have been used to study the duration of the FADH• + → FADH– + O2 reaction in cryptochrome (see Fig. 2). In the following, the magnetic field dependence of the reduction of cryptochrome's FAD cofactor into its FADH– state is analyzed by means of the reaction duration time 〈τ〉 stated in Eq. 13. The value 〈τ〉 is studied as a function of magnetic field strength B0 and it is demonstrated that in weak magnetic fields, comparable with typical geomagnetic fields, this time can change significantly upon reorientation in the field. The dependence of 〈τ〉 on the magnetic field strength is also analyzed. It is shown that 〈τ〉 satisfies all conditions necessary for the construction of an animal's inclination compass.
Magnetic field dependence of reaction time
Fig. 3 shows the relative duration 〈τ〉/〈τ0〉 of the FADH• + → FADH– + O2 reaction as a function of external magnetic field strength B0, calculated for different values of the electron transfer rate constant ket and for different values of the O2•– radical escape rate constant kb. The value 〈τ〉 is evaluated according to Eq. 13 and 〈τ0〉 is the duration of the reaction at zero magnetic field. For this evaluation, the z axis of the radical pair is assumed to be aligned at an angle of 36°, with respect to the magnetic field vector.
Figure 3.
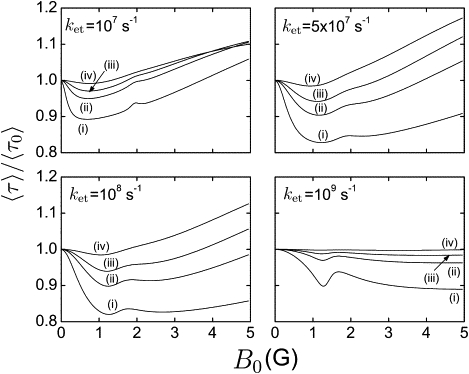
Relative reaction time 〈τ〉/〈τ0〉 of the FADH• + →FADH– + O2 reaction. The reaction time is shown as a function of the external magnetic field strength B0, calculated for different values of electron transfer rate constants ket and for different values of the escape rate constant kb: i), kb = 106 s–1; ii), kb = 3 × 106 s–1; iii), kb = 5 × 106 s–1; and iv), kb = 107 s–1. 〈τ〉 has been evaluated according to Eq. 13; 〈τ0〉 is the duration of the reaction at zero magnetic field. The z axis of the radical pair is assumed to be aligned at an angle of 36° with respect to the applied magnetic field.
As seen in Fig. 3, the dependence of 〈τ〉 on B0 is nonmonotonic and magnetic fields weaker than 0.5 G can produce a significant change in the reaction duration time. The effect of a 0.5 G magnetic field is most pronounced for the smallest O2•– radical escape rates presented in Fig. 3, namely, for kb = 106 s–1. When the escape rate constant is large (≳ 3 × 106 s−1), the radical pair separates too fast, preventing significant singlet↔triplet mixing and, hence, a magnetic field effect.
The rate constant kb is expected to be ∼106 s–1 in reality, since this is a radical pair decay rate constant characteristic for biological systems (7,18,77). For instance, by means of flash photolysis it was demonstrated (36,77) that radical pairs in a protein environment have either reacted with their geminate partner or succeeded in separating after 1–2 μs. On the other hand, one can assume that the rate constant kb developed in the course of evolution such that it furnishes today a maximal magnetic field effect.
The duration 〈τ〉 of the reduction reaction also depends on the electron transfer rate constant ket. Fig. 3 shows that the largest relative change in 〈τ〉 at 0.5 G is expected for ket = 108 s–1, which is a realistic value for the electron transfer in proteins. For example, this ket matches the experimentally determined value of the electron transfer rate constant in the tryptophan chain of DNA photolyase (78,79) and is close to the value estimated in Solov'yov et al. (7) for the same process. ket = 108 s–1 is also of the same order of magnitude as the singlet↔triplet interconversion rate for typical radical pairs (80). In Solov'yov et al. (7), it was shown that the singlet↔triplet interconversion rate constant in a radical pair with one spin-1/2 nucleus is ∼8.3 × 107 s–1.
The dependence of 〈τ〉 on B0 (see Fig. 3) due to singlet ↔triplet state mixing is brought about by a competition between Zeeman and hyperfine interaction as well as the decay processes described by ket and kb. The fact that 〈τ〉 experiences the most pronounced changes at realistic values ket = 108 s–1 and kb = 106 s–1 supports the choice of hyperfine coupling constants in our model and demonstrates the feasibility of the suggested magnetoreception mechanism. The chosen model for the putative [FADH• + O2•–] radical pair involves hyperfine coupling constants that are of the same order of magnitude as the known hyperfine coupling constants in the FADH• radical (37–40).
For the particular values of hyperfine coupling used in this article, the calculation predicts an enhancement in the duration of the reduction reaction of ∼18%, which for ket = 108 s–1 and kb = 106 s–1 is expected for a magnetic field strength of ∼1.25 G (see Fig. 3). This enhancement shows that significant magnetic field effects in the reduction reaction at Earth magnetic field strengths are possible.
Angular dependence of reaction time
To obtain directional information from the geomagnetic field, the reaction time must exhibit variation with respect to reorientation of cryptochrome in the external magnetic field. Such orientational dependence could modulate the visual sense of a bird to produce the avian magnetic compass, as described in Ritz et al. (18). Fig. 4 shows the relative duration, 〈τ〉/〈τ0〉, of the FADH• + → FADH– + O2 reaction calculated as a function of the direction of the magnetic field vector, characterized by the angle θ (see Eq. 12). 〈τ〉/〈τ0〉 in Fig. 4 is calculated for an external magnetic field of 0.5 G for different values of the electron transfer rate constant ket and for different values of the rate constant kb. The value 〈τ0〉 is the duration time of the reduction reaction at θ = 0°.
Figure 4.
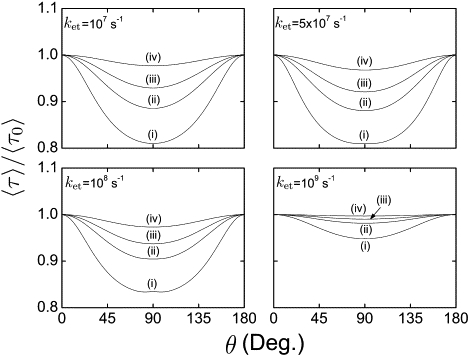
Relative reaction time 〈τ〉/〈τ0〉 of the FADH• + →FADH– + O2 reaction serving as an inclination compass. The reaction time has been evaluated as in Fig. 3 for different directions of the applied magnetic field characterized by the angle θ (see Eq. 12). The assumed strength of the applied magnetic field B0 is 0.5 G, i.e., the value characteristic for the geomagnetic field.
The angle θ between the z axis of the radical pair and the magnetic field varies from 0° to 180°. As seen in Fig. 4, the dependence of 〈τ〉 on θ is symmetric with respect to θ = 90°. This symmetry derives from a nearly isotropic distribution of the nuclear spins in the initial state of the radical pair and renders the magnetic-field-dependent reaction to be an inclination compass (16). An inclination compass should not distinguish between the angles θ and 180° – θ (13) and, therefore, any inclination compass-based receptor should produce identical signals at these two orientations.
The results show that the variation (through reorientation) in the reaction duration 〈τ〉 can be as large as 19% for the external field of 0.5 G. The largest change in 〈τ〉 is expected for rate constants ket = 5 × 107 s–1 and kb = 106 s–1; for rate constants ket = 108 s–1 and kb = 106 s–1, it measures 17%.
As noted already, for the studied radical pair reaction to be sensitive to reorientation in the external magnetic field, it is necessary to employ an anisotropic hyperfine coupling tensor. Such an anisotropy is perfectly realized in the FADH• radical, where the hyperfine interaction is dominated by two strong axially anisotropic 14N hyperfine couplings (38). In our model, we introduce anisotropy of the hyperfine coupling tensor (see the Supporting Material) to qualitatively describe this effect. The actual orientation dependencies shown in Fig. 4 stem from the simplicity of the model assumed, and are intended to demonstrate only that a significant magnetic compass effect can be expected at 0.5 G and that the suggested reaction leads to an inclination compass.
It is interesting that in magnetic fields of 0–5 G the duration of the FADH• + → FADH– + O2 reaction in cryptochrome can be enhanced by ∼22%. Fig. 5 illustrates this by showing 〈τ〉/〈τ0〉 calculated as a function of the angle θ between magnetic field and radical pair and for different field strengths. In this calculation the electron transfer rate constant and the O2•– radical escape rate constant are assumed again to be ket = 108 s–1 and kb = 106 s–1. Fig. 5 shows that the most pronounced change in 〈τ〉 is expected for magnetic field strengths of 1.14 G and 5 G. This suggests that in a system with slightly different hyperfine interaction than assumed in the present model, the influence of an external magnetic field on the reduction reaction at 0.5 G might be stronger than seen here, i.e., leads to a maximal angular variation of up to 22%.
Figure 5.
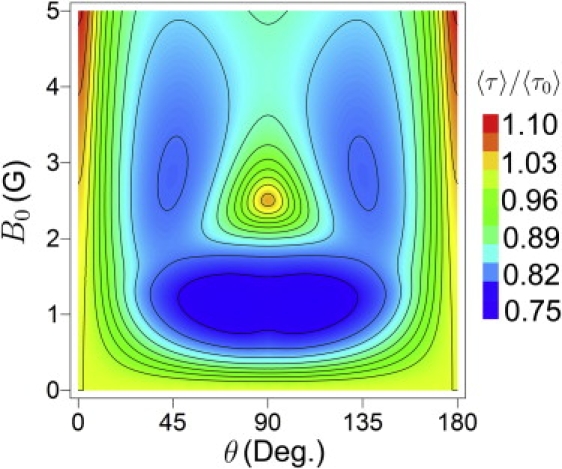
Relative time 〈τ〉/〈τ0〉 of the FADH• + → FADH– + O2 reaction calculated as a function of magnetic field orientation and field strength. The calculations were done as for Figs. 3 and 4 with electron transfer rate constant ket = 108 s–1 and O2•– escape rate constant kb = 106 s–1. The value 〈τ0〉 is the duration of the reduction reaction calculated at B0 = 0 G and θ = 0°.
The result shown in Fig. 5 is in qualitative agreement with the observation that the avian compass operates only in a narrow range of field intensities, while for field intensities differing from the natural geomagnetic field, birds require a certain time for adaptation (25). Such behavior is only possible if the putative receptor functions differently at different field intensities. An explanation of the experimental observation was given in Ritz et al. (18), where it was suggested that, with increase of the magnetic field strength, the action of the magnetic sensor should become less pronounced and that, therefore, a bird requires more time to find the correct flight direction. However, a bird might also become disoriented for a certain period of time if the magnetic sensor suddenly starts operating differently.
Conclusion
The hypothesis that the magnetic sense in animals is related to the photoreceptor cryptochrome has been suggested in several studies (4,7,18–20) and is pursued in this study, too. Experimental observations speak strongly for the involvement of the radical-pair mechanism in animal magnetoreception. Such a magnetic field-sensing mechanism can explain many long-observed properties of avian magnetoreception (1,2,18,23,24). The fact that the geomagnetic field is ∼0.5 G puts a severe constraint on the radical pair involved in the magnetic compass sense. For a noticeable change of the reaction yield in a redirected geomagnetic field, the hyperfine interaction has to be of the same strength as the Zeeman interaction due to the geomagnetic field, i.e., has to be unusually low for organic molecules. Such weak hyperfine coupling can be achieved, however, if one of the radicals is devoid of hyperfine interactions altogether, as realized in a radical pair containing the oxygen molecule as one of the radicals. Accordingly, we investigated here a possible radical-pair-based reaction in cryptochrome that reduces cryptochrome's FAD cofactor in its FADH• oxidation state by means of the superoxide radical O2•– and, thereby, shifts the protein from its signaling to its inactive state.
For this purpose we studied computationally whether a weak (i.e., the Earth's) external magnetic field can alter the duration of cryptochrome's FADH• + → FADH– + O2 reaction. For a simple radical pair model, we demonstrated that the suggested reaction can act as a geomagnetic inclination compass by showing that a field of 0.5 G produces effects that vary significantly during reorientation of cryptochrome.
To our knowledge, this article presents the first attempt to demonstrate how the FADH• + →FADH– + O2 reaction of cryptochrome may be influenced by an external magnetic field and be linked to avian magnetoreception. Therefore, we illustrate the feasibility of the suggested magnetoreception mechanism here only qualitatively, rather than describing the mechanism in quantitative detail.
The main assumption made—namely, that superoxide is involved in magnetoreception—still has to be verified experimentally, as such involvement has been corroborated so far only indirectly. The involvement of a radical pair in which one of the radical partners is devoid of the hyperfine interaction in the magnetoreception process is consistent with studies on the effects of weak radio-frequency oscillating magnetic fields on migratory bird orientation (63,65–67), investigations that had been inspired by earlier theoretical work (18,81,82). Another argument, that speaks for the suggested reaction is its robustness. Indeed, the suggested reaction is much simpler than the magnetic field-dependent reactions that have been suggested earlier (7) and, therefore, is expected to function more reliably in a weak magnetic field. The involvement of superoxide in magnetoreception is a clearcut suggestion that should attract experimental investigation.
The purpose of the suggested model is to provide a framework that connects the molecular magnetoreception mechanism to animal behavior. The model presented here links existing experiments to the mechanism, and points to new experiments that can be performed to test our rationale.
A key aspect of the proposed mechanism is the involvement of the superoxide radical. In this regard, experiments in vitro can study the change of cryptochrome activity in an applied magnetic field by varying the concentration of oxygen. It is also important to continue studies of bird behavior in radio frequency magnetic fields. The superoxide radical is devoid of hyperfine interactions and, therefore, its unpaired electron should exhibit a resonance behavior at a Larmor frequency for a free electron.
Clearly a controversial aspect of our suggestion is the involvement of superoxide, O2•–, in the magnetic-field-dependent backreaction of cryptochrome. It seems odd that an organism should relay on a toxic substance for a sensory mechanism. However, one should note that superoxide arises naturally in organisms, and is well controlled by superoxide dismutase (83–85), which keeps the concentration of superoxide low. This low concentration level, though, is key to the suggested mechanism as the reaction back to the nonsignaling state of cryptochrome should be slow, i.e., should take ∼10 ms (41,55). Such slow rate of diffusion-controlled encounter is ensured through the small O2•– concentration. The formation rate of the encounter pair [FADH• + O2•–], kox, can be estimated through the well-known diffusive encounter rate (which applies strictly only for a homogeneous three-dimensional space surrounding an encounter sphere)
| (14) |
where D ≈ 2 × 10−5 cm2/s is the oxygen diffusion coefficient in water (86), L ≈ 20 Å is the size of the molecular pocket in cryptochrome (see Fig. S1), and [O2•–] is the concentration of the superoxide radical in the cell. At a concentration of [O2•–] = 3 nM, which is tolerable to an organism (70,71), the formation of FADH• + O2•– is estimated to take ∼τox = 1/kox = 1.1 ms, which is indeed the time needed for the suggested mechanism to function optimally. Addition of superoxide dismutase in large concentrations might be a means whereby to test the suggested mechanism.
The influence of superoxide on the cellular function is still not fully understood. Besides the well- established toxicity of the radical, it also seems to have additional signaling functions (87). A recent report (87) demonstrates that O2•– is an important local signaling molecule required in normal physiology, which may serve to increase cell or tissue responsiveness to growth and/or differentiation-enhancing factors. The involvement of superoxide in magnetoreception may be another property of O2•– to be revealed in the future.
Supporting Material
Two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00777-2.
Supporting Material
Acknowledgments
I.S. thanks the Theoretical and Computational Biophysics group at the University of Illinois at Urbana-Champaign for a visit in which the research for this article was accomplished, and acknowledges use of resources at the Frankfurt Center for Scientific Computing.
K.S. thanks the Alexander von Humboldt Foundation for support. This work has been supported also by the European Commission within the Network of Excellence project EXCELL, by the Stiftung Polytechnische Gesellschaft Frankfurt am Main, and by National Science Foundation grants Nos. NSF MCB-0744057, NSF PHY0822613, and NIH P41-RR05969.
References
- 1.Mouritsen H., Ritz T. Magnetoreception and its use in bird navigation. Curr. Opin. Neurobiol. 2005;15:406–414. doi: 10.1016/j.conb.2005.06.003. [DOI] [PubMed] [Google Scholar]
- 2.Wiltschko R., Wiltschko W. Magnetoreception. Bioessays. 2006;28:157–168. doi: 10.1002/bies.20363. [DOI] [PubMed] [Google Scholar]
- 3.Johnsen S., Lohmann K.J. The physics and neurobiology of magnetoreception. Neuroscience. 2005;6:703–712. doi: 10.1038/nrn1745. [DOI] [PubMed] [Google Scholar]
- 4.Johnsen S., Lohmann K.J. Magnetoreception in animals. Phys. Today. 2008;61:29–35. [Google Scholar]
- 5.Lohmann J., Johnson S. The neurobiology of magnetoreception in vertebrate animals. Trends Neurosci. 2000;23:153–159. doi: 10.1016/s0166-2236(99)01542-8. [DOI] [PubMed] [Google Scholar]
- 6.Ahmad M., Galland P., Ritz T., Wiltschko R., Wiltschko W. Magnetic intensity affects cryptochrome-dependent responses in Arabidopsis thaliana. Planta. 2007;225:615–624. doi: 10.1007/s00425-006-0383-0. [DOI] [PubMed] [Google Scholar]
- 7.Solov'yov I.A., Chandler D., Schulten K. Magnetic field effects in Arabidopsis thaliana Cryptochrome-1. Biophys. J. 2007;92:2711–2726. doi: 10.1529/biophysj.106.097139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Solov'yov I.A., Greiner W. Theoretical analysis of an iron mineral-based magnetoreceptor model in birds. Biophys. J. 2007;93:1493–1509. doi: 10.1529/biophysj.107.105098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hanzlik M., Heunemann C., Holtkamp-Rötzler E., Winklhofer M., Petersen N. Superparamagnetic magnetite in the upper beak tissue of homing pigeons. Biometals. 2000;13:325–331. doi: 10.1023/a:1009214526685. [DOI] [PubMed] [Google Scholar]
- 10.Fleissner G., Holtkamp-Rötzler E., Hanzlik M., Winklhofer M., Fleissner G. Ultrastructural analysis of a putative magnetoreceptor in the beak of homing pigeons. J. Comp. Neurol. 2003;458:350–360. doi: 10.1002/cne.10579. [DOI] [PubMed] [Google Scholar]
- 11.Fleissner G., Stahl B., Thalau P., Falkenberg G., Fleissner G. A novel concept of Fe-mineral based magnetoreception: histological and physicochemical data from the upper beak of homing pigeons. Naturwissenschaften. 2007;94:631–642. doi: 10.1007/s00114-007-0236-0. [DOI] [PubMed] [Google Scholar]
- 12.Davila A.F., Winklhofer M., Shcherbakov V.P., Petersen N. Magnetic pulse affects a putative magnetoreceptor mechanism. Biophys. J. 2005;89:56–63. doi: 10.1529/biophysj.104.049346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Solov'yov I.A., Greiner W. Iron-mineral-based magnetoreceptor in birds: polarity or inclination compass? Eur. Phys. J. D. 2009;51:161–172. [Google Scholar]
- 14.Walker M., Dennis T., Kirschvink J. The magnetic sense and its use in long-distance navigation by animals. Curr. Opin. Neurobiol. 2002;12:735–744. doi: 10.1016/s0959-4388(02)00389-6. [DOI] [PubMed] [Google Scholar]
- 15.Schulten K., Swenberg C.E., Weller A. A biomagnetic sensory mechanism based on magnetic field modulated coherent electron spin motion. Z. Phys. Chem. 1978;NF111:1–5. [Google Scholar]
- 16.Schulten K. Magnetic field effects in chemistry and biology. In: Treusch J., editor. Festkörperprobleme (Solid State Problems), Vol. 22. Vieweg, Braunschweig; Germany: 1982. [Google Scholar]
- 17.Schulten K., Windemuth A. Model for a physiological magnetic compass. In: Maret G., Boccara N., Kiepenheuer J., editors. Biophysical Effects of Steady Magnetic Fields. Vol. 11 of Proceedings in Physics. Springer; Berlin, Germany: 1986. [Google Scholar]
- 18.Ritz T., Adem S., Schulten K. A model for photoreceptor-based magnetoreception in birds. Biophys. J. 2000;78:707–718. doi: 10.1016/S0006-3495(00)76629-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Solov'yov I.A., Chandler D.E., Schulten K. Exploring the possibilities for radical pair effects in cryptochrome. Plant Signal. Behav. 2008;3:676–677. doi: 10.4161/psb.3.9.5809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maeda K., Henbest K.B., Cintolesi F., Kuprov I., Rodgers C.T. Chemical compass model of avian magnetoreception. Nature. 2008;453:387–390. doi: 10.1038/nature06834. [DOI] [PubMed] [Google Scholar]
- 21.Schulten K. Magnetic field effects on radical pair processes in chemistry and biology. In: Bernhard J.H., editor. Biological Effects of Static and Extremely Low Frequency Magnetic Fields. MMV Medizin Verlag; Munich, Germany: 1986. [Google Scholar]
- 22.Wiltschko W., Wiltschko R. Magnetic compass of European robins. Science. 1972;176:62–64. doi: 10.1126/science.176.4030.62. [DOI] [PubMed] [Google Scholar]
- 23.Wiltschko W., Wiltschko R. Magnetic compass orientation in birds and its physiological basis. Naturwissenschaften. 2002;89:445–452. doi: 10.1007/s00114-002-0356-5. [DOI] [PubMed] [Google Scholar]
- 24.Wiltschko W., Wiltschko R. Magnetic orientation and magnetoreception in birds and other animals. J. Comp. Physiol. [A]. 2005;191:675–693. doi: 10.1007/s00359-005-0627-7. [DOI] [PubMed] [Google Scholar]
- 25.Wiltschko W., Stapput K., Thalau P., Wiltschko R. Avian magnetic compass: fast adjustment to intensities outside the normal functional window. Naturwissenschaften. 2006;93:300–304. doi: 10.1007/s00114-006-0102-5. [DOI] [PubMed] [Google Scholar]
- 26.Wiltschko W., Munro U., Ford H., Wiltschko R. Red light disrupts magnetic orientation of migratory birds. Nature. 1993;364:525–527. [Google Scholar]
- 27.Wiltschko W., Wiltschko R. Light-dependent magnetoreception in birds: the behavior of European robins, Erithacus rubecula, under monochromatic light of various wavelengths and intensities. J. Exp. Biol. 2001;204:3295–3302. doi: 10.1242/jeb.204.19.3295. [DOI] [PubMed] [Google Scholar]
- 28.Wiltschko W., Traudt J., Güntürkün O., Prior H., Wiltschko R. Lateralization of magnetic compass orientation in a migratory bird. Nature. 2002;419:467–470. doi: 10.1038/nature00958. [DOI] [PubMed] [Google Scholar]
- 29.Schulten K., Weller A. Exploring fast electron transfer processes by magnetic fields. Biophys. J. 1978;24:295–305. doi: 10.1016/S0006-3495(78)85378-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schulten K., Wolynes P.G. Semiclassical description of electron spin motion in radicals including the effect of electron hopping. J. Chem. Phys. 1978;68:3292–3297. [Google Scholar]
- 31.Timmel C.R., Till U., Brocklehurst B., Mclauchlan K., Hore P. Effects of weak magnetic fields on free radical recombination reactions. Mol. Phys. 1998;95:71–89. doi: 10.1080/09553000050176270. [DOI] [PubMed] [Google Scholar]
- 32.Schulten K., Staerk H., Weller A., Werner H.-J., Nickel B. Magnetic field dependence of the geminate recombination of radical ion pairs in polar solvents. Z. Phys. Chem. 1976;NF101:371–390. [Google Scholar]
- 33.Werner H.-J., Schulten Z., Schulten K. Theory of the magnetic field modulated geminate recombination of radical ion pairs in polar solvents: Application to the pyrene-N,N-dimethylaniline system. J. Chem. Phys. 1977;67:646–663. [Google Scholar]
- 34.Schulten K. Ensemble averaged spin pair dynamics of doublet and triplet molecules. J. Chem. Phys. 1984;80:3668–3679. [Google Scholar]
- 35.Efimova O., Hore P. Role of exchange and dipolar interactions in the radical pair model of the avian magnetic compass. Biophys. J. 2008;94:1565–1574. doi: 10.1529/biophysj.107.119362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rodgers C.T., Norman S.A., Henbest K.B., Timmel C.R., Hore P.J. Determination of radical re-encounter probability distributions from magnetic field effects on reaction yields. J. Am. Chem. Soc. 2007;129:6746–6755. doi: 10.1021/ja068209l. [DOI] [PubMed] [Google Scholar]
- 37.Himo F., Eriksson L.A. Theoretical study of model tryptophan radicals and radical cations: comparison with experimental data of DNA photolyase, cytochrome c peroxidase, and ribonucleotide reductase. J. Phys. Chem. B. 1997;101:9811–9819. [Google Scholar]
- 38.Cintolesi F., Ritz T., Kay C., Timmel C., Hore P. Anisotropic recombination of an immobilized photoinduced radical pair in a 50-μT magnetic field: a model avian photomagnetoreceptor. Chem. Phys. 2003;294:707–718. [Google Scholar]
- 39.Kay C.W.M., Feicht R., Schulz K., Sadewater P., Sancar A. EPR, ENDOR, and TRIPLE resonance spectroscopy of the neutral flavin radical in E. coli DNA photolyase. Biochemistry. 1999;38:16740–16748. doi: 10.1021/bi991442u. [DOI] [PubMed] [Google Scholar]
- 40.Lendzian F., Sahlin M., MacMillan F., Bittl R., Fiege R. Electronic structure of neutral tryptophan radicals in ribonucleotide reductase studied by EPR and ENDOR spectroscopy. J. Am. Chem. Soc. 1996;118:8111–8120. [Google Scholar]
- 41.Liedvogel M., Maeda K., Henbest K., Schleicher E., Simon T. Chemical magnetoreception: Bird cryptochrome 1a is excited by blue light and forms long-lived radical-pairs. PLoS ONE. 2007;2:e1106. doi: 10.1371/journal.pone.0001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mouritsen H., Janssen-Bienhold U., Liedvogel M., Feenders G., Stalleicken J. Cryptochromes and neuronal-activity markers colocalize in the retina of migratory birds during magnetic orientation. Proc. Natl. Acad. Sci. USA. 2004;101:14294–14299. doi: 10.1073/pnas.0405968101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Möller A., Sagasser S., Wiltschko W., Schierwater B. Retinal cryptochrome in a migratory passerine bird: a possible transducer for the avian magnetic compass. Naturwissenschaften. 2004;91:585–588. doi: 10.1007/s00114-004-0578-9. [DOI] [PubMed] [Google Scholar]
- 44.Ahmad M., Cashmore A.R. Seeing blue: the discovery of cryptochrome. Plant Mol. Biol. 1996;30:851–861. doi: 10.1007/BF00020798. [DOI] [PubMed] [Google Scholar]
- 45.Cashmore A.R., Jarillo J.A., Wu Y.-J., Liu D. Cryptochromes: blue light receptors for plants and animals. Science. 1999;284:760–765. doi: 10.1126/science.284.5415.760. [DOI] [PubMed] [Google Scholar]
- 46.Sancar A. Structure and function of DNA photolyase and cryptochrome blue-light photoreceptors. Chem. Rev. 2003;103:2203–2237. doi: 10.1021/cr0204348. [DOI] [PubMed] [Google Scholar]
- 47.Hoang N., Schleicher E., Kacprzak S., Bouly J.-P., Picot M. Human and Drosophila cryptochromes are light activated by flavin photoreduction in living cells. PLoS Biol. 2008;6:1559–1569. doi: 10.1371/journal.pbio.0060160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lin C., Todo T. The cryptochromes. Gen. Biol. 2005;6:220.1–220.9. doi: 10.1186/gb-2005-6-5-220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Partch C.L., Sancar A. Cryptochromes and circadian photoreception in animals. Methods Enzymol. 2005;393:726–745. doi: 10.1016/S0076-6879(05)93038-3. [DOI] [PubMed] [Google Scholar]
- 50.Christie J.M., Briggs W.R. Blue light sensing in higher plants. J. Biol. Chem. 2001;276:11457–11460. doi: 10.1074/jbc.R100004200. [DOI] [PubMed] [Google Scholar]
- 51.Mouritsen H., Feenders G., Liedvogel M., Wada K., Jarvis E. A night vision brain area in migratory songbirds. Proc. Natl. Acad. Sci. USA. 2005;102:8339–8344. doi: 10.1073/pnas.0409575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Heyers D., Manns M., Luksch H., Güntürkün O., Mouritsen H. A visual pathway links brain structures active during magnetic compass orientation in migratory birds. PLoS ONE. 2007;2:e937. doi: 10.1371/journal.pone.0000937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liedvogel M., Feenders G., Wada K., Troje N., Jarvis E. Lateralized activation of Cluster N in the brains of migratory songbirds. Eur. J. Neurosci. 2007;25:1166–1173. doi: 10.1111/j.1460-9568.2007.05350.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Brautigam C.A., Smith B.S., Ma Z., Palnitkar M., Tomchick D.R. Structure of the photolyase-like domain of cryptochrome 1 from Arabidopsis thaliana. Proc. Natl. Acad. Sci. USA. 2004;101:12142–12147. doi: 10.1073/pnas.0404851101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Giovanni B., Byrdin M., Ahmad M., Brettel K. Light-induced electronic transfer in a cryptochrome blue-light photoreceptor. Nat. Struct. Biol. 2003;10:489–490. doi: 10.1038/nsb933. [DOI] [PubMed] [Google Scholar]
- 56.Bouly J.-P., Schleicher E., Dionisio-Sese M., Vandenbussche F., Van Der Straeten D. Cryptochrome blue light photoreceptors are activated through interconversion of flavin redox states. J. Biol. Chem. 2007;282:9383–9391. doi: 10.1074/jbc.M609842200. [DOI] [PubMed] [Google Scholar]
- 57.Banerjee R., Schleicher E., Meier S., Viana R.M., Pokorny R. The signaling state of Arabidopsis cryptochrome 2 contains flavin semiquinone. J. Biol. Chem. 2007;282:14916–14922. doi: 10.1074/jbc.M700616200. [DOI] [PubMed] [Google Scholar]
- 58.Zeugner A., Byrdin M., Bouly J.-P., Bakrim N., Giovani B. Light-induced electron transfer in Arabidopsis cryptochrome-1 correlates with in-vivo function. J. Biol. Chem. 2005;280:19437–19440. doi: 10.1074/jbc.C500077200. [DOI] [PubMed] [Google Scholar]
- 59.Biskup T., Schleicher E., Okafuji A., Link G., Hitomi K. Direct observation of a photoinduced radical pair in a cryptochrome blue-light photoreceptor. Angew. Chem. Int. Ed. Engl. 2009;48:404–407. doi: 10.1002/anie.200803102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.O'Day K.E. Shedding light on animal cryptochromes. PLoS Biol. 2008;6:1359–1360. doi: 10.1371/journal.pbio.0060168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kao Y.-T., Tan C., Song S.-H., Öztürk N., Li J. Ultrafast dynamics and anionic active states of the flavin cofactor in cryptochrome and photolyase. J. Am. Chem. Soc. 2008;130:7695–7701. doi: 10.1021/ja801152h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Henbest K.B., Maeda K., Hore P.J., Joshi M., Bacher A. Magnetic-field effect on the photoactivation reaction of Escherichia coli DNA photolyase. Proc. Natl. Acad. Sci. USA. 2008;105:14395–14399. doi: 10.1073/pnas.0803620105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ritz T., Wiltschko R., Hore P., Rodgers C.T., Stapput K. Magnetic compass of birds is based on a molecule with optimal directional sensitivity. Biophys. J. 2009;96:3451–3457. doi: 10.1016/j.bpj.2008.11.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Prabhakar R., Siegbahn P.E., Minaev B.F., Ågren H. Activation of triplet dioxygen by glucose oxidase: spin-orbit coupling in the superoxide ion. J. Phys. Chem. B. 2002;106:3742–3750. [Google Scholar]
- 65.Ritz T., Thalau P., Phillips J.B., Wiltschko R., Wiltschko W. Resonance effects indicate a radical-pair mechanism for avian magnetic compass. Nature. 2004;429:177–180. doi: 10.1038/nature02534. [DOI] [PubMed] [Google Scholar]
- 66.Thalau P., Ritz T., Stapput K., Wiltschko R., Wiltschko W. Magnetic compass orientation of migratory birds in the presence of a 1.315 MHz oscillating field. Naturwissenschaften. 2005;92:86–90. doi: 10.1007/s00114-004-0595-8. [DOI] [PubMed] [Google Scholar]
- 67.Wang K., Ritz T. Zeeman resonances for radical-pair reactions in weak static magnetic fields. Mol. Phys. 2006;104:1649–1658. [Google Scholar]
- 68.Sawyer, D.T., Superoxide chemistry. AccessScience@McGraw-Hill. DOI 10.1036/1097–8542.669650.
- 69.Muller F. The nature and mechanism of superoxide production by the electron transport chain: its relevance to aging. J. Amer. Aging Assoc. 2000;23:227–253. doi: 10.1007/s11357-000-0022-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wali M.A., Suleiman S.A., Kadoumi O.F., Nasr M.A. Superoxide radical concentration and superoxide dismutase (SOD) enzyme activity in varicose veins. Ann. Thorac. Cardiovasc. Surg. 2002;8:286–290. [PubMed] [Google Scholar]
- 71.Mishra B., Priyadarsini K.I., Bhide M.K., Kadam R.M., Mohan H. Reactions of superoxide radicals with curcumin: probable mechanisms by optical spectroscopy and EPR. Free Radic. Res. 2004;38:355–362. doi: 10.1080/10715760310001660259. [DOI] [PubMed] [Google Scholar]
- 72.Cozens F., Scaiano J. A comparative study of magnetic field effects on the dynamics of geminate and random radical pair processes in micelles. J. Am. Chem. Soc. 1993;115:5204–5211. [Google Scholar]
- 73.Foresman J.B., Frisch Æ. Gaussian Inc.; Pittsburgh, PA: 1996. Exploring Chemistry with Electronic Structure Methods. [Google Scholar]
- 74.Frisch, M.J., G.W. Trucks, H.B. Schlegel, G. Scuseria, M.A. Robb, et al. 2003. Gaussian 03 (Rev. B.05). Gaussian, Inc., Pittsburgh, PA.
- 75.Kubo R. Stochastic Liouville equations. J. Math. Phys. 1963;4:174–183. [Google Scholar]
- 76.Shankar R. Plenum Press; New York: 1994. Principles of Quantum Mechanics. [Google Scholar]
- 77.Mohtat N., Cozens F., Hancock-Chen T., Scaiano J., McLean J. Magnetic field effects on the behavior of radicals in protein and DNA environment. Photochem. Photobiol. 1998;67:111–118. [PubMed] [Google Scholar]
- 78.Cheung M., Daizadeh I., Stuchebrukhov A., Heelis P. Pathways of electron transfer in E. coli DNA photolyase—Trp306 to FADH. Biophys. J. 1999;76:1241–1249. doi: 10.1016/S0006-3495(99)77287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Aubert C., Vos M.H., Mathis P., Eker A.P., Brettel K. Intraprotein radical transfer during photoactivation of DNA photolyase. Nature. 2000;405:586–590. doi: 10.1038/35014644. [DOI] [PubMed] [Google Scholar]
- 80.Hayashi H. World Scientific Publishing; Singapore: 2004. Introduction to Dynamic Spin Chemistry: Magnetic Field Effects on Chemical and Biochemical Reactions. [Google Scholar]
- 81.Canfield J.M., Belford R.L., Debrunner P.G., Schulten K. A perturbation theory treatment of oscillating magnetic fields in the radical pair mechanism. Chem. Phys. 1994;182:1–18. [Google Scholar]
- 82.Canfield J.M., Belford R.L., Debrunner P.G., Schulten K. A perturbation treatment of oscillating magnetic fields in the radical pair mechanism using the Liouville equation. Chem. Phys. 1995;195:59–69. [Google Scholar]
- 83.Campana F. Topical superoxide dismutase reduces post-irradiation breast cancer fibrosis. J. Cell. Mol. Med. 2004;8:109–116. doi: 10.1111/j.1582-4934.2004.tb00265.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Corpas F., Barroso J., del Rio L. Peroxisomes as a source of reactive oxygen species and nitric oxide signal molecules in plant cells. Trends Plant Sci. 2001;6:145–150. doi: 10.1016/s1360-1385(01)01898-2. [DOI] [PubMed] [Google Scholar]
- 85.Segui J., Gironella M., Sans M., Granell S., Gil F. Superoxide dismutase ameliorates TNBS-induced colitis by reducing oxidative stress, adhesion molecule expression, and leukocyte recruitment into the inflamed intestine. J. Leukoc. Biol. 2004;76:537–544. doi: 10.1189/jlb.0304196. [DOI] [PubMed] [Google Scholar]
- 86.Lide D.R. CRC Press; Boca Raton, FL: 2008. Handbook of Chemistry and Physics. [Google Scholar]
- 87.Buetler T.M., Krauskopf A., Ruegg U.T. Role of superoxide as a signaling molecule. News Physiol. Sci. 2004;19:120–123. doi: 10.1152/nips.01514.2003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


