A Link between Hinge-Bending Domain Motions and the Temperature Dependence of Catalysis in 3-Isopropylmalate Dehydrogenase

Abstract

Enzyme function depends on specific conformational motions. We show that the temperature dependence of enzyme kinetic parameters can provide insight into these functionally relevant motions. While investigating the catalytic properties of IPMDH from Escherichia coli, we found that its catalytic efficiency (k_cat/K_M,IPM) for the substrate IPM has an unusual temperature dependence, showing a local minimum at ∼35°C. In search of an explanation, we measured the individual constants k_cat and K_M,IPM as a function of temperature, and found that the van 't Hoff plot of K_M,IPM shows sigmoid-like transition in the 20–40°C temperature range. By means of various measurements including hydrogen-deuterium exchange and fluorescence resonance energy transfer, we showed that the conformational fluctuations, including hinge-bending domain motions increase more steeply with temperatures >30°C. The thermodynamic parameters of ligand binding determined by isothermal titration calorimetry as a function of temperature were found to be strongly correlated to the conformational fluctuations of the enzyme. Because the binding of IPM is associated with a hinge-bending domain closure, the more intense hinge-bending fluctuations at higher temperatures increasingly interfere with IPM binding, thereby abruptly increasing its dissociation constant and leading to the observed unusual temperature dependence of the catalytic efficiency.

Introduction

The temperature dependence of the rate constant of chemical reactions is generally described by the Arrhenius equation, which, in simple terms, states that the rate constant grows with temperature as an exponential function of −E_a/T. For an enzyme-catalyzed reaction, however, the rate constant is determined by the conformation and the dynamics of the enzyme, and its temperature dependence reflects how these properties are influenced by temperature. Enzymes usually have a temperature where they function optimally; at lower temperatures, activity is limited by the slower conformational dynamics, whereas at higher temperatures, the protein may denature. The kinetics of enzymes is commonly described by the Michaelis-Menten equation, using parameters such as the Michaelis constant K_M, the turnover number k_cat, and the maximum conversion rate V_max. To characterize the “efficiency” of an enzyme, the quantity k_cat/K_M, called “catalytic efficiency” or “specificity constant”, is commonly used, despite the fact that it is not generally applicable for comparison of different enzymes (1). The temperature dependence of k_cat usually follows the Arrhenius rate law, although nonlinear Arrhenius plots (plots of ln k_cat versus 1/T) are sometimes found (2–4). The temperature dependence of K_M is rarely studied. If product formation is the rate-limiting step during the enzyme reaction then K_M is identical to the dissociation constant of the substrate, and its temperature dependence is described by the van 't Hoff equation. Assuming a constant standard enthalpy (and entropy) of dissociation, a plot of ln K_M versus 1/T (the van 't Hoff plot) should be linear. A deviation from linearity may indicate a change in the rate-limiting step or the binding mode (5,6). The temperature dependence of K_M can be markedly different for orthologous enzymes from organisms adapted to different temperatures, e.g., when enzymes from psychrophiles and mesophiles are compared (7,8). The temperature dependence of k_cat/K_M is often measured to calculate individual rate constants, especially for proteases (9,10). In an earlier study, we investigated the role of conformational flexibility in cold-adaptation by comparing the psychrotrophic, mesophilic, and thermophilic variants of IPMDH (11). When plotting the catalytic efficiencies of these three enzymes versus temperature (see Fig. 5 A in Svingor et al. (11)), an unusual feature in the plots stood out. For all the three enzyme variants, k_cat/K_M,IPM increases with temperature over the 10–60°C range, but for the psychrotrophic and the mesophilic variants, a local minimum is observed around the middle of this range. The mesophilic variant, from E. coli, shows the more pronounced minimum.

Figure 5.

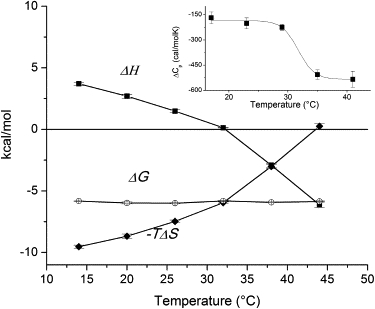
Temperature dependence of enthalpy (■), entropy (♦), and Gibbs free energy (○) of the binding of IPM to IPMDH measured by ITC. The data were analyzed by assuming a 1:1 binding stoichiometry using MicroCal Origin 5.0 software. Standard deviation was calculated according to the fit by Origin. Inset: The temperature dependence of heat capacity change associated with substrate binding was calculated from the temperature dependence of binding enthalpy. The solid lines are visual guides to the eye.

Through the unusual temperature dependence of k_cat/K_M,IPM, the temperature profile of the enzyme is flatter than expected, with the catalytic efficiency being about the same at ∼20°C as at ∼50°C. In fact, thanks to the anomalous temperature dependence of the specificity constant, the enzyme can function with an almost uniform efficiency in a wide temperature range. For an organism that must be able to grow in environments of varying temperatures, this type of enzyme regulation may be of advantage.

In this study, we investigate the anomalous temperature dependence of the catalytic efficiency of IPMDH from Escherichia coli in more detail to find the mechanism behind it.

Isopropylmalate dehydrogenase (EC 1.1.1.85) catalyzes the penultimate step of leucine biosynthesis in microorganisms and plants. The reaction involves a dehydrogenation and subsequent decarboxylation of threo-D-3-isopropylmalate to 2-oxoisocaproate with the concomitant reduction of NAD⁺. IPMDH is a homodimer, with each subunit composed of two domains. The crystallographic structures of IPMDH from eight species are available in the Protein Data Bank, namely Thermus thermophilus (12), Thiobacillus ferrooxidans (13), Bacillus coagulans (14), Thermotoga maritima, Salmonella typhimurium, Escherichia coli (15), Sulfolobus tokodaii, and Mycobacterium tuberculosis (16). In IPMDH from E. coli, the first domain consists of residues 1–105 and 256–363, and the second domain includes residues 106–255. The domains are linked by a 10-stranded central antiparallel β-sheet, with arm-like regions protruding from each subunit to stabilize the quaternary structure of the enzyme. The catalytic properties and thermal stability of E. coli IPMDH were studied previously (11,17).

To find the mechanism underlying the observed anomalous temperature dependence of the catalytic efficiency of E. coli IPMDH, we carried out a range of experiments including the measurement of k_cat and both K_M separately, as a function of temperature, differential scanning calorimetry to characterize the thermal stability of the protein under various conditions, hydrogen-deuterium exchange measurements to describe conformational flexibility, isothermal titration calorimetry to describe the thermodynamics of substrate binding, as well as measurements of fluorescence resonance energy transfer to determine dissociation constants and to characterize relative domain-domain motions. We suggest that the anomalous temperature dependence of k_cat/K_M,IPM can be attributed to an abrupt increase in K_M,IPM at ∼35°C, due to increased thermal domain-domain motions interfering with substrate-induced domain closure.

Materials and Methods

Materials

Threo-DL-3-isopropylmalic acid was purchased from Wako Pure Chemicals (Osaka, Japan) and NAD⁺ from Roche Applied Science (Penzberg, Germany). D₂O (99.95% purity) was obtained from Merck (Darmstadt, Germany). Other chemicals (high purity grade) were products of Merck, Reanal (Budapest, Hungary), Sigma (St. Louis, MO), and Fluka (St. Louis, MO).

Enzyme preparation

E. coli IPMDH was expressed in recombinant form in E. coli and purified as described previously (18,19).

CD measurements

CD measurements were carried out on a JASCO J-720 spectropolarimeter (Tokyo, Japan) equipped with a Neslab RTE-111 computer-controlled thermostat (Thermo Fisher, Waltham, MA), using cylindrical, water-jacketed quartz cells. Protein concentrations were set to 0.25 mg/mL for far-ultraviolet (UV), and 0.12 mg/mL for near-UV in 20 mM potassium phosphate buffer (pH 7.6) containing 0.3 M KCl. Cells of 0.1 cm path length were used for recording far-UV spectra, and 5 cm path length for near-UV spectra. Measurements were carried out in 3°C steps in the temperature range 14–65°C. Conformational changes were monitored at 220 nm in the far-UV and 280 nm in the near-UV region in continuous heating experiments at a heating rate of 60°C/h, in the temperature range 15–60°C.

DSC measurements

Measurements were carried out on a VP-DSC instrument (MicroCal, Northampton, MA). The protein concentration was adjusted to 0.5 mg/mL and a heating rate of 1°C/min was used. The samples were dialyzed against the buffers used in the activity measurements, and the dialysis buffer was used as a reference. The substrate and coenzyme concentration was 1 mM to insure saturating level.

ITC measurements

ITC was carried out using a VP-ITC instrument (MicroCal) between 20–50°C with 6°C steps. Protein and the titrating ligand samples were prepared in the same buffer, containing 20 mM KH₂PO₄, 300 mM KCl, and 1 mM MgCl₂, pH 7.6. The protein concentration was set to 45 μM and the ligand concentration was 6.6 mM. A titration experiment consisted of 25 injections of 5 μL of the titrating ligand into the cell at 300–400 s intervals. The titration data were corrected for the small heat changes observed in control titrations of ligands into the buffer. The data were analyzed by assuming a 1:1 binding stoichiometry using MicroCal Origin software. The data at 50°C was not used for evaluation due to the aggregation of the concentrated protein solution induced by the intense stirring. Standard deviation was calculated according to the fit by Origin.

Kinetic analysis

Determination of the k_cat and K_M values was carried out by global analysis of the saturation curves for IPM and NAD⁺ according to (11). Standard errors for k_cat and K_M were obtained from the nonlinear fitting; the standard error of k_cat/K_M was calculated using Gaussian error propagation.

The kinetic parameters were determined at various temperatures in 20 mM potassium phosphate buffer (pH 7.6) containing 0.3 M KCl, 0.2 mM MnCl₂, and various concentrations of NAD⁺ and IPM. Initial rates were measured by monitoring the absorbance of the formed NADH at 340 nm on a JASCO V-550 spectrophotometer equipped with a Grant thermostat (Cambridge, UK). Measurements were carried out in 3°C steps in the 14–65°C temperature range. (The temperature dependence of pH of the phosphate buffer is negligible.) Enzyme concentrations were set to 0.3 μM at each temperature.

Hydrogen/deuterium exchange

Hydrogen/deuterium (H/D) exchange of amide protons was measured and analyzed according to Závodszky et al. (18). Measurements were carried out in 3°C steps in the 20–59°C temperature range for the apoenzyme and in 5°C steps in the 20–50°C temperature range for the IPMDH-IPM complex, where the IPM concentration was fixed at a saturating concentration of 1.2 mM. To compare overall conformational flexibilities measured under different conditions, we calculated from these curves the “microstability” ΔG^mic, the average Gibbs free-energy associated with the local, reversible, noncooperative “unfolding” reactions within the folded state (20,21). The usual van 't Hoff analysis was applied for determination of ΔH. The standard deviations were calculated from the results of three independent measurements.

Fluorescence

Fluorescence resonance energy transfer (FRET) measurements were carried out as described by Dean and Dvorak (22). Data were collected on a Jobin Yvon Horiba FluoroMax3 spectrofluorometer (Kyoto, Japan) equipped with a Peltier thermostated cell holder. One centimeter quartz cells were used. Emission was monitored at 340 and 420 nm using excitation at 295 nm. The enzyme concentration was kept at 30 μg/mL, NADH concentration was 12 μM, and IPM concentration was varied between 10–500 μM. The measurements were carried out at 3°C intervals in the 14–50°C temperature range. To determine K_d for IPM binding, the emission of NADH at 420 nm was evaluated as a function of IPM concentration. The K_d values, and their standard errors were calculated from a nonlinear fit to the modified Michaelis-Menten equation:

$$F=F_{\text{MAX}}\left[S\right]/\left(K_{\mathrm{d}}+\left[S\right]\right)\text{.}$$ (1)

The temperature dependence of transfer efficiency was determined by examining the excitation spectra of NADH, with the emission measured at 420 nm. The transfer efficiency was calculated according to Stryer (23):

$$E=\left[\left(F_{\text{NADH},295\mathrm{nm}}/F_{\text{NADH},340\mathrm{nm}}\right)-\left({\varepsilon }_{\text{NADH},295\mathrm{nm}}/{\varepsilon }_{\text{NADH},340\mathrm{nm}}\right)\right]\times \left({\varepsilon }_{\text{NADH},340\mathrm{nm}}/{\varepsilon }_{\text{apoIPMDH},295\mathrm{nm}}\right),$$ (2)

where F denotes the fluorescence emission intensity and ɛ the extinction coefficient of the respective molecules at the specified wavelengths.

Results and Discussion

Temperature dependence of enzyme kinetic parameters

An unusual temperature profile of k_cat/K_M,IPM was observed by us previously for the reaction catalyzed by E. coli IPMDH (11). These results led us to reproduce these experiments with a more frequent sampling as a function of temperature. The more detailed data set (Fig. 1) resembles the previous one (see Fig. 5 A in Svingor et al. (11)). For a better understanding of the nature of the temperature-induced changes, we separately examined the k_cat and K_M components. The Arrhenius plot (ln k_cat versus 1/T) is curved, with the apparent activation energy dropping from ∼60 to ∼30 kJ/mol as temperature increases from 14°C to 65°C (Fig. 2). The van 't Hoff plots (ln K_M versus 1/T) describing the temperature dependence of the Michaelis-Menten constants are markedly different for IPM and NAD⁺. For the coenzyme NAD⁺, the plot is perfectly linear, whereas for the substrate IPM, it is sigmoid shaped (Fig. 3). For IPM, K_M increases from ∼20 to ∼100 μM in the 20–40°C temperature range.

Figure 1.

Specificity constants (k_cat/K_M) of the reaction catalyzed by E. coli IPMDH for NAD⁺ (A) and IPM (B) as a function of temperature. The specificity constant k_cat/K_M,IPM has an unusual temperature dependence, having a local minimum at ∼35°C. The specificity constant k_cat/K_M,NAD has no unusual features. Error bars represent standard errors obtained as described in Materials and Methods. The solid lines are visual guides to the eye.

Figure 2.

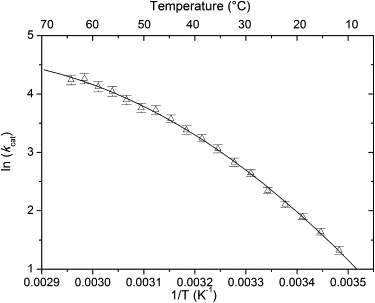
Temperature dependence of the catalytic constant (k_cat) of the reaction catalyzed by E. coli IPMDH displayed as an Arrhenius plot. The observed curvature of the plot is not unexpected, given the complexity of the catalytic mechanism in which individual rate constant may have different temperature dependences. Error bars represent standard errors obtained as described in Materials and Methods. The solid line is a quadratic function fitted to the data.

Figure 3.

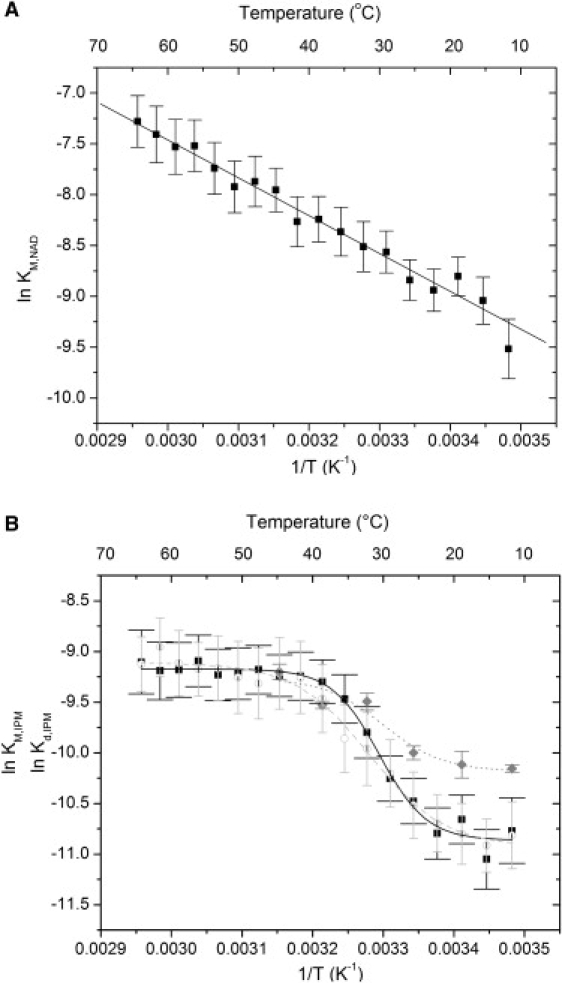
Temperature dependence of Michaelis-Menten constants of the reaction catalyzed by E. coli IPMDH displayed as van 't Hoff plots for NAD (A) and IPM (B). For NAD, the plot is linear; the straight line was obtained by linear fitting. For IPM, a sigmoid-like transition is observed in the 20–40°C temperature range. In plot B, the dissociation constant K_d,IPM (○) of IPM, as measured by a FRET based method is also shown, demonstrating that it is equal to K_M,IPM (■) over the whole temperature range. K_d,IPM measured by ITC (shaded diamond) is also shown. Sigmoidal (logistic) functions were fitted to all three sets of data, and represented by solid (K_M,IPM), dashed (K_d,IPM,FRET), and dotted K_d,IPM,ITC lines, respectively. Error bars represent standard errors obtained as described in Materials and Methods.

For a correct interpretation of these findings, it is important to know whether K_M,IPM is equal to the dissociation constant K_d,IPM of IPM in the entire temperature range studied. In a previous study, an assay was developed to determine K_d,IPM for IPMDH from T. thermophilus (22), based on the change in the fluorescence of a solution of the enzyme with NADH when IPM is added. A similar approach has been used successfully in other enzymatic systems (24,25). We used this method to determine K_d,IPM in the 14–65°C temperature range. The results are practically indistinguishable from K_M,IPM, showing that the Michaelis constant is in this case equal to the dissociation constant of the substrate (Fig. 3 B).

It can be concluded, therefore, that the observed unusual temperature dependence of the catalytic efficiency k_cat/K_M,IPM is related to the sigmoid-like increase of the dissociation constant K_d,IPM in the 20–40°C temperature range, i.e., substrate binding gets nonlinearly (referring to the van 't Hoff plot) weaker in a relatively narrow temperature range. This suggests a sudden change in the enthalpy and entropy of binding in this range. What mechanism may cause this change, whereas nothing unusual can be seen in the temperature dependence of NAD binding (at least as judged from the behavior of K_M,NAD)?

The binding modes of NAD and IPM

There are two structures available in the Protein Data Bank of IPMDHs crystallized in complex with a ligand: 1A05 (13), a structure of IPMDH from T. ferrooxidans, in complex with IPM, and 1HEX (26), a structure of IPMDH from T. thermophilus, in complex with NAD. The homodimer has two identical binding sites for each of NAD and IPM. By comparisons with the numerous available crystallographic structures of unliganded IPMDHs, the conformational changes related to substrate binding have been identified. The coenzyme NAD binds to Domain 1 and induces small structural changes, of up to 2.5 Å, in five loops (13). The binding of the substrate, IPM, induces a much larger conformational change. Its binding site is in a deep cleft between Domain 1 of one subunit and Domain 2 of the other subunit. The binding of IPM induces a rigid-body rotation of Domain 1 relative to Domain 2 by ∼27° around a hinge axis between the two domains. This closure of the two domains results in the formation of a hydrophobic pocket for the substrate (26). See Fig. 4 for a schematic representation of the structure of IPMDH.

Figure 4.

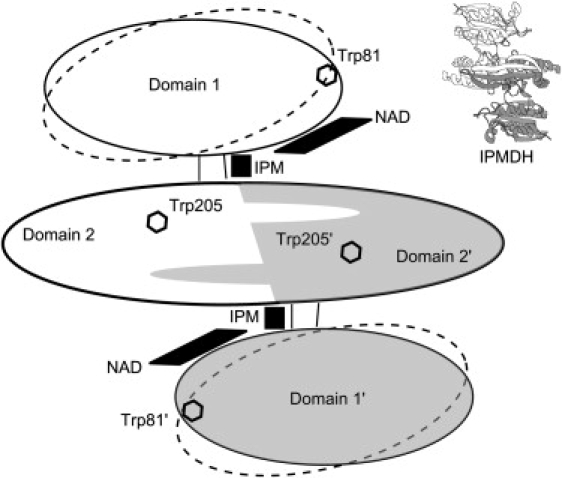
Schematic representation of the structure of IPMDH. Each subunit (white and gray, respectively) consists of two domains; Domain 2 from each subunit interacts with Domain 2 of the other subunit to form a homodimer. The coenzyme NAD binds to Domain 1; the substrate IPM binds in a cleft between the two subunits. The binding of IPM induces domain closure; ellipses drawn with dashed lines indicate the conformation of the enzyme in the open state. The locations of tryptophan residues are shown to facilitate the interpretation of FRET experiments. Top right: A cartoon model of IPMDH, prepared with the PMV program (35), shown in the same orientation as the main figure.

A superposition of over a dozen various IPMDH subunit structures available in the Protein Data Bank showed that there is a large number of intermediate states between the fully open and fully closed conformations (16). It is probably safe to assume that the free energy differences between these states are small, and in solution, there is an equilibrium between all these states. Ligand binding shifts the equilibrium toward more closed states: solution phase SAXS studies showed that both NADH and IPM induce partial domain closure, but with different intermediate states, and the nonproductive ternary complex (IPMDH + NADH + IPM) is fully closed (27). Because the binding of IPM is associated with domain closure, it is reasonable to assume that the observed unusual temperature dependence of the dissociation constant is somehow related to the temperature dependence of relative domain-domain motions.

Conformational transition or a change in conformational fluctuations?

The sigmoid shape of the van 't Hoff plot of the dissociation constant of IPM may indicate a temperature-induced two-state conformational transition. However, because IPM binding is likely to be also affected by the conformational fluctuations (especially the relative domain-domain motions), it may also reflect a change in the amplitude or mode of these fluctuations. The situation is somewhat analogous to the classic example of d-amino acid oxidase, whose tryptophan fluorescence decreases according to a sigmoid-like curve on raising the temperature (28). This phenomenon was first attributed to a conformational change (28) but later shown to be a consequence of dynamic quenching (29). To decide whether the change we observed could be due to a temperature-induced two-state conformational transition, we carried out CD, DSC, and ITC measurements.

CD measurements

We detected no changes in the CD spectra of the ligand-free enzyme either in the far-UV or the near-UV region in the 14–65°C temperature range (data not shown), showing that both the secondary and the tertiary structures remain intact in this temperature range. The holoenzyme is not suitable for CD measurements because of the high absorbance of NAD⁺.

DSC

DSC is the most direct method to investigate whether the observed sigmoidal behavior of K_M,IPM is due to a temperature-induced two-state conformational change. Let us assume that the sigmoid-like curve seen in Fig. 3 B is the result of a temperature-dependent equilibrium between two static conformational states of IPMDH with different affinities toward IPM. In this case, the apparent (van 't Hoff) enthalpy ΔH_vH of a reversible transition between the two states can be calculated from the curve and turns out to be 26 kcal/mol. Setting the midpoint of the transition at 31°C, the expected heat capacity curve can be calculated as well. If such a transition is present, the actual heat capacity curve, as measured by DSC, should also exhibit a peak centered around ∼31°C, with the area under the peak corresponding to the calorimetric enthalpy ΔH_cal ≥ ΔH_vH (30). Supporting Material, Fig. S1 shows the calculated and the measured heat capacity curves of IPMDH, both in the apo and the IPM-bound states. The peak expected in the case of a hypothetical temperature-induced transition is not present in the actual, measured curves. Although the expected peak is small compared to the unfolding transition of the enzyme observed at ∼68°C, it should still be an order of magnitude above the noise level of the measurement (see Fig. S1, magnified insets); thus, it would be fairly detectable with the DSC instrument used. The absence of a peak indicates that no temperature-induced conformational change occurs under the conditions of the measurement in the temperature range where the sigmoid-like behavior of K_M,IPM is observed.

ITC

DSC was carried out on the IPM-free and the IPM-saturated states of the enzyme. That measurement, however, does not provide us with a full thermodynamic description of a system in which ligand binding and a conformational transition are coupled. Eftink et al. (31) showed that in such a situation, the apparent dissociation constant and the apparent enthalpy and entropy of ligand binding depend on a number of parameters including the equilibrium constant between the two conformational states, the enthalpy difference between them, as well as the enthalpies and entropies of ligand binding to each state. Besides, an apparent heat capacity change associated with ligand binding will also arise. Therefore, to obtain a full thermodynamic description of IPM binding, we carried out ITC measurements at 6°C intervals at temperatures ranging from 14–44°C. (Unfortunately, aggregation of the protein under the conditions of the ITC measurement prevented us from measuring at higher temperatures.)

The results are shown in Fig. 5 (ΔH, −TΔS, ΔG, and ΔC_p) and Fig. 3 B (van 't Hoff plot for K_d). Although there is a slight difference between the K_d values obtained from fluorescence and those from the ITC measurement, the first part of the sigmoidal van 't Hoff plot, i.e., the upward curvature of ln K_d with increasing temperature, is clearly seen. Unfortunately, because no ITC measurement could be carried out at temperatures >44°C, the high-temperature regime is not seen, and therefore the ITC results do not offer an explanation for the downward curvature and flattening seen at these higher temperatures on the van 't Hoff plot as obtained from fluorescence measurements. The thermodynamic parameters (Fig. 5), however, provide insight into the changes occurring as temperature is varied. The favorable free energy (ΔG) of ligand binding is predominantly entropy-driven at lower temperatures; however, the entropic (−TΔS) and enthalpic (ΔH) contributions change steeply, in opposite directions, as temperature is increased, with the entropic contribution reaching zero at ∼44°C and thereby making the binding purely enthalpic. The slope of the change is not constant: it increases at ∼32°C, leading to a drop in the heat capacity change ΔC_p (Fig. 5, inset).

Are these observations consistent with a two-state conformational transition with a midpoint at ∼31°C, as the van 't Hoff plot may suggest? An analysis of Eqs. 1–4 in Eftink et al. (31) shows that in the case of a two-state transition coupled with ligand binding, the apparent binding enthalpy versus temperature plot should be either sigmoidal or contain a peak (depending on the parameters), and correspondingly, heat capacity should show a peak or change its sign at the midpoint of the transition. We do not see any of those features in our plots; therefore our ITC results are not consistent with a two-state conformational change of the enzyme at ∼31°C.

Rather, the ITC results suggest a gradual population shift toward states with higher entropies: there is an increasing, favorable contribution to the entropy of the unbound state as temperature is increased. The findings are consistent with a model described by Eftink et al. (31) (see Scheme II in that article), which assumes a multitude of protein states spanning a range of energy levels. In this model, ligand binding induces a shift of the distribution toward lower-energy states. This model predicts a negative ΔC_p of ligand binding, in accordance to what we observed.

Assuming that this model is appropriate for our case, it follows that an increasing number of protein states become populated as temperature increases; in other words, the protein becomes more flexible, which also affects substrate binding. We used hydrogen/deuterium exchange and fluorescence measurements to characterize the conformational dynamics of IPMDH.

Thus, we conclude that the observed sigmoid-like temperature dependence of K_M,IPM cannot be explained by assuming a temperature-induced two-state conformational change. For an alternative explanation, change in conformational dynamics of IPMDH was investigated.

H/D exchange versus temperature

Hydrogen/deuterium exchange of both IPM-bound and ligand-free IPMDH dissolved in D₂O was monitored by infrared spectrometry, which measures the amount of exchanged amide protons versus time (Fig. S2) and provides a measure of global conformational flexibility, the microstability ΔG^mic (see Materials and Methods) (Fig. 6 A). There is a marked difference between the behavior of the ligand-bound and ligand-free forms (Fig. 6 A). The conformational flexibility of the ligand-bound form increases nearly linearly with temperature. The conformational flexibility of the ligand-free form is close to that of the ligand-bound form at low temperatures, but curves upward with increasing temperature, in a nonlinear way: the curve is almost flat up to 30°C, becoming much steeper above this and at temperatures >30°C, it is markedly higher than that of the ligand-bound form. Although we do not have atomic-level information on what parts of the protein become more flexible at higher temperatures, the sudden increase in the slope of the microstability ΔG^mic versus temperature curve at ∼30°C may signal the appearance of new fluctuation modes. This temperature also roughly coincides with the middle of the sigmoid-like transition of K_M,IPM suggesting that this transition may be related to certain conformational fluctuations.

Figure 6.

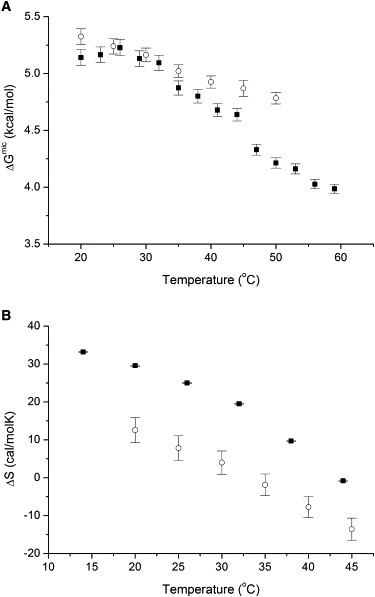
Temperature dependence of the conformational flexibility of E. coli IPMDH. (A) The “microstability”, i.e., the Gibbs free energy ΔG^mic associated with the local, reversible, noncooperative ”unfolding” reactions within the folded state (20) was calculated as a function of temperature. Measurements were carried out in the absence (■) and the presence (○) of 1.2 mM IPM. The points are averages from two independent measurements; error bars represent standard deviations. (B) The temperature dependence of substrate binding (■) was directly determined by ITC measurements. The temperature dependence of the entropy change associated to binding, was also calculated independently from H/D exchange measurements ΔS^mic in the absence and the presence IPM (○). The two entropies vary in an almost parallel way, with a nearly constant difference between them, suggesting that the change in entropy from conformational fluctuations on ligand binding has a major influence on the temperature dependence of the total entropy of binding. Error bars represent standard deviations.

Using a van 't Hoff type analysis an estimated average entropy change associated with conformational fluctuations detected by H/D exchange can be calculated converting the ΔG^mic values to equilibrium constants and determining the associated ΔH^mic values from the slope of the van 't Hoff plot, and then calculating ΔS^mic as (ΔG^mic − ΔH^mic)/T. We calculated these entropies for both the ligand-bound and ligand-free states. The difference between these two values, ΔS^mic (binding) = ΔS^mic (bound) −ΔS^mic (free) is an estimate of the change in entropy associated with fluctuations on ligand binding. A plot of ΔS^mic (binding) versus temperature, compared with the temperature dependence of the entropy of ligand binding (Fig. 6 B) shows that these two entropies vary in an almost parallel way, with a nearly constant difference between them. This finding suggests that the change in entropy from conformational fluctuations on ligand binding has a dominant contribution to the total entropy of binding, and it has a major influence on its temperature dependence. Thus, the comparison shown in Fig. 6 B indicates a quantitative relationship between protein dynamics and ligand binding.

H/D exchange and DSC measurements were also carried out on IPMDH + NAD and IPMDH + NADH + IPM complexes (see the Supporting Material for details).

Domain motions studied by FRET

The notion that FRET can be used as a probe for changes in protein conformational fluctuations is well established and well described by a simple oscillator model (32). FRET between NADH bound to Domain 1 and the tryptophan residues in the protein allows us to study the relative domain-domain motions in the absence and in the presence of IPM, as a function of temperature. There are two Trp residues in E. coli IPMDH per subunit: Trp-81 (in Domain 1) and Trp-205 (in Domain 2). In the open conformation (as measured in the NAD-bound T. thermophilus IPMDH structure 1HEX (26)), each coenzyme is 11, 27, 54, and 24 Å away from Trp-81, Trp-205, Trp-81′, and Trp-205′, respectively (primed numbers refer to residues in the other subunit). In the closed conformation (as estimated from the IPM-bound T. ferrooxidans IPMDH structure 1A05 (13), with a NAD⁺ molecule inserted), these distances are 10, 28, 44, and 17 Å. (See also Fig. 4 for an illustration of Trp positions.) Thus, the largest change in FRET efficiency on domain closure can be expected from the coenzyme moving ∼7 Å closer to Trp-205′. (Although Trp-81′ moves ∼10 Å closer, the resulting distance, 44 Å, remains too large for a measurable transfer.)

All FRET measurements on IPMDH were carried out in the presence of 12 μM NADH. At 14°C, the FRET efficiency in the absence of IPM is very low (E = 0.09 ± 0.01), which suggests that Trp-81, which is only 11 Å away from the bound NADH group, has a negligible contribution to FRET. In the presence of IPM, the FRET efficiency is significantly higher (E = 0.41 ± 0.03), which is consistent with a decrease of the distance between NADH and Trp-205′, and suggests an induced fit mechanism for IPM binding. From the distances taken from the crystallographic structures and the measured FRET efficiencies, the Förster distance R₀ (the distance between the donor and the acceptor where the transfer efficiency is 50%) can be calculated using the relationship E = 1/(1 + (r/R₀)⁶). Assuming that transfer occurs only between Trp-205′ and NADH, the resulting R₀ is 16.3 Å, both from the IPM-bound (closed) and IPM-free (open) structures. Assuming that Trp-205 also contributes to the FRET signal with the same R₀ as Trp-205′, the value of R₀ would be 16.0 Å, a very similar value. These Förster distances are similar to those found in other studies (33,34). However, the distance of Trp-205 from NADH does not shorten on IPM-binding (rather, it slightly increases, by 1 Å). Therefore, given the geometries in the crystal structures, it is likely that the Trp-205′ to NADH transfer provides the dominant contribution to the transfer efficiency increase observed on domain closure.

We measured the temperature dependence of FRET in the 14–50°C range. To be able to monitor changes in conformational fluctuations and/or states, we used the parameter f' = E/F_DA, i.e., the FRET efficiency normalized by the donor fluorescence intensity, as defined by Somogyi et al. (32). This parameter was shown to be sensitive to changes in amplitudes of local fluctuations (32). Fig. 7 shows the percent change in f' as the temperature is increased from 14°C to 50°C, taking the value at 14°C as 100%, both in the absence and the presence of IPM. There is a striking difference between the two curves: whereas f' only increases slightly in this temperature range in the presence of IPM, it dramatically increases (to ∼300% of its initial value) in the absence of IPM, with a slight increase in the slope of the curve at ∼30°C.

Figure 7.

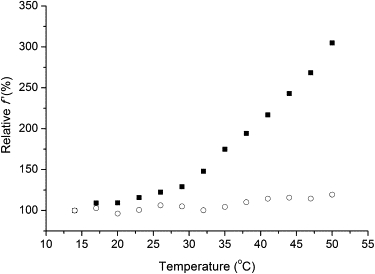
Temperature dependence of f'. Percent change of the f' parameter in the absence (■) and presence (○) of 500 μM IPM, taking the value at 14°C as 100%. Without IPM, the increase of the efficiency with temperature suggests an increasing amplitude of hinge-bending fluctuations.

An increase in f' indicates an increase in the amplitude of conformational fluctuations (domain-domain motions in this case) unless a conformational transition occurs that also changes the equilibrium donor-acceptor distance. We have already ruled out the possibility of a temperature-induced conformational change (see the earlier sections on DSC and CD measurements). The lack of a conformational transition is further confirmed by the unaltered structure of fluorescence spectra (data not shown). There is a slight change (∼15%) in the value of the overlap integral between the Trp emission and NADH absorption spectra as temperature increases from 14°C to 50°C, but this is clearly not sufficient to account for the observed 300% increase in f'. A change in the orientation factor κ² might also contribute to the change in f', but near-UV CD spectra do not indicate any temperature-dependent change in tryptophan orientations. We conclude, therefore, that the variation of f' with temperature mainly reflects the variation of the amplitude of hinge-bending domain-domain fluctuations.

The data displayed in Fig. 7 suggest that in the IPM-bound, closed conformation, temperature has little effect on the amplitude of fluctuations; the closed structure obviously suppresses the fluctuations. In the IPM-less, open conformation, however, the domains are free to move, and the amplitude of hinge-bending fluctuations strongly increases with temperature.

Judged from the varying slope of the curve, this increase becomes even more pronounced above ∼30°C. This temperature coincides with the one at which the overall flexibility of the protein starts to grow rapidly according to our H/D exchange relaxation experiments (see Fig. 6 A).

Considering the fact that the binding of IPM induces domain closure in IPMDH, higher-amplitude hinge-bending fluctuations may interfere with IPM binding at higher temperatures, reducing the observed affinity of the enzyme to IPM. We suggest that this is the explanation for the sigmoid-like increase in K_M,IPM in the 20°C to 40°C temperature range, leading to the unusual temperature dependence of the catalytic efficiency.

Conclusions

The focus of this study was to find the explanation of the unusual temperature dependence of the catalytic efficiency k_cat/K_M,IPM of E. coli IPMDH (Fig. 1 A). Measuring the individual constants as a function of temperature, we found that k_cat behaves regularly, apart from a curvature of the Arrhenius plot (Fig. 2), which is, however, not unexpected given the kinetic complexity of the enzyme-catalyzed reaction. On the other hand, we found that the van 't Hoff plot of K_M,IPM shows a sigmoid-like transition in the 20–40°C temperature range (Fig. 3 B). We showed that K_M,IPM is equal to the dissociation constant K_d,IPM of the substrate. Thus, the sigmoid-like transition signifies an unexpected increase of K_d,IPM in the 20–40°C temperature range. In contrast to these findings, nothing unusual is seen in the temperature dependence of NAD binding; the van 't Hoff plot for K_M,NAD is perfectly linear (Fig. 3 A).

The different temperature dependence of IPM and NAD binding reflects the fact that they bind to the enzyme by entirely different mechanisms. Although NAD binds to Domain 1 and only induces small conformational changes in a few loops, IPM binds in a deep cleft between Domain 1 of one subunit and Domain 2 of the other subunit, inducing a hinge-bending rigid-body rotation of Domain 1 relative to Domain 2, resulting in a closed conformation.

We showed that no significant conformational change occurs in the 20–40°C temperature range that could explain the sigmoid-like van 't Hoff plot of the substrate dissociation constant, and that the observations cannot be explained by assuming a two-state conformational transition in this temperature range. On the other hand, both H/D exchange experiments and FRET measurements indicate that the conformational flexibility of the protein grows more steeply with temperature above ∼30°C. FRET measurements, in particular, suggest that the amplitude of hinge-bending fluctuations increases more steeply above 30°C. A comparison of entropies calculated from the flexibilities measured by H/D exchange and the entropies of ligand binding obtained from ITC measurements indicates a strong, quantitative relationship between the thermodynamics of conformational fluctuations and ligand binding. We suggest that the more intense fluctuations as temperature is increased to above 30°C interfere with substrate binding (that requires domain closure) by sharply increasing the entropy of the unbound state, and this is the main reason why the substrate dissociation constant shows an upward curvature (as temperature increases) in the van 't Hoff plot. This explains the first part of the sigmoidal van 't Hoff plot, up to ∼45°C. The high-temperature part, showing a downward curvature, however, remains unexplained; increases in a sigmoid-like fashion. ITC measurements could not be carried out in this range, and an extrapolation of the ITC results to higher temperatures would indicate a continuing upward curvature rather than a downward one. We think that the flat part of the van 't Hoff plot might be an artifact. Experiments requiring high protein concentrations are increasingly difficult to perform in this temperature range because of the onset of thermal denaturation and aggregation.

The unusual temperature dependence of k_cat/K_M,IPM makes the catalytic efficiency of the enzyme flatter as a function of temperature than it would be otherwise. At higher temperatures, catalytic efficiency is high because the catalytic constant k_cat is high; at lower temperatures the catalytic efficiency is again high because K_M,IPM is low. Therefore, the domain-closure mechanism of IPM binding makes the optimum temperature range of IPMDH wider than it were if IPM bound by a mechanism similar to NAD binding. This flattening of the catalytic efficiency curve may have biological implications. Organisms have many ways of regulating their function, the most important way being the regulation of gene expression, but other mechanisms may also be at work at the molecular level. Our results raise the possibility that the domain-closure mechanism of IPMDH might actually serve as an indirect means of regulating enzyme activity over the temperature range the organism (E. coli in this case) may encounter. However, given that E. coli typically grows in an environment with a rather constant temperature (i.e., ∼37°C), this may not be the case for this particular organism.

Our results underline the role of conformational flexibility and domain motions in the catalytic function of IPMDH. From our experiments, a putative model of how conformation and flexibility vary during the catalytic cycle emerges.

To our knowledge, a sigmoid-like transition in the temperature dependence of a substrate dissociation constant has not been described for other enzymes. We suggest that a similar phenomenon may occur with other enzymes in which substrate binding induces domain closure and hinge-bending fluctuations influence the process.

Supporting Material

Results and discussion, three figures, and a table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00801-7.