Membrane-Mediated Interactions Measured Using Membrane Domains

Abstract

Cell membrane organization is the result of the collective effect of many driving forces. Several of these, such as electrostatic and van der Waals forces, have been identified and studied in detail. In this article, we investigate and quantify another force, the interaction between inclusions via deformations of the membrane shape. For electrically neutral systems, this interaction is the dominant organizing force. As a model system to study membrane-mediated interactions, we use phase-separated biomimetic vesicles that exhibit coexistence of liquid-ordered and liquid-disordered lipid domains. The membrane-mediated interactions between these domains lead to a rich variety of effects, including the creation of long-range order and the setting of a preferred domain size. Our findings also apply to the interaction of membrane protein patches, which induce similar membrane shape deformations and hence experience similar interactions.

Introduction

Lipid bilayer membranes enclose and compartmentalize the living cell, and as such represent the single most important barrier that cellular sensing and transport processes face (1). The detection of, and adequate response to, extracellular cues in particular is strongly bound to the membrane. Rather than allow ligands to pass through the membrane, changes in external concentrations of specific agonists are typically registered by transmembrane proteins and protein complexes. The spatial organization of such proteins is crucial to the successful transduction of signals across the membrane, and facilitates many cellular processes (1,2). This organization within the membrane has been the subject of intense studies, and represents a fundamental biological challenge: How is it that supramolecular organization comes about, and persists in the two-dimensional fluid environment of the membrane? After all, in a perfectly liquid environment, diffusion would tend to strongly counteract pattern formation and would quickly erase any significant density gradients. Moreover, traditionally considered protein-protein interactions (hydrophilic/hydrophobic, electrostatic, van der Waals) tend to be either too short-ranged or too weak to effectively drive the formation of heterogeneities.

Protein interactions mediated by the membrane have been suggested as a possible mechanism to overcome the limitations set by short-ranged conventional interactions. The membrane may effectively mediate protein interactions in several ways. The first is by creating local inhomogeneities in membrane composition, particularly in the emergence of small domains enriched in particular lipid species (3,4). These domains may present transient or persistent target sites for protein aggregation due to protein confinement or specific lipid-protein interactions. A second possibility is that single lipids or proteins interact via hydrophobic mismatches. If the length of the hydrophobic domain of a protein or lipid does not match the thickness of the surrounding membrane, this configuration will carry an energy penalty. To reduce that penalty, lipids or proteins may aggregate with similar-sized ones. The interaction due to hydrophobic mismatch is short-ranged and independent of overall membrane curvature (5). A final possibility is that proteins locally distort the membrane shape (6–9). Such distortions lead to an effective interaction between them through the differential curvature they impart. Aggregates of proteins, especially, could interact via membrane curvature. Such interactions would have biological implications, for example, for the assembly of protein coats and endocytosis (2).

In this article, we study the existence and magnitude of the last type of membrane-mediated interactions. We do so by considering the dynamics of domains on partially phase-separated vesicles containing cholesterol and two other species of lipids (10). While no proteins are present in our system, these small lipid domains mimic the proposed behavior of proteins (11). They, too, locally distort the shape of the membrane. Working with domains carries two great advantages over using actual proteins. Firstly, the domains interact only through the membrane shape deformations they induce. Secondly, they are straightforward to visualize and track. Earlier studies of the same system by Yanagisawa et al. (12) focused on the dynamics of domain growth. They described a slowing down of domain coalescence due to membrane-mediated interactions. Rozovsky et al. (13) reported the formation of regular patterns in a similar system. In their experiments, the shape of the vesicle was strongly coupled to phase separation due to substrate adhesion. In this study, we use domains on freely suspended giant vesicles as a probe to demonstrate the existence of membrane-mediated interactions. We develop a theoretical model that predicts the existence of partially budded domains in this system, which is a prerequisite for membrane-mediated interactions. We measure the distribution of domain sizes and find a pronounced preferred length scale. By analysis of the fluctuations of domain positions, we quantify the strength of membrane interactions and find a nontrivial dependence of the interaction strength on domain size. Those effects are captured qualitatively in a simple model. Our findings shed new light on intramembrane interactions between protein patches. Moreover, they also yield new information on the domain size distribution and the stability of the widely reported microphase separation in multicomponent biomimetic membranes.

Materials and Methods

GUV formation

Giant unilamellar vesicles (GUVs) were produced by electroformation in a flow chamber (14,15) from a mixture of 30% DOPC, 50% brain sphingomyelin, and 20% cholesterol at 55°C. The liquid-disordered L_d phase was stained by a small amount of Rhodamine-DOPE (0.2–0.4%), and the liquid-ordered L_o with a small amount (0.2–0.4%) of perylene. The DOPC (1,2-di-oleoyl-sn-glycero-3-phosphocholine), sphingomyelin, cholesterol, and Rhodamine-DOPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-n-(Lissamine Rhodamine B Sulfonyl)) were obtained from Avanti Polar Lipids (Alabaster, AL); the perylene from Sigma-Aldrich Chemie (Zwijndrecht, The Netherlands).

After formation of the GUVs the buffer (256 mM sucrose) was partially exchanged by a buffer with a higher osmolarity (335 mM sucrose), resulting in a difference of osmolarity of ∼40–50 mM between inside and outside of the vesicles. Subsequently lowering the temperature to 20°C resulted in the spontaneous nucleation of liquid-ordered L_o and liquid-disordered L_d domains on the vesicles. All reported observations were made on vesicles that show partially budded domains, which are stable over extended periods of time (see Movie S1 in the Supporting Material). In total, 21 vesicles were recorded.

Vesicles were imaged at video rate with a model No. 902H2 Supreme charge-coupled device camera (Watec, Orangeburg, NY) attached to an inverted microscope (Axiovert 40 CFL, Carl Zeiss, Oberkochen, Germany). The sample was illuminated continuously by a mercury lamp (HBO 50, Zeiss) and suitable excitation filters. Fluorescence signal was collected using appropriate dichroic mirrors and emission filters.

Image analysis

First, an equatorial image of the vesicle is taken to determine its radius and center position (see Fig. S1). After taking the equatorial image, the focus is moved to the top of the vesicle and the movement of domains is followed for several minutes. Every frame of those movies (Fig. 1 c) is treated with a bandpass Fourier filter to eliminate noise and background and a region of interest around the center of the vesicle is chosen (Fig. 1 d). The filtered grayscale image is subsequently transformed to a binary image by thresholding (Fig. 1 e). The positions of the domains are determined from the centroids of the domains (i.e., the center-of-mass, where mass corresponds to pixel intensity here). The short and long axes of the domains are calculated from the moment-of-inertia tensor (Fig. 1 f). Since the domains are in a liquid phase, their boundaries are circular. They appear elliptical due to the projection onto a plane. The real radius of a domain is given by the long axis of the observed ellipse.

Figure 1.

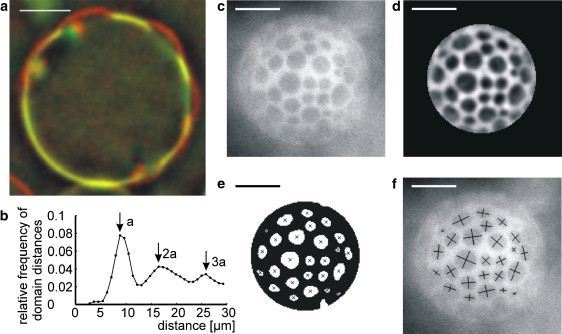
Analysis of experimental data. (a) Cross section of a partially budded vesicle. Overlay of 405-nm excitation (perylene, red/dark shaded) and 546-nm excitation (rhodamine, yellow/light shaded). (b) Typical radial distribution function for the center-center distances of the domains on a single vesicle. The nearest-neighbor distance is denoted by a. (c–f) Image analysis. The L_d phase is stained and appears bright in the images; the L_o phase appears dark. (c) Raw image; (d) filtered image with region of interest on top of the vesicle; (e) filtered image converted to binary image by thresholding, crosses marking the centroids of the domains; and (f) raw image with long and short axes of the domains overlayed. All scale bars: 20 μm.

The vesicle is assumed to be approximately spherical. Hence, the z position of the domains relative to the equatorial plane can be calculated from the position of the centroids and the center of the vesicle. All domain radii and distances between domains are measured along the vesicle surface.

Evidence for Interactions

We experimentally studied the dynamics of tricomponent GUVs. Under appropriate conditions on composition and temperature, the lipids in such vesicles phase separate into liquid-ordered (L_o) and liquid-disordered (L_d) domains (16). In our system, we typically observe many L_o domains in an L_d background (see Fig. 1). After preparation by means of electroformation, the vesicles have a spherical shape. By increasing the osmotic pressure outside the vesicle, we produce a slight increase in surface/volume ratio. For this reason some of the vesicles show partially budded L_o domains (see Fig. 1 a). Those domains posses long-term stability (see Movie S1; in experiments we observed stability on the timescale of several hours). In contrast, flat domains, which have the same curvature as the vesicle as a whole, rapidly fuse until complete phase separation is attained (12,17).

The stability of the vesicles with budded domains indicates that the domains experience a repulsive interaction that prevents them from fusing. This interaction also affects the distribution of domain distances (radial distribution function) and domain sizes.

Radial distribution function

Fig. 1 b shows the radial distribution function (rdf) of the center-to-center distance of domains for a typical vesicle. The first (and highest) maximum in the rdf corresponds to the first coordination shell, i.e., the nearest neighbors. The distance between nearest neighbors is denoted by a. On average a = 9 μm, while the radius of a domain is on average 3 μm and the vesicle radius equals 34 μm on average. Fig. 1 b clearly shows two additional maxima roughly at 2a and 3a, which correspond to the second and third coordination shell. The rdf therefore indicates that the domains are not randomly distributed but, that instead, their positions are correlated. Consequently, the system of diffusing domains can be characterized as a two-dimensional liquid with interactions. Since a exceeds the typical domain radius by a factor of 3, this interaction is different from mere hard-core repulsion between the domains.

Size distribution

Fig. 2 shows the domain size distribution of all observed vesicles. The distribution is not uniform, but instead shows an absolute maximum, corresponding to a preferred domain size. Moreover, there is a long tail to larger domain sizes that drops off exponentially, as can be seen in a logscale plot (Fig. 2 inset). This nonuniform distribution can be understood in a picture that includes both domain fusions and domain interactions.

Figure 2.

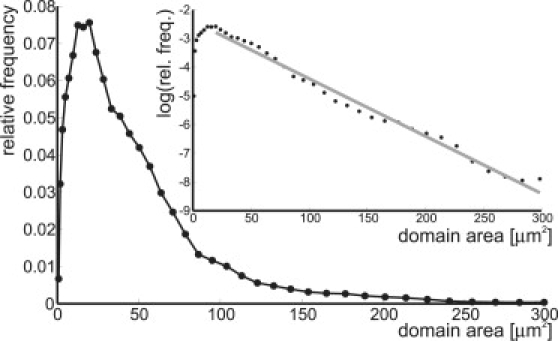
Distribution of domain sizes on all 24 vesicles. (Inset) Logarithmic plot of the domain size distribution shows an exponential decay toward large domains (solid line).

As was already observed by Yanagisawa et al. (12), we find that domains fuse when they are small. However, due to the repulsive interaction, the fusion of domains becomes kinetically hindered, and slows down significantly with increasing domain size. When the repulsive interaction has grown to the size of the thermal energy (k_BT), the fusion process will come to a halt and the vesicle with multiple domains enters the (metastable) kinetically arrested state that we observe in the experiments. Due to the finite available amount of domain area, the frequency-of-size occurrence decays exponentially for large domains (Fig. 2).

To check whether the local maximum and the exponential tail observed in the experimental domain size distribution can be explained by mutual repulsion of domains, we performed Monte Carlo simulations of domain coalescence. We assume that the rate for the fusion of two domains of areas n and m can be written as the product of two factors: the rate for random encounter by diffusion k_diff({N_n}), which may depend on the distribution of domain sizes {N_n}, and the probability $p_{\text{n,m}}^{\text{merge}}$ for domain merger if the domains are close to each other:

$$k_{\text{n,m}}=p_{\text{n,m}}^{\text{merge}}{k}_{\text{diff}}\left(\right\{N_{\text{n}}\left\}\right)\text{.}$$ (1)

Our simulations start with 1/ɛ domains of identical size, where ɛ is defined as the initial domain area. During the simulation, the domains are fused randomly with the rates given above. The fusion rate is converted to a fusion probability p_n,m by multiplication with a small time step Δt. Since there are $\frac{1}{2}N(N-1)$possible pairings of N domains, we write the fusion probability as

$$p_{\text{n,m}}=k_{\text{n,m}}\Delta t=\frac{1}{\frac{1}{2}N(N-1)}{p}_{\text{n,m}}^{\text{merge}}\left(\frac{1}{2}N(N-1)\right)k_{\text{diff}}\left(\right\{N_{\text{n}}\left\}\right)\Delta t,$$ (2)

with the total number of domains given by $N={\sum }_{\text{n}}{N}_{\text{n}}$.

If the time step Δt is chosen to be $\Delta t={\left[\left(\frac{1}{2}N(N-1)\right)k_{\text{diff}}\left(\right\{N_{\text{n}}\left\}\right)\right]}^{-1}$, the fusion probability becomes $p_{\text{n,m}}=\frac{1}{\frac{1}{2}\text{N}(\text{N}-1)}{p}_{\text{n,m}}^{\text{merge}}$.

In the following, we briefly sketch the Monte Carlo algorithm we used; details can be found in Semrau et al. (18). In each Monte Carlo step, first a pair of domains is chosen randomly (which corresponds to the factor $1/\left(\frac{1}{2}N(N-1)\right)$ in p_n,m) and the Monte Carlo time is increased by Δt. With a probability of $p_{\text{n,m}}^{\text{merge}}$, the domain fusion is executed. In the Supporting Material, we show that this Monte Carlo scheme results in the correct domain fusion dynamics. For short enough timescales, the system can be described by a master equation (19)

$${\dot{N}}_{\text{n}}=\frac{1}{2}\sum _{\text{m}=1}^{\text{n}-1}{k}_{\text{m,n}-\text{m}}{N}_{\text{m}}{N}_{\text{n}-\text{m}}-\sum _{\text{m}=1}^{\mathrm{\infty }}{k}_{\text{n,m}}{N}_{\text{n}}{N}_{\text{m}},$$ (3)

where N_n is the number of domains with area n; k_n,m is the fusion rate for domains of area n and m; and the dot refers to the time derivative. A master equation approach disregards the discrete nature of domain numbers and is therefore only applicable for domain numbers much bigger than 1, i.e., a long time before complete phase separation.

For a simple case (k_n,m = k and $p_{\text{n,m}}^{\text{merge}}$ = 1), the master equation (Eq. 3) is exactly solvable (see Supporting Material). The solution for this case is an exponential distribution for all times

$$N_{\text{n}}\left(t\right)=\varepsilon \frac{4}{{\left(kt\right)}^2}\exp \left(-\frac{2n}{kt}\right),$$ (4)

which suggests that the exponential tail observed in experiments is simply a consequence of conserved total domain area.

To take the spatial distribution and diffusion of domains into consideration, we adopt the scaling argument used in the literature (12,19): The time τ_diff for two domains to encounter each other at random, due to diffusion scales like τ_diff ∝ 〈d²〉/D(d) with d the domain radius and D(d) the diffusion constant. Since we observe only a weak dependence of the diffusion coefficient on domain size (D(d) ≈ D; see Fig. S4), we set k_diff({N_n}) = π/〈A〉 with the average domain area $\langle A\rangle =\frac{1}{\text{N}}\sum _{\text{n}}n{N}_{\text{n}}$. This rate should give the correct timescale for domain fusion apart from a constant prefactor. To gauge the simulations with real experimental timescales, we let the system evolve to complete phase separation for noninteracting domains ($p_{\text{n,m}}^{\text{merge}}$= 1) and compare the resulting Monte Carlo time to measured timescales. In the case of unbudded domains, which are free to fuse, the time needed for complete separation was determined experimentally (see (12), normal coarsening) and is ∼1–10 min. The corresponding Monte Carlo time in our simulations is T_MC ∼ 2. Fig. 3 a shows intermediate domain size distributions for four different Monte Carlo times. Clearly, the exponential behavior is conserved in the presence of diffusion, and the typical lengthscale of that distribution (i.e., domain size) increases over time.

Figure 3.

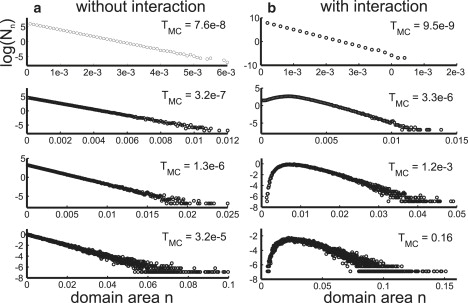
Domain size distributions determined using Monte Carlo simulations. (a) Distribution for four different Monte Carlo times averaged over 1000 simulation runs (open circles) including diffusion. Initial condition: 10⁴ domains of area ɛ = 10⁻⁴. (b) Distribution for four different Monte Carlo times averaged over 1000 simulation runs (open circles), including diffusion and interaction of domains. Here p^merge_n,m = 10⁻⁶/(n^∗m). Initial condition: 10⁴ domains of area ɛ = 10⁻⁴.

In the kinetic hindrance model for budded domains the probability for merger of two neighboring domains decreases with domain size. Hence we assume $p_{\text{n,m}}^{\text{merge}}$ = c/(n^∗m). (Since we do not attempt to obtain quantitative agreement with the experimental results, any probability that decreases monotonically with domain sizes would be acceptable as well. See the Supporting Material for the results of a simulation with $p_{\text{n,m}}^{\text{merge}}=c/\sqrt{n\ast m}$, which are qualitatively identical to the results presented below). Fig. 3 b shows intermediate domain size distributions for four different Monte Carlo times. The simulations reproduce the two qualitative features observed in experiments: the local maximum and the exponential tail (see Fig. 2). We find that at T_MC ∼ 175, phase separation is still not complete. This is much longer than the time we found for complete phase separation in the case without interactions (T_MC ∼ 2). The Monte Carlo simulations therefore show that incomplete phase separation is a quasistatic state.

Domain Budding

The experimentally observed distributions of domain distances and sizes can be explained by a repulsive membrane-mediated interaction between the domains. Domains that partially bud out from the vesicle locally deform the membrane around them. Placing two budded domains close together causes this deformation to be larger, carrying a larger energy and resulting in an effective force between them. This membrane-mediated force is therefore a direct consequence of the fact that the domains partially bud out from the vesicle. In this section, we analyze the energetics of this partial budding process.

The first systematic study of domain budding was performed by Lipowsky (20). He modeled the domains as either circular disks in, or spherical caps on, a flat background. Domain budding is then a consequence of a tradeoff between two competing forces, which we will treat here in a coarse-grained, mean-field manner. For a more detailed view on the microscopic processes involved, we refer to reviews by Lipowsky and Dimova (21) and Seifert (22). The first force is the line tension between the L_o domain and the L_d background, which favors budding because it reduces the length of the domain boundary. On the other hand, the bending energy of the L_o domain resists budding because a budded domain has a higher curvature. Lipowsky found that there is a critical domain size at which there is a transition between an unbudded (or flat) state and a fully budded domain. This lengthscale is called the invagination length, given by ξ = κ_o/τ, with κ_o the bending modulus of the L_o phase and τ the line tension on the domain boundary; in our experimental vesicles we have κ_o ∼8.0 × 10⁻¹⁹ J and τ ∼1.2 pN, giving ξ ∼ 0.7 μm (17). The invagination length therefore sets the length scale at which we expect to find the first occurrence of domain budding. Although we occasionally see domains splitting off from the vesicle completely, we mostly observe partially budded domains. In the model proposed by Lipowsky, partial budding is not possible, suggesting that we need to consider additional constraints on, for example, the vesicle area and volume, and/or additional energy contributions. Such constraints were also studied by Jülicher and Lipowsky (23,24). They used numerical methods to find the minimal-energy shape of a L_d vesicle with a single L_o domain. Their results confirm the finding by Lipowsky that there is a critical domain size for budding. Moreover, they found that a constraint on the volume of the vesicle only changes the budding point but does not modify the qualitative budding behavior. In the following, we show that it is not sufficient to just include area and volume constraints to explain the shape of our experimental vesicles. If we also allow for stretching of the membrane, we do get the partially budded vesicle shapes.

In general, the equilibrium shape of the membrane of a GUV is found by minimizing the associated shape energy functional under appropriate constraints on the total membrane area and enclosed volume. The functional is composed of several contributions, reflecting the energy associated with the deformation of the membrane and the effect of phase separation of the different lipids into domains. The contribution due to bending of the membrane (i.e., the bending energy) is given by the Canham-Helfrich energy functional (25,26):

$${\text{E}}_{\text{CH}}={\text{E}}_{\text{curvature}}+{\text{E}}_{\text{Gauss}}=\mathrm{\int }\left[\frac{\kappa }{2}{\left(2H\right)}^2+{\kappa }_{\text{G}}K\right]dS\text{.}$$ (5)

Here H and K are the mean and Gaussian curvature of the membrane respectively, and κ and κ_G the bending and Gaussian moduli. We have not included a spontaneous curvature, because in our experimental system the membrane has ample time to relax any asymmetries between the membrane leaflets. Using the Gauss-Bonnet theorem, we find that the integral over the Gaussian curvature over a continuous patch of membrane, such as one of our L_o domains or the L_d background, yields a constant bulk contribution (which we can disregard) plus a boundary term (27).

For a GUV with a uniform membrane, the shape that minimizes the bending energy (Eq. 5) is found to be a sphere. If the membrane contains domains with different bending moduli κ, the sphere is no longer the optimal solution. However, within the bulk of each domain, far away from any domain boundary, the sphere is still a good approximation of the actual membrane shape. For the case at hand, where we have many small and relatively stiff domains in a more flexible background, we follow Lipowsky (20) and model the small domains as spherical caps on a vesicle that also has spherical shape itself (see Fig. 4 d). Although this model has the serious shortcoming that it suggests infinite curvature at the domain edge, it remains a good approximation for the overall vesicle shape, because it corresponds to the minimal-curvature solution of the shape equation on the entire vesicle except a few special points. For the special case that all domains are equal in size, we can describe them with a curvature radius R_c and opening angle θ_c, and the background sphere with its radius R_b and opening angle θ_b (see Fig. 4 d). For the mean curvature energy of a system with N domains, we then have

$${\text{E}}_{\text{curvature}}=4\pi {\kappa }_{\text{o}}N(1-\cos {\theta }_{\text{c}})+4\pi {\kappa }_{\text{d}}(2-N(1-\cos {\theta }_{\text{b}})),$$ (6)

where κ_o and κ_d are the bending moduli of the L_o and L_d phases, respectively. The Gaussian curvature contribution is given by the boundary term

$${\text{E}}_{\text{Gauss}}=2\pi N\Delta {\kappa }_{\text{G}}\cos {\theta }_{\text{c}},$$ (7)

with Δκ_G the difference in Gaussian curvature modulus between the L_o and L_d domains. As mentioned above, we model the fact that the lipids separate into two phases by assigning a line tension to the phase boundary. The energy associated with that line tension τ in the spherical cap model is given by

$${\text{E}}_{\text{tension}}=2\pi \tau N{R}_{\text{b}}\sin {\theta }_{\text{b}}\text{.}$$ (8)

Figure 4.

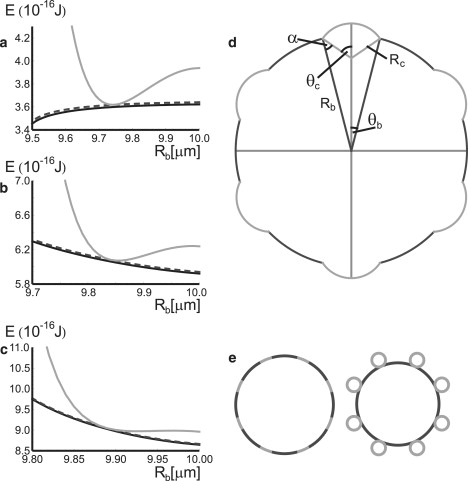
Energies of the sphere-with-domains system for 10 (a), 25 (b), and 50 (c) domains as a function of the radius R_b of the background sphere in micrometers. In each case, the geometrical (Eq. 9) and volume constraints (Eq. 10) are met and the total area of the domains is fixed. The vesicle has a surface/volume ratio that is slightly larger than that of a sphere, to create area for the domains to bud out. For the material parameters, we use the values we obtained in an earlier study on phase-separated membrane vesicles (17). The solid line shows just the contributions of curvature and line tension; the dashed line shows the contributions of curvature and line tension, plus a surface tension term; and the shaded line shows all contributions, including a surface elasticity term (Eq. 15). Without the surface elasticity term, the minimum of the energy is located at the maximum vesicle radius (b and c), implying flat domains (e, left), or the minimum vesicle radius (a), implying full budding (e, right). In the case of 50 domains, the line tension is not strong enough yet to create buds, but when there are only 25 it forces the domains to bud out and deform the membrane around, halting or at least slowing down further fusion of domains. The energy without the surface elasticity term predicts that the buds form complete spheres, whereas the one with the surface elasticity predicts spherical caps, as observed. In these plots, the excess area fraction $\frac{R_{\text{A}}-R_{\text{V}}}{R_{\text{V}}}={\left(\frac{A}{4\pi }\right)}^{\frac{1}{2}}{\left(\frac{3V}{4\pi }\right)}^{-\frac{1}{3}}-1$ is equal to 0.012. Panel d shows the coordinate system for the spherical caps model and panel e the two extremal situations—complete budding (right) and no budding at all (left).

If the total number N of domains is fixed, the energy given by the sum of Eqs. 6–8 is a function of four variables: R_b, R_c, θ_b, and θ_c. These variables are not independent, since they are subject to constraints. The first is that the membrane must be continuous at the domain boundary, which gives the geometric constraint

$$R_{\text{c}}\sin {\theta }_{\text{c}}=R_{\text{b}}\sin {\theta }_{\text{b}}\text{.}$$ (9)

Since the volume of the vesicle will change only over long timescales (hours) (28), we assume it is constant in our experiment (minutes), leading to a volume constraint on our system

$$\frac{4\pi }{3}\left[R_{\text{b}}^3+N{R}_{\text{c}}^3{(1-\cos {\theta }_{\text{c}})}^2(2+\cos {\theta }_{\text{c}})-N{R}_{\text{b}}^{\text{3}}{(1-\cos {\theta }_{\text{b}})}^2(2+\cos {\theta }_{\text{b}})\right]=V_0,$$ (10)

where V₀ is the volume of the vesicle. Finally we consider the area of the vesicle. We have to treat the (total) area of the domains and that of the bulk phase separately. If we fix both of them, we obtain two additional constraints:

$$2\pi N{R}_{\text{c}}^2(1-\cos {\theta }_{\text{c}})=A_{\text{c},0},$$ (11)

and

$$2\pi R_{\text{b}}^2(2-N(1-\cos {\theta }_{\text{b}}))=A_{\text{b},0}\text{.}$$ (12)

If all four constraints given by Eqs. 9–12 are imposed rigorously, the shape of the vesicle is fixed, because there were only four unknowns in the system. For an experimental system at temperature T > 0, however, the total area is not conserved. Thermal fluctuations cause undulations in the membrane, resulting in a larger area than the projected area given by A_{c, 0} and A_{b, 0} (29). For T > 0 we should therefore not work in a fixed-area ensemble, but rather in a fixed surface-tension ensemble. We drop the constraints given by Eqs. 11 and 12 and instead add an area energy term to the total energy

$${\text{E}}_{\text{area}}=2\pi {\sigma }_{\text{o}}N{R}_{\text{c}}^2(1-\cos {\theta }_{\text{c}})+2\pi {\sigma }_{\text{d}}{R}_{\text{b}}^{\text{2}}(2-N(1-\cos {\theta }_{\text{b}})),$$ (13)

with σ_o and σ_d the surface tensions of the L_o and L_d phases, respectively. Note that Eq. 13 can be interpreted in two ways: in the fixed area ensemble, it contains two freely adjustable Lagrange-multipliers (σ_o and σ_d), which enforce the conditions given by Eqs. 11 and 12. In the fixed surface tension ensemble, σ_o and σ_d are set and the shape is found by minimizing the total energy with respect to the free parameters, considering the remaining geometrical and volume constraints given by Eqs. 9 and 10. These constraints can, of course, be included in the total energy using Lagrange multipliers as well. This is often done for the volume constraint, and the associated Lagrange multiplier is usually identified as the pressure difference across the membrane. We stress that since we fix the total volume (i.e., work in a fixed volume ensemble), this pressure is selected by the system and is not an input parameter. The Lagrange-multiplier approach is mathematically equivalent to imposing an external volume constraint as we do here for practical purposes.

Equation 13 correctly gives the free energy contribution of the area energy in what is called the entropic regime, where the dominant contribution to the area term is due to the thermal fluctuations of the membrane (29). To account for the fact that the membrane itself can be stretched or compressed away from its natural area, A₀, we include a quadratic term in the area of the membrane (30):

$${\mathrm{E}}_{\text{elastic}}=\gamma {\left(\frac{A-A_0}{A_0}\right)}^2\text{.}$$ (14)

The elastic modulus γ is ∼10⁻¹⁴ J in the tricomponent system considered here (28). One way to understand Eq. 14 is that in the high-tension or elastic regime, the surface tension is no longer a fixed number, but itself depends linearly on the area (29). The total shape energy is given by the sum of the five contributions (Eqs. 6–8, 13, and 14)

$$\text{E}={\text{E}}_{\text{curvature}}+{\text{E}}_{\text{Gauss}}+{\text{E}}_{\text{tension}}+{\text{E}}_{\text{area}}+{\text{E}}_{\text{elastic}}\text{.}$$ (15)

With the constraints from Eqs. 9 and 10, we are left with two independent variables for the minimization of the total energy. Since the surface tension and elastic modulus of the L_o phase are much larger than that of the L_d phase (17,28), we further assume that the area of the L_o domains is fixed. This leaves us with a single variable minimization problem, which we solve numerically. For the material parameters, we use the values we obtained in an earlier study on phase-separated membrane vesicles (17). The results are shown in Fig. 4. In the same figure we plot the energy without the membrane-stretching term (Eq. 14). In this case we find no partial budding, showing that the area elasticity term is required to reproduce the experimental results, and that our experimental vesicles are well within the elastic regime. Plotting the minima of the energy as a function of the number of budded domains on the vesicle, we find that it decreases with the number of domains (Fig. S2). Therefore the fully phase-separated vesicle is the ground state, as we expected from the fact that the line tension is strong enough to dominate the shape.

Measuring the Interactions

Domain position tracking

To determine quantitatively the interaction strength between the domains, we tracked their positions over time. In particular, we regarded situations like the one shown in Fig. 5, in which a single domain is surrounded and held in place by a shell of 4–6 neighbor domains. We recorded the distance between the central domain and the center-of-mass of the shell domains (projected on the vesicle surface) over time and calculated the mean-squared displacement (msd); see Fig. 5 for a typical example. Using only relative distances eliminates any influence of putative flow or overall movement of domains.

Figure 5.

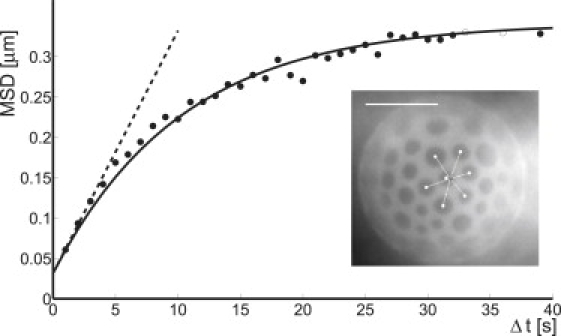
Typical example of the mean-square displacement (msd) of the distance between central domain and center-of-mass of the surrounding domains (dots); (solid line) fit to the Ornstein-Uhlenbeck model (Eq. 16); and (dashed line) linear fit to the first three data points. (Inset) Example for tracking configuration. (Open dots) Centroids of domains; (solid dot) center-of-mass of domains constituting the shell; and (shaded line) vector connecting the centroid of the central domain and the center-of-mass of the shell domains. The msd of this distance is used to determine the diffusional behavior of the central domain. Scale bar, 20 μm.

Although the precise form of the potential that confines the central domain is not known, we can approximate it around the local minimum by a harmonic potential $U\left(x\right)=\frac{1}{2}k{x}^2$ with spring constant k. If we treat the domain as a random walker with diffusion constant D, our model is formally equivalent to an Ornstein-Uhlenbeck process (31). Alternatively, one can imagine all domains connected by harmonic springs. This approach also leads to an isotropic harmonic confining potential for the central domain. The msd of the domain is given by

$$\langle \Delta x^2(\Delta t)\rangle =\frac{4k_{\text{B}}T}{k}\left[1-\exp \left(-\frac{kD}{k_{\text{B}}T}\Delta t\right)\right]\approx 4D\Delta t\text{for small}\Delta t\text{.}$$ (16)

In practice, we determined the diffusion coefficient D (and a small offset due to the finite positional accuracy) from a linear fit to the first three time lags (see Fig. 5), since the reliability of the data points is highest in that region. Fig. S4 shows the diffusion coefficient as a function of the size of the central domain. The other parameter of the Ornstein-Uhlenbeck model for the msd of a domain (Eq. 16) is the spring constant k. We determined its value from a fit of Eq. 16 to the full experimental data set, where D was fixed to the value determined before. Fig. 6 shows k normalized by the number of nearest neighbors as a function of the size of the central domain. On average, k = 1.4 ± 0.5 k_BT/μm². This value supports the observation that domains are stable over extended periods of time: since the distance between domains is typically several μm, the energy barrier that the domains have to overcome in order to fuse is well above k_BT. Due to the limited amount of available trajectories, the error in the determination of k is fairly large. Hence, it is not possible to deduce the quantitative dependence of k on the domain size. Therefore, we determined k more precisely in a separate, independent way, based on domain distance statistics.

Figure 6.

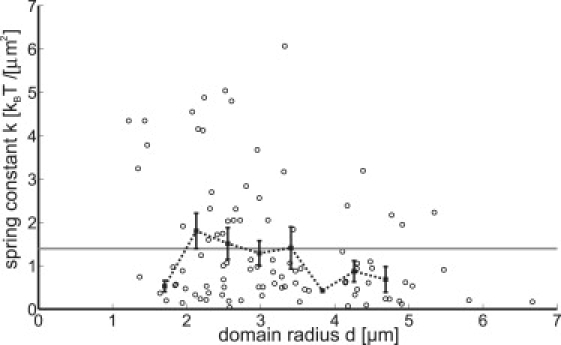
Spring constant k corrected for the number of nearest neighbors versus domain radius (open circles); the solid squares correspond to binned data. The shaded line marks the average k = 1.4 ± 0.5 k_BT/μm². Reported error bars are standard errors of the mean.

Domain distance statistics

The interaction potential between two domains can be directly inferred from the distribution of domain distances, as already demonstrated by Rozovsky et al. (13). We consider a central domain surrounded by N nearest neighbors, whose combined imposed potential is given by U. Then the probability p(x) to find the central domain a distance x from the center-of-mass of the neighbors is proportional to the Boltzmann factor $p\left(x\right)\propto \exp \left(-\frac{U\left(x\right)}{k_{\text{B}}T}\right)$. As before, we assume the imposed potential, at least locally, to be harmonic, $U\left(x\right)=\frac{1}{2}k{x}^2$, which gives for p(x)

$$-\ln \left(p\left(x\right)\right)=\text{const}\text{.}+\frac{1}{2}k{x}^2\text{.}$$ (17)

To determine k, we used Eq. 17 to fit $-\ln \left(p\left(x\right)\right)$, where p(x) was determined from the distances of the four nearest neighbors of each domain. When determining p(x), the data was binned according to the size of the central domain. Fig. S5 shows an example of the distance distribution and a fit of the potential to $-\ln \left(p\left(x\right)\right)$.

The available data set for domain distances is much larger than the one we obtained from domain tracking. Consequently, the spring constant k can be determined with a smaller error (see Fig. 7). The average k = 1.6 ± 0.2 k_BT/μm² coincides with the result found from domain tracking k = 1.4 ± 0.5 k_BT/μm². Interestingly, k shows a nonlinear behavior with a clear maximum for domains of an intermediate size which roughly coincides with the size of the most abundant domains (see Fig. 2).

Figure 7.

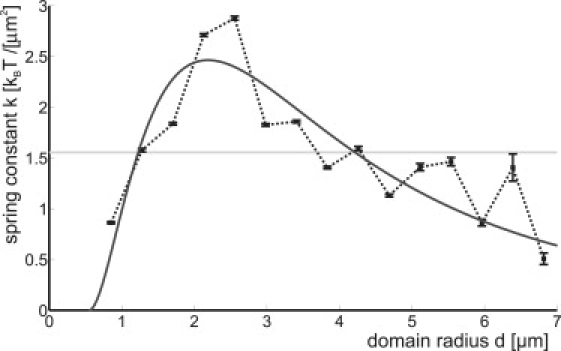
Effective spring constant k versus domain radius (solid squares). The light-shaded line marks the average k = 1.6 ± 0.2 k_BT/μm² and the dark-shaded line the theoretical fit (determined using Eq. 22).

Due to the fact that the membrane of a GUV is both curved and finite in size, the calculation of the interaction potential between two distortions on such a membrane is a very difficult task. However, in the case where we are dealing with a large number of small domains on a big vesicle, the situation approaches that of domains on an infinite and asymptotically flat membrane. For two such domains with the shape of spherical caps, the interaction potential was first calculated by Goulian et al. (6) and reads

$$V=4\pi \kappa ({\alpha }_1^2+{\alpha }_2^2){\left(\frac{a}{r}\right)}^4,$$ (18)

where r is the center-to-center distance between the two domains, a is a cutoff lengthscale taken to be the membrane thickness (a few nanometers), α₁ and α₂ are the domain's contact angles with the surrounding membrane (see Fig. 4 d), and κ is the bending modulus of the background membrane. The domains themselves are again assumed to be nondeformable spherical caps, which is a good approximation given that the ratio of their bending modulus with that of the surrounding membrane is significantly larger than 1 ($\frac{{\kappa }_{\text{o}}}{{\kappa }_{\text{d}}}\approx 4$) (17).

As Dommersnes and Fournier showed (7), the interaction between multiple inclusions is not equal to the sum of their pairwise interactions. However, the scaling of the interaction with the distance between the domains r and the contact angles α_i does not change; only the prefactor does. For any budded domain surrounded by several other budded domains, we can therefore assume a potential of the form

$$V=\overline{C}\kappa a^4\sum _{\text{i}=1}^{\text{N}}\frac{{\alpha }_0^2+{\alpha }_{\text{i}}^{\text{2}}}{r_{0\text{i}}^4},$$ (19)

where $\overline{C}$ is an (unknown) numerical constant; α₀ is the contact angle of the domain in which we are interested; α_i is that of the i^th neighbor; and r_0i is the distance between the central domain and its i^th neighbor. The number of neighbors is N, which in experimental vesicles is typically 5 or 6, corresponding to a relatively dense packing of domains. Let us assume for simplicity that the equilibrium of the potential (Eq. 19) is such that the nearest neighbors form a circle of radius r₀ around it, on which they are, on average, equally distributed. This mean-field assumption means that the central domain sees its environment as isotropic (it is not pushed in any particular direction) and its potential has a unique global minimum at the center of the circle. The energy of any displacement Δr of the central domain away from its energy minimum can then be calculated by an expansion in Δr of Eq. 19. The linear term in that expansion vanishes because of the isotropic distribution of the neighbors, in agreement with the assumption of the existence of a global potential minimum at Δr = 0. The first term of interest is therefore the quadratic term, which is given by

$$V_{\text{quadratic}}=\frac{C\kappa a^4}{2}\frac{{\alpha }_0^2+{\beta }^2}{r_0^6}{(\Delta r)}^2,$$ (20)

where C is another constant and β is the contact angle of a neighboring domain that would correspond to the time-average isotropic potential assumed above. Equation 20 allows us to experimentally determine the strength of the interactions between budded domains, since it yields an effective spring constant that can be measured

$$k=C\kappa a^4\frac{{\alpha }_0^2+{\beta }^2}{r_0^6}\text{.}$$ (21)

To be able to predict the behavior of the spring constant k as a function of the domain size d (the length of its projected radius), we need to establish how α and r₀ vary with d. At present we have no way of determining α(d) from first principles, since that would require having a full description of the complete vesicle membrane. We can argue, though, that at least it should be an increasing function of d for small domains. When a domain has just grown large enough to bud out, its circumference will still be small, and the amount of membrane bending and stretching it can induce to reduce the line tension term will also be small. As the domain grows in size, this balance shifts, and by budding-out further it makes its presence felt more strongly in the surrounding membrane. Because in our experimental system we always consider vesicles with many small domains, we assume α(d) to be in the linear regime. We therefore phenomenologically write α ∝ (d – d₀), where d₀ is the domain size at which budding first occurs, which should be of the order of the invagination length (0.5–1.0 μm; see Domain Budding).

For r₀(d), we do not need to make a guess, but can simply rely on experimental results, which show that r₀ depends linearly on d (Fig. S6). Finally, we will assume that α₀ ∼ β, since in experiments we always find that domains are typically surrounded by domains of approximately equal size (T. Idema, S. Semrau, C. Storm, and T. Schmidt, unpublished). Using the linear dependencies of α₀ and r₀ on d in the expression for the spring constant (Eq. 21), we find

$$k=A\frac{{(d-d_0)}^2}{{({\overline{r}}_0+cd)}^6}\text{.}$$ (22)

Equation 22 has two fitting parameters (A and d₀). The best fit of the experimental data is given by the dark-shaded line in Fig. 7. We find A = 1.5 × 10⁵ k_BT μm² and d₀ = 0.55 μm, which indeed is approximately the size of the invagination length (0.7 μm). Qualitatively, we find that due to the increase in repulsion strength with growing domain size, the spring constant increases with domain size for small domains. For very large domains, on the other hand, the interdomain distance also grows, and because the interactions fall off very steeply with distance, the spring constant decreases. In between, we find a maximum that corresponds to the most abundantly present domain size in the experimental vesicles.

Conclusion

We have experimentally demonstrated the presence of membrane-mediated interactions in lipid bilayer membranes and quantified their strength. We have shown that these interactions originate in locally imposed curvature from the domains on their immediate environment. We have also shown that the phenomenon of partial domain budding can be explained as a competition between curvature and elastic forces, on the one hand, and tensile forces, on the other hand. Furthermore we found that the membrane-mediated interaction influences the fusion behavior of domains, resulting in a preferred domain size. Using a simple Monte Carlo simulation, we were able to reproduce the experimental domain size distribution. Finally we found that the dependence of the interaction strength on distance is consistent with existing theory, which gives a 1/r⁴ dependence.

Proteins in the membranes of living cells distort their surrounding membrane in the same fashion as lipid domains do. We therefore predict that similar membrane-mediated interaction forces play a significant role in membrane structuring. Coarse-grained simulations show that membrane-mediated interactions can lead to the aggregation of membrane inclusions (9). In our experiments we do not observe such attractive behavior, which suggests that our model system is more comparable to larger structures, like protein aggregates. We expect that such aggregates experience repulsive interaction if they impose a curvature on the membrane. If this curvature exceeds a certain critical size, the aggregates will not be able to grow further, just like the domains stop growing after reaching a certain size. Moreover, the membrane-mediated interaction reported here has a longer range (1/r⁴) than van der Waals interactions (1/r⁶) and should therefore be the dominant interaction effect in the absence of electrical charges. We therefore expect this interaction to play an important role in many biological processes.

Supporting Material

Six figures and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00780-2.