Optimal Feedback Strength for Noise Suppression in Autoregulatory Gene Networks

Abstract

Autoregulatory feedback loops, where the protein expressed from a gene inhibits or activates its own expression are common gene network motifs within cells. In these networks, stochastic fluctuations in protein levels are attributed to two factors: intrinsic noise (i.e., the randomness associated with mRNA/protein expression and degradation) and extrinsic noise (i.e., the noise caused by fluctuations in cellular components such as enzyme levels and gene-copy numbers). We present results that predict the level of both intrinsic and extrinsic noise in protein numbers as a function of quantities that can be experimentally determined and/or manipulated, such as the response time of the protein and the level of feedback strength. In particular, we show that for a fixed average number of protein molecules, decreasing response times leads to attenuation of both protein intrinsic and extrinsic noise, with the extrinsic noise being more sensitive to changes in the response time. We further show that for autoregulatory networks with negative feedback, the protein noise levels can be minimal at an optimal level of feedback strength. For such cases, we provide an analytical expression for the highest level of noise suppression and the amount of feedback that achieves this minimal noise. These theoretical results are shown to be consistent and explain recent experimental observations. Finally, we illustrate how measuring changes in the protein noise levels as the feedback strength is manipulated can be used to determine the level of extrinsic noise in these gene networks.

Introduction

Gene expression and regulation is inherently a noisy process. The origins of this stochasticity lie in the probabilistic nature of transcription and translation and low copy numbers of RNAs and proteins within cells, which can lead to large statistical fluctuations in molecule numbers. Recent work (1–6) has provided considerable experimental evidence for these stochastic fluctuations and may explain the large amounts of cell-to-cell variation observed in genetically identical cells exposed to the same environmental conditions (7,8). Various gene network motifs within cells decrease these stochastic fluctuations. A common such motif is an autoregulatory gene network where the protein expressed from the gene inhibits its own transcription (9,10). Both theoretical and experimental studies have shown that negative feedback in these autoregulatory gene networks reduces stochastic fluctuations in the protein population (11–19), whereas positive feedback has the opposite effect (20,21).

Autoregulatory gene networks are characterized by their transcriptional response g(x), which determines the transcription rate of the gene as a nonlinear function g of the protein molecular count x within the cell. Monotonic decreasing and increasing functions g(x) denote negative and positive feedback, respectively. The noise in the protein population is quantified by its coefficient of variation defined as the ratio of the standard deviation to the average number of protein molecules. Previous work has shown that this protein noise level is determined by a combination of two components (22,23). The first is the intrinsic noise, which represents the stochastic fluctuations in the protein population arising due to random mRNA and protein formation/degradation events. The second component is the extrinsic noise, which corresponds to fluctuations in the protein numbers arising due to an exogenous noise source driving the autoregulatory gene network, e.g., fluctuations in gene copy numbers, enzyme levels, and/or environmental stimuli.

Using a gene expression model where each expression event produces a burst of random numbers of protein molecules, we decompose the total noise in the protein population into its extrinsic and intrinsic components. In particular, both these components of noise are expressed in terms of the response time defined as follows: assuming x^∗ to be the steady-state average protein count, the response time T_r is the time taken for any initial perturbation about x^∗ to decay by 50% of its initial value. The response time is intrinsically connected to the stability of the equilibrium x^∗ with more stable equilibriums having smaller values of T_r. We show that for a fixed average number of protein molecules, decreasing response times leads to attenuation of both protein intrinsic and extrinsic noise, with the extrinsic noise being more sensitive to changes in the response time.

We next quantify noise in autoregulatory gene networks that involve a common negative feedback with transcriptional response given by

$$g\left(\mathbf{x}\right)=\frac{g_0}{1+{\left(a\mathbf{x}\right)}^{\text{M}}},$$ (1)

where M ≥ 1 denotes the Hill coefficient, g₀ corresponds to the maximum transcription rate, and the constant a characterizes the negative feedback strength. We perform a systematic analysis of how the protein noise level changes as the feedback strength is increased, keeping all the other kinetic parameters of the gene network fixed. In this procedure of varying the feedback strength a, the steady-state average protein level monotonically decreases with increasing a. We show that in this case, the total noise in the protein population is minimal at some optimal level of feedback strength, and decreasing or increasing feedback strength away from this optima always causes an increase in the noise level. We quantify both the optimal level of feedback strength and the limit of noise suppression, which is defined as the ratio of the minimum possible noise in the protein population to the protein noise level when there is no feedback. We show that this limit of noise suppression can be used to estimate the noise in the exogenous signal that is the source of protein extrinsic noise. These theoretical results are validated using experimental data from Dublanche et al. (24) for a synthetic autoregulatory gene network.

Finally, we investigate how the protein noise level changes as the feedback strength is increased, keeping the steady-state average protein level x^∗ fixed. Here increasing feedback strength is also accompanied by a change in one of the gene network parameters (for example, the maximum transcription rate g₀) such that x^∗ does not change. We show that depending on which gene network parameter is varied with the feedback strength, the protein noise level can either monotonically decrease with increasing feedback strength or can be minimal at an optimal level of feedback strength.

Unregulated Gene Expression

We consider a simple model of gene expression where a gene expresses a protein X in bursts that occur at a rate K_x. Each expression event leads to a burst of N_x molecules of the protein X. Recent work suggests that the burst of proteins from each mRNA transcript follows a geometric distribution (25–27). Thus, instead of assuming N_x to be a constant, we assume it to be a random variable with mean N_x and variance V²_x. We also assume that the protein decays at a constant rate d_x. Our model omits the mRNA dynamics. This is a valid approximation as long as the protein's half-life is much longer than the mRNA's half-life (26,28). Shahrezaei and Swain (26) does a survey of ∼2000 genes in budding yeast and shows that most genes do indeed satisfy this condition. Ignoring the mRNA dynamics leads to relatively simple expressions for the protein noise level, which help develop a qualitative understanding of how noise level changes in response to alterations of the gene network parameters.

In a stochastic formulation, gene expression and protein degradation are treated as probabilistic events with probabilities of occurring in an infinitesimal time interval (t, t + dt] given by

$$\text{Pr}\{\mathbf{x}(t+dt)=x+{\mathit{N}}_{\text{x}}|\mathbf{x}\left(t\right)=x\}=K_{\text{x}}dt,$$ (2a)

$$\text{Pr}\{\mathbf{x}(t+dt)=x-1|\mathbf{x}\left(t\right)=x\}=d_{\text{x}}xdt,$$ (2b)

respectively, where x(t) denotes the number of molecules of protein X at time t.

A convenient way to model the time evolution of the number of molecules x is through a stochastic hybrid system (SHS) characterized by trivial continuous dynamics

$$\mathbf{x}\dot{}=0,$$ (3)

and two reset maps

$$\mathbf{x}{\varphi }_1(\mathbf{x})=\mathbf{x}+N_{\text{x}},\mathbf{x}{\varphi }_2\left(\mathbf{x}\right)=\mathbf{x}-1$$ (4)

with corresponding transition intensities given by

$${\lambda }_1\left(\mathbf{x}\right)=K_{\text{x}},{\lambda }_2\left(\mathbf{x}\right)=d_{\text{x}}\mathbf{x}$$ (5)

(29). To gauge the noise level in the protein population, we determine the time evolution of the first- and second-order moments of x, i.e., the expected values E[x] and E[x²]. The moment dynamics can be obtained using the Dynkin's formula for the above SHS, according to which, for every differentiable function ψ(x), we have that

$$\frac{d\mathbf{E}\left[\psi \left(\mathbf{x}\right)\right]}{dt}=\mathbf{E}\left[\sum _{\text{i}=1}^2\left(\psi \left({\varphi }_{\text{i}}\left(\mathbf{x}\right)\right)-\psi \left(\mathbf{x}\right)\right){\lambda }_{\text{i}}\left(\mathbf{x}\right)\right]$$ (6)

(30,31). Taking ψ(x) = x and ψ(x) = x² in Eq. 6, we obtain the following moment dynamics:

$$\frac{d\mathbf{E}\left[\mathbf{x}\right]}{dt}=N_{\text{x}}{K}_{\text{x}}-d_{\text{x}}\mathbf{E}\left[\mathbf{x}\right],$$ (7a)

$$\frac{d\mathbf{E}\left[{\mathbf{x}}^2\right]}{dt}=K_{\text{x}}(N_{\text{x}}^2+V_{\text{x}}^2)+d_{\text{x}}\mathbf{E}\left[\mathbf{x}\right]+2K_{\text{x}}{N}_{\text{x}}\mathbf{E}\left[\mathbf{x}\right]-2d_{\text{x}}\mathbf{E}\left[{\mathbf{x}}^2\right]\text{.}$$ (7b)

As t → ∞, the first- and second-order moments converge to constant steady-state values given by

$${\mathbf{x}}^{\ast }=\underset{t\to \mathrm{\infty }}{\lim }\mathbf{E}\left[\mathbf{x}\left(t\right)\right]=\frac{N_{\text{x}}{K}_{\text{x}}}{d_{\text{x}}},$$ (8a)

$${\mathbf{E}}^{\ast }\left[{\mathbf{x}}^2\right]=\underset{t\to \mathrm{\infty }}{\lim }\mathbf{E}\left[{\mathbf{x}}^2\left(t\right)\right]=\frac{K_{\text{x}}{d}_{\text{x}}{N}_{\text{x}}+2K_{\text{x}}^2{N}_{\text{x}}^2+K_{\text{x}}{d}_{\text{x}}(N_{\text{x}}^2+V_{\text{x}}^2)}{2d_{\text{x}}^2}\text{.}$$ (8b)

We quantify the noise in x(t) by its coefficient of variation defined as the ratio of the standard deviation in protein numbers to the average number of protein molecules. Using the above steady-state values, we obtain

$$C{V}_{\text{int-nr}}^2=\frac{{\mathbf{E}}^{\ast }\left[{\mathbf{x}}^2\right]-{\mathbf{x}}^2}{{\mathbf{x}}^2}=\frac{d_{\text{x}}(N_{\text{x}}^2+V_{\text{x}}^2+N_{\text{x}})}{2K_{\text{x}}{N}_{\text{x}}^2}=\frac{N_{\text{x}}^2+V_{\text{x}}^2+N_{\text{x}}}{2{\mathbf{x}}^{\ast }{N}_{\text{x}}}\text{.}$$ (9)

This quantity quantifies the noise in the protein X solely due to random gene expression and protein degradation, and is referred to as the intrinsic noise in the protein population when there is no regulation. Table 1 provides a summary of the notations used for the different forms of noise in the protein population. Note that the noise in the protein increases with the variance V²_x in the number of protein molecules produced in each transcription event. A special case of Eq. 9 is obtained for N_x = 1 and V_x = 0, for which x(t) has a Poisson distribution and CV_int–nr² = 1/x^∗. In the next section, we examine what happens to this intrinsic noise when the gene expression rate is not a constant but a function of the number of protein molecules.

Table 1.

Summary of notation used in this article

CVtot	Total noise in protein numbers.
CVext	Extrinsic noise in protein numbers.
CVint	Intrinsic noise in protein numbers.
CVz	Noise in the exogenous signal driving the gene network.
CVtot–nr	Total noise in protein numbers when there is no feedback.
CVext–nr	Extrinsic noise in protein numbers when there is no feedback.
CVint–nr	Intrinsic noise in protein numbers when there is no feedback.
CVtot–min	Minimum possible total noise in protein numbers with optimal negative feedback.
CVext–min	Minimum possible extrinsic noise in protein numbers with optimal negative feedback.
CVint–min	Minimum possible intrinsic noise in protein numbers with optimal negative feedback.
amin	Feedback strength where the total noise in the protein is minimum.
x∗	Steady-state mean protein level.
Tr	Protein response time.
Tnr	Protein's half-life.
Tz	Response time of the exogenous signal.

Autoregulatory Gene Expression

Often the expressed protein binds to the promoter region of its own gene. In doing so, it either recruits the enzyme RNA polymerase to the promoter (which leads to an increase in gene expression) or blocks RNA polymerase from binding to the promoter (which causes a decrease in gene expression). Such gene expression is referred to as an autoregulatory gene network. Recent work has reported that >40% of Escherichia coli transcription factors regulate their own expression through these mechanisms (32).

We model this network by assuming that the rate of gene expression is no longer a constant and is instead a function g(x) of the number of protein molecules x. We refer to the function g(x) as the transcriptional response of the network. This transcriptional response can be formally derived assuming that the rate of binding and dissociation between the protein and its promoter is much faster than the dynamics of protein production and degradation (9), or it can be determined directly from experiments. Monotonic decreasing and increasing functions g(x) denote negative and positive feedback, respectively.

When an autoregulation mechanism is present, the probabilities of gene expression and protein degradation events occurring in an infinitesimal time interval (t, t + dt] are given by

$$\text{Pr}\{\text{x}(t+dt)=x+{\mathit{N}}_{\text{x}}|\mathbf{x}\left(t\right)=x\}=g\left(x\right)dt,$$ (10a)

$$\text{Pr}\{\mathbf{x}(t+dt)=x-{\mathit{N}}_{\mathbf{x}}|\text{x}\left(t\right)=x\}=d_{\text{x}}xdt\text{.}$$ (10b)

To write the moment dynamics of x we approximate g(x) by a linear transcriptional response,

$$g\left(\mathbf{x}\right)\approx g\left({\mathbf{x}}^{\ast }\right)+{\text{g}}^{\prime }\left({\mathbf{x}}^{\ast }\right)(\mathbf{x}-{\mathbf{x}}^{\ast }),$$ (11)

where x^∗ is the steady-state average protein count. This approximation is valid as long as the stochastic fluctuations in the protein do not leave the region in which g(x) is approximately linear.

As in the section on Unregulated Gene Expression, we model the time evolution of x through an SHS, but now the transition intensities are given by λ₁(x) = g(x^∗) + g′(x^∗)(x – x^∗) and λ₂(x) = d_xx. Using the Dynkin's formula for this modified SHS, we obtain the following dynamics for the mean E[x],

$$\frac{d\mathbf{E}\left[\mathbf{x}\right]}{dt}=N_{\text{x}}g\left({\mathbf{x}}^{\ast }\right)-d_{\text{x}}{\mathbf{x}}^{\ast }+(N_{\text{x}}{g}^{\prime }\left({\mathbf{x}}^{\ast }\right)-d_{\text{x}})(\mathbf{E}\left[\mathbf{x}\right]-{\mathbf{x}}^{\ast }),$$ (12)

and the steady-state value x^∗ for the mean population E[x] must satisfy

$$N_{\text{x}}g\left({\mathbf{x}}^{\ast }\right)=d_{\text{x}}{\mathbf{x}}^{\ast }\text{.}$$ (13)

Assuming that this steady state is stable, we have a negative eigenvalue

$$\lambda =N_{\text{x}}{g}^{\prime }\left({\mathbf{x}}^{\ast }\right)-d_{\text{x}}<0$$ (14)

for the linear system given by Eq. 12. This eigenvalue λ can be expressed in terms of the response time T_r of the protein. The response time is defined as the time taken for any perturbation around x^∗ to decay by 50% of its initial value, and is given by

$$T_{\text{r}}=-\frac{\ln \left(2\right)}{\lambda }>0,\lambda =N_{\text{x}}{g}^{\prime }\left({\mathbf{x}}^{\ast }\right)-d_{\text{x}}<0\text{.}$$ (15)

The above equation shows that for a fixed mean protein count x^∗, average burst size N_x, and protein degradation rate d_x, making the slope g′(x^∗) more negative decreases the response time T_r.

We now compute the coefficient of variation of x(t) by writing the moment dynamics for the second-order moment E[x²]. Using Eq. 6, with ψ(x) = x² we obtain the following time derivative for E[x²]:

$$\frac{d\mathbf{E}\left[{\mathbf{x}}^2\right]}{dt}=[g\left({\mathbf{x}}^{\ast }\right)-{\mathbf{x}}^{\ast }{g}^{\prime }\left({\mathbf{x}}^{\ast }\right)](N_{\text{x}}^2+V_{\text{x}}^2)+d_{\text{x}}\mathbf{E}\left[\mathbf{x}\right]+2[g\left({\mathbf{x}}^{\ast }\right)-{\mathbf{x}}^{\ast }{g}^{\prime }\left({\mathbf{x}}^{\ast }\right)]N_{\text{x}}\mathbf{E}\left[\mathbf{x}\right]-2d_{\text{x}}\mathbf{E}\left[{\mathbf{x}}^2\right]+g^{\prime }\left({\mathbf{x}}^{\ast }\right)(N_{\text{x}}^2+V_{\text{x}}^2)\mathbf{E}\left[\mathbf{x}\right]+2g^{\prime }\left({\mathbf{x}}^{\ast }\right)N_{\text{x}}\mathbf{E}\left[{\mathbf{x}}^2\right]\text{.}$$ (16)

Performing a steady-state analysis of the above equations and using Eq. 13, we obtain the following steady-state coefficient of variation,

$$C{V}_{\text{int}}=\sqrt{\frac{d_{\text{x}}(N_{\text{x}}^2+V_{\text{x}}^2+N_{\text{x}})}{2I{N}_{\text{x}}^2}},I=g\left({\mathbf{x}}^{\ast }\right)-{\mathbf{x}}^{\ast }{g}^{\prime }\left({\mathbf{x}}^{\ast }\right),$$ (17)

where I can be interpreted as the y intercept of the tangent to the transcriptional response g(x) at x = x^∗ (see Fig. 1). Using Eqs. 13, 15, and 17, we can also relate the intrinsic noise to the response time T_r of the protein as

$$C{V}_{\text{int}}=\sqrt{\frac{T_{\text{r}}}{T_{\text{nr}}}\frac{N_{\text{x}}^2+V_{\text{x}}^2+N_{\text{x}}}{2{\mathbf{x}}^{\ast }{N}_{\text{x}}}},$$ (18)

where T_nr = ln(2)/d_x is the protein's half-life. The formula in Eq. 18 shows that the intrinsic noise level in autoregulatory gene networks is determined by three factors: the average number of protein molecules x^∗; the response time of the protein T_r; and the gene expression burst-characteristics, i.e., N_x and V²_x. From Eqs. 15 and 18, we also conclude that for a fixed x^∗, N_x, V²_x, and d_x, making the slope g′(x^∗) more negative causes a decrease in the response time and leads to attenuation of intrinsic noise in the protein population. For example, for a fixed x^∗ a fivefold decrease in response time (i.e., T_r = T_nr/5) will reduce the intrinsic noise levels in the protein population by a factor of $\sqrt{5}\approx 2.2$.

Figure 1.

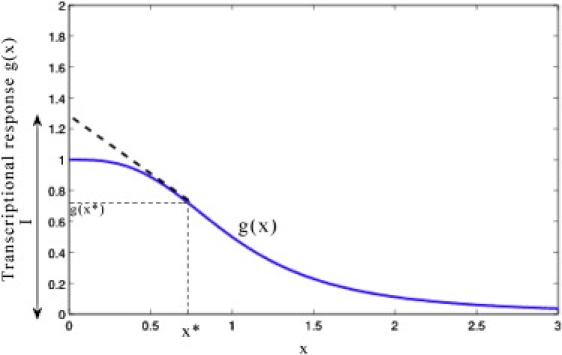
A graphical interpretation of the quantity I = g(x^∗) – x^∗g′(x^∗) in Eq. 17 for any arbitrary transcriptional response g(x): I is the intercept of the tangent to the transcriptional response g(x) at x = x^∗ with the y axis.

An important feature of Eq. 18 is that it relates the noise in the protein to parameters that can be experimentally determined. In particular, the average burst size N_x = L_x/d_r, where L_x is the translation rate of the mRNA and d_r is the mRNA degradation rate. As mentioned before, protein half-lives are typically much longer than mRNA half-lives. In this case, N_x follows a geometric distribution and V²_x = N²_x + N_x (26,27). Finally, the response times can be measured by tracking the time evolution of fluorescently tagged protein molecules (32).

Extrinsic and Intrinsic Contributions to Noise

We now consider extrinsic noise in the protein population arising due to an exogenous noise source driving the autoregulatory gene network. Toward that end, we consider a transcriptional response g(x, z) that depends on a noisy exogenous signal z. The transcriptional response g(x, z) may take different forms. For example, if the gene is encoded on a low-copy plasmid, then fluctuations in the number of copies of the plasmid are known to be a major source of extrinsic noise (24). In this case, the transcriptional response takes the form zg(x), where z represents the number of copies of the plasmid. Alternatively, z could represent the number of molecules of the RNA polymerase, in which case, the transcriptional response (assuming a feedback with a Hill coefficient equal to one) would be

$$g(\mathbf{x},\mathbf{z})=\frac{k_0\mathbf{z}}{1+k_1\mathbf{z}+k_2\mathbf{x}},$$ (19)

where k₀, k₁, and k₂ are positive constants (14).

We model the stochastic fluctuations in z by a birth-death process. In particular, the probabilities of formation and degradation of z in the infinitesimal time interval (t, t + dt] are given by

$$\text{Pr}\{\text{z}(t+dt)=z+{\text{N}}_{\text{z}}|\text{z}\left(t\right)=z\}=K_{\text{z}}dt,$$ (20a)

$$\text{Pr}\{\text{z}(t+dt)=z-1|\text{z}\left(t\right)=z\}=d_{\text{z}}zdt,$$ (20b)

where K_z and d_z represent the production and degradation rate of z, respectively, and N_z is a random variable with mean N_z and variance V²_z. In the sequel we refer to T_z = ln(2)/d_z as the response time of the exogenous signal. Following steps such as those outlined in Unregulated Gene Expression, we can conclude from Eqs. 8 and 9 that the steady-state average level and the coefficient of variation of z are given by

$${\mathbf{z}}^{\ast }=\frac{N_{\text{z}}{K}_{\text{z}}}{d_{\text{z}}}$$ (21)

and

$$C{V}_{\text{z}}=\sqrt{\frac{N_{\text{z}}^2+V_{\text{z}}^2+N_{\text{z}}}{2{\mathbf{z}}^{\ast }{N}_{\text{z}}}},$$ (22)

respectively. The quantity CV_z represents the amount of noise that enters the autoregulatory gene network through the exogenous signal z. Assuming that stochastic fluctuations around the means are sufficiently small, we linearize the transcriptional response with respect to both x and z. This gives us the transcriptional response

$$g(\mathbf{x},\mathbf{z})\approx g({\mathbf{x}}^{\ast },{\mathbf{z}}^{\ast })+\frac{dg(\mathbf{x},{\mathbf{z}}^{\ast })}{d\mathbf{x}}{|}_{\mathbf{x}={\mathbf{x}}^{\ast }}(\mathbf{x}-{\mathbf{x}}^{\ast })+\frac{dg({\mathbf{x}}^{\ast },\mathbf{z})}{d\mathbf{z}}{|}_{\mathbf{z}={\mathbf{z}}^{\ast }}(\mathbf{z}-{\mathbf{z}}^{\ast }),$$ (23)

where x^∗ and z^∗ are steady-state means of x and z, respectively. In the sequel, g(x) refers to g(x, z^∗), the transcriptional response when there is no noise in the exogenous signal. Details are presented in Appendix A (see Supporting Material) where we show that for this linearized transcriptional response, x^∗ is the solution to Eq. 13 and the total protein noise CV_tot is given by

$$C{V}_{\text{tot}}^2=C{V}_{\mathrm{int}}^2+C{V}_{\text{ext}}^2,$$ (24)

where CV_int is the previously computed intrinsic noise and

$$C{V}_{\text{ext}}=\frac{T_{\text{r}}}{T_{\text{nr}}}\sqrt{\frac{T_{\text{z}}}{T_{\text{z}}+T_{\text{r}}}}SC{V}_{\text{z}},S=\frac{{\mathbf{z}}^{\ast }}{g({\mathbf{x}}^{\ast },{\mathbf{z}}^{\ast })}\frac{dg({\mathbf{x}}^{\ast },\mathbf{z})}{d\mathbf{z}}{|}_{\mathbf{z}={\mathbf{z}}^{\ast }},T_{\text{z}}=\frac{\ln \left(2\right)}{d_{\text{z}}}$$ (25)

represents the extrinsic noise in the protein population. Note that signals z with small response times T_z result in smaller values of CV_ext because rapid fluctuations in the exogenous signal are averaged out by the dynamics of the gene network. Typically, only those exogenous signals that have response times much larger than the protein's response time contribute significantly to the extrinsic component of protein noise.

Equation 25 shows that the extrinsic component of noise CV_ext is related to the protein response time T_r, which in turn is determined by the slope of the transcriptional response g(x) at x = x^∗ (see Eq. 15). This is in contrast to the intrinsic noise CV_int, which is determined by the y intercept of the tangent to the transcriptional response g(x) at x = x^∗ (see Eq. 17).

We recall that for a fixed mean protein count x^∗, average burst size N_x, and protein degradation rate d_x, making the slope g′(x^∗) more negative decreases the response time T_r. Equation 25 predicts that like intrinsic noise, here decreasing response time also reduces the extrinsic component of noise CV_ext. We now contrast how rapidly intrinsic and extrinsic noise attenuate as the response time decreases. We first express CV_ext as a function of the extrinsic noise level CV_ext–nr that would be observed in the absence of feedback,

$$C{V}_{\text{ext}}=\frac{T_{\text{r}}}{T_{\text{nr}}}\sqrt{\frac{T_{\text{nr}}+T_{\text{z}}}{T_{\text{r}}+T_{\text{z}}}}C{V}_{\text{ext}-\text{nr}},$$ (26)

where

$$C{V}_{\text{ext}-\text{nr}}=\sqrt{\frac{T_{\text{z}}}{T_{\text{z}}+T_{\text{nr}}}}SC{V}_{\text{z}}\text{.}$$ (27)

Note from the previous section that a fivefold decrease in the response time (i.e., T_r = T_nr/5) reduced protein intrinsic noise levels by a factor of 2.2 (assuming that x^∗ is kept fixed). From Eq. 26, we conclude that this fivefold decrease in the response time corresponds to a reduction of CV_ext by a factor of 3.9 compared to CV_ext–nr when T_z ≈ T_nr, or a reduction by a factor of 5 when T_z >> T_nr. This illustrates an important point: in these autoregulatory gene networks, negative feedback is much more effective in reducing the extrinsic component of protein noise than its intrinsic component.

Autoregulatory Gene Networks with Negative Feedback

We next consider autoregulatory gene networks where transcriptional response is given by the Hill equation

$$g\left(\mathbf{x}\right)=\frac{g_0}{1+{\left(a\mathbf{x}\right)}^{\text{M}}},$$ (28)

where M ≥ 1 denotes the Hill coefficient and g₀ is the maximal transcription rate (9,33). The constant a is the feedback strength that depends on the binding affinity of the protein to the promoter, with lower binding affinities corresponding to smaller values of a. Note that a = 0 corresponds to no negative feedback in gene expression. This is because when a = 0, the transcription rate is simply g(x)|_a=0 = g₀, which is independent of the protein count. For this transcriptional response, we conclude from Eq. 13 that the steady-state average protein count x^∗ is the unique solution to

$$N_{\text{x}}g\left({\mathbf{x}}^{\ast }\right)=\frac{N_{\text{x}}{g}_0}{1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}}=d_{\text{x}}{\mathbf{x}}^{\ast },$$ (29)

and monotonically decreases as we increase the feedback strength a.

Our goal is to understand how the noise in the protein numbers change as the negative feedback strength varies. In particular, we vary the feedback strength in two different ways. Firstly, we vary a by keeping the gene network kinetics (i.e., the constants g₀, N_x, and d_x) fixed. As mentioned above, here the protein count x^∗ decreases with increasing feedback strength a. Alternatively, we vary a by keeping x^∗ fixed. In this later procedure, any increase in a is also accompanied by a change in g₀, N_x, or d_x. As we show below, in both these methods of varying the feedback strength, noise in protein numbers can be minimal at an optimal level of feedback strength.

Changing Feedback Strength by Keeping the Kinetics Fixed

We investigate how the different components of the noise and the total noise in the protein numbers change as the feedback strength is varied, keeping the constants g₀, N_x, and d_x fixed.

Suppression of intrinsic noise in the protein

We first investigate the intrinsic component of noise given by Eq. 18 for this specific transcriptional response. Substituting Eq. 28 in Eq. 18, and using Eq. 29, we conclude that the intrinsic noise CV_int in the protein is given by

$$C{V}_{\text{int}}=\sqrt{\frac{T_{\text{r}}\left[1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}\right]}{T_{\text{nr}}}}C{V}_{\text{int}-\text{nr}},$$ (30)

where

$$C{V}_{\text{int}-\text{nr}}=\sqrt{\frac{d_{\text{x}}(N_{\text{x}}^2+V_{\text{x}}^2+N_{\text{x}})}{2g_0{N}_{\text{x}}^2}}$$ (31)

is the intrinsic noise in the protein when there is no feedback (i.e., a = 0). Using Eqs. 15 and 28, we have that the response time T_r is given by

$$\frac{T_{\text{r}}}{T_{\text{nr}}}=\frac{1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}}{1+(1+M){\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}},T_{\text{nr}}=\frac{\ln \left(2\right)}{d_{\text{x}}},$$ (32)

and it monotonically decreases as we increase the feedback strength a (keeping g₀, N_x, and d_x fixed) with the asymptote

$$\underset{a\to \mathrm{\infty }}{\lim }{T}_{\text{r}}=\frac{T_{\text{nr}}}{M+1}\text{.}$$ (33)

Substituting Eq. 32 in Eq. 30, we get

$$C{V}_{\text{int}}=\sqrt{\frac{{\left[1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}\right]}^2}{1+(1+M){\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}}}C{V}_{\text{int}-\text{nr}}\text{.}$$ (34)

Straightforward calculus shows that the above intrinsic noise is smallest when the feedback strength is equal to

$$a_{\text{int}-\text{min}}=\frac{d_{\text{x}}}{N_{\text{x}}{g}_0}\frac{2M}{M+1}{\left(\frac{M-1}{M+1}\right)}^{\frac{1}{\text{M}}}$$ (35)

and the corresponding minimum intrinsic noise CV_int–min is given by

$$C{V}_{\text{int}-\text{min}}=\frac{\sqrt{4M}}{M+1}C{V}_{\text{int}-\text{nr}}\le C{V}_{\text{int}-\text{nr}}\text{.}$$ (36)

When M = 1, then a_int–min = 0 and CV_int–min = CV_int–nr, i.e., the intrinsic noise level is minimum when there is no feedback. In this particular case, increasing a causes CV_int to monotonically increase (see Fig. 2). This happens because as we increase a from zero, both T_r and x^∗ decrease in Eq. 18. However, as x^∗ decreases at a faster rate than T_r, their ratio T_r/x^∗ increases, and hence, the intrinsic noise increases as we increase the feedback strength a. When M > 1, the intrinsic noise first decreases when we increase a from zero and achieves a minimum at some optimal value a = a_int–min > 0. Increasing a beyond a_int–min causes an increase in the intrinsic noise level (see Fig. 2). Note from Fig. 2 that, for large levels of feedback strength, the intrinsic component of protein noise always increases with increasing feedback strength, irrespective of the value of the Hill coefficient.

Figure 2.

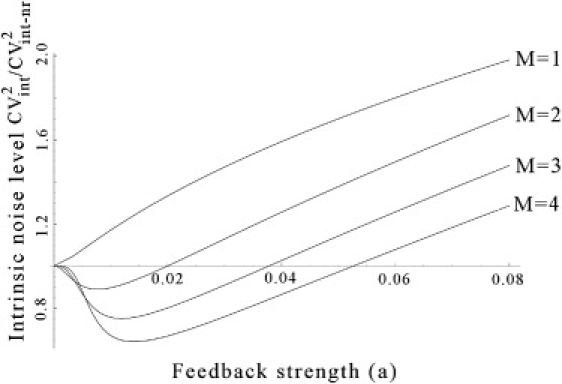
Intrinsic noise CV_int in the protein as a function of the feedback strength a and Hill coefficient M. CV_int is normalized by CV_int–nr, the intrinsic noise in the protein when there is no feedback. Other parameters taken as g₀ = 1, N_x = 1, V_x = 0, and d_x = 0.01.

From Eq. 36, the quantity

$$\frac{C{V}_{\text{int}-\text{min}}}{C{V}_{\text{int}-\text{nr}}}=\frac{\sqrt{4M}}{M+1}$$ (37)

represents the highest suppression of intrinsic noise in the protein from CV_int–nr that can be achieved with the transcriptional response given by Eq. 28. This limit of noise suppression is completely determined by the Hill coefficient M, with larger values of M causing more reduction in the protein intrinsic noise. This is consistent with results in the literature, which show that a large Hill coefficient is more effective in reducing stochastic fluctuations in the protein (12,17,33). For example, when M = 2, there can be, at most, a $1-\sqrt{4M}/(M+1)=5.7\%$ reduction in intrinsic noise from CV_int–nr, whereas for M = 4, we can have a 20% reduction.

In summary, depending on the Hill coefficient, the protein intrinsic noise levels can either monotonically increase or exhibit a U-shaped curve as the feedback strength is increased. Moreover, large Hill coefficients are much more effective in reducing noise.

Suppression of extrinsic noise in the protein

We now investigate the extrinsic component of protein noise CV_ext. As the response time T_r is a monotonically decreasing function of the feedback strength (see Eq. 32), we conclude from Eq. 25 that the extrinsic noise in protein numbers decreases with increasing feedback strength. Using Eqs. 26 and 33, the minimum level of extrinsic noise is given by

$$\frac{C{V}_{\text{ext}-\text{min}}}{C{V}_{\text{ext}-\text{nr}}}=\frac{T_{\text{rmin}}}{T_{\text{nr}}}\sqrt{\frac{T_{\text{nr}}+T_{\text{z}}}{T_{\text{rmin}}+T_{\text{z}}}},\frac{T_{\text{rmin}}}{T_{\text{nr}}}=\frac{1}{1+M},$$ (38)

and is achieved in the limit a → ∞.

Equation 38 represents the limit of extrinsic noise suppression. If the response time of the exogenous signal is much slower than the protein half-life (i.e., T_z >> T_nr), then this limit reduces to

$$\frac{C{V}_{\text{ext}-\text{min}}}{C{V}_{\text{ext}-\text{nr}}}=\frac{1}{M+1}\text{.}$$ (39)

As we increase M, these limits decrease at a much faster rate than the limit of intrinsic noise suppression (compare with right-hand side of Eq. 37). For example, when T_z ≈ T_nr and M = 2, we have a maximum reduction in extrinsic noise of $1-\sqrt{2/\left[(M+1)(M+2)\right]}$≈42%, whereas for M = 4 we have a reduction of 74%. These reductions are much larger than the maximum reductions of 5.7% and 20% in the protein intrinsic noise level for the same values of M (see previous section). This reinforces the earlier point that negative feedback is much more efficient in reducing the extrinsic component of the noise than its intrinsic component.

Suppression of total noise in the protein

Finally, we investigate how the total noise in the protein population varies with the feedback strength. As derived in Extrinsic and Intrinsic Contributions to Noise, the total protein noise level is given by

$$C{V}_{\text{tot}}^2=C{V}_{\mathrm{int}}^2+C{V}_{\text{ext}}^2\text{.}$$ (40)

By which, using Eq. 25, Eqs. 32 and 34 can be written as

$$C{V}_{\text{tot}}^2=C{V}_{\text{int}-\text{nr}}^2\frac{T_{\text{r}}\left[1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}\right]}{T_{\text{nr}}}+S^{2}C{V}_{\text{z}}^2{\left(\frac{T_{\text{r}}}{T_{\text{nr}}}\right)}^2\frac{T_{\text{z}}}{T_{\text{z}}+T_{\text{r}}},$$ (41a)

$$\frac{T_{\text{r}}}{T_{\text{nr}}}=\frac{1+{\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}}{1+(1+M){\left(a{\mathbf{x}}^{\ast }\right)}^{\text{M}}}\text{.}$$ (41b)

Now, for all M ≥ 1 and CV_z > 0, we have that

$$\underset{a\to 0}{\lim }\frac{dC{V}_{\text{tot}}^2}{d{a}^{\text{M}}}=-{\left(\frac{g_0{N}_{\text{x}}}{d_x}\right)}^{\text{M}}\left[C{V}_{\text{int}-\text{nr}}^2(M-1)+S^{2}C{V}_{\text{z}}^{2}M\frac{(2T_{\text{z}}^2+T_{\text{nr}}{T}_{\text{z}})}{{(T_{\text{z}}+T_{\text{nr}})}^2}\right]<0,$$ (42)

which means that in the presence of extrinsic noise, the total protein noise level will always decrease as we increase the feedback strength from a = 0, irrespective of the value of the Hill coefficient, but eventually will start to increase for sufficiently large values of a past an optimal feedback strength a_min. In summary, in the presence of extrinsic noise, the total noise in the protein is always minimized at some optimal feedback strength and decreasing or increasing feedback strength away from this optima will always causes an increase in the noise level. This point is shown in Fig. 3, which plots CV_tot/CV_tot–nr as a function of a when the Hill coefficient is one, where

$$C{V}_{\text{tot}-\text{nr}}^2=C{V}_{\text{int}-\text{nr}}^2+S^{2}C{V}_{\text{z}}^2\frac{T_{\text{z}}}{T_{\text{z}}+T_{\text{nr}}}$$ (43)

represents the protein noise level when there is no feedback. We can see that in the absence of extrinsic noise (CV_z = 0), CV_tot/CV_tot–nr monotonically increases as the feedback strength is increased. However, in the presence of extrinsic noise, it follows a U-shaped profile and is minimized at some a = a_min > 0.

Figure 3.

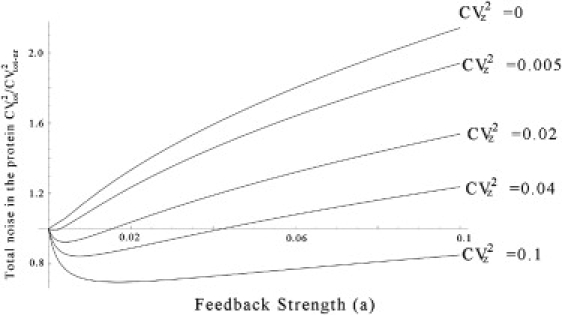
Total noise CV_tot as a function of the feedback strength a when the Hill coefficient is one (M = 1) for different values of noise CV_z in the exogenous signal. CV_tot is normalized by CV_tot–nr, the total noise in the protein when there is no feedback. Other parameters are taken as g₀ = 1, N_x = 4, V²_x = N²_x + N_x, S = 1, and d_x = 0.04. The response time T_z is assumed be much larger than T_nr.

As shown in Fig. 4, when the Hill coefficient is larger than one (M > 1), then even in the absence of any extrinsic noise (CV_z = 0), the protein noise level will show a U-shaped profile as the feedback strength is altered. In particular, for CV_z = 0, we conclude from Eq. 37 that the minimum value of CV_tot/CV_tot–nr, i.e., the limit of noise suppression, is given by

$$\frac{C{V}_{\text{tot}-\text{min}}}{C{V}_{\text{tot}-\text{nr}}}=\frac{\sqrt{4M}}{M+1}$$ (44)

and is attained when the feedback strength is equal to

$$a_{\text{min}}=\frac{d_{\text{x}}}{N_{\text{x}}{g}_0}\frac{2M}{M+1}{\left(\frac{M-1}{M+1}\right)}^{\frac{1}{\text{M}}}\text{.}$$ (45)

Figure 4.

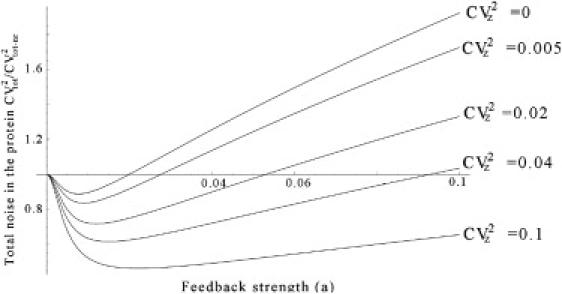
Total noise CV_tot as a function of the feedback strength a when the Hill coefficient is two (M = 2) for different values of noise CV_z in the exogenous signal. CV_tot is normalized by CV_tot–nr, the total noise in the protein when there is no feedback. Other parameters are taken as g₀ = 1, N_x = 4, V²_x = N²_x + N_x, S = 1, and d_x = 0.04. The response time T_z is assumed be much larger than T_nr.

As shown in Fig. 3 (for M = 1) and Fig. 4 (for M = 2), when we now increase CV_z away from zero, this limit of noise suppression decreases and is much lower than what is predicted by Eq. 44. On the other hand, the optimal feedback strength a_min, at which the protein noise is minimum, increases and is much higher than Eq. 45. As we further increase the noise CV_z in the exogenous signal, CV_tot–min/CV_tot–nr approaches Eq. 38, which corresponds to the scenario where extrinsic noise dominates the total noise in protein numbers.

In Appendix B (see Supporting Material), we provide formulas that predict both the minimum level of noise CV_tot–min and the optimal feedback strength when both intrinsic and extrinsic noise are present but neither dominates the total noise in the protein population. As we will illustrate later, an important application of these formulas is that one can estimate the noise in the exogenous signal from the experimentally obtained value of CV_tot–min without directly measuring the exogenous signal.

Experimental verification

We now validate our theoretical results with recent experimental measurements of protein noise levels that were obtained as the feedback strength was changed via experimental manipulation. In Dublanche et al. (24), a synthetic autoregulatory gene network is constructed where the protein inhibits its own transcription. The feedback strength is altered by adding a compound aTc that binds to the protein and the resulting complex has a significantly smaller binding affinity to the promoter. As the feedback strength is directly related to the binding affinity of the protein to its promoter, increasing the concentration of aTc corresponds to decreasing the feedback strength a. The gene is encoded on a low-copy plasmid with high variability in plasmid population contributing to large levels of extrinsic noise in the protein population. Based on our theoretical analysis, the protein noise level should show a U-shaped profile as the feedback strength is changed. In particular, at low values of a (i.e., high levels of aTc), increasing a (i.e., deceasing aTc) should lead to a decrease in protein noise levels. However, at high values of a (i.e., low levels of aTc), increasing a (i.e., deceasing aTc) should increase the protein noise levels. Such a U-shaped profile is indeed what is experimentally observed and the protein noise level is minimized at an optimal level of feedback strength (see bottom-left plot of Fig. 4 in (24)).

In Dublanche et al. (24), the results from detailed stochastic simulations of the autoregulatory gene network are also reported. The authors observe in simulation that both in the absence of any extrinsic noise or when the extrinsic noise from only the enzyme RNA polymerase is included, instead of seeing a U-shaped profile, the protein noise level monotonically increased as the feedback strength is increased (i.e., aTc concentration is decreased). Our theoretical results fully explain this phenomenon: Since in this synthetic gene network the Hill coefficient is one (M = 1), our analysis in Changing Feedback Strength by Keeping the Kinetics Fixed shows that the intrinsic noise level will always increase when the feedback strength is increased. As the extrinsic noise associated with fluctuations in RNA polymerase numbers is very small (we calculate CV_{RNA polymerase} ≈ 0.02 using Eq. 22 and the reaction rates provided in Table I of (24)), in both the above cases the protein noise is dominated by the intrinsic noise, which always increases with the feedback strength, and hence, no U-shaped profile should be observed.

As mentioned earlier, our results also allow us to predict the level of noise in the exogenous signal that drives the synthetic autoregulated gene network. Hypothesizing that the source of extrinsic noise is the plasmid population, and using the experimentally obtained minimal protein noise level of ∼0.4, we estimate in Appendix C (see Supporting Material) that

$$C{V}_{plasmid}\approx 0.64\text{.}$$ (46)

Independent measurements of plasmid noise (using Eq. 22 and the reaction rates provided in Table I of (24)) show that CV_plasmid is equal to 0.51, which is just slightly smaller than given by Eq. 46. This indicates that variability in plasmid numbers is indeed the major source of extrinsic noise in the protein population. The fact that the estimate in Eq. 46 is larger than the actual plasmid noise suggests that variability in other cellular components or fluctuations in number of aTc molecules also make (minor) contributions to the extrinsic noise.

In summary, the experimental results of Dublanche et al. (24) provide an experimental verification of our theoretical predictions. They also indicate that measuring changes in the protein noise level as a function of the feedback strength could be useful in determining the level of noise in the exogenous signal.

Changing Feedback Strength by Keeping the Protein Level Fixed

We finally investigate how the protein noise levels change as the feedback strength is varied, keeping the steady-state average protein level x^∗ fixed. As can be seen from Eq. 29, x^∗ can be held at a fixed level if increasing feedback strength a is also accompanied by: 1), an increase in the maximum transcription rate g₀; 2), a decrease in the protein degradation rate d_x; and 3), an increase in the average protein burst size N_x. Recall that the average burst size N_x = L_x/d_r, where L_x is the translation rate of the mRNA and d_r is the mRNA degradation rate. Thus, increasing both mRNA translational rate and/or decreasing mRNA degradation rate will result in an increase in N_x. In Appendix D (see Supporting Material), we derive formulas for the total noise in the protein level for each of these three different ways of changing the feedback strength but keeping the average protein level fixed.

We show that if the feedback strength is varied along with either the maximum transcription rate g₀ or the protein degradation rate d_x, then noise in protein numbers always decreases with increasing feedback strength. On the other hand, if feedback strength is varied by changing the mRNA translation or degradation rate (i.e., the average protein burst size), then there exists an optimal levels of feedback strength where protein noise level is minimum. The above points are illustrated in Fig. 5, where, for a given fixed x^∗, we observe a U-shaped noise profile when feedback strength is varied along with the average protein burst size. However, this U-shaped profile vanishes if feedback strength is varied along with the maximum transcription rate g₀ or protein degradation rate d_x.

Figure 5.

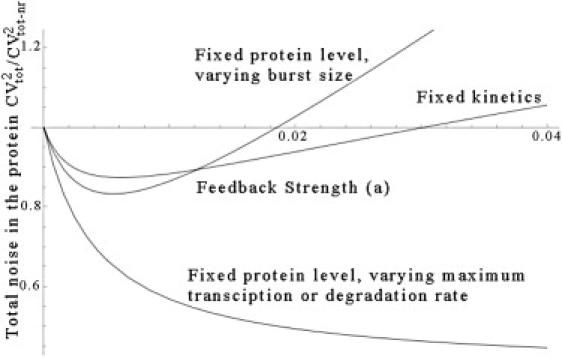
Total noise CV_tot as a function of the feedback strength a when the Hill coefficient is one (M = 1). The feedback strength is increased in three different ways: 1), keeping the gene network kinetics fixed; 2), keeping the average protein level fixed by varying the average protein burst size; and 3), keeping the average protein level fixed by varying the maximum transcription rate or protein degradation rate. The response time T_z is chosen such that it is much larger than the protein's response time when there is no feedback.

Discussion

Autoregulatory gene networks where the protein inhibits/activates its own transcription are common motifs occurring within living cell. These networks are characterized by their transcriptional response g(x), which provides information on how the transcription rate of the gene varies as a function of the number of protein molecules x present in the cell.

Noise and the shape of the transcriptional response

We developed a full understanding of how the protein noise levels are related to the functional form of the transcriptional response. Using a linear approximation for g(x), we showed that the extrinsic noise levels are determined by the slope g′(x^∗) of the transcriptional response at x^∗, with more negative values of the slope (i.e., more stable equilibriums x^∗) leading to smaller levels of extrinsic noise. On the other hand, the intrinsic noise levels are determined by I = g(x^∗) – x^∗g′(x^∗), which is the y intercept of the tangent to the transcriptional response at x = x^∗ (as shown in Fig. 1), and larger values of I lead to smaller levels of intrinsic noise. Consequently, given two gene networks with same protein degradation rate, gene expression characteristics (i.e., N_x and V²_x) but different hypothetical transcriptional responses g₁(x) = 1 and g₂(x) = 1 − x/2, the response g₂(x) will give lower levels of extrinsic noise. However, since both transcriptional responses have the same intercept I equal to one, they both yield the same level of intrinsic noise in the protein population.

Analytical formulas that relate the noise levels to the response time of the protein show key differences between extrinsic and intrinsic noise. For a fixed mean protein level, burst size, and protein degradation rate, as one decreases the protein response time T_r through feedback (by decreasing the slope g′(x^∗)), the levels of extrinsic noise decrease much more than those of intrinsic noise. This leads to an important conclusion that negative feedback is much more effective in reducing the extrinsic component of protein noise than its intrinsic component, which is consistent with other theoretical and experimental studies (23,34–36). At a qualitative level, this arises because intrinsic noise is equivalent to white noise driving gene expression (16,37). On the other hand, the exogenous noisy signal z that comes from Eq. 20 is colored noise in the sense that it has noise shifted to lower frequencies, and hence, can be more easily attenuated with feedback than white noise.

Changing feedback strength with fixed kinetics

We investigated how protein noise levels change as we vary the feedback strength keeping the kinetics of the gene network fixed. This was done for a biologically meaningful class of autoregulatory gene networks with negative feedback and characterized by the transcriptional response

$$g\left(\mathbf{x}\right)=\frac{g_0}{1+{\left(a\mathbf{x}\right)}^{\text{M}}}\text{.}$$ (47)

Our main result shows that in this procedure of varying the feedback strength, the total noise level in the protein population is minimized at an optimal level of feedback strength. This is in contrast to the Fano factor, defined as the ratio of the variance to the average number of protein molecules. As illustrated in Appendix E (see Supporting Material), in this case the Fano factor always decreases with increasing feedback strength, irrespective of whether noise in protein numbers is intrinsic or extrinsic.

Recall from Autoregulatory Gene Networks with Negative Feedback that increasing the feedback strength causes a decrease in the average number of protein molecules, which results in an increase in the intrinsic noise level. On the other hand, increasing the feedback strength causes the protein response time to decrease, which attenuates both the intrinsic and extrinsic noise. The net result of these two opposing effects is a U-shaped profile, where increasing feedback strength first causes the noise level to decrease and then increase. This U-shaped profile was shown to be in good agreement with experimental data for a synthetic autoregulatory gene network. We also identified a scenario where noise is minimum when there is no feedback and any amount of negative feedback will always increase the noise: the case where intrinsic noise dominates the total noise in the protein population and the Hill coefficient is close to one. This explained the observation that when the source of the extrinsic noise was removed, the U-shaped profile vanished, and instead, the noise level monotonically increased with the feedback strength. However, for synthetic gene networks characterized by a large Hill coefficient, our theory predicts that, even in the absence of extrinsic noise, a U-shaped profile should be observed. This remains to be experimentally verified.

Limit of noise suppression

We characterized the smallest level of noise when feedback strength is varied keeping the gene network kinetics fixed. This was done through the limit of noise suppression, which is defined to be the ratio of the minimum possible noise with feedback to the protein noise level when there is no feedback (i.e., a = 0), and corresponds to the depth of the U-shape profile in Figs. 3 and 4. This limit is given by

$$\frac{\sqrt{4M}}{M+1},$$ (48)

when the intrinsic noise dominates the total noise in the protein (see Eq. 37). However, as the amount of extrinsic noise increases, this limit decreases and asymptotically approaches a value of

$$\sqrt{\frac{T_{\text{nr}}+T_{\text{z}}}{[T_{\text{nr}}+T_{\text{z}}(M+1)](M+1)}},$$ (49)

which corresponds to the situation where extrinsic noise completely dominates the total noise in the protein (see Eq. 38).

The above results can be used to quantify the level of extrinsic noise in the protein population. This is useful for synthetic and natural autoregulatory gene networks where the feedback strength can be manipulated. As illustrated, noise in the exogenous signal can then be estimated from the minimum possible protein noise. Matching these estimates with independent measurements of noise in the exogenous signal can be used to confirm that a particular noise source is the major contributor of extrinsic noise to the protein population.

Relaxing the assumptions of the model

Our analysis made two important assumptions about the autoregulatory gene network model. Firstly, we omitted the mRNA dynamics. This is a valid approximation for any gene network, with or without transcriptional feedback, as long as the protein's half-life time is much longer than the mRNA's half-life (26,28,38). Secondly, we assumed that the minimum level of transcription rate for the transcriptional response g(x) (also called the basal level of transcription rate and achieved when x → ∞) is zero. The PhD thesis (38) relaxes both these assumptions and shows that our above results hold even when the mRNA dynamics is slower than the protein dynamics and the basal rate of transcription is nonzero. The only difference is that the limit of noise suppression is now slightly larger than predicted by Eqs. 48 and 49.

Changing feedback strength with fixed mean protein level

We also investigated how the protein noise levels change as the feedback strength is varied, keeping the steady-state mean protein level fixed. We showed that in this comparison the shape of protein noise profile depends on which particular gene network parameter is varied with the feedback strength. In particular, if the feedback strength is varied along with the maximum transcription rate or the protein degradation rate, then there is no optimality, and protein noise level always decreases with increasing feedback strength.

If the feedback strength is varied with the mean protein burst size N_x (i.e., mRNA translation or degradation rate), then we get a U-shaped protein noise profile. Such a noise profile arises because for a fixed x^∗, a large feedback strength a corresponds to having a high mean burst size N_x ≈ a^Mx^∗Md_x/g₀ (see Eq. 29), and hence, high levels of intrinsic noise in the protein population (see Eq. 18). Thus, in this case, small levels of a yield high noise levels because there is no negative feedback in the system, while large levels of a also yield high noise levels because of very bursty gene expression. This results in a U-shaped profile in which total noise in protein numbers is minimum at an optimal level of feedback strength.

In summary, we have developed results relating the noise levels to the feedback strength in autoregulatory gene networks. We have shown that depending on how the feedback strength is increased in these networks, the protein noise levels can monotonically increase, decrease, or be minimal at an optimal level of feedback strength. These results were not only consistent but also helped explain experimental observation from a synthetic autoregulatory gene network. Finally, we illustrated how measuring changes in protein noise level as the feedback strength is altered can be a useful tool to determine the level of extrinsic noise in autoregulatory gene networks.