A New Computational Approach for Mechanical Folding Kinetics of RNA Hairpins

Abstract

Based on an ensemble of kinetically accessible conformations, we propose a new analytical model for RNA folding kinetics. The model gives populational kinetics, kinetic rates, transition states, and pathways from the rate matrix. Applications of the new kinetic model to mechanical folding of RNA hairpins such as trans-activation-responsive RNA reveal distinct kinetic behaviors in different force regimes, from zero force to forces much stronger than the critical force for the folding-unfolding transition. In the absence of force or a low force, folding can be initiated (nucleated) at any position by forming the first base stack and there exist many pathways for the folding process. In contrast, for a higher force, the folding/unfolding would predominantly proceed along a single zipping/unzipping pathway. Studies for different hairpin-forming sequences indicate that depending on the nucleotide sequence, a kinetic intermediate can emerge in the low force regime but disappear in high force regime, and a new kinetic intermediate, which is absent in the low and high force regimes, can emerge in the medium force range. Variations of the force lead to changes in folding cooperativity and rate-limiting steps. The predicted network of pathways for trans-activation-responsive RNA suggests two parallel dominant pathways. The rate-limiting folding steps (at f = 8 pN) are the formation of specific basepairs that are 2–4 basepairs away from the loop. At a higher force (f = 11 pN), the folding rate is controlled by the formation of the bulge loop. The predicted rates and transition states are in good agreement with the experimental data for a broad force regime.

Introduction

Elucidation of RNA folding mechanism at the level of both secondary and tertiary structures is essential to understanding RNA functions in transcription, splicing, and translation. RNA hairpins are important for biological functions, partly because they can be uniquely recognized by different proteins (1). In a cell, RNAs often undertake the force exerted by its environments, e.g., the messenger RNA can be pulled into the decoding site so that ribosome can read the message (2,3). Moreover, many RNA functions are kinetically controlled. Therefore, modeling RNA hairpin folding kinetics under force is significant for quantitative predictions of functions and rational design of RNAs for therapeutic applications.

Recently, an increasing amount of theoretical and experimental studies for force-free folding (4–7) led to the conclusion that even for simple hairpins, the free energy landscape can be quite rugged and folding can involve misfolded intermediates (4–15). These studies on RNA hairpin folding energy landscapes suggested several different mechanisms for the rate-limiting steps, from loop closure, disruption of misfolded states, or single-stranded base stacks (for loop formation), to slow formation of specific base stacks in the helix stem. The kinetic rates show strong temperature and sequence-dependence. At high temperatures or a temperature around the folding-unfolding transition, folding can be two-state and have a positive or a negative activation barrier; however, for lower temperatures, folding can become noncooperative and involve a positive apparent activation barrier, presumably corresponding to the energy cost to break the misfolded states. Recently, a theory based on the kinetic cluster method systematically explored a broad range of kinetic behaviors for RNA hairpin folding for different temperatures and different helix and loop sequence contexts and lengths (15).

Recent experiments on force-induced RNA folding probed by atomic force microscopes, laser tweezers, and magnetic tweezers (16–19) greatly expanded the scope of RNA folding (20–29). Mechanical folding in these experiments provided a highly effective tool for probing the mechanical properties of RNA folding, mapping the free energy landscape, and controlling the folding-unfolding trajectories. From the force-extension curve and the time series of the extension, the mechanical folding experiments reveal kinetic information for the conformational switches and the presence or absence of kinetic intermediates. For example, the time-dependence of the end-to-end distance for P5ab hairpin under an external force suggests that the folding-unfolding transition is two-state, without detectable intermediates (16).

These remarkable experiments have greatly inspired theoretical studies of force-induced unfolding (30–40). Theoretical studies found that the force-extension curve of a single-stranded RNA could be well modeled as an elastic, freely jointed chain (31). Moreover, theoretical predictions for unfolding along one pathway (unzipping from the end of helix stem) yielded good agreements with experimental data (41). RNA can fold/unfold along many different pathways, and the folding kinetic behavior can strongly depend on the force range. Therefore, studies based on a specific force range used in experiments and theories may not reveal the full landscape of the force-dependence of the folding kinetics. It is thus desirable to investigate the folding kinetics, including the folding rate, transition state, kinetic intermediates, and folding pathways, for a broad force range.

The force range probed experimentally and theoretically was limited to the narrow range around the point at which the folding/unfolding transition takes place. In this article, based on a new kinetic model, we discuss the effect of force on the folding/unfolding kinetics for several sequences in the full range of the force from zero to the point at which the hairpin is fully unfolded. We aim to understand the general principles for the effect of force on the folding/unfolding kinetics. We will first develop a new kinetic theory that allows us to effectively account for the kinetically accessible conformational ensemble. We will then apply the new theory to study the mechanical folding-unfolding of RNA hairpins under external pulling force. We will compare our theoretical prediction with the experimental data. We will also combine the free energy landscape analysis and the kinetic master equation to investigate the force-dependence of the folding rate and the folding pathways and rate-limiting steps for different sequences. Because the model is mainly analytical and deterministic, it enables stable, deterministic predictions for the long time dynamics and detailed analysis for the folding mechanisms. Furthermore, the new kinetic model developed here, which is validated through experimental tests, can effectively reduce a huge conformational ensemble down to a manageable size. This new model may be potentially useful for future theoretical studies regarding more-complex RNAs, beyond hairpins.

Kinetic Analysis

Based on the virtual bond representation of polynucleotide conformations, we recently developed a new model (i.e., V-fold) for RNA conformational entropy and folding free energy landscape. Experimental tests for the thermally induced equilibrium RNA folding thermodynamics indicate that the model is reliable (42,43). We first test the validity of the new conformational model for mechanical folding-unfolding through theory-experiment comparisons for the force-extension curves in the equilibrium folding process. We show the thermodynamic analysis for the constant force ensemble and constant distance ensemble in the Supporting Material. Our theoretical predictions agree with the experimental results by Li et al. (24). In what follows, we will focus on the kinetics of the mechanical folding of RNA hairpins.

A new kinetic model

Due to the large number of possible states for a long chain, the master equation (7) (see Supporting Material) approach is limited to short sequences. The kinetic cluster theory (15,44,45) (see Supporting Material), based on the classification of conformations into reduced states, can effectively reduce the size of the conformational ensemble. Our kinetic cluster approach is useful for kinetic systems with a manageable number of clusters (∼6000). However, the kinetic cluster method would become highly convoluted for larger RNAs, which can have a much larger number of clusters. Thus, it is desirable to develop a new kinetic model which, in combination with the kinetic cluster method, can treat the kinetics efficiently for large RNAs. Such a model may have the advantage over the simulational methods (46–48), which are often limited by stochastic conformational sampling.

We note that a vast number of conformational states may not be significantly sampled in the folding process. These states are usually slow to form (due to large entropic loss) and fast to disrupt (with small enthalpic cost). As a result, the stability of these states ΔG = ΔH − T ΔS is usually low (high free energy ΔG). Based on the above observation, we developed the following new method for generating the conformational ensemble for the kinetic analysis.

• 1.We select the first Ω_c low-free energy states whose (force-free) folding stability ΔG is lower than a threshold ΔG_c (Fig. 1 a). We treat each such state as a parent state. Basepairs contained in a parent are called parent basepairs. Note that a parent state can be either nativelike or misfolded.
• 2.For each parent state i (i = 1, 2, 3,…, and Ω_c), we enumerate all the daughter states that stem from the parent state. A daughter state contains 0, 1, 2,…., parent basepairs and no non-parent basepairs (see Fig. 1, b and c). Moreover, a daughter state can form all the possible loops that satisfy the following conditions: x′₁ = x₁ and x′₂ = x₂; x′₃ ≤ x₃ and y′₃ ≥ y₃; and y′₂ = y₂ and y′₁ = y₁.
• 3.All the parents and their daughters form a reduced conformational ensemble for the kinetic analysis. We construct the rate matrix for this reduced conformational ensemble. The size of the reduced conformational ensemble is much smaller and grows much more slowly with the chain length than the original complete ensemble (see Fig. 2). Depending on the sequence length, the number of conformations can be reduced by a factor of 10 for a 26-nt chain and >10³ for a 42-nt chain. The smaller size of the conformational ensemble enables viable and efficient computations with the master equation and the kinetic cluster analysis.

Figure 1.

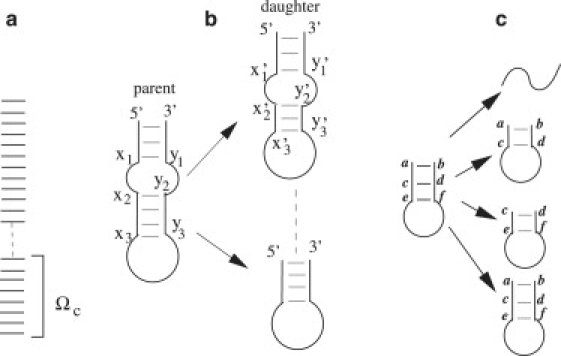
(a) The selected Ω_c conformations based on the thermal stability. (b) A parent and the possible daughter states derived from the parent. (c) A parent with two base stacks. The four daughter states include a coil state, two states with only one base stack, and one state with two base stacks.

Figure 2.

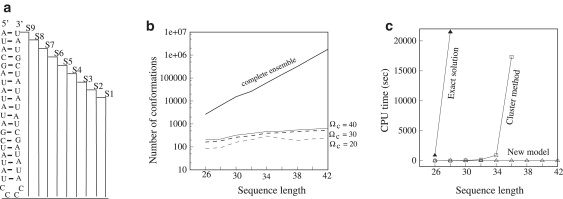
(a) S1–S9 are the nine sequences with different stem lengths and hence different sequence lengths. These sequences are used to compute the data for panel b. (b) The number of conformations from the complete conformational ensemble model and the new kinetic model based on the number of parent states Ω_c = 20, 30, and 40. We find the number of conformations from the complete conformational ensemble model grows exponentially as the chain length increases. However, the number of conformations from the new kinetic model increases much more slowly with the chain length. (c) The computational time for the exact master equation (solid triangle), kinetic cluster method (open rectangle), and the new kinetic method (Ω_c = 20) (open triangle). The new kinetic method can significantly improve the computational speed. The computational time for the nine sequences is <1 s. In contrast, both the exact master equation and the cluster method are computationally expensive and can only treat short RNA sequences.

In practice, to choose the number of parent conformations for a given RNA sequence, we perform a series of tests from a small Ω_c to larger Ω_c values until the results of the relaxation rates (eigenvalues of the rate matrix) converges. For the sequences to be investigated in this study (sequence ≤120 nt), we find that Ω_c = 20 is sufficient for a robust prediction of the folding kinetics. The tested sequences are HP1 and HP2 in Fig. 3, a and b, HP3 and HP4 in Fig. S7, a and b, trans-activation-responsive (TAR) RNA in Fig. 6 a, and S13 in Fig. S5 b.

Figure 3.

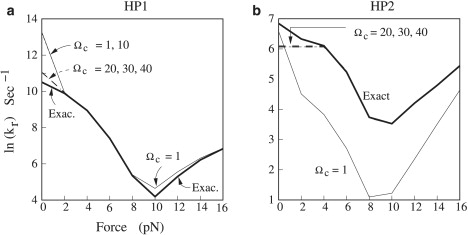
The force dependence of the relaxation rate for (a) HP1 (Fig. S3a) and (b) HP2 (Fig. S3b) at T = 25°C. We compare the results from the complete ensemble model and from the new kinetic model. We test the dependence of the predicted rate constant on the parameter Ω_c (the number of parent states) used in the new kinetic model. For HP1, we find that the folding rate is the same for Ω_c = 1 and 10 at force ≤ 2 pN. For force ≥ 2 pN, the predicted rate constant is the same for Ω_c = 10, 20, 30, and 40.

Figure 6.

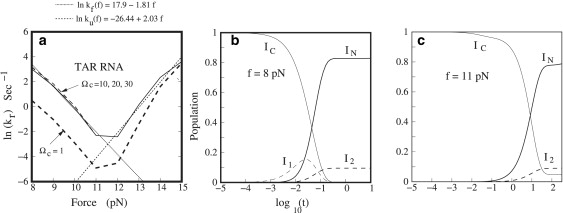
(a) The calculated folding rates at different forces. The temperature is fixed at 22°C. We use different parameters Ω_c (the number of parent states) to test the convergence of the new kinetic model. We find that the folding rates are identical for Ω_c = 10, 20, and 30. The folding rate from the new kinetic model agrees with the experimental results. We obtain a force-dependence for the folding/unfolding rates as follows: ln k_f = 17.9–1.8f for the folding rate and ln k_u = −26.4 + 2.0f for the unfolding rate. In the experiment by Li et al. (24), the folding rate is (21 ± 8) − (1.92 ± 0.72) f and the unfolding rate is (−24 ± 16) + (1.68 ± 1.2) f. Therefore, our theoretical prediction is consistent with the experiment. The populational kinetics at different forces: (b) f = 8 pN and (c) f = 11 pN.

Force-dependence of the rate and the rate-limiting step

Because hydrogen-bonding and base-stacking interactions are short-ranged, the transition from the basepaired state to the unpaired state may occur over a small displacement (∼0.1 nm) (41). In an earlier article, Cocco et al. (41) estimated that the mechanical work done by a pulling force f is (0.1 nm) f ∼0.3 k_BT for a typical force of 15 pN at room temperature. The work is much smaller than the base-stacking enthalpy parameter ΔH, which is ≥6 k_BT (49). Therefore, for the disruption of a basepair, we neglect the perturbation of the force on the kinetic barrier. In contrast, for the formation of a basepair, two originally separated (unpaired) nucleotides are juxtaposed into close proximity from a larger separation; thus, the force causes a large excess kinetic barrier. The work done by the force can be estimated as 2g_s(f), where g_s(f) is the free energy per nucleotide under external force f per nucleotide (see Eq. S8 and Fig. S1 b in Supporting Material) and the factor 2 is the number of the nucleotides involved in the formation of the base pair. Therefore, we obtain the following rate constants for the formation (k₊) and disruption (k_–) of a basepair (or a base stack):

$$k_{+}\left(f\right)=k_{+}\left(0\right)e^{-2g_{\text{s}}\left(f\right)/k_{\text{B}}T}=k_0{e}^{-(T\Delta S+2g_{\text{s}}\left(f\right))/k_{\text{B}}T}\text{,}$$ (1)

$$k_{-}\left(f\right)=k_0{e}^{-\Delta H/k_{\text{B}}T}\text{.}$$ (2)

The kinetic barrier for the formation of a basepair comes from two contributions: TΔS from the entropy decrease and 2g_s(f) from the force. The barrier to break a basepair comes from the ΔH of the enthalpy increase of the base stack. Therefore, the rate-limiting steps for folding would be 1), the formation of the native base stacks of the largest TΔS + 2g_s(f); and/or 2), the disruption of nonnative stacks of the largest ΔH. In contrast, the rate-limiting steps for unfolding would be the disruption of the native base stacks of the largest ΔH. To estimate how strong the effect of force is on the rate constant, we calculate the force-induced barrier 2g_s(f). We found that for temperature T = 25°C and force f = 12 pN, g_s(f) = 0.64 kcal/mol, which is small compared to TΔS and ΔH of a base stack. Therefore, the effect of the force on the slowest folding step is weak.

Although the force may not cause a significant change to the rate constant for a single kinetic move (Eqs. 1 and 2), its effect on a structure containing multiple base stacks can be significant due to the base-to-base accumulation. From Eq. S12, the overall rate is determined not only by the rate of individual kinetic moves, but also by the populational distribution of the states. In the kinetic cluster framework, the populational distribution is related to the stabilities of the conformations in the respective local preequilibrated cluster. The pulling force can significantly change the populational distribution of different states, which often contain multiple base stacks. As a result, the external force can cause notable changes to the overall folding and unfolding rate and the partitioning of the pathways.

Force dependence of the kinetics

We first study the folding kinetics for two short hairpin-forming sequences. These sequences are short. Therefore, we can exactly solve the kinetics based on the complete conformational ensemble. We will also apply our new kinetic model, which is based on the reduced conformational ensemble, to solve the kinetics. Our motivation here is twofold: 1), to evaluate the effect of force on the misfolded intermediates and the transition states in different force regimes; and 2), to validate the new kinetic model for hairpin folding kinetics. Because the temperature dependence of folding kinetics has been thoroughly studied (36,50), below we mainly focus on the force dependence of folding and unfolding kinetics at a fixed temperature T = 25°C (unless explicitly stated otherwise).

We will then apply the model to study the folding kinetics of TAR RNA. The complete conformational ensemble of TAR RNA (52-nt) is too large to be treated by the master equation method or the kinetic cluster method. Our control tests suggested that the maximum number of conformations that we can treat using the kinetic cluster method is ∼10⁶, corresponding to chain length ∼40 nt for a generic sequence (Fig. 2, a and b). In addition, for such large number of conformations, the kinetic cluster method yields ∼6000 clusters for the system. It takes ∼7 h to obtain the eigenvectors and eigenvalues for the rate matrix on a Dell EM65T cluster computer system with one Intel Xeon 5150 (2.66 GHz) processor. Fig. 2 c shows the computational time for different kinetic models. The new kinetic model significantly improves the computational efficiency. For example, the new model takes <1 s to compute the folding rate for a 42-nt sequence. Further tests suggest that the new method can efficiently handle much larger RNA hairpins (>100 nt) (see Fig. S4 and Fig. S5, a and b). In contrast, both the exact master equation method based on the complete conformational ensemble and the kinetic cluster method are computationally expensive and can only treat much shorter sequences. To treat a long sequence such as TAR RNA, the new model developed here is essential.

UAUAGCUAUAUCCCCAUAUAGCUAUA

For this sequence (labeled as HP1), the force-free native structure is a hairpin with loop-length L_loop = 4 (see Fig. S3 a). With the external force, the thermodynamic model based on the complete conformational ensemble predicts that at temperature T = 25°C, the hairpin unfolds at critical force f_c = 10.0 pN for a constant force ensemble. At f = f_c, the native state is almost unzipped completely (data not shown).

Analysis based on the exact complete conformational ensemble model. For the 26-nt sequence, exhaustive enumeration of all the possible states (described by base stacks) gives 2617 conformational states. For the force range 0 ≤ f ≤ 16 pN (see Fig. 3 a), the eigenvalue spectrum of the rate matrix for the complete conformational ensemble has a gap between the first (λ₁) and the second (λ₂) nonzero eigenvalues (rates). Therefore, the slowest mode (λ₁) in Eq. S10 controls the folding rate and the folding time is ∼t_fold ∼1/λ₁.

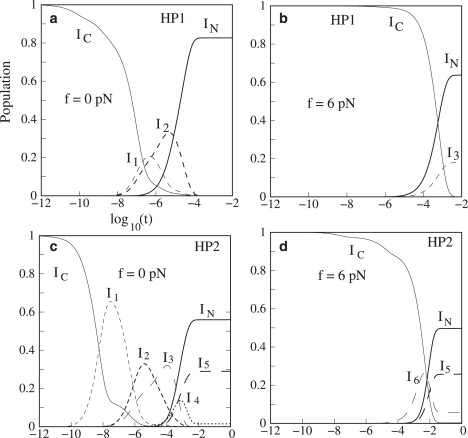
Formation of the misfolded intermediates in the low-force limit. Without the external force, the populational kinetics of the native state follows P_N(t) ≃ P^eq_N −0.67 e^−λ₁t, with λ₁ = 3.6 × 10⁴ s⁻¹ and the equilibrium fractional population of the native hairpin P^eq_N = 0.83. Among all the native base stacks, we find that 5GC6-21GC22 has the largest |ΔS|, thus the formation of this native base stack is an on-pathway rate-limiting step. Among all the nonnative base stacks, 7UA8-25UA26 has the largest |ΔH|, thus, detrapping from the misfolded base stack 7UA8-25UA26 (see I₂ in Fig. S6 a) is an off-pathway rate-limiting step. In summary, folding of the hairpin is biphasic:

• 1.Rapid formation of the misfolded state I₂. The large entropic barrier for the on-pathway rate-limiting step (formation of the native stack 5GC6-21GC22) and, thus, the slow formation of the native structure, causes the formation of the misfolded state.
• 2.Slow detrapping from the misfolded state I₂. Detrapping from I₂ is the major rate-limiting step for the overall folding process. As shown in Fig. 4 a, the populational kinetics solved from the master equation for the 2617 states shows that the misfolded state I₂ indeed emerges as an intermediate in the absence of the external force.

Figure 4.

The populational kinetics for HP1 (Fig. S3a) and HP2 (Fig. S3b) at different forces.

Force-induced destabilization of the misfolded intermediates. Increasing the force can lower the barrier for breaking the misfolded state. For detrapping from the misfolded states, though the rate to break a (misfolded) base stack (∼e^−ΔH/k_BT) is assumed to be force-independent, the probability for the chain to take the folding pathway through detrapping is force-sensitive due to the force-dependent stability of the misfolded states. A large force would destabilize the misfolded intermediates and cause the chain to have a smaller probability to take the folding route through the intermediates. For example, in the absence of the force, intermediates I₁ and I₂ appear as a transient kinetic intermediate. For force f = 6 pN, the intermediates I₁ and I₂ disappear (see Fig. 4 b). The folding pathways through I₁ and I₂ become kinetically silent (probability ≃ 0%). A nativelike on-pathway intermediate I₃ appears. Therefore, through changing the stability of the (misfolded) kinetically trapped state, the force can significantly alter the partitioning of the kinetic pathways, resulting in the change of the kinetic cooperativity of folding. In this example, an increase of the force would turn a noncooperative (non-single-exponential) folding reaction into a cooperative (single-exponential) kinetics.

Analysis based on the new kinetic model with reduced conformational ensemble

Validity of the new kinetics model. Using the new kinetic model, we can greatly reduce the number of conformations (and hence the size of the rate matrix). For the 26-nt hairpin sequence, the total numbers of conformations in the reduced ensemble are 50, 56, 86, 162, and 203 for the number of parent conformations Ω_c = 1, 10, 20, 30, and 40, respectively. From Fig. 3 c, we find that the predicted folding rates for different Ω_c values are convergent for Ω_c >20. Comparisons with the results from the complete conformational ensemble show excellent agreement except for the low-force limit f ≤ 2 pN, where the new kinetic model underestimates the folding rate. This is because at low force, more intermediates, such as I₁ and I₂ in Fig. 4 a, can form. These states may be out of the first Ω_c states and thus neglected in the reduced conformational ensemble. Since these intermediates can contribute to the folding process, neglecting their contribution leads to underestimation of the rate. Under a large pulling force f, I₁ and I₂ become unstable compared to the coil state: ΔG ∼7g_s(f) for I₁ with a 7-nt single-stranded RNA tail and 6g_s(f) for I₂ with a 6-nt tail compared to 26g_s(f) for the coil state, respectively (see Fig. S1 b for g_s(f)). I₁ and I₂ disappear at large forces, and neglecting them will not cause notable error in the prediction of the folding rates. Therefore, the new kinetic model works better for the forces that are not too low. In contrast, the increase of the force stabilizes state I₃, which has two unpaired nucleotides, ΔG ∼2g_s(f). Therefore, I₃ instead of I₁ or I₂ emerges as a subpopulated states for f = 6 pN.

Folding under folding condition f < f_c. We first investigate the folding kinetics under folding condition f = 6 pN < f_c (= 10 pN). To obtain the detailed information about the folding pathways, rates, and rate-limiting steps, we perform the kinetic cluster analysis for the ensemble of 86 conformations (based on the Ω_c = 20 parent states). We first identify the slow-forming native stacks and slow-breaking nonnative base stacks. We find five rate-limiting stacks 1UA2-25UA26, 3UA4-23UA24, 5GC6-21GC22, 7UA8-19UA20, and 9UA10-17UA18. They are slow-forming native stacks. These stacks are slow to form due to the large entropic decrease accompanying the formation of the base stacks (49). Using the five stacks, we can classify the 86 conformations (with Ω_c = 20 parent conformations) into 16 kinetic clusters.

The 16 × 16 rate matrix (for the 16 kinetic clusters) gives the folding rate of 1813 s⁻¹, which is close to the folding rate 1639 s⁻¹ predicted from the exact master equation based on the complete conformational ensemble. In addition, the fast intercluster transitions give the dominant folding pathway (see Fig. 5 a). Furthermore, applying Eq. S15 to the dominant folding pathway in Fig. 5 a gives a folding rate of 1711 s⁻¹, which again is close to the rate 1813 s⁻¹. From Fig. 5 a, folding is rate-limited by the transition from cluster C₁ to C₂. The dominant pathway for C₁ → C₂ is from conformation I_{(2, 0)} in cluster C₁ to I_{(3, 0)} in cluster C₂ through the slow formation of the base stack 9UA10-17UA18. We can estimate the rate from Eq. S12 as $p_{I_{(2,0)}}{k}_{I_{(2,0)}\to I_{(3,0)}}=(6.4\times {10}^{-3}\%)(2.9\times {10}^7{\text{s}}^{-1})=1856{\text{s}}^{-1}\text{.}$ The slow rate is caused by the very low fractional population of state I_{(2, 0)} in cluster C₁. This rate is much slower than the formation of a stack (in I_{(2, 0)}) from a fully unfolded state because the fully unfolded state has a large fractional population in cluster C₁.

Figure 5.

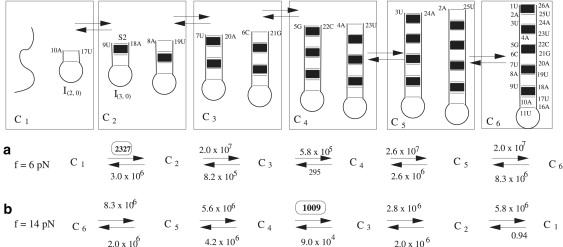
(a) The dominant folding pathway and the intercluster transition rates for the hairpin in Fig. 3a at f = 6 pN and T = 25°C. (b) The unfolding pathway at f = 14 pN and T = 25°C. We find the rate-limiting step for folding is the formation of the native base stack 9UA10-17UA18 (C₁ → C₂) due to the large entropic barrier, while the rate-limiting step for the unfolding is the disruption of the nonnative base stack 5GC6-21GC22 (C₄ → C₃) due to the large enthalpic cost for breaking the base stack. I_{(N, NN)} denotes a conformation with N native basepairs and NN nonnative basepairs. The figure also shows the intercluster transition rates in s⁻¹.

Unfolding under folding condition f < f_c. Under the unfolding condition with a higher force f = 14 pN, the 16 × 16 rate matrix for the kinetic clusters gives nearly the same unfolding rate (504 s⁻¹) as that from the exact master equation(500 s⁻¹). On the predicted dominant pathway (Fig. 5 b) at f = 14 pN, the rate-limiting step is the unfolding process from cluster U₃ to U₄, which involves disruption of the 5GC6-21GC22 native stack. The GC-GC stack has the largest enthalpic parameter (9.4 kcal/mol) (49). The folding rate from cluster U₃ to U₄ is 1000 s⁻¹ from Eq. S12, which is roughly on the same scale as the rate 504 s⁻¹ solved from the exact master equation. The slow U₃ → U₄ rate is not caused by the fractional population of I_{(7, 0)} (32%). Instead, it is caused by the slow I_{(7, 0)} → I_{(6, 0)} rate (2967 s⁻¹) for the breaking of the 5GC6-21GC22 base stack.

Bending of the rate-force curve in the low-force regime. The rate-force dependence in Fig. 3 a shows bending of the curve at the low force region. The bending is a result of two effects. First, at low force, misfolded intermediates would be stabilized and emerge in the folding process (Fig. 4 a). The formation and detrapping of these misfolded intermediates would cause the slowdown of the folding kinetics. Second, the force-induced barrier is related to the elastic free energy g_s(f). The nonlinearity of the g_s(f) curve at the low force region (Fig. S1 b) would contribute to the low-force bending of the rate-force curve in Fig. 3 a.

CGCUCAAAUGUCUAAAAGACAGAGCG

We next study the effect of force on the folding of a more complex hairpin-hairpin with a bulge loop (see HP2 in Fig. S3 b). From Fig. 3 b, we find that 1), the folding rate predicted from the new kinetic model converges for Ω_c ≥ 20; and 2), the results from the new kinetic model and from the original, complete ensemble model show excellent agreement for forces not too weak (f ≥ 4 pN). For weak forces f ≤ 4 pN, the new kinetic model underestimates the folding rate.

The force-free populational kinetics (Fig. 4 c) shows the formation of five intermediates, including four misfolded states (I₁, I₂, I_3, and I₄); see Fig. S6 b for the structures. These states have low stabilities and thus are not included in the reduced conformational ensemble. We find that these misfolded states I₁ and I₂ are still populated at low force f = 2 pN. For low forces, the folding can be complex due to the formation of the misfolded states and multiple folding pathways. The conclusion is consistent with the Monte Carlo simulation by Hyeon and Thirumalai (51).

For a large force f ≥ 4 pN, these misfolded states become kinetically inaccessible. For example, for the misfolded states I₁, because the misfolded state (kinetic trap) involves the formation of a 7-nt tail in the 3′ end of the helix, its relative stability compared to the coil state would be greatly decreased as the force f is increased. For f = 6 pN, there exists only one transient nativelike intermediate state I₆ (see Fig. 4 d) in the folding process. Folding at larger force (6 pN) is more cooperative than the folding at f = 0 pN.

TAR RNA

TAR RNA plays a critical role in HIV viral replication (52). Recent mechanical folding experiments suggested that RNA hairpin folding kinetics can be multistate (20,21,24). Inspired by the biological significance and the intriguing experimental results, we apply our new kinetic model to analyze the folding rates, pathways, and intermediates for TAR RNA here. Unlike the 26-nt hairpin-forming sequences studied above, for the 52-nt TAR RNA sequence, the number of conformations is so large that neither the exact rate matrix/master equation approach nor the kinetic cluster method would be viable. Previous theoretical studies on the folding kinetics for large RNAs mainly use Gō-like model or Monte Carlo simulations (41,51). Our new kinetic model here can give the analytical and stable solution for the populational kinetics folding rates, rate-limiting steps, pathways, and intermediates.

We study the folding kinetics for TAR RNA using the number of parent conformations Ω_c =1, 10, 20, and 30. The corresponding total number (parent plus daughter) of conformations are 235, 683, 1352, and 1982, respectively. The manageable size of the conformation ensemble allows for the exact solution using the master equation. Fig. 6 shows the folding rate at different forces. We find that the results with different Ω_c values converge for Ω_c ≥ 10, and that Ω_c = 1 is not sufficient to give reliable results. This result suggests that having information on the native structure only (Ω_c = 1) might not be sufficient for prediction of the full kinetics.

Folding and unfolding rates. The rate-force (Fig. 6 a) curve shows an apparent turn at f = 12 pN. For force range ≤12 pN, the kinetic process is dominated by the folding reaction. We find that the folding rate decreases as the force increases. For force range ≥12 pN, the kinetics is dominated by the unfolding reaction. We find that the unfolding rate increases as the force increases. For force range f ≤ 12 pN, we can fit our theoretically predicted folding rate versus force k_r – f curve using the analytical formula

$$\ln k_f=17.9-1.8f\text{,}$$

which is in good agreement with experimental result (24) ln k_f = (21 ± 8) − (1.92 ± 0.72)f. Under a large pulling force f > f_c = 12 pN, our predicted unfolding rate k_u leads to the fitted analytical expression

$$\ln k_u=-26.4+2.0f\text{,}$$

which is again in good agreement with experimental result ln k_u = (−24 ± 16) + (1.68 ± 1.2)f.

Folding and unfolding pathways. The populational kinetics (Fig. 6 b) solved from the master equation (Eq. S10) based on the (parent plus daughter) conformations shows a kinetic intermediate I₁ at f = 8 pN. Fig. S8 shows the secondary structures of the intermediates. To unveil the detailed folding pathway at f = 8 pN, we use the kinetic cluster method to classify the 683 conformations (based on the Ω_c = 10 parent states) into kinetic clusters, from which we predict the dominant folding pathways (15,45). Among the 683 conformations, we find six rate-limiting stacks: 2GC3-50GC51, 3CU4-49GG50, 7GG8-45CU46, 17GA18-36UC37, 22GA23-34UC35, and 24GC25-32GC33. The formation of these stacks involves large entropic decrease ΔS, and is thus, slow. Based on the six rate-limiting stacks, we classify the 684 conformations into 35 clusters. Solving the rate matrix for the 35 clusters, we obtain a folding rate of 41 (s⁻¹). From the intercluster transitions (Eq. S12), we identify two major folding pathways from the coil state (I_C) to the native structure (I_N of cluster C₇) (see Fig. 7): C₁ → C₃ either through C₂ or C′₂ followed by the pathway → C₃ → C₄ → C₅ → C₆ → C₇. Furthermore, Eq. S15 gives a folding rate of 23 s⁻¹ for pathway 1 and 17 s⁻¹ for pathway 2. The total folding rate is k_f^{path 1} + k_f^{path 2} = 40 s⁻¹, which is close to 41 s⁻¹ from the exact master equation. The rate-limiting steps are C₁ → C₂ for pathway 1 and C₁ → C′₂ for pathway 2, corresponding to the slow formation of the native base stacks 22GA23-34UC35 and 24GC25-32GC33, respectively. The finding is consistent with the experimental results, which suggest that the rate-limiting steps involve the formation of 1.5–5 bp adjacent to the loop depending on the sequence (13).

Figure 7.

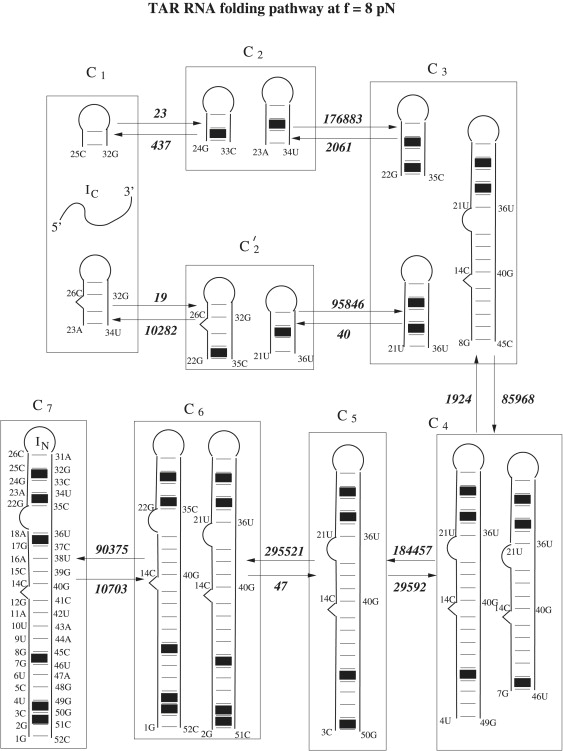
The folding of TAR RNA at force f = 8 pN and T = 22°C involves two parallel pathways: C₁ → C₂ → C₃ → C₄ → C₅ → C₆ → C₇ and C₁ → C′₂ → C₃ → C₄ → C₅ → C₆ → C₇. The intercluster transition rate (in s⁻¹) and the dominant micro-pathways between adjacent clusters are shown in the figure. The solid squares denote the rate-limiting base stacks.

To further investigate the force effect on the folding kinetics, we compute the populational kinetics at a different force (f = 11 pN). We find that the kinetic intermediate I₁ formed at f = 8 pN (Fig. 6 b) now disappears at a larger force f = 11 pN (Fig. 6 c). This is due to the decreased stability of structure I₁ at the larger stretching force f = 11 pN. Furthermore, we use the kinetic cluster method to investigate the folding pathways. Based on the three slow-forming rate-limiting base stacks: 14CC15-39GG40, 15CA16-38UG39, and 17GA18-36UC37, we classify the original 683 conformations into seven kinetic clusters. The seven-cluster system leads to a folding rate of 0.1 s⁻¹, which agrees exactly with the rate constant determined from the master equation for the original complete 683 conformations. The kinetic cluster method gives the dominant folding pathway (Fig. 8) from the coil state (I_C) to the native structure (I_N of cluster C₄). We find that the process is rate-limited by the slow folding from cluster C₁ to cluster C₂. We can estimate the rate for this pathway using Eq. S12 as $p_{I_{(7,1)}}{k}_{I_{(7,1)}\to I_{(8,1)}}=(2\times {10}^{-5}\%)(5\times {10}^5{\text{s}}^{-1})=0.1{\text{s}}^{-1}\text{.}$ The slow rate is caused by the very low fractional population (stability) of state I_{(7, 1)} in cluster C₁. Because the low stability of I_{(7, 1)} comes from the bulge loop between nucleotides 18A and 20C, we conclude that the formation of the bulge loop determines the slow folding rate at f = 11 pN.

Figure 8.

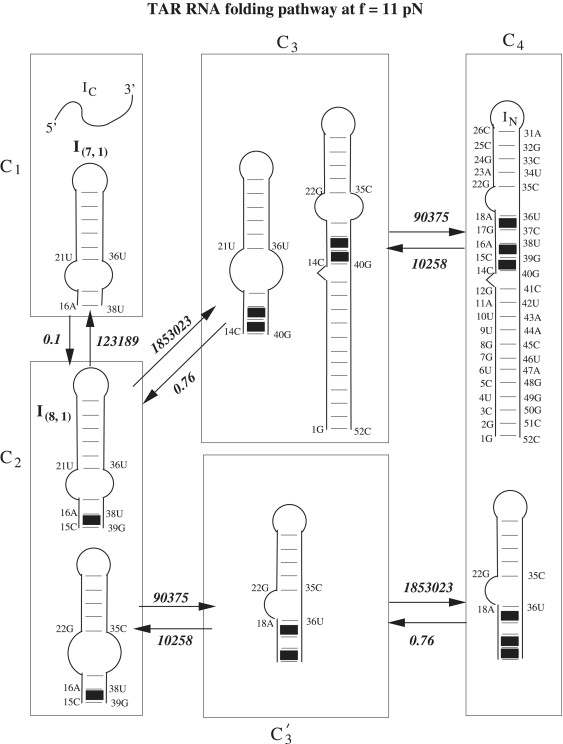
The folding of TAR RNA at the transition force (∼11 pN) and T = 22°C involves two parallel pathways: C₁ → C₂ → C₃ → C₄ and C₁ → C′₂ → C₃ → C₄. The intercluster transition rate (in s⁻¹) and the dominant micropathways between adjacent clusters are shown in the figure. The solid squares denote the rate-limiting base stacks.

Conclusion

Combining the newly developed folding kinetics model with the previously developed kinetic cluster model and the master equation approach, we investigate the effect of the pulling force on RNA folding mechanism such as the folding rate, transition state, kinetic intermediates, and folding pathways for hairpin RNA sequences. This new model, which can predict the misfolded intermediates and pathways, is fundamentally different from the previous Gō-like approaches. The Gō-like model (41) is based only on the native structure and cannot predict the formation of misfolded states in RNA folding. Other simulational methods (36,39,53), which are based on the incomplete sampling of the conformation ensemble, have been useful for the analysis of folding kinetics. However, what distinguishes the new model here from the simulational approaches is the deterministic treatment for the conformational ensemble and the ability to make stable predictions for the long-time folding kinetics.

From our study, we find that the force can significantly alter the kinetic folding pathways, resulting in the change of folding kinetic cooperativity. An increase of the force would turn a noncooperative (non-single-exponential) folding reaction into a cooperative (single-exponential) kinetics. For the folding process at low force, we find that the rate-limiting step is the formation of only a few (such as two) basepairs adjacent to the loop, which is consistent with the nanomechanical measurements (13). The very low population of the transition state contributes to the slow folding rate. For the unfolding process at high force, we find that the rate-limiting step is to break the base stack of the largest enthalpic barrier. For TAR RNA, using our newly developed kinetic model, we can effectively reduce the number of kinetically accessible conformations to a few hundreds. The folding rate obtained from the new method agrees with the experiment (24) for a wide force regime. In that experiment, the force is >8 pN. We find that the force can change the folding pathways and rate-limiting steps. At f = 8 pN, folding involves a single rate-limiting step, namely the formation of the native stack 24GC25-32GC33. At a high force (f = 11 pN), the rate-limiting step is the formation of a different native stack, namely, 15CA16-38UG39. The slow folding rate is due to the low stability of the transition state, mainly caused by the formation of a bulge loop. Recent experiments found that the folding process is more complex at low force (20), such as the formation of nonnative base pairs and kinetic trapping in the misfolded state. Further improvement of the model may be required to account for the low-stability misfolded state. In addition, because the approach developed here is independent of any specific structural features, it can be generalized to treat more complex nonhairpin conformations. For more-complex RNA folds, we might need to include a larger number of low-lying parent conformations. Therefore, further calibration of the model may be needed to extend the model to treat general complex RNA folds.