Visualization of Membrane Loss during the Shrinkage of Giant Vesicles under Electropulsation

Abstract

We study the effect of permeabilizing electric fields applied to two different types of giant unilamellar vesicles, the first formed from EggPC lipids and the second formed from DOPC lipids. Experiments on vesicles of both lipid types show a decrease in vesicle radius, which is interpreted as being due to lipid loss during the permeabilization process. We show that the decrease in size can be qualitatively explained as a loss of lipid area, which is proportional to the area of the vesicle that is permeabilized. Three possible modes of membrane loss were directly observed: pore formation, vesicle formation, and tubule formation.

Introduction

Electropermeabilization is a commonly used physical method in which electric pulses are applied to cells and vesicles, and has been widely reviewed in the literature (1–7). An effect of major importance is that, under certain circumstances, the electric pulses can induce the transient permeabilization of the cell plasma membrane. This permeabilization manifests itself via the crossing of the cell membrane by molecules that would normally not be able to permeate the cell membrane. When subjected to sufficiently large electric fields, vesicle membranes become permeable to small molecules (8,9) and flat membranes show a marked increase in their electrical conductance (10). Small molecules appear to cross the permeabilized membranes via simple diffusion. However, complex processes, such as electrophoresis and direct interactions with the membrane, come into play for larger molecules such as DNA. Electropermeabilization is now regularly employed as a delivery method for a large variety of molecules such as drugs, antibodies, oligonucleotides, RNA, and DNA (6,9,11–13). Initial studies were carried out in vitro on cells in culture, but as the technique has developed, an increasing amount of data has been obtained in vivo on tissues (14–16); this method is being adapted to the clinical context (17,18). Clearly the method has a huge potential in the fields of cancer treatment and gene therapy, offering, in some cases, more efficient, more controllable, and safer treatment protocols (when compared to viral transfection methods, for example). From a purely physical point of view, the application of an electric field to a lipid membrane has two notable effects. The first is a mechanical one in which the stresses caused by the field can deform the membrane; for instance, causing a spherical vesicle to deform into an ellipsoidal or cylindrical one (19–22). This deformation can be thoroughly understood in terms of a macroscopic continuum description of the cell membrane in terms of its bulk electrical and mechanical properties. The second phenomenon of electropermeabilization is much less well understood. Despite its increasing popularity as a therapeutic method, there are still many open questions about the underlying physical mechanisms involved in electropermeabilization. Indeed, at the simplest level, the basic structural changes induced by the field on the membrane structure are still to be fully understood. A number of physical theories have been put forward to explain the phenomenon of electropermeabilization. Historically, the first explanations of electropermeabilization were based on classical continuum theories, which predict dielectric breakdown of the membrane at a critical field strength (23–28). The main problem with such theories is that, although predicting a dielectric/mechanical breakdown transition, they do not provide a description of the physical state of the permeabilized membrane. Currently, the most popular explanation for electropermeabilization is that pores are formed because of a local increase in the surface tension due to the electric field (29–33). This increase in surface tension energetically favors the formation of pores, which is otherwise energetically defavored by their line tension. A similar theory was first introduced to explain the rupture of soap films (34). In this theory, the pores can become stabilized in a hydrophobic-to-hydrophilic pore transition via the rearrangement of the lipids at the pore edges. Because the permeabilization is explained by the formation of pores, the phenomenon described by this theory is referred to as electroporation. Recently, numerical simulations have confirmed that pores can be induced by strong electric fields (35–41); typically, the systems simulated are small, and no significant lipid loss during pore formation has been reported.

When discussing the phenomenon of electropermeabilization, we must distinguish between two key stages of the process:

• Step 1. The physical change induced in the membrane by the field (in the absence of molecules to be transported).

• Step 2. The interaction of the molecules that are to be transported with the modified membrane.

At the simplest level, combination of Steps 1 and 2 can be observed experimentally as a transport phenomenon using marked molecules or via conductivity experiments. In this article, we demonstrate that Step 1 can be indirectly detected via a change in the size of giant liposomes under electropulsation and an associated direct visualization of the expulsion of lipids from the liposomes. Concretely we study the effect of a series of permeabilizing pulses, well separated in time, on the size of giant unilamellar vesicles (GUVs). In the experiments, the radius of the GUV is measured after each pulse and we find that each GUV studied shows, on average, a decrease in its radius down to a critical radius beyond which its size no longer changes. This decrease in size points to the fact that, during the physical processes leading to electropermeabilization, lipids are lost from the vesicle—thus leading to a reduction in their size.

Our experiments are not a direct study of permeabilization; however, they constitute an indirect method of studying electropermeabilization that is relatively straightforward to carry out and interpret in terms of simple physical models that are relatively well established. From an experimental point of view, the crucial advantage of using GUVs is that their composition can be varied and controlled, and in addition, their membrane is not subjected to internal mechanical constraints, as is the case for living cells with cellular cytoskeletons. Furthermore, their size is similar to that of mammalian cells, which allows a direct visualization by an optical microscope.

Lipid loss during electropermeabilization seems likely as if, for instance, pores are formed the lipids near the edges of these pores will be subject to strong variations in the local electric potential and the electric field. Charges and dipole moments on lipids will interact strongly with the electric field and variations of the electric field, respectively. The forces involved may well be capable of tearing lipids from the membrane structure. However, our experiments suggest that the mechanism of lipid loss is a collective one, which involves the formation of small structures such as tubules and vesicles as well as pores. A simple comparison of electrostatic (dipole electric field interaction) energy and hydrophobic free energy suggests that individual lipids cannot be removed from the membrane.

The phenomenon of lipid loss due to an applied field has previously been studied in Tekle et al. (42) but from quite a different point of view (in that study, the effect of single pulses was examined). DOPC vesicles of sizes of ∼20 μm were subjected to pulsed electric fields of ∼1 kV/cm and duration 700 μs. The vesicles were observed using a standard fluorescent microscope and at the cathode-facing side, single pores of the size of ∼7 μm were observed. Such pores were, however, seldom found on the anode-facing side. However, it was inferred that this side was also permeabilized but that the pores responsible were too small to be observed. In the experiments, it was also noted that up to 14% of the vesicle surface could be lost during the process of pore formation/permeabilization.

See Table 1 for a list of terms and parameters used in this article.

Table 1.

Abbreviations used

a	Membrane thickness.
ae	Membrane electrical thickness.
A	Area of the vesicle.
Ap	Permeabilized area.
C	Constant depending on R, a, and the various conductivities of the problem.
DiIC18	1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate.
DOPC	1,2-Dioleoyl-sn-glycero-3-phosphocholine.
EggPC	L-α-Phosphatidylcholine (egg, chicken).
E	Magnitude of the applied electric field.
l	Length of the hydrocarbon chain.
Nc	Number of pulses needed to enter the shrinking regime.
p	Dipole moment of the PC headgroup.
PR	Preshrinking regime.
q	Probability that one pulse induces a transition from the pre-shrinking to the shrinking regime.
Rc	Critical radius.
λ	Fraction of the permeabilized area lost per pulse.
Rhodamine PE	L-α-Phosphatidylethanolamine-n-(Egg Lissamine Rhodamine PE).
R(n)	Radius of the vesicle after n pulses.
Wc	Rescaled critical radius, Rc/R(0)
SR	Shrinking regime.
W(n)	Rescaled radius of the vesicle after n pulses, R(n)/R(0)
ΔΨ	Transmembrane voltage.
ΔΨ0	Initial transmembrane voltage induced by the first pulse at the poles of the liposomes.
ΔΨc	Critical transmembrane voltage n: number of pulses.
θ	Angle on the cell surface with respect to the direction of the applied field.
θc	Critical angle.
Σ0	Initial surface tension.
Σel	Surface tension induced by the electric field.
Σlys	Lysis tension.
ɛm	Membrane dielectric constant.
ρ	Effective radius of the lipid hydrocarbon tail viewed as a cylinder.
μ	Lipid tail hydrophobic free energy per unit of area.

Experimental Setup

We decided to work with two different lipids. However, we wanted phospholipids with identical head groups to obtain the same dipole behavior. Thus, we used DOPC and EggPC, purchased from Avanti Polar Lipids (Alabaster, AL). The formation medium is an aqueous solution with 240 mM sucrose. The pulsation buffer is an aqueous solution of 260 mM glucose that also contains 1 mM phosphate buffer KH₂PO₄/K₂HPO₄ (Merck, Darmstadt, Germany) to impose a physiological pH of 7.4, and 1 mM sodium chloride (Prolabo, Briare, France) to achieve an electrical conductivity in the range of a few hundreds of μS/cm. Conductivities of internal and external solutions are measured with an HI 8820 conductimeter (Hanna Instruments, Lingolsheim, France), and have the values σ_i ≈ 15 μS/cm and σ_e ≈ 460 μS/cm, respectively. The osmolarities are 285 mOsm/kg for the formation medium, and 305 mOsm/kg for the pulsation buffer. These measurements were performed with an Osmomat 030 osmometer (Gonotec, Berlin, Germany). The different refractive indexes of the internal and external media yields a contrast which enables the vesicles to be visualized using a microscope, and the density difference allows the sedimentation of the vesicles on the bottom of the chamber, thus reducing their distance from the objective. EggPC liposomes are visualized by phase contrast, and DOPC liposomes by fluorescence microscopy. We worked with two different dyes (Rhodamine PE (Avanti Polar Lipids) and DiIC₁₈ (Molecular Probes, Eugene, OR)) without any noticeable change in our experimental results. The vesicle formation method employed here is electroformation, as described in Angelova and Dimitrov (43). We chose this technique because it is simple, easily reproducible, and has a good yield. Furthermore, a large amount of the produced vesicles is unilamellar, as demonstrated in Rodriguez et al. (44).

Electroformation

Lipid solution

The lipids are diluted in chloroform, at a mass concentration of 0.5 mg/mL. For DOPC vesicles, the fluorescent probe is added at 0.005 mg/mL. This preparation and the following steps can be performed at room temperature, because the gel-phase/liquid-phase transition temperature of the lipids used is much lower.

Formation chamber

The chamber is made of two glass layers covered with Indium Tin Oxide to ensure the electrical conductivity of the surface. The two layers are separated by an adhesive silicone joint of 1 mm width. The connection with the generator (model 128, AC Exact; Hillsboro, OR) is maintained by two wires, each one soldered on a small copper strip stuck on the ITO slide. Then, 15 μL of lipid solution is deposited on the conducting sides of the glass slides. The deposition is carried out slowly and at constant rate in a chamber held at 4°C to slowly evaporate the chloroform and then the slides are dried under vacuum for a couple of hours to entirely remove the remaining solvent molecules.

Finally, the slides are sealed together, and the chamber is filled with the formation medium.

Voltage application

We apply a sinusoidal voltage of 25 mV peak to peak at 8 Hz. The voltage is increased by 100 mV steps every 5 min, up to a value of 1225 mV. It is maintained under these conditions overnight. Next, we apply a square wave of same amplitude at 4 Hz for 1 h to detach the liposomes from the slides.

Electropulsation

Pulsation chamber

The chamber where the GUVs are subjected to the electric field is composed of a glass slide and a coverslip. Two parallel copper strips of thickness 70 μm are stuck on the slide at a distance of 1-cm apart. The coverslip is then stuck onto the slide and strips with heated parafilm. The chamber is 1-cm long (between electrodes), 2.6-cm wide (width of the coverslip), and 250-μm high (value estimated via measurements with a microscope). We first introduce 60 μL of pulsation buffer between the slide and the coverslip, while taking care of filling the whole chamber to ensure the conductivity of our medium. Next, we add 5 μL of our GUV preparation. Capillarity phenomena prevent the solution from leaking out of the chamber.

The electrode thickness is about the size of our biggest liposomes, which represents only a quarter of the chamber height. We could not a priori be certain of the homogeneity of the field. However, we solved numerically Laplace's equation with the finite element software Comsol Multiphysics (Comsol, Burlington, MA) for the case of our geometry. We found that the field was almost homogeneous in the bottom part of the chamber between the electrodes, and that the size and shape of the permeabilized area were not significantly different from that computed for a geometry with much bigger electrodes (data not shown).

Pulsation method

Electropulsation is carried out using a CNRS cell electropulsator (Jouan, St. Herblain, France), which delivered square-wave electric pulses. An oscilloscope (Enertec, St. Etienne, France) is used to monitor the pulse shape and amplitude. The process of electropulsation is performed directly under the microscope. For the phase contrast visualization, we used an inverted epifluorescence microscope (Leica model No. DM IRB; Leica Microsystems, Wetzlar, Germany) equipped with a camera (Princeton model No. RTE/CCD-1317-K/0; Princeton Instruments, Trenton, NJ) and a 40× Leica phase contrast objective, and an inverted confocal microscope (Zeiss model No. LSM 510; Carl Zeiss, Jena, Germany) with a 63× Zeiss objective for fluorescence imaging. Excitation at 543 nm was provided by a HeNe laser, and emission filter was a 560-nm long-pass. The pulse duration was not set to a few hundreds of microseconds as in the literature (21,22,42), but to 5 ms, because this value is commonly used for gene transfer protocols in mammalian cells (9). In most cases, we apply pulses at 0.5 Hz. However, we sometimes have to interrupt the pulse train for a few seconds to recenter the image on the liposome of interest. Indeed, the observed vesicle does not always stay immobile. It often experiences a translational motion toward the positive electrode, because of which we sometimes have to modify the centering. This displacement was always directed toward the anode, irrespective of the net electric charge of the fluorescent probe that we used (negative for Rhodamine PE and positive for DiIC₁₈). As we will see later, the direction of this motion is coherent with the sign of the ζ-potentials of the vesicles, which does not depend on the type of dye chosen. Due to the need to recenter the image from time to time, the frequency of the pulses is not constant over a whole experiment, but we checked that this did not affect our results. The time delay between two consecutive pulses is of the same order of magnitude, ranging from 2 s to a few tens of seconds. This duration seems to be much longer than the time needed by the vesicle to relax after one pulse, therefore it does not matter if pulses are separated by 2 or 20 s. Direct observation showed that vesicles were distorted rapidly after the pulse application, but as far as the eye could see, there was no visible size or shape change between two consecutive pulses. The pulse amplitude is chosen according to the rule ED = (4/3)ΔΨ₀ = Const (see details later for this choice), where E denotes the amplitude of the electric field, and D the initial diameter of the GUV. The constant is chosen to be 1.7 V. This choice means that at the beginning of every experiment the potential difference drop, ΔΨ₀, across the GUV membrane at the poles facing the electrodes is theoretically (see later) equal to ∼1.3 V; this value is well beyond the value of 200 mV typically cited as the permeabilization threshold for Chinese hamster ovary cells (45,46) and of the order of that cited for artificial vesicles and other cell types (3,26,47). In the pulsation chamber, the distance between the electrodes is 1 cm and so the potential applied between the electrodes is 1.7/D V, where D is measured in centimeters or conveniently 17/D kV if we measure D in μm. The idea behind this large choice of initial transmembrane potential ΔΨ₀ is that the field will initially permeabilize the membrane and continue to do so until the vesicle size becomes significantly smaller than the initial one. We note that our protocol yields initial transmembrane potentials that are slightly lower but of the same order as those in the experiments of Tekle et al. (42), which varied between 1.4 and 2.5 V.

The experimental strategy is simple. We focus on a liposome and we measure its initial diameter. We then tune the voltage amplitude according to the rule described above, and we apply a pulse train until the GUV does not shrink anymore. We acquire one image between two consecutive pulses (∼1 s after each pulse), so we are sure that the vesicle has experienced an electric pulse between two consecutive values of the diameters we measure. Image processing tasks are performed with ImageJ (National Institutes of Health, Bethesda, MD).

ζ-Potentials measurements

We measured the average ζ-potentials of our GUVs by photon correlation spectroscopy (Zetasizer 3000 HS; Malvern, Worcestershire, United Kingdom), using the following method. We diluted 1 mL of the GUV solution obtained after electroformation in 2 mL of a special buffer containing 240 mM sucrose, 1.5 mM phosphate buffer, and 1.5 mM sodium chloride. Vesicles are thus suspended in a medium containing 1 mM sodium chloride, 1 mM phosphate buffer, and 240 mM sucrose. This composition is the same as that of our pulsation medium, except for the 260 mM glucose replaced by 240 mM sucrose to avoid sedimentation of the vesicles, which would make the measurement impossible. We then split the 3 mL into two samples, on which we performed two series of 10 measurements each.

Theory

The basic theory that explains electroporation is based on the modeling of the vesicle electrode system in terms of a weakly conductive cell membrane of conductivity denoted by σ_m, with external and internal media of much higher conductivities denoted by σ_e and σ_i, respectively. We denote by R the radius of the vesicle assumed spherical, and which stays spherical throughout the experiments. In our experiments, R lies typically between 10 and 100 μm. The thickness of the vesicle membrane is denoted by a and typically has the value of 4 nm. In the steady state, which is achieved on timescales much shorter than the time over which the pulse is applied, the electric potential Ψ obeys Laplace's equation, and if θ denotes the angle on the cell surface with respect to the direction of the applied field, which is of magnitude E, then the potential drop across the membrane at that point is given by (see (1) for instance for a detailed derivation)

$$\Delta \Psi =-CRE\cos \left(\theta \right),$$ (1)

where C is a constant depending on R, a, and the various conductivities of the problem. In the limits where σ_m << σ_i, σ_m << σ_e, and a << R, the constant C becomes very simple and takes the value C = 3/2. For the parameters of the experiments carried out here, we are close to the limit where C takes this limiting value. The most important point for our analysis here is that C is independent of R. We thus find that, for a thin membrane, the electric field inside the membrane and normal to its surface, denoted by E_n, is given by

$$E_{\mathrm{n}}\left(\theta \right)=\frac{CRE\text{cos}\left(\theta \right)}{a}\text{.}$$ (2)

Equation 2 demonstrates that there is a huge amplification of the externally applied field across the membrane. This huge electric field internal to the membrane causes structural changes. Whether this structural change corresponds to the formation of pores, dielectric breakdown, or the formation of defects or vesicles, is still open to debate. However, in experiments where permeabilization is measured either via conductivity measurements of planar membranes or by direct optical observation of the entry of marker molecules, a consensus exists that permeabilization occurs locally in the membrane when the magnitude of the potential drop across the membrane ΔΨ exceeds a certain threshold ΔΨ_c, which is estimated to be ∼0.25–1.0 V (3,26,45–47). This corresponds to a field within the membrane of ∼50–250,000 kV/m (for a membrane of thickness 4 nm). This critical threshold is seemingly quite universal, being largely independent of cell and vesicle composition. There is an alternative though largely equivalent physical explanation of field-induced breakdown of the membrane. The effect of a local potential drop ΔΨ across the membrane is to induce a local electrical surface tension Σ_el, which can be computed via the Maxwell stress tensor and is given by Σ_el = ɛ_mΔΨ²a/2a_e², where ɛ_m is the dielectric constant of the membrane, a is its thickness, and a_e its electrical thickness (7,26). If the initial surface tension of the membrane is Σ₀, then, upon applying the field, the total tension is Σ = Σ₀ + Σ_el. The tension of rupture of a lipid membrane is called the lysis tension Σ_lys and thus, when the local tension Σ exceeds Σ_lys, we expect the membrane to be destabilized. This formulation is strictly equivalent to the existence of a critical value of the local electric field in the membrane at which breakdown will occur. However, in this formulation we see that ΔΨ_c will depend on the initial surface tension of the vesicle Σ₀. Indeed, such a dependence on Σ₀ has been reported experimentally (21). In terms of the initial and lysis tension, the critical potential is given by

$$\Delta {\Psi }_{\mathrm{c}}=\sqrt{\frac{2a_{\mathrm{e}}^2}{{\varepsilon }_{\mathrm{m}}a}\left({\Sigma }_{\text{lys}}-{\Sigma }_0\right)},$$ (3)

and thus, we see that the value of the applied field required to affect the membrane will depend on the initial tension of the vesicle. In our study, we are interested in the mechanism of lipid loss, and the ΔΨ_c that induces lipid loss does not necessarily correspond to that necessary to induce permeabilization; however, it is reasonable to expect that the two critical potentials have the same order of magnitude. Studies of electropermeabilization phenomena show that the critical potential depends on the duration of the applied pulse, the critical potential being smaller for longer pulses (11). This means that the underlying physical mechanisms rely on activated processes such as nucleation events for first-order phase transitions. This means that an applied pulse may have no effect with some probability, and this probability should decrease with the amplitude and duration of the pulse. In our experimental setup, the liposomes are visibly under an initial tension, and we expect that there is some distribution of initial tensions even for vesicles of the same composition and similar sizes. The critical potential for each vesicle should therefore be expected to vary.

As we are looking at vesicles, we can neglect any possible modification of the transmembrane potential due to cellular activity and thus assume that it is given purely by Eq. 1. Assuming that the mechanical and electric membrane thickness a and a_e remains constant, there is a critical transmembrane potential drop beyond which the membrane becomes permeabilized or susceptible to lipid loss. Clearly, at fixed electric field parameters (amplitude and duration), a cell can no longer be permeabilized when its radius is smaller than a certain critical radius R_c, beyond which no part of the cell is permeabilized. We thus expect that the permeabilization and thus, vesicle shrinkage will stop once the vesicle has this critical radius. The region where the magnitude of ΔΨ is maximal is clearly that facing the electrodes, corresponding to θ = 0 and θ = π, and so these are the last points where the membrane is permeabilizable. The value of R_c is thus given by

$$\Delta {\Psi }_{\mathrm{c}}=CE{R}_{\mathrm{c}}\text{.}$$ (4)

If we are in the situation where R > R_c, then about the pole at θ = 0 the region where θ is between 0 and θ_c is permeabilized and θ_c is given by

$${\theta }_{\mathrm{c}}=\arccos \left(\frac{\Delta {\Psi }_{\mathrm{c}}}{CRE}\right)\text{.}$$ (5)

This region gives one-half of the total permeabilized area of the vesicle, which we denote by A_p. We thus find that

$$\frac{1}{2}{A}_{\text{p}}=2\pi {\int }_0^{{\theta }_{\mathrm{c}}}{R}^2\text{sin}\left(\theta \right)d\theta =2\pi R^2\left(1-\frac{R_{\mathrm{c}}}{R}\right)\text{.}$$ (6)

Now we consider how the area loss upon a pulsation can be related to the physical parameters of the system. The simplest idea is to assume that the area lost is simply proportional to the permeabilized membrane area. This does not presuppose the mechanism of lipid loss; we simply assume that, in the region where the field exceeds the critical value, the membrane structure is altered. This alteration can be interpreted as a form of dielectric breakdown, and where it occurs, we assume that lipids can be effectively lost from the membrane surface.

If n denotes the number of pulses, treating n as a continuous variable, we can write that, on average,

$$\frac{dA}{dn}=-\lambda A_{\text{p}},$$ (7)

that is to say, the average area lost per pulse is simply proportional to the area where the critical membrane potential (or equivalently surface tension) is exceeded. Note that we should really use a discrete difference equation rather than the continuous one above; however, we have, numerically, checked that the difference behavior is insignificant when compared to the typical experimental errors. Now if we assume that ΔΨ_c remains constant throughout the experiment, Eq. 7 can be solved using A = 4πR² to obtain

$$R\left(n\right)=R_{\mathrm{c}}+(R\left(0\right)-R_{\mathrm{c}})\text{exp}\left(-\frac{\lambda }{2}n\right)\text{.}$$ (8)

Thus, we expect an exponential decay to the critical value of R_c, as given by Eq. 4. If we define the dimensionless variable

$$W\left(n\right)=\frac{R\left(n\right)}{R\left(0\right)},$$ (9)

then W(n) obeys

$$W\left(n\right)=W_{\mathrm{c}}+(1-W_{\mathrm{c}})\text{exp}\left(-\frac{\lambda }{2}n\right),$$ (10)

and W_c is the asymptotic value of W after a large number of pulses have been applied and beyond which the vesicle is no longer permeabilizable; it is given by

$$W_{\mathrm{c}}=\frac{R_{\mathrm{c}}}{R\left(0\right)}=\frac{\Delta {\Psi }_{\mathrm{c}}}{CER\left(0\right)}\text{.}$$ (11)

Now, in the experiments, if we choose to apply fields E such that ER(0) is constant, then if ΔΨ_c and C are constant we find that

$$W_{\mathrm{c}}=\frac{\Delta {\Psi }_{\mathrm{c}}}{\Delta {\Psi }_0},$$ (12)

where ΔΨ₀ is the initial experimentally imposed potential drop at the poles of the cells and is by construction (i.e., via the choice of E) the same for all vesicles. With this choice of E, all plots of W as a function of the number of pulses n should collapse onto the same curve if ΔΨ_c remains constant during the experiment and if it is the same for all vesicles. All plots will have W(0) = 1, and should attain the asymptotic value W_c after the same characteristic number of pulses (as we have assumed that λ is independent of R).

We stress here that, if ER(0) is taken to be constant, then the normal component of the electric field within the membrane is the same for every vesicle studied at the beginning of each experiment and thus, independently of any theory used to analyze the results, we are always looking at systems where the local electric fields in the membranes are the same.

Clearly three sources of additional complexity are neglected in the above analysis:

• 1.The surface tension will fluctuate during the permeabilization/lipid loss process.
• 2.The local electric field seen by the vesicles will fluctuate due to the presence of other vesicles (48).
• 3.We shall see in the section on experimental results that several mechanisms can be involved in the process of lipid loss (pore, vesicle, and tubule formation) and clearly, the choice of a single fitting parameter for lipid loss per permeabilized area λ is another simplification. Indeed, λ should be interpreted as an average area loss parameter due to the (at least) three visualized mechanisms of lipid expulsion.

The initial surface tension (which will have some distribution about an average value) will also play a role in the initiation of the permeabilization and lipid loss process. The extent to which the vesicle retains a memory of this initial tension, is an important point. If, after each pulse, it had the same tension, then the distribution of the values of W_c would be a direct reflection of this initial surface tension distribution. However, it is likely that the tension will vary after each pulse and indeed, that the tension is a dynamical variable. Our experimental results imply that the reduction of the radius is due to expulsion of lipid from the main vesicle, but that some expelled lipid is still in contact with the main vesicle (as in the case of tubules). These attached lipids will constitute a reservoir, which will modify the effective surface tension of the main vesicle, and this tension itself will evolve if the system has not had time to equilibrate between pulses. We conclude that, in fitting the data with the simple model presented here, we should find a scatter in the resulting values of λ and W_c due to points 1–3, mentioned above.

Experimental Results

Observations and data fitting

The existence of the critical radius R_c was confirmed by the two following observations:

• Observation 1. After a sufficiently large number of pulses had been applied, all the vesicles we could find in our sample had sizes lower than the one of the initial liposome of interest.

• Observation 2. We noticed that a liposome that had reached its critical radius could experience another shrinkage if the field magnitude was increased.

We should mention that we sometimes saw vesicles disintegrating, and thus we could not observe the size stabilization. We only kept data corresponding to shrinking and stabilizing GUVs, and we finally gathered 51 data sets for DOPC and 47 for EggPC. Another fact that must be mentioned is the following. In some cases, the size diminution did not begin immediately after the first pulse. We had to apply several electric pulses before being able to detect radius decrease. A possible explanation for this fact is that, like the permeabilization process, the mechanism for lipid loss requires a change in the physical state of the membrane—the formation of defects or pores, for example. The effect of the field is therefore twofold; it allows for the formation of defects, and once defects are present, the field, along with the presence of the defects, allows for lipid loss. We may assume that the creation of defects is an activated process, and at each pulse, the membrane develops defects with some probability q. Note that we assume it is only the defect creation process that has this probabilistic nature (once the vesicle size has begun to decrease, lipids are expelled after each pulse as long as the vesicle radius is >R_c). To describe this phenomenon, we suppose that one vesicle can be found either in a preshrinking (no defects) or in a shrinking (with defects) regime (preshrinking regime, i.e., PR or shrinking regime, i.e., SR, respectively), the transition to the SR after a pulse being a stochastic event occurring with constant probability q, independent of the number of pulses applied before. This hypothesis of a random event is legitimate because our model should incorporate the intrinsic stochastic nature of permeabilization processes (3). The fact that q does not depend on n is justified if we assume that a vesicle having experienced a harmless pulse recovers the same state it had in the PR. Within this modified framework, the former expression of the scaled variable W(n) (Eq. 10) now reads

$$W\left(n\right)=\mathrm{H}(N_{\mathrm{c}}-n-1)+\mathrm{H}(n+1-N_{\mathrm{c}})\left[W_{\mathrm{c}}^{\text{fit}}+(1-W_{\mathrm{c}}^{\text{fit}})\exp \left(-\frac{{\lambda }^{\text{fit}}}{2}n\right)\right],$$ (13)

where H denotes a Heaviside function taking the value 1 for a positive argument and 0 otherwise, and N_c the critical number of pulses needed before entrance in the SR. This means that the fitted curve will be constant up until N_c, and then decay exponentially after n = N_c. We have denoted the critical value of W_c given by the fit as W_c^fit and the effective value of λ estimated from fitting is denoted by λ^fit. In terms of our theory, we expect the average value of W_c^fit to be concentrated at W_c with fluctuations around this value. All fits were performed with the formula given by Eq. 13, so we obtained values of N_c, W_c^fit, and λ^fit for each of the 51 DOPC data sets. With assumptions described above, the random variable N_c should follow a geometric (discrete and memory-less) distribution. We checked this by plotting the normalized histogram of N_c, and as Fig. 1 shows, the values of N_c are well fitted by a geometric distribution of the form

$$\text{Probability}(N_{\mathrm{c}}=n)=q{(1-q)}^{n-1}\text{.}$$ (14)

Figure 1.

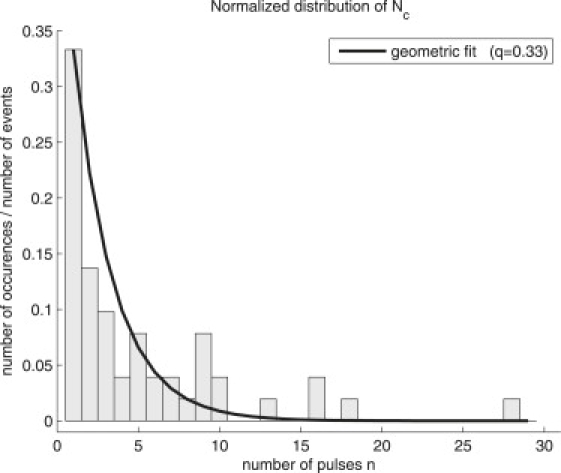
Normalized distribution of the values of N_c obtained after fitting of experimental data for DOPC vesicles. Solid line is a fit to a geometric distribution of the form given in Eq. 14, yielding the value q = 0.33.

The shown fit yields the value q = 0.33, which means that N_c has the average value 〈N_c〉 = 1/q = 3. In Fig. 2, we present four examples of data sets (crosses) and associated fits (full lines). Diamond marks correspond to the images shown later in Figs. 5 and 6 depicting the different mechanisms of lipid loss (see details below). Except for liposome C that immediately starts to shrink, we can clearly identify the PRs, the SRs, and the stabilization of sizes. Detailed information about pulse spacing for data from Fig. 2, which is not constant over a whole experiment because of the lateral motion of the vesicles, can be found in Table S1 in the Supporting Material.

Figure 2.

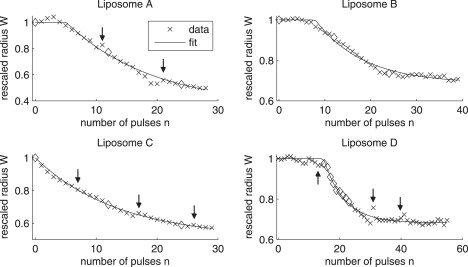
Examples of experimental data and corresponding fits for DOPC liposomes. (Top left) Liposome A; fit results are N_c = 6, λ = 0.13, and W_c^fit = 0.35. (Top right) Liposome B; fit results are N_c = 9, λ = 0.19, and W_c^fit = 0.69. (Bottom left) Liposome C; fit results are N_c = 1, λ = 0.15, and W_c^fit = 0.51. (Bottom right) Liposome D; fit results are N_c = 16, λ = 0.30, and W_c^fit = 0.68. Pulse magnitudes are 290, 360, 235, and 300 V/cm, respectively. Pulse duration is 5 ms. Arrows, if present, indicate data just before which we had to recenter the image on the liposome of interest. There is thus a time interval of ≈10 s before the indicated point, instead of 2 s as in all other cases.

Figure 5.

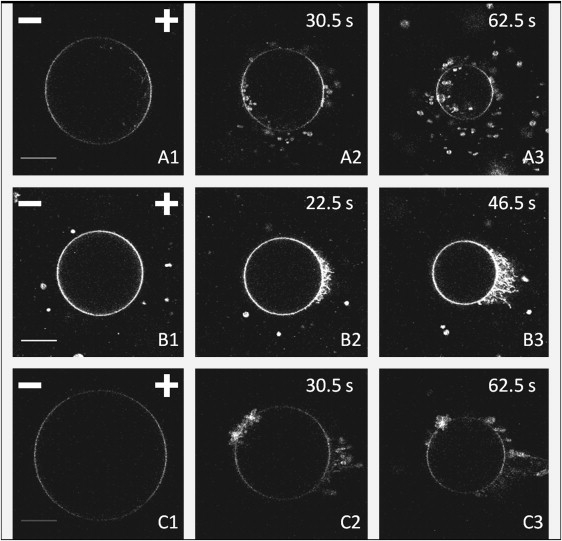
Images of liposomes A, B, and C, composed of DOPC and labeled with Rhodamine PE, at times indicated by the diamonds in Fig. 2, corresponding to 0, 12, and 24 applied pulses. Liposomes A and C lose lipids by formation of vesicles, and liposome B by formation of tubules. Scalebars (20-μm length) and positions of the electrodes appear in the first photograph of each vesicle. Pulse magnitudes are 290, 360, and 235 V/cm, respectively. Pulse duration is 5 ms. Times in upper-right corners indicate when images were acquired, the time origin being the onset of the first pulse. No time indication means that the picture was taken before the first pulse.

Figure 6.

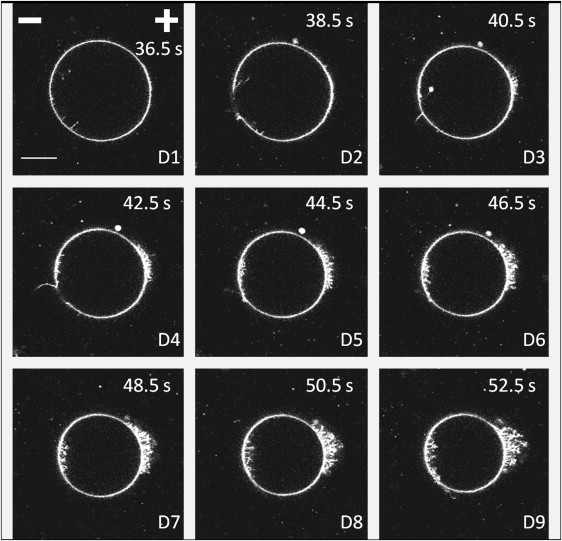
Images of liposome D, composed of DOPC and labeled with Rhodamine PE, at times indicated by the diamonds in Fig. 2. Image D1 is acquired after 15 pulses, D2 after 16 pulses, D3 after 17 pulses, etc. We can see pores on pictures D2 and D4 on the cathode-facing hemisphere. Scalebar (20 μm length) and position of the electrodes appear in the first photograph. Pulse magnitude and duration are 300 V/cm and 5 ms. Times in upper-right corners indicate when images were acquired, the time origin being the onset of the first pulse.

Quantitative analysis—DOPC

As a first step in our data analysis, we can take the average of all the experimental curves and then carry out a fit; this yields the values λ = 0.16 and W_c = 0.65. The fit also yields the number of pulses necessary to put the liposome in the active state, where lipid loss can be induced, to be N_c = 1.73. The experimental data was also examined to see whether there was any correlation between the fitted value of W_c and λ with the initial vesicle radius R(0). No appreciable correlation was seen, thus validating our hypothesis that the vesicle shrinkage can be well described in terms of the rescaled (dimensionless) quantity W(n). A second way to estimate the parameters of the model is to fit λ and W_c for each curve individually to obtain 〈λ^fit〉, 〈W_c^fit〉, and 〈N_c〉, with the average value of the fitting parameters averaged over the individual experiments. The values obtained were 〈λ^fit〉 = 0.25, 〈W_c^fit〉 = 0.58, and 〈N_c〉 = 4.99. This value of 〈N_c〉 agrees well with that of 3, estimated by the geometric distribution fit to the histogram of the fitted values for N_c.

Figs. 3 and 4 show the histograms of λ^fit and W_c^fit, respectively. As mentioned in the section called Theory, in fitting the data with our simple model we should expect to see variation in the values of λ and W_c obtained due to fluctuations of the surface tension (both initial and during the permeabilization process), local electric field, and possibly the effective number of defects created after the N_c pulses needed to enter into the permeabilized state. We note that it has been demonstrated in the literature (21,22) that the critical potential necessary to induce permeabilization is indeed dependent on the surface tension.

Figure 3.

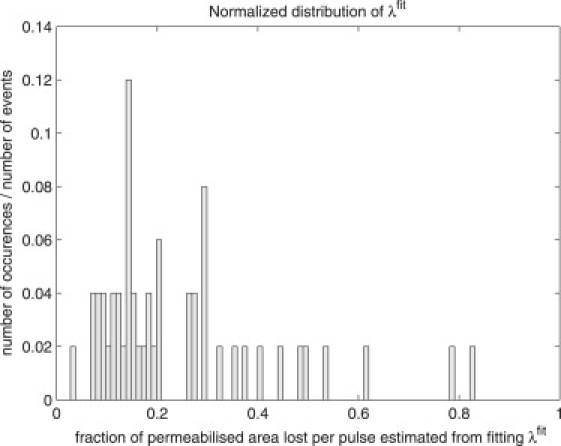
Distribution of the values of λ^fit obtained after data fitting for DOPC liposomes.

Figure 4.

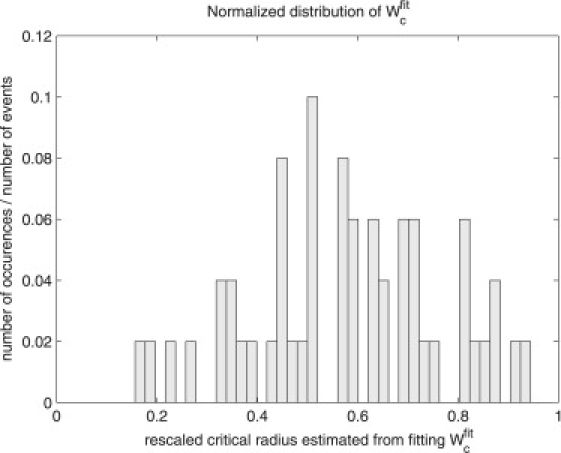
Distribution of the values of W_c^fit obtained after data fitting for DOPC liposomes.

Quantitative analysis—EggPC

The experiments with EggPC were performed first and at that time, we had not yet made the considerations about the PR and the SR. We only kept data sets corresponding to immediately shrinking vesicles, therefore in this section N_c = 1 for each liposome. Despite this simplification, we did the same data processing as that described for DOPC. The fit on the average of all experimental curves yields the values λ = 0.27 and W_c = 0.77. The values of the fitting parameters averaged over the individual experiments are 〈λ^fit〉 = 0.31 and 〈W_c^fit〉 = 0.69.

About the anode-directed motion of the vesicles

The translational motion we observed was always directed toward the anode, suggesting that the GUVs could carry a net negative charge, even with a positively charged fluorescent dye. We checked this by measuring the ζ-potential of the vesicles in a medium with ionic composition equivalent to that of our pulsation medium, the sugar composition being different to avoid vesicle sedimentation making the measure impossible. We examined four different types of vesicles: EggPC alone, DOPC alone, DOPC labeled with Rhodamine PE, and DOPC labeled with DiIC₁₈. We did not use EggPC vesicles with a fluorescent dye, because our experiments involving EggPC were performed via phase contrast microscopy, without any probe.

For all four vesicle compositions, we find an average ζ-potential of ∼−20 mV, a value in agreement with that found in Carvalho et al. (49) for DOPC GUVs, and whose sign is consistent with our observations. This corresponds to a negligible negative surface charge for the GUVs, <1 elementary charge per thousand of lipids. This residual electric charge possibly due to lipid impurities manifests itself only via the anode-directed motion of the vesicles, because of the large magnitude of the applied electric field.

About the initial pH asymmetry

Internal and external media of our GUVs were not at the same pH conditions (6.6 and 7.4, respectively). It was thus questionable whether this pH asymmetry had any significant influence in our experiments. The answer is no, based on the three following arguments. First, it is true that local pH gradients can induce the formation of tubular structures (50). However, such gradients have a magnitude of ∼4 pH units, much higher than our 0.8 pH units. Second, as can be seen on our phase contrast images (data not shown), GUVs become permeabilized during pulsation, and experience a mixing of their internal and external media. Thus, the initial pH asymmetry should disappear after a few permeabilizing pulses. Third, the observation that the vesicles are stable and do not exhibit any shape changes until the electric field is applied corroborates the fact that the initial pH asymmetry of our GUVs has no significant effect.

Mechanisms of lipid loss

One of the most fascinating aspects of the experiments is the wide variety of mechanisms of lipid loss that can be observed. Three different mechanisms of lipid loss are observed when the lipids are fluorescently marked, as is the case on our experiments on DOPC liposomes (these observed mechanisms do not show any appreciable dependence on the probe employed). (We emphasize here that the term “lipid loss” implies loss of lipid from the bulk spherical part of the vesicle; the lipid ejected appears, in most cases, to remain attached to or close to the parent vesicle.)

The three basic mechanisms are shown in Figs. 5 and 6. Images were taken with the confocal microscope.

The first and most frequent mechanism is the formation of small vesicles at both the anode-and cathode-facing poles. Those vesicles are mainly thrown out of the GUVs, but some of them were also driven inside the GUVs. Liposomes A and C of Fig. 5 lost their lipids in such a manner (Movie S1 in the Supporting Material shows that mechanism for another GUV). Interestingly, a similar phenomenon has been reported when high-frequency alternating electric fields are applied to sea urchin eggs (51)—firstly, the cell is deformed and elongated by the field; and secondly, this cell splits into two smaller cells and a number of much smaller vesicles.

The second phenomenon we could observe (see photographs for liposome B in Fig. 5) was the creation of lipid tubules on the exterior of the anode-facing hemisphere (Movie S2 shows that mechanism for liposome B). DOPC molecules expelled from the membrane rearranged in the form of tubular structures, whose lengths grew with the number of applied pulses. These structures initiated from the pole facing the positive electrode and remained attached to the vesicle. However, they then appeared to diffuse away from the pole toward the equator (while remaining attached to the membrane) and appeared to cover most of the anode-facing hemisphere, as shown in Fig. 5. We also saw on the cathode-facing side of Fig. 6 that tubules can grow on the interior surface of the liposome. These structures also diffuse toward the equatorial regions, the number and size of tubules, however, being smaller. This mechanism of tubule formation appears to be stronger on the anode-facing hemisphere.

Finally, we also noticed the presence of pores on the cathode-facing hemisphere (as did (42)). This was a quite rare observation, but it is normal because our acquisition times were of a few hundreds of milliseconds, the same order of magnitude as the lifetimes of such pores (42). Liposome D, which has entered the SR after 16 pulses, is found to have pores after 16 and 18 pulses, as shown by images D2 and D4 of Fig. 6. On the next images, we can see the beginning of the formation of the tubular structures described previously. We thus conclude that those two mechanisms could occur together for a same vesicle. The fact that we detected only a few GUVs exhibiting pore formation is certainly due to the too-low acquisition speed of our experimental setup. Recently, it has been shown that pore formation can be induced in vesicles by solubilizing the membrane (52), and that this process of pore formation is also associated with membrane loss and thus, vesicle shrinkage. An animation of the shrinkage of liposome D associated with pores and tubules formation is available in Movie S3.

The eventual long-term evolution of the structures described above (after pulsation has been stopped) varied from one experiment to another. The small vesicles, in most cases, diffused away from the liposome and the vesicle radius stayed constant. However, the behavior of the tubular structures exhibited wide variation. Some of the tubules broke away from the GUV and diffused away, sometimes forming vesicles and sometimes not. Other tubules remained attached to the vesicles, exhibiting polymerlike fluctuations. In some cases, they were reabsorbed into the GUV membrane after a time of approximately minutes. In fact, the eventual fate of tubules was strongly dependent on their environment, notably on whether other vesicles came in contact with them or not. In the cases where tubules were reabsorbed, the volume of the vesicle they were attached to increased, and the final state of the vesicle was often nonspherical, and appeared to be under little tension (in agreement with the idea that the attached lipids act as reservoir of lipid for the main vesicle).

Discussion

Giant liposomes subjected to pulsed DC electric fields diminish in size and lose lipids via several observable mechanisms—vesicle ejection, tubule formation, and pore formation. This is quite different to what is observed in living cells, which tend to swell under electroporation (53–56). The experiments, along with the associated model, provide us with the following picture of lipid loss due to applied pulses. The lipid loss proceeds by a two-stage process. First, if the applied field is high enough, a membrane passes from an inactive state where it has no induced defects to one where defects are present. We have seen that this process is of an exponential character reminiscent of radioactive decay. Secondly, for DOPC composed vesicles, once defects are present the membrane loss per pulse is ∼λ ≈ 0.20 of the area in which the transmembrane potential exceeds the critical value, denoted here by ΔΨ_c. From our estimate W_c = 0.65 obtained by fitting the average of all curves, we find that, on average, ΔΨ_c = W_c × ΔΨ₀ = 0.65 × 1.3 V ≈ 0.85 V. If we use the average value of 〈W_c^fit〉 obtained by fitting the individual curves, we obtain ΔΨ_c ≈ 0.75 V.

These values of ΔΨ_c are to be compared with those reported for certain cell membranes ΔΨ_c ≈ 1 V (3,47) and tension free vesicles (1-stearoyl-2-oleoyl phosphatidylcholine and dioleoyl phosphatidyglycerol) (26), where ΔΨ_c ≈ 1.1 V. Similar results apply for EggPC but in this case, λ ≈ 0.29 and there is thus, with comparison to DOPC, more lipid loss per unit area of where the critical transmembrane potential is exceeded. The estimated value of W_c obtained by fitting the average of all curves is 0.77, which gives a critical transmembrane voltage of 1 V. The estimate from the average values obtained over individual fits yields a value of 0.69 for W_c, thus leading to a critical transmembrane voltage ΔΨ_c ≈ 0.89 V.

Recently numerical simulations have provided much insight into the membrane organization occurring during the membrane permeabilization process (35–41). The picture emerging is one where the strong electric field present in the membrane causes water molecules (via their dipole interaction with the applied field) to penetrate into the membrane. There is an initial formation of so-called hydrophobic pores because the water molecules are in proximity to the hydrophobic core of the membrane. Subsequently, the lipid head dipoles reorient to form hydrophilic pores where the lipid heads line the inside of the pore. The mechanism behind this reorientation involves hydrophobic effects and electrostatic effects. For example, dipole moments that are oriented normal to the membrane surface (which is roughly the case for DOPC) are favorably aligned on one side of the membrane but not on the other. This means that, on the side where they are well oriented, the field keeps them straight toward the normal. However, on the side where they are maloriented, they can lower their energy by turning in toward the core of the membrane. This tendency to turn inside the membrane lowers their electrostatic energy and aids the formation of hydrophilic pores. The same effect is clearly present before water penetration into the bilayer core, and helps to form defects that favor penetration by water molecules. This explains why formation appears to be initiated from a particular membrane side in electrically neutral membranes. However, in numerical simulations, lipid loss from the membrane is not generally observed during pore formation and pore resealing. This could be because the timescales over which the simulations are carried out are too short. Indeed, it is difficult to see, if we accept the above image of the pore formation mechanism, how lipid loss to the extent observed in our experiments can be explained by such processes. The main differences between the experiments here and numerical simulations is that the system here is much larger and that the pores formed are an order-of-magnitude larger than those seen in simulations (which can be interpreted as prepores). We have seen that vesicle formation seems to make a major contribution to the observed lipid loss, and there is presumably a minimal size that a vesicle can have (for thermodynamic and mechanical reasons); thus, if the simulated system contains less lipids than required to build a vesicle of minimal size, then lipid loss by vesiculization cannot be observed. Another possible mechanism for lipid loss is that lipid headgroup dipoles, which are maloriented, instead of turning into the membrane to be better oriented, are simply expelled from the membrane. This expulsion will increase the free energy of the lipid due to hydrophobic interactions but lower the electrostatic energy. The hydrophobic component of the free energy increase could be lowered by the formation of small vesicles into which these expelled lipids could be incorporated. We recall that, in smaller vesicles, the electrostatic energy of maloriented lipid headgroup dipoles is much smaller due to the scaling with R, the vesicle radius, of the potential drop across the membrane. The idea that single lipids can be extracted due to the field turns out to be unrealistic. The dipole moment p of the PC headgroup is ∼20 Debye (see (57) and references therein), which means that the maximal electrostatic energy of a maloriented dipole is ∼E_D ≈ p(ΔΨ/a), where ΔΨ is the potential drop across the membrane. However, the hydrophobic energy of a lipid tail placed in water is given by E_hydro ≈ 2πρlμ, where l is the total length of the hydrocarbon chain and ρ is its effective radius (viewed as a cylinder). Clearly, the tail length is approximately related to the membrane thickness by l ≈ a/2. The term μ is a hydrophobic free energy per unit of area and takes a value of ∼40 mJ/m² (58). The effective cylindrical radius of the lipid hydrocarbon tail is estimated at 0.8 nm (there is, of course, really two tails each of radius ∼0.4 nm (58)). Equating these two energies yields a critical transmembrane potential beyond which lipids can be torn out directly by the field as

$$\Delta {\Psi }^{\mathrm{\ast }}\approx \frac{\pi a^2\rho \mu }{p}\approx 24V\text{.}$$ (15)

This value of ΔΨ^∗ is to be compared with the value given typically for the critical potential drop across the membrane necessary to achieve permeabilization which, as previously mentioned, is ∼200 mV for a wide range of membrane types. In addition, the electric field seen by the lipid heads is only the amplified one if we assume that the head region is of low conductivity, having a value close to that cited for the total membrane conductivity. We thus conclude that, for permeabilization seen in the range of voltages of our experiments, a simple mechanism of tearing out lipids is unlikely to occur (although this mechanism could conceivably play a role when high intensity short pulses are applied). The conclusion of the above estimation is that lipids must be ejected together in structures that minimize their hydrophobic energy such as micelles, tubules, and vesicles, as is indeed seen in our experimental results.

There is a clear asymmetry in our observations of lipid loss, in agreement with the observations of Tekle et al. (42); when we observed pore formation, it was on the cathode-facing side of the liposome. However, the anode-facing side was the one where the formation of tubules was favored. The mechanism of symmetry breaking could well be related to the anisotropic dielectric structure of the membrane due to the behavior of its lipid components.

Another interesting feature of our results is that the vesicle does not always lose lipid material from the first pulse onwards. This implies that the vesicle needs to be in a particular state (induced by the field with some probability) to enter into the shrinking regime (SR). The difference between the SR and preshrinking regime is unclear, but one could speculate that, in the SR, the membrane has defects that facilitate the loss of lipids. The number and nature of defects created at the inception of the SR is presumably stochastic in nature and could be responsible for the variations in the parameter λ seen in our experiments. The continued application of pulses then leads to a number of visible modes of membrane loss, vesicle formation, tubule formation, and pore formation. In the context of applied DC pulses, only pore formation had been previously reported (42). Vesicle formation due to alternating fields has been reported (51), but the underlying physics appears quite different, as, in the presence of AC fields, the formation of small vesicles occurs via the fission of the initial cell into two similar-sized daughter cells. Perhaps the most striking phenomenon is that of tubule formation, which leads to a hairlike structure of tubules around the liposome. Thus repeated application of short DC pulses leads to the shrinkage of artificial vesicles and a rich phenomenology of lipid structure formation. As a final comment, the phenomenon of lipid loss observed here seems to support aspects of the phase transition model of electropermeabilization (59). In this model, the electric field can induce a transition from a state where the bilayer is thermodynamically stable to one where smaller units, for example micelles, are thermodynamically preferred. The fact that the lipid loss process is not always immediately initiated when N_c ≠ 1, supports the first-order nature of the transition.