Spike Train Probability Models for Stimulus-Driven Leaky Integrate-and-Fire Neurons

Abstract

Mathematical models of neurons are widely used to improve understanding of neuronal spiking behavior. These models can produce artificial spike trains that resemble actual spike train data in important ways, but they are not very easy to apply to the analysis of spike train data. Instead, statistical methods based on point process models of spike trains provide a wide range of data-analytical techniques. Two simplified point process models have been introduced in the literature: the time-rescaled renewal process (TRRP) and the multiplicative inhomogeneous Markov interval (m-IMI) model. In this letter we investigate the extent to which the TRRP and m-IMI models are able to fit spike trains produced by stimulus-driven leaky integrate-and-fire (LIF) neurons.

With a constant stimulus, the LIF spike train is a renewal process, and the m-IMI and TRRP models will describe accurately the LIF spike train variability. With a time-varying stimulus, the probability of spiking under all three of these models depends on both the experimental clock time relative to the stimulus and the time since the previous spike, but it does so differently for the LIF, m-IMI, and TRRP models. We assessed the distance between the LIF model and each of the two empirical models in the presence of a time-varying stimulus. We found that while lack of fit of a Poisson model to LIF spike train data can be evident even in small samples, the m-IMI and TRRP models tend to fit well, and much larger samples are required before there is statistical evidence of lack of fit of the m-IMI or TRRP models. We also found that when the mean of the stimulus varies across time, the m-IMI model provides a better fit to the LIF data than the TRRP, and when the variance of the stimulus varies across time, the TRRP provides the better fit.

1 Introduction

The leaky integrate-and-fire (LIF) model is one of the fundamental building blocks of theoretical neuroscience (Dayan & Abbott, 2001; Gerstner & Kistler, 2002; Koch, 1999; Tuckwell, 1988). Its use in examining spike train data is limited, however, because its full parameter vector cannot be estimated uniquely from spike trains in the absence of subthreshold measurements, and estimation of a reduced set of parameters is somewhat subtle (Iyengar & Mullowney, 2007; Paninski, Pillow, & Simoncelli, 2004). An alternative is to use likelihood methods based on the conditional intensity function λ(t | H_t), where H_t is the complete history of spiking preceding time t (Kass, Ventura, & Brown, 2005 and references therein). The stimulus-driven LIF model depends on only the experimental clock time t, relative to stimulus onset, and the elapsed time t − s _*(t) since the preceding spike s _*(t), that is, it satisfies

$$\lambda (t|H_t)=\lambda (t,t-s_{*}(t)).$$ (1.1)

Models of the general form of equation 1.1 have been called inhomogeneous Markov interval (IMI) models by Kass and Ventura, 2001 (following Cox & Lewis, 1972) and 1-memory point processes by Snyder and Miller (1991). Two special cases of equation 1.1 have been considered in the literature: multiplicative IMI models (Kass & Ventura, 2001, and references therein) and time-rescaled renewal-process models (Barbieri, Quirk, Frank, Wilson, & Brown, 2001; Koyama & Shinomoto, 2005; Reich, Victor, & Knight, 1998). We label these, respectively, m-IMI and TRRP models. Both models separate the dependence on t from the dependence on t − s _*(t), but they do so differently. The purpose of this letter is to investigate their relationship to the stimulus-driven LIF model. Specifically, given a joint probability distribution of spike trains generated by an LIF model, we ask how close this distribution is to each of the best-fitting m-IMI and TRRP models, where closeness is measured using Ku¨llback-Leibler divergence. This quantifies the extent to which the m-IMI and TRRP models can capture the dynamics of a stimulus-driven LIF neuron. It also provides an interpretative distinction between the m-IMI and TRRP models themselves.

2 Method

2.1 Leaky Integrate-and-Fire Model

The LIF model is the simplest model that retains the minimal ingredients of membrane dynamics (Dayan & Abbott, 2001; Gerstner & Kistler, 2002; Koch, 1999; Tuckwell, 1988). The dynamics of the model are represented by the equation,

$$\tau \frac{dV(t)}{dt}=-V(t)+I(t),$$ (2.1)

where V(t) is the membrane potential of the cell body measured from its resting level, τ is the membrane decay time constant, and I(t) represents an input current. When the membrane potential reaches the threshold, υ_th, a spike is evoked, and the membrane potential is reset to υ₀ immediately.

By suitable scale transformation, the original model can be reduced to a normalized one,

$$\frac{dX(t)}{dt}=-X(t)+I(t).$$ (2.2)

The threshold value and reset potential are given by x_th and x₀, respectively. While I(t) represents an external input, x_th and x₀ could be interpreted as “intrinsic” parameters of the neuron model and are directly related to biophysical properties (Lansky, Sanda, & He, 2006). In this letter, we consider stimuli that have the form

$$I(t)=\mu (t)+\sigma (t)\xi (t),$$ (2.3)

where ξ(t) is gaussian white noise with E[ξ(t)] = 0, V(ξ(t)) = 1, and Cov(ξ(t), ξ(t′)) = 0, for t ≠ t′.

2.2 Probability Models of Spike Trains

A point process can be fully characterized by a conditional intensity function (Daley & Vere-Jones, 2003; Snyder & Miller, 1991). We consider two classes of models. First, the conditional intensity function of the m-IMI model has the form

$$\lambda (t,s_{*}(t))={\lambda }_1(t)g_1(t-s_{*}(t)).$$ (2.4)

Here, λ₁(t) modulates the firing rate only as a function of experimental clock, while g ₁(t − s _*(t)) represents non-Poisson spiking behavior.

Second, the TRRP model has the form

$$\lambda (t,s_{*}(t))={\lambda }_0(t)g_0({\mathrm{\Lambda }}_0(t)-{\mathrm{\Lambda }}_0(s_{*}(t))),$$ (2.5)

where g₀ is the hazard function of a renewal process and Λ₀(t) is defined as

$${\mathrm{\Lambda }}_0(t)={{\displaystyle \int }}_0^t{\lambda }_0(u)du.$$ (2.6)

In this letter, we call λ₀ and λ₁ excitability functions to indicate that they modulate the amplitude of the firing rate, and we call g₀ and g₁ recovery functions to indicate that they affect the way the neuron recovers its ability to fire after generating an action potential. The fundamental difference between the two models is the way the excitability interacts with the recovery function. In the m-IMI model, the refractory period represented in the recovery function is not affected by excitability or firing rate variations. In the TRRP model, however, the refractory period is no longer fixed but is scaled by the firing rate (Reich et al., 1998).

Note that in both the m-IMI and the TRRP models, the excitability and recovery functions are defined only up to a multiplicative constant: replacing λ₁(t) and g₁(t − s_*(t)) cλ₁(t) and g₁(t − s_*(t))/c, for any positive c, leaves the model unchanged, and similarly for λ₀ and g₀. This arbitrary constant must be fixed by some convention in implementation.

2.3 Küllback-Leibler Divergence

We use the Küllback-Leibler (KL) divergence to evaluate closeness between the LIF model and the two empirical models. The KL divergence is a coefficient measuring a nonnegative asymmetrical “distance” from one probability distribution to another, and the model distribution with a lower value of the KL divergence approximates the original probability distribution better. For two probability densities p_f and p_q of a spike train {t₁,…,t_n} in the interval [0, T′), the KL divergence per spike between the two densities is given by

$$\begin{array}{cc}\hfill D(p_f\parallel p_q)=\hfill & \underset{T\prime \to \infty }{\text{lim}}\frac{1}{E[n]}{\displaystyle \sum _{n=1}^{\infty }}{\displaystyle {\int }_0^{T\prime }}{\displaystyle {\int }_{t_1}^{T\prime }\cdots }{\displaystyle {\int }_{t_{n-1}}^{T\prime }{p}_f(t_1,\dots ,t_n)}\hfill \\ \hfill \hfill & \hfill \times \text{log}\frac{p_f(t_1,\dots ,t_n)}{p_q(t_1,\dots ,t_n)}d{t}_{1}d{t}_2\cdots d{t}_n,\hfill \end{array}$$ (2.7)

where E[n] is the mean spike count in the interval [0, T′), the expectation being taken over replications (trials). For simplicity, in considering first μ(t) and then σ(t) to be time-varying functions, we will assume in each case that they are periodic with period T, so that spike train segments across time intervals of the form [kT, (k + 1)T) for nonnegative integers k may be considered replications (in other words, the spike train generated from the LIF neuron becomes periodically stationary). Let θ(t) = t mod T be the phase of the periodic stimulus where we take the phase of the stimulus to be zero at t = 0 and λ(t, s _*) be a conditional intensity of an IMI model. The conditional interspike interval density given the previous spike phase θ, q(u|θ), is obtained as

$$q(t-s_{*}|\theta (s_{*}))=\lambda (t,s_{*})\text{exp}(-{{\displaystyle \int }}_{s_{*}}^t\lambda (x,s_{*})dx).$$ (2.8)

Since the LIF model belongs to the class of IMI model, it is completely characterized by a conditional interspike interval density, f(u|θ). Then, as shown in appendix A, under the condition of $E[n]={{\displaystyle \int }}_0^{T\prime }{\lambda }_0(t)dt\to \infty$ as T′ → ∞, where λ₀(t) is the instantaneous firing rate given by λ₀(t) = E[λ(t, s _*(t))], equation 2.7 is reduced to

$$D(p_f||p_q)={{\displaystyle \int }}_0^T({{\displaystyle \int }}_0^{\infty }f(u|\theta )\text{log}\frac{f(u|\theta )}{q(u|\theta )}du)\chi (\theta )d\theta ,$$ (2.9)

where χ(θ) ≡ p{spike at θ|one spike in [0, T)} is a stationary spike phase density. Under the periodic stationary condition, the KL divergence between two probability densities of spike trains of IMI models (see equation 2.7) is reduced to the KL divergence between the conditional interspike interval densities (see equation 2.9). Note that the KL divergence of the conditional interspike interval density is averaged over the spike phase distribution, χ(θ), since spikes are distributed by χ(θ) over time.

For calculating the KL divergence given by equation 2.9, we need to calculate f(u|θ) and χ(θ), which can be obtained as follows. Since the membrane potential of the LIF model is a Markov diffusion process, f(u|θ) satisfies the renewal equation (van Kampen, 1992),

$$p(x,t|x_0,0;\theta )={{\displaystyle \int }}_0^{t}f(t\prime |\theta )p(x,t|x_{th},t\prime ;\theta )dt\prime ,x\ge x_{th},$$ (2.10)

where p(x, t|x₁, t₁; θ) is the conditional probability density that the voltage is x at time t if it is x₁ at time t₁ < t. This conditional probability density can be obtained by solving the stochastic differential equation 2.2 as

$$p(x,t|x_1,t_1;\theta )=\frac{1}{\sqrt{2\pi \eta (t)}}\text{exp}[-\frac{(x-\gamma (t){)}^2}{2\eta (t)}],$$ (2.11)

where

$$\gamma (t)=x_1{e}^{t_1-t}+{{\displaystyle \int }}_{t_1}^t{e}^{t\prime -t}\mu (t\prime +\theta )dt\prime ,$$ (2.12)

and

$$\eta (t)={{\displaystyle \int }}_{t_1}^t{e}^{2(t\prime -t)}{\sigma }^2(t\prime +\theta )dt\prime ,$$ (2.13)

(see van Kampen, 1992). Inserting equation 2.11 to equation 2.13 into equation 2.10, we can solve equation 2.10 numerically to obtain f(u|θ). (See Burkitt & Clark, 2001, for numerical solution of the integral equation.)

The stationary spike phase distribution χ(θ) can be obtained as follows. The phase transition density, which is the probability density that a spike occurs at phase θ′ given the previous spike at phase θ, is given by

$$g(\theta \prime |\theta )={{\displaystyle \int }}_0^{\infty }f(u|\theta )\delta ([u+\theta {]}_{\text{mod}T}-\theta \prime )du.$$ (2.14)

Following the standard theory of Markov processes (see van Kampen, 1992), the stationary spike phase distribution χ(θ) is obtained as a solution of

$$\chi (\theta \prime )={{\displaystyle \int }}_0^{T}g(\theta \prime |\theta )\chi (\theta )d\theta .$$ (2.15)

The stationary phase distribution χ(θ) is the eigenfunction of g(θ′|θ) corresponding to the unique eigenvalue 1. In practice, the spike phase distribution χ(θ) can be calculated by discretizing the phase and calculating the eigenvector corresponding to eigenvalue 1 of the transition probability matrix using standard eigenvector routines (Plesser & Geisel, 1999).

2.4 Fitting the IMI Model

We fit the m-IMI and TRRP models to spike trains derived from the LIF model via maximum likelihood.

2.4.1 Fitting the m-IMI Model

We follow Kass and Ventura (2001) to fit the m-IMI model to data. For fitting m-IMI model in equation 2.4, we use the additive form:

$$\text{log}\lambda (t,s_{*}(t))=\text{log}{\lambda }_1(t)+\text{log}{g}_1(t-s_{*}(t)).$$ (2.16)

We first represent a spike train as a binary sequence of 0s and 1s by discretizing time into small intervals of length Δ, letting 1 indicate that a spike occurred within the corresponding time interval. We represent log λ₁(t) and log g ₁(t − s _*(t)) with cubic splines. Given suitable knots for both terms, cubic splines may be described by linear combinations of B-spline basis functions (de Boor, 2001),

$$\text{log}{\lambda }_1(i\Delta )={\displaystyle \sum }_{k=1}^M{\alpha }_k{A}_k(i\Delta ),$$ (2.17)

$$\text{log}{g}_1(i\Delta -s_{*}(i\Delta ))={\displaystyle \sum }_{k=1}^L{\beta }_k{B}_k(i\Delta -s_{*}(i\Delta )),$$ (2.18)

where M and L are the numbers of basis functions that are determined by the order of splines and the number of knots. Note that the shapes of B-spline basis functions {A_k} and {B_k} also depend on the location of knots. Fitting of the model is accomplished easily via maximum likelihood: for fixed knots, the model is binary generalized linear model (McCullagh & Nelder, 1989) with

$$\text{log}\lambda (i\Delta ,s_{*}(i\Delta ))={\displaystyle \sum }_{k=1}^M{\alpha }_k{A}_k(i\Delta )+{\displaystyle \sum }_{k=1}^L{\beta }_k{B}_k(i\Delta -s_{*}(i\Delta )),$$ (2.19)

where {A_k(iΔ)} and {B_k(iΔ)} play the role of explanatory variables. The coefficients of the spline basis elements, {α_k} and {β_k}, are determined via maximum likelihood. This can be performed by using a standard software such as R and Matlab Statistics Toolbox.

In the following simulations we chose the knots by preliminary examination of data. We conducted the fitting procedure for several candidates of knots and then chose the one that minimizes the KL divergence between the estimate and the LIF model.

2.4.2 Fitting the TRRP Model

We begin by noting that λ₀(t) is a constant multiple of the trial-averaged conditional intensity (see appendix B). To fix the arbitrary constant, we normalize so that the constant multiple becomes 1. We may then first estimate λ₀(t) from data pooled across trials (effectively smoothing the PSTH), which we do by representing it with a cubic spline and using a binary regression generalized linear model. Then we apply the time-rescaled transformation given by equation 2.6 to spike train {t_i} to obtain a rescaled spike train, {Λ₀(t_i)}. Finally we determine an interspike interval distribution of {Λ₀(t_i)} by representing the log density with a cubic spline and again using binary regression.

3 Results

3.1 Time-Varying Mean Input

We first considered the case that the input to the LIF neuron was

$$I(t)=a\text{sin}\frac{t}{{\tau }_s}+\xi (t),$$ (3.1)

where a and τ_s are amplitude and timescale of the mean of the input, respectively. We took (x_th, x₀) = (0.5, 0) and τ_s = 5/π. In the following simulation, we used the Euler integration with a time step Δ = 10⁻³. We first simulated the LIF model over the time interval 10⁷Δ to generate a spike train and fitted the m-IMI and TRRP models to data. For each model we used 4 knots for fitting the excitability function and 3 knots each for fitting the recovery function and the interspike interval distribution. Then we calculated the KL divergence between the LIF model and those fitted probability models as described in section 2.3. We repeated this procedure 10 times to calculate the mean and the standard error of the value of the KL divergence.

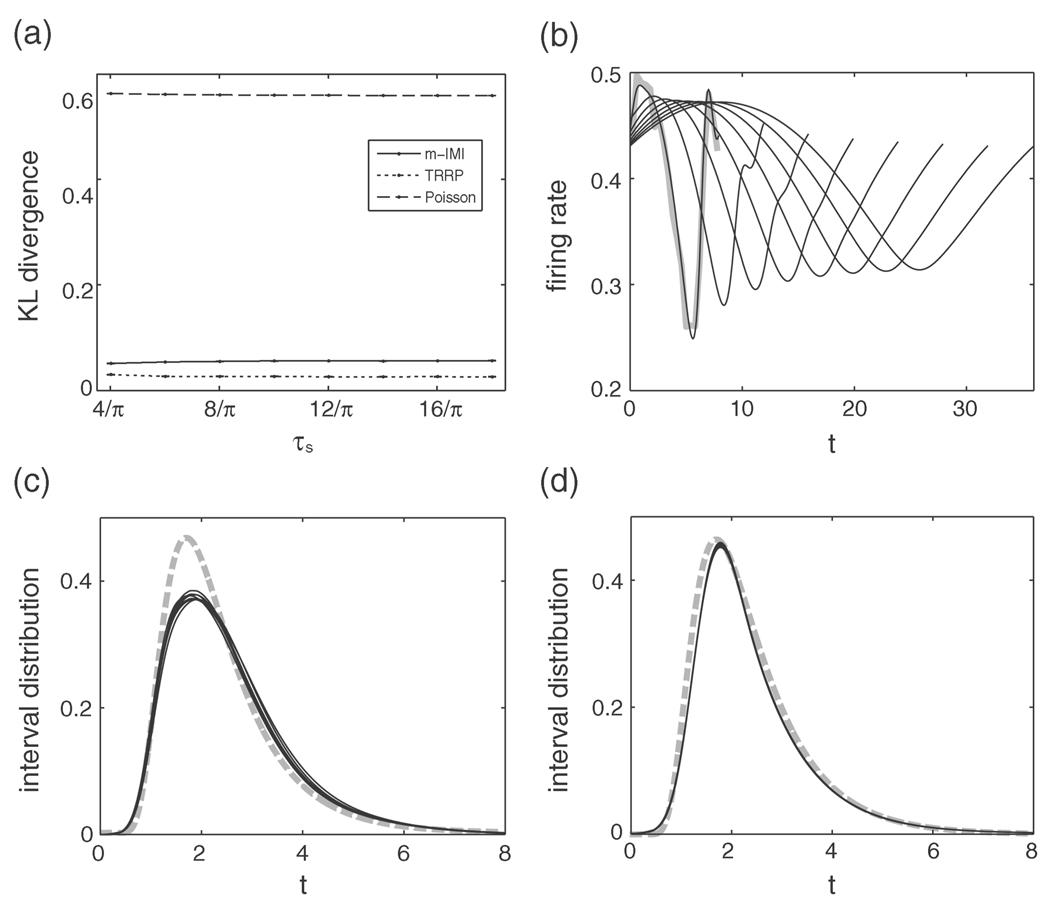
Figure 1a depicts the KL divergences as a function of the amplitude of the mean of the input. We also show in this figure the KL divergence between the LIF model and the inhomogeneous Poisson process for comparison. As shown in this figure, the KL divergence of the m-IMI model is the smallest among three models. When the amplitude of the mean input is increased, the KL divergences of these models get increased. It is remarkable that even when the firing rate is highly modulated, as seen in Figure 1b, the KL divergence of the m-IMI model remains small.

Figure 1.

Results for the case that the mean input is varying in time. (a) The KL divergence as a function of the amplitude of the mean input, a. The solid line, dotted line, and dashed lines represent the KL divergence of the m-IMI model, the TRRP model, and the inhomogeneous Poisson process, respectively. The mean and the standard error at each point were calculated with 10 repetitions. The KL divergence of the inhomogeneous Poisson process is much larger than that of the m-IMI model and the TRRP model. (b) The instantaneous firing rates of the LIF neuron for various values of a. Thin solid lines represent the instantaneous firing rates of the LIF model, and the thick gray lines are raw traces. The amplitude of the instantaneous firing rate is increasing as a is increasing. (c) The solid lines represent rescaled interval distributions of the m-IMI model for various values of a, which are obtained from the recovery function by equation 3.2. The gray dashed line is the interval distribution of the LIF model for a = 0. (d) Same as c for the TRRP model. The rescaled interval distributions in both c and d are departing from the interval distribution of the LIF model as a is increasing, but the LIF model shows less variation for the m-IMI model than for the TRRP model.

Figures 1c and 1d display rescaled interval distributions, which are calculated from recovery functions of the m-IMI and the TRRP models, respectively, as

$$p(t)=\widehat{g}(t)\text{exp}(-{{\displaystyle \int }}_0^t\widehat{g}(u)du),$$ (3.2)

where ĝ(t) denotes the fitted recovery function. Note that this is not the actual interval distribution of spike trains, but the one that is extracted from a spike train after removing the effects of the stimulus. (Here we show p(t) but ĝ(t) since the shape of p(t) is more stable in the tail of the distribution: the tail of p(t) converges to zero as t → ∞, while the estimation of the tail of ĝ(t) is rather variable because there are few spikes at large t in data.) The gray dashed line in Figures 1c and 1d represents the interspike interval distribution of the LIF model with a = 0. The interval distribution plot shows less variation for the m-IMI model than for the TRRP model as the amplitude of the stimuli is increased, especially in the range of the short timescale of the refractory period. This indicates that the dynamics of LIF model in the range of the short timescale is not affected by the stimuli, and the recovery function of the m-IMI model can capture the stimulus-independent spiking characteristics of the LIF model.

Figure 2 displays the results for various values of τ_s and fixed value of a. Parameter values of the LIF model were taken as (x_th, x₀) = (0.5, 0) and a = 1. The results are qualitatively the same as in Figure 1: the m-IMI model fits better than the TRRP model, and the interval distribution of the m-IMI model shows less variation than that of the TRRP model. These results depicted in Figure 1 and Figure 2 suggest that for various amplitudes and timescales of a stimulus, the fitted m-IMI model is closer than the TRRP model to the true LIF model when a stimulus is applied to mean of the LIF model.

Figure 2.

Results for various values of the time constant of the time-varying mean input, τ_s. (a–d) The same as Figure 1.

3.2 Statistical Interpretation of the KL Divergence

The scale of KL divergence is, by itself, somewhat difficult to interpret. However, in general terms, the value of the KL divergence is related to the probability that a test will reject a false null hypothesis: as the KL divergence increases, the probability of rejecting the hypothesis increases. We used the Kolmogorov-Smirnov (K-S) test to provide a statistical interpretation of the KL divergence, and we obtained corresponding K-S plots (Brown, Barbieri, Ventura, & Kass, 2002) to provide visual display of fit in particular cases.

The K-S plot begins with rescaled interspike intervals,

$$y_i=\mathrm{\Lambda }(t_i)-\mathrm{\Lambda }(t_{i-1}),$$ (3.3)

where Λ(t) is the time-rescaling transformation obtained from the estimated conditional intensity,

$$\mathrm{\Lambda }(t)={{\displaystyle \int }}_0^t\widehat{\lambda }(u,s_{*}(u))du.$$ (3.4)

If the conditional intensity were correct, then according to the time-rescaling theorem, the y_is would be independent exponential random variables with mean 1. Using the further transformation,

$$z_i=1-\text{exp}(-y_i),$$ (3.5)

z_is would then be independent uniform random variables on the interval (0,1). In the K-S plot, we order the z_is from smallest to largest and, denoting the ordered values as z_(i), plot the values of the cumulative distribution function of the uniform density, that is, $b_i=\frac{i-\frac{1}{2}}{n}$ for i = 1,…,n, against the z _(i)s. If the model were correct, then the points would lie close to a 45 degree line. For moderate to large sample sizes the 95% probability bands are well approximated as b_i ± 1.36/n^1/2 (Johnson & Kotz, 1970). The K-S test rejects the null-hypothetical model if any of the plotted points lie outside these bands.

Using this procedure, we first generated spike trains from the LIF model with parameter values (x_th, x₀) = (0.5, 1) and (a, τ_s) = (1.4, 5/π) (the same as in Figure 1) and fitted the empirical models to the data. The integral in the time-rescaling transformation (see equation 3.4) was computed with discrete time step, Δ = 10⁻³. We also confirmed that the results did not change with the temporal precision Δ = 10⁻⁴. In order to calculate the rate at which the empirical models are rejected by the K-S test, we generated 100 sets of repeated spike train trials, with varying numbers of trials—and thus varying total numbers of spikes (ISIs).

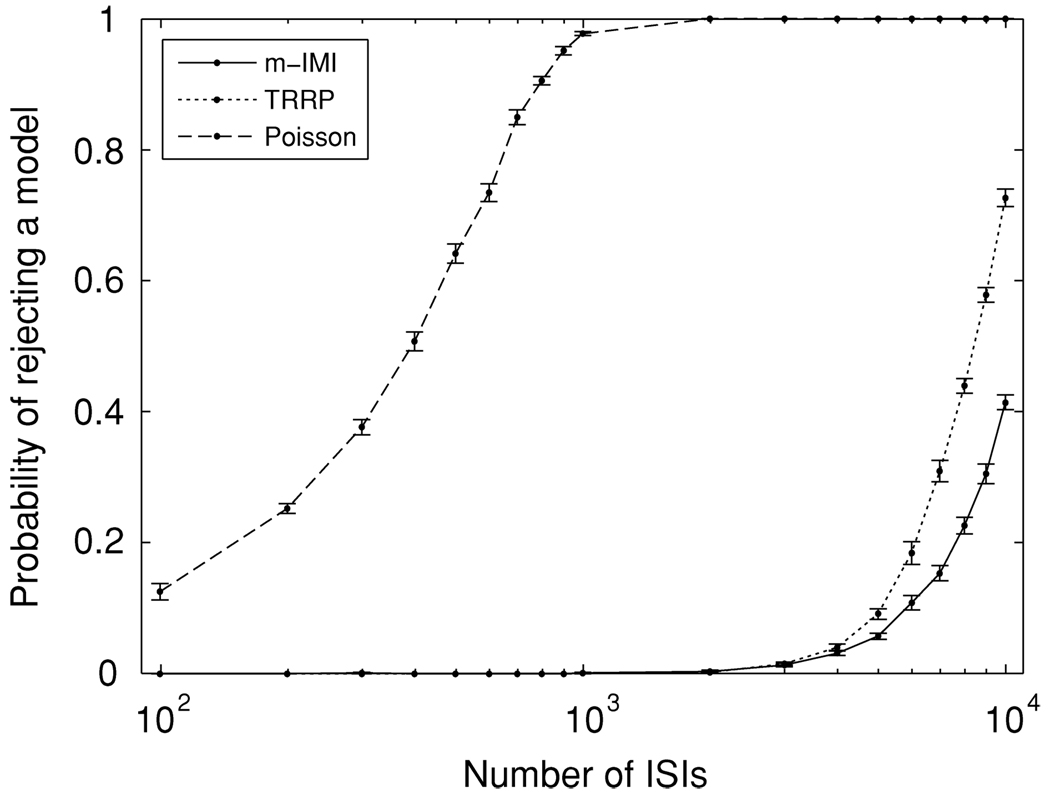
Figure 3 displays the rate of rejecting the models as a function of the number of spikes. The probability of rejecting the inhomogeneous Poisson process rises very fast, while it takes much larger data sets to reject the m-IMI model and the TRRP. Figures 4a and 4b depict examples of K-S plots. With only 200 ISIs (see Figure 4a), there is clear lack of fit of the Poisson model. With 7000 ISIs (see Figure 4b), lack of fit of the TRRP becomes apparent, though the m-IMI model continues to fit the mean-modulated LIF data. From Figure 3, in this example, roughly 10⁴ ISIs are necessary to reject the TRRP with probability 0.8.

Figure 3.

The probability of rejecting probability models as a function of the number of ISIs. The solid line, dotted line, and dashed lines represent the m-IMI model, the TRRP model, and the inhomogeneous Poisson process, respectively. The mean and the standard error at each point were calculated with 10 repetitions. With relatively small sample sizes, it can be easy to reject the hypothesis of Poisson firing but very hard to distinguish m-IMI models from TRRP models.

Figure 4.

(a) The Kolmogorov-Smirnov plot using 200 ISIs showing the Poisson model does not fit but the two other models do. (b) Same as a using 7000 ISIs showing that the m-IMI model fits, but the two other models do not.

3.3 Time-Varying Input Variance

Next we considered the input whose variance varies across time,

$$I(t)=\sigma (t)\xi (t),$$ (3.6)

where

$${\sigma }^2(t)=1+a\text{sin}\frac{t}{{\tau }_s}.$$ (3.7)

This form could be interpreted as a signal in the variance of the input, of which Silberberg, Bethge, Markram, Pawelzik, and Tsodyks (2004) considered the possibility in the cortex. We set the parameter values of the LIF neuron to (x_th, x₀) = (0, −4) and τ_s = 10/π. We simulated the LIF model over the time interval 10⁷Δ to generate a spike sequence, fit the three probability models to data, and calculate the KL divergence.

The result of the KL divergence is displayed in Figure 5a. In contrast to the case of time-varying mean input, the TRRP model best fits the LIF neuron for this case. The value of the KL divergence of the TRRP model remains small even when the firing rate varies largely (see Figure 5b).

Figure 5.

Results for the case that the input variance is varying in time. (a–d) The same as Figure 1. Only the raw trace of the firing rate for a = 0.9 is shown in b. In this case, the KL divergence of the TRRP model is the smallest among the three models, and the interval distribution for the TRRP model shows less variation than for the m-IMI model.

Figures 5c and 5d depict the rescaled interval distributions of the m-IMI model and the TRRP model, respectively. The interval distributions of the TRRP model are almost identical even when the amplitude of the variance modulation is changed, whereas interval distributions of the m-IMI model show variation.

Figure 6 displays the results for various values of τ_s and fixed value of a. The parameter values of the LIF model in this figure are (x_th, x₀) = (0, −4) and a = 0.8. It is confirmed from this figure that the results are qualitatively the same as Figure 5. That is, the time-rescaled renewal process shows the best agreement with the LIF neuron, and the best fitted interval distribution of the TRRP model is invariant for different values of τ_s.

Figure 6.

Results for the various values of the time constant of the time-varying variance of the input, τ_s. (a–d) The same as Figure 5. Only the raw trace of the firing rate for τ_s = 4/π is shown in b.

3.4 Another Example

So far we have examined the ability of the statistical models to accommodate data from the LIF model driven by sinusoidal stimuli. We performed another simulation to confirm that the results are robust against different stimuli. In this example, we took f(t) to be a stimulus with the form represented in Figure 7a. Two cases were considered: the mean of the input to the LIF neuron varies across time, I(t) = f(t) + ξ(t), and the variance of the input varies across time, I(t) = f(t)ξ(t). The parameter values of the LIF neuron were taken to be (x_th, x₀) = (0.5, 0). We simulated the LIF model to generate sequences of spikes; fitted the m-IMI, TRRP, and the Poisson model to data; and conducted the KS test. Figures 7b and 7c depict examples of K-S plots. For the mean-modulated case (see Figure 7a), the lack of fit of the TRRP model becomes apparent, though the m-IMI model continues to fit the LIF model with 6000 ISIs. For the case of the variance-modulated version (see Figure 7b), however, the m-IMI model shows lack of fit with 1000 ISIs, while the TRRP model continues to fit the LIF model.

Figure 7.

(a) The shape of the stimulus, f(t). (b) Kolmogorov-Smirnov plot using 6000 ISIs showing that the m-IMI model fits, but the two other models do not for the mean-modulated stimulus. (c) Same as b using 1000 ISIs showing that the TRRP model fits but the two other models do not for the variance-modulated stimulus.

4 Discussion

Our results examined the extent to which regularity and variability in spike trains generated by a stimulus-driven LIF neuron could be captured by two empirical models, the m-IMI model and the TRRP. Although the LIF model involves a gross simplification of neuronal biophysics, it remains widely applied in theoretical studies. This is one reason we investigated the performance of statistical models for stimulus-driven LIF spike trains. Our more fundamental motivation, however, was that LIF spike trains serve as a vehicle for quantifying the similarity and differences between the m-IMI and TRRP specifications of history effects. For a constant stimulus, the LIF model becomes stationary, generating a renewal process of spike trains, and the m-IMI and TRRP models become identical. The qualitative distinction between the m-IMI and TRRP models in the nonstationary case may be understood by considering the way the refractory period is treated: if, during an interval of stationarity, for which the neuron has a constant firing rate, there is a refractory period of length δ, then when the firing rate changes, the TRPP model will vary the refractory period away from δ while the m-IMI model will leave it fixed. More complicated effects, described under stationarity by a renewal process, will, similarly, according to the two empirical models, either vary in time with the firing rate or remain time invariant. Thus, it is perhaps not surprising that when a stimulus was applied to the mean of the LIF model, the fitted m-IMI model was closer than the TRRP model to the true LIF model that generated the data. The interval distribution plots in Figure 1 and Figure 2 are consistent with this interpretation.

On the other hand, when the variance in the LIF model is temporally modulated, the renewal effects, such as the refractory period, become distorted in time. In this case, we observed that the TRRP model fits better than the m-IMI model, and the interval distribution plot in Figure 5 shows less variation for the TRRP model than for the m-IMI model.

We also computed the power of the K-S test as a function of the number of spikes. We found that with relatively small sample sizes, it can be easy to reject the hypothesis of Poisson firing but very hard to distinguish m-IMI from TRRP models. This is demonstrated in the K-S plot of Figure 3b. For the very large data set used in the K-S plot of Figure 3c, the m-IMI model provided a satisfactory fit, while the TRRP did not. Overall we would conclude, first, that in most practical circumstances, it is unlikely to matter much whether one uses the m-IMI model or the TRRP to produce empirical fits to spike train data, but, second, m-IMI models would be preferred when a mean-modulated LIF conception might be thought to represent reality better than the variance-modulated version, and vice versa.

Statistical models used to characterize such things as a receptive field, or the effect of an oscillatory local field potential, must account for spike history effects. A successful approach has been to include m-IMI or TRRP terms in a log-linear model for the conditional intensity (Brown, Frank, Tang, Quirk, & Wilson, 1998; Okatan, Wilson, & Brown, 2005; Paninski, 2004; Truccolo, Eden, Fellows, Donoghue, & Brown, 2005). As special cases of equation 1.1, the m-IMI and TRRP models studied here may be considered simplified versions of the more realistic models used in the literature. Because we are focusing on history effects, we would anticipate that results for more complicated settings would be similar to those reported here.

Appendix A: Derivation of the KL Divergence

In this appendix we derive equation 2.9 from equation 2.7 under the conditions that p_f and p_q are periodically stationary with period T and E[n] → ∞ as T′ → ∞. Let {t₁,…, t_n} be a sequence of spikes, θ_i = θ(t_i) be the phase of spike time t_i, and u_i = t_i − t_i−1 be the ith interspike interval. The probability density of a spike sequence {t₁, …, t_n} in the time interval [0, T′) for T′ → ∞ whose conditional ISI density is f(u|θ) is given by

$$\begin{array}{cc}{p}_f(t_1,\dots ,t_n)\hfill & =Q(n)\chi (\theta (t_1))f(t_2-t_1|\theta (t_1))\cdots f(t_n-t_{n-1}|\theta (t_{n-1}))\hfill \\ \hfill & =Q(n)\chi ({\theta }_1)f(u_2|{\theta }_1)\cdots f(u_n|{\theta }_{n-1}),\hfill \end{array}$$ (A.1)

where Q(n) is a probability distribution of spike count in the interval [0, ∞). Equation A.1 satisfies the normalization condition:

$$\begin{array}{c}\begin{array}{cc}Q(0)\hfill & +\underset{T\prime \to \infty }{\text{lim}}{\displaystyle \sum _{n=1}^{\infty }{\displaystyle {\int }_0^{T\prime }{\displaystyle {\int }_{t_1}^{T\prime }\cdots }{\displaystyle {\int }_{t_{n-1}}^{T\prime }{p}_f(t_1,\dots ,t_n)d{t}_{1}d{t}_2\dots d{t}_n}}}\hfill \\ \hfill & =Q(0){\displaystyle \sum _{n=1}^{\infty }Q(n){\displaystyle {\int }_0^T\chi }({\theta }_1)d{\theta }_1{\displaystyle {\int }_0^{\infty }f(u_2|{\theta }_1)d{u}_2\cdots {\displaystyle {\int }_0^{\infty }f(u_n|{\theta }_{n-1})d{u}_n}}}\hfill \\ \hfill & ={\displaystyle \sum _{n=0}^{\infty }Q(n)}=1.\hfill \end{array}\hfill \\ \hfill \end{array}$$ (A.2)

In equation 2.7, taking the limit of T′ → ∞,

$$\begin{array}{c}{\displaystyle {\int }_0^{T\prime }{\displaystyle {\int }_{t_1}^{T\prime }\cdots {\displaystyle {\int }_{t_{n-1}}^{T\prime }{p}_f(t_1,\dots ,t_n)\text{log}\frac{p_f(t_1,\dots ,t_n)}{p_q(t_1,\dots ,t_n)}d{t}_{1}d{t}_2\dots d{t}_n}}}\hfill \\ \begin{array}{ccc}\hfill & \to Q(n){\displaystyle {\int }_0^T{\displaystyle {\int }_0^{\infty }\cdots }{\displaystyle {\int }_0^{\infty }\chi ({\theta }_1)}\left({\displaystyle \prod _{i=2}^{n}f(u_i|{\theta }_{i-1})}\right)}\hfill & \hfill \\ \hfill & \times {\displaystyle \sum _{j=2}^n\text{log}\frac{f(u_j|{\theta }_{j-1})}{q(u_j|{\theta }_{j-1})}d{\theta }_{1}d{u}_2\cdots d{u}_n}\hfill & \hfill \\ \hfill & =Q(n){\displaystyle \sum _{i=2}^n{\displaystyle {\int }_0^T\chi ({\theta }_1)\left({\displaystyle \prod _{j=2}^{i-1}{\displaystyle {\int }_0^{\infty }f(u_j|{\theta }_{j-1})d{u}_j}}\right)d{\theta }_1}}\hfill & \hfill \\ \hfill & \times \left({\displaystyle {\int }_0^{\infty }f(u_i|{\theta }_{i-1})\text{log}\frac{f(u_i|{\theta }_{i-1})}{q(u_i|{\theta }_{i-1})}d{u}_i}\right)\left({\displaystyle \prod _{k=i+1}^n{\displaystyle {\int }_0^{\infty }f(u_k|{\theta }_{k-1})d{u}_k}}\right)\hfill & \hfill \\ \hfill & =Q(n){\displaystyle \sum _{i=2}^n{\displaystyle {\int }_0^T{\displaystyle {\int }_0^{\infty }\chi ({\theta }_{i-1})f(u_i|{\theta }_{i-1})\text{log}\frac{f(u_i|{\theta }_{i-1})}{q(u_i|{\theta }_{i-1})}d{\theta }_{i-1}d{u}_i}}}\hfill & \hfill \end{array}\hfill \\ \begin{array}{ccc}\hfill & =Q(n)(n-1){\displaystyle {\int }_0^T{\displaystyle {\int }_0^{\infty }\chi (\theta )f(u|\theta )\text{log}}\frac{f(u|\theta )}{q(u|\theta )}d\theta du,}\hfill & \hfill \end{array}\hfill \end{array}$$ (A.3)

where we use

$${{\displaystyle \int }}_0^T\chi ({\theta }_1)({\displaystyle \prod }_{j=2}^{i-1}{{\displaystyle \int }}_0^{\infty }f(u_j|{\theta }_{j-1})d{u}_j)d{\theta }_1={{\displaystyle \int }}_0^T\chi ({\theta }_{i-1})d{\theta }_{i-1}.$$ (A.4)

Substituting equation A.3 into equation 2.7 leads to

$$\begin{array}{cc}D(p_f\Vert p_q)\hfill & =\underset{T\prime \to \infty }{\text{lim}}\frac{1}{E[n]}{\displaystyle \sum _{n=1}^{\infty }Q(n)(n-1)}{\displaystyle {\int }_0^T{\displaystyle {\int }_0^{\infty }\chi (\theta )f(u|\theta )\text{log}\frac{f(u|\theta )}{q(u|\theta )}d\theta du}}\hfill \\ \hfill & =\underset{T\prime \to \infty }{\text{lim}}\left(1-\frac{1-Q(0)}{E[n]}\right){\displaystyle {\int }_0^T{\displaystyle {\int }_0^{\infty }\chi (\theta )f(u|\theta )\text{log}\frac{f(u|\theta )}{q(u|\theta )}d\theta du}}\hfill \\ \hfill & {\displaystyle ={\int }_0^T{\displaystyle {\int }_0^{\infty }\chi (\theta )f(u|\theta )\text{log}\frac{f(u|\theta )}{q(u|\theta )}d\theta du.}}\hfill \end{array}$$ (A.5)

Appendix B: TRRP Model

In this appendix we show that the rescaling function of the TRRP model, λ₀(t), corresponds to the trial-averaged conditional intensity function, up to an arbitrary multiplicative constant. Let g ₀(u) be the hazard function of a renewal process, and, to avoid transient start-time effects, suppose that the renewal point process starts from u = −∞. Let e _*(u) be the event time prior to u. By the renewal theorem (theorem 4.4.1 in Daley & Vere-Jones, 2003), the expectation of g₀(u − e_*(u)) is constant,

$$E{g}_0(u-e_{*}(u))=c,$$ (B.1)

for some positive c. Now transform time from u to t with a monotonic time-rescaling function $t={\mathrm{\Lambda }}_0^{-1}(u)$, where Λ₀(t) is given by equation 2.6. By the change-of-variables formula, the conditional intensity as a function of time t is given by equation 2.5. Taking expectations of both sides and applying equation B.1, we get

$$E[\lambda (t,s_{*}(t))]={\lambda }_0(t)c.$$ (B.2)

If we replace g₀(t) with h(t) = g₀(t)/c, then λ₀(t) becomes the expected (trial-averaged) conditional intensity function. This is convenient because λ₀(t) may then be estimated by pooling data across trials, that is, by smoothing the PSTH.