Instantaneous Normal Modes and the Protein Glass Transition

Abstract

In the instantaneous normal mode method, normal mode analysis is performed at instantaneous configurations of a condensed-phase system, leading to modes with negative eigenvalues. These negative modes provide a means of characterizing local anharmonicities of the potential energy surface. Here, we apply instantaneous normal mode to analyze temperature-dependent diffusive dynamics in molecular dynamics simulations of a small protein (a scorpion toxin). Those characteristics of the negative modes are determined that correlate with the dynamical (or glass) transition behavior of the protein, as manifested as an increase in the gradient with T of the average atomic mean-square displacement at ∼220 K. The number of negative eigenvalues shows no transition with temperature. Further, although filtering the negative modes to retain only those with eigenvectors corresponding to double-well potentials does reveal a transition in the hydration water, again, no transition in the protein is seen. However, additional filtering of the protein double-well modes, so as to retain only those that, on energy minimization, escape to different regions of configurational space, finally leads to clear protein dynamical transition behavior. Partial minimization of instantaneous configurations is also found to remove nondiffusive imaginary modes. In summary, examination of the form of negative instantaneous normal modes is shown to furnish a physical picture of local diffusive dynamics accompanying the protein glass transition.

Introduction

The importance of internal dynamics in the function of proteins is widely recognized (1–3). Proteins exhibit a wide spectrum of dynamical processes ranging from localized femtosecond-timescale harmonic vibrations to collective diffusive movements with timescales up to the millisecond range or longer (4).

Among the computational methods used to characterize protein dynamics are normal mode analysis (NMA) and molecular dynamics simulation (MD). NMA makes the harmonic approximation to the potential energy around an equilibrium configuration. In the realm of validity of this approximation, the dynamics is determined completely by the second-derivative (Hessian) matrix of the potential energy with respect to the mass-weighted atomic coordinates. The vibrational dynamics of the system around the local minimum is described by the eigenvectors and eigenvalues of the Hessian matrix.

Standard NMA cannot be used to characterize anharmonic dynamics. Instead, MD simulation, involving stepwise integration of the equations of motion with the full, anharmonic potential, can be used. However, the analysis of MD trajectories to extract useful information on anharmonic motion is nontrivial. Here, we examine the application to proteins of the Instantaneous Normal Mode (INM) method, which has proven to be a useful analysis tool for diffusive dynamics in condensed phase systems (5–8). INM is a statistical mechanical theory connecting dynamic properties (e.g., diffusion constants) to equilibrium averages of the curvatures of the potential energy surface at sample configurations. As in NMA, INM is based on the second derivative of the potential energy. However, unlike in NMA, the Hessian matrix is computed for snapshot configurations generated, for example, during MD or Monte Carlo simulation, instead of at fully energy-minimized configurations. Negative eigenvalues thus result.

INM theory, which has been developed based on the concept of inherent structure (9–11) and on a random energy model (6,12–14), predicts that the self-diffusion constant and the configurational entropy are proportional to the average fraction of diffusive instantaneous normal modes (7,8,15–19). However, although much progress has been made, present theoretical derivations rely on significant approximations and still have open questions (6,8,20–28). It has therefore been necessary to employ computational techniques to examine the relation between diffusive modes and dynamical properties of liquids (15,28). Instantaneous normal modes with negative curvature are called unstable modes. To relate INM to diffusive properties filtering methods have been proposed for separating diffusive from nondiffusive unstable modes (see later) (19).

Computational INM studies have been hitherto performed mainly on simple, supercooled liquids, with a focus on glass transition, mode-coupling, and crystallization behavior (6,15,23,25,27,29). These results have demonstrated that it is possible to calculate useful temperature-dependent dynamical properties, such as the self-diffusion constant, from INM on a small number of sampled configurations. For proteins, an integral equation connecting the fraction of unstable INM modes with the barrier height distribution has been derived and shown to aid in exploring the energy landscape (30,31). Also, vibrational energy relaxation rates of selected vibrational modes of proteins have been computed using INM analysis (32). However, research connecting dynamical properties to unstable INM modes has not been documented for proteins. The goal in this work is to investigate this connection, and we examine which INM properties are related to diffusive dynamics in proteins.

We concentrate on the dynamical or glass transition in internal protein dynamics. Many experiments and simulations (33–39) have shown that, for proteins at 180–220 K, the average mean-square displacement exhibits a change in gradient with temperature, involving the excitation of anharmonic displacements (40,41). The role of hydration in the dynamical transition is an area of active research (37,42,43). Calculations are performed here for a small protein as a function of temperature to determine which INM properties are related to the physical nature of the transition. As for liquids, it is essential to accurately compute the subset of unstable modes from the set of negative modes, and so the filtering methods proposed for liquids are evaluated here for proteins. It is found that the number of unfiltered negative-eigenvalue modes does not correlate with dynamical transition behavior. However, selection of double-well modes that escape to distinct regions of configurational space does mirror the behavior of the temperature-dependent mean-square displacement.

Methods

We first provide a brief overview of INM filtering methods. INM studies on simple liquids have shown that some negative modes are not connected to diffusion (26). Therefore, the nondiffusive negative modes should be filtered out. In an early study on a Lennard-Jones liquid (6), the filtering was performed by subtracting the number of negative modes observed for a crystal (none of which are diffusive) from the number of negative modes for the liquid. After this work, a cutoff-based filtering method was proposed in which those unstable modes with frequency |ω| above a cutoff value were considered to be diffusive (19). However, it was found that both of the above filtering methods are material-specific. Subsequently, improved filtering methods were developed, based on the topology of the potential energy landscape (16,22), and these will now be outlined.

In the double-well filtering method, one-dimensional potential energy profiles along the negative modes are calculated and used to classify them into double-well or shoulder modes (22,44). For the double-well modes, the one-dimensional potential energy profiles consist of two minima separated by a barrier, while the shoulder modes exhibit single wells with shoulders. It has been suggested that double-well modes are diffusive whereas shoulder modes are not, and therefore the diffusive dynamics should be associated only with the former (27). The filtering was further refined by classifying the double-well modes as extended or localized depending on the fraction of atoms that participate in these modes (22), the extended double-well modes being assumed to make the primary contribution to the diffusive dynamics. However, it was later demonstrated that the double-well filtering method failed to provide a satisfactory description of the diffusive dynamics of various materials, particularly ionic melts (45). Moreover, it was shown that, for some double-well modes, quenching from either side of the barrier converged to the same inherent structure, thus suggesting that these double-well modes do not play any special role in diffusion (26).

A further problem arises when the one-dimensional potential energy profile is computed along a straight-line in the direction of the eigenvector computed at the instantaneous configuration. Because of the anharmonicity of the energy landscape, the frequency, and thus curvature, changes quickly along this line, due to a fast increase of the potential energy arising from van der Waals repulsion between neighboring atoms (16). This fast increase prohibits finding more distant saddles, and hence the evaluated number of double-well modes corresponds to only those double wells with close-by saddles.

The finding that double-well modes do not always minimize to different inherent structure basins led to the definition of escape modes (16,46). In escape filtering, the configurations corresponding to the two one-dimensional minima along the mode on either side of the saddle are minimized. An inherent structure basin is defined as the region of the potential energy surface that minimizes to the same point. By quenching the configurations corresponding to one-dimensional minima, it is possible to determine whether or not these minima belong to the same inherent structure basin. Those modes for which the minima do not belong to the same basin are escape or true double-well modes, the others being false double-well modes. In an analysis of liquid water, the temperature dependence of the number of escape modes was found to exhibit a behavior similar to that of the self-diffusion constant (15,21).

As well as the energy landscape-based methods discussed above, two minimization-based methods have been suggested: the saddle-order (SO) and the partial quenching (PQ) methods. The SO method suggests that by minimizing the squared gradient of the potential energy (|∇U|²) the system can be driven to the nearest stationary point (which can be a minimum or a saddle). The number of imaginary frequency modes calculated at the stationary point gives an estimate of the saddle order and thus the number of diffusive modes (47).

In the PQ approach the instantaneous configuration is partially quenched and the INM analysis performed at the partially quenched configuration so as to remove spurious, nondiffusive, negative modes. It has been found that the negative nondiffusive modes in a Lennard-Jones crystal vanish after the first minimization steps, while only the diffusive modes persist in the liquid state (47).

For all the filtering methods described above, linear proportionality to the self-diffusion constant was found for at least some materials. The computational methods used here to examine the relation between the self-diffusion constant and the number of diffusive modes for proteins will be discussed in the next section.

Simulation details

MD simulations were performed on Toxin II from the Scorpion Androctonus australis Hector (PDB (48) id: 1PTX), solved at 1.3 Å resolution (49), in the crystalline state. This protein was chosen for computational convenience, as it is small enough (64 residues) to permit ready evaluation of a large number of Hessian matrices for all atoms in a unit cell replicated with periodic boundary conditions. Toxin II crystallizes in an orthorhombic unit cell with the following lattice parameters: a = 45.94 Å, b = 40.68 Å, and c = 29.93 Å. The unit cell consists of four proteins. Explicit water molecules that were resolved in the crystallographic analysis were included, i.e., 107 water molecules per protein molecule. This model of a partially hydrated protein in crystalline form, although experimentally unrealizable, provides an appropriate model of a powder system as has been used in neutron scattering experiments on the dynamical transition and corresponding simulations (50).

Calculations were performed with the CHARMM program (51) using the CHARMM27 force field (52). Water molecules were represented by the TIP3P model (53). Electrostatic interactions were computed using the particle mesh Ewald method (54) for which the direct sum cutoff was 14 Å and the reciprocal space interaction were computed on a 48 × 48 × 32 grid using sixth-degree B-splines.

Simulations were carried out in the isothermal-isobaric (NPT) ensemble at temperatures starting at 20 K and increasing to 300 K in steps of 20 K. The system at each temperature was equilibrated for 1 ns followed by a production run of 1 ns during which atomic coordinates were written out every 50 fs. The starting structure for each temperature was the final structure from the preceding temperature.

For each temperature, 40 equally spaced configurations (separated by 5 ps) were extracted from the last 200-ps segment of MD trajectory and were used for the INM analysis. For mean-square displacement (MSD) computations, the full production run was used. This procedure determines whether the diffusion constant calculated using the INM analysis from a few configurations over a short timescale can furnish information pertaining to the diffusion constant computed from the MSD of a longer trajectory.

The computation of the Hessian matrix followed by its diagonalization is computationally demanding for a complex system studied here (with long-range electrostatic interactions treated with PME). In this investigation, the Hessian matrices were computed with a finite difference method using CHARMM on a single processor. The finite difference method computes the first derivative of the energy function (the force) for a small displacement to either side of the minimum for each of the 3N directions (where N is the number of atoms). In total, ∼660 Hessian matrices were calculated (with finite difference method followed by diagonalization), each requiring ∼6.5 CPU hours for the system studied here. Compute times are summarized in Table 1.

Table 1.

Approximate CPU times for the INM analysis of scorpion toxin at 15 temperatures on an ∼2 GHz CPU (see text for number of configurations)

Computation	CPU-time
Double-well filtering	300 days
Minimization for escape filtering	2 years
Escape filtering	3 years
Partial minimization (45 matrices)	10 days
Gradient minimization	10 days

The landscape-based filtering methods were implemented in the CHARMM program as follows. The eigenvectors and the atomic coordinates were read and one-dimensional energy profiles calculated by displacing the atomic coordinates along the eigenvector directions. An energy threshold of 0.6 kcal/mol was used for exploring the potential energy profile. The energy profiles were used to classify the imaginary modes into shoulder or double-well types. In total, there were ∼400,000 negative modes (evaluated at 600 instantaneous configurations) and all modes were thus classified.

To identify escape modes, the configurations corresponding to the two one-dimensional minima along each double-well mode were energy-minimized. The adopted basis Newton-Raphson (ABNR) method was used for these minimizations. After the minimization, the RMS distance between the pair of quenched configurations was computed. It was assumed that the minimized structures converge to a single minimum if the RMS distance is less than a threshold value. The number of minimization steps (1000 steps) and the distance cutoff (0.01–0.02 Å) were chosen after a few convergence tests. The same procedure was applied to both the double-well and shoulder modes so as to determine which of these types behave like escape modes. For shoulder modes, the starting structures were chosen either with energy or distance criteria.

The two minimization-based methods were implemented in CHARMM. In the PQ method, instantaneous configurations were partially minimized for 4–16 steps and the Hessian matrices computed and diagonalized so as to determine the fraction of unstable modes.

The SO method uses generalized stationary points on the potential energy landscape to describe the diffusive dynamics (47). In this method, the squared gradient of the potential energy is minimized, leading to minima and saddles around the instantaneous configurations. Here again the second-derivative matrix was required, to minimize the squared gradient, thus making this procedure computationally intensive.

Results

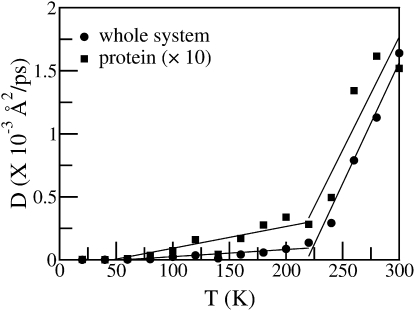
The mean-square displacement (MSD) averaged over the atoms as a function of temperature was calculated from the MD trajectories, and the self-diffusion constant computed from the long-time slope of the time-dependent MSD. In Fig. 1 is shown the temperature dependence of the diffusion constant for both the whole system (including the solvent) and the protein. A significant change in the diffusion constant at ∼220 K is evident, originating from the dynamical transition as observed in many biological systems (1,2,33,37,42,55–67). The temperature dependence of the diffusion constant in Fig. 1 was used as a benchmark with which to compare the INM results.

Figure 1.

Diffusion constant of the protein (squares, scaled by 10×) and the full system (circles) as a function of temperature.

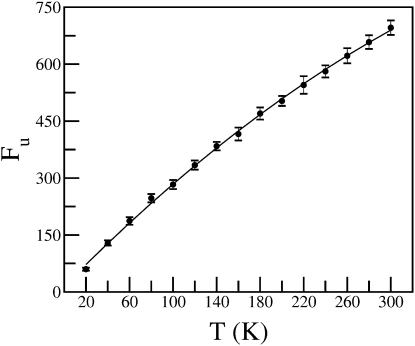
As a first necessary step for the INM method, the Hessian matrices were computed. This was performed from the simulations of 15 temperatures, for 40 configurations each, taken from the last 200 ps of the MD production runs in steps of 5 ps. In Fig. 2 is shown the number of imaginary frequency modes (F_u) as a function of temperature. As expected, F_u increases with temperature, as anharmonic regions of the potential energy surface become explored. However, unlike the diffusion constant, F_u does not exhibit any slope change at ∼220 K and instead shows an almost constant slope. Thus, it is evident that F_u cannot be equated with D and does not adequately describe internal diffusion in proteins.

Figure 2.

Number of negative modes (F_u) as a function of temperature. The total number of modes (negative and positive) is 15,348.

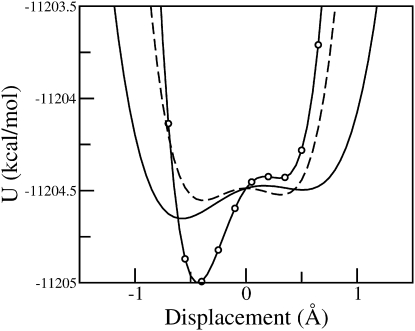
In the landscape-based filtering methods the energy profiles are explored by evaluating the potential energy along the modes. Inspection of the profiles revealed that a small number of negative modes correspond to double wells while no double wells were found for positive frequency modes  (as described in Methods, the potential energy profile can only reveal saddles close to the instantaneous position; because no saddle can be close in the direction of a positive frequency mode, no double well can be found for positive frequencies). Representative double-well profiles are shown in Fig. 3.

Figure 3.

Representative double-well potential energy profiles evaluated at a randomly-chosen instantaneous configurations sampled at 300 K.

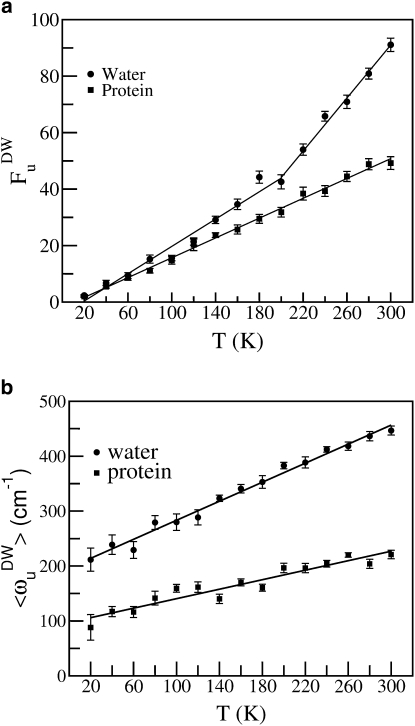
The temperature dependence of the number of diffusive modes (F_u^DW) after double-well filtering, and the temperature dependence of the average negative frequency of the double-well modes 〈ω_u^DW〉, are shown in Fig. 4, panels a and b, respectively. In this analysis, the contribution to the number of negative modes by the protein was computed by decomposing the normalized eigenvectors ($\overrightarrow{n}$) into protein (${\overrightarrow{n}}_{\text{p}}$) and water (${\overrightarrow{n}}_{\text{w}}$) components such that $\overrightarrow{n}$ = ${\overrightarrow{n}}_{\text{p}}$ + ${\overrightarrow{n}}_{\text{w}}$. We compute the projection r of protein atoms as

$$r=\overrightarrow{n}\cdot {\overrightarrow{n}}_{\text{p}}\text{.}$$ (1)

The negative modes for which r ∼ 1 are assumed to be dominated by diffusive protein dynamics while modes withr ∼ 0 are dominated by solvent dynamics. Fig. 4 a exhibits a small slope change in the number of double-well modes contributing to the motion of the water. However, similar to the unfiltered case, no change of slope is observed for the protein atoms, and thus the dynamical transition seen in the temperature-dependent protein MSD is not seen in the double-well filtered modes. The average frequency is proportional to the temperature without inflection. The variation of 〈ω_u^DW〉 as a function of temperature is one of the reasons for the weak T-dependence of the D ∝ f_u relation observed for simple liquids (19).

Figure 4.

Temperature dependence of (a) number of double-well modes (F_u^DW). (b) Average frequency 〈ω_u^DW〉 of double-well modes.

The double-well modes were further classified into escape modes and false double-well modes. The two one-dimensional minima of an escape mode belong to different inherent structure basins, while for false double wells they belong to the same inherent structure. To check whether a given double-well mode is an escape mode, the pair of configurations corresponding to two minima of the double well was energy-minimized (see Methods). This requires an efficient minimization scheme and a suitable criterion to check whether the minimized configurations belong to the same inherent structure. To determine a satisfactory minimization scheme, a few modes were selected and escape-mode classification was performed using different minimization methods (steepest descent, conjugate gradient, and Adopted Basis Newton-Raphson (ABNR)) and numbers of steps. ABNR was found to be the most suitable method for this classification.

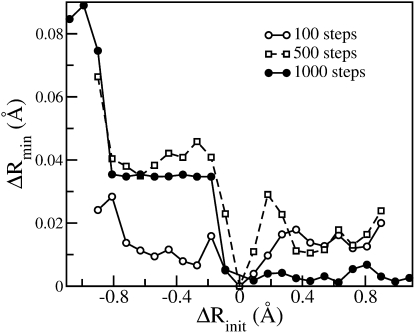
To select the optimal number of minimization steps required to filter escape modes, the following procedure was carried out: Let R_pert denote a perturbed configuration, obtained by displacing the instantaneous configuration, R_inst along a randomly-chosen double-well mode such that R_pert = R_inst + ΔR_initu_dw, where u_dw is the eigenvector corresponding to a double-well mode and ΔR_init denotes the RMSD between R_pert and R_inst. Let R_pert^min and R_inst^min denote configurations obtained by energy minimizing R_pert and R_inst, respectively. The RMSD between R_pert^min and R_inst^min is denoted as ΔR_min. For various values of ΔR_init and the number of minimization steps, ΔR_min was calculated and the results are presented in Fig. 5. It is evident that ΔR_min is sensitive to the number of minimization steps: increasing the number of steps leads to more highly-converged results. For instance, the variations in ΔR_min (for −0.8 Å < ΔR_init < −0.2 Å and 0.2 Å < ΔR_init < 0.8 Å) decrease as the number of minimization steps increases, indicating that increasing the number of minimization steps leads to more unique inherent structures. Moreover, the diffusive nature of double-well modes is evident in Fig. 5: a small displacement along the negative direction of the mode leads to an inherent structure (after 1000 steps of minimization) with ΔR_min ∼ 0.04 Å while a small displacement along the positive direction leads to a different inherent structure with ΔR_min = 0.0 Å. This analysis suggests that 1000 minimization steps are sufficient to filter out escape-modes.

Figure 5.

Distance (ΔR_min) between a pair of configurations obtained by minimizing the instantaneous structure and a perturbed structure obtained by displacing (by ΔR_init) along a randomly-chosen double-well mode for three different numbers of minimization steps.

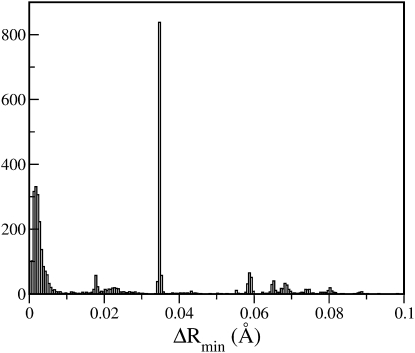
In addition to selecting the optimal number of minimization steps, a suitable cutoff for the RMSD between the inherent structures is required, so as to allow a decision to be made as to whether perturbations to either side of a double-well mode lead to the same inherent structure. To estimate this cutoff, a set of perturbed configurations were generated by displacing randomly-chosen instantaneous configurations (sampled at 300 K) by ΔR_init = 0.014 Å along the double-well modes. The value of ΔR_init = 0.014 Å was obtained by averaging the distances along the double-well modes at which the potential energy is 0.6 kcal/mol (K_BT at 300 K) higher than that at the instantaneous configuration. These perturbed configurations were further energy-minimized (with 1000 ABNR steps) resulting in an ensemble of inherent structures. The RMSD (ΔR_min) between these quenched configurations and R_inst^min was calculated as described above and the histogram of ΔR_min is shown in Fig. 6. Two most-probable inherent structures are found: one at ΔR_min ∼ 0.0 Å and the other at ΔR_min ∼ 0.038 Å: these values are consistent with the data presented in Fig. 5.

Figure 6.

Histogram of (ΔR_min).

The first minimum seen at ΔR_min ∼ 0.01 Å clearly separates the probable inherent structures, suggesting that ΔR_min ∼ 0.01 Å is a suitable cutoff for distinguishing between a pair of inherent structures. Consequently, for each double-well mode, a pair of configurations corresponding to two minima of the double well was minimized with 1000 ABNR steps and the double-well mode was classified as an escape mode if the Euclidean distance between the two minimized configurations thus obtained was >0.01 Å.

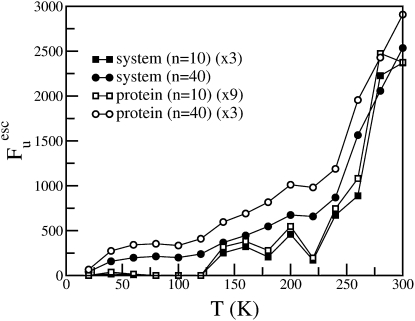
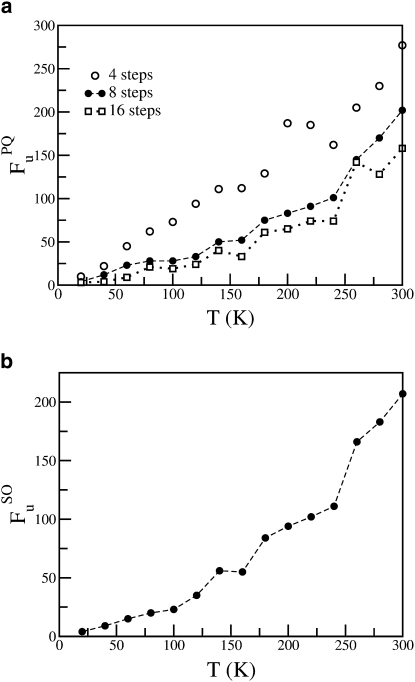
The number of escape modes F_u^esc, computed with a cutoff of 0.01 Å, is shown as a function of temperature in Fig. 7. F_u^esc increases gradually with temperature until ∼200 K and an abrupt change is observed at ∼220 K. The large increase in the population of escape modes at ∼220 K is concomitant with the onset of large amplitude displacements observed in the MSD (Fig. 1). This observation indicates that the number of barrier-crossing, diffusive degrees of freedom accessible to the protein increases at the dynamical transition temperature.

Figure 7.

Number of escape modes (F_u^esc) calculated from INM analysis performed at 10 (squares) and 40 (circles) configurations as a function of temperature. A distance cutoff of 0.01 Å was used for the escape filtering method.

To further characterize the escape modes, we have calculated for each escape mode the participation ratio (P) using the equation

$$P={\left(\sum _{i=1}^N|{\mathbf{u}}_{\text{i}}{|}^2\right)}^2{\left(N\sum _{i=1}^N|{\mathbf{u}}_{\text{i}}{|}^4\right)}^{-1},$$ (2)

with u_i being the component of the eigenvector contributed by atom i. P ∼ 1 for an extended eigenmode while P ∼ 0for strongly localized modes (68).

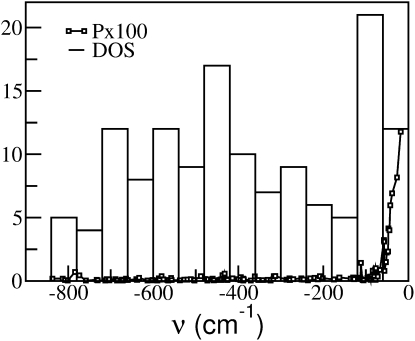
Fig. 8 shows the frequency dependence of P together with the density of states of the escape modes. The escape modes are almost equally distributed across the negative frequencies. The escape modes with frequencies >−75 cm⁻¹ have relatively larger P values compared to those with frequencies <−100 cm⁻¹, indicating that a large number of protein atoms exhibit diffusive dynamics along these high-frequency escape modes. A large fraction of escape modes (∼80 % at 300 K) are located below −100 cm⁻¹ with P ∼ 0 leading to an overall average P value of 0.005 (∼4 times smaller than the P value averaged over all negative modes, i.e., including those removed by escape filtering) at 300 K. This indicates that a large fraction of the INM escape modes activated at the transition describe diffusive processes that involve excitation of a few protein atoms while only a minor fraction of escape modes, i.e., those with frequencies above −75 cm⁻¹ (∼10 % at 300 K), describe collective diffusive dynamics in which a large number of protein atoms take part.

Figure 8.

Participation ratio (P) and density of states for escape modes at 300 K.

To investigate the nature of the delocalized escape modes, a normal mode calculation of the Toxin II crystal was performed and an essential space formed by the vibrational modes below 100 cm⁻¹ (7.3% of the total modes) was defined. The delocalized escape modes (those with absolute frequencies <100 cm⁻¹) were projected onto this subspace. It was found that ∼75% of the atomic fluctuations in these escape modes are captured by the essential space, thus indicating that the delocalized escape modes effectively span the same space as that of the low-frequency normal modes. A large number of studies have shown that the low-frequency collective normal modes are essential for biological functions of proteins (69). This investigation suggests that those collective normal modes that become escape modes across the protein dynamical transition may be key players of protein functions.

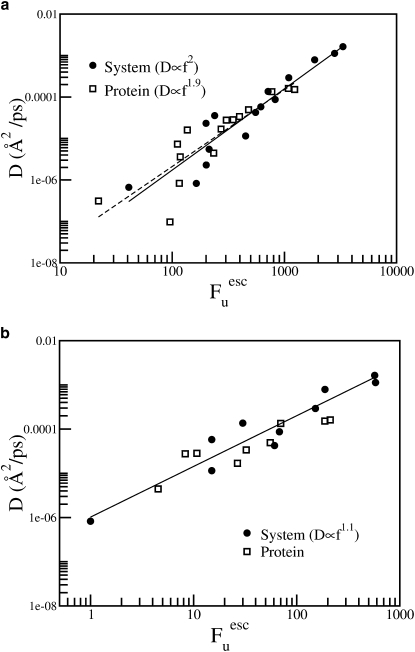
Fig. 9 shows the number of escape modes (calculated with two different distance cutoffs) plotted against the diffusion constant calculated from the MSD. A strong correlation of D with F_u^esc is seen, confirming that the escape filtering method can provide instantaneous modes related to internal protein diffusion.

Figure 9.

Number of escape modes (F_u^esc) calculated with a distance cutoff of (a) 0.01Å and (b) 0.02 Å versus the diffusion constant computed from the MSD. Calculations performed using (a) 40 and (b) 10 configurations. Straight lines (solid line, whole system; dashed line, protein) are fitted (using y = Ax^B) to the data.

Two minimization-based filtering methods were also tested: 1), the PQ and 2), SO approaches. In PQ the instantaneous configuration is partially minimized and a complete INM analysis is performed, involving computing and diagonalizing the Hessian for the minimized configurations, then counting the number of imaginary modes. In SO, the squared gradient of the potential energy is minimized, resulting in configurations corresponding to stationary points, including saddles, on the potential energy surface. After the application of SO, a complete INM analysis was performed at these stationary points. The imaginary modes thus obtained are considered as diffusive.

The results of the minimization-based methods are shown in Fig. 10. No change in the slope of F_u^PQ versus T is observed at ∼240 K when the instantaneous configurations are not energy-minimized (see Fig. 2). As observed for simple liquids, partial energy minimization of the instantaneous configuration removes a significant fraction of the nondiffusive imaginary modes. The temperature dependence of the number of diffusive modes obtained from the PQ method, F_u^PQ, is sensitive to the number of minimization steps (n). As n increases from 4 to 8, the number of diffusive modes decreases significantly for temperatures <220 K. Further increase in n from 8 to 16 does not greatly change the number of diffusive modes for T < 220 K, indicating that convergence has been reached. Although the number of diffusive modes decreases as n increases for T > 220 K, there is no significant change in the slope. For n = 8 and n = 16, the number of diffusive modes increases almost linearly with temperature up to ∼160 K, above which the slope increases slightly, with signs of a further increase at ∼240 K. The ∼160 K increase may correspond to the low-T dynamical transition in proteins that is solvent-independent and may involve activation of methyl group rotation (43,70–73). In Fig. 10 b is shown the temperature dependence of the number of diffusive modes, F_u^SO, obtained from the SO approach. The temperature dependence of F_u^SO exhibits gradual increase in gradient from ∼100 K with a small further increase at ∼240 K.

Figure 10.

Number of diffusive modes obtained from (a) partial quenching method (F_u^PQ) and (b) saddle order approach (F_u^SO) as a function of temperature.

Conclusions

The connection between the topography of the underlying potential energy surface (PES) and the diffusive dynamics of proteins has been investigated for several decades (74,75). This article has examined the possibility of employing the INM-based theoretical methods to provide PES-based insight into the anharmonic, diffusive dynamics of proteins. One potential advantage of using INM is that, in principle, it furnishes a picture of diffusive dynamics from a few sampled configurations. Based on the curvature of the local potential, the INM method determines the negative modes on the PES.

An important question concerns the identification of those negative modes that contribute to diffusive displacements. Here, filtering methods that have been proposed for simple liquids are evaluated for a small protein. For comparison, the temperature-dependent diffusion constant of the protein was computed from the slope of the average mean-square displacement obtained from molecular dynamics trajectories generated over a temperature range of 20–300 K. A significant change in the MD diffusion constant is found at ∼220 K, corresponding to the dynamical transition observed in many biological systems. In contrast, the number of INM negative eigenvalues increases almost linearly with temperature, exhibiting no transition with temperature. This indicates that many negative modes are not diffusive. These may correspond to, for example, local van der Waals repulsions.

Partial minimization (quenching) of the instantaneous configurations is found to remove nondiffusive imaginary modes, as has been seen for simple liquids (76), suggesting that the nondiffusive modes correspond to regions of the configuration space that are relatively high in energy. Filtering the negative modes so as to retain only those corresponding locally to double-well potentials does reveal a transition in the hydration water, consistent with results seen previously for simple liquids (22,44), but again, no transition in the protein is seen. This may be due to the relative simplicity of the water energy landscape, in that most effective double-well potentials on the water landscape may lead to diffusive dynamics. In contrast, the protein interior possesses double wells that, on energy minimization, return to the same inherent structure. Once these are filtered, retaining only those modes that escape to different regions of configurational space, clear dynamical transition behavior is seen, i.e., the number of escape modes follows the dynamical transition, with a good correlation with the diffusion constant calculated from the MD MSD. The filtered INM results obtained over a 200-ps segment of the MD trajectories provides physical information pertaining to the full 1 ns.

Previous work has demonstrated that the incipient dynamical transition in myoglobin can be represented by a very small number of solvent-driven, large-amplitude, multi-minimum principal component modes involving hundreds of atoms moving collectively (57,58). These results show that the instantaneous diffusive escape modes activated span a wide range of frequencies, from a few to several hundred wave-numbers. The relatively small number of collective, large-amplitude escape modes with low absolute frequencies will make the largest contribution to the diffusive MSD and are likely to bear similarities with the largest-amplitude principal components. Interestingly, however, a number of relatively localized, low-amplitude escape modes with high absolute frequencies also exist.

This analysis demonstrates that the negative normal modes derived from instantaneous protein configurations furnish, after appropriate filtering, a physical picture of local diffusive dynamics accompanying protein glass transition behavior. It will be of interest in the future to understand the environmental and functional relevance of the diffusive and nondiffusive imaginary modes in biological macromolecular systems, and to examine their relationship to measurable quantities such as, for example, neutron spectroscopic intensities.