Kinetics of Genetic Switching into the State of Bacterial Competence

Abstract

Nonlinear amplification of gene expression of master regulators is essential for cellular differentiation. Here we investigated determinants that control the kinetics of the genetic switching process from the vegetative state (B-state) to the competent state (K-state) of Bacillus subtilis, explicitly including the switching window which controls the probability for competence initiation in a cell population. For individual cells, we found that after initiation of switching, the levels of the master regulator [ComK](t) increased with sigmoid shape and saturation occurred at two distinct levels of [ComK]. We analyzed the switching kinetics into the state with highest [ComK] and found saturation after a switching period of length 1.4 ± 0.3 h. The duration of the switching period was robust against variations in the gene regulatory network of the master regulator, whereas the saturation levels showed large variations between individual isogenic cells. We developed a nonlinear dynamics model, taking into account low-number stochastic effects. The model quantitatively describes the probability and timescale of switching at the single cell level and explains why the ComK level in the K-state is highly sensitive to extrinsic parameter variations. Furthermore, the model predicts a transition from stochastic to deterministic switching at increased production rates of ComK in agreement with experimental data.

Introduction

Populations of genetically identical cells often maintain a diversity of phenotypes, characterized by different patterns of gene expression. This is usually triggered by stochastic fluctuations, which are amplified by the underlying gene regulatory networks (1–4). The benefits of such non-genotype-derived heterogeneity lie in the enhanced adaptability to environmental changes of the population as a whole (5–8). To analyze phenotypic heterogeneity it is necessary to monitor gene expression in individual cells (9). Real-time kinetics of gene expression have been extensively measured in individual cells to characterize noise in gene expression (10–14), multistability (1,5,15,16), oscillations (16–19), and timing of gene activities (20), but the determinants for genetic switching kinetics are not well characterized so far.

Competence development in Bacillus subtilis is one example in which a genetic switch determines cell fate. At low cell density, a homogeneous cell population undergoes exponential growth, but at high cell density (stationary growth phase), the cell population becomes heterogeneous in its phenotype, with a well-defined fraction of 15% expressing genes that code for a strong DNA import machine and recombination proteins (21). These cells are called competent for DNA transformation and they express the master regulator comK at high level (22–24). In this study, the state in which comK expression levels are high is denoted the K-state. The entry into the K-state is switchlike (25,26). The positive feedback loop in the genetic control circuit is important for the establishment of the competent phenotype in Bacillus subtilis (27,28). In noncompetent cells, the positive autoregulatory loop is not activated and comK expression is low (B-state). During exponential growth, ComK is kept at a basal level through degradation by the MecA/ClpC/ClpP protease complex, and by transcriptional repressors including Rok, AbrB, and CodY (Fig. 1). Due to a quorum-sensing mechanism, the concentration of ComS (an inhibitor of MecA/ClpC/ClpP) rises with increasing cell density. Work by Maamar et al. (29) revealed that at T₀ (i.e., at the entry into stationary phase, T_x=x h after transition point) the average number of mRNA coding for ComK per cell is of order 1. In this regime, small number fluctuations are, relative to the mean, of paramount importance. This is especially noteworthy since the reaction kinetics of ComK is highly nonlinear. Experiments and simulation have shown that the fraction of cells that switch into the K-state is determined by the magnitude of intrinsic fluctuations in comK expression (16,29). The second important determinant of the fraction of cells in the K-state is the length of a switching window in which basal comK expression rate is enhanced, which facilitates switching (30). Under conditions in which nutrient concentrations are constantly low, cycles of competence initiation and decay have been observed in real-time experiments in individual cells and a mathematical model described the system as an excitable regulatory circuit (15,16). Escape from the K-state has been attributed to negative feedback between ComK and the inhibitor of ComK proteolysis, ComS. Theoretical models of the competence decision system can be divided into two different categories, by the description of the system as excitable (15,16,31) as opposed to bistable (5,27–29,32).

Figure 1.

Core of the competence circuit. Arrows denote upregulation, blunt ends denote downregulation.

Here we investigated the switching kinetics of individual cells of Bacillus subtilis both experimentally and theoretically. We quantified the expression rate of the promoter of comK in real-time and mimicked increasing cell density with individual cells by continuously adjusting the growth medium. Using this method, we investigated the variability in the length of switching period, switching kinetics, and accumulated comK expression against varying external conditions due to growth phase and against genetic modification of the competence circuit. We developed a mathematical model predicting bistability during cell growth that retrieved the length of the switching period and the fraction of competent cells. The model explains why the saturation level of the K-state is highly sensitive to external fluctuations as observed in the experiments. Transition to deterministic switching, i.e., independence of fluctuations, as found for a mutant strain with increased transcription rates, is neatly explained by loss of the B-state in the stationary phase.

Materials and Methods

Materials and strains

All B. subtilis strains used were derived from strain BD630 and are described in Table S1 in Supporting Material. Bacillus strains were grown in liquid competence medium (33) supplemented with glucose (0.5%), L-histidine, L-leucine, L-methionine (50 μg/ml), and chloramphenicol, kanamycin (5 μg/ml), or spectinomycin (100 μg/ml) at 37°C. Competent cells were prepared as described previously (33). BM101 was created by transformation of genomic DNA of BD2711 into BD2955 ((28,41) (Table S1)).

Microscopy

Cells were taken at T₀ ± 1 h (where T₀ is the transition from the exponential to the stationary growth phase, T_x = x h after the transition point), permitted to attach to a polystyrene-coated cover slide and mounted onto a flow chamber. An image was acquired every 15 min. To confirm that the conditions under the microscope were equal to the conditions in an Erlenmeyer flask, the medium was exchanged directly after every exposure for the supernatant of a parallel culture grown in an Erlenmeyer flask (shaken at 300 rpm, at 37°C).

Microscopy was performed with a Axiovert 200 M microscope (Carl Zeiss, Jena, Germany) equipped with a digital camera (Andor, Belfast, UK), and an EC Plan-Neofluar 100×/1.30 oil immersion objective (Zeiss). Andor software was used for image acquisition. Stability of absolute fluorescence values was verified using a microscope image intensity calibration kit (Focal-Check fluorescence microscope test slide #3, F 36914; Molecular Probes, Eugene, OR). Homogeneity of illumination was tested using fluorescent slides and the maximum deviation was <5%.

Analysis

To analyze the ComK protein levels in single cells, we used strains containing a gfp-comK reporter construct standing under the control of the promoter of comK (P_comK) in addition to the original copy of the comK gene. As the green fluorescent protein (GFP) molecule is not likely to be a substrate for MecA/ClpC/ClpP proteolysis, the concentration of GFP controlled by P_comK is not a direct measure of ComK. However, the expression rates, i.e., the production rate of ComK and GFP, are expected to be similar, as the complete native promoter of comK including all native signals for comK expression is present. We analyzed ComK expression in single cells as the fluorescence intensity (FI) represented by the mean shaded value (measured in arbitrary fluorescence units (FU)).

Images were processed using ImageJ software (National Institutes of Health, Bethesda, MD). The image background was corrected using a rolling ball algorithm with a radius of 50. An intensity threshold tool was used to delimit the boundaries of the cells in the bright-field image (Fig. 2 a). The areas encircled by the boundaries were then selected as a region of interest using the ImageJ wand tool. These regions of interest were then applied to the fluorescence images and the mean shaded value of each cell was obtained using the ImageJ measurement tool.

Figure 2.

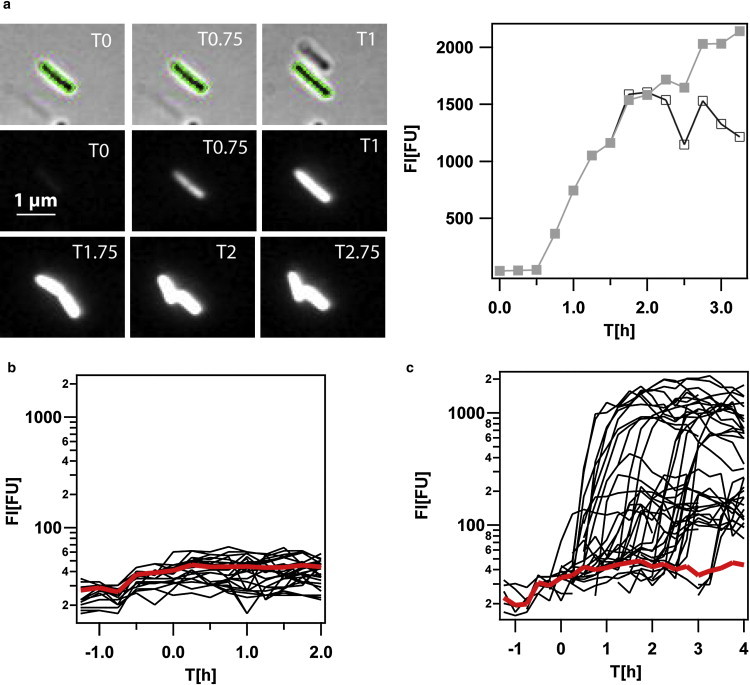
Time course of P_comK-gfp expression in individual cells. (a) Time-lapse of a switching cell and corresponding plot of fluorescence intensity FI as a function of time. (Green contour) Outline of the cell. Scale bar 1 μm. (b) Time course of fluorescence intensity of cells remaining in the B-state. Red line indicates the average fluorescence intensity of cells remaining in the B-state. (c) Time course of fluorescence intensity of cells switching into the K-state. Red line indicates the average fluorescence intensity of cells still in the B-state before switching.

The autofluorescence level of noncompetent BD630 was FI_{auto T−2} = 23 ± 1 FU, and the width of the Gaussian fit was FI_{auto T−2} = 9.2 ± 1 FU. We verified recently that the autofluorescence level did not shift until the basal fluorescence level reached its maximum (30). Since the time delay between the expression of the GFP reporter and the onset of fluorescence is 5 min (30), but switching into the K-state occurred on a significantly longer timescale, we did not correct our data for GFP-folding. In addition, no significant GFP degradation could be found on the relevant timescale of 3 h (30).

We defined the switching threshold differently as in previous work with fixed cells (30). Instead of defining the threshold from the histogram of fluorescence intensity, we defined the switching time as the point where the intensity increased sharply in the FI(t) plot (Fig. 2 a). This led to slightly lower values for the threshold but the fraction of competent cells was not affected (Fig. S4).

Results

The basal comK expression rate increases within the whole cell population

We quantified the expression of the master regulator comK in individual cells by measuring the fluorescence intensity of GFP fused to the promoter of comK (Fig. 2) (see Materials and Methods). To stimulate growth-phase-dependent development of cells on the microscope and to supply the cells with oxygen, we exchanged the medium in the flow chamber with medium from a cell culture growing under standard competence conditions every 15 min. We quantified the expression from the comK promoter by measuring the average fluorescence intensity FI of individual cells (Fig. 2 a). In agreement with previous experiments, we found that in our real-time experiments 15% of the cells switched into the K-state (Fig. S4). Initiation of switching was defined as a sharp increase in fluorescence intensity, which was followed by a sigmoidal increase in fluorescence intensity as a function of time. Before entry into the stationary phase at T₀, basal expression of comK increased significantly in all cells between T_−0.75 and T_−0.5 (Fig. 2, b and c). The basal level of comK expression was indistinguishable for cells that later triggered the switch and cells that remained in the B-state, indicating that no preselection had taken place as yet.

A fraction of cells switches into a state with intermediate comK expression

The saturation levels showed a large variation between individual cells with two distinct peaks of saturation fluorescence intensity (Figs. 2 c and 3 a). An intermediate peak was distributed at ∼200 FU, i.e., at a level between the basal fluorescence level at 50 FU (B-state) and high fluorescence level (K-state) at 1300 FU. We did not observe switching between the intermediate fluorescence mode and the K-state. Furthermore, we found no correlation between saturation fluorescence intensity and basal fluorescence, daughter cells after cell division, or cell length (data not shown). The intermediate fluorescence peak disappeared in the rok-strain (Fig. S5) in which the major repressor of comK transcription, Rok, was knocked-out. Since the characterization of functionality and molecular determinants for switching into the intermediate fluorescence mode is subject to future experiments, we decided to analyze the kinetics of switching into the K-state in the following, i.e., we concentrated on cells that obtained saturation fluorescence values exceeding 300 FU.

Figure 3.

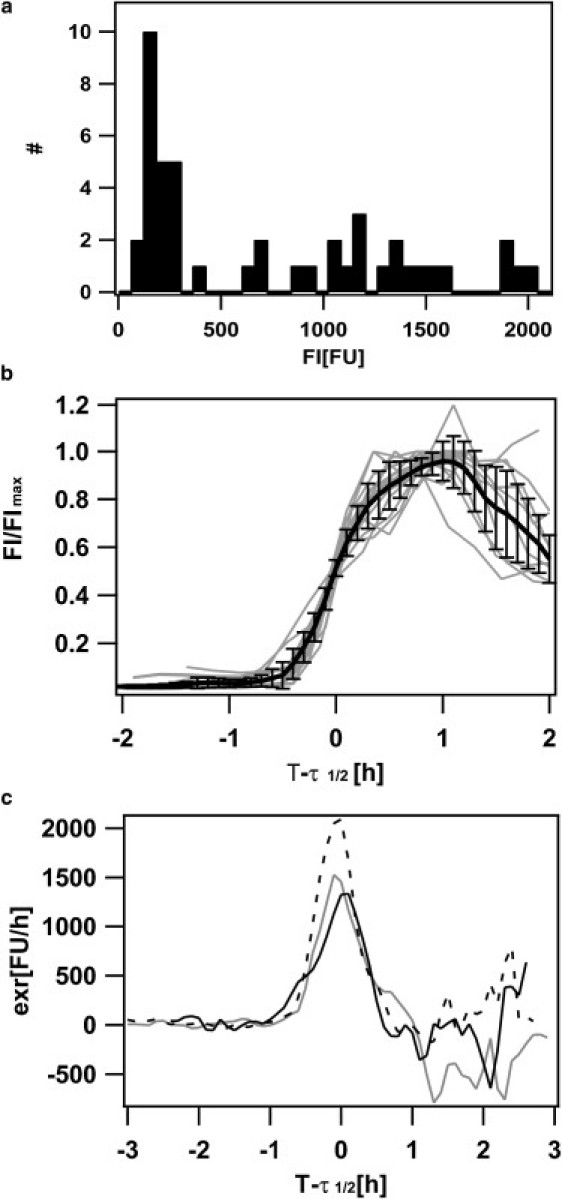
Switching characteristics of wild-type (wt) cells. (a) Distribution of maximum fluorescence intensity in the wild-type (BD2711). (b) The fluorescence intensity in 28 individual cells was normalized to the cumulative expression (maximum fluorescence intensity). The time axis was shifted to τ_1/2, where cells had half-maximum fluorescence intensity. (Solid line) Averaged fluorescence intensity; (shaded lines) individual cells. (c) Expression rates exr of wt (shaded), rok-strain (dotted), and ComS (solid) overproducing strain. Expression rates were obtained by multiplication of the normalized values with the average maximum value of 28–50 cells.

The length of the switching period of individual cells is well defined and independent of growth phase

To quantify the switching kinetics, we normalized the individual switching curves to their saturation level and shifted the T-axis to overlay all curves at half-maximum expression level at τ_1/2 (Fig. 3 b). To investigate whether the switching kinetics were dependent on growth phase, we sampled switching curves between T_−0.25 and T_2.5. The overlay showed very little variation, indicating that the duration of the switching period is well defined and independent of growth phase (data not shown). The expression rate exr was defined as the first derivative with respect to time of the fluorescence intensity, FI (Fig. 3 c). Please note that the cells did not grow during ≈1 h after the onset of switching (M. Leisner, K. Stingl, and B. Maier, unpublished data), and therefore we did not correct the expression rate for cell length. However, we attribute the negative expression rate at T − τ_1/2 > 1 h to cell growth, since GFP fluorescence was stable within several hours (Materials and Methods). We defined the length of the switching period ρ as the time during which exr exceeded 0.1exr_max. The average period for switching into the K-state was ρ = 1.4 ± 0.3 h, with a standard deviation of 0.3 h (Fig. S7 a). To address the question whether the length of the switching period was well defined in individual cells, we plotted the switching period ρ as a function of growth phase T and found no significant variation (Fig. S7 b).

With increasing ComS concentration, the probability for proteolysis of ComK by the MecA/ClpC/ClpP complex decreases, leading to increased ComK levels. We investigated whether the levels of ComS influenced the kinetics of switching using a ComS overproducing strain comS++. Although the fraction of switching cells increased from 15% to 85%, the switching kinetics of the individual bacteria did not alter significantly as compared to the wild-type (Fig. S6). In particular, the expression rate exr was comparable to the wild-type (Fig. 3 c).

A two-variable model elucidates the switching process

Nonlinear dynamics together with fluctuations can lead to bimodal protein distributions (34). Here we analyze a fully stochastic model for competence development. It incorporates production and degradation of both ComK proteins (K) and corresponding mRNA molecules (M). Mathematically the model is captured by a Master equation; a formal description of the model in terms of transition rates is given in the Supporting Material. Since analytical solutions are not feasible, we analyze the model by employing stochastic simulations (see below).

To give a frame of reference for the dynamics of competence development, and to explain the emergence of distinct phenotypes, it is instructive to analyze the equations:

$$\frac{\partial \text{K}}{\partial t}=\beta \text{K}\text{M}-\frac{{\delta }_{\text{K}}\text{K}}{q\text{K}+\text{S}+\text{K}}-{\delta }_0\text{K},$$ (1)

$$\frac{\mathrm{\partial }\text{M}}{\mathrm{\partial }t}\mathrm{=}\mathrm{\alpha }\text{M}+\frac{\mathrm{\beta }\text{M}}{{1+(\mathit{p}\text{K}/K_{\text{f}})}^{{\gamma }_{\text{K}}}}-\mathrm{\delta }\text{M}\text{M}\text{.}$$ (2)

While these equations disregard stochastic effects (see further below), they are easily discussed by a nonlinear dynamics analysis.

The first term in Eq. 1 represents translation of K, which happens with rate β_K for each M. The second term describes degradation of K according to Michaelis-Menten kinetics. For very high K this happens at a maximal rate δ_K, and half-maximal degradation of K is found where K = S + q_K. S corresponds to the number of ComS (S) proteins which compete with ComK for degradation by the MecA/ClpC/ClpP protease complex (see Supporting Material). Representing the effect of quorum sensing, S(t) communicates the cell density which rises sigmoidal with time to the individual cell. In our model, S(t) takes the role of an externally determined control function (Fig. S1). The third term covers linear degradation of ComK with rate δ₀ < < δ_K, which must always be present owing to nonspecific degradation/denaturation of ComK. This term is important only for large K and ensures that K cannot rise arbitrarily, as is biologically necessary. In Eq. 2, α_M is the basal transcription rate in absence of K. The next term describes autocatalytic feedback of ComK: Two ComK dimers bind cooperatively to the comK-promoter (35,36), thereby strongly activating transcription. Assuming dimer formation and dissociation as well as promoter binding and unbinding are fast enough to equilibrate, autocatalytic transcription can be modeled by a Hill function, with maximal (for large K) transcription rate β_M, half-maximal concentration p_K, and cooperativity γ_K. The value K_f, appearing in the denominator, is the number of free ComK, i.e., not bound to the MecA/ClpC/ClpP protease complex (see Supporting Material). Finally, degradation of mRNA is proportional to M and the rate δ_M. For further details on the model and its parameters, see Table S2.

Using nonlinear dynamics analysis (37) and literature data to set parameters, we investigated whether our two variable model (Eqs. 1 and 2) could reproduce the switching behavior. For low numbers of ComS we find only one stable fixed point corresponding to the vegetative state (K ≈ 100, M ≈ 1) (Fig. 4 a). As S rises, a saddle-node bifurcation appears, creating a further stable fixed point with higher K and M values and an intermediate unstable fixed point. This, in principle, allows cells to stochastically switch to the state with higher K and M. However, due to the high activation threshold, this is highly unlikely. At S ∼ 1500, the lower stable and the unstable fixed point almost meet in another bifurcation. The lower stable fixed point (now shifted to K ≈ 200, M ≈ 1) corresponds to the B-state. The intermediate unstable fixed point at K ≈ 600, M ≈ 3 is very close to the B-state (Fig. 4 b). Under these conditions, intrinsic noise is strong enough to carry some cells across the switching threshold. A sample path in phase space is given in Fig. S2, illustrating escape from B-state and passing of threshold. Cells that cross the threshold evolve toward the upper stable fixed point (K-state, K ≈ 7000, M ≈ 10), i.e., bacteria switch into the K-state. Back-transitions from the K-state into the B-state are highly improbable, because in the K-state, fluctuations are too small compared to the distance between the K-state and the threshold to revert switching.

Figure 4.

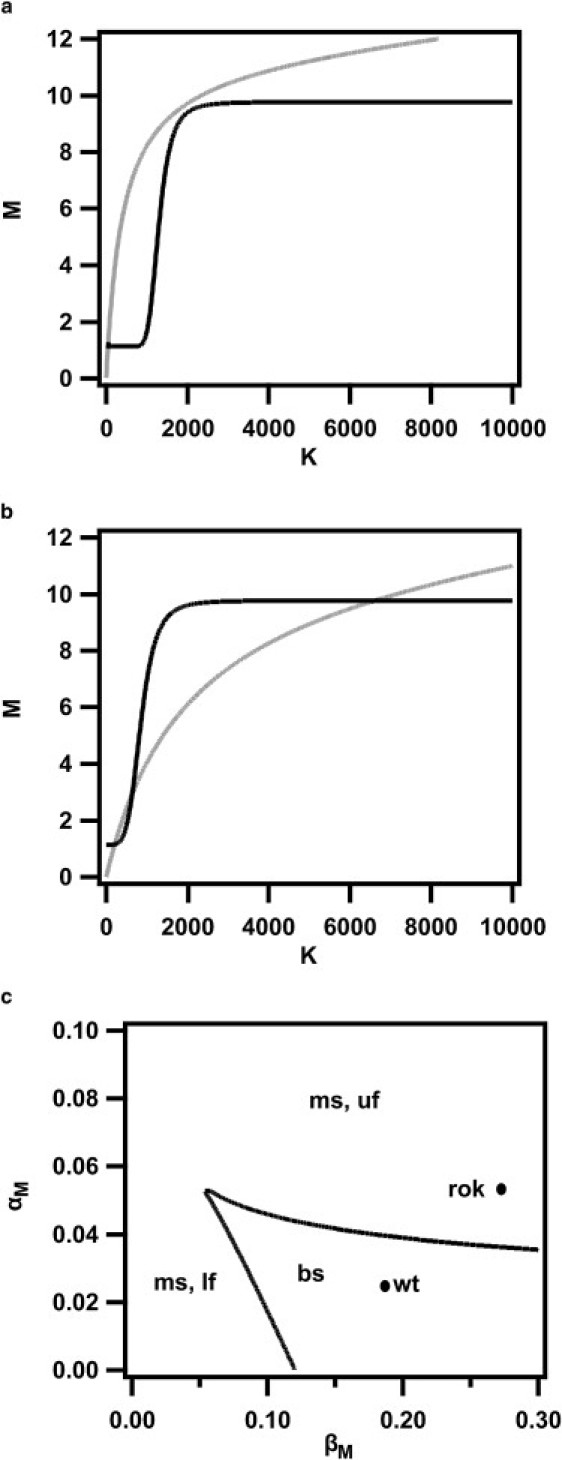
Nonlinear dynamics model. (a and b) Bifurcation analysis. Nullclines of Eqs. 1 and 2. (a) S=0. (b) S=1500 are plotted (solid, dM/dt=0; shaded, dK/dt=0). (c) A stability diagram, α_M versus β_M is plotted, monostable (ms) and bistable (bs) regions with only upper (uf) or only lower (lf) are indicated. Parameter combinations of the model for the wild-type (wt) and rok-strain (rok) are indicated.

Noise-driven switching requires vicinity to region with quantitatively different dynamics

The above scheme describes the evolution for a standard wild-type cell as it evolves from the low cell density exponential growth phase to the high cell density stationary phase. In that sense, it can be considered as averaged description, while for single cells reaction rates may vary, which is usually termed extrinsic noise (13). This can have major influence on the single cell dynamics to the point of loss of stochastic switching. To explore the consequences of variation in the rates we performed a stability analysis by examining the topology of nullclines and fixed points of the model. If the topology changes, one expects to find qualitatively different dynamics to that described above. Fixed points of the dynamics may emerge or disappear in bifurcations, changing the switching behavior significantly. Since the expression rates are experimentally accessible, we show the stability diagram (a cut through the parameter space) for variation in the basal transcription rate α_M and the transcription rate with feedback β_M (Fig. 4 c). Similar stability diagrams can be drawn for any pair of parameters.

A general result for bistable systems exhibiting stochastically induced switching is that they are located close to lines that separate regions with different topology. This is necessary, since only then are random fluctuations frequent and wide enough to enable a trajectory (an individual cell in our case) to cross the threshold with a sufficiently high probability. It follows that the switching probability per unit time is sensitive to the distance to the line of separation. This feature is likely to be present in systems similar to ours (38).

Effects of perturbing the promoter activity of comK on initiation probability, switching kinetics, and saturation levels

The stability diagram (Fig. 4 c) predicts the loss of bistability at increased transcription rates of comK. Previous experiments using a rok-strain showed that the rok-strain has a twofold increased basal expression (29,30,39). We further measured that the maximum expression rate during switching increased ∼1.5-fold (Fig. 3 c). We therefore analyzed how the dynamics of the model qualitatively changes when α_M and β_M vary strongly. For the rok-strain, one would expect α_M → 2 α_M and (α_M + β_M) → 1.5 (α_M + β_M). In this regime, as the stationary phase is reached (S ∼ 1500), the system has lost its lower and intermediate fixed point, corresponding to B-state and threshold. This means achievement of competence is independent of fluctuations and is initiated in all cells. In this altered reaction network a transition from a bistable system with stochastic switching to a monostable, deterministic system occurs.

Experimental data showed indeed that 99 ± 3% of all cells reach high FI for the rok-strain (30). We further investigated experimentally whether deletion of the major repressor protein of comK transcription, Rok, affected switching characteristics (Fig. S5). The sigmoidal shape of [ComK](t) and the switching period of ρ = 1.4 h were not altered, while the maximum expression rate and the cumulative expression increased by a factor of ∼1.5 as compared to the wild-type strain (Fig. 3 c and Fig. S5 a).

Extrinsic noise determines the saturation value of individual cells in the K-state

The observed spread in saturation levels (Figs. 2 c and 3 a) is explained by extrinsic noise, which is present in any cell population. This does not alter the behavior of the population as a whole but affects every individual bacterium differently. Besides altering dynamics of a few cells qualitatively (as discussed above), the value of K at the upper fixed point is highly sensitive to these fluctuations. This results from the fact that the nullclines in Fig. 4 b are close to parallel at the upper fixed point. Variations in the model's parameters thus shift the K-state to higher or lower values of K.

We quantified the effect of variation of the parameters on the saturation value of ComK. Computing the relative change of K at the upper fixed point due to a relative change in a given parameter yields the sensitivity (see Supporting Material). We find that variation in the overall degradation rates δ_M and (δ_K + δ₀) alter the fixed point's position by the same magnitudes, but opposite sign as the overall production rates (α_M + β_M) and β_K. By comparison, the half-maximal degradation of ComK, q_K, has a minor effect on the fixed point's position, while variations in the other parameters can be neglected (see Table S2).

Stochastic simulations with well-motivated parameters fortify predictive character of the model

Quantitative data, obtained by stochastic simulations (40), corroborated the predictive value of the model (Fig. 5 and Fig. S2). As found in earlier experiments of the whole bacterial population (30), single cell time-lapse microscopy revealed a transient increase in comK transcription α_M before T₀ (Fig. 2, b and c), which we introduced in our simulations (Fig. S1).

Figure 5.

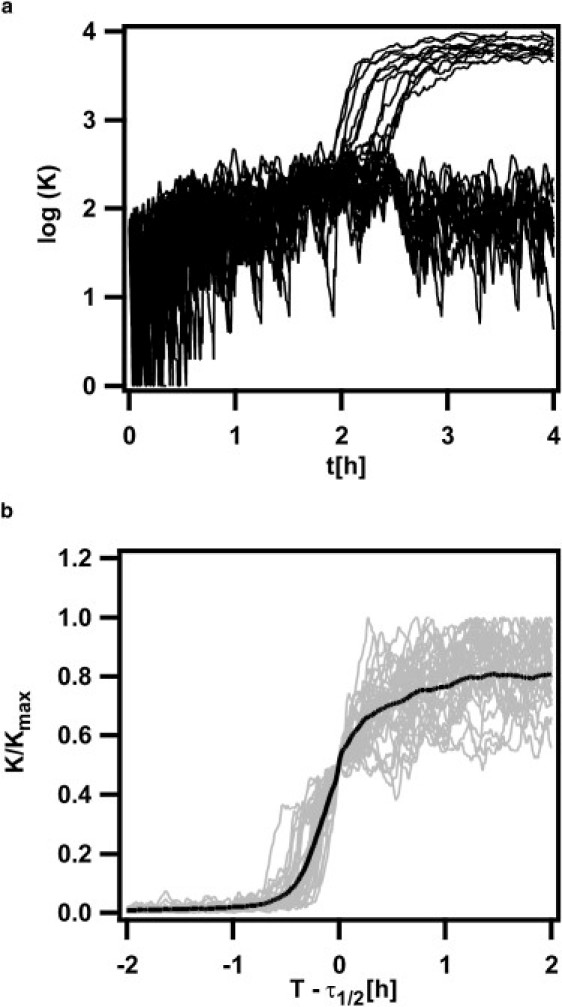
Stochastic simulations. (a) 100 realizations of the stochastic simulation of the model are shown. (b) Time courses of cells that entered the K-state were normalized to the maximal value. The time axis was shifted to τ_1/2, where cells had half-maximal K values; compare to Fig. 3b.

Extrinsic noise was introduced in the stochastic simulations by choosing model parameters from a Gaussian with a standard deviation of 5% about their mean for each realization (see Supporting Material for details). Theses variations in the model parameters can change number and positions of fixed points. The former can be addressed analytically by stability analysis (see above, Fig. 4 c), the latter by computation of sensitivities, as was done for the position of the upper stable fixed point (Table S2).

Before entry into stationary phase, i.e., at values of S ≪ 1500, cells showed fluctuations about the vegetative state, but no escape was possible. Approximately 14.7% of all cells entered the K-state, showing saturation in ComK level within ρ = 1.2 h, in accordance with experimental findings of ∼15% competent cells and a length of the switching period of ρ ∼1.4 h. Further, we find a wide spread in saturation levels and expression curves very much like those recorded in the experiment (Fig. 2 c), indicating that extrinsic noise is an important determinant of ComK levels.

These findings show that an effective two-component model with well-motivated parameters is not only sufficient to explain switching dynamics qualitatively but also returns quantitative data in excellent agreement with the experiment.

Discussion

Competence development in B. subtilis provides an interesting regulatory network to study the kinetics of genetic switching between different phenotypes. We developed an experimental approach and a stochastic nonlinear dynamics model to quantify the switching behavior of individual cells of B. subtilis into the K-state in response to quorum sensing. Both experiment and theory reveal that the switching period is a robust property of the genetic switch whereas the saturation levels show strong variability most likely due to external fluctuations.

Rise in basal expression from the comK promoter does not select cells for switching

In agreement with previous studies that concentrated on cell populations, we found that the basal expression rate of ComK increased before entry into stationary phase (30). Increased expression rate of comK may be explained by decreasing expression of the repressor AbrB and by deactivation of the GTP-dependent repressor function of CodY. Using real-time experiments with individual cells, we were able to distinguish the rise in basal expression rate between cells that switched eventually after entry into the stationary phase and cells that did not switch before the switching window closed. The magnitude of increase was similar in cells that remained in the B-state and cells that switched into the K-state. This result indicates that the sharp rise in the expression rate of the comK promoter upon switching is not a result of predetermination in the B-state. Interestingly, in the simulations, switching of individual cells could not be predicted from the corresponding timecourses before switching. While different cells must have different switching probabilities (due to extrinsic noise), the ones which actually switch are picked randomly by fluctuations in the number of molecules. This observation is in agreement with the finding that noise in transcription from the comK promoter was mainly intrinsic, i.e., that the transcription probability from two copies of P_comK is uncorrelated (29).

Is the competence system multimodal?

We found that the maximum levels of ComK in the wild-type strain were highly variable with two distinct levels. This observation is reminiscent of a previous result reported by Maamar and Dubnau (28) showing the existence of two subpopulations with an intermediate and a high ComK-expressing class of cells. Since their setup only allowed for snapshots in time for a whole-cell population, they could not resolve whether the cells expressing comK at intermediate levels had already reached their maximum. Using single cell time-lapse microscopy, we showed that indeed the intermediate fraction has already reached their maximum ComK concentration.

Multimodality in the distribution of ComK of cells in the K-state hints toward further distinguishable phenotypes. There are two possible sources for multimodal expression: stochastic bursting or a deterministic mechanism due to additional regulation circuits. Transcriptional bursts mediated by slow promoter dynamics could lead to different protein levels. Then, however, typical times for binding/unbinding of transcription factors would need to be on the order of several hours, as no transitions between the two levels are evident. This is unlikely, as for prokaryotes it is known that promoter dynamics are usually very fast. Translational bursts might also lead to multimodality if mRNA dynamics are much slower than protein dynamics. In that case, one would expect to find multiple peaks in the protein distribution which are equidistant to each other. Again, the timescale of mRNA dynamics would need to be on the order of hours to explain the absence of transitions between the distribution's modes. Since these two stochastic explanations seem unlikely we suppose that a deterministic mechanism due to additional regulatory circuits is responsible for the observed multimodality. The circuit could couple into the dynamics of the comK promoter, thereby altering the maximal transcription rate (α_M + β_M) by a significant amount. This assumption would be consistent with the observation that the intermediate peak is not present in the rok-strain, where transcription rates are elevated. A more thorough understanding of the observed multimodality has to await further experimental investigations.

A minimal model can describe the time course of switching in individual cells

Here we presented a plausible two-component model incorporating well-known processes, intrinsic and extrinsic noise. All parameters are taken directly from literature or within biological meaningful ranges, and quantitative results remarkably match those of the experimental system. Our model covers the development of competence on the single cell level which we also recorded experimentally. To include escape from competence, extended models with further interactions and more molecular species are necessary. Since the mechanisms of escape from competence are as yet sketchy and extended models tend to be less descriptive, we decided to focus on competence onset and clarify it in detail. Of special significance is the accordance in the timescale for reaching the K-state, as well as in the fraction of cells attaining competence. A discussion of the system gives straight explanations of probabilistic and deterministic switching in different B. subtilis strains.

For the wild-type, we identify the low-number mRNA fluctuations about the mean value 1, together with a large burst factor, as the outstanding source of fluctuations in the vegetative state. While in exponential phase our model predicts monostability (thereby forbidding switching), in stationary phase, switching initiation is facilitated due to the vicinity of B-state and threshold. Values of ComK saturate in K-state, whose position is highly sensitive to extrinsic noise, explaining broad distributions in saturation levels.

We see the minimal number of species and reaction parameters as an advantage of our model as compared to others (16,29). It grants an intuitive understanding of the key properties of competence decision: the interplay of low-number fluctuations and nonlinear dynamics.

Bistable versus excitable models

We focused on the time interval of transition from exponential to stationary phase. Similar to independent research (5,27–29,32), we find that a model featuring bistability is well fit to explain experiments performed in that temporal regime. Studies characterizing the competence system as excitable (15,16,31) focus on longer time intervals later in stationary phase. They find that an indirect inhibition of comS expression by ComK acts as a further feedback loop, rendering the system excitable in a region of parameter space. These two different approaches appear to be contradictory at first sight only: The models address experiments using different strains and growth conditions. In particular, these differences led to different length scales of the switching period, to different fractions of competent cells and length of cell cycle. Another highly important difference is that Suel et al. (16) observed initiation and decay of competence over a timescale of days without actively changing the medium. The effect of quorum sensing and nutrient limitation (that is known to initiate competence development during entry into the stationary growth phase) is not explicitly involved in these studies, although change in cell concentration under microscope conditions may have an effect on the probability of switching initiation. In our experiments, we explicitly included the effect of cell density by continuously adjusting the medium thus simulating quorum sensing.

At the transition from exponential to stationary phase, the environment of a single cell, which couples into its dynamics by quorum sensing, is not in equilibrium yet. This constantly pushes the system away from steady state dynamics so that slow processes (like indirect feedback) are of less importance. Furthermore, model parameters are influenced by the overall state of the cell, so that the relative importance of network components might change over time. These variations in parameters can also carry excitable systems into regions of mono- or bistability (15,31). If indirect feedback is bypassed cells are no longer excitable (15). From an evolutionary point of view a system that initially reacts fast and in a bistable manner to stressful conditions and then transits to an excitable mode is meaningful: A fast response enhances fitness, but only cells that can exit competence and reproduce can make use of that advantage. If a first wave of transient competent cells does not succeed in producing a beneficial phenotype, there are always other individuals entering and leaving the competent state.

All models identify noise as a necessary ingredient of the competence decision network of B. subtilis, supporting the idea of functional noise. Noise is needed to leave the vicinity of a stable fixed and cross a threshold, which either leads to an excursion in phase space or to the approach of another stable fixed point. The origin of these fluctuations can be manifold but were analyzed by Schultz et al. (31) in a systematic way. There it was found that fluctuations in binding to the protease complex can be neglected which we accounted for by adiabatic elimination of this fast reaction. In previous theoretical studies (31,32), fluctuations in the mRNA were ignored. However, since transcript numbers per cell are extremely low, and promoter dynamics are usually assumed to be fast in prokaryotes (4) we regard the finite number effect of mRNA and the consequential translational bursting as the main source of noise (1,4). Quantitative switching times cannot be determined reliably if noise in mRNA levels is neglected (38). If promoter dynamics are slow, the corresponding fluctuations will leave their mark in the downstream mRNA, which amounts to large fluctuations in mRNA. Here we showed that extremely low mRNA numbers coupled to transcriptional bursting suffice to trigger crossing of threshold and onset of competence in a stochastic manner.

The duration of the switching period is intrinsically defined and robust toward variations of the regulation circuit

We studied the switching kinetics of individual cells, dependent on growth phase. Switching was accomplished after a period of ρ = 1.4 h in individual cells. One explanation could be that dependent on growth phase an external signal accumulated in the surrounding medium. However we found, that overlaying switching curves between T₀ and T₄ did not reveal large variation, indicating the expression rate and switching period did not depend on growth phase. We therefore conclude that in the K-state expression of comK and degradation of the protein equilibrate to a new steady state, without further extracellular regulation. Furthermore, we found that neither overproduction of the proteolysis inhibitor ComS nor knockout of the repressor for comK transcription had an effect on the length of the switching period, indicating that the period is a robust property of the system.

Transition from stochastic to deterministic switching at increased promoter activity

In the rok-strain, B-state and threshold are nonexistent in stationary phase and render the system monostable, forcing individuals into the K-state in a deterministic manner. Smits et al. (27,39) and Maamar et al. (28) showed bistable behavior in their rok-strain. Since we found deterministic switching with different rok-strains both in real-time and in bulk experiments, we attribute the difference to our more rigorous quantification of fluorescence levels to determine the threshold between cells in the B-state and cells in the K-state. Furthermore, the close proximity to the stability transition (Fig. 4 c) could explain that slightly different growth conditions may have a strong effect on the stability of the system.

Conclusion

Our combined experimental and theoretical approach showed that the length of the switching period from the B-state to the K-state of Bacillus subtilis is robust against variations of regulation circuit of the master regulator for competence and against the growth phase. Switching characteristics of B. subtilis can be understood by a well-defined two-component mathematical model that couples nonlinear dynamics to probabilistic effects. The model quantitatively retrieves the fraction of competent cells and the switching period and predicts a transition from stochastic to deterministic genetic switching at increased basal transcription rate. Experiments verified this prediction. Furthermore, the model explains the large fluctuations between individual cells in comK expression in the K-state. We hypothesize that the expression of late competence proteins may be induced once a threshold concentration of ComK is reached and that therefore the cell does not require tight control over the saturation level of ComK.