What Determines the Structure and Stability of KFFE Monomers, Dimers, and Protofibrils?

Abstract

The self-assembly of the KFFE peptide was studied using replica exchange molecular dynamics simulations with a fully atomic description of the peptide and explicit solvent. The relative roles of the aromatic residues and oppositely charged end groups in stabilizing the earliest oligomers and the end-products of aggregation were investigated. β and non-β-peptide conformations compete in the monomeric state as a result of a balancing between the high β-sheet propensity of the phenylalanine residues and charge-charge interactions that favor non-β-conformations. Dimers are present in β- and non-β-sheet conformations and are stabilized primarily by direct and water-mediated charge-charge interactions between oppositely charged side chains and between oppositely charged termini, with forces between aromatic residues playing a minor role. Dimerization to a β-sheet, fibril-competent state, is seen to be a cooperative process, with the association process inducing β-structure in otherwise non-β-monomers. We propose a model for the KFFE fibril, with mixed interface and antiparallel sheet and strand arrangements, which is consistent with experimental electron microscopy measurements. Both aromatic and charge-charge interactions contribute to the fibril stability, although the dominant contribution arises from electrostatic interactions.

Introduction

The aggregation of proteins and peptides in the body is often a pathological process that can lead to debilitating diseases (1). Alzheimer's, Huntington's, and Parkinson's diseases, for instance, are associated with the formation of toxic oligomers and fibrillar aggregates that deposit on tissue in the body in the form of amyloid plaques (2–5). Approximately 20 different proteins, sharing low sequence and low native structure homology, are involved in amyloid diseases.

The aggregation process involves in a first step the misfolding of globular proteins, or the structuring of natively unfolded proteins and peptides, followed by their self-assembly. The initial stages of aggregation (partial structuring of the monomer, dimerization, and formation of higher order oligomers) are poorly characterized experimentally. Simulations have been instrumental in providing insight into the conformations populated in the early steps of aggregation (6–9). The final product of aggregation, the amyloid fibril, has been extensively studied through a combination of cryo-electron microscopy (EM), x-ray, and solid-state nuclear magnetic resonance studies (2,10). When complemented with molecular modeling (6,7,11,12), these studies have provided atomically detailed information of the fibrillar structures. All amyloid fibrils, regardless of the sequence and native fold of the protein, possess a common β-sheet core structure, the cross-β structure. In this structure, the β-strands align perpendicular to the fibrils axis, and assemble side-by-side to form long β-sheets running parallel to the fibril axis. Pairs of β-sheets assemble into double-layered (or higher order) protofibrils stabilized by side chain-side chain interactions. The interplay between the intrinsic chirality of the single peptides and the short-ranged cohesive interactions between neighboring strands within the aggregates (mainly hydrogen bonds and side chain-side chain interactions) leads to different supramolecular fibril geometries (morphologies). These geometries range from virtually flat fibrils, when the cohesive intermolecular interactions nearly balance the chiral deformation of the peptides, to helicoids with saddlelike curvature, cylindrical helices, and chiral tubules (13–15). The kinetics of amyloid formation for any sequence follows a nucleation-growth mechanism (7).

There is compelling experimental evidence that amyloid fibril self-assembly is based, to a large extent, on fundamental properties of the polypeptide chain. These intrinsic properties govern the stabilization of the common cross-β structure, with specific interactions between side chains playing an auxiliary role in defining the different morphologies of the mature fibrils. Indeed, several experiments have shown that even nonpathogenic globular proteins can self-assemble into amyloid fibrils under partial denaturation conditions (such as low pH or in solution with trifluoroethanol) (16–18). Furthermore, fragments of aggregating peptides (such as the Aβ-peptide implicated in Alzheimer's disease and the islet amyloid polypeptide linked with Type II diabetes), as well as synthetic peptides with de novo sequences, have also been shown to form amyloids in vitro (13–15). Many of these fragments exhibit aggregates possessing some of the toxicity of their full length counterparts (19). The implication of these findings is that aggregation is an inherent property of polypeptide chains.

An interesting question pertains to the minimum requirements in terms of peptide length and sequence for forming amyloid fibrils. Recently, Tjernberg et al. (20) showed that synthetic peptides as short as four residues can self-assemble and form amyloid fibrils in vitro. The aim of this work is to investigate the nature of the different forces stabilizing the structure of small oligomers and fibrils of KFFE, the tetrapeptide with the highest fibrillization propensity identified by Tjernberg. Amyloid fibrils of KFFE were seen in Tjernberg's experiments to form in aqueous solution after incubation at c = 300 μM for 10 days at T = 310 Kelvin in phosphate buffer (pH = 7.0) or water (pH = 5.0). The amyloid nature of the fibrils formed by the KFFE peptide was confirmed by both EM and Congo red staining. The dimensions of the fibrils calculated directly from electron micrographs appear to be consistent with a double layered cross-β structure (20). The secondary structure of the solvated KFFE peptide was analyzed by circular dichroism (CD) spectroscopy. CD spectra recorded immediately after solubilization, at T = 293 Kelvin and at c = 300 μM, showed a coexistence of β-strand and random structures. The CD results suggest the presence of some degree of β-strand conformation in monomers and small oligomers formed in the first steps of the aggregation process.

The KFFE peptide is a minimal model system to investigate the balance of forces involved in amyloid formation as it is one of the smallest peptides to possess the two key elements that are commonly believed to contribute to aggregation, namely, an aromatic, hydrophobic core (F-F) with high β-sheet propensity and two oppositely charged terminal groups (K and E). Both aromatic and electrostatic effects have been identified as key contributors to aggregation, although their relative importance may differ in different peptide systems and under different solution conditions (14,20–23). In the case of aromatic interactions, Reches and Gazit have shown that a dipeptide consisting of only two F residues (NH2-Phe-Phe-COOH) possesses all the necessary elements to form supramolecular assemblies (24). Pawar et al. (25) defined an amyloid aggregation propensity scale for the 20 naturally occurring amino acids and identified phenylalanine as having high amyloid aggregation propensity. The aggregation propensity scale was successfully applied to calculate the aggregation propensity profiles of three peptides associated with neurodegenerative diseases (Aβ42, α-synuclein, and τ). Many naturally existing and synthetic peptides that aggregate to form fibrils contain aromatic residues. These peptides include, in addition to the KFFE peptide studied here, the 16-22 fragment of the Alzheimer Amyloid-β peptide (KLVFFAE), the NFGAIL fragment of Amylin, as well as various fragments of calcitonin (15,26,27). While aromatic residues clearly play an important role in aggregation, recent experiments have questioned whether they are essential for aggregation (14,20,28). Indeed, while dramatic mutations (F to A) abolish aggregation in the small peptides mentioned above, lesser mutations, such as F to L, preserve the peptide's ability to aggregate. Recent experiments by Tracz et al. (22) and Marek et al. (23) on the islet amyloid polypeptide and on small fragments derived from human amylin have shown that the F residues may play a role in accelerating aggregation, as peptides with an F-to-L mutation aggregate more slowly than their wild-type counterparts. Electrostatic interactions, in turn, can also play an important role in promoting aggregation. Peptides with oppositely charged side chains (such as K and E) can promote self-assembly into antiparallel β-sheet structures through favorable electrostatic interactions. KFFE, Aβ(16–22), and certain fragments of calcitonin, are all examples of peptides with oppositely charged residues in flanking positions that aggregate.

In this article, we use replica exchange molecular dynamics simulations with an atomistic representation of the peptide in explicit solvent to explore the conformations adopted by monomeric, dimeric, and fibrillar forms of KFFE. This work provides detailed atomic information not accessible using current experimental techniques and augments earlier computational work that made use of simplified representations of the peptide, solvent, and long-range electrostatic interactions (29–33). Specifically, our simulations show that β and non-β peptide conformations are competing in the first steps of the aggregation process as a result of a balancing between 1), the high, intrinsic β-sheet propensity of the phenylalanine residues (34) and 2), charge-charge interactions that favor non-β conformations. Our simulations reveal a cooperative dimerization process to form β-sheet dimers in which the presence of a second peptide induces β-strand structure into an otherwise non-β strand peptide. The stability of KFFE protofibrils results from both close contacts between charged groups (lysine and glutamic acid, as well as between the charged termini) and between phenylalanines residues at the interface level. An important result from our simulations is that the major contribution to protofibril stability arises from charge-charge interactions rather than from aromatic interactions between phenylalanines residues.

Methods

We performed Langevin dynamics simulations using the NAMD software (35), with the OPLS/AA force field (36) and the TIP3P explicit water model (37). The damping coefficient for the Langevin integrator was set to b = 1.0 ps⁻¹, the time step was ts = 2.0 fs, and the cutoff for the nonbonded interactions in the direct space was fixed at 10.0 Å. All the simulations were performed under periodic boundary conditions and the long-range electrostatic interactions were calculated by using the Ewald summation method with the particle mesh Ewald algorithm. The particle mesh Ewald accuracy was fixed at 10⁻⁶, the order of the interpolation functions on the grid was set to 4 (cubic), and the grid size was ∼1 Å. The peptides were spatially constrained within a sphere, centered in the water box center. In more detail, spherical harmonic boundary conditions were enforced on the peptides by means of a single potential function,

$$E_{\text{sphere}}=\{\begin{array}{ll}{k}_{\text{sphere}}{\left(|{\mathbf{r}}_i-{\mathbf{r}}_{\text{center}}|-r_{\text{sphere}}\right)}^2,\hfill & \text{if}|{\mathbf{r}}_i-{\mathbf{r}}_{\text{center}}|>r_{\text{sphere}},\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$ (1)

where k_sphere = 10 Kcal/mol, ${\overrightarrow{r}}_i$ is the current position of atom i, r_center is the center of the sphere, and r_sphere is the radius of the sphere. In all the simulations performed in our study, the radius for the enclosing sphere (see Eq. 1) was set so to obtain a constant peptide concentration of 400 mM. We found that the magnitude of the spherical harmonic potential is negligible when compared to the total potential energy of the KFFE monomers, dimers, and protofibrils studied in our simulations (<0.01% of the total potential energy). We therefore do not expect the details of the spherical harmonic potential used in this study to affect our results and conclusions.

Replica exchange Langevin dynamics simulations: KFFE monomer and dimer

Random conformations for both the monomer and the dimer systems were generated, in vacuum, by running, first, a short Langevin Dynamics simulation at a temperature T = 600 K. Then, the peptides were solvated in a cubic water box and underwent a local optimization followed by a short (0.1 ns) Langevin dynamics simulation under periodic boundary conditions, at a pressure p = 1.0 atm and a temperature T = 310 K (NPT-MD simulation) for equilibrating the box dimension and to obtain the correct water density. The equilibrium periodic box dimension after the NPT-MD simulation was L = 22.60 Å for the monomer and L = 28.50 Å for the dimer. The radius of the enclosing sphere (see Eq. 1) was r_sphere = 9.97 Å for the monomer and r_sphere = 12.6 Å for the dimer. The final geometry obtained from the NPT-MD simulation was used as initial configuration for the replica exchange Langevin dynamics simulations (REX-LD). We ran the REX-LD simulations using 24 temperatures T ∈ [310–480] Kelvin. The total simulation time for each replica was 50 ns and 120 ns for the monomer and the dimer, respectively. Swaps between replicas were attempted every 40 ps and the acceptance ratio varied between 15% and 35%. The last 40 ns and the last 100 ns have been considered for the analysis of the monomer and the dimer, respectively.

Langevin dynamics simulations: stability of small KFFE protofibrils

In addition to the REX-LD simulations of the monomer and the dimer, we ran additional Langevin dynamics (LD) simulations of small protofibrils formed by the KFFE peptide. EM measurements show that the width of the KFFE fibrils is 12–16 Å and suggest that the fibrils are formed by two β-sheet layers (20). Therefore, we analyzed the relative stability of small double-layered protofibrils considering four different arrangements of two antiparallel β-sheet tapes (double tapes). All initial structures were generated using the Hyperchem software. The β-sheet tapes were manually generated by placing eight peptides into a planar, antiparallel β-sheet arrangement. Four flat double tapes with different interfaces were then obtained by assembling two planar tapes. (The details of the different interfaces are shown later in Fig. 7.) For the local optimization, the solvation, and the initial NPT equilibration of the double tapes, we followed the same procedure employed for the monomer and dimer simulations (see Replica Exchange Langevin Dynamics Simulations: KFFE Monomer and Dimer). The four final geometries obtained from the molecular dynamics simulations under NPT conditions were used as initial configurations for the LD simulations which were carried out at a temperature T = 310 K and for a time length t = 50 ns. The dimension of the periodic box was L_box = 58.5 Å and the radius of the enclosing sphere (see Eq. 1) was r_sphere = 25.0 Å. The last 40 ns have been considered for data analysis.

Figure 7.

(Top) The four different protofibril interfaces considered in our simulations. AP-KF and AP-MIXED have antiparallel, interlayer orientation while P-KF and P-MIXED have parallel, interlayer orientation. The protofibrils named AP-KF and P-KF have, at least, one close contact between lysine (K) and phenylalanine (F) at the interface level while the protofibrils named AP-MIXED and P-MIXED have a close contact between two phenylalanine residues at the interface level. All protofibrils have antiparallel intralayer orientation. (Middle) Time series for the backbone RMSD obtained from the single temperature simulations of the four different KFFE protofibrils. Only the P-KF and the AP-MIXED protofibrils are stable over a simulation time length of 50 ns. The RMSD time series eventually show that the structure labeled as “AP-MIXED” was the most stable over the simulation time length. (Bottom) Representative/average structure of the stable AP-MIXED protofibril. The average dimension of the stable AP-MIXED protofibril is consistent with the values of the fibril dimension (12–16 Å) calculated directly from electron micrographs.

Definition of order parameters

We defined a dimer to be formed when the average of the nearest neighbor C_α-C_α intermolecular distances between two peptides was <6.5 Å. To distinguish between parallel and antiparallel dimers, in the REX-LD simulations, the cosine of the angle γ between the main axes of the two peptides has been considered,

$$\text{cos}\left(\gamma \right)=\frac{{({\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}}\left(C_{\alpha }\right))}_{\left(1\right)}·{({\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}}\left(C_{\alpha }\right))}_{\left(2\right)}}{\Vert ({\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}}\left(C_{\alpha }\right)){\Vert }_{\left(1\right)}\Vert ({\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}}\left(C_{\alpha }\right)){\Vert }_{\left(2\right)}},$$ (2)

where the indexes 1 and 2 refer to the two peptides and ${\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)$ and ${\mathit{r}}_{\text{E}}\left(C_{\alpha }\right)$ are the positions of the C_α carbons for lysine and glutamic acid, respectively. The two-dimensional free energy landscape of the KFFE dimer has been calculated as a function of two order parameters: 1), r_ee^tot = r_ee⁽¹⁾ + r_ee⁽²⁾ and 2), χ^tot = χ⁽¹⁾ + χ⁽²⁾, where the indexes 1 and 2 refer again to the two peptides. The quantity

$$r_{\text{ee}}^{\left(i\right)}=\Vert {\mathit{r}}_{\text{K}}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}}\left(C_{\alpha }\right)\Vert$$ (3)

is defined as the end-to-end distance for the i^th KFFE peptide. The quantity χ⁽ⁱ⁾ is calculated, for the i^th KFFE peptide, as the absolute value of the dihedral angle defined by the quadruplet ${\mathit{r}}_{\text{K}1}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{F}2}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{F}3}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}4}\left(C_{\alpha }\right)$, where the indexes K1, F2, F3, and E4 refer to the residue name and position along the peptide backbone:

$${\chi }^{\left(i\right)}=\Vert \text{dihe}({\mathit{r}}_{\text{K}1}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{F}2}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{F}3}\left(C_{\alpha }\right)-{\mathit{r}}_{\text{E}4}\left(C_{\alpha }\right))\Vert \text{.}$$ (4)

Results and Discussion

Structure of the KFFE monomer: coexistence of extended β-strand and compact U-shaped structures

Analysis of the replica exchange simulation trajectories reveals that the KFFE monomer populates extended β-strand as well as compact, U-shaped conformations. In Fig. 1, we show two representative snapshots for the β-strand (bottom left) and the U-shape conformation (bottom right) seen in our replica exchange simulations. To discriminate between these conformations, we use the two order parameters described in Methods: the end-to-end distance r_ee and the dihedral angle χ (see Eqs. 3 and 4). For the ideal extended β-strand (Fig. 1, top left), χ = π, while for the other extremum, the compact U-shaped structure (Fig. 1, top right), χ = 0. The end-to-end distance r_ee is larger in the ideal extended β-structure than in the U-shaped structure. In Fig. 2 we plot the free energy landscape for the monomer as a function of the two order parameters r_ee and χ at T = 310 Kelvin, the temperature at which the experiments of Tjernberg et al. were performed (20).

Figure 1.

(Top left) Ideal, planar structure for the extended, β-strand conformation of the peptide. (Bottom left) Representative snapshot of the β-strand monomer conformation obtained from REX-LD simulations. (Top right) Ideal, planar structure for the compact, U-shape conformation of the peptide. (Bottom right) Representative snapshot of the U-shape monomer conformation obtained from REX-LD simulations.

Figure 2.

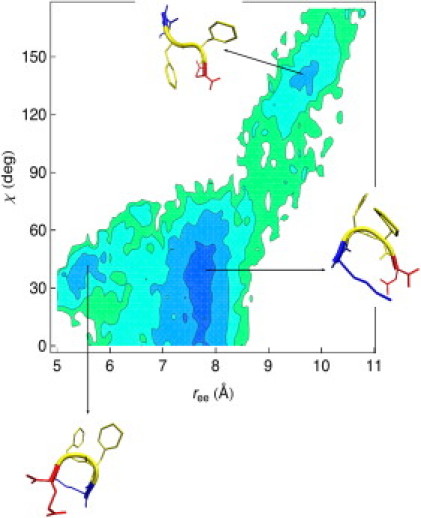
Free energy landscape of the monomer as a function of the two order parameters r_ee and χ obtained from REX-LD simulations at 310 K. The deepest blue color corresponds to the lowest value for the free energy (in Kcal/mol). Contour lines are drawn every 0.5 Kcal/mol. The free energy minimum at the top-right corner of the free energy map corresponds to the ensemble of the β-strand monomer conformations. The two free energy minima at the bottom left corner of the free energy map correspond to the ensemble of the U-shape monomers. The less compact U-shape monomers populate the larger of the two basins, while the more compact U-shape monomers populate the small basin. At the temperature T = 310 K, the non-β structures have the highest statistical weight, with the less compact non-β structures more populated that the more compact ones. The barrier height between the free energy basins of the β-strand monomers and of the U-shape monomers is ≈1.0 Kcal/mol.

The free energy map shows three major basins: the first basin is located at the top-right corner of the map and is defined by r_ee ∈ [8.9:10.5]Å and χ ∈ [105°:180°]. The two other basins are located at the bottom-left corner of the map and are defined by r_ee ∈ [5.0:6.5]Å and χ ∈ [20°:50°] (small basin) and by r_ee ∈ [6.5:8.6]Å and χ ∈ [0°:69°] (large basin), respectively. We can partition the three basins into two main families: the basin at the top-right corner of the map corresponds to extended β-strand monomer conformations, while the two basins at the bottom-left are compact, U-shape monomer structures, with slightly different degrees of compactness. At the temperature considered (T = 310 K), the non-β structures have the highest statistical weight (broader basin with lowest free energy at the bottom-left corner of Fig. 2), with the less compact non-β structures more populated that the more compact ones.

Since the REX-LD simulations give us information uniquely on the thermodynamics, we performed separate Langevin dynamics (LD) simulations for the monomer to explore the dynamics of the system. Each simulation was run at T = 310 K for 70 ns, using as starting coordinates the representative structures of the β-strand monomer and of the U-shape monomer, shown later in Fig. 4 (top). The time series of the root mean-square deviation (RMSD, calculated from the two starting configurations) show that both structures are stable during the first 10 ns, after which we observe several structural transitions between β-strand and U-shape conformations. The probability distributions of the two order parameters r_ee and χ obtained from the first 10 ns were used to define the boundaries of the three free energy basins in Fig. 2. The LD trajectories show that the simulation started from the U-shape structure explores extensively, on the timescale studied, the conformations associated with the two basins at the bottom left in the free energy map of Fig. 2. In contrast, the β-strand monomer is stable only during the first 10 ns and then it converts to the U-shape structure and rarely (and for very short time intervals) converts back to the β-structure. A detailed analysis of the factors responsible for the stability of the different monomer conformations is given in Stability of Early Oligomers: β-Sheet Propensity and Charge-Charge Interactions.

Figure 4.

Representative structures for the free energy basins in Figs. 2 and 3. (Top) Snapshots of the two representative monomer conformations: U-shape (left) and β-strand (right). (Bottom) Snapshots of the representative dimer conformations: U-shape (left), mixed (center), and β-sheet (right) The competition between β and non-β structures in both monomer and dimer conformational phase space is the result of the balance between the high, intrinsic β-sheet propensity of the phenylalanine residues and charge-charge interactions that favor non-β conformations. At the temperature T = 310 K, the non-β monomers and dimers (top-right and bottom-right) have the highest statistical weight. The combined analysis of the relative statistical weights for monomer and dimer structures is presented in Structural Ensembles and Cooperativity Effects in the KFFE Dimer Formation.

Structure of the KFFE dimer: coexistence of β-sheet, U-shaped, and mixed dimers

To characterize the dimer population, we collected and analyzed all the structures in which a dimer was formed. The fraction of the dimer population calculated over the last 100 ns varies between 0.79 and 0.48 in the temperature interval considered in our REX-LD simulations ([310–480] Kelvin). We calculate the distribution of the cosine of the angle γ between the main axes of the two peptides at T = 310 K (see Eq. 2) and we observe that the antiparallel dimers dominate the conformational phase space (see Supporting Material, Fig. S1). In Fig. 3 we plot the free energy map for the dimer at T = 310 K. We consider two order parameters related to the end-to-end distances and the dihedral angles: $r_{\text{ee}}^{\left(1\right)}+r_{\text{ee}}^{\left(2\right)}$ and χ⁽¹⁾ + χ⁽²⁾, where the sum is over the two peptides. Three main basins are present. The first one (bottom left, snapshots A–C) consists of an ensemble of U-shaped dimers ($r_{\text{ee}}^{\left(1\right)}+r_{\text{ee}}^{\left(2\right)}$ ∈ [10:16.5]Å and χ⁽¹⁾ + χ⁽²⁾ ∈ [0°:138°]), the second one to β-sheet dimers (top-right, snapshot E; r_ee⁽¹⁾ + r_ee⁽²⁾ ∈ [17.8:22.0]Å and χ⁽¹⁾ + χ⁽²⁾ ∈ [220°:360°]) and the third one (center of the map ($r_{\text{ee}}^{\left(1\right)}+r_{\text{ee}}^{\left(2\right)}$ ∈ [16.5:17.8]Å and χ⁽¹⁾ + χ⁽²⁾ ∈ [138°:220°]) to dimer conformations with one peptide in the β-strand conformation and the other in the U-shape conformation (snapshot D). The representative structures for the three different basins seen in the dimer free energy maps are shown at the bottom of Fig. 4.

Figure 3.

Free energy landscape of the dimer as a function of the two order parameters r⁽¹⁾_ee + r⁽²⁾_ee and χ⁽¹⁾ + χ⁽²⁾ obtained from REX-LD simulations at 310 K. The deepest blue color corresponds to the lowest value for the free energy (in Kcal/mol). Contour lines are drawn every 0.5 Kcal/mol. Three main basins are present. The first one (bottom left, snapshots A–C) consists of an ensemble of U-shaped dimers, the second one at the top-right of the free energy map is populated by the β-sheet dimers (snapshot E), and the third one (center of the map) corresponds to dimer conformations with one peptide in the β-strand conformation and the other in the U-shape conformation (snapshot D). At the temperature T = 310 K, the non-β dimers (snapshots A–C) have the highest statistical weight. The barrier heights between the three main free energy basins are ≈0.5–1.0 Kcal/mol.

In addition to the REX-LD simulations, we ran two separate Langevin dynamics (LD) simulations for the dimer (at T = 310 K and for 80 ns each) considering as starting coordinates the representative structures of the β-sheet dimer and of the U-shape dimer shown in Fig. 4 (bottom). The time series of the RMSD from the initial structure for the two Langevin simulations show that both the U-shape and the β-sheet dimer are stable over the simulation time length (data not shown). The probability distributions of the two order parameters $r_{\text{ee}}^{\left(1\right)}+r_{\text{ee}}^{\left(2\right)}$ and χ⁽¹⁾ + χ⁽²⁾ obtained from the LD trajectories were used to define the boundaries of the three free energy basins in Fig. 3. The time-averaged RMSDs are 0.8 Å and 1.2 Å for the U-shape and the β-sheet dimer, respectively, and suggest, along with the free energy map in Fig. 3, that the U-shape dimer is slightly more stable than the β-sheet dimer at T = 310 K. A detailed analysis of the factors responsible for the stability of the different dimer conformations is given in Stability of Early Oligomers: β-Sheet Propensity and Charge-Charge Interactions.

Stability of early oligomers: β-sheet propensity and charge-charge interactions

Monomer stability

The free energy surface of the monomer (Fig. 2) shows two families of structures: extended β-strand conformations and U-shaped conformations. In this section, we probe the various factors contributing to the stability of the structures. To understand the role of electrostatic (ES) interactions (charge-charge interactions) in the stabilization of the different monomer conformations we calculate the distribution of the distances between positively and negatively charged atoms in both the termini and the polar side chains. Specifically, we analyze intra- and intermolecular mutual distances considering the nitrogen atom in the N-terminus (${\text{N}}_{\text{NT}}^{+}$), the oxygen atom in the C-terminus (${\text{O}}_{\text{CT}}^{-}$), and the charged nitrogen (${\text{N}}_{\text{k}}^{+}$) and oxygen (${\text{O}}_{\text{E}}^{-}$) atoms in lysine and glutamic acid side chains, respectively. The distributions show two significant peaks: a first peak at ∼2.6 Å corresponding to the formation of a direct salt bridge between oppositely charged atoms and a second peak located at ∼4.7 Å, which is consistent with a water-mediated contact. This water-mediated contact can involve a hydrogen bond between the water oxygen atom and one of the hydrogens in the ${\text{NH}}_2^{+}$ moiety (either of the lysine side chain or of the N-terminus) and/or a hydrogen bond between one of the water hydrogen atoms and one of the oxygen atoms in the ${\text{CO}}_2^{-}$ moiety (of the glutamic acid side chain or of the C-terminus). This assignment is made by considering the location of the first peak in the water-peptide radial distribution functions (see Fig. S2).

Both direct salt bridges and water-mediated charge-charge interactions play a more important stabilization role for the U-shape monomer than for the β-strand conformation. We observe a major contribution from direct salt bridges and water-mediated charge-charge interactions for the atom pair ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (see Fig. 5, top left) for the compact U-shaped structures. A much smaller contribution is given by ${\text{N}}_{\text{NT}}^{+}-{\text{O}}_{\text{E}}^{-}$ and ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{CT}}^{-}$ contacts (data not shown). Analysis of the different U-shape monomer structures in the two U-shaped basins (bottom of the free energy map in Fig. 2) reveals that structures with close ES contact between the charged side groups K and E (atom pair ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$) correspond to the less compact, U-shape monomer structures (larger basin in Fig. 2). The structure of the more compact U-shape monomers (small basin in Fig. 2)), on the other hand, is consistent with ES contacts involving the termini (atom pairs ${\text{N}}_{\text{NT}}^{+}-{\text{O}}_{\text{E}}^{-}$ and ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{CT}}^{-}$).

Figure 5.

Distance distributions for different, oppositely charged atom pairs at T = 310 K. The distributions show two significant peaks: a first peak at ∼2.6 Å corresponding to the formation of a direct salt bridge between oppositely charged atoms and a second peak located at ∼4.7 Å, which is consistent with a water-mediated contact. All the plots show that both 1), direct salt bridges and 2), water-mediated charge-charge interactions play a more important stabilization role for the U-shape monomer and dimer conformation than for the β-conformations. (Top left) ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (monomer). Direct salt bridges and water-mediated contacts between the charged atoms on the lysine (+) and glutamic acid (−) side chains represent the major ES contribution to the stability of the U-shape monomer structures. (Top right) ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (dimer, intramolecular). Intramolecular ES contacts (i) and (ii) between the charged atoms on the lysine and glutamic acid side chains are important only for the U-shape, non-β dimers. (Bottom left) ${\text{N}}_{\text{NT}}^{+}-{\text{O}}_{\text{CT}}^{-}$ (dimer, intermolecular). Intermolecular ES contacts (i) and (ii) between charged termini are common to U-shape and β-sheet dimers. (Bottom right) ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (dimer, intermolecular). Intermolecular contacts between lysine and glutamic acid are important only for β-sheet dimers.

For the β-strand monomer, the only contribution to stability by charge-charge interactions originates from the charged atoms on the lysine and glutamic acid side chains (see Fig. 5, top left). As charge-charge interactions clearly favor the U-shape conformation, other energetic contributions have to be considered to explain the relative stability of the β-strand monomer. Hydrophobic forces between the two phenylalanine residues are certainly negligible since both residues are exposed to the solvent, side chain-side chain, and backbone hydrogen bonds energy contributions are also negligible compared to the charge-charge contribution (this holds both for the U-shape and β-strand monomers) (data not shown). An estimate of the contribution of β-sheet propensity (a factor that would encourage the population of extended structures over U-shaped ones) can be obtained by considering the potentials of mean force plotted as a function of the ϕ and ψ angles (Ramachandran maps) for the two central phenylalanine. The Ramachandran plots shown in Fig. 6 were calculated from single temperature LD simulations for the U-shape (bottom) and β-strand monomers (top). The Ramachandran maps reflect the fact that, as a result of the balancing between the high intrinsic β-strand propensities of the phenylalanine residues (34) and the influence of the local environment on secondary structure (38–40), the two F residues sample slightly different regions of the dihedral space. While the phenylalanine residue close to the lysine residue (left of Fig. 6) samples α-helix regions in the U-shape and β-sheet regions in the β-strand conformation, the phenylalanine residue close to the glutamic acid residue (right of Fig. 6) samples extensively the β-sheet region in both the U-shape and β-strand monomers. The implication is that β- and non-β-monomer conformations are competing as a result of a balancing between 1), the intrinsic β-sheet propensity of the phenylalanine residues and 2), charge-charge interactions that favor non-β conformations.

Figure 6.

Monomer system: potential of the mean force in the Ramachandran space for the two central phenylalanine residues at T = 310 K. (Left) Phenylalanine in position 2. (Right) phenylalanine in position 3. (Top) Both phenylalanine residues in the β-strand monomers sample extensively the β-sheet region of the Ramachandran map. (Bottom) The phenylalanine residue close to the lysine residue (left) samples α-helix regions in the U-shape monomer while the phenylalanine residue close to the glutamic acid residue (right) samples the β-sheet region. The implication is that β- and non-β-monomer conformations are competing as a result of a balancing between 1), the intrinsic β-sheet propensity of the phenylalanine residues and 2), charge-charge interactions that favor non-β conformations.

Dimer stability

In an analogous manner, we analyzed for the case of the dimer the intra- and intermolecular mutual distances involving the charges in the termini and in the side chains of residues K and E. As in the monomer case, the distributions showed two main peaks—a direct salt-bridge at ∼2.6 Å and a water-mediated charge-charge interaction at 4.7 Å. Both types of interactions (salt bridges and water-mediated charge-charge contacts) contribute significantly to dimer stabilization. In the U-shape dimer, intramolecular contacts involving the atom pairs ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (Fig. 5, top right) together with intermolecular contacts between the atom pairs ${\text{N}}_{\text{NT}}^{+}-{\text{O}}_{\text{CT}}^{-}$ are the only contributions to structure stability (Fig. 5, bottom left). For the β-sheet dimer, we observe that only intermolecular contacts are important. Specifically, the major contribution is given by intermolecular contacts between the oppositely charged N- and C-termini groups (Fig. 5, bottom left). Smaller contributions are given by (in order of magnitude/peaks heights) ${\text{N}}_{\text{k}}^{+}-{\text{O}}_{\text{E}}^{-}$ (Fig. 5, bottom right) and ${\text{N}}_{\text{NT}}^{+}-{\text{O}}_{\text{E}}^{-}$ atom pairs. Further support for the role of electrostatics in governing dimer stability comes from the fact that the distribution of the cosine of the angle γ between the main axes of the two peptides (shown at T = 310 in Fig. S1) does not vary much with temperature. This implies that the Coulombic interactions between oppositely charged side chains and between charged termini control the dimerization process to drive antiparallel dimer formation over a wide range of temperatures. Experimental confirmation of the importance of favorable charge-charge interactions can be found in the work of Tjernberg et al. (20). Indeed, sequences with same charges at the termini (EFFE and KFFK) only aggregate when placed in an equimolar mixture. Furthermore, removal of the termini charges by acetylating the N-terminus and amidating the C-terminus of the KFFE peptide significantly reduced fibril formation (20). In terms of other contributions to dimer stability, we find that 1), the hydrophobic and side-chain hydrogen bonds energies are negligible compared with charge-charge interactions; and 2), backbone hydrogen bonds contribute to dimer stability to a similar extent for the two structures (U-shape and β-sheet). We calculated the average number of backbone hydrogen bonds within a finite interval of angle and distance cutoffs (20–40° and 3.0–4.0 Å, respectively) and found that its value varies from 2 to 3. To analyze possible differences in the energetic contribution of the solvent degrees of freedom between the two different dimers we calculated the potential of mean force (PMF) as −k_BT ln(g(r)), where g(r) is the radial distribution function (41). Although water molecules give an important contribution to dimer stability with the formation of water-mediated salt-bridges, analysis of a set of PMFs for the water oxygens with different atoms of the dimer show that the solvent energetic contribution, as a whole, does not play a significant role in determining the structure of the dimer (U-shape or β-sheet). Pairs of analogous PMFs calculated from single temperature LD simulations for the two structures are, in fact, almost identical (see Fig. S3).

Structural ensembles and cooperativity effects in the KFFE dimer formation

The β-sheet dimer conformations seen in our simulations are of particular interest, as these structures are direct precursors of the extended β-sheets structures found in amyloid fibrils. To gain insight into the formation of the β-sheet dimers from the β-strands monomers, we partitioned the free energy maps (Figs. 2 and 3) and consequently the conformational phase space, as follows. For the monomer, we partition the free energy map into two regions (see Structure of the KFFE Monomer: Coexistence of Extended β-Strand and Compact U-Shaped Structures): one for the β-strand conformation with a statistical weight related to the top-right region of the free energy map and one for the non-β, U-shape conformation with a statistical weight related to the bottom-left region of the free energy map. The representative structures for the two monomer structural ensembles are shown in Fig. 4 (top line). For the dimer, we partition the free energy into three regions (see Structure of the KFFE Dimer: Coexistence of the β-Sheet, U-Shaped and Mixed Dimers): one for the β-sheet dimer conformation with a statistical weight related to the top-right region of the free energy map, one for the U-shape dimer conformation with a statistical weight related to the bottom-left region of the free energy map and, finally, a third region in the center of the map linked to dimers with mixed conformations (one peptide in the β-strand conformation and the other in the U-shape conformation). The representative structures for the three dimer structural ensembles are shown in Fig. 4 (bottom line).

The boundaries of the different regions (basins) in the free energy maps for both the monomer and the dimer were obtained from the two-dimensional probability distributions of the order parameters (r_ee and χ for the monomer, and r_ee⁽¹⁾ + r_ee⁽²⁾ and χ⁽¹⁾ + χ⁽²⁾ for the dimer) calculated from the single temperature LD simulations (see Structure of the KFFE Monomer: Coexistence of Extended β-Strand and Compact U-Shaped Structures and Structure of the KFFE Dimer: Coexistence of the β-Sheet, U-Shaped, and Mixed Dimers, for details). Once these boundaries have been defined, we can calculate the statistical weights for the U-shape, β-sheet, and mixed dimers as well as for U-shape and β-strand monomers by integrating the related 2D-normalized probability distributions of the order parameters on the proper intervals. The calculated statistical weights for the monomer are P_B = 0.2 and P_U = 0.8 for the β-strand and for the U-shape conformations, respectively (see Fig. 4, top line). Under the assumption that the dimer formation is an additive process we can calculate the statistical weights for the structural ensembles of the dimer as $P_{\text{BB}}^{\ast }=P_{\text{B}}^2$ = 0.04 (β-sheet dimer), $P_{\text{UU}}^{\ast }=P_{\text{U}}^2$ = 0.64 (U-shape dimer) and $P_{\text{UB}}^{\ast }=P_{\text{BU}}^{\ast }$ = P_BP_U = 0.16 (mixed dimer). On the other hand, the calculations from the actual REX-LD simulations of the dimer give

$$\{\begin{array}{l}{P}_{\text{BB}}=0.2\gg P_{\text{BB}}^{\ast }\hfill \\ P_{\text{UU}}=0.6\simeq P_{\text{UU}}^{\ast }\hfill \\ P_{\text{UB}}=0.1<P_{\text{UB}}^{\ast },(P_{\text{BU}}=0.1<P_{\text{BU}}^{\ast })\hfill \end{array},$$ (5)

and show a positive cooperative effect only in the formation of the β-sheet dimer. In other words, significantly more β-sheet dimers are present than would be expected based solely on the population of β-strand monomers. The process of association hence induces the formation of β structure. In contrast, the U-shape dimer formation appears to be a quasiadditive process (small negative cooperativity) while the formation of the mixed dimers (central snapshot in the bottom line of Fig. 4) appears to be an anticooperative process. The statistical weight for a given monomer or dimer conformation P(r_ee, χ) (P($r_{\text{ee}}^{\left(1\right)}+r_{\text{ee}}^{\left(2\right)}$, χ⁽¹⁾ + χ⁽²⁾) for the dimer) is related to the free energy F(r_ee, χ) (F(r_ee⁽¹⁾ + r_ee⁽²⁾, χ⁽¹⁾ + χ⁽²⁾) for the dimer) by the formula F = −k_BT ln(NP), where N is the normalization factor for the statistical weight P (probability). Therefore, there is a large negative contribution to the total dimer free energy when a β-sheet dimer is formed, and the thermodynamic picture emerging from this analysis shows that the dimerization process favors the β-sheet conformation over both the U-shape and the mixed dimers. The definition of the β-sheet dimer formation as a thermodynamically favorable process is also consistent with the major role played by intermolecular charge-charge interactions in the β-sheet dimer (see Stability of Early Oligomers: β-Sheet Propensity and Charge-Charge Interactions). In a similar way, the definition of the U-shape dimer formation as a quasiadditive process is consistent with the equal contributions given by intramolecular and intermolecular charge-charge interactions to the U-shape dimer stability (see Stability of Early Oligomers: β-Sheet Propensity and Charge-Charge Interactions).

Stability of small KFFE protofibrils

Tjernberg et al. characterized the fibrils of KFFE using electron microscopy and obtained an average KFFE fibril dimension consistent with double-layered protofibrils (20). Because of the inherent limited atomic resolution of the EM technique, their study was unable to generate a detailed molecular picture of the interface stabilizing the fibrils. To determine the structure of the KFFE fibrils, we considered four double-layered protofibrils, two with antiparallel, interlayer orientation (AP-KF and AP-MIXED) and two with parallel, interlayer orientation (P-KF and P-MIXED), with different interfaces and ran LDBP simulations to assess their relative stabilities (see Fig. 7, top). The protofibrils named AP-KF and P-KF have, at least, one close contact between lysine (K) and phenylalanine (F) at the interface level while the protofibrils name AP-MIXED and P-MIXED have a close contact between two phenylalanine residues at the interface level.

The protofibrils named P-MIXED and AP-KF have unfavorable charge-charge contacts and from both the analysis of the RMSD time series (see Fig. 7, middle line) and the visualization of the LD trajectory, we observe that they are, in fact, unstable. Conversely, the P-KF protofibril does not have any unfavorable charge-charge contact and its RMSD time series seems to converge to a plateau value of ∼5 Å. The RMSD time series eventually show that the structure labeled as “AP-MIXED” was the most stable over the simulation time length. The AP-MIXED protofibril is the only one with both close contacts between lysine and glutamic acid (Coulombic interactions) and between phenylalanines at the interface level (see Fig. 7, top left).

We performed a structural analysis of the AP-MIXED protofibril, first, calculating an average/representative structure using a clustering-averaging procedure (42) over 10⁴ structures taken from the last 40 ns of our simulation. The RMSDs from the representative structure were 1.5 Å for the backbone atoms-only and 1.8 Å for all the heavy atoms in the protofibril. The representative structure for the AP-MIXED protofibril is shown at the bottom of Fig. 7. Second, we measured the average structural parameters of the protofibril considering the average interpeptide distance and found a value of 4.9 Å consistent with the typical experimental values found in β-sheets (4.7–5.0 Å (5)). We finally calculated the average peptide end-to-end distance and interlayer distance as these can be compared with average measurements from electron micrographs (20). The average value calculated from our simulations is 13 Å for both the end-to-end distance and the interlayer distance and is consistent with the values of the fibril dimension (12–16 Å) calculated directly from electron micrographs. The analysis of the nonbonded energy contributions at the interface level for the two stable protofibrils P-KF and AP-MIXED shows that for both structures the major contribution to stability (∼90% of the total potential energy between side chains within the interface) comes from electrostatic interactions between lysine and glutamic acid. The total, nonbonded potential energy at the interface level for the AP-MIXED protofibril is ∼2.2 times lower than the one of the P-KF protofibril (−374.4 vs. −165.9 kcal/mol). The lower energy of the AP-MIXED protofibril is mainly due to favorable contacts between lysine and glutamic acid residues. Interactions between phenylalanine residues lead to a small contribution to the stability of both protofibrils: −27.2 to −16.0 kcal/mol for the AP-MIXED and P-KF protofibrils, respectively. It is interesting to notice that the value of −27.2 kcal/mol for the nonbonded potential energy at the interface level between phenylalanine residues in the AP-MIXED protofibril is in agreement with an analogous calculation performed on a small protofibril formed by the Aβ_16–22 peptide with sequence KLVFFAE (43). We note that in the Aβ_16–22 study (43), the contribution of the phenylalanine residues to the interface stability is dominant because there are no charged residues at the interface level (the protofibril interface is purely hydrophobic: LFA-LFA). In contrast, in the KFFE AP-MIXED protofibril there are 16 charged residues (eight lysine residues and eight glutamic acid residues in close favorable contact) buried in the interface. In this case, both the ES interactions between charged residues at the interface level and the analogous ES contacts between oppositely charged termini groups represent the highest energy contribution to protofibril stability. The comparison with the Aβ_16–22 study shows that for short peptides 1), aromatic interactions play an important role in stabilizing the protofibrils only when there are no ES interactions between oppositely charged residues at the interface level; and 2), although the KFFE and KLVFFAE peptides have similar amino acid sequences, the relative energetic contributions to protofibril stability are different in the two systems. Therefore, one should be careful when considering the KFFE peptide as a minimalistic version of the hydrophobic core of the full Aβ_1–42 peptide.

Conclusions

In this article, we presented an extensive computational study of the KFFE tetrapeptide. KFFE is a minimal model system to investigate the balance of forces driving peptide aggregation, as it is one of the smallest sequences that combines both an aromatic hydrophobic core with high β-sheet propensity and oppositely charged terminal side chains. Our work sought to address the question of the relative importance of aromatic and electrostatic interactions in the early and late stages of aggregation. We used a fully atomic model of the peptide in explicit solvent. While other researchers have also explored the self-assembly of this peptide, their simulations employed either a coarse-grained description of the peptide that lacked a proper description of the electrostatics (no Coulombic terms) and had no solvent (30–32), or fully atomic simulations in implicit solvent (29,33). The coarse-grained simulations, while valuable, are not able to answer questions related to the role of electrostatics in aggregation. Furthermore, these simulations (32) were not able to generate a bilayer fibril structure consistent with experiment. The importance of using an explicit representation of the solvent was highlighted in a recent work by Strodel and Wales (33). The authors examined the monomer and dimeric conformations of KFFE using a given force field and four different implicit solvent models. None of the implicit solvent models could capture the complexity of both the monomer and the dimer free energy surfaces that we obtain from our explicit solvent REX simulations (see Figs. 2 and 3). For the monomer, each implicit solvent model yielded only a very partial view of the free energy surface, each resolving only one of the free energy minima corresponding to one of the three representative monomer conformations populating the free energy surface in Fig. 2. Similarly, for the dimer, the individual implicit solvent models were not able to reproduce the complexity of the free energy surface in Fig. 3. Our simulations reveal several new aspects of the KFFE aggregation process that could not be resolved in prior coarse-grained and implicit solvent models simulations. In particular, our simulations show that the monomer structure coexists between β- and non-β-conformations, and that these structures are the result of a competition between the high β-propensity of the F residues and the favorable attraction between the oppositely charged termini (both end groups and the K and E residues). We see three major structural ensembles for the KFFE dimer: 1), U-shape, antiparallel dimers; 2), β-sheet, antiparallel dimers; and 3), mixed dimers where one peptide is in the U-shape conformation while the other is in the β-strand conformation. We also observe that the β-conformation of the peptide is the same in the monomeric state, dimeric state, and in the double-layered protofibril (See Figs. 4 and 7). Our results are in agreement with experimental observations of the KFFE peptide showing partial β-strand conformation in the early steps of aggregation. Our simulations show that charge-charge interactions between charged side chains and charged termini play a dominant role in stabilizing the various monomer and dimer structures. In particular, we found that both direct and solvent-mediated salt bridges give an important contribution to structure stabilization. Aromatic stacking does not appear to be the primary driving force for dimer formation, although such interactions can help further stabilize the associated complex. The high intrinsic β-strand propensity of the phenylalanine residues plays a more dominant role than aromatic stacking in the early stages of aggregation. We observe a significant cooperativity in the formation of the β-sheet dimers, in which dimerization induces the formation of β-structure from U-shaped monomer. By considering fibrils with different interfaces, we were able to propose a fibril model consistent with experimental electron microscopy measurements (20). The most stable interface involved both close contacts between lysine and glutamic acid (Coulombic interactions) and between phenylalanines. While this construct highlights the role of both aromatic and electrostatic interactions in fibril stability, our calculations show that charge-charge interactions within the interface are by far the most important energetic factor stabilizing the protofibrils. Nonetheless, the combination of high β-propensity in addition to the favorable aromatic stacking interactions that arise with F residues may make F-rich peptides particularly prone to aggregate. This may explain why KFFE has a much higher aggregation propensity than the other tetrapeptides studied by Tjernberg (KLLE that aggregates and KVVE and KAAE that do not). We note that the relative importance of electrostatic versus aromatic interactions will differ for different peptide sequences and for different experimental solution conditions. Indeed for the Alzheimer Amyloid-β KLVFFAE peptide that we studied earlier (43,44), aromatic interactions were dominant in stabilizing the protofibril as a result of the absence of electrostatic interactions between oppositely charged residues in the interface. KFFE may be a special case in which the importance of electrostatic interactions is magnified. It is conceivable that solution conditions (or perhaps more realistic in vivo conditions) in which the charges become screened may alter the balance of interactions stabilizing KFFE fibrils.