Interaction of Tea Catechin (—)-Epigallocatechin Gallate with Lipid Bilayers

Abstract

A major component of green tea extracts, catechin (—)-Epigallocatechin gallate (EGCg), has been reported to be biologically active and interacting with membranes. A recent study reported drastic effects of EGCg on giant unilamellar vesicles (GUVs). In particular, EGCg above 30 μM caused GUVs to burst. Here we investigated the effect of EGCg on single GUVs at lower concentrations, believing that its molecular mechanism would be more clearly revealed. We used the micropipette aspiration method, by which the changes of surface area and volume of a GUV could be measured as a result of interaction with EGCg. We also used x-ray diffraction to measure the membrane thinning effect by EGCg. To understand the property of EGCg, we compared its effect with other membrane-active molecules, including pore-forming peptide magainin, the turmeric (curry) extract curcumin, and detergent Triton X100. We found the effect of EGCg somewhat unique. Although EGCg readily binds to lipid bilayers, its membrane area expansion effect is one order of magnitude smaller than curcumin. EGCg also solubilizes lipid molecules from lipid bilayers without forming pores, but its effect is different from that of Triton X100.

Like ginseng and curry, green tea is popularly believed to have health benefits. Green tea extracts, particularly catechins, have been reported to have a wide variety of biological activities (see references in (1)). Because many of these activities seemed to affect membrane-dependent cellular processes (2), such as cell signaling, cell cycle, arachidonic acid metabolism and mitochondrial functionality, there have been a long series of reports on catechin-membrane interactions (2–11). Earlier investigations (2–9) demonstrated that tea catechins bound to lipid bilayers caused aggregation of lipid vesicles and leaked contents from a suspension of vesicles. A more extensive study was done recently by Tamba et al. (10) who concentrated on a major catechin from tea extract, (—)-Epigallocatechin gallate (EGCg). Noting that in an earlier study with magainin (12) they had demonstrated the advantage of observing individual giant unilamellar vesicles (GUVs) over measuring collective responses from a suspension of vesicles, Tamba et al. observed the effect of EGCg on individual GUVs in several ways. They found that EGCg had the effects of 1), causing shape change of GUVs 2), inducing aggregation of vesicles, and 3), causing GUVs to burst through a large hole. They suggested that the bursting effect is a possible mechanism for catchins' antibacterial activity. They attributed all these activities to the binding of EGCg exclusively to the outer leaflet of the GUV membranes.

The methods used by Tamba et al. required relatively high concentrations of EGCg. Below 30 μM, EGCg showed the effect of shape change and aggregation of GUVs, but no leakage. The bursting effect was seen only for concentrations above 30 μM. It is difficult to discern the molecular mechanism of EGCg from such drastic effects on membranes. Here we will study the effect of EGCg on membranes by using a different GUV method which is more sensitive than the methods used by Tamba et al. and can measure the effect at lower EGCg concentrations. We believe that low concentration phenomena are more likely to reveal the molecular mechanism.

We used the micropipette aspiration method (13) to monitor the area and volume change of a GUV exposed to EGCg in solution. We also measured the effect of EGCg on the thickness of lipid bilayers by x-ray diffraction. We have previously used the combination of these methods to study other membrane-active molecules (14,15). We found that the molecular effect of EGCg on membranes is best understood by comparing its action with membrane-active molecules whose actions are understood, such as pore-forming peptides (14), the turmeric (curry) extract curcumin (15,16), and detergents. The comparative studies led us to conclude that EGCg has a mild detergent-like effect. At concentrations below 10 μM, it binds to lipid bilayers but also slowly dissolves the lipid molecules from the bilayer without making pores. We did not observe any effect indicating that EGCg binds exclusively to the outer leaflet of GUV membranes. Thus the effect of EGCg on membranes is somewhat unique. Its binding effect (i.e., the membrane area expansion effect) is one order of magnitude smaller than curcumin, and its lipid-solubilization effect is also different from detergents.

Experiment

Materials

(—)-Epigallocatechin gallate (EGCg) (product number E4143), HEPES (product number H3375), Triton X100 (product number T8787) and bovine serum albumin (product number A9418) were purchased from Sigma-Aldrich (St. Louis, MO). 1,2-dieicosenoyl-sn-glycero-3-phosphocholine (Di 20:1PC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), chicken egg L-α-phosphatidylcholine 95% (EggPC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(Lissamine Rhodamine B Sulfonyl) (Rh-DOPE) were purchased from Avanti Polar Lipids (Alabaster, AL). Magainin 2-amide was purchased from GenScript Corporation (Piscataway, NJ). Polyethylene glycol (PEG) (PEG400) was purchased from Merk Co. (Hohenfrunn, Germany). All materials were used as delivered.

X-ray lamellar diffraction

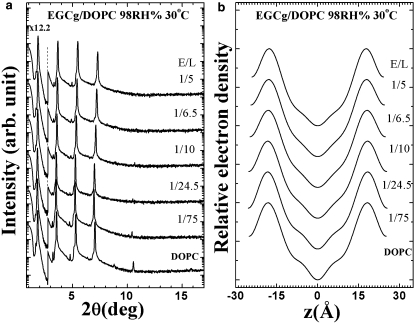
EGCg (Fig. 1 for its molecular structure) and lipid in molar ratio E/L were co-dissolved in a solvent of 1:1 (v/v) methanol and chloroform. An appropriate amount of the solution was spread onto a cleaned quartz surface (3 mg of lipid on 18×18 mm² area). After the solvent evaporated, the sample was placed in vacuum to remove the remaining solvent residues, and then slowly hydrated with saturated water vapor until it appeared transparent. The results were oriented multiple bilayers of lipid/EGCg mixtures parallel to the substrate.

Figure 1.

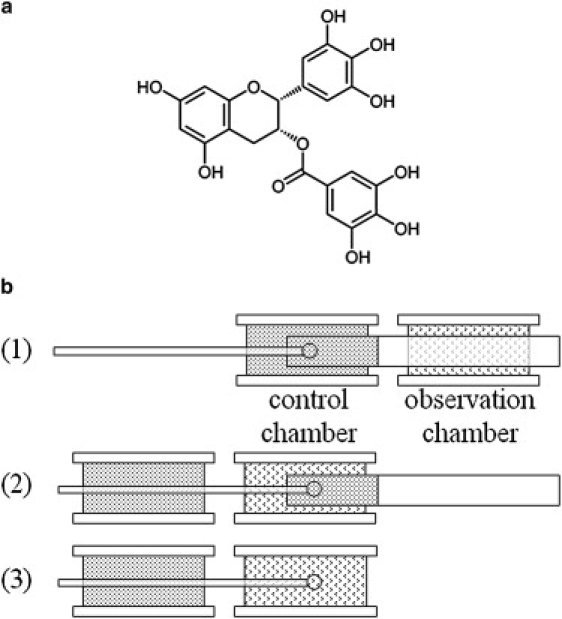
(a) Chemical structure of EGCg. (b) Schematic of the GUV experiment: (1) An aspirated GUV was inserted ∼0.7mm into the transfer pipette in the control chamber. (2) The aspirated GUV in the transfer pipette was moved from the control chamber to the observation chamber. (3) Then the transfer pipette was moved away, so that the GUV was exposed to the EGCg/sucrose/HEPES solution (marked as t = 0).

For x-ray lamellar diffraction measurement, the sample was kept in a thermally insulated chamber (±0.1°C) that was equipped with mylar windows for x-ray passage. The chamber also enclosed a PEG solution for the humidity control. The relative humidity corresponding to a PEG solution was measured by a hygrometer (Rotronic Instrument Co., Huntington, NY) in a calibration chamber provided by the manufacturer. For example, 1.0 g of PEG400 dissolved in 4.0 g of water gave a vapor pressure equivalent to 98% relative humidity (RH) at 30°C.

The diffractometer consisted of a two-circle goniometer and a Cu K_α radiation source filtered by Ni and operated at 40kV/30mA. The two-circle goniometer was designed for vertical θ-2θ scan, so that the sample substrate was kept nearly horizontal during the entire measurement. This allowed us to measure the lipid samples at high hydration levels without the problem of sample-running that would otherwise occur if the substrate were oriented vertically as in a horizontal θ-2θ scan experiment. Both the incident and the diffracted x rays were collimated by two sets of x-y slits. An attenuator was used to prevent the first order Bragg peak from saturating the detector. Each θ-2θ scan was measured from θ=0.5 to 10.5° with a step size Δθ=0.01° at 1 s per step. Each sample was measured at several different hydration levels from 90%RH to 98%RH, for the purpose of using the swelling method to determine the phases of diffraction amplitudes (17–19). The equilibrium of the sample at each humidity setting was ensured by an agreement of at least three consecutive diffraction patterns whose average was subsequently analyzed. Each EGCg-lipid mixture was measured with at least two separately prepared samples. Each sample was measured twice to check its reproducibility. This procedure also ensured that the samples were not damaged by radiation. In previous experiments, we observed diffraction pattern changes when a sample was overexposed; such samples also produced extra spots in the thin layer chromatogram (18).

The procedure for data reduction was described in many of our previous articles (17–19). Briefly, data reduction started with the background removal and corrections for absorption and diffraction volume. Then the integrated peak intensities were corrected for the polarization and the Lorentz factors. The magnitude of the diffraction amplitude was the square root of the integrated intensity. The phases were determined by the swelling method (20). With their phases determined, the diffraction amplitudes were Fourier transformed to obtain the trans-bilayer electron density profiles. The profiles were not normalized to the absolute scale, but they gave the correct phosphate peak-to-phosphate peak distances (19).

Isothermal titration calorimetry (ITC)

EGCg was first dissolved in a buffer solution of 20mM HEPES (pH7.4) and 150mM NaCl. Monodispersed large unilamellar vesicles (LUVs) of DOPC with a diameter ∼100nm were made by an extruder. ITC was performed by injecting a series of aliquots (volume10 μL) from an LUV suspension into an EGCg solution of concentration E_t at 25°C. The heat flow for EGCg binding to the vesicles was measured by a high-sensitivity ITC instrument (MicroCal LLC, Northampton, MA) with a reaction cell volume of 1.4144 ml. Before ITC experiment, the EGCg solution was put in a vacuum degas system (provide by MicroCal) to remove the possible air bubbles. The data of heat flow were acquired by computer software developed by MicroCal. The solution in the reaction cell was continually stirred during the measurement. The reaction heat for each injection was determined by integration of the heat flow tracing. In a control experiment, the corresponding LUVs were injected into a buffer solution in reaction cell. The resultant heat (usually called dilution heat) for each injection was subtracted from the corresponding reaction heat of LUVs injected into the EGCg solution. The reaction heat per injection thus obtained was that for EGCg binding to lipid vesicles. We have performed the following ITC measurements. EGCg solutions of concentration (E_t) 10, 50, 100 and 300 μM were each titrated by DOPC LUVs of 4mM lipid concentration. The data reduction described below was similar to that employed in Hung et al. (21), but with a small modification.

Denote the reaction heat for the i^th injection as h_i. The cumulative heat up to the k^th injection is defined as,

$$h^{\left(k\right)}=\sum _{i=1}^k{h}_i\text{.}$$ (1)

The cumulative heat will be saturated once all the EGCg molecules in the reaction cell are bound to lipid vesicles. Denote the saturated cumulative heat as h^(sat) and the initial molar concentration of EGCg molecules in the reaction cell as E_t, then the molar fraction of the vesicle-bound EGCg up to the k^th injection is,

$$E^{\left(k\right)}/\left({\eta }^{\left(k\right)}{E}_t\right)=h^{\left(k\right)}/h^{\left(\text{sat}\right)},$$ (2)

where the dilution factor η^(k) is defined as follows. The injection of each LUV aliquot increased the volume by δv. The volume of the solution in the reaction cell up to the k^th injection is $V_{\text{cell}}^{\left(k\right)}=V_{\text{cell}}^o+k\mathrm{\delta }v,$ where $V_{\text{cell}}^{\text{o}}$ is the original volume of solution in the reaction cell. The dilution factor is ${\eta }^{\left(k\right)}=V_{\text{cell}}^o/V_{\text{cell}}^{\left(k\right)}\text{.}$ The lipid concentration in the reaction cell up to the k^th injection is

$$L^{\left(k\right)}=L_o(k\mathrm{\delta }v/V_{\text{cell}}^{\left(k\right)}),$$ (3)

where L_o is the molar concentration of lipid injected into the reaction cell. Then the partition coefficient K is defined by

$$E^{\left(k\right)}/\left({\eta }^{\left(k\right)}{E}_t\right)=K{L}^{\left(k\right)}/(1+K{L}^{\left(k\right)})\text{or}{E}^{\left(k\right)}/L^{\left(k\right)}=K{E}_f^{\left(k\right)},$$ (4)

where $E_f^{\left(k\right)}={\eta }^{\left(k\right)}{E}_t-E^{\left(k\right)}$ is the concentration of EGCg dissolved in solution at the end of k^th injection. Combining Eqs (2). and (4), one obtains

$$h^{\left(k\right)}=h^{\left(\text{sat}\right)}K{L}^{\left(k\right)}/(1+K{L}^{\left(k\right)})\text{.}$$ (5)

We used Eq (5). to fit the data of h^(k)vs L^(k), from which Kand h^(sat) were obtained. The binding enthalpy per mole of EGCg can be obtained by

$$\mathrm{\Delta }H=h^{\left(\text{sat}\right)}/\left(E_t{V}_{\text{cell}}^{\text{o}}\right)\text{.}$$ (6)

GUV experiment

EGCg was first dissolved in 10mM HEPES (pH 7.4) at 10mM and then diluted with a HEPES/sucrose solution to desired concentrations. Triton X100 and magainin 2 were first dissolved in distilled water at 10mM and then diluted with sucrose solution to desired concentration.

GUVs were produced in a 200mM sucrose solution by the electroformation method (22). 1.25 mg of DOPC (or 1.34 mg of Di20:1PC) and 0.0083 mg of Rh-DOPE were dissolved in 1ml chloroform. The mole/mole ratio of the PC to Rh-DOPE was always kept at 99.6% to 0.4%. Rh-DOPE was used to enhance the image contrast of the GUV boundary. 60μl of the lipid/chloroform solution was dried onto two platinum electrodes in a Teflon chamber. The solvent was completely removed by placing the chamber in vacuum for at least one hour. The chamber was then filled with 200mM sucrose solution. An alternating AC field with amplitude 1.5V and frequency 10Hz was applied across the electrodes for 10 min. Then the amplitude was changed to 3V and the frequency was adjusted in the sequence of 10Hz, 40 min; 3Hz 15 min; 1Hz 10 min; 0.5Hz 30min. This electroformation method has been shown to produce unilamellar large vesicles (22). The vesicle suspension was gently collected into a glass vial. The vesicles were used within 24 h of production.

GUV experiments were performed in a setup described in Sun et al. (15)—see the schematic in Fig. 1. The vesicles were first transferred to a control chamber containing a 200mM sucrose solution. The osmolality of each solution used in the experiment was measured by the Wescor Model 5520 Vapor Pressure Osmometer (Wescor, Logan, UT). The osmolality of the solution in the control chamber was the same as the sucrose solution inside the vesicles so that the vesicles were kept in an isotonic environment. A selected vesicle (diameter ∼50–70μm) was aspirated at a low constant negative pressure (which created a membrane tension 0.5 to 1 dyn/cm) by a micropipette connected to a pressure control system. [Before the experiment, micropipettes (with inner diameter 16–20μm) and the chamber walls were coated with 0.5% bovine serum albumin to dissipating charge on the glass surface (23) and then washed extensively by 200mM sucrose solution.] The pressure control system was similar to the setup described by Fygenson et al. (24). The negative pressure was produced by connecting the micropipette to a syringe and was referenced to the atmosphere pressure by a water-filled U tube. The pressure was measured by a pressure transducer MKS Baratron 223 with a digital readout MKS 660 (Andover, MA).

To observe the effect of EGCg on GUVs, the aspirated vesicle was transferred to an observation chamber that contained the EGCg solution. The observation chamber was set side-by-side with the control chamber and separated by ∼1cm. A transfer pipette (with inner diameter 0.75mm) filled with the control solution was inserted into the control chamber through the observation chamber from the opposite side of the aspiration micropipette (Fig. 1). The aspiration pipette and the transfer pipette were each held by a motor-driven micromanipulator Narishige MM-188 (East Meadow, NY). The aspirated vesicle was inserted ∼0.7mm into the transfer pipette in the control chamber. By moving the microscope stage, the aspirated vesicle in the transfer pipette was moved from the control chamber to the observation chamber. Then the transfer pipette was moved away, so that the vesicle was exposed to the EGCg solution (marked as t = 0). The solution in the observation chamber also had the same osmolality as the solution in the control chamber, unless otherwise specified.

An aspirated GUV consisted of a cylindrical protrusion (length L_p) in the micropipette (radius R_p) connected to the spherical vesicle (radius R_v) at the tip of the micropipette (see Fig. 2). The protrusion length would change if there was a change in the surface area A and/or the volume V of the GUV, as a result of interaction with EGCg.

Figure 2.

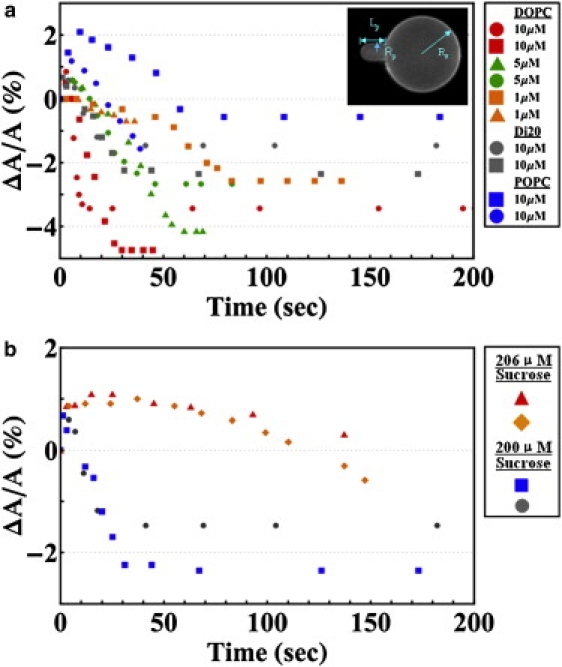
(a) Time sequence of fractional area changes ΔA/A of individual GUVs exposed to various concentrations of EGCg. Different symbols represent different runs: the lipid of GUV and the EGCg concentration are given in the side panel. For each run, the osmolality of the solution in the observation chamber, including the buffer and EGCg, was made the same as the 200 mM sucrose solution inside the GUV. (b) Comparison of runs when the solution in the observation chamber had osmolality 206 mM and the corresponding runs when the osmolality was 200 mM. The lipid was di20:1PC, EGCg was 10 μM, and the sucrose solution inside the GUV was 200 mM. Inset in a shows the definitions for L_p, R_p and R_v.

Control experiment was performed with the observation chamber filled with 190mM sucrose and 10mM HEPES solution which was isotonic to the sucrose solution in the control chamber. After the GUV was transferred to the observation chamber, the length of the aspirated protrusion reminded unchanged for 6 min, as expected. To minimize the osmolality change due to evaporation, each run of the experiment were kept within 6 min and the solutions were changed after each run. The video image of the experiment was recorded by a Nikon NS-5 MC camera (Nikon, Melville, NY).

Turbidity measurement

A suspension of lipid vesicles was prepared for turbidity measurement. From a stock solution of DOPC (25 mg of lipid in 1 ml chloroform), 2.5 mg of DOPC was placed in a glass vial and blow-dried with nitrogen for 30 min. Three samples were prepared by adding 4 ml of HEPES or EGCg and HEPES or Triton X-100 solutions into the glass vial, making the lipid's final concentration 0.8 mM, and the concentration of EGCg or Triton 10 mM. The glass vial was put in a sonicator for 10 min to form vesicles. The vesicle suspension was immediately transferred to a cuvette for the transmission measurement in a spectrophotometer (Shimadzu UV-2101PC, Tokyo, Japan). For background subtraction, the same solution without lipid was used for each sample.

Result

GUV experiment

The general response of a GUV exposed to an isotonic EGCg/HEPES/sucrose solution was that the protrusion length L_p initially increased slightly and then within seconds decreased until diminished. In ∼50% of the cases, the GUV ruptured after the protrusion diminished. The rupture was not correlated with the concentration of EGCg. From the geometry of an aspirated GUV, the change of the surface area A is related to the changes of L_p and the GUV radius R_v (see Fig. 2) by $\mathrm{\Delta }A=2\pi R_p\mathrm{\Delta }{L}_p+8\pi R_v\mathrm{\Delta }{R}_v,$ and the change of the GUV volume V by $\mathrm{\Delta }V=\pi R_p^2\mathrm{\Delta }{L}_p+4\pi R_v^2\mathrm{\Delta }{R}_v$ (13). In general, the changes of GUV radius ΔR_v were too small to be measured accurately. However, since the inside and outside of the GUVs were always isotonic, the change of volume should be zero. This will be further demonstrated by comparative GUV experiments with other types of membrane-active molecules below. Under the condition ΔV = 0, ΔL_p is directly proportional to ΔA: $\mathrm{\Delta }A=2\pi R_p(1-L_p/R_v)\mathrm{\Delta }{L}_p\text{.}$ From the recorded video images, we measure ΔL_p as a function of time by using the Nikon NIS-Elements BR 2.30 software. The responses of GUVs of different sizes can be compared by their ΔA/A as a function of time, as shown in Fig. 2 A. The data include GUVs of DOPC, POPC, and Di20:1PC exposed to EGCg of concentrations ranging from 1 to 10 μM.

X-ray diffraction

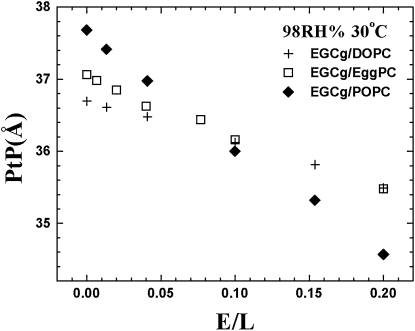
Lipid-EGCg mixtures formed excellent bilayers as shown by their x-ray lamellar diffraction patterns and their reconstructed electron density profiles. The example of EGCg-DOPC mixtures in a series of mixing molar ratios (E/L) is shown in Fig. 3. The results of EGCg-POPC, and EGCg-EggPC mixtures were similar in quality. In such bilayers, EGCg was in its equilibrium bound state. The peaks of the electron density profile are the positions of the phosphate groups on the surfaces of the bilayer. Hence the peak-to-peak distance (PtP) across the bilayer is a good measure of the bilayer thickness. The presence of EGCg apparently caused membrane thinning. The thinning is linearly proportional to the E/L for all three lipids measured here (Fig. 4).

Figure 3.

(a) X-ray diffraction patterns for a series of EGCg-DOPC mixtures of molar ratios E/L in aligned multiple bilayers. An attenuator was used to prevent the first order Bragg peak from saturating the detector. The patterns are displaced for clarity. (b) Electron density profiles for DOPC bilayers containing EGCg at different E/L, all at 30°C and 98% RH.

Figure 4.

The peak-to-peak distance (PtP) of the electron density profiles plotted as a function of E/L. The profiles were obtained from x-ray diffraction of EGCg/DOPC (Figure 3), EGCg/POPC and EGCg/EggPC mixtures.

ITC

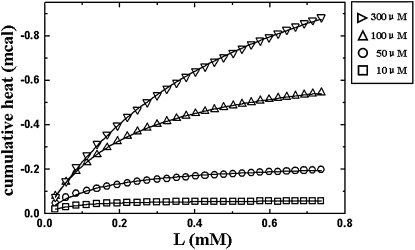
ITC measurement was performed by injecting lipid vesicles into an EGCg solution of concentration E_t. The measured cumulative reaction heat as a function of injected lipid concentration is shown in Fig. 5 for four values of E_t. Equation 5 was used to fit the data, from which Kand h^(sat) were obtained. The binding enthalpy per mole of EGCg, ΔH, was obtained from Eq. 6. The results were K = 1.8 × 10⁴ M⁻¹, ΔH = −4.3 kcal/mol for E_t = 10 μM; K = 7.0 × 10³ M⁻¹, ΔH = −3.3 kcal/mol for E_t = 50 μM; K = 4.3 × 10³ M⁻¹, ΔH = −5.1 kcal/mol for E_t = 100 μM; K = 1.8 × 10³ M⁻¹, ΔH = −3.7 kcal/mol for E_t = 300 μM. It is clear that the measured apparent partition coefficients decrease with increasing EGCg concentration, whereas the measured binding enthalpy remains within a narrow range of value. We attribute this result to the effect of vesicle aggregation caused by bound EGCg (see Discussion section). Aggregation reduces the amount of vesicle's lipids available for EGCg binding. The effect of aggregation is greater at higher EGCg concentration, which makes the apparent partition coefficient decrease with EGCg concentration.

Figure 5.

ITC measurement of EGCg solution titrated by DOPC vesicles, the cumulative heat h^(k) versus lipid concentration L^(k). The series of data points represent different k. The symbols are square for the initial EGCg concentration E_t =10 μM; circle for 50 μM; triangle for 100 μM; inverted triangle for 300 μM. The solid curves are the fittings by Eq. 5, from which Kand h^(sat) were obtained.

We have also performed ITC on several other lipids including POPC, DOPC/DOPG(9:1) and DOPC/DOPG(1:1). We obtained similar results, namely, the measured apparent binding coefficients decreased with increasing EGCg concentration whereas the binding enthalpy remained within a narrow range of value.

Comparative experiments

To understand the effect of EGCg on membranes, we compared EGCg with other membrane-active molecules whose behaviors are to a large degree understood, including the turmeric (curry) extract curcumin, detergent Triton ×100, and pore-forming peptide magainin.

Comparison with curcumin

Experiment with curcumin was previously performed (15) exactly as for EGCg described above. In all concentrations of curcumin from 1.35 to 13.5 μM, the vesicle protrusion invariably lengthened to an equilibrium value (Fig. 6). x-ray diffraction of curcumin-lipid mixtures showed a nonlinear membrane thinning effect by curcumin. The data showed that the initial binding of curcumin had a large thinning effect, but above C/L∼0.032 (C stands for curcumin) the thinning effect became considerably smaller. These results indicate that at low concentrations, curcumin mainly adsorbs to the water-lipid chain interface where the adsorption expands the interfacial area. But as C/L increases, the energy cost of the area expansion elevates the energy level of interfacial adsorption, so curcumin binding shifts to a second bound state inside the hydrocarbon region. This makes the membrane area expansion per curcurmin and the corresponding thinning effect much smaller at high C/Ls > 0.032 (15).

Figure 6.

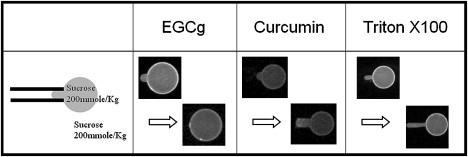
Comparative studies of EGCg with curcumin and Triton X100. The inside and outside solutions of GUVs were isotonic. In the presence of EGCg, the protrusion length initially increased and then decreased until diminished. In the presence of curcumin, the protrusion length steadily increased to an equilibrium length (data from (15)). In the presence of Triton X100, the protrusion length steadily increased at a decelerating rate during the entire six minutes of observation time.

Comparison with Triton X100

Experiment with Triton X100 was performed exactly as for EGCg described above at Triton concentration 10 μM. The GUV protrusion length continuously increased, with a decelerating growth rate, to a length corresponding to ΔA/A∼10% at the end of the observation period of six minutes (Fig. 6). The effect of Triton X100 on lipid vesicles has been studied previously. Two independent studies (25,26) found no bilayer solubilization at Triton concentrations below its critical micelle concentration (CMC) which was estimated to be 0.22–0.24 mM. Thus in the GUV experiment with 10 μM Triton, Triton molecules appeared to incorporate into the bilayer and expanded the GUV surface area.

Comparison with magainin

Magainin is a well-understood pore-forming peptide (12,27,28). Like many other well studied antimicrobial peptides (29,30), magainin spontaneously binds to lipid bilayers; at low concentrations the binding expands the bilayer area without changing its permeability; but above a lipid-dependent critical concentration, magainin induces finite-sized stable pores in the membranes (27,31) —the vesicles remain intact under this condition (12,14). This description of molecular action is in complete agreement with the extensive results obtained by Tamba et al. (12) who, among many experiments, observed the responses of individual GUVs to the introduction of magainin into the vicinity.

To find out if EGCg induces pores in membranes, we performed same experiments with EGCg and magainin. Systematic pore-forming experiments with an aspirated GUV have been performed with another pore-forming peptide melittin (14). Therefore we could predict the response of a GUV if pores were formed in the bilayer. As a control, we repeated the melittin experiment with magainin. The observation chamber was filled with 200 mM glucose solution and 10 μM magainin. We observed the protrusion length initially increased and then decreased (due to the formation of pores when the ΔA/A exceeded a threshold), exactly the same reaction as in the melittin experiment (14,32). The decrease of the protrusion length was due to the finite-size of the peptide-induced pores that allowed the permeation of the smaller glucose more than the permeation of the larger sucrose; and the resulted osmolality imbalance induced a net water influx (14,32). Thus the response of GUVs in this control experiment was similar to the EGCg experiments reported above. To test if EGCg formed pores in membranes, we designed experiments in which the protrusion length should grow if pores were formed.

In the first comparative experiment, we used a 206 mM sucrose solution in the observation chamber, slightly higher in osmolality than the 200 mM sucrose solution inside the GUV. If pores were formed in the membrane of the GUV, the osmolality imbalance would cause a rapid efflux of water from the GUV and reduce its volume. Under the circumstance the GUV surface area would not change, because area changing is a high energy process (33) and also it has been experimentally shown that membrane area is constant once the pores are formed (14,34). Then the relation between ΔL_p and ΔV is $\mathrm{\Delta }V=-\pi R_p(R_v-R_p)\mathrm{\Delta }{L}_p,$ i.e., the GUV protrusion in the micropipette would grow. This was exactly what happened when the observation chamber included 3 μM magainin (Fig. 7). On the contrary the response of a GUV to 10 μM EGCg was similar to the response when the observation chamber contained 200 mM sucrose solution, i.e., the protrusion length initially increased slightly and then decreased. However due to the osmolality imbalance, there was a slow water efflux from the GUV through the lipid bilayer; therefore there was a larger initial increase of L_p compared with the 200 mM sucrose solution experiment. To make a comparison between the experiments of 206 mM and 200 mM sucrose solutions, we used the formula $\mathrm{\Delta }A=2\pi R_p(1-L_p/R_v)\mathrm{\Delta }{L}_p$ to translate ΔL_p to ΔA in Fig. 2 b, even though part of ΔL_p in the case of 206 mM was due to volume decrease. The point is that the effect of EGCg in reducing the GUV protrusion (negative ΔL_p) was stronger than the positive ΔL_p from the volume decrease due to the slow water efflux through the membrane.

Figure 7.

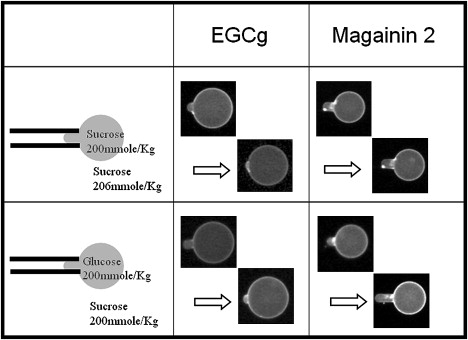
Comparative studies of EGCg with magainin to detect the formation of pores in GUVs. In case one, the outside solution had a slightly higher osmolality. Magainin induced pores made the protrusion length increased before the GUV ruptured. On the contrary, the presence of EGCg made the protrusion length decrease after an initial increase, despite the water outflow by the osmolality imbalance that favored the protrusion length increase. In case two, an isotonic glucose solution was inside the GUVs. Since the magainin-induced pores were of finite size, the permeation of the smaller glucose from inside was faster than the permeation of the larger sucrose from outside, there was a net outflow of water as in case one for magainin. On the other hand, the replacement of sucrose to glucose inside GUV did not affect the response of GUV to EGCg.

In the second experiment, we produced GUVs in 200 mM glucose solution, and used an isotonic 200 mM sucrose solution in the observation chamber. This was the reversal of the control experiment for magainin described above. Therefore if magainin were in the observation chamber and formed pores in the GUV, the GUV protrusion would lengthen. This was exactly what we observed when we introduced 10 μM magainin in the observation chamber (Fig. 7). On the contrary, in the presence of 10 μM EGCg, the protrusion length initially increased slightly and then decreased, exactly the same as when 200 mM sucrose solution was inside the GUV.

These comparisons clearly showed that EGCg did not induced pores or altered the permeability of the membranes. EGCg clearly reduced the GUV surface area, after a small initial expansion due to the EGCg binding.

Discussion

EGCg binds to the bilayer interface

All molecular binding to a membrane expands the membrane area, as we saw in the above examples. The membrane expansion can be correlated with the membrane thinning. If the molecules bind to the water-lipid chain interface, the interfacial area expansion will stretch the hydrocarbon region, making its thickness thinner. Due to the very small volume compressibility of the hydrocarbon chains (35), the fractional area increase is closely equal to the fractional thickness decrease of the hydrocarbon region: $\mathrm{\Delta }A/A\approx -\mathrm{\Delta }h/h$ where h is the thickness of the hydrocarbon region. This relation is valid only for interfacial binding; it does not hold for molecules binding in the hydrocarbon region (15). Until now all water-soluble membrane-active molecules we have studied, including many antimicrobial peptides (36) and curcumin (15), exhibited a nonlinear thinning effect as a function of the bound molecule/lipid ratio (M_B/L). At low M_B/L's, the initial thinning rate is large and linear, but at high M_B/L's the thinning rate diminishes. The energetic reason for this nonlinear thinning effect has been explained (15,34).

The effect of membrane thinning by EGCg is shown in Fig. 4 in PtP. The thickness of the hydrocarbon region is h≈PtP−10 Å, or PtP minus twice the length of the glycerol region (from the phosphate to the first methylene of the hydrocarbon chains). It is important to point out that this relation is valid not only for pure lipid bilayers (16,37,38) but also for bilayers with bound molecules (21). Note that the electron density profile of the glycerol region did not change with the EGCg concentration E/L in Fig. 3–the main changes occurred in the central chain region. Also in numerous measurements on lipid bilayers containing antimicrobial peptides (18,34,39), the PtP initially thinned by an amount ranging from 0.5 to 2 Å and then became almost constant with increasing concentrations of peptides, indicating no significant effect on the glycerol configuration by high concentrations of peptide binding. This means that the length of the glycerol region (∼5 Å) is approximately a constant even when there are bound molecules in the bilayer. Thus the linear thinning in PtP (Fig. 4) indicates a linear thinning in the hydrocarbon region h. This implies that, at least up to E/L = 0.2, all EGCg molecules are bound to the interface.

From the slope of Δh vs. E/L, and the relation $\mathrm{\Delta }A/A\approx -\mathrm{\Delta }h/h$, one can calculate the area expansion by the binding of one EGCg molecule, A_S: $-\mathrm{\Delta }h/h=A_{S}E/A_{L}L$ (21). From Fig. 4, we obtained h of pure lipid (26.7, 27.7. 27.1 Å for DOPC, POPC, EggPC), and from the volume of chains (40) divided by h we obtained the cross sectional area per lipid A_L (73.0, 67.7, 67.7 Ų for DOPC, POPC, EggPC). The results are: A_S = 16.2 Ų, 37.4 Ų, and 19.6 Ų for DOPC, POPC and EggPC, respectively. The larger A_S for POPC is reflected in the larger initial protrusion growth in the GUV experiment (Fig. 2 A). But compared with the similar size curcumin, which has A_S ∼ 240Ų (15), the membrane expansion effect of EGCg is very small. Note that these values are not to be interpreted as the physical dimensions of the bound molecule. (The molecular weight of EGCg and curcumin are, respectively, 458 and 368.) When a molecule binds to a lipid bilayer, the molecule might bring in additional water molecules or release some water molecules associated with the bilayer before binding. Such a redistribution of water molecules would affect the value of area expansion by molecular binding. In the study of curcumin interaction with membranes (15), we showed that the energy level of the interfacial binding state contained a term proportional to $A_S^2(M_B/L)$ due to the energy cost of membrane thinning (Eq. 2 of ref. 14). It was this term that made the transition of curcumin binding from the interfacial state to another bound state embedded in the hydrocarbon region at high M_B/L's. But for EGCg, the values of A_S is so small that energy level of the interfacial state remains sufficiently low (at least up to E/L∼0.2) compared with the energy level of a potential binding state in the hydrocarbon region. That is why EGCg bound only to the interface and did not show any nonlinear thinning effect.

However, there was no indication in our GUV experiments that EGCg bound exclusively to the outer leaflet of the GUV bilayer, as proposed by Tamba et al. (10). For example, in the experiment with POPC (Fig. 2 a), the initial ΔA/A reached ∼+2%. If there were a 2% area difference between the outer leaflet and inner leaflet, we would have seen an obvious shape change to the GUV (41,42). Yet all the GUVs subject to EGCg binding remained a sphere plus a protrusion during experiment. Many experiments (14,32,43) have demonstrated that molecules bound to the outer leaflet of a GUV redistributed rapidly to the inner leaflet due to the high energy of asymmetric distribution. Tamba et al. proposed that the surface pressure from the asymmetric binding caused the shape changes of the GUVs (10), for example, from sphere to prolate to dumbbell or pearls. But it is well known that such shape changes can also be explained by a change in the area to volume ratio due to the membrane area expansion by the EGCg binding, without invoking bilayer asymmetry (44,45).

EGCg solubilizes lipid molecules from a bilayer but does not form pores

The binding of EGCg to a GUV caused an initial growth of the protrusion length due to the area increase of the vesicle. But within seconds, the protrusion length began to decrease, contrary to the case of curcumin binding to lipid bilayers. There are two possible reasons for the decrease of the protrusion length: either due to a decrease of the GUV surface area and/or due to an increase of the GUV volume. Because we kept the solutions inside and outside of the GUV isotonic, it could not be the volume change. Thus it was the GUV's surface area that had decreased. This implies that EGCg solubilized the lipid molecules from the lipid bilayer of GUVs. Through the comparative studies with pore-forming peptide magainin, we also showed that the solubilization effect of EGCg did not create pores in the bilayer.

The solubilization effect apparently increased with EGCg concentration, as Fig. 2 A shows that the decrease of the protrusion length was faster with higher concentrations of EGCg. However, the rupture of the GUV after the protrusion diminished appeared to be stochastic, not correlated with the concentration of EGCg. It has been shown that the event of GUV rupture is initiated by nucleation of precursor defects in the lipid bilayer, therefore it is a stochastic happening (46,47).

The solubilization effect of EGCg is compared with Triton X100 by their capacities of reducing the turbidity of a vesicle suspension. Fig. 8 shows the attenuation of light passing through three samples, each containing 0.8 mM of DOPC: a lipid vesicle suspension and the same suspension with 10 mM of EGCg or Triton added. Triton diminished the attenuation by two orders of magnitude, whereas EGCg reduced the attenuation by one order of magnitude. Therefore the solubilization effect of EGCg is much less than that of Triton × 100.

Figure 8.

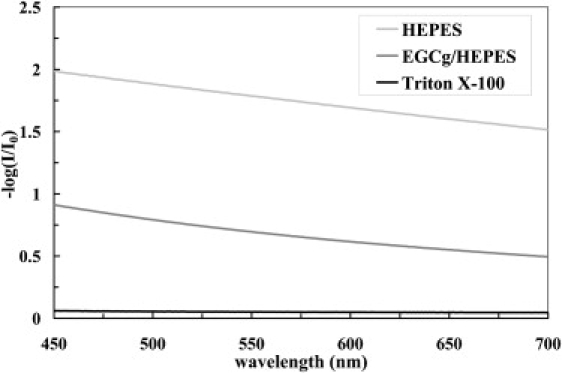
Attenuation of light passing three samples: A vesicle suspension of 0.8 mM DOPC, the same suspension with 10 mM EGCg added, and the same suspension with 10 mM Triton X100 added.

It is not clear what caused the bursting of GUVs observed by Tamba et al. at EGCg concentrations above 30 μM. It could be due to the initial rapid GUV area expansion at high EGCg concentrations or due to the solubilization effect or the combination of both. As observed by Tamba et al. (10), the bursting was a stochastic event—its time of occurrence was not predictable from the time EGCg was introduced.

Partition coefficient

The partition coefficient of EGCg to lipid bilayers has been reported in many prior publications (6,7,10) and were used to correlate with biological activities (8,9). Initially our intention was to quantitatively compare the membrane thinning effect measured by x-ray diffraction with the changes of membrane area measured by GUVs, as we did for curcumin binding (15). For that purpose we would need to know the amount of EGCg bound to the GUV by a calculation based on the partition coefficient.

Although the ITC measurement for the partition coefficient looked normal for each EGCg concentration (Fig. 5), the measured partition coefficients showed a strong dependence on the EGCg concentration. This made the very concept of partition coefficient invalid. We believe that this was due to a greater degree of vesicle aggregation with increasing EGCg concentration that correspondingly decreased the lipid surface area for binding EGCg. The same conclusion was reached by Tamba et al. (10). This calls into question all the previously reported partition coefficients (6,7,10).

Conclusion

Experiments with antimicrobial peptides, curcumin, EGCg and Triton X100 showed that there are many types of membrane-active molecules. Their different characteristics are clarified most effectively by comparative studies. The combination of GUV kinetic experiment with x-ray measurement of the binding effect on membrane thickness has been very successful in revealing the molecular mechanism of membrane-active molecules (14,15). Antimicrobial peptides bind to the interface of membranes, but they make a transition to form stable finite-sized pores in membranes when the concentration exceeds a critical value (14). Curcumin binds to the membranes in two states, first on the interface and then in the hydrocarbon region (15). Triton X100 strongly solubilizes lipid bilayers when its concentration is above its CMC (25,26); but below CMC it incorporates into the lipid bilayers. EGCg binds only to the interface of membranes but also solubilizes the lipid molecules. Its effect of membrane area expansion is one order of magnitude smaller than the similar size curcumin, and its solubilization effect is mild compared with Triton.

EGCg is known to inhibit growth of both Gram-positive and Gram-negative bacteria when added into the bacterial culture medium, and these antibacterial effects were correlated with some measured effects of EGCg on lipid bilayers (2–4,6–9,11). These effects included binding coefficients (6–8), leakage from vesicles (2,3), ³¹P chemical shift and ²H quadrupole splitting by NMR (9) and spin probe parameter by electron paramagnetic resonance (11). Recently Tamba et al. (10) suggested that the bursting of GUVs by EGCg is a possible mechanism for catchins' antibacterial activity. However the GUV bursting was observed only at high EGCg concentrations (>30 μM). The results presented here help clarifying the molecular effect of EGCg on lipid bilayers. We hope that the understanding of the molecular effect of EGCg on lipid bilayers will help clarifying the molecular mechanism of its antibacterial effect.