Microscopic Mechanics of Hairpin DNA Translocation through Synthetic Nanopores

Abstract

Nanoscale pores have proved useful as a means to assay DNA and are actively being developed as the basis of genome sequencing methods. Hairpin DNA (hpDNA), having both double-helical and overhanging coil portions, can be trapped in a nanopore, giving ample time to execute a sequence measurement. In this article, we provide a detailed account of hpDNA interaction with a synthetic nanopore obtained through extensive all-atom molecular dynamics simulations. For synthetic pores with minimum diameters from 1.3 to 2.2 nm, we find that hpDNA can translocate by three modes: unzipping of the double helix and—in two distinct orientations—stretching/distortion of the double helix. Furthermore, each of these modes can be selected by an appropriate choice of the pore size and voltage applied transverse to the membrane. We demonstrate that the presence of hpDNA can dramatically alter the distribution of ions within the pore, substantially affecting the ionic current through it. In experiments and simulations, the ionic current relative to that in the absence of DNA can drop below 10% and rise beyond 200%. Simulations associate the former with the double helix occupying the constriction and the latter with accumulation of DNA that has passed through the constriction.

Introduction

Nanometer-diameter pores in nanometer-thick membranes have proved useful as a means to characterize DNA. In the so-called DNA translocation experiments, electrodes are immersed in electrolytic solution on each side of the membrane, allowing a transmembrane bias to be imposed. When DNA molecules, which are negatively charged, are added to the solution on the negatively biased side of the membrane (the cis side), some molecules are forced through the pore by the electric field and enter the compartment containing the positive electrode (the trans side). As single molecules of nucleic acids pass through the pore, transients in the ionic current through the pore are measured between the electrodes. The duration and magnitude of these transients can be used to determine the translocating molecule's length (1), orientation (2,3), and some details of its nucleotide sequence (4–11). Furthermore, the electric field of the nanopore provides a convenient way to apply force to single DNA molecules and, thereby, nanopores can be used for force spectroscopy experiments (8,12–18).

Hairpin DNA (hpDNA), having both a double-helical portion (stabilized by hydrogen bonds) and an overhanging coil portion, is an exceptionally attractive system for the purposes of nanopore force spectroscopy and DNA sequencing. Using a pore of the appropriate minimum diameter (1.0 < d < 2.5 nm), the double helix can become trapped in the pore with the coil threaded through the constriction. The probability of translocation can therefore be controlled by varying—through adjustment of the transmembrane voltage—the probability of the double helix's rupture, which is required for the translocation. Ashkenasy et al. (9) halted translocation in this way, giving ample time to execute a sequence measurement. Furthermore, Nakane et al. (8) have shown that single nucleotide polymorphisms can be detected by measuring the average time required for unzipping a DNA duplex, while Soni and Meller (10) demonstrated the feasibility of an ultrafast sequencing method in which the DNA sequence is read optically by means of fluorescent markers as the double helix unzips.

The proteinaceous pore α-hemolysin originally was the nanopore of choice for assaying DNA because it has the appropriate dimensions to allow the passage of single-stranded DNA (ssDNA) (13,19,20). Recently, many researchers have focused on synthetic nanopores, which are stable under a wider range of voltage biases, pH values, electrolyte concentrations, and temperatures (10,21–26). Furthermore, synthetic nanopores can be easily integrated into semiconductor devices, suggesting a host of possibilities for sequencing DNA electronically (27–29).

Synthetic pores have another key advantage over biological pores: their geometries can be controlled and optimized. As we demonstrate below, the geometry of the pore strongly affects the conformation of the hpDNA during translocation. Knowledge of the hpDNA's conformation is essential for its use in the DNA sequencing schemes. In this work, we describe the effect of the pore size and transmembrane voltage on the translocation of hpDNA through synthetic pores.

For molecules with heterogeneous structures such as hpDNA, there exist multiple plausible scenarios for how translocation occurs. In simulations of translocation of β-hairpin peptides through α-hemolysin, Goodrich et al. (30) observed different modes of translocation whose occurrence depended on the pore-peptide interaction. Likewise, hpDNA can permeate the pore by different modes, depending on the pore-hpDNA interaction. These modes differ by the orientation of the hpDNA and the pathway by which the double helix transits the pore. Fig. 1 a (see Movie S1 in the Supporting Material) illustrates the mode of translocation prevalent in α-hemolysin, which is also possible in synthetic pores as illustrated in Fig. 1 b (Movie S2). In this mode, translocation begins with the coil threading through the constriction. The portion of the hpDNA initially forming the double helix subsequently passes through the pore by the unzipping pathway, wherein the basepairs are dissociated one by one and only a single strand passes through the pore's constriction. For a synthetic pore with a constriction somewhat larger than that of α-hemolysin, the double helix can pass through the pore by another pathway, which will be referred to as the stretching/distortion pathway because the double helix is elongated and distorted from its original shape (that of canonical B-DNA) while transiting the constriction. As shown in Fig. 1 c (Movie S3), this pathway is typified by the simultaneous presence of two portions of the strand in the constriction and the possibility that some of the hydrogen bonds linking the basepairs are maintained during permeation. Both the unzipping and stretching/distortion pathways have been seen for hpDNA in simulations of synthetic nanopores (31). The translocation of hpDNA oriented such that the loop at the apex of the double-helix transits the constriction first cannot occur by the unzipping pathway because the loop covalently joins the two strands forming the double helix. However, the stretching/distortion pathway allows hpDNA to permeate the pore in the loop-first orientation as illustrated in Fig. 1 d (Movie S4). Note that these modes of translocation are not necessarily exclusive and that alternative mechanisms operating on timescales beyond the reach of molecular dynamics (MD) simulation may also be relevant.

Figure 1.

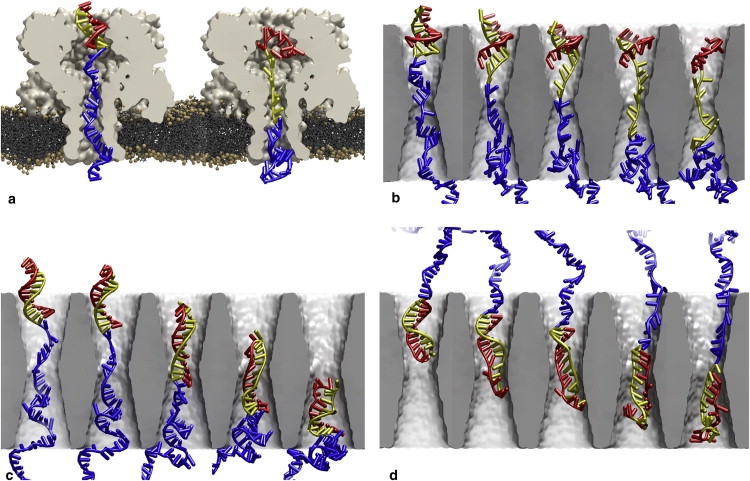
Possible modes of hpDNA translocation through α-hemolysin and synthetic nanopores. In α-hemolysin, hpDNA can permeate only by (a) unzipping in the coil-first orientation. In synthetic pores, hpDNA can translocate by (b) unzipping in the coil-first orientation, (c) stretching/distortion in the coil-first orientation, or (d) stretching/distortion in the loop-first orientation. In all cases, the portion of the hpDNA initially forming the double helices shown in yellow (nearest to the coil) and red, while the portion initially forming the coil is shown in blue. The loop is colored the same as the nearest portion of the double helix. Water molecules and ions are not shown. The snapshots are derived from MD simulations where the transmembrane electric field is oriented upwards.

Details of the molecule's conformation would ideally be determined from ionic current measurements, which have long been used to probe DNA's interaction with a nanopore. However, without the ability to simultaneously image the conformation of hpDNA in a nanopore and measure the current, one cannot develop criteria for inferring changes in the conformation from changes in the current. Here computer simulation can play a role by allowing us to both see the conformation and determine the corresponding ionic current.

Ionic currents >I₀, where I₀ is the ionic current through the pores in the absence of DNA, have been observed (23,32) and were attributed to increases in the ion concentration within the pore due to DNA. While only reductions of the current were seen at high salt concentrations (≥0.5 M) and only enhancements seen at low salt concentrations (≤0.15 M), at a bulk KCl concentration of 0.3 M, Smeets et al. (32) occasionally observed events composed of a current reduction followed by an enhancement. Furthermore, using a smaller pore (<2 nm in diameter), currents <0.1I₀ and >2I₀, due to hpDNA interaction with the pore were observed at a bulk salt concentration of 1 M (31). The observation of both large enhancements and large reductions of ionic current in the same pore at the same bulk ion concentration suggests that whether enhanced or reduced currents are measured can depend on the conformation of the nanopore/DNA system. In this work, we demonstrate that the ion distribution within the pore depends strongly on the conformation of the nanopore/hpDNA system and that ionic currents <0.1I₀ and >2I₀ can indeed be attained by placing the DNA in different conformations within the pore.

The remainder of the article is organized as follows. First, in Methods, we describe the experimental procedures, computational models, and numerical methods used in this study. In Results and Discussion, we present the outcomes of our simulations and relate them to experimental observations. Here we focus first on determining which modes of translocation (as illustrated in Fig. 1), if any, are likely under various conditions and then how the mode of translocation might be inferred from experimentally measurable ionic currents. Finally, in the Conclusions, we discuss how the results of this study might be relevant for future work on DNA translocation through synthetic pores and the development of sequencing devices.

Methods

Our experimental procedures are described below in Experimental Methods. We employed two computational methods, Metropolis Monte Carlo (MC) and classical molecular dynamics (MD), to relate the microscopic behavior of DNA to experimental measurements. The implementations of these methods are elaborated in MC Model and Methods, MD Model, MD Force Field, and MD Methods.

Experimental methods

We used two hpDNA molecules in our experiments: the first was a 150-mer hairpin that consisted of an overhanging coil (50-mer poly-dA) and double helix of 12 basepairs with an intervening 76-nucleotide loop and had the following sequence (the self-complementary parts are underlined): 5′-GCTCTGTTGC TTGGGCGCGT TATTTATCGG AGTTGCAGTT GCGCCCGCGA ACGACATTTA TAATGAACGT GAATTGCTCA ACAGTATGAA GCAACAGAGC AAAAAAAAAAAAAAAAAAAA AAAAAAAAAA AAAAAAAAAA AAAAAAAAAA-3′; the second was a 110-mer hairpin that consisted of a 50-mer poly-dA strand of DNA and a double helix of 10 basepairs with an intervening 6-nucleotide loop and had the following sequence (the self-complementary parts are underlined): 5′-GCTCTGTTGC TCTCTCGCAA CAGAGC ATGA ACG TGAAAAG GTCTACAGTA AAAAAAAAAAAAAAAAAAAA AAAAAAAAAA AAAAAAAAAA AAAAAAAAA GAA TCG CAG TG-3′. The rationale for these designs is described elsewhere (31).

The procedures used to fabricate and characterize the synthetic nanopores in Si₃N₄ membranes used in our experiments are also described elsewhere (31). The nanopores were formed in Si₃N₄ membranes, which had nominal thicknesses of 10 nm. Each membrane including a nanopore was mounted in a membrane transport bi-cell made from acrylic using silicone O-rings coated with polydimethylsiloxane to seal the membrane to the acrylic (with >5 TΩ resistance). The membrane separated two reservoirs in the bi-cell: one with a 140 μL volume on the cis side; and the other with 15 mL volume on the trans side. Each reservoir contained microfiltered and buffered (10 mM Tris, pH 8.0) 1.0 M KCl and a Ag/AgCl electrode that was connected to an Axopatch 200B current amplifier (Molecular Devices, Sunnyvale, CA) used in resistive feedback mode to measure the current. LabVIEW (National Instruments, Austin, TX) software was used to record the electrolytic current at 23.5 ± 1°C and to apply voltages in range of ±5 V. We injected hpDNA, double-stranded DNA (dsDNA), or ssDNA at a concentration of 1 μg/140 μL (or 10¹¹ molecules/μL) into the cis chamber containing the (negative) Ag/AgCl cathode, and then applied a voltage across the membrane, and monitored the current through the pore for 4 h typically. A DAQ card (National Instruments) was used to sample the output of the current amplifier. The signal was filtered with an eight-pole 10 kHz Bessel filter and was sampled at 20 kilosamples/s. For analysis of the long duration events (>10 ms), the data was filtered with an eight-pole 100 Hz Bessel filter and down-sampled to 200 samples/s.

MC model and methods

In the MC simulations, the hpDNA's coil was modeled as an extensible freely jointed chain in 3D with a Kuhn length of 1.6 nm and a stretching modulus of 123.5 k_BT/nm² (33). Analysis of MD simulations of ssDNA in 1.0 M KCl solution showed that 1.6-nm-long segments spanned 2.3 nucleotides. Thus, 0.43 segments represented one nucleotide. Because of its large persistence length (∼50 nm), the double helix of 10 basepairs was modeled to a good approximation as a rigid cylinder with a length of 3.4 nm, which was attached to one end of the freely jointed chain. A Markov chain of states was generated from a random initial conformation by the Metropolis algorithm (34) through the four types of moves discussed by Zhang et al. (33). These moves consisted of 1), rotation of a randomly chosen subchain about the line connecting the ends of the subchain; 2), rotation of the subchain between a randomly chosen vertex and the free end about an arbitrary axis; 3), scaling the length of a randomly chosen segment; and 4), swapping a randomly chosen set of three consecutive nodes with a randomly chosen set of two consecutive nodes. The double helix and coil segments were treated as hard cylinders with diameters of 2.2 nm and 0.8 nm, respectively; hence, conformations for which there was overlap of nonconsecutive segments were rejected. Because our experimental setup contained a high concentration of ions (1.0 M), electrostatic interactions were neglected. The elastic energy was computed as $1/2\sum _{i=1}^{N}Y{\left(\right|{\mathbf{r}}_i-{\mathbf{r}}_{i-1}|-b)}^2$, where Y is the stretching modulus, b is the Kuhn length, and r_i values are the positions of the N + 1 nodes.

MD model

To model the synthetic membranes, two right hexagonal prisms of Si₃N₄, with hexagonal side lengths of 4.56 nm and respective thicknesses of 10.5 and 20.0 nm, were constructed by replication of the β-Si₃N₄ cell (35). The hexagonal surfaces were oriented perpendicular to the z axis. Covalent bonds were assigned to pairs of adjacent Si₃N₄ conforming to hexagonal periodic boundary conditions in the xy plane. To form free surfaces at the top and bottom of the membrane, no periodicity was invoked along the z axis.

Double-cone pores were created in the membranes by the removal of atoms from the structures (35). Each pore had its minimum cross section at the middle of the membrane along z axis and made an angle of γ = 10° with the z axis, which is the geometry suggested by transmission electron microscopy images of real pores at oblique angles (36,37). However, the detailed shape of the pore surface is not known and the presence of irregularities and deviations from a symmetrical double-cone structure could affect the motion of DNA through the pore. To produce the pores, atoms with their centers satisfying

$${\left(\frac{x}{d_x/2+\left|z\right|\text{tan}\left(\gamma \right)}\right)}^2+{\left(\frac{y}{d_y/2+\left|z\right|\text{tan}\left(\gamma \right)}\right)}^2<1$$ (1)

were removed. In the thicker membrane (20.0 nm), a pore having an elliptical cross section was formed with the values d_x = 1.8 nm and d_y = 2.1 nm (pore A). The thinner membrane (10.5 nm) was used to create three axially symmetric pores (d = d_x = d_y) with d = 2.2 nm (pore B), d = 1.6 nm (pore C), and d = 1.3 nm (pore D). The nonzero charge due to the removal of atoms was neutralized by shifting the charges on all nitrogen atoms by an insignificant amount (<2% of the absolute value of a single atom's charge).

A model of an hpDNA molecule was created by grafting a published hpDNA structure (Protein Data Bank code 1QE7) onto a model of dsDNA. Through deletions and base mutations, a strand of the following sequence was generated (complementary portions are underlined): 5′-GCTCTGTTGCTCTCTCGCAACAGAGCA₅₀-3′. At the beginning of the simulations, the complementary portions adopt a double-helical secondary structure and will henceforth be referred to as the double helix. The hpDNA bends back on itself in the region between the complementary portions, which is referred to as the loop. The overhang, comprising 50 adenine bases, will be referred to as the coil. The structure was equilibrated for 0.5 ns in a volume containing TIP3P (38) water molecules and 1.0 M NaCl solution, using a protocol that will be subsequently described. The water and ions were then removed and the hpDNA was combined with the Si₃N₄ pores. For the coil-first simulations, the hpDNA was placed inside the pore using only translations and rotations, while for all other hpDNA simulations the coil portion was mapped along a smooth spline curve to obtain the desired conformation. The dsDNA systems were generated as described by Heng et al. (39).

The combined Si₃N₄/hpDNA systems were solvated in TIP3P water molecules, with the solvent filling the pore and extending ∼8 nm above and below the Si₃N₄ membrane. K⁺ and Cl⁻ ions were added to obtain a 1.0-M KCl solution. Additional K⁺ ions were added to bring the net charge of the systems to zero.

MD force field

The simulations were performed using the AMBER parm94 (40) force field describing nucleic acids, water, and ions. However, because the force field was recently modified to correct spurious irreversible transitions of the α/γ torsions, we repeated some simulations with the new AMBER parmbsc0 force field (41) to determine how the imperfections in the older force field might have affected the results (see Supporting Material for details).

In previous simulations we observed adhesion of ssDNA to the surfaces of pores cut from crystalline Si₃N₄ (35,39), which halted the process of ssDNA translocation. This adhesion was dominated by hydrophobic attraction of the nucleobases to the pore walls and sticking of the charged phosphate groups of DNA to cavities in the surface. Although surfaces of silicon-based pores have not been fully characterized and the composition of the surfaces is dependent on the details of the pore's fabrication (42), relaxation of the surface from the crystalline structure should occur in real pores, resulting in fewer cavities and fewer dangling atoms than are present in the cut crystalline structures (43). It is possible to produce models of relaxed surfaces by annealing in MD simulations (43). Here, we instead used an approach in which an additional force was applied to DNA to effectively reduce the atomic-scale roughness of the pore. While it is not clear that the addition of this DNA-specific force substantially improved the realism of the interaction between the pore surface and the DNA, it permitted translocation of DNA in the coil conformation to be observed.

The custom force field describing crystalline Si₃N₄ was divided into three parts: electrostatic and van der Waals forces, restraint forces, and the DNA-specific interaction that effectively reduced the surface roughness. The van der Waals parameters and charges were taken from Heng et al. (39) and Wendel and Goddard (44). Next, to obtain a relative permittivity of 7.5, harmonic restraints with a force constant of 695 pN/nm were applied to bulk Si₃N₄ atoms and harmonic bonds with a force constant of 3470 pN/nm were applied between neighboring atoms (39). Similar restraint forces were applied to surface atoms, except with force constants of 6950 pN/nm. The third portion of the force field was a DNA-specific interaction. The latter was introduced by adding the repulsive radial term to the force on atom i of the DNA due to Si₃N₄ atom j,

$${\mathbf{F}}_{ij}^{\text{surf}}=\{\begin{array}{ll}{F}_0{\mathbf{e}}_{ij}\hfill & \text{if}{r}_{ij}\le R\hfill \\ F_0(1-(r_{ij}-R)/\sigma ){\mathbf{e}}_{ij}\hfill & \text{if}R<r_{ij}<R+\sigma \hfill \\ \mathbf{0}\hfill & \text{otherwise}\hfill \end{array},$$ (2)

where r_ij is the distance between the atoms i and j and e_ij is the unit vector from atom j to atom i. The parameters R, σ, and F₀ describe the distance within which the force is constant, the distance over which the force drops linearly to zero, and the scale of the force, respectively. We find that values R = 0.18 nm, σ = 0.16 nm, and F₀ = 139 pN obtain the desired result, i.e., translocation of ssDNA occurs within the timescales accessible to our simulations and the threshold voltage for the translocation of dsDNA remains within the same range as for the unmodified pore. The choice of R and σ implies that the DNA-specific force is applied primarily to hydrogen atoms because the repulsive portion of the van der Waals potential discourages larger atoms from entering the range where the DNA-specific force is significant. The DNA-specific force could reduce the effective diameter of the pores by as much as 0.2 nm; the relationship between the pore diameter and translocation of mode of hpDNA described later in this work should be interpreted with this in mind.

The DNA-specific force is implemented by sampling the potential energy due to this force term from the Si₃N₄ atoms in their equilibrium positions onto a uniform grid. During the simulation, the DNA-specific force is applied using the grid-steered molecular dynamics techniques (45) recently implemented in NAMD (46). The use of a static grid is justified in that the atoms on the surface of the pore deviate little from their equilibrium positions.

MD methods

The all-atom MD simulations described herein were performed using the program NAMD2 (46). In all simulations, hexagonal prism periodic boundary conditions were applied and nonbonded energies were calculated using particle mesh Ewald full electrostatics (47) (grid spacing < 0.15 nm) and a smooth (1.0–1.2 nm) cutoff of the van der Waals energy. Each hpDNA system underwent 2000 steps of energy minimization, 2 ps of equilibration at fixed volume during which time the temperature rose from 0 to 295 K by rescaling of velocities, and 600 ps using Nosé-Hoover Langevin piston pressure control (48). In the last stage, the volume of each system fluctuated at an approximate fixed value at a pressure of 1.0 atm after ∼400 ps and Langevin dynamics (applied to nonhydrogen atoms) with a damping constant of 5 ps⁻¹ maintained a temperature of 295 K.

All production simulations, for both dsDNA and hpDNA, were performed at fixed volume with the temperature maintained by Langevin dynamics applied only to the atoms of the Si₃N₄ with a damping constant of 1.0 ps⁻¹. A constant electric field was applied to produce the desired transmembrane voltage across the system. Ionic currents were computed from the simulated trajectories by (49)

$$I(t+\Delta t/2)=\frac{1}{\Delta t{l}_z}\sum _{i=1}^N{q}_i(z_i(t+\Delta t)-z_i\left(t\right)),$$ (3)

where z_i and q_i are, respectively, the z coordinate and charge of ion i, N is the total number of ions, l_z is the length simulated system along the z axis, and Δt = 5 ps is the time between trajectory frames. The interval z_i(t + Δt) − z_i(t) was computed respecting the periodic boundary conditions.

Results and Discussion

First, we describe experiments that led us to probe the hpDNA-nanopore interaction through simulations. Second, we investigate possible conformations in which hpDNA can encounter a nanopore. After that, we determine how the mode of hpDNA translocation depends on pore geometry and transmembrane bias. Finally, we discuss what experimentally measurable ionic current can reveal about the conformation of hpDNA in a nanopore.

Experimental measurements of hpDNA–nanopore interactions

We have previously reported (31) the observation of a threshold voltage for translocation of hpDNA that depends sensitively on the pore diameter. We also reported finding transients in the electrolytic current through the pore in the presence of hpDNA. These transients, some with a very long duration (>1 s), were superimposed on the open pore electrolytic current and associated with a molecule or molecules of hpDNA interacting with the pore. Here we report on experiments in the same Si₃N₄ pores that show multiple recurring levels of the current transients, which we ascribe to nanopore/hpDNA conformations.

Fig. 2 relates a series of observations made using three separate pores with cross sections of 0.8 nm × 1.0 nm, 1.2 nm × 1.4 nm, and 1.9 nm × 2.0 nm ± 0.2 nm through membranes that were nominally 10-nm-thick, which initially motivated our experimental work. Fig. 2 a shows a transmission electron micrograph of the 1.9-nm × 2.0-nm pore along with gel arrays comprised of horizontal lanes with bands indicating the permeability of 105-mer ssDNA, 150-mer hpDNA, 110-mer hpDNA, and 105-basepair dsDNA through it as a function of the transmembrane voltage, ϕ. The fluorescent bands in the figure indicate that DNA is collected at the positive electrode, which implies that the molecule translocates across the membrane through the pore (24,31,50). Apparently, 105-mer ssDNA permeates the pore at very low voltage (ϕ > 0.5 V), while dsDNA only permeates through the same pore for ϕ >3.00 V. We have previously described these phenomena (39). While ssDNA can permeate through pores as small as 1 nm in diameter at low field, dsDNA is sterically inhibited when the pore diameter is <3 nm. On the other hand, dsDNA can permeate a pore <3 nm in diameter if the electric field exceeds a threshold value, which corresponds to the force gradient inside the pore required to stretch the leading nucleotides in the double helix according to MD simulations.

Figure 2.

Experimental determination of threshold voltage. (a) (Left) A transmission electron micrograph of a 1.9-nm × 2.0-nm pore in a nominally 10-nm-thick nitride membrane. The shot noise in the center of the images is associated with the pore. (Right) Gel arrays indicating the voltage at which 105-mer ssDNA, 150-mer hpDNA (12-basepair double helix with a 76-basepair loop), 110-mer hpDNA (10-basepair double helix with a six-basepair loop), and 105-basepair dsDNA permeate the pore. NC and PC indicate the negative and positive control samples taken from the same solutions used in the anode and cathode chambers. For reference, a 100-basepair ladder is shown in the top lane of each gel. We find that ssDNA permeates the pore for voltages ϕ > 0.5 V, while 105-basepair dsDNA permeates the pore only for voltages ϕ > 3.0 V. The hairpins permeate at voltages intermediate to these: 150-mer hpDNA permeates the same pore for ϕ > 2.0 V and 110-mer hpDNA for ϕ > 2.5 V. (b and c) High resolution transmission electron micrographs of 0.8-nm × 1.0-nm, and 1.2-nm × 1.4-nm pores through Si₃N₄ membranes nominally 10-nm-thick, respectively. The gel arrays next to each micrograph contain horizontal lanes with bands indicating the voltage, ϕ, at which 150-mer hpDNA permeates the pore. For reference, a 100-basepair ladder is shown in the top lane of each gel. The negative control is represented by the 0-V lanes. The 150-mer hpDNA permeates the 1-nm pore at low voltage ϕ > 0.25 V, but only permeates the 1.4-nm pore for ϕ > 1.5 V. Thus, the threshold depends on the pore diameter.

The double helix of hpDNA confronts a similar dilemma. If the pore diameter is smaller than the cross section of the double helix, then it cannot easily translocate at low field. The gels in Fig. 2 a also show that hpDNA with a 76-mer loop permeate the 2-nm pore only for ϕ > 2.0 V, while the hpDNA with a 6-mer loop permeates the same pore only for ϕ > 2.5 V. Calculations indicate that the 76-mer loop is more stable (31) than the 6-mer loop. So apparently, the threshold voltage is not a measure of molecular stability alone. Rather, the more flexibility or disorder in the loop, the deeper it penetrates into the pore and the lower the voltage threshold.

The threshold seems to depend on the pore diameter too. Fig. 2, b and c, epitomizes experimental work presented elsewhere (31) with hpDNA in Si₃N₄ nanopores with cross sections of 0.8 nm × 1.0 nm and 1.2 nm × 1.4 nm, respectively. Fig. 2 b shows a transmission electron micrograph of a 0.8-nm × 1.0-nm pore and the corresponding gel array comprised of eight horizontal lanes with bands indicating the permeability of 150-mer hpDNA through the pore as a function of ϕ. We find that the 150-mer hpDNA permeated the 1-nm pore only for ϕ ≥ 0.25 V. On the other hand, the threshold for pore diameters in the range 1.4 < d < 2.3 nm is ϕ > 1.5 V, which corresponds to the force required to stretch the double helix of the hpDNA according to molecular dynamics simulations (31). Fig. 2 c shows a transmission electron micrograph of a 1.2-nm × 1.4-nm pore and the corresponding gel array indicating that 150-mer hpDNA permeates the pore for ϕ > 1.5 V.

Associated with interactions with the hpDNA, we observe transients in the electrolytic current through the pore. Fig. 3, a–d, illustrates some of the variety of current transients observed in the 1.2-nm × 1.4-nm pore for a voltage bias below threshold. We observe both blockades of the current as well as current enhancements of greater than twice the open pore current value. In particular, Fig. 3, b and c, shows current enhancements >5.5 nA, above the open pore current of ∼I₀ = 2.6 nA. These events can be short-lived; occurring for only milliseconds as illustrated in Fig. 3 c, but we also observed extraordinarily long duration transients (>1 s) in the electrolytic current through the pore. These transients are easily resolved from the electronic noise (as indicated by the red traces shown in Fig. 3 a, but the narrow bandwidth (10 kHz) of the nanopore mechanism combined with the current amplifier precludes the observation of events shorter than 10-100 μs. The duration of these events may represent an extended residence time of one or more of the hpDNA molecules over the pore that terminates either through translocation across the membrane through the pore or with the hpDNA uneventfully exiting the pore due to thermal agitation. For voltages below the threshold, the latter is more likely.

Figure 3.

Experimental measurement of ionic current. (a) The electrolytic current through the 1.2-nm × 1.4-nm pore shown in Fig. 2c as a function of time with the membrane voltage at ϕ = 0.5 V. The open pore current, I₀, at this voltage is ∼0.9 nA (dotted line). Also shown (shaded) is the current through the pore with no DNA at ϕ = 0.25 and 0.5 V. (b) The electrolytic current through the same pore as a function of time with the membrane voltage at ϕ = 1.5 V (below the threshold) illustrating current enhancement above the open pore current and blockades. The open pore current, I₀, at this voltage is ∼2.6 nA (dotted line). (c) The same trace as panel b expanded ∼5.76 s to reveal current enhancement and current blockades occurring on a millisecond timescale. (d) The electrolytic current measured at ϕ = 1.5 V through the same pore over a longer timescale illustrating the long duration of the current transients and the persistence of the levels. (e) A histogram showing the frequency of values of the current observed over the 12-s interval shown in panel c. The shaded background is amplified ×25 to illustrate the frequency of current enhancements at twice the open pore current. For reference, arrows are shown at 4.33, 1.93, and 0.87 nA top to bottom.

We hypothesize that the current transients are caused by hpDNA molecules modulating the current through the pore. According to this hypothesis, the modulation depends on the molecular configuration in or near the pore. We followed the pore current flowing through the 1.2-nm × 1.4-nm pore for ∼4 h and observed some familiar and some new features, but generally found long duration current transients both above and below the open pore value. Fig. 3 e is a histogram that tallies the values of the current observed over the 12 s interval, including the data shown in Fig. 3, b–d. The salient features are: current blockades that peak near 900 pA and 1.9 nA, along with current enhancements, which peak near 4.3 nA but range to >200% of the open pore value of 2.6 nA. The histogram reflects the observation that the current through the pore assumes well-defined levels for extended periods of time and some of these recur over time with approximately the same value.

Orientation of hpDNA at the onset of translocation

Before we could simulate translocation of hpDNA, we needed to determine in which orientation, if either, hpDNA is most likely to encounter the nanopore. Because the electric field decreases rapidly away from the pore's constriction (39), the timescale associated with a translocation of hpDNA starting from a random conformation a few nanometers away from the pore opening is beyond the reach of all-atom MD simulations. We were thus unable to directly sample the respective probabilities of coil- and loop-first translocation using this method. Instead, we performed both all-atom MD and MC simulations to determine the likely conformations of the hpDNA as it approached the pore.

With a sufficiently long coil, the double helix is surrounded by a cloud of coil DNA, making arrival in the loop-first orientation unlikely. Thus, for a double helix of fixed length, increasing the length of the coil should increase the probability of arriving in the coil-first orientation. On the other hand, both orientations should be nearly equally likely for a sufficiently short coil. To determine whether the probability of loop-first translocation was at all significant for systems similar to ours, we performed MC simulations using a rigid double helix of fixed length and a freely jointed and extensible coil of 25, 50, or 100 nucleotides. Fig. 4, a–c shows typical conformations generated by the MC procedure. The potential energies of the systems were seen to fluctuate at an approximate mean value of $\sim k_{\text{B}}T/2$ per nucleotide after fewer than 5000 MC steps. To ensure that the systems were properly equilibrated, analysis of hpDNA conformations was performed excluding the first 10,000 MC steps.

Figure 4.

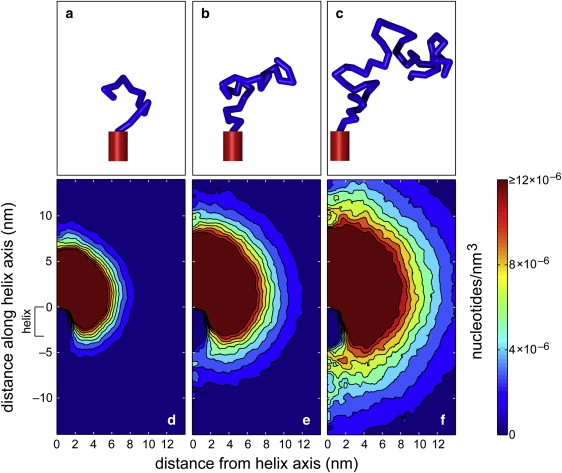
Conformational statistics of hpDNA. (a–c) Typical conformations generated by a Monte Carlo procedure for hpDNA with a coil of 25 (a), 50 (b), or 100 (c) nucleotides attached to a double helix of 10 basepairs. (d–f) The density of nucleotides averaged over 90,000 three-dimensional conformations of hpDNA with the three different coil lengths shown as a function of the distance from the axis of the double helix and the distance along the axis of the double helix. The position of the double helix is indicated at the left.

Fig. 4, d–f, shows the density of nucleotides averaged about the axis of the double helix for 90,000 MC steps. For a coil of 25 nucleotides, there is a significant probability that no portion of the coil extends below the loop of the double helix as seen in Fig. 4 d. Thus, the double helix is often exposed and there is a significant probability that it reaches the membrane before any portion of the coil. This probability decreases as the length of the coil increases. As shown in Fig. 4 f, the density of nucleotides shielding the bottom of the double helix is much larger for a coil of 100 nucleotides than for the two shorter coils.

To get an idea of the likelihood that the hpDNA arrives at the pore in the loop-first orientation, we computed the fraction of MC-generated conformations in which the double helix was closer to the membrane than any part of the coil. The membrane was considered to be a plane at a large distance from the hpDNA with a randomly oriented normal chosen from a spherically symmetric distribution. The fractions of conformations in which the double helix was closest to the membrane were 0.36 ± 0.01, 0.28 ± 0.01, and 0.20 ± 0.01 for coils of 25, 50, and 100 nucleotides, respectively. Thus, the MC simulations suggested that reaching the pore in the loop-first orientation had a significant probability.

Furthermore, all-atom MD simulations implied that the MC simulations might have underestimated the probability of hpDNA arriving at the pore mouth loop-first. Simulations performed in 1.0-M KCl solution without a pore or membrane showed that instead of acting as a freely jointed chain, the coil had a disordered but relatively compact secondary structure due to interactions between the nucleotides. Hence, for a coil length of 50 nucleotides, we consider both orientations as plausible initial states for hpDNA translocation.

Threshold voltage for DNA translocation

We have previously reported on experiments and MD simulations demonstrating the existence of a threshold voltage for translocation of dsDNA through synthetic nanopores <2.5 nm in diameter (39). At the same time, ssDNA was found to permeate through all pores at all voltage biases probed (≥120 mV) (24,39). Because hpDNA contains a double-helical fragment, one could expect that a threshold voltage for hpDNA translocation would also exist in pores with constrictions <2.5 nm. Indeed, threshold voltages were experimentally observed for hpDNA (31). The orientation of hpDNA at the threshold and the origin of the threshold reduction in comparison to dsDNA were not resolved.

To determine a threshold voltage using the MD method, a DNA molecule was placed near the opening of the pore. Transmembrane biases of various magnitudes were imposed and the subsequent translocation or lack thereof was observed. Note that the transmembrane voltages applied in our simulations (see below) are in the range of those applied in experiments (31,39,51). Furthermore, translocation times approximately a few tens of nanoseconds are consistent with experiment. Fologea et al. (25) reported a translocation velocity of ∼3 basepairs/(100 ns) at 120 mV in synthetic nanopores. The velocity is expected to grow faster than linearly with the transmembrane voltage for the DNA lengths considered here (52); thus, the velocities seen in our simulations, which generally increase with pore size and transmembrane voltage, do not disagree with experiments. For example, in the 1.8-nm × 2.2-nm pore, we observe translocation at 1 basepair/(7.3 ns) and 10 basepairs/(3.9 ns) at transmembrane voltages of 2.0 and 3.0 V, respectively.

Threshold voltage for dsDNA

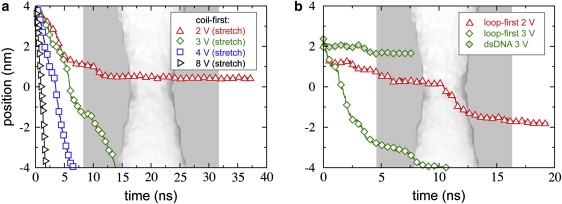
Fig. 5 a shows the center of mass of the two nucleotides at the leading edge of a dsDNA molecule as a function of time for simulations performed at the indicated transmembrane voltages ϕ. The pore used here had a minimum elliptical cross section of 1.8 nm × 2.2 nm and resided in a 20.0-nm-thick membrane (pore A). The molecule translocated rapidly at ϕ = 6.0 and 5.0 V, with the leading end passing through the constriction (at z = 0) in <4 ns. Reducing the voltage to 4.0 V caused a dramatic decrease in the rate of motion. Finally, at ϕ = 3.0 V, the molecule stalled near z = 3.1 nm, where the cross section of the pore is 2.2 nm × 2.6 nm. As indicated by the slight rise in the trace at ∼6 ns, the free end of the molecule eventually bent back on itself, making deeper permeation of the molecule even less likely. As permeation occurred at 5.0 V, but not at 3.0 V, we predict that the threshold voltage for translocation of dsDNA lies between 3.0 and 5.0 V for this pore.

Figure 5.

Threshold voltages for dsDNA and hpDNA translocation. (a–c) The position of the leading edge of dsDNA (a) or hpDNA in the coil-first (b) or the loop-first (c) orientation as a function of time for the indicated transmembrane voltages. The pore has a minimum elliptical cross section of 1.8 nm × 2.2 nm and resides in a 20.0-nm-thick membrane (pore A). The initial conformation of each system is shown to the right of the plots. The background image of the pore faithfully overlays each plot.

Threshold voltage for hpDNA in the coil-first orientation

The center of mass of the nucleotide in the double helix adjacent to the coil is plotted as a function of time in Fig. 5 b. First, we see that the hpDNA translocated at ϕ = 3.0, 2.0, and 1.5 V, implying that the threshold voltage is less for hpDNA than for dsDNA, in agreement with experiments (31). Permeation did not occur at 1.0 V; hence, we estimate the threshold to be between 1.0 and 1.5 V. The motion hpDNA through the pore at the higher voltages is qualitatively distinct from that at lower voltages. At ϕ = 3.0, 4.0, and 6.0 V, the hpDNA moves more or less continuously, while at ϕ = 1.0, 1.5, and 2.0 V there are pauses separated by relatively rapid advances.

While one might assume that the behavior of hpDNA in synthetic pores is similar to that in α-hemolysin as long as the constriction is small enough not to admit the double helix, we find that the behavior in synthetic pores can be qualitatively different. In all simulations of pore A, hpDNA permeated the pore by the stretching/distortion pathway, as in Fig. 1 c; the unzipping pathway taken in the α-hemolysin system (Fig. 1 a) was not observed. Furthermore, in contrast to when the unzipping pathway is taken, a number of basepairs in the double helix remained intact at the end of the translocation. Exactly two basepairs (out of 10) dissociated at 1.0, 1.5, 2.0, and 3.0 V. The first basepair to break was the one initially nearest to the constriction (farthest from the loop). The second basepair to dissociate was 1–3 basepairs away from the first. More basepairs dissociated at larger voltages: four and six at 4.0 and 6.0 V, respectively. In no case did the two bases nearest the loop dissociate.

Threshold voltage for hpDNA in the loop-first orientation

Furthermore, we find that translocation is also possible when the loop of the hpDNA leads, which is illustrated in Fig. 1 d. Fig. 5 c shows the center of mass of the two bases at the apex of the loop as a function of time at ϕ = 1.0, 1.5, 2.0, 2.5, 3.0, and 4.0 V. As in the coil-first orientation, permeation occurred at all ϕ except 1.0 V and hence the threshold voltage was estimated to lie between 1.0 and 1.5 V. Fewer basepairs dissociated in the loop-first orientation than in the coil-first orientation. None were broken at 1.0 V. Only the basepair adjacent to the loop dissociated at 1.5, 2.0, and 3.0 V. Three dissociated at 2.5 and 4.0 V. Thus, it seems that dissociation of the leading basepairs is more likely than the dissociation of those on the trailing end of the molecule, irrespective of the orientation.

Within the resolution of our simulations, we could not determine whether the coil-first orientation or loop-first orientation had a lower threshold for permeation through pore A. Any difference in the threshold between the two orientations was not substantial compared to that between dsDNA and hpDNA in either orientation. Note that the threshold voltage predicted by the simulations may not exactly correspond to that of the experiments on the 150-mer hpDNA due to the difference in the structure of the hpDNA. Experiments have been performed using both the hpDNA with the six-nucleotide loop similar to our computational model and the hpDNA with the 76-nucleotide loop (31). A larger voltage was required for permeation of the molecule with the shorter loop (ϕ > 2.5 V) than for permeation of the molecule with the longer loop (ϕ > 2.0 V).

As for the difference in the threshold voltage between dsDNA and hpDNA, our simulations provide the following explanation. As the double helix travels along the pore axis, its leading end eventually reaches a critical position where the diameter of the pore is ∼2.5 nm. At this point, the double-helical structure must be disrupted for hpDNA to proceed further. In both orientations, hpDNA extends deeper (due to either the loop or the coil) into the pore at this position than dsDNA. The electric field within a double-cone pore rises sharply to its maximum value near the constriction (39); hence, a greater electrostatic force is applied to hpDNA than to dsDNA at the same transmembrane bias. Therefore, translocation of hpDNA can occur at a lower transmembrane voltage than for dsDNA.

Effects of pore diameter on the translocation process

To determine the influence of the pore diameter on the translocation process, we performed simulations of hpDNA in both orientations in three pores: 1.3, 1.6, and 2.2 nm in diameter; the length of these pores was 10.5 nm. For each pore, different orientations and transmembrane biases were tested, revealing a variety of outcomes.

2.2-nm-diameter pore

Fig. 6 illustrates the trajectories of hpDNA in the pore with a constriction of 2.2 nm (pore B). For this pore, we observe translocation only by the stretching/distortion pathway. We find, however, that loop-first translocation occurs at a transmembrane voltage of 2.0 V while hpDNA in the coil-first orientation stalls at the same transmembrane voltage. These simulations suggest that at ϕ = 2.0 V, translocation of hpDNA through this pore can occur only in the loop-first orientation. Fig. 7 a shows a typical conformation of the double helix while passing through the constriction in this pore. The bases near the constriction make an angle of ∼50° with the pore axis and many of the basepairs do not dissociate. The bases assume a similar conformation when hpDNA translocates through this pore in the loop-first orientation.

Figure 6.

hpDNA in a 2.2-nm-diameter pore (pore B). (a) The position of the leading edge of the double helix of the hpDNA introduced in the coil-first orientation as a function of time for the indicated transmembrane voltages. (b) The position of the leading edge of the hpDNA in the loop-first orientation or dsDNA as a function of time. The background image of the pore faithfully overlays each plot. In all cases, the membrane has a thickness of 10.5 nm.

Figure 7.

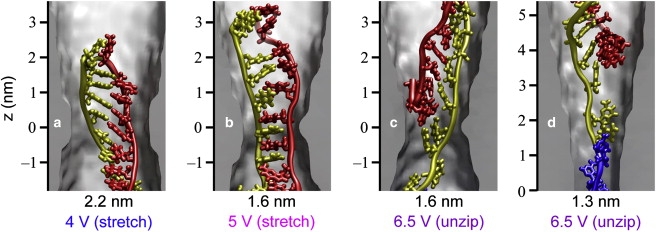
Possible conformations of hpDNA during translocation. (a) Conformation of the bases as the double helix passes by stretching/distortion through the 2.2-nm pore. (b) Conformation of the bases as the double helix passes by stretching/distortion through the 1.6-nm pore. Note the difference between the conformation here and that in panel a. (c) Conformation of the bases as the double helix unzips in the 1.6-nm pore. Note the difference in the orientation of the bases as compared to the stretching/distortion pathway. (d) Conformation of the bases as the double helix unzips in the 1.3-nm pore.

1.6-nm-diameter pore

Fig. 8 a plots the position of the leading edge of hpDNA in the coil-first orientation (pore C). In this pore, we observed a striking change in behavior for the coil-first orientation. At ϕ = 4.0 or 5.0 V, the two portions of the strand pass through the constriction simultaneously, as shown in Fig. 7 b. However, at ϕ = 6.5 or 8.0 V, translocation occurs by the unzipping pathway. The double helix begins to unzip above the constriction and passes through it having only a single portion of the strand at one time (Fig. 7 c). The bases make a smaller angle with the pore axis (<30°) during unzipping than they do during stretching/distortion. Note that three simulations were performed at 6.5 V using different initial conditions and that in each a similar unzipping process was observed.

Figure 8.

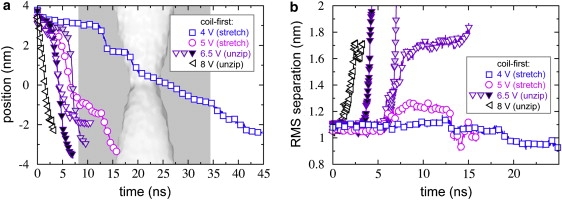
hpDNA in a 1.6-nm-diameter pore (pore C). (a) The position of the leading edge of the double helix of the hpDNA introduced in the coil-first orientation as a function of time for the indicated transmembrane voltages. (b) Root mean-square distance between C1′ atoms of initially paired nucleotides.

To contrast the unzipping pathway with the stretching/distortion pathway, in Fig. 8 b we plot the root mean-square (RMS) distance between the C1′ atoms of initially paired nucleotides for the trajectories shown in Fig. 8 a. At ϕ = 4.0 V, only the leading basepair unzipped before reaching the pore constriction, causing the small rise in the trace near t = 12.5 ns. The remaining basepairs did not dissociate until they neared the constriction, where the bases were forced to interleave as illustrated in Fig. 7 b. In this interleaved conformation, the initially paired portions of the strand were forced closer together than in the double helix, which is why the RMS separation eventually drops below its initial value in Fig. 8 b. The situation at ϕ = 5.0 V was nearly identical, except that after the leading basepair dissociated, the newly freed portion of the strand bent back on itself, causing the rise in the trace between 5.0 and 12.5 ns. After this portion passed through the constriction, the molecule adopted the interleaved conformation much like at 4.0 V. In contrast, at ϕ ≥ 6.5 V, the 5′-end of the molecule never reached the constriction, but remained nearly fixed as the complementary portion of the strand moved through the constriction (Fig. 7 c). Unzipping of the double helix is reflected by the rapid rise in the RMS separation (Fig. 8 b). Before unzipping, each basepair was observed to tilt with respect to the pore axis. When the angle between the basepair and the pore axis reduced to ∼30°, dissociation of the basepairs was observed, which is analogous to the process of DNA melting during the overstretched transition (53).

Neither hpDNA in the loop-first orientation nor dsDNA translocates through the 1.6-nm-diameter pore at 4.0 V (Fig. S2). Hence, it might be possible to select the coil-first orientation over the loop-first orientation, which is the opposite of what was observed for the 2.2-nm-diameter pore. In contrast to the larger pore, we found that all basepairs must dissociate to pass the 1.6-nm constriction, regardless of the translocation pathway. While, for convenience, we refer to all situations in which two portions of the strand simultaneously pass through the constriction as the stretching/distortion pathway, one should note that the conformation of the bases for this pathway in a constriction of 1.6 nm (Fig. 7 b) is distinct from that in a constriction of 2.2 nm (Fig. 7 a).

1.3-nm-diameter pore

Finally, in the 1.3-nm-diameter pore (pore D), translocation of hpDNA took place only in the coil-first orientation by the unzipping pathway at ϕ = 6.5 V (Fig. S3). The manner of unzipping, as illustrated in Fig. 7 d, was similar to that with the constriction of 1.6 nm except that it occurred farther from the constriction. Due to the limited timescales accessible to all-atom MD simulations, the threshold voltage for hpDNA in the coil-first orientation could not be determined in this pore. At ϕ = 13.0 V, hpDNA in the loop-first orientation was able to permeate. We note, however, that this transmembrane voltage is much higher than those typically used in experiment.

Modes of hpDNA translocation

Fig. 9 shows diagrammatically which hpDNA translocation modes are likely to occur as a function of the transmembrane voltage and constriction size. We observe that either the unzipping or stretching/distortion pathway occurs for given parameter values, but not both. For instance, for the 1.6-nm pore, only the unzipping pathway was observed for the three simulations with different initial conditions at 6.5 V, while only the stretching/distortion pathway was observed for the simulations at 4.0 and 5.0 V, which also had different initial conditions. In the coil-first orientation, translocation can occur by unzipping, stretching/distortion, or not at all, while in the loop-first orientation, translocation occurs either by stretching/distortion or not at all. There are then six possible scenarios when the behavior in both orientations is considered. Surprisingly, we find that all six occur for some parameter values. The complexity of the diagram is a consequence of the fact that the pore geometry affects both the electric field near the pore and the steric constraints on the molecule. As the constriction becomes larger, the electric field profile along the pore axis changes more smoothly, while the double helix can penetrate more deeply without being distorted. These two effects act to produce the strikingly different behavior observed across pores of different geometries.

Figure 9.

Diagram of translocation modes. The diagram indicates which hpDNA translocation modes occur, on average, as a function of the transmembrane voltage and constriction size of a double-cone pore in a 10.5-nm-thick membrane. The circles show points that have been probed by MD simulations. The positions of the curves delineating the various regions are approximate.

In Fig. 9, the dashed curve separates the region where coil-first translocation is possible from that where it is not, while the dotted curves do likewise for loop-first translocation. Clearly, for sufficiently small pores or sufficiently low transmembrane voltages, translocation will not occur in either orientation. At sufficiently large voltages, it is possible to force hpDNA through pores with constrictions ≥1.3 nm in both orientations; thus, we find regions at the top of the diagram where both coil- and loop-first translocation were observed.

In our simulations of a 2.2-nm-diameter pore (pore B), we found that permeation in the loop-first orientation occurred at 2.0 V, while it did not in the coil-first orientation. Hence, we predict the existence of a region in the lower right of the diagram where translocation can proceed only in the loop-first orientation. This region appears to exist because the linear charge density of the loop along the pore axis is higher than that of the rest of the molecule. For large pores, the double helix can nearly reach the constriction without being stretched, so the force on the intact hpDNA is largest when the loop leads and is in the region where the electric field is relatively high. However, for smaller pores, the loop cannot extend into the region where the electric field is highest while the double helix is intact. A sufficiently long coil, however, can extend all the way through the constriction and the force is highest when this occurs. Thus, the simulations for constrictions of 1.6 and 1.3 nm showed only coil-first permeation below 4.0 and 6.5 V, respectively. However, the preference of the coil-first orientation over the loop-first orientation should depend on the length of the loop, likely reducing the threshold voltage in the loop-first orientation for molecules with longer loops and expanding the region of the diagram where loop-first translocation is possible.

Furthermore, the force at which the overstretching transition occurs for B-DNA depends on the sequence (54); thus, it is likely that altering the sequence would change the position of the curves on the diagram.

The shaded curve in Fig. 9 separates regions where unzipping of the double helix was observed from those where the stretching/distortion of double helix was observed. Clearly smaller pores should disfavor the stretching/distortion pathway, because the passage of two portions of the strand through the constriction simultaneously becomes more difficult. In accord with this, we observed only the unzipping pathway with the constriction of 1.3 nm. On the other hand, only the stretching/distortion pathway was seen with a constriction of 2.2 nm. The bias toward this pathway might be expected because basepairs need not be dissociated for translocation through a constriction of 2.2 nm. Thus, the energy cost for translocation by stretching/distortion could be less than that for unzipping, since all basepairs must dissociate in the latter case. The location of the turnover from unzipping to stretching/distortion could then be sequence-dependent because more energy is required to dissociate C·G pairs than to dissociate A·T pairs. The constriction of 1.6 nm appears to be an intermediate case where the pathway shows a dependence on the transmembrane voltage: unzipping was observed at 6.5 V and above and stretching/distortion at 5.0 V and below. Experiments have shown a large decrease in the threshold voltage for translocation from pores with constrictions of 2.2 nm to those with constrictions of 1.3 nm (31). However, due to the timescales accessible to our simulations, we have been unable to determine the threshold voltage for a pore with a 1.3-nm constriction.

Our results are consistent with previous simulations (31) in which hpDNA was driven through the pore by applying an external force directly to the coil rather than by applying an external electrostatic field to the system. In the previous work, the unzipping pathway was observed in pores having constrictions <1.6 nm, while the stretching/distortion pathway occurred in larger pores. However, due to the way the force was applied in the previous work, dependence of the pathway on the transmembrane voltage, as seen here for the 1.6-nm-diameter pore, could not be determined.

The modes of translocation described here are only those that can be observed in the timescales amenable to simulation. We cannot rule out alternative mechanisms that occur on longer timescales, such as spontaneous thermal unzipping of the double helix. Thus, when we suggest that translocation does not occur for particular parameter values, we are not excluding translocation by these alternative mechanisms. However, quantitative polymerase chain reaction analyses (31) show a threshold voltage for permeation of hpDNA below which the number of molecules that translocate through the pore falls dramatically to a noise-limited detection threshold of N molecules, suggesting that translocations due to mechanisms such as thermal unzipping do not predominate for nanopores fabricated as described.

Ionic current

The presence of hpDNA within the pore changes its conductivity and causes a departure of the ionic current from its open pore value I₀. To relate the microscopic conformation of hpDNA to the level of the ionic current, the latter was computed using a standard method (49) for all simulations performed. The results allowed us to associate particular values of the relative current I(ϕ, r_i)/I₀(ϕ) with the microscopic conformation of the hpDNA. For all pores considered, I₀ was found to scale approximately linearly with the transmembrane bias ϕ. Hence, simulations performed under different transmembrane voltages could be compared. Typical values of the open pore currents are given in Table 1.

Table 1.

Open pore currents

Pore	deff (nm)	Lpore (nm)	ϕ (V)	I0 (nA)	G0 (nS)	Origin
A	2.0	20.0	4.00	5.81 ± 0.08	1.45 ± 0.02	sim
B	2.2	10.5	4.00	8.52 ± 0.13	2.13 ± 0.03	sim
C	1.6	10.5	4.00	5.10 ± 0.14	1.27 ± 0.04	sim
D	1.3	10.5	4.00	2.15 ± 0.11	0.54 ± 0.03	sim
E	2.2	9–16	0.50	1.60 ± 0.02	3.20 ± 0.03	exp
F	1.4	9–16	0.50	0.99 ± 0.02	1.98 ± 0.03	exp
G	1.0	9–16	0.50	0.41 ± 0.02	0.82 ± 0.03	exp

Experimental values are from Zhao et al. (31).

In general, we found the ionic current to depend on the microscopic details of the hpDNA's conformation. An illustrative example is shown in Fig. 10. Comparing the current trace, Fig. 10 a, to the snapshots of the hpDNA conformation, Fig. 10, b–f, reveals that the position of the double helix relative to the constriction does not uniquely determine the relative current. While the double helix penetrates the pore more deeply in Fig. 10 e than in Fig. 10 c, the current in the former conformation is greater than in the latter because the double helix stretches in the constriction.

Figure 10.

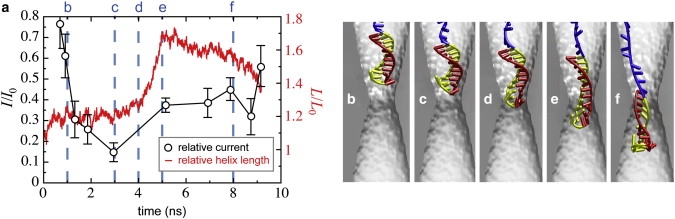
Stretching of the double helix and ionic current. (a) Ionic current (black, left abscissa) derived from the MD simulation illustrated by the snapshots in panels b–f and the strain of the helix (red, right abscissa) shown at the corresponding times. The elongation of the helix, which reaches a maximum value at ∼5 ns, reduces its cross section, causing an increase in the current through the pore.

Despite the ambiguities in determining the conformation of hpDNA from ionic current transients, several general rules are formulated below.

Current blockades

We found that the deepest blockades of the ionic current in the pores ≥1.6 nm in diameter were produced by hpDNA in the loop-first orientation. The smallest relative current through the 1.8-nm × 2.2-nm pore (pore A), I/I₀ = 0.20 ± 0.01, was observed when hpDNA stalled at the constriction in the loop-first orientation. For the 2.2-nm pore (pore B), the minimum mean relative current was 0.16 ± 0.03 in the loop-first orientation and 0.20 ± 0.03 in the coil-first orientation. For the 1.6-nm-diameter pore (pore C), the current for the loop-first orientation of hpDNA was found to be reduced more than that for the coil-first orientation, irrespective of whether the stretching/distortion or unzipping pathway was taken. Thus, in the loop-first orientation, the mean relative currents were I/I₀ = 0.083 ± 0.014 and 0.08 ± 0.02 at ϕ = 4.0 and 6.5 V, respectively, while in the coil-first orientation I/I₀ = 0.131 ± 0.013 and 0.24 ± 0.02. Because the associated relative currents are identical to the precision of the data for 4.0 and 6.5 V, the hpDNA/pore system acts as a linear resistor in the loop-first orientation. However, this is not true in the coil-first orientation due to the change in the translocation pathway.

The observation that hpDNA in the loop-first orientation causes the lowest current, however, is valid only when the double helix is not stretched beyond 1.2L₀, where L₀ is its equilibrium length. If the double helix is stretched beyond 1.3L₀, the ionic current depends very little on the hpDNA orientation (Fig. S4).

For the 1.3-nm pore (pore D), only coil-first translocations are likely. For this pore, we found that hpDNA can almost completely block the passage of ions in the timescale of our simulation, so we predict a mean current <0.003I₀. Overall, the smallest relative currents were found to decrease with the pore diameter.

Stretching/distortion versus unzipping

In the 1.6-nm-diameter pore (pore C), we observed translocation by both stretching/distortion (ϕ ≤ 5.0 V) and unzipping (ϕ ≥ 6.5 V) pathways, which enabled direct comparison of the resulting ionic current traces. We found that because only a single DNA strand blocks the constriction in the unzipping pathway, the relative ionic current is much larger, on average, than in the stretching/distortion pathway. For this pore, we found the ionic current during unzipping (I/I₀ = 0.24 ± 0.02 at ϕ = 6.5 V) to be nearly twice of that obtained during stretching/distortion (I/I₀ = 0.131 ± 0.013 at ϕ = 4 V).

Current enhancements

Long-duration enhancement of the current well above the open pore level was observed when hpDNA occupied the trans side of pore A for a prolonged period of time. Fig. 11 illustrates a simulation in which such enhancement of the current was observed. At the beginning of the simulation, the current was just below the open pore value. As the double helix neared the constriction the relative current drops to near I/I₀ = 0.25. However, the DNA began to gather on the trans side of the pore, causing a rise in the ion concentrations there. The relative current then jumped above 2.0. Note that such current enhancement persists as long as a portion of the hpDNA remains in the pore on the trans side, which is different from transient current enhancements reported in Aksimentiev et al. (35). The current enhancements are more likely to be observed for the pores in thicker membranes, as hpDNA can adopt a more compact conformation. Indeed, currents near 2I₀ and above were not observed for the pore of similar diameter in the 10.5-nm-thick membrane (pore B).

Figure 11.

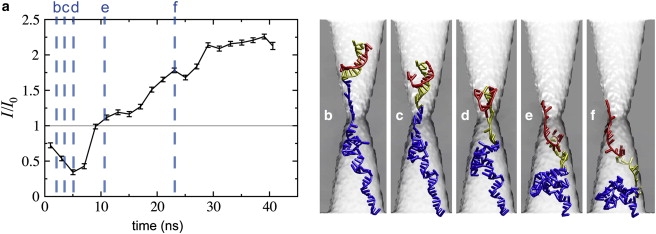
Enhancement of the ionic current. (a) Ionic current as a function of time. (b–f) Snapshots of hpDNA conformation. The simulation times are indicated by dotted lines in panel a.

DNA alters distribution of ions

To understand the reason for observing both reduction and enhancement of ionic current in the same pore, we investigated the influence of the hpDNA conformation on the distribution of ions in the pore. Fig. 12 shows the concentration of K⁺ (Fig. 12 d) and Cl⁻ (Fig. 12 e) ions for the three nanopore/hpDNA systems shown in Fig. 12, a–c. Steady-state currents were observed in the above three systems. The concentration as a function of z for each time step was calculated by c(z_i) = (55.523 M) N_ion(z_i)/N_water(z_i), where N_ion(z_i) and N_water(z_i) were the number of ions and the number of water molecules, respectively, in a thin segment of the system z_i − Δz/2 < z < z_i + Δz/2. The values were then averaged over the steady-state portions of the simulation trajectories. It was suggested earlier (23,32), that the existence of both reduction and enhancement of ionic current is caused by the competition of the following two phenomena. First, DNA sterically excludes ions from occupying the pore, which lowers the number of charge carriers and thus the ionic current (equivalent to reducing the pore's cross section). At the same time, the presence of DNA in the pore increases the concentration of counterions, as they are required to neutralize the DNA's charge. Complicating the matter is the fact the concentration of ions within the pore in the absence of DNA is not the same as that of the bulk solution.

Figure 12.

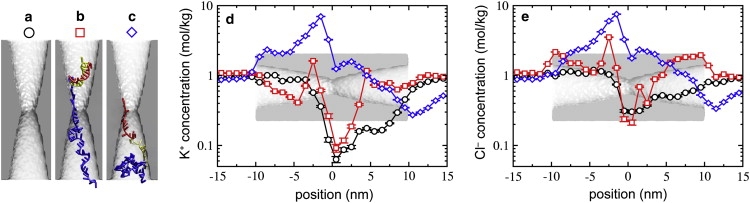
Effect of hpDNA on the ion concentration within the pore. (a) Open pore. (b) Nanopore/hpDNA conformation for reduced current. (c) Nanopore/hpDNA conformation for enhanced current. (d and e) Concentration profile of K⁺ (d) and Cl⁻ (e) along the pore axis for the systems illustrated in panels a–c.

In the absence of DNA, the concentration of both K⁺ and Cl⁻ was found to be smaller than that in the bulk, which is consistent with experimental suggestions (25). Fig. 12 reveals that the concentration of K⁺ drops below 0.1 M near the constriction, whereas the concentration of Cl⁻ shows a similar but less substantial drop to 0.3 M. Note that the abscissa is shown on a logarithmic scale. The Cl⁻ current was greater than that for K⁺, consistent with the larger concentration of Cl⁻.

For the system shown in Fig. 12 b, the concentration of ions is enhanced at some places and reduced at the others. Despite the enhancements of the pore's ion concentration, the increased concentrations are not large enough to overcome the reduction of the cross-sectional area by the DNA. Moreover, there is a reduction of the Cl⁻ concentration at the pore constriction from 0.3 to 0.2 M due to the presence of DNA. The total relative current for this configuration is approximately half of that for the open pore, I/I₀ = 0.49 ± 0.02.

For the conformation shown in Fig. 12 c, the total ion current is enhanced to I/I₀ = 2.17 ± 0.04. Fig. 12, d and e, shows that the concentrations of both types of ions near the constriction are greater than their bulk values. Furthermore, at z = −1.5 nm, the concentrations of Cl⁻ and K⁺ are greater than seven times their bulk values. These increases in ion concentration are responsible for the enhancement of the total current.

Conclusions

In summary, we find that, even when the constriction is small enough to forestall the translocation of dsDNA, hpDNA translocation through nanopores can occur in different orientations and by different pathways, depending on the geometry of the pore and the transmembrane voltage. Our simulations suggest that translocation led by the loop of the double helix rather than the overhanging coil is possible for pores with constrictions ≥1.6 nm and that the loop-first orientation may even dominate at low voltages in large pores. Furthermore, it appears that larger pores tend to favor the translocation pathway in which the portion of the hpDNA initially forming the double helix passes through the constriction as two strands, maintaining some if not all of the hydrogen bonds between the paired nucleotides.

The MD simulations demonstrate that changes in the conformation of the nanopore/hpDNA system dramatically alter the ion distribution within the pore and are sufficient to produce the range of ionic current values seen in experiment. Furthermore, our simulations have given us some insight into the possible origin of the multiple ionic current levels shown in Fig. 3 e. In simulations, we found that the highest current levels (>2I₀) corresponded to having a large portion of the hpDNA in the trans chamber of the pore. Because the transmembrane voltage applied in the experiment was much less than the expected threshold voltage for the pore, it was not likely that double helix was able to pass the constriction in the experiments. Thus, the enhanced levels shown in Fig. 3 e were likely produced by a flexible portion of the molecule, either the coil or the long loop of the hpDNA used in experiment, threading into the trans side of the pore while the double helix remained in the cis side. The lowest levels of current observed in simulation occurred when the hpDNA stalled with the loop blocking the constriction. However, this observation likely depends on the length and structure of the loop and may not apply to experiments using the hpDNA with the 76-nucleotide loop. In addition, because having two portions of the strand in the constriction blocks the current more efficiently than having only one, the simulations showed that translocation by the stretching/distortion pathway should be distinguishable from that by the unzipping pathway.

Our results demonstrate that the geometry of the pore must be chosen carefully so that the molecule adopts a desirable conformation for the application in mind. Some sequencing schemes might require that only a single strand of DNA passes through the constriction; hence, pores with constrictions of ∼1.3 nm may be more suited for these schemes than larger pores. For sequencing methods in which the knowledge of the orientation of the bases is crucial, such as those proposed by Gracheva et al. (27) and Lagerqvist et al. (55), it is possible that the ordered interleaving of bases (Fig. 7 b) as seen in the constriction of 1.6 nm is optimal.

Supporting Material

Animations of simulation trajectories, a comparison of results with different force fields, and supporting figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00030-1.