DNA as Membrane-Bound Ligand-Receptor Pairs: Duplex Stability Is Tuned by Intermembrane Forces

Abstract

We use membrane-anchored DNA as model adhesion receptors between lipid vesicles. By studying the thermal stability of DNA duplex formation, which tethers the vesicles into superstructures, we show that the melting temperature of a 10-base DNA sequence is dependent on the lipid composition of the tethered vesicles. We propose a simple model that describes how the intermembrane interactions tilt the free energy landscape for DNA binding. From our model, we estimate the area per DNA in the binding sites between vesicles and also the total area of the adhesion plaques. We find that vesicles containing a small proportion of cationic lipid that are modified with membrane-anchored DNA can be reversibly tethered by specific DNA interactions and that the DNA also induces a small attraction between these membranes, which stabilizes the DNA duplex. By increasing the equilibrium intermembrane distance on binding, we show that intermembrane interactions become negligible for the binding thermodynamics of the DNA and hence the thermal stability of vesicle aggregates becomes independent of lipid composition at large enough intervesicle separations. We discuss the implications of our findings with regards to cell adhesion and fusion receptors, and the programmable self-assembly of nano-structured materials by DNA hybridization.

Introduction

Recognition and signaling between organelles in nature is mediated through a wealth of ligand-receptor pairs that are localized to lipid membrane structures (1–3). These abundant ligand-receptor pairs differ in binding strength and range of interaction from the membrane surface, but generally have the common attributes of interaction specificity and diffusion within their fluid, lipid matrix. Recent studies have reported adhesion of lipid vesicles to solid supported membranes (4,5) and other lipid vesicles (6,7) mediated by membrane-anchored single-stranded DNA (ssDNA), which act as artificial adhesion receptors (Fig. 1). These membrane-anchored ssDNA offer a model system to study generic phenomena of membrane-bound ligand-receptor interactions: the interaction range and strength can be systematically varied by, for instance, selecting the length of the DNA base sequence, the number and location of complementary basepairs and inserting repeated base sequences. Membrane-anchored DNA acting as adhesion ligand-receptor pairs between lipid vesicles are engineered to bind in a conformation such that membrane-distal portion of the first DNA is complementary to the membrane-proximal portion of the second DNA (and vice versa) as shown in Fig. 1.

Figure 1.

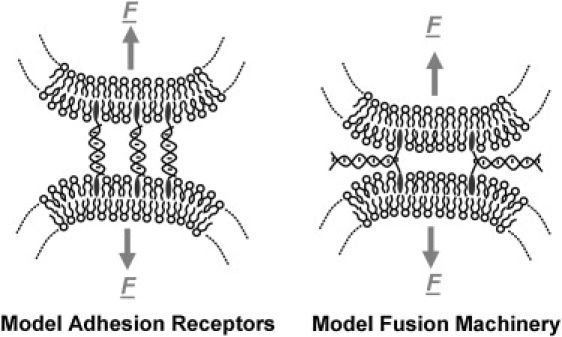
(Left) Membrane-anchored ssDNA acting as model adhesion receptors between lipid vesicles (both ssDNA anchored to the membranes by either the 5′ or 3′ end, i.e., symmetric anchoring). (Right) Membrane-anchored ssDNA acting as model fusion machinery, “zipping” two lipid vesicles into close opposition (ssDNA in opposing vesicles are anchored asymmetrically, i.e., one is anchored at the 5′ end and the other is anchored at the 3′ end).

Membrane-anchored DNA can also be engineered to act as model systems for membrane fusion receptors (Fig. 1) (8,9). In this mode, the membrane-distal sections of the two complementary ssDNAs are engineered to bind to each other in a manner that “zips” the membranes into close apposition. This is analogous to the action of the SNARE fusion machinery (10,11).

More generically, the specific recognition of complementary DNA strands is a wide-spread tool in bionanotechnology (12–17). Programmable assembly of nanoscale building blocks by the specific interactions between complementary DNA strands is viewed as a promising route to the fabrication of functional, nanotechnological devices. Because the digital base coding of the DNA sequence has extremely high specificity for its complementary sequence and the binding stability is sensitive even to single base mismatches, highly complex systems with multiple DNA sequences can be conceived. A further advantage of DNA is the reversibility of binding by heating above the melting temperature of the DNA sequence that is sensitive to its external environment, e.g., DNA concentration, pH and ionic strength. This attribute can be used to disassemble or anneal structures created by DNA self-assembly. An accurate predictive framework for the calculation of DNA duplex stabilities when confined by or anchored to nanoscale components would be necessary for the melting characteristic of DNA to be controllably exploited in the manipulation of self-assembling DNA devices.

The inclusion of lipid vesicles in the programmable self-assembly tool-kit has technological appeal. Vesicles are deformable, self-healing containers that exhibit many advantageous biomimetic properties such as fusion, controlled leakage, and exotic morphological transitions. These and other properties have the potential to be exploited in multicompartment supravesicular structures or hybrid materials where vesicles are incorporated into nanostructures with other components: gold nanoparticles, quantum dots, and carbon nanotubes numbering among the many possibilities.

The melting temperatures (T_m) of unmodified, short DNA duplexes have been well-characterized and a thermodynamic model exists for their prediction over a range of environmental conditions (18–27). It has also been found that the modification of DNA strands with “dangling ends” of small molecules, such as fluorophores and quenchers, can increase T_m by up to 4.3°C (20). Comparatively, very little is understood about how the melting stability of DNA is affected by being anchored to much larger, mesoscopic entities.

Melting temperatures of DNA-linked nanoparticle assemblies cannot be understood directly from models of the thermodynamics of single DNA strands in solution (28–31). Many physical factors may contribute to these differences: i), the entropy cost of tethering one end of the ssDNA to a particle, ii), the entropy loss of the particles when bound, iii), locally increased concentration and orientational restriction of the surface-anchored DNA, and iv), the influence of interparticle interactions on the stability of DNA binding. Sharp melting profiles have been reported for DNA-tethered particles due to the necessity of several DNA strands to unbind to allow particle dissociation (32–35). This increased sharpness in melting profile compared to ordinary DNA increases the sensitivity to single base mismatches in oligonucleotide detection assays (36). Experimental studies have explored the effects of DNA surface concentration, salt concentration, particle size and interparticle separation on the thermodynamics of melting (29,30). However, a systematic series of experiments that decouple the effect of interparticle forces from other perturbations to DNA binding stability has yet to be reported. For instance, changes in the salt concentration affect the screening of electrostatic double layer forces between particles but simultaneously influence DNA stability through the electrostatic screening of the charged phosphate backbones. Although changing the particle separation modulates the interparticle forces, the methods that have been used to achieve this either altered the DNA binding geometry or the total number of DNA linkages between particles, the effects of which too cannot be discounted (29).

We study the thermodynamic stability of assemblies of lipid vesicles tethered by DNA. We tune the intervesicle interactions by choice of lipid composition, a strategy inaccessible to the more extensively investigated DNA self-assembly systems of gold nanoparticles or polystyrene microspheres. We keep the DNA sequence, vesicle anchoring method, and solvent properties constant, allowing us to quantitatively explore how interparticle forces modify the DNA binding stability. We propose a simple model to quantify how the forces between vesicles tune the free energy of DNA hybridization and thereby modulate the melting temperature of tethered vesicles. We then re-examine our data in light of this model to show that it predicts physically rational values for the area per DNA in the binding site and the osculating area between tethered vesicles.

Materials and Methods

Materials

The lipids 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (sodium salt) (POPG), and 1,2-dioleoyl-3-trimethylammonium-propane (chloride salt) (DOTAP) were purchased from Avanti Polar Lipids (Alabaster, AL). Cholesterol-modified oligonucleotides cholesteryl-TEG-5′-ACAGACTACC-3′ (chol-DNA-10A), cholesteryl-TEG-5′-GGTAGTCTGT-3′ (chol-DNA-10B), cholesteryl-TEG-3′-TTTGGCCCGCGCCCCGCCCC-5′ (chol-DNA-20), cholesteryl-TEG-5′-TTTCCGGGCGCGGGGCGGGGACAGACTACC-3′ (chol-DNA-30A), and cholesteryl-TEG-5′-TTTCCGGGCGCGGGGCGGGGGGTAGTCTGT-3′ (chol-DNA-30B) were purchased from Eurogentec North America (San Diego, CA) and had been purified by HPLC. DNA sequences 5′-ACAGACTACC-3′ (DNA-10A) and 5′-GGTAGTCTGT-3′ (DNA-10B) were purchased from IDT (Coralville, IA) and had also undergone HPLC purification.

Preparation and characterization of DNA-modified vesicles

Large unilamellar vesicles (LUVs) were prepared by extrusion; ∼600 μL of 25 mg/mL lipid in chloroform was added to a glass scintillation vial and the chloroform was evaporated under vacuum for at least 4 h; 2 ml of buffer (125 mM sodium chloride, 10 mM HEPES, pH 7.4, and measured osmolarity 260 mOsm) was pipetted into the vial. The sample was vortexed until all the lipid was in solution. The sample was frozen under liquid nitrogen and then thawed in a warm water bath. This vortex-freeze-thaw cycle was repeated five times. The lipid solution was then extruded 10 times through two polycarbonate membranes with a pore size of 0.1 μm.

Final lipid concentrations were measured by a standard phosphate assay. Vesicle size distributions were checked by dynamic light scattering (DLS) and found to have a mean hydrodynamic radius of ∼50 nm with a polydispersity in the range 0.07–0.12.

Cholesterol-DNA (chol-DNA) solutions were added to the vesicles in the desired molar ratio, mixed and left to stand for at least 30 min so that the chol-DNA could diffuse into the membranes. Samples contained vesicles with average DNA surface concentrations in the range 10–155 DNA per vesicle (D/V).

DLS

Samples of LUVs were studied by DLS using a Brookhaven Instruments BI-200SM goniometer (Brookhaven Instruments, Holtsville, NY), an ALV-5000E digital correlator, and a Coherent Compass 315M 100 mW (Coherent, Santa Clara, CA), double-pumped, continuous wave, solid-state NdYAG laser with 532 nm emission wavelength. For the determination of the size distribution of LUVs, the goniometer bath temperature was set to 20°C. The size distribution of vesicle aggregates in the sample was calculated from the apparent diffusion constant obtained from the normalized intensity correlation function at a scattering angle of 90° using a second order cumulant data analysis. Scattered intensities were collected for 2 min per measurement. Repeat measurements were taken to ensure the reproducibility of the apparent size distribution.

For experiments to estimate the melting temperature of vesicle aggregates, temperature-dependent DLS measurements were collected. The goniometer bath temperature was varied in steps of 5°C and samples were allowed 30 min to equilibrate at each temperature. The temperature was increased continually until the measured size distribution of the sample returned to that of single vesicles.

Ultraviolet absorption spectroscopy

Temperature-dependent ultraviolet (UV) absorption measurements were conducted on an Evolution 300 UV-visible spectrophotometer with a Smart Peltier thermostated single cell holder (Thermoelectron). Samples were degassed before being transferred to a semimicro, stoppered quartz spectrophotometer cell (Starna Cells, Atascadero, CA) with a path length of 10 mm. A temperature probe connected to the Peltier controller was placed into the samples so that the absorption could be recorded against the actual sample temperature rather than that of the sample-holder base. Samples were heated and cooled at 0.4°C/min and absorption measurements were taken every 15 s (i.e., every 0.1°C). Absorption at 260 nm (at which DNA absorbs) and 320 nm (at which DNA does not absorb; this shows any turbidity changes within the sample) were measured with an integration time of 1 s. Samples were heated and cooled repeatedly through two heat-cool cycles to confirm the reproducibility of the DNA melting transition.

UV absorption measurements of DNA at 260 nm are a result of an electronic π − π^∗ transition in the DNA bases. This transition is quenched in the double-stranded form. A sigmoidal transition curve for the DNA melting profile is recorded on heating and cooling. The transition curves are smoothed and lower and upper sloping baselines are normalized to f = 0 and 1 respectively, where f is the fraction of unbound bases in the sample. The melting temperature (T_M) is defined as the temperature at which f = 1/2 (22).

A thermodynamic model for the melting of short DNA strands in solutions has been derived from the van 't Hoff equation (22,24). The melting temperature, T_M, is calculated by

$$T_{\mathrm{M}}=\frac{\Delta H^0}{\Delta S^0+k_{\mathrm{B}}\text{ln}\left(C_{\mathrm{T}}/4\right)},$$ (1)

where ΔH⁰ is the enthalpy change per molecule and ΔS⁰ is the entropy change per molecule between single-stranded and double-stranded DNA. C_T is the total concentration of single DNA strands and k_B is Boltzmann constant. Linear fits to plots of 1/T_M against ln(C_T/4), often referred to as van 't Hoff plots, allow the enthalpy and entropy changes for DNA hybridization to be extracted from the data.

In samples where vesicles aggregate due to DNA hybridization, the increase in sample turbidity is too great for the sigmoidal UV transition curve due to DNA basepairing to be resolved. In these samples, the turbidity due to vesicle-vesicle association and dissociation on cooling and heating was used as the signature of the binding and unbinding transition. A linear fit to the absorption curve above and below the vesicle melting temperature was used to determine the transition temperature, an example of which is shown in Fig. 2.

Figure 2.

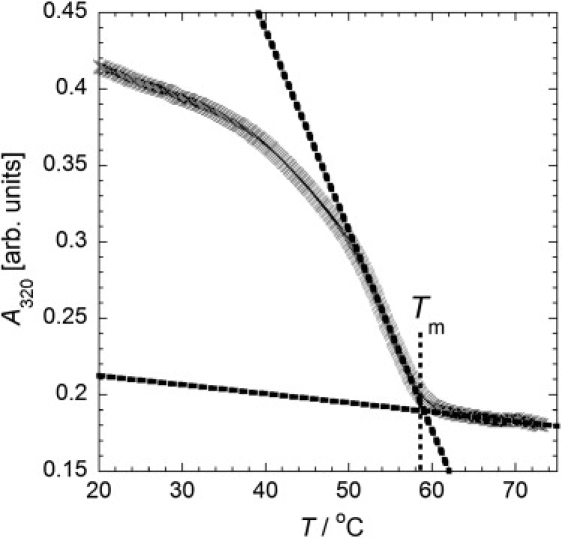
Example data (absorption at 320 nm against temperature) for the cooling of a sample of 10% DOTAP vesicles with an average of 39 D/V. Linear fits of the data just above and below the melting temperature are shown (dashed lines). The melting temperature, T_m, is determined from the point of intersection of these two lines.

Model for the stability of DNA duplexes in a nonuniform force field

In this section we derive an equation to predict how intermembrane interactions will modulate the melting temperature of anchored DNA molecules. A theoretical framework for how a constant applied force modifies the binding free energy of specific cell adhesion molecules has been proposed by George Bell (37). The forces between lipid membranes however are not constant with separation and so we modify the Bell model for a nonconstant force field,

$$\Delta G^{\mathbf{F}}=\Delta G^0-U^{\mathbf{F}},$$ (2)

$$U^{\mathbf{F}}={\int }_{D_0}^{D_0+\Delta x}\mathbf{F}\left(\mathbf{X}\right)\cdot d\mathbf{X}\text{.}$$ (3)

Here, ΔG^F is the difference in Gibbs free energy between bound and unbound states in the applied force field F(X), where X is the reaction coordinate (in this case, the direction normal to the membranes). U^F is the work done by the intermembrane forces on the DNA duplex. ΔG⁰ is the difference in Gibbs free energy between bound and unbound states under conditions of no applied force, D₀ is the separation between membranes when bound together by DNA bonds and Δx is the distance along the reaction coordinate between bound and unbound states.

The change in free energy under an applied force field (Eq. 2) can be inserted into the derivation of the van 't Hoff equation (Eq. 1). Therefore we obtain an expression for the equilibrium melting temperature of DNA duplexes in an applied force field:

$$T_{\mathrm{M}}=\frac{\Delta H^0-U^{\mathbf{F}}}{\Delta S^0+k_{\mathrm{B}}\text{ln}\left(C_{\mathrm{T}}/4\right)}\text{.}$$ (4)

The van 't Hoff equation that we have applied here is a two-state model that assumes no intermediate states between single-stranded and double-stranded state forms. Although this assumption may seem overly simplistic for the complexity of hybridization between two nucleic acid chains, single-molecule experiments on RNA hairpins showing equilibrium hopping under applied force between folded and unfolded conformations suggest that this is an accurate description of the free energy landscape for nucleic acids (38).

The model we have derived in Eq. 4 is generically applicable to the melting of DNA in any applied force field. So far, there is nothing about this model that is specific to lipid membranes and should be applicable to the melting of DNA anchored to any materials where an expression for the force field can be derived and inserted into Eq. 3. We will present our experimental results before examining this model with the specific case of lipid vesicles.

Results

We will present our data in three subsections. First, we will compare melting data from DLS and UV spectroscopy to show that the melting data we present truly represents dissociation to monomeric vesicles in our samples. Second, we will compare the melting temperatures of the soluble, unmodified DNA sequence to the melting temperatures of vesicle-anchored DNA and show that the local increase in concentration of DNA on the vesicle surface is insufficient to explain the melting temperatures of the vesicle assemblies. Finally, we will examine the effects of lipid composition on the melting temperatures of the DNA-tethered vesicle superstructures.

Comparison of DLS and UV spectroscopy

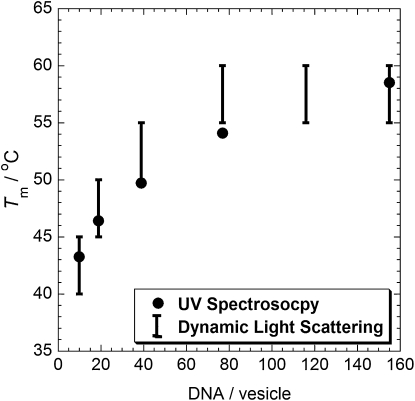
Vesicle melting temperatures measured by UV spectroscopy and DLS are in good agreement with each other. DLS gives information about the size distribution of vesicles or aggregates in the samples, whereas UV spectroscopy offers higher temperature resolution and longer experimental run times. Samples of two populations of POPC vesicles modified by complementary, single-cholesterol-anchored DNA (chol-DNA-10A and chol-DNA-10B) were heated in the goniometer bath of the DLS until the measured size distribution (mean size and polydispersity) returned to that of single vesicles. Samples of untethered vesicles were measured to have a mean hydrodynamic radius of ∼50 nm and polydispersities in the range of 0.07–0.12. Fig. 3 shows estimates of the vesicle melting temperatures obtained from DLS measurements as a function of the average DNA per vesicle in the samples. The data is plotted as error bars where the lower bound of the error bar is the last temperature measurement where the sample contained aggregated vesicles and the upper bound of the error bar represents the first temperature that yielded the size distribution of single vesicles. The melting temperature data of these DNA-functionalized vesicles obtained by UV spectroscopy, and plotted on the same graph for comparison, is also shown in Fig. 3. Good agreement is seen between vesicle melting temperatures obtained by the two techniques. The DLS data shows that the melting temperatures we report by UV spectroscopy represent the temperatures at which the vesicles become fully dissociated from one another.

Figure 3.

Comparison of melting temperatures for POPC vesicles decorated with single-cholesterol-anchored DNA obtained by DLS and UV spectroscopy.

Comparison of soluble DNA and membrane-anchored DNA

We find the melting temperature of the unmodified, soluble DNA sequences (DNA-10A and DNA-10B) in the 125 mM NaCl buffer solution are in excellent agreement with theoretical calculations from empirical, single base, nearest-neighbor thermodynamics using the online IDT oligo-analyzer database (39). We measure T_m over a range of concentrations comparable to the range of the bulk concentrations of chol-DNA in our vesicle samples. Melting temperatures as a function of total DNA concentration are plotted in Fig. 4 and are within the ±2°C error quoted for these theoretical estimates (39). A van 't Hoff plot of 1/T_m against ln(C_T/4) for the unmodified DNA is shown in the lower inset of Fig. 4. This is used to calculate the enthalpy and entropy change for hybridization of these DNA sequences using Eq. 1 (22,24). These thermodynamic quantities were calculated to be ΔH = −276 ± 17 kJ mol⁻¹ and ΔS = −767 ± 55 J K⁻¹ mol⁻¹, as shown in Table 1.

Figure 4.

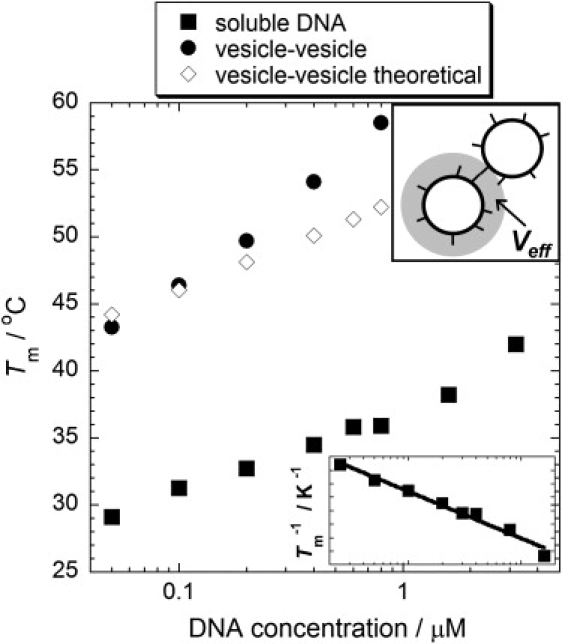
Total DNA concentration against melting temperature for unmodified (soluble) DNA (■), complementary DNA-modified vesicles (●) and a theoretical estimate of the melting temperature of the vesicles from the effective volume of DNA (inset, top) confined to the vesicle surface (⋄). (inset, bottom) A van 't Hoff plot for the soluble DNA (T_m⁻¹ against C_T/4). A logarithmic fit to the data gives the enthalpy and entropy changes for the hybridization of the soluble DNA.

Table 1.

Approximate enthalpy and entropy changes obtained from van 't Hoff plots for the melting of our 10-base DNA sequence in solution and when anchored to lipid vesicles

	Soluble DNA	Single cholesterol anchor			Double cholesterol anchor
		POPC	POPG	10% DOTAP	POPC	POPG
ΔH/kJ mol−1	−276 ± 17	−157 ± 6	−135 ± 10	−147 ± 11	−171 ± 8	−161 ± 11
ΔS/J K−1 mol−1	−767 ± 55	−412 ± 18	−361 ± 39	−371 ± 33	−443 ± 24	−413 ± 13

DOTAP, 1,2-dioleoyl-3-trimethylammonium-propane (chloride salt); POPC, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine; POPG, 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (sodium salt).

Samples containing two populations of POPC vesicles modified with the complementary chol-DNA pair show a greatly increased DNA duplex stability compared to the unmodified DNA (Fig. 4). This is expected to be partly due to the enhanced local concentration of DNA when they are confined to the surface of vesicles. It should be noted that our measurements of T_m for DNA-modified vesicles represent temperatures at which almost all DNA is unbound. Although T_m for soluble DNA is defined as the temperature at which half the DNA is bound and half unbound, melting profiles of DNA anchored to surfaces and colloids are known to be sharp (28–31) and therefore we expect T_m(vesicles) ≈ T_m(DNA) in our experiments.

The increase in effective local concentrations of DNA when anchored to the vesicle membranes cannot fully explain the vesicle melting temperatures that we measure. We estimate the local enhancement in DNA concentrations (Fig. 4, upper inset) by considering the effective volume in which these chol-DNA exist and can interact with chol-DNA on the surface of other vesicles in solution. This is calculated from the mean vesicle radius of 50 nm and that the maximum range of interaction of ssDNA anchored to opposing vesicles being twice their maximum contour length (the contour length of ssDNA is 0.59 nm/base (40)). We use these effective concentrations to calculate expected vesicle melting temperatures based on theoretical thermodynamic quantities for the unmodified 10-base sequences in solution: this does not reproduce our experimentally measured data for the vesicle samples (Fig. 4). This is not due simply to a discrepancy in our calculation of effective volumes because the trend in melting temperatures as a function of DNA concentration that we measure has the wrong slope compared to any theoretical estimates based on the thermodynamic quantities measured for the unmodified DNA. This was expected because the enthalpic and entropic contributions to the free energy are expected to differ from those of soluble DNA, as we discussed in the Introduction.

Effect of lipid composition on duplex stability

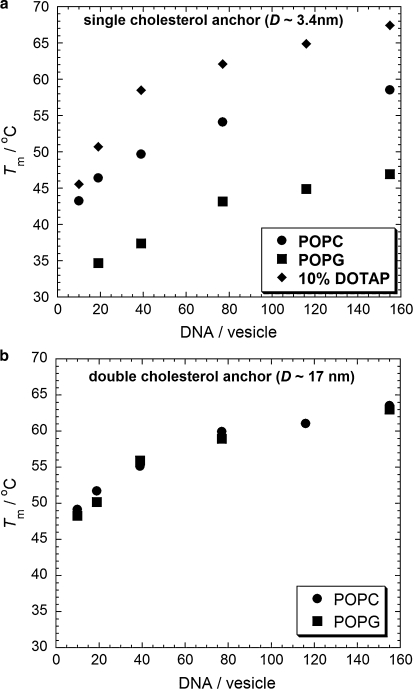
We explore the perturbation of the DNA binding stability brought about by intervesicle interactions. We will look at vesicles composed of the zwitterionic lipid POPC, the anionic lipid POPG (-1e/lipid), and vesicles with 10 mol % of the cationic lipid analog DOTAP (+1e/lipid) in POPC. We will also look at two different DNA binding geometries: the single-cholesterol anchored pair chol-DNA-10A and chol-DNA-10B, and the double-cholesterol anchored pair of chol-DNA-20/chol-DNA-30A and chol-DNA-20/chol-DNA-30B. These two DNA binding systems have the same 10-base recognition sequence, but change the intermembrane separation on vesicle tethering (Fig. 5). In the double-cholesterol binding geometry, DNA-chol-20 binds to the membrane-proximal portion of the 30mer DNA to reinforce its anchoring in the membrane (4). We use an anchoring sequence with 17 complementary bases and 100% GC content to maximize its binding strength, ensuring that the anchoring sequence does not unbind during the vesicle melting experiments. Fig. 6 shows the variation of melting temperatures for vesicles with different lipid compositions at different DNA surface coverage on the vesicles.

Figure 5.

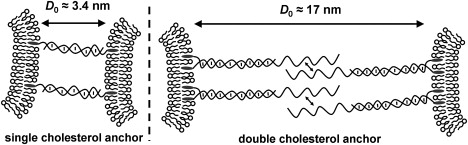
Anchoring and binding geometries of vesicles modified with single-cholesterol-anchored DNA (left) compared to double-cholesterol-anchored DNA (right).

Figure 6.

Graphs of T_m against ssDNA per vesicle. (a) Single-cholesterol-anchored ssDNA. (b) Double-cholesterol-anchored ssDNA. (●) POPC vesicles, (■) POPG vesicles, and (♦) 10% DOTAP vesicles.

Significant changes in the thermal stability of the DNA duplex are observed for vesicles consisting of different lipid compositions. Fig. 6 a shows vesicle melting temperatures for samples of vesicles modified with chol-DNA-10A and chol-DNA-10B. Aggregates of anionic POPG vesicles melt at lower temperatures than neutral POPC vesicles. We propose that the repulsion of the electrostatic double layer between POPG vesicles destabilizes the DNA duplexes that are tethering the vesicles together and hence lowers the melting temperature. Melting temperatures of 10% DOTAP vesicles are found to be higher than those of POPC vesicles. This might suggest an attractive interaction between these cationic vesicles when tethered to one another by the polyanionic DNA. Indeed, this is not unreasonable because DNA is known to form complexes with cationic membranes (41–43) and polycations (e.g., Ca²⁺) are known to induce aggregation and fusion between anionic lipid vesicles (44).

If there is a nonspecific attraction between 10% DOTAP vesicles that have been modified with anchored DNA then it might be expected that the vesicles aggregate nonspecifically and irreversibly. However, the reversible thermal binding and unbinding observed in the UV spectroscopy data implies that any attractive interaction is not strong enough to permanently aggregate these vesicles; we will revisit this idea later. We note that DNA-modified vesicles consisting of 50 mol % DOTAP did not show thermally reversible aggregation, probably due to the nonspecific attraction being larger at higher DOTAP concentrations, causing permanent aggregation and perhaps even morphological changes in these samples (i.e., DNA-cationic lipid complexes other than aggregation of DNA-functionalized vesicles). An increased turbidity above that of single vesicles was measured for these samples, and hence some form of nonspecific electrostatic aggregation can be inferred.

No significant, resolvable differences in the melting temperatures of POPC and POPG vesicles modified by double-cholesterol-anchored DNA are observed (Fig. 6 b). This binding technique, using a double-cholesterol-anchor, results in an increased separation between vesicles on DNA tethering compared to single-cholesterol-anchored DNA. Because double-stranded DNA has a persistence length of ∼50 nm (45), we expect it to act as a rigid rod between the vesicles on the length-scale of these short, membrane-anchored oligonucleotides. Because the contour length of double-stranded DNA is known to be 0.34 nm/base (40), the intermembrane separation (D₀) between vesicles tethered by single-cholesterol-anchored DNA is ∼3.4 nm and, between vesicles tethered by double-cholesterol-anchored DNA, D₀ ≈ 17 nm. At these greater intermembrane separations, it seems that any differences in forces between POPC and POPG membranes are not large enough to cause any resolvable differences between the stabilities of the DNA duplexes.

Vesicles composed of 10% DOTAP could not be reversibly bound and unbound using double-cholesterol-anchored DNA. We postulate that this is due to the larger anionic charge per DNA adhesion receptor (−50e for double-cholesterol-anchored DNA compared to −10e for single-cholesterol-anchored DNA) that results in a larger attraction between 10% DOTAP vesicles that prohibits reversible aggregation by specific DNA hybridization.

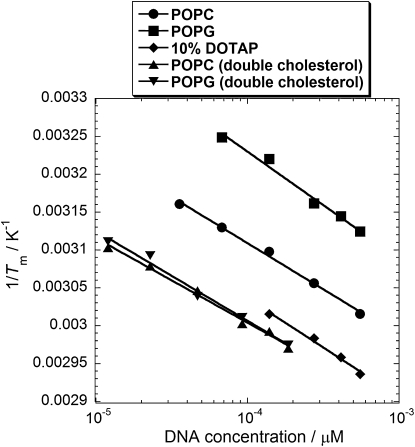
Van 't Hoff plots of 1/Tm against our calculated effective DNA concentrations when confined to the vesicle surface yield estimates of the enthalpy and entropy change for hybridization of the membrane-anchored DNA (Fig. 7). The thermodynamic quantities obtained from these fits are shown in Table 1. We only use the data points for surface concentrations ≥39 D/V for 10% DOTAP vesicles because below this concentration the melting temperatures converge toward the values obtained for POPC vesicles. We assume that the interaction between DNA-functionalized cationic vesicles is sensitive to the concentration of DNA in the adhesion plaques between vesicles, because bare cationic membranes would repel each other and the polyanionic DNA is required to induce a nonspecific electrostatic attraction between the membranes. At DNA surface concentrations below 39 D/V, small stable aggregates are known to form for POPC vesicles where these adhesion plaques between vesicles are not saturated in DNA i.e., the adhesion plaques do not grow to the maximum size that is physically attainable by populations of 10mer DNA anchored on 100 nm diameter vesicles. At 39 D/V and above, adhesion plaques between vesicles can saturate with DNA and continuous aggregation occurs until the sample becomes flocculated (6). If the binding sites between 10% DOTAP have a reduced number of polyanionic DNA molecules that induce an attraction between vesicles, then the attractive interaction between these vesicles would be reduced and therefore the free energy landscape of DNA that is bound between these vesicles will not be the same as those occupying saturated adhesion plaques in systems with a larger number of DNA per vesicle. This trend can be observed in the data (Fig. 5 a), as the melting temperatures for 10 and 19 D/V 10% DOTAP vesicles converge toward the respective data points for POPC vesicles compared to 10% DOTAP vesicles surface concentrations of 39 D/V or more.

Figure 7.

Van 't Hoff plot for the melting of DNA-tethered vesicles. The effective DNA concentration on the vesicle surface is plotted against inverse temperature.

The values obtained in Table 1 show that membrane-anchored DNA has a lower binding enthalpy and a reduced entropic benefit for dehybridization when compared to the same sequence in free solution. Enthalpy changes, ΔH, were found to be in the range −135 to −171 kJ mol⁻¹ (cf. −276 kJ mol⁻¹ for the same DNA sequence in free solution) and the average entropy change for single-cholesterol-anchored DNA is ΔS = −381 J K⁻¹ mol⁻¹, compared to ΔS = −767 J K⁻¹ mol⁻¹ for the same sequence in free solution. Although there are differences in binding geometries, a similar entropy change for the double-cholesterol-anchored DNA is predicted.

In the next section we will examine the differences in melting temperatures that we observe with respect to our proposed model for the modulation of DNA duplex stability by intermembrane interactions. We first examine the differences between POPC and POPG vesicles where intermembrane forces can be calculated from well-established theoretical models. This will allow us to make predictions for the area per DNA in the osculating region and the total area of these adhesive plaques between vesicles. We then examine the differences between POPC and 10% DOTAP vesicles to estimate the additional adhesive energy between the cationic vesicles induced by the polyanionic DNA molecules.

Application of the model to DNA anchored between lipid membranes

DNA duplex destabilization by the repulsive pressures between anionic vesicles

To use our model (Eqs. 3 and 4) for the modulation of the DNA melting temperature caused by intermembrane interactions, we must calculate the forces between the membranes as a function of the intermembrane separation. The total intermembrane force per unit area between lipid membranes, P_tot(X), can be calculated by (46–52)

$${\mathbf{P}}_{\text{tot}}\left(\mathbf{X}\right)={\mathbf{P}}_{\text{vdw}}\left(\mathbf{X}\right)+{\mathbf{P}}_{\text{edl}}\left(\mathbf{X}\right)+{\mathbf{P}}_{\text{und}}\left(\mathbf{X}\right)+{\mathbf{P}}_{\text{hyd}}\left(\mathbf{X}\right)\text{.}$$ (5)

P_vdw(X) is the attractive pressure due to van der Waals dispersion forces, P_edl(X) is the repulsive pressure due to the electrostatic double layer, P_und(X) is the repulsive steric pressure due to thermal undulations of the bilayer and P_hyd(X) is the repulsive short-range hydration pressure. In calculating the intermembrane pressure between vesicles we assume that the membranes flatten on adhesion and so models for the interactions between planar bilayers are applicable (i.e., we do not use the Derjaguin approximation to convert to forces between spheres) and that contributions to the intermembrane pressure from parts of the membranes outside of the adhesion plaque do not make a significant contribution, as has convincingly been argued previously by Rand and Parsegian (52).

The van der Waals and electrostatic double layer forces can be modeled by the theory of Derjaguin, Landau, Verwey, and Overbeek (DLVO) (47), that has been calculated explicitly for the interactions between lipid bilayers (46–49,51):

$${\mathbf{P}}_{\text{vdw}}\left(\mathbf{X}\right)=-\frac{A}{6\pi }\left[\frac{1}{X^3}-\frac{2}{{\left(X+\delta \right)}^3}+\frac{1}{{\left(X+2\delta \right)}^3}\right],$$ (6)

where A is the Hamaker constant (A ≈ 3 × 10⁻²¹ J for lipid bilayers in 0.1 M NaCl solution (47,53)) and δ is the bilayer thickness (δ ≈ 4 nm). The intermembrane pressure due to the electrostatic double layer can be calculated by (47,50)

$${\mathbf{P}}_{\text{edl}}\left(\mathbf{X}\right)=64k_{\mathrm{B}}T{\rho }_{\infty }{\gamma }^2{e}^{-\kappa \mathrm{X}},$$ (7)

where k_B is Boltzmann constant, T is temperature, ρ_∞ is the bulk concentration of NaCl. $\gamma =\text{tanh}(\mathit{ze}{\psi }_0/4k_{\mathrm{B}}T)$, where z is the valency of the counterions (z = 1 for all our experiments), e is the charge on an electron and ψ₀ is the surface potential of the membrane, which we take to be −123 mV for POPG membranes in 0.1 M NaCl (47). The Debye screening length, κ⁻¹, is determined by the bulk concentration of counterions and for monovalent NaCl counterions in water is given by ${\kappa }^{-1}=0.304/{\left[\text{NaCl}\right]}^{1/2}\text{nm}$. (47)

The steric repulsion due to thermal undulations of the membranes was first calculated by Helfrich (54). For membranes of bending energy κ_b (≈ 10⁻¹⁹ J (55)),

$${\mathbf{P}}_{\text{und}}\left(\mathbf{X}\right)=\frac{3{\pi }^2{\left(k_{\mathrm{B}}T\right)}^2}{64{\kappa }_{\mathrm{b}}{X}^3}\text{.}$$ (8)

The short range hydration repulsion decays exponentially with a characteristic decay length λ_h (48,49,51,52),

$${\mathbf{P}}_{\text{hyd}}\left(\mathbf{X}\right)=P_0\text{exp}(-X/{\lambda }_{\mathrm{h}})\text{.}$$ (9)

This model for an exponentially decaying, short range, repulsive pressure is an empirical fit to experimentally measured repulsive forces between lipid bilayers. Typical values for PC membranes are P₀ = 4.0 × 10⁹ Nm⁻² and λ_h = 0.21 nm (52).

Because we have a model that describes the pressure rather than the forces between membranes, we must slightly modify Eq. 3 to

$$U^{\mathbf{F}}=A_{\text{DNA}}{\int }_{D_0}^{D_0+\Delta x}{\mathbf{P}}_{\text{tot}}\left(\mathbf{X}\right)\cdot d\mathbf{X},$$ (10)

where A_DNA is the area per DNA in the binding site between vesicles. We will now proceed to use this model to make predictions about the system from our data.

The pressures between POPC and POPG membranes experienced during DNA binding can be evaluated for the relevant intermembrane separations. Using Eqs. 5–9, the magnitude of the intermembrane pressures between POPC and POPG membranes are plotted in Fig. 8. We assume that the electrostatic contribution of the headgroup dipoles of POPC lipids to the intermembrane pressure is not significant, as is normally presumed (46,48,51,52). Note that the total pressure between POPC membranes is predicted to be attractive for intermembrane separations between ∼3 and 9 nm, whereas the total pressures between POPC and POPG membranes are repulsive at all other separations that we consider.

Figure 8.

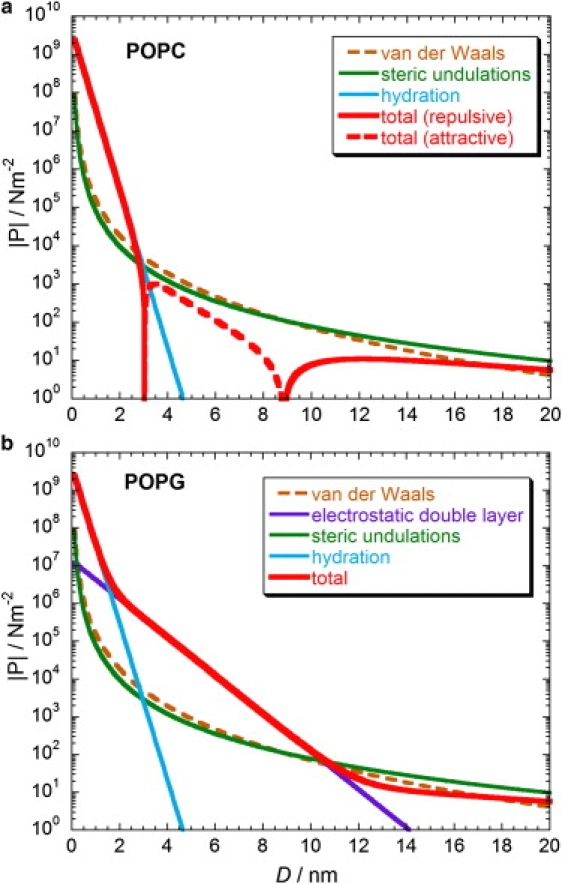
Theoretical models for the absolute intermembrane pressures as a function of separation: (a) POPC membranes; (b) POPG membranes. Repulsive forces are denoted by solid lines and attractive forces are represented by dashed lines.

We estimate the distance along the reaction coordinate between the bound and unbound state, Δx, to be the change in contour length between double-stranded and single-stranded DNA, therefore Δx = n(l_ss − l_ds), where n is the number of DNA bases, l_ss is the length per base of ssDNA (= 0.59 nm) and l_ds is the length per base of double-stranded DNA (= 0.34 nm). Therefore for a 10-base binding segment, Δx = 2.5 nm. This is consistent with single molecule force spectroscopy experiments that measure the distance to the free energy barrier between double-stranded and single-stranded states for short DNA oligonucleotides to be Δx_b = 0.7 + 0.07n nm = 1.4 nm for a 10-base sequences (56), located roughly half way between our estimate for the distance between the bound and unbound state.

We use our theoretical model to estimate the area per DNA in the adhesion plaque that would be necessary to cause the observed shift in melting temperatures between POPC and POPG vesicles for our single-cholesterol anchored DNA. This calculation will assume that the area per DNA (A_DNA) is independent of the lipid composition of the vesicle. The average difference in melting temperatures between POPC and POPG vesicles in Fig. 5 a is ΔT_m = 11.6°C. Assuming that ΔS⁰_POPC = ΔS⁰_POPG = −381/N_A J K⁻¹ (where N_A is Avogadro's number) and ΔH⁰_POPC = ΔH⁰_POPG, then, from Eq. 9, we can write $\Delta U^{\mathbf{F}}=\Delta T_{\mathrm{M}}\left(\Delta S^0+k_{\mathrm{B}}\text{ln}\left(C_{\mathrm{T}}/4\right)\right)=A_{\text{DNA}}\Delta \xi$, where we define ΔU^F = U^F_POPG − U^F_POPC, $\xi ={\int }_{D_0}^{D_0+\Delta x}{\mathbf{P}}_{\text{tot}}\left(\mathbf{X}\right)\cdot d\mathbf{X}$ and Δξ = ξ_POPG − ξ_POPC. We take C_T to be the effective concentration of DNA when anchored to the vesicle surface, as described earlier. In the range D₀ to D₀ + Δx (= 3.4–5.9 nm), P_tot(X) for POPG is repulsive in the range of 10⁵–10⁴ Nm⁻² and dominated by the electrostatic double layer (Fig. 8 b), whereas P_tot(X) for POPC is attractive in the range 10³–10² Nm⁻² (Fig. 8 a). Therefore, it is reasonable to make the simplifications Δξ = ξ_POPG, because ξ_POPG >> ξ_POPC, and for POPG P_tot(X) = P_edl(X). Taking an average effective concentration for the DNA at membrane surface coverages investigated, this predicts A_DNA ≈ 41 nm², i.e., an average separation between DNA in the adhesion plaque of approximately (A_DNA)^1/2 ≈ 6.4 nm. This seems reasonable because double-stranded DNA has a diameter of 2.0 nm, which would be the lower, close-packed limit.

We can use this estimate to extrapolate to an average total area for the adhesion plaque between vesicles. Because we have already reported for POPC vesicles that the aggregation behavior of these vesicles undergoes a transition from small, stable aggregates to continuous aggregation between 19 and 39 DNA per vesicles, which results from the binding sites between vesicles becoming saturated and sufficient free DNA on the remaining vesicle surface being available to bind to further vesicles in the sample (6). Therefore we can estimate that the adhesion plaque saturates at ∼20 DNA per vesicle, which would predict an average area of an adhesion plaque on vesicles with a mean diameter of 100 nm, A_plaque ≈ 812 nm². This is equivalent to a circular adhesion plaque of diameter 32 nm, a perfectly reasonable estimate given the geometric constraints of a deformable, 100 nm diameter vesicle.

No significant difference between the intermembrane pressures of POPC and POPG vesicles is predicted by our model in the range D₀ to D₀ + Δx (= 17–19.5 nm) for the double-cholesterol-anchored adhesion geometry (Fig. 8). This is consistent with our experimental measurements of the melting temperatures in these systems (Fig. 5 b), where no obvious difference in T_m is observed for the different lipid compositions. Therefore, specific adhesion molecules that separate the vesicles (or other particles) by a sufficiently large distance do not gain a sufficient contribution to the free energy landscape for binding from the interparticle forces.

The adhesive energy between cationic vesicles induced by DNA

Our model is insufficient to be used to directly predict the melting temperatures of the vesicles containing 10% DOTAP because superimposing the work done by the intermembrane interactions onto the free energy landscape of the DNA does not capture the physics of the attraction induced between the membranes by the intermediary polyanionic DNA strands. A more sophisticated model for the separation-dependent intermembrane pressure that includes a consideration of the membrane-DNA in addition to membrane-membrane interactions would need to be developed. However, from our current model, it is possible to estimate the work of adhesion per DNA, U^F_10%DOTAP, contributed by the membranes to increase the thermal stability of the DNA. The average difference in melting temperature between POPC and 10% DOTAP vesicles, ΔT_m = 8.6°C. Again assuming ΔS⁰ is independent of lipid composition, this predicts an attractive contribution from the membranes of U^F_10%DOTAP ≈ −1.4 k_BT per DNA at T = 323 K. This would imply that the total adhesion energy between vesicles with an adhesion plaque of 20 DNA is ∼−28 k_BT, a strong attraction. This is sufficiently high that it seems surprising that specific interactions between DNA strands still dominate the system behavior as opposed to nonspecific electrostatic aggregation. However, as each DNA in the binding site unbinds, it will be able to diffuse out of the osculating area, reducing the total attractive energy between vesicles. Therefore, once all of the DNA molecules are unbound, the attractive energy is reduced to a point that is insufficient to result in permanent, irreversible aggregation of the vesicles. This is evident from our experimental data as we find reversible aggregation for 10% DOTAP vesicles decorated with the single-cholesterol-anchored 10-base DNA sequences. It should be noted, however, that experiments with DNA-modified 50% DOTAP vesicles and 10% DOTAP vesicles modified with the double-cholesterol-anchored DNA did not show thermally-reversible aggregation, probably due to the nonspecific attraction between the vesicles dominating the behavior of the system.

Possible implications

We explore some possible implications of how nature might use lipid composition as a signaling mechanism to tune the free energy landscape of membrane-bound ligand-receptor pairs and also the implications to the nanotechnology of programmable assembly by DNA hybridization. First, it should be noted that the force acting on the DNA in the binding geometry of our system is in the shearing mode (Fig. 9) as opposed to the unzipping geometry. Force spectroscopy experiments on the same DNA sequence in both shearing and unzipping modes show that DNA strands unbind at much lower forces when unzipped (57), this is analogous to the force unfolding of proteins being dependent on the pulling geometry (58,59). Experiments that use membrane-anchored DNA as model membrane fusion receptors (8,9) will experience intermembrane pressures that act to unzip the DNA as opposed to shearing (Fig. 1). Vesicle fusion also requires bringing the bound membranes into closer apposition, where the hydration forces dominate and therefore much larger repulsive forces between membranes contribute to the free energy landscape of DNA binding, acting to destabilize the DNA duplex. Low fusion efficiencies (as measured by vesicle contents mixing assays (8), although higher fusion efficiencies are reported using lipid mixing assays (8,9)) have been reported for vesicles in these experiments and this has been considered to be due to weaknesses in the hydrophobic coupling of the DNA to the membrane. Although this may be a significant contribution to the low efficiencies reported, it should also be considered that the intermembrane pressures that approach 10⁹ Nm⁻² when intermembrane separations are of the order of the size of a water molecule (0.25 nm) will significantly contribute to destabilizing DNA duplexes that attempt to pull apposing membranes into close contact. This analysis suggests that nature must design efficient membrane fusion machinery to have high binding strengths that will not be destabilized by these short-range repulsive forces.

Figure 9.

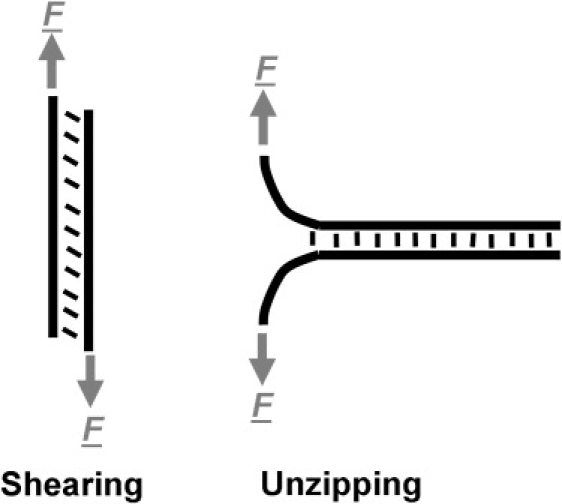
Two modes of force-induced dehybridization of DNA strands: (left) shearing; (right) unzipping.

Nature could use intermembrane forces to subtly tune the binding affinities of intermembrane ligand-receptor pairs. Recruiting or excluding charged lipids to or from osculating regions of membrane could be used as a signaling mechanism to tilt the free energy landscape of intermembrane adhesion molecules in a controlled manner. Our results for 10% DOTAP vesicles show that binding of macro ions between oppositely charged membranes can stabilize the binding between a ligand-receptor pair. Natural lipid membranes are anionic, therefore controlling the number of cationic (lysine and arginine) or anionic (glutamic acid and aspartic acid) amino acids in the intermembrane binding domains of receptor proteins could provide an evolutionary mechanism for regulating their binding strengths. Posttranslational modifications to receptors that alter their net charge could also be a signaling mechanism that tilts the free energy landscape for the association of membrane-bound ligand-receptor pairs.

From a nanotechnology perspective, accurate quantitative prediction of melting temperatures is crucial for the design of many nanoscale self-assembly strategies. Examples include the annealing of architectures at temperatures close to T_m and disassembly of sections of structures assembled using several different complementary DNA sequences. Precise prediction of DNA association temperatures is also inherent to more intricate approaches such as the hierarchical assembly of multiple components by the controlled cooling through the melting transitions of numerous DNA sequences. Therefore the effect of interparticle forces in modulating DNA stability is an important consideration for engineering the self-assembly of these structures.

Summary

By varying the lipid composition of nanoscale vesicles, we have shown how interparticle forces can modulate the thermodynamics of DNA-mediated self-assembly by contributing to the binding free energy of the system. We propose a simple quantitative model to evaluate this effect and use this to predict physically rational estimates for the area per DNA in the binding sites and the total size of the osculating regions between 100 nm vesicles. We have shown that increasing the separation between tethered vesicles to significantly reduce the intermembrane pressures effectively eliminates the contribution of intermembrane interactions to the free energy landscape of DNA binding. Vesicles containing a small proportion (10%) cationic lipid experienced a small nonspecific electrostatic attraction induced by the polyanionic DNA. This attraction was not strong enough for the case of the single-cholesterol anchored 10-base DNA sequences to prevent specific binding and unbinding of vesicles but contributed to increase the thermal stability of the DNA duplex. The impact of interparticle interactions on DNA stability should be considered in the rational design of programmable self-assembly of nano- and microstructured materials. These results may also hold important biological implications to the coupling of local lipid composition to signaling processes between the myriad of membrane-associated ligand-receptor pairs.