Three-dimensional integrated microfluidic architectures enabled through electrically switchable nanocapillary array membranes

Abstract

The extension of microfluidic devices to three dimensions requires innovative methods to interface fluidic layers. Externally controllable interconnects employing nanocapillary array membranes (NCAMs) have been exploited to produce hybrid three-dimensional fluidic architectures capable of performing linked sequential chemical manipulations of great power and utility. Because the solution Debye length, κ⁻¹, is of the order of the channel diameter, a, in the nanopores, fluidic transfer is controlled through applied bias, polarity and density of the immobile nanopore surface charge, solution ionic strength and the impedance of the nanopore relative to the microfluidic channels. Analyte transport between vertically separated microchannels can be saturated at two stable transfer levels, corresponding to reverse and forward bias. These NCAM-mediated integrated microfluidic architectures have been used to achieve highly reproducible and tunable injections down to attoliter volumes, sample stacking for preconcentration, preparative analyte band collection from an electrophoretic separation, and an actively-tunable size-dependent transport in hybrid structures with grafted polymers displaying thermally-regulated swelling behavior. The synthetic elaboration of the nanopore interior has also been used to great effect to realize molecular separations of high efficiency. All of these manipulations depend critically on the transport properties of individual nanocapillaries, and the study of transport in single nanopores has recently attracted significant attention. Both computation and experimental studies have utilized single nanopores as test beds to understand the fundamental chemical and physical properties of chemistry and fluid flow at nanometer length scales.

INTRODUCTION

The goal of micrototal analysis systems (μ-TAS) (Refs. ^{1, 2}) is to develop a single, miniature device that performs vastly scaled-down versions of traditional analytical laboratory functions resulting in fast analysis times, increased sensitivity, and significant reductions in the volume and cost of reagents. A comprehensive μ-TAS system would, within itself, have the capability to accept and pretreat a sample, then subsequently implement the analytical unit operations required to isolate and either identify or determine the analyte. These latter two steps might be comprised of sequential independent steps so that the entire system could carry out a multidimensional chemical analysis. As an example, one might perform an electrophoretic separation in an on-chip capillary channel,³ selecting and isolating a single band from the separation,⁴ then injecting just that single isolated band into an electrospray mass spectrometer for identification.⁵

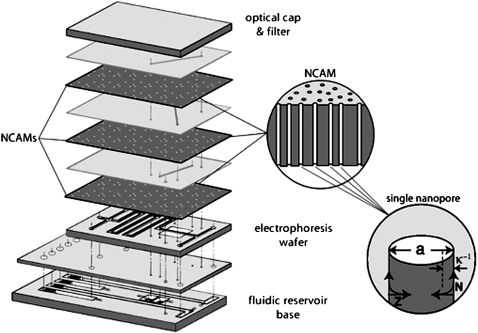
Microfluidic technology has developed such that separations⁶ and detection⁷ can be accomplished with high efficiency. However, sample injection, isolation, and mixing are difficult to achieve within a μ-TAS device without the use of mechanical pumps, valves, and mixers.⁸ Furthermore, increasing the complexity of the chemical analysis by sequentially linking steps places demands on the physical architecture that ultimately are difficult to satisfy in two-dimensional, i.e., planar structures. Nanofluidic technology can complement and greatly expand the functionality of μ-TAS devices by accessing the third dimension, thereby creating three-dimensional μ-TAS devices and increasing the degree of spatial and temporal control of molecular movement. Hybrid nanofluidic-microfluidic structures can greatly simplify multidimensional chemical analyses in μ-TAS formats by enabling the physical isolation of analyte-bearing fluid volume elements, i.e., voxels, as shown in Fig. 1.

Figure 1.

Exploded view schematic diagram of an integrated fluidic μ-TAS structure with nanocapillary array membranes (NCAMs) providing electrically switchable fluidic communication between adjacent layers. The composite diagram (left) shows the vertically separated planar layers, each of which can be assigned a unique analytical unit operation. NCAM switching layers are interposed between layers carrying perpendicular microfluidic channels. Inset (middle) shows a schematic cross section of an NCAM exhibiting nonintersecting high aspect ratio nanopores spanning the thickness of the membrane. Second inset (right) shows a single nanopore and the relationship between the pore diameter, a, and the inverse Debye length, κ.

Nanofluidics specifically refers to fluid flow in structures of comparable size to fundamental physical scaling lengths, e.g., the Debye length in ionic solutions. Consequently, fluids confined in these structures may display physical behavior not observed at the micrometer and longer length scales. Furthermore, the large surface area-to-volume ratio characteristic of these structures makes a significant impact by enhancing interfacial interactions which can result in improved physical separation efficiencies and reaction rates, and drastically reduced Joule heating effects during electrokinetic flow. Finally, at the reduced dimensions characteristic of nanoscale structural features, diffusion becomes a viable mass transport mechanism and the restriction to laminar flow placed on microfluidic channels by the reduced Reynolds numbers can be circumvented. Thus, the fact that nanopore diameters are commensurate with natural scaling lengths in nanofluidic structures opens new avenues for the manipulation of fluid flow.

NANOFLUIDIC TRANSPORT

In microfluidic devices, fluid transport is generally accomplished by applying pressure or an electric field. Rice and Whitehead, in a seminal 1965 publication,⁹ described the flow of a charged fluid through an infinitely long cylindrical capillary with a small zeta potential, ζ. In such structures the potential, φ, at a radial distance, r, is given by the Poisson-Boltzmann equation,

$$\frac{1}{r}\frac{d}{dr}\left(r\frac{d\phi }{dr}\right)={\kappa }^2\phi ,$$ (1)

where κ, the inverse Debye length,

$$\kappa =\sqrt{\frac{8\pi n{e}^2}{\epsilon kT}}$$ (2)

is determined by the ion number density, n, the dielectric constant, ε, the Boltzmann constant, k, and the temperature T. Knowing the potential, ϕ(r), the charge density can be recovered from the Poisson equation, the solution of which may be expressed as a modified Bessel function of the first kind, I₀(κr), scaled to the capillary radius, a. An equation of motion under combined pressure and electrically driven flow can then be written,

$$\frac{1}{r}\frac{d}{dr}\left(r\frac{d{\upsilon }_z}{dr}\right)=\frac{1}{\eta }\frac{dp}{dz}-\frac{F_z}{\eta },$$ (3)

where η is the viscosity, dp∕dz is the pressure gradient, and F_z is the body force driven by the action of the applied field, E_z, on the net charge density in the double layer. When there is no net applied pressure, the velocity is given by

$${\upsilon }_z\left(r\right)=\frac{\epsilon {\phi }_o}{4\pi \eta }{E}_z[1-\frac{I_o\left(\kappa r\right)}{I_o\left(\kappa a\right)}].$$ (4)

From 4 it follows that fluid flow in nanocapillaries is governed by the dimensionless κa product, that is, the relative sizes of the Debye length and the pore radius.

The Debye length, κ⁻¹, which characterizes the length scale of ionic interactions in solutions spans the range 1 nm<κ⁻¹<10 nm for buffered solutions of singly-charged ions 100 mM>μ>1 mM. Thus, in the presence of an axial electric field at constant pore radius, simply adjusting the ionic strength, μ, of the solution can shift the fluidic behavior between regimes where electrokinetic flow is dominated by electro-osmosis (small μ) or ion migration (large μ). In addition, the enhanced surface-to-volume ratio in nanofluidic systems magnifies the importance of the nanopore surface charge density, σ, in determining fluid transport, because the total charge associated with the walls is immobile. Since it determines the magnitude of the surface potential and the applicability of the Debye-Hückel approximation, surface charge density provides an experimental handle to adjust the microscopic processes that determine transport in nanopores. For example, a single 50 nm diameter nanopore of 5 μm length, l∕a∼100, with σ=2×10⁻³ C m⁻² would display ∼10⁴ elemental charges. Under these conditions a 1.6 mM solution of 1:1 monovalent electrolyte would have just enough counterions to balance the surface charge at the nominal solution concentration. Note that in order to maintain intrapore electroneutrality under these conditions, every mobile ion in the pore is a counterion—there are no coions. In contrast, the ratio of the number of surface charges to the number of solution charges enclosed by a given cylindrical region, N_S∕N_V, is governed by a, σ, and the solution concentration, C, according to N_S∕N_V=4σ∕aC, so increasing the diameter from 50 nm to 50 μm decreases the importance of the surface charge by a factor of 10³. Thus, the experimentalist is presented with a rich array of possible handles for the control of nanofluidic flow, including varying the applied bias, charge density (e.g., through control of pH), pore diameter, charge polarity, and∕or solution ionic strength.

NANOCAPILLARY ARRAY MEMBRANES

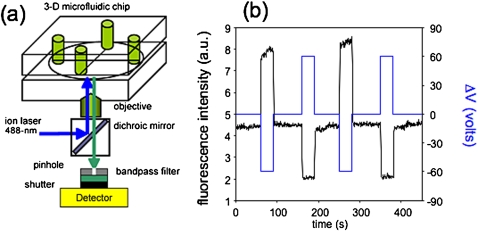
One immediate application of these nanofluidic control phenomena lies in constructing multilevel, i.e., three-dimensional, integrated microfluidic structures by incorporating nanocapillary array membranes (NCAMs) between orthogonal microfluidic channels.¹⁰ Typically NCAMs are polycarbonate, nuclear track etched membranes ca. 5–10 μm thick, containing 10⁸ cm⁻²–10⁹ cm⁻² pores with diameters in the range 10–500 nm. When an NCAM is placed between two vertically separated microfluidic channels and an electrical potential is applied across the membrane, fluid voxels can be transferred from one microfluidic channel to the other. The essentially digital character of this transfer, cf. Fig. 2, was demonstrated by Kuo et al.³ who showed that above a condition-dependent threshold potential, 100% mass transfer efficiency is achieved. That is, under saturated bias conditions all ionic and molecular species entering the cross-section spanned by the NCAM transit the NCAM pores and are transferred between source and receiving microchannels. In contrast, at bias potentials below the threshold, the efficiency of analyte mass transfer is pore size-dependent, showing that NCAMs display hindered transport characteristics which can be exploited for sample stacking and preconcentration, cf. Fig. 3,¹¹ in microfluidic devices and for desalting biological samples in complex ionic solutions.⁵

Figure 2.

(a) Schematic diagram of the confocal laser induced fluorescence (LIF) apparatus used to characterize the fluid flow in three-dimensional microfluidic-nanofluidic hybrid architectures. (b) Illustration of the digital character of NCAM-mediated fluidic transfer. The bias (blue) is applied in three polarities (negative, neutral, positive), corresponding to the three states of fluorescent probe transfer to the receiving microchannel (purple). LIF measurements are acquired from the microfluidic receiving channel directly under the NCAM. Fluid flow is maintained in the microfluidic channels when forward bias potentials are not applied.

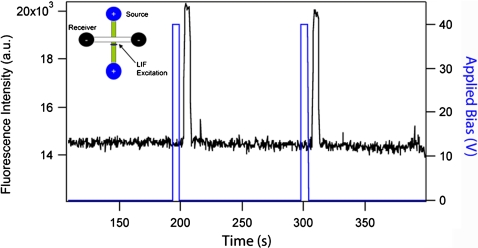
Figure 3.

Illustration of sample stacking. Fluorescence signal (black) monitored in the source channel as a function of time and applied bias (red). (Inset) LIF signal acquisition geometry. LIF is monitored ∼1 mm away from the microchannel cross-section in a channel prepared with 1 μM fluorescein in 10 mM pH 9 phosphate buffer.

The robust and controllable transfer properties of NCAMs opens possibilities for numerous applications within μ-TAS devices. For example, Cannon et al.¹² designed an NCAM-based sample injection scheme for chip-based separations. In this approach, the magnitude and length of the forward bias pulse are adjusted to control the volume of analyte solution injected into an electrophoresis column, thereby achieving gated injections. The inverse of sample injection is sample collection, and the ability to selectively remove separated bands from an on-chip electrophoresis run constitutes de facto a preparative separation, one with the capacity to isolate exceedingly small mass analyte bands. Tulock et al.⁴ exploited this idea to sequester individual analyte bands from the electrophoretic separation of multicomponent peptide mixtures into fluidically isolated channels. Of course, once the bands have been isolated into separate microfluidic channels they may be subjected to subsequent processing, e.g., to accomplish 2D separations, an object of active investigation in our laboratory.

Fluid flow in microfluidic channels is laminar, owing to the low Reynolds numbers, R_e<10⁻², typical of flow in these structures. This inherently limits passive mixing in the microfluidic channel to diffusive mechanisms, which, at length scales of tens to hundreds of micrometers, are slow. However, if an array of nanopores, i.e., an NCAM, is placed between two vertically separated microfluidic channels, the nanopores can act as micromixers facilitating mixing via diffusion. The key concept is that adjacent nanopores are separated by distances determined by the pore density, and, to first order, complete mixing requires only that the volume between pores be completely accessed. For a nominal density of N_p∼4×10⁸ cm⁻², the average separation is 500 nm. Thus, simple linear diffusion yields characteristic diffusive mixing times of 2.5 ms for D=10⁻⁶ cm² s⁻¹. Kuo et al.¹³ demonstrated the fast micromixing capabilities of NCAM-based nanopore arrays in a three-dimensional device by successfully performing two chemical reactions: a binding reaction between Ca²⁺ and calcium green-labeled dextrans, and a fluorigenic reaction between derivatized glycine and o-phthaldialdehyde in the presence of 2-mercaptoethanol. Chang et al.¹⁴ then incorporated these ideas into a miniature Pb²⁺ sensor. In this sensor, the NCAM is used to deliver small volumes of Pb²⁺-containing samples to a DNAzyme molecular beacon reagent contained in another channel. The rapid mixing characteristics of the NCAM-based fluid injection means that the analytical signal is developed within a small confined volume, typically a few pL, thereby dramatically enhancing the concentration sensitivity of the measurement.

Finally, fluidic isolation within a multidimensional device can be critical to realizing single step sample determinations. Consider, for instance, a sample whose separation is optimized in an acidic, low ionic strength environment but whose detection is optimized in a basic, high ionic strength environment. Keeping these two disparate chemical environments isolated within the same device would be highly advantageous. Given the predominance of the surface charge density in establishing a huge disparity between counterions and coions in the fluid environment inside a small diameter nanopore, it is not surprising that NCAMs exhibit excellent fluidic isolation properties. For example, NCAMs with 15 nm pores can maintain excellent fluidic isolation between two microfluidic channels containing solutions whose ionic strengths differ by a factor of 100. Protons with their inherently high mobility present the ultimate challenge in separating microfluidic environments with different properties. Fa et al.¹⁵ showed that NCAMs with a pore diameter less than 50 nm could maintain two distinctively different pH solution environments. The NCAMs studied were characterized by a positive zeta potential, ζ>0, so at small nanocapillary diameters the electrical double layer overlap established an energy barrier for either diffusion or electrokinetic transport of cations. Proton transfer through an NCAM into microchannels was observed to be reduced for pore diameters, d⩽50 nm and ionic strengths ⩽50 mM, while for large pore diameters or higher solution ionic strengths, the incomplete overlap of the electric double layer allowed more facile ionic transfer across the membranes, viz. Table 1.

Table 1.

pH gradient changes without microchannel flow.

Initial ΔpHa	2.0	3.0	4.0
Pore diameter (nm)	Δ(ΔpH)b
10	0.08	0.12	0.23
50	0.1	0.16	0.39
200		1.3

^aΔpH=pH (source)−pH (receiving).

^bΔ(ΔpH)=shift in pH difference at steady state.

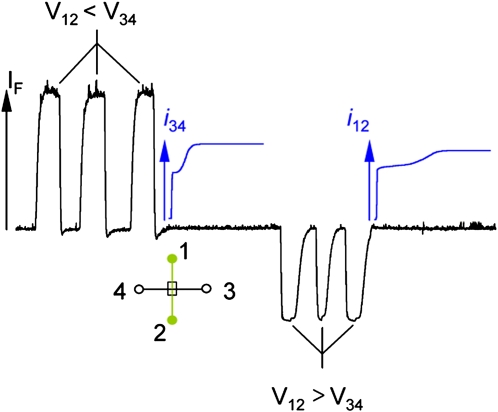
The ability of NCAMs to function as fluidic isolators, gated injectors, and microreactors is principally controlled by applied potential. However, the electrical behavior of fluid flow in coupled microfluidic-nanofluidic architectures cannot be understood from experiment alone. Computational modeling and simulations correlated with experimental data are needed to produce detailed pictures of molecular level phenomena characteristic of these architectures. One example of the type of unexpected behavior encountered in these structures is illustrated in Fig. 4. Here a series of forward bias pulses are applied to the simple NCAM junction shown schematically in the inset. The current measured immediately after the last bias pulse exhibits a clear biphasic response upon re-establishing fluid flow in the microchannel. The same qualitative current recovery response is observed independent of which spatial direction the bias pulse is applied. The details of the spatial and temporal behavior of the solution compositional changes encountered upon transporting ionic solutions from one microfluidic channel to another through an NCAM were recovered from a compact model simulation for the electrical parameters obtained from a self consistent solution of the Poisson-Boltzmann, Nernst-Plank, and Navier-Stokes equations as discussed by Chatterjee et al.¹⁶ The observed biphasic response reflects underlying transport dynamics that highlight the differential transport characteristics of different ionic components of the solution; Na⁺, $\mathrm{H}\mathrm{P}{\mathrm{O}}_4^{2-}$, and ${\mathrm{H}}_2\mathrm{P}{\mathrm{O}}_4^{-}$ in this specific instance.

Figure 4.

Plot of the current recovery (blue) in the receiving channel after solution transfer across the NCAM. (Left) Transfer of solution by three successive forward bias pulses (V₁₂<V₃₄), as monitored by the increase of fluorescence (black), is followed by monitoring the current in the 3-4 channel, i₃₄. (Right) Transfer of solution by three successive reverse bias pulses (V₁₂>V₃₄), as monitored by the decrease in fluorescence, is followed by monitoring the current in the 1-2 channel, i₁₂. (Inset) Schematic diagram of the sample structure. Channel 1-2 is nominally the source channel, and channel 3-4 is the receiving channel. LIF is monitored directly at the microchannel cross-section in a channel prepared with 1 μM fluorescein in 10 mM pH 9 phosphate buffer.

SINGLE NANOCAPILLARIES

The utility of NCAMs in a wide variety of lab-on-a-chip applications has been demonstrated. However, as useful as the membrane systems are in a practical sense, they leave much to be desired as model systems to understand fluid flow and chemical reactions in confined geometries. Nanocapillary array membranes, containing 10⁸–10⁹ pores cm⁻² are naturally characterized by dispersion in pore characteristics. In the NCAMs used for intelligent control of fluid flow, there are three types of structural irregularities: (a) different pores have slightly different angles relative to the surface plane, and therefore slightly different lengths, (b) the pores do not have uniform diameters along their length, i.e., they are not strictly cylindrical, and (c) over sufficiently large areas, defects, such as branched pores, always exist. In contrast, the study of individual, well-defined cylindrical nanopores circumvents all of the above difficulties. Because the properties of individual nanopores may be characterized in detail, they are much more useful in testing theoretical predictions of potential-driven molecular transport. Building up the ensemble properties of nanopore transport from statistical averages of individual transport events through single nanopores allows the distribution of events to be understood from the outset. Furthermore, because a single pore is fabricated specifically for studying transport, its structure can be carefully controlled and it can approach the mathematical ideal used in theoretical studies of nanocapillary transport. Thus, it is advantageous from both computational and experimental perspectives to work with systems containing a single nanocapillary as a test bed for studies into fundamental physical behavior of nanoscale fluid transport and chemistry.

Computational studies of single nanopores are critically important in that they can provide significant, molecular-level insights into fundamental fluid behavior in nanopores. Furthermore, it is clear that studying transport in individual nanopores is advantageous, because computational complexity is reduced both by the smaller number of pores and by eliminating the need to calculate interpore coupling effects. Thus, single pore computational studies can yield significant insight not available from experiment alone. Molecular dynamics simulations carried out by Qiao and Aluru have shown significant deviations from continuum behavior in 1-D Si nanofluidic channels, i.e., slit-pores, due to greatly increased counterion viscosity near the pore wall.¹⁷ Other simulations by Qiao and Aluru, focusing on the coupling between electrical and mechanical properties in single nanopores, have determined that conductivity is dominated by surface charge density.¹⁸ Quite detailed descriptions of fluid physics are possible when working at this limit. Petsev Dimiter et al. have developed analytical expressions for fluid transport in nanofluidic channels, including the effects of flow modulation by the application of an electrical potential transverse to the channel (i.e., fluidic field effect transistors).¹⁹

Experiments with single nanocapillaries also exhibit clear advantages. The experiments eliminate polydispersity in pore characteristics such as length, diameter, tapering (i.e., nonparallel sidewalls), and angle with respect to the substrate plane. Concurrently, the properties of single pores can be rationally controlled and fully characterized. Systems incorporating thousands of pores necessitate measuring ensemble averages, whereas single pore systems inherently allow single event resolution. The observation of outlying events and subpopulations is thus facilitated.

SINGLE NANOCAPILLARY EXPERIMENTS

A variety of strategies have been employed to fabricate structures incorporating single nanopores. Sun and Crooks performed the seminal work in the area²⁰ developing a template-based fabrication strategy in which a single glass fiber is inserted through an electrochemically generated seed pore in a gold membrane. Gold is subsequently electrodeposited to fully enclose the fiber which is then dissolved to leave a single 0.5<a<2 μm pore in the Au membrane. Harrell, Lee, and Martin developed an alternative single nanocapillary fabrication paradigm in which the pores of a low-density track etched membrane are filled with fluorescein, visualized via fluorescence microscopy, and a single pore is isolated by masking the remainder of the membrane.²¹ Other investigations in their laboratory have created asymmetric nanopores in track-etched polymer membranes via etching of the nuclear damage tracks with KOH∕ethanol from one side of the membrane with an acidic “stop” solution opposite.²² Half-angles up to 4.4° were obtained yielding entrance to exit aperture ratios as large as 2:1.

Our laboratory has demonstrated a rational fabrication strategy for single, high aspect ratio (ca. 100) nanopores in polymer films via focused-ion beam (FIB) milling, cf. Fig. 5.²³ Briefly, poly(methyl methacrylate) (PMMA) is spin-coated into a ∼5 μm film on Si carrier wafers. Exposure to 1–50 pA ion currents from a 30 kV Ga⁺ ion beam yields pores 75 nm<a<400 nm with either parallel or tapered sidewalls. This process enables the creation of small arrays of nanocapillaries with arbitrary relative position, number, and density. Release of the pore-containing film from the sacrificial Si carrier is facilitated by the addition of trace amounts of poly(ethylene oxide)∕poly(dimethylsiloxane) diblock copolymer to the initial PMMA solution, allowing incorporation into the previously described hybrid micro∕nanofluidic devices.

Figure 5.

(Left) Plan view SEM image of a 5×5 array of nanopores on 50 μm centers milled into a 5 μm thick PMMA sheet. The array is surrounded by a fiducial mark prepared by a milling a 10 μm wide trench to a depth of a few nanometers in a circular pattern. The pattern is readily visible in the optical microscope and facilitates alignment between microfluidic channels. (Right) A high resolution SEM image of a single nanopore in the array. The scoring apparent near the pore mouth results from the partial redistribution of the conductive Au coating during FIB milling.

CHEMICALLY ELABORATED NANOPORES

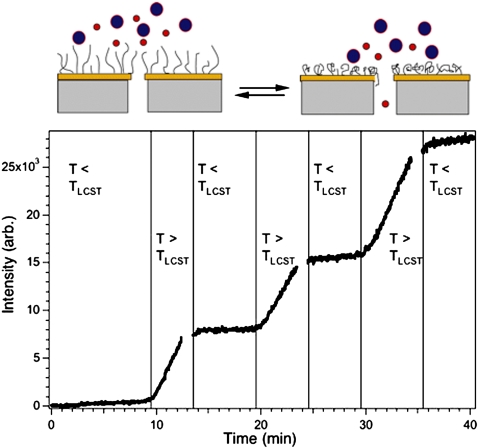
Optimization of transport and separation efficiency in nanopores requires control of the internal nanochannel environment, especially surface charge density. Lee and Martin have functionalized the interior surface of Au nanopores via chemisorption of thiols,²⁴ achieving both chemical and ionic selectivity through the adsorption of electrically neutral or charged thiols, respectively. Additionally, chemisorption of zwitterionic thiols (e.g., cysteine) onto the nanopore walls allows active control of ion transport selectivity by tuning solution pH.²⁵ pH has also been used to modulate nanopore transport by grafting pH-responsive polyelectrolyte brushes to the membrane surface, occluding the pore entrance or exit apertures.²⁶ A similar paradigm has been employed in our laboratory. We have grafted voltage,²⁷ pH, and temperature²⁸ responsive polymer brushes to membrane surfaces by atom transfer radical polymerization (ATRP) and studied their ability to modulate nanofluidic transport as shown in Fig. 6. Here, tuning the temperature through the lower critical solution temperature (LCST) of a poly(N-isopropylacrylamide) (PNIPAAm) brush grafted to the surface of an NCAM repeatedly switches between states permeable and impermeable to diffusion of a 77 kDa dextran. A comparable strategy was followed by Karnik et al. who used aminosilane chemistry to functionalize nanopore walls with proteins such as biotin and streptavidin.²⁹ Of course, once the chemistry of the nanopore is understood then an array of possibilities for control present themselves. For instance, affinity interactions in nanochannels have been harnessed by Sun et al. and used as matrix-assisted laser desorption ionization mass spectrometry preconcentration substrates.³⁰ Our laboratory has developed robust chemistries for immobilization of proteins and DNAzyme reagents on planar gold surfaces and has transferred these chemistries to nanopores with resulting enhancements in limits of detection for determinations of environmental pollutants.³¹

Figure 6.

(Top) Schematic diagram showing the manner in which the ATRP surface-grafted film regulates access to the entrance of the cylindrical nanopores, thereby establishing size-dependent transport across the NCAM. (Bottom) Reversible switching capability of a PNIPAAm grafted membrane. Permeation of 77 kDa dextran over several heating-cooling cycles through membrane prepared by first evaporating 50 nm of Au and then growing 10 nm of PNIPAAm onto an NCAM exhibiting 200 nm pores.

Clearly rational control of intrapore chemistry is a powerful capability in that it can modulate various physical interactions experienced by analyte molecules during nanopore translocation. Molecular size, shape, and charge, as well as affinity interactions can be exploited as the basis for separations. The transport of ions and analyte species is typically studied by measuring nanopore electrical transconductance. Coulter counting is a limiting case of this modality, in which molecules whose characteristic size relative to the nanopore diameter transiently diminish the measured current as they transit the nanopore. Ito et al. demonstrated nanoparticle counting in a carbon nanotube-based Coulter counting device.³² Closely related to Coulter counting are stochastic sensing applications in which specific molecular binding events in nanopores (typically biological pores such as α-hemolysin) modulate conductance.³³ In both of these applications, ensemble averages are measured through the observation of single events.

Our laboratory has pioneered the use of coupled conductance and laser induced fluorescence measurements to study fluid flow in NCAMs. As discussed above, combining these measurements with molecular dynamics simulations provides powerful molecular-level insight into transport processes. We are currently extending these methods to the study of single nanopores by developing optical techniques to measure the fluorescence of single fluorescent molecules passing the entrance and exit apertures of single nanocapillaries integrated into hybrid micro∕nanofluidic devices. Coupling optical and electrical measurements with single event resolution will allow very detailed models of processes, such as hindered electrokinetic translocation and chemical kinetics in spatially constrained environments to be developed.