Impact of Emission Anisotropy on Fluorescence Spectroscopy and FRET Distance Measurements

Abstract

The objective of this report is to provide a practical and improved method for estimating Förster resonance energy transfer distance measurement error due to unknown angles in the dipole orientation factor based on emission anisotropy measurements. We improve on the method of Dale et al. (1979), which has minor mistakes and is frequently interpreted in overly optimistic ways in the literature. To facilitate proper fluorescence intensity measurements, we also evaluated instrument parameters that could impact the measurement. The apparent fluorescence intensity of isotropic samples depends on the sample emission anisotropy, fluorometer geometry, and optical apertures. We separate parameters of the sample, and those of the cylindrically symmetric illumination source and detector in the equations describing results of unpolarized and polarized fluorescence intensity measurements. This approach greatly simplifies calculations compared with the more universal method of Axelrod (1989). We provide a full computational method for calculating the Förster resonance energy transfer distance error and present a graph describing distance error in the simplest case.

Introduction

Förster resonance energy transfer (FRET) is widely used in biophysics for tracking on-off type interactions (1). The measurement of FRET efficiency between donor and acceptor fluorophores attached to the same macromolecule can also be used to estimate the distance between fluorophore attachment points (2–5). However, FRET efficiency depends not only on the distance, but also on the orientation of the fluorophore dipoles described by the dipole orientation factor (DOF), which can take values from 0 to 4. Iqbal et al. (6) used the known structure of the short DNA double helix for the prediction of the DOF and FRET efficiency. In the case of large, multiprotein complexes, complete structural knowledge is usually missing and the orientation of the fluorophores attached to the different points might be uncorrelated, which produces distance uncertainties scattered over the whole calculated error range. Although it is impossible to measure the distribution of all three angles contributing to the DOF, with certain assumptions we can estimate the diffusion limits of the dyes during the excitation lifetime and the angle between donor and acceptor from the emission anisotropies (EAs) measured for the donor alone, the acceptor alone, and the FRET signal. The admissible range of the DOF values is restricted, because any statistical distribution narrows upon averaging and restricting values of its random variables. This method was originally derived by Dale et al. (7), but simple use of the average value of 2/3 for the DOF, regardless of its uncertainty range, is still a common practice. We updated the equation for the DOF derived in the work by Dale et al. (7) with the additional geometric constraint for unknown angles (inequality 17, missing in Dale et al. (7)). The extrema search in Dale et al. (7) was performed incorrectly, and the plots are complicated, but extrema search and plots can now be easily performed using a computer.

The typical reported values of EA for fluorophores attached to protein-DNA complexes (2–5) are 0.1–0.3, which leads to a significant uncertainty in FRET distance measurement from −15 + 20% to −25 + 30%. In this article, we use, as an example of FRET distance measurements, the human immunodeficiency virus type 1 (HIV-1) stable synaptic complex involved in HIV-1 DNA integration into the host genome. Detailed results of the FRET study of the HIV-1 integrase complex will be published separately.

In the first part of the article, we describe effects of the sample EA, fluorometer geometry, and optics apertures on the intensity and polarization measurements. Next, we calculate a sample EA from the intensity measurements. The novelty of our approach is complete separation of the illumination parameters, detector parameters, and sample EA for cylindrically symmetric illumination and detector profiles. Our results are applicable for bulk fluorescence intensity and EA measurements on isotropic samples using a fluorometer, laser gel scanner, or microscope with transillumination or total internal reflection fluorescence through a prism. In the second part of the article, we discuss effects of the sample EA on distance measurements using FRET.

Of the aspects of fluorophore behavior that contribute to FRET efficiency, we discuss only distance between fluorophores and DOF in this article. We consider isotropic samples with simple fluorophores with one absorption dipole and one emission dipole parallel to the absorption dipole. We do not cover time-resolved measurements explicitly, but most of our equations can be directly applied to each moment after excitation. We do not discuss single-molecule techniques (8–12) or anisotropic samples (13–15), but our results can be generalized for these cases with the help of books by Lakowicz (16) or Valeur (17).

Methods

Effects of EA on intensity measurements

Fluorescence light scattering partially preserves polarization of the emitted light parallel to the polarization of excitation light if the dipole orientation is not lost completely due to rotational diffusion during the excitation lifetime. The components of fluorescence intensity with polarization parallel to and perpendicular to the excitation polarization are called the parallel (I_‖) and perpendicular (I_⊥) intensity components (section 5.1.1.1 of Valeur (17)). The perpendicular/parallel ratio of the intensity components depends on the EA of the sample only: I_⊥/I_‖ = (1 − r)/(1 + 2r). For isotropic samples, any measured fluorescence intensity I is a linear combination of the parallel and perpendicular intensity components with coefficients depending only on the fluorometer configuration, not on the sample properties:

$$I=\left(p{I}_{\Vert }+\left(1-p\right)I_{\perp }\right)w,$$ (1)

where w, the weight, depends on illumination intensity and monochromator and detector efficiencies, and the fraction of parallel illumination, p, depends on the fluorometer configuration only and can be calculated as the average cosine squared of the angle between the illumination and detection polarizations over illumination and detector intensity profiles. The fluorometer averaging signal over the whole sphere has a value of p = ²/₃. Values of p different from ¹/₃ lead to a discrepancy between the measured intensity and the intensity averaged over the whole sphere 〈I〉:

$$\delta \equiv \left(I-\langle I\rangle \right)/\langle I\rangle =\left(3p-1\right)r\text{.}$$ (2)

We calculated values of p for a fluorometer with cylindrically symmetric illumination and light collection profiles. In the remainder of this section, we use calculated values of coefficient p to find EA from the intensity measurements.

We consider the illumination and detector sensitivity profiles as thin conical shells. If the coefficient p is a bilinear sum of terms linear by light source parameters and terms linear by detector parameters, with coefficients dependent on the angle between the light source and detector, the light source and detector coefficients can be averaged independently of each other over arbitrary cylindrically symmetric profiles. The fluorometer geometry is described in Fig. 1. The optical axes of illumination and detector systems are located in the horizontal plane and cross in the middle of the sample chamber at the angle ϕ. The fluorometer is assumed to be infinity-corrected with parallel beams before the excitation collimator and after the emission collimator. The fluorometer is equipped with excitation and emission linear polarizers located in the parallel beams. We first assume that the monochromators of the light source and detector have no polarization bias, i.e., the weight, w,is the same for all polarizer orientations. Monochromators with polarization bias will be discussed later. The EA will be calculated from four intensity measurements, $I_{\text{HH}}$, $I_{\text{HV}}$, $I_{\text{VH}}$, and $I_{\text{VV}}$, with horizontal (H) or vertical (V) orientations of the source (first index) and detector (second index) polarizers.

Figure 1.

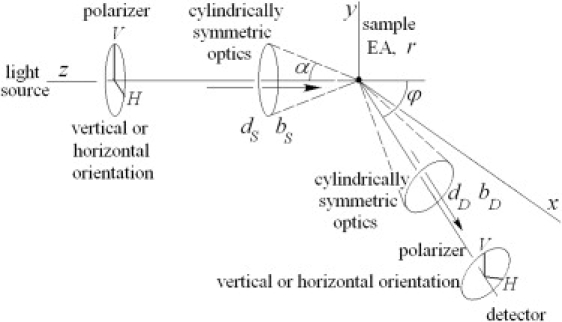
Geometry of the fluorometer. The parallel light beam from the source located on the z axis propagates through the linear polarizer and cylindrically symmetric collimating optics to the small sample located at the origin of the coordinate system. Fluorescence signal from the sample is collected by cylindrically symmetric collimating optics into a parallel beam that is passed through the linear polarizer into the detector. The detector is located in the horizontal xz plane under angle ϕ with the z axis. The cylindrically symmetric collimating optics of the light source and detector can be characterized by b- and d-factors, respectively.

The fractions of parallel illumination for the intensity components are calculated using Mathematica software (Wolfram Research, Champaign, IL) as a function of the light source (S) and detector (D) polarizer angles, ${\psi }_{\text{S}}$ and ${\psi }_{\text{D}}$, respectively, counted from the horizontal plane $\left(\psi =0\right)$:

$$p\left({\psi }_{\text{S}},{\psi }_{\text{D}}\right)=\frac{1}{6}[2+d_{\text{S}}{d}_{\text{D}}+3b_{\text{S}}{b}_{\text{D}}\left(\cos \left(2{\psi }_{\text{S}}\right)\cos \left(2{\psi }_{\text{D}}\right)+\cos \varphi \sin \left(2{\psi }_{\text{S}}\right)\sin \left(2{\psi }_{\text{D}}\right)\right)+\left(P_2\left(\cos \varphi \right)-1\right)\left(d_{\text{S}}+b_{\text{S}}\cos \left(2{\psi }_{\text{S}}\right)\right)\left(d_{\text{D}}+b_{\text{D}}\cos \left(2{\psi }_{\text{D}}\right)\right)],$$ (3)

where the factors d = 〈P₂(cosα)〉 and $b=\langle {\cos }^4\left(\alpha /2\right)\rangle$ are averaged over corresponding illumination (subscript S) or light collection (subscript D) profiles with weights proportional to normalized light intensity, α is the cone angle between the beam direction in the sample chamber and the optical axis, $P_2\left(x\right)\equiv \frac{1}{2}\left(3x^2-1\right)$ is the second Legendre polynomial. The b- and d-factors are equal to 1 for collimators with small numerical aperture (NA), which can cause polarization of the measured signal $\left(p\ne \frac{1}{3}\right)$. The higher values of NA lead to smaller b- and d-factors, which causes depolarization $\left(p\cong \frac{1}{3}\right)$. Values of d- and b-factors for typical optical configurations are calculated below. The fractions of parallel illumination for four orthogonal polarizer orientations are $p_{\text{HH}}=p\left(0,0\right)$, $p_{\text{HV}}=p\left(0,\frac{\pi }{2}\right)$, $p_{\text{VH}}=p\left(\frac{\pi }{2},0\right)$, and $p_{\text{VV}}=p\left(\frac{\pi }{2},\frac{\pi }{2}\right)$. If no polarizer is used for intensity measurements, $p={\langle p\left({\psi }_{\text{S}},{\psi }_{\text{D}}\right)\rangle }_{{\psi }_{\text{S}},{\psi }_{\text{D}}}=\frac{1}{3}+\frac{1}{6}{P}_2\left(\cos \varphi \right)d_{\text{S}}{d}_{\text{D}}$ and the uncertainty in the intensity measurement is

$$\delta =\frac{1}{2}r{P}_2\left(\cos \varphi \right)d_S{d}_{\text{D}}\text{.}$$ (4)

We noticed that this result can be derived directly from the Soleillet theorem (17–19) if d-factors are treated as “depolarization factors” for the light source and detector.

The EA of the fluorescent sample can be calculated from four intensity measurements using Eq. 3 as

$$r\equiv \frac{I_{\Vert }-I_{\perp }}{I_{\Vert }+2I_{\perp }}=\frac{a_1-\sqrt{a_1^2-4\left({\Im }^2-1\right)a_2}}{2a_2},$$ (5)

where

$${\Im }^2\equiv \left(I_{\text{VV}}{I}_{\text{HH}}\right)/\left(I_{\text{VH}}{I}_{\text{HV}}\right),$$ (6)

$$a_1=\left(3p_{\text{VV}}-1\right)+\left(3p_{\text{HH}}-1\right)-{\Im }^2\left[\left(3p_{\text{VH}}-1\right)+\left(3p_{\text{HV}}-1\right)\right],$$ (7)

$$a_2={\Im }^2\left(3p_{\text{VH}}-1\right)\left(3p_{\text{HV}}-1\right)-\left(3p_{\text{VV}}-1\right)\left(3p_{\text{HH}}-1\right)\text{.}$$ (8)

Only two intensity measurements are sufficient for a laser gel scanner or microscope with $\varphi =0°$ or $180°$ (because $I_{\text{VV}}=I_{\text{HH}}$ and $I_{\text{VH}}=I_{\text{HV}}$), and Eq. 5 can be simplified as

$$r=2/\left[3b_{\text{S}}{b}_{\text{D}}\left(\Im +1\right)/\left(\Im -1\right)-d_{\text{S}}{d}_{\text{D}}\right],$$ (9)

where $\Im =I_{\text{VV}}/I_{\text{HV}}$. Equation 9 is useful and EA can be measured unless $b_{\text{S}}{b}_{\text{D}}=0$.

Now we take into account that the efficiency of diffraction gratings used in fluorometer monochromators can vary by an order of magnitude with wavelength and polarization change. The efficiencies of the light source or detector monochromators (with vertical or horizontal slits) for vertical or horizontal polarizations are $E_{\text{SV}}$, $E_{\text{SH}}$, $E_{\text{DV}}$, $E_{\text{DH}}$, respectively; they are wavelength functions. The weight factor in Eq. 1 depends on the efficiencies and the orientation of polarizers as

$$w\left({\psi }_{\text{S}},{\psi }_{\text{D}}\right)=\left(E_{\text{SH}}{\cos }^2{\psi }_{\text{S}}+E_{\text{SV}}{\sin }^2{\psi }_{\text{S}}\right)\left(E_{\text{DH}}{\cos }^2{\psi }_{\text{D}}+E_{\text{DV}}{\sin }^2{\psi }_{\text{D}}\right)\text{.}$$ (10)

It is possible to calculate the fraction of the parallel intensity component for unpolarized measurement analytically using a computer for arbitrary cylindrically symmetric illumination and detection profiles, but we could not simplify the bulky result to a short form. In the limit of small NAs of the illumination and detector optics, the b- and d-factors are approaching to 1 from below, and the fraction of parallel illumination is

$$p=\left(gG+{\cos }^2\varphi \right)/\left(1+g+G+gG\right),$$ (11)

where factors $G\equiv E_{\text{DV}}/E_{\text{DH}}$ and $g\equiv E_{\text{SV}}/E_{\text{SH}}$ can be calculated from the four polarized intensity measurements as

$$G=\left(\frac{1}{2}{\sin }^2\varphi +\sqrt{{\left(\frac{1}{2}{\sin }^2\varphi \right)}^2+{\Im }^2{\cos }^2\varphi }\right)\left(I_{\text{HV}}/I_{\text{HH}}\right),$$ (12)

$$g=\left(\frac{1}{2}{\sin }^2\varphi +\sqrt{{\left(\frac{1}{2}{\sin }^2\varphi \right)}^2+{\Im }^2{\cos }^2\varphi }\right)\left(I_{\text{VH}}/I_{\text{HH}}\right)\text{.}$$ (13)

The g-factor is a function of the light source wavelength describing the light source polarization bias. Its definition is straightforward, but we cannot find it in the literature, so we introduced it by analogy with the G-factor, which is a function of emission wavelength that describes the detector polarization bias. If $\varphi ={\text{90}}^{\text{o}}$, the brackets in Eqs. 12 and 13 are equal to 1, and Eq. 12 takes the common form $G=I_{\text{HV}}/I_{\text{HH}}$.

Example: b- and d-factors for typical hardware configurations

If a parallel linearly polarized laser beam overfills the light source collimator lens with uniform intensity, its d- and b-factors are

$$d_{\text{S}}=P_2\left(\sqrt{\left(1-x^{-2}\right)\ln \left(1-x^2\right)}\right),b_{\text{S}}=\frac{5}{4}-x^{-2}\left(1-\sqrt{1-x^2}\right)+\frac{1}{4}\left(1-x^{-2}\right)\ln \left(1-x^2\right),$$ (14)

where $x=\text{NA}/n$ is the ratio of the numeric aperture of the lens and the refractive index of the media. If an objective lens has 100% light collection efficiency for all aperture angles, its d- and b-factors are (Fig. 2)

$$d_{\text{D}}=\left(1-x^2+\sqrt{1-x^2}\right)/2,b_{\text{D}}=\left(2+\sqrt{1-x^2}-x^2/4\right)/3\text{.}$$ (15)

The EA of an isotropic sample can be measured using a microscope with total internal reflection fluorescence illumination through a prism with a linearly polarized laser beam. The EA can be calculated using Eq. 9 if the b- and d-factors are known, the illumination polarization is fixed, and only emission polarization is changed by a linear polarizer in the observation channel. There are two polarizations of the laser beam creating the evanescent wave: s-polarized with the electric field of the incident light and the evanescent wave parallel to the interface of two media, and p-polarized with the electric field in the plane of the incident and reflected beams. The ratio of the polarization components perpendicular and parallel to the media interface for the p-polarized evanescent wave is $\text{1}-n^2{\sin }^{-2}\theta$, where $n<\text{1}$ is the ratio of refractive indexes of buffer and the glass, and θ is the incidence angle (Eqs. 5 and 6 of Axelrod (20)). For p-polarization, the b- and d-factors are d_S = 1 and $b_{\text{S}}=-n^2/(2{\sin }^2\theta -n^2)$. For the s-polarized illumination there is no depolarization, and d_S = b_S = 1. The d- and b-factors of the detector are calculated above for the microscope objective (Eq. 15). The results can be generalized for single-molecule observation.

Figure 2.

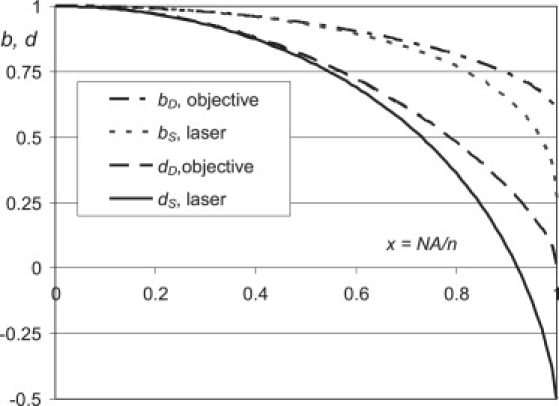
The b- and d-factors as functions of $\text{NA}/n$ for the laser illumination overfilling the condenser lens with uniform intensity and for the objective collecting fluorescence light with the same efficiency for all solid angles within its aperture, calculated using Eqs. 14 and 15.

We describe the GE Healthcare (Waukesha, WI) Typhoon Trio gel laser scanner as an example of real hardware equipment. According to the company's technical support, the Typhoon series laser scanners use two objectives with focal lengths of 6 mm (setting: platen) and 9 mm (setting: +3 mm), both with NA = 0.7. The same objective is used for the illumination and detection, but the illumination beam diameter, 0.7 mm, is much smaller than the objective aperture, and the NA aperture of the objective is applicable only for detection. The effect of illumination NA can be neglected: $N{A}_{\text{S}}\cong 0$, $b_{\text{S}}=d_{\text{S}}=1$. The b- and d-factors for the detector can be calculated using Eq. 15: $b_{\text{D}}=0.86$, $d_{\text{D}}=0.61$. The Typhoon laser scanner uses fixed filters and a photomultiplier tube as the detector, and is assumed to have no polarization or wavelength bias. Using Eq. 4 we calculate the unpolarized intensity error as a function of the sample EA: $\delta =0.31r$. If the EA of the sample is unknown $\left(-0.2\le r\le 0.4\right)$, the possible intensity error is between −6% and +12%.

Estimate of the FRET DOF from the EA

Nonradiative transfer of the excitation energy between fluorophores or from a fluorophore to a quencher in classical electrodynamics can be described as a nearfield dipole-dipole interaction. Here, we assume that the donor and acceptor dyes are two simple dipoles. The more complex cases might be studied as a combination of several dipoles (21), but such an undertaking is beyond the scope of this article. We describe the geometry of a FRET pair by the polar angles for donor, ${\theta }_{\text{d}}$, and acceptor, ${\theta }_{\text{a}}$, counted from the axis connecting the donor and acceptor, and the dihedral angle between dipole planes, ${\varphi }_{\text{da}}$ (Fig. 3). The angle between donor and acceptor ${\beta }_{\text{da}}$ can be calculated as a function of other angles

$$\cos {\beta }_{\text{da}}=\cos {\theta }_{\text{a}}\cos {\theta }_{\text{d}}+\sin {\theta }_{\text{a}}\sin {\theta }_{\text{d}}\cos {\varphi }_{\text{da}}\text{.}$$ (16)

Figure 3.

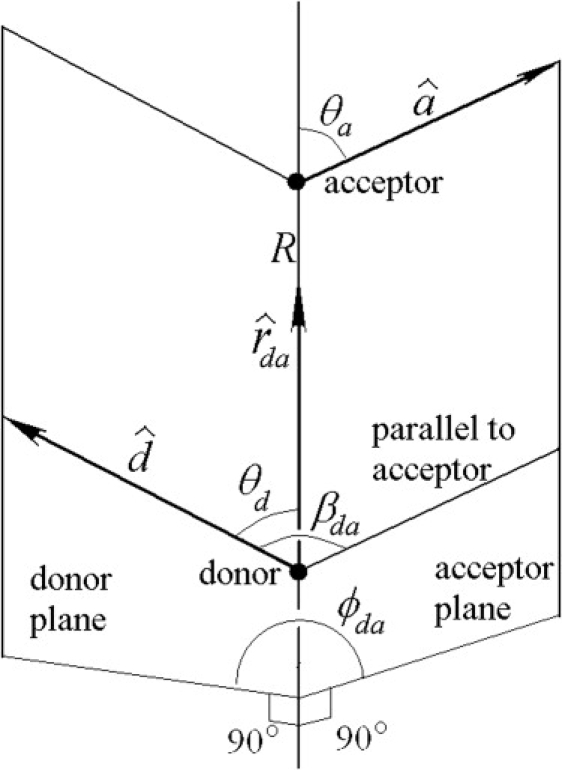
Geometry of the FRET pair. The donor fluorophore is located at distance R from the acceptor fluorophore. Donor and acceptor dipole orientations are described by the unit vectors $\widehat{d}$ and $\widehat{a}$, but in reality they are unit projective vectors (opposite directions are equivalent), which is reflected in all equations describing observable physical quantities. The donor plane is formed by the donor vector $\widehat{d}$ and the unit vector ${\widehat{r}}_{\text{da}}$ in the direction from the donor to acceptor, the angle ${\theta }_{\text{d}}$ is the angle between these two vectors. The acceptor plane and the angle ${\theta }_{\text{a}}$ are defined similarly. The angle ${\varphi }_{\text{da}}$ is the angle between the donor and acceptor planes. The angle ${\beta }_{\text{da}}$ is the angle between $\widehat{d}$ and $\widehat{a}$.

From Eq. 16, and from the fact that $-1\le \cos {\varphi }_{\text{da}}\le 1$, it is easy to derive the trivial but important geometric inequality missing in the Dale et al. (7):

$$\cos \left({\theta }_{\text{d}}+{\theta }_{\text{a}}\right)\le \cos {\beta }_{\text{da}}\le \cos \left({\theta }_{\text{d}}-{\theta }_{\text{a}}\right)\text{.}$$ (17)

If the value of $\cos {\beta }_{\text{da}}$ is known, we can use inequality 17 as a constraint on the admissible area for the polar angles.

According to Förster theory (chapter 9 of Lakowicz (17)), the rate of the energy transfer is proportional to the DOF, ${\kappa }^2={\left(3\cos {\theta }_{\text{a}}\cos {\theta }_{\text{d}}-\cos {\beta }_{\text{da}}\right)}^2$. The Förster radius, $R_0$, is defined as the distance at which FRET efficiency is 50% for the given value of the DOF; thus, it is proportional to $\sqrt[6]{{\kappa }^2}$ (7,17). The distance between fluorophores can be calculated from the FRET efficiency, E, and R₀ as $R=R_0\sqrt[6]{E^{-1}-1}\propto \sqrt[6]{{\kappa }^{\text{2}}}$. The solid-angle average value of the DOF is equal to ²/₃. Orientation averaging of ${\kappa }^2$ is only valid if the donor and acceptor dipole orientations are redistributed isotropically over the whole sphere during the donor excitation lifetime (i.e., there is no depletion of population for states with higher values of DOF compared with surviving states with smaller DOF). The discrepancy in distance measurements due to DOF values that are different from the angle-averaged value can be described by the correction factor $\Delta \equiv \sqrt[6]{{\kappa }^2/\frac{2}{3}}$, equal to the ratio of the true distance and apparent distance calculated for ${\kappa }^2=\frac{2}{3}$. Below, we estimate the correction factor range from EA measurements.

Let us consider that the donor and acceptor fluorophores are attached to a big and motionless (during excitation lifetime) macromolecule; the fluorophores are diffusing only angularly with respect to the whole macromolecule and the distance between the donor and acceptor is fixed. According to the Soleillet theorem, the FRET signal's EA is a product of the limiting anisotropy $\frac{2}{5}$, the donor and acceptor axial depolarization factors $d_{\text{d}}^{x_{\text{d}}}$ and $d_{\text{a}}^{x_{\text{d}}}$, and the depolarization factor, $P_2\left(\cos {\beta }_{\text{da}}\right)$, corresponding to the angle between the centers of the donor and acceptor distribution symmetry axes, ${\beta }_{\text{da}}$ (7):

$$r_{\text{FRET}}=\frac{2}{5}{d}_{\text{d}}^{x_{\text{d}}}{d}_{\text{a}}^{x_{\text{a}}}{P}_2\left(\cos {\beta }_{\text{da}}\right)\text{.}$$ (18)

We can calculate $d_{\text{d}}^{x_{\text{d}}}$ from the EA, $r_{\text{d}}=\frac{2}{5}{d}_{\text{d}}=\frac{2}{5}{\left(d_{\text{d}}^{x_{\text{d}}}\right)}^2$, for the donor fluorophore attached to the macromolecule in the absence of acceptor fluorophore:

$$d_{\text{d}}^{x_{\text{d}}}=\sqrt{d_{\text{d}}}=\sqrt{\frac{5}{2}{r}_{\text{d}}},$$ (19)

where $d_{\text{d}}$ is the depolarization factor for the donor alone, which is equal to the square of axial depolarization factor, $d_{\text{d}}^{x_{\text{d}}}$. The acceptor axial depolarization factor, $d_{\text{a}}^{x_{\text{a}}}$, can be calculated similarly. (If the acceptor is not a fluorophore, but a dark quencher, its axial depolarization factor cannot be derived from measured EA. This problem could be overcome if the acceptor is not a simple dipole and can be almost intrinsically isotropic.) The sign of $d_{\text{d}}^{x_{\text{d}}}$ might be negative if $r_{\text{d}}\le 0.1$ for the rotating bond or $r_{\text{d}}\le 1/160$ for the filled-cone angular distributions of the donor dipole with respect to the macromolecule (7). The negative sign of the depolarization factors might lead to two or even four different possibilities for the DOF, but it is not hard to consider all of them using a computer. The widest range for the error estimation has to be chosen in general.

We can calculate $\cos {\beta }_{\text{da}}$ from FRET polarization using Eq. 18:

$$\cos {\beta }_{\text{da}}=\sqrt{\frac{1}{3}+\frac{5}{3}\frac{r_{\text{FRET}}}{d_{\text{d}}^{x_{\text{d}}}{d}_{\text{a}}^{x_{\text{a}}}}}\text{.}$$ (20)

The sign of $\cos {\beta }_{\text{da}}$ is not defined, but one can consider $\cos {\beta }_{\text{da}}$ to be always positive and $0^{\text{o}}\le {\beta }_{\text{da}}\le {90}^{\text{o}}$ in all equations describing dipole coupling, because radiative dipole moments (unlike orientation of the fluorescent molecules) is defined not by vectors but by projective vectors, i.e., opposite orientations are equivalent. By the same reasoning, we can restrict $0°\le {\theta }_{\text{d}}\le 90°$ and $0°\le {\theta }_{\text{a}}\le 90°$ if necessary. The angle between the donor and acceptor, ${\beta }_{\text{da}}$, is the only angle that can be found from EA measurements or any other polarization measurements over isotropic samples. Measurements of the other angles contributing to the DOF require some extra knowledge about the macromolecule, its fluorophore attachment points, and its conformational dynamics, and such knowledge is hard to acquire experimentally (1).

The DOF averaged over cylindrically symmetric distributions of the acceptor and donor was derived in Dale et al. (7):

$${\kappa }^2=d_{\text{d}}^{x_{\text{d}}}{d}_{\text{a}}^{x_{\text{a}}}{\kappa }_0^2+\left(1-d_{\text{a}}^{x_{\text{a}}}\right)\left(d_{\text{d}}^{x_{\text{d}}}{\cos }^2{\theta }_{\text{d}}+\frac{1}{3}\right)+\left(1-d_{\text{d}}^{x_{\text{d}}}\right)\left(d_{\text{a}}^{x_{\text{a}}}{\cos }^2{\theta }_{\text{a}}+\frac{1}{3}\right),$$ (21)

where

$${\kappa }_0^2={\left(3\cos {\theta }_{\text{a}}\cos {\theta }_{\text{d}}-\cos {\beta }_{\text{da}}\right)}^2\text{.}$$ (22)

The DOF in Eq. 21 depends only on two unknown angles, ${\theta }_{\text{d}}$ and ${\theta }_{\text{a}}$, restricted by constraint 17; $\cos {\beta }_{\text{da}}$ can be found from Eq. 20. The minima and maxima of the DOF from Eq. 21 were calculated incorrectly in Dale et al. (7) regardless of use of constraint 17 (this can be verified numerically). The possible range of the DOF can be found using a computer.

If the EA of the FRET signal is not known, or if Eq. 18 cannot be solved for ${\beta }_{\text{da}}$ with good precision, the minimal and maximal values of the DOF with the positive depolarization factors (7) are

$${\kappa }_{\min }^2=\frac{2}{3}\left(1-\left(\sqrt{\frac{5}{2}{r}_{\text{d}}}+\sqrt{\frac{5}{2}{r}_{\text{a}}}\right)/2\right),{\kappa }_{\max }^2=\frac{2}{3}\left(1+\sqrt{\frac{5}{2}{r}_{\text{d}}}+\sqrt{\frac{5}{2}{r}_{\text{a}}}+3\sqrt{\frac{5}{2}{r}_{\text{d}}}\sqrt{\frac{5}{2}{r}_{\text{a}}}\right)\text{.}$$ (23)

If the negative depolarization factors are possible (see Eq. 19 and ensuing discussion), the minimal and maximal values of the DOF can be found using a computer by trying all sign combinations in Eq. 21 (Fig. 6).

Figure 6.

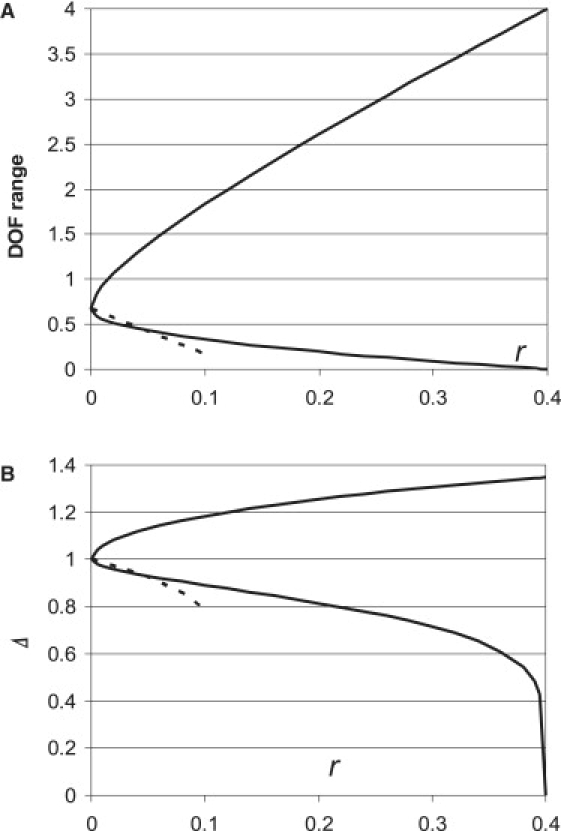
Minimal and maximal values of the DOF (A) and the distance correction factor (B) as a function of EA, if the donor and the acceptor have the same value of EA: $r_{\text{d}}=r_{\text{a}}=r$. The graph is calculated using Eq. 23 for positive (solid line) and negative (dashed line (only possible for $r\le 0.1$)) axial depolarization factors. It is easy to see that the range for the DOF slowly converges to $\frac{2}{3}$ at $r_{\text{d},\text{a}}\to 0$. The typical range of the EA, 0.15–0.25, corresponds to $-15+\text{20}\%$, or even $-20+\text{25}\%$, uncertainty for the FRET distance measurements.

Example: DOF uncertainty for the HIV-1 integrase complex

The HIV-1 integrase complex consists of four integrase molecules and two double-stranded DNA fragments (22). The DNA fragments in the complex can be the two ends of a single long DNA molecule, as in the case of the real HIV-1 DNA, or could take the form of two shorter DNA fragments. The complex is difficult to purify in vitro, but it can be separated from unreacted substrate by native gel electrophoresis. The atomic force microscopy images of the complexes lack sufficiently high resolution information and also suffer from possible deformations of the complexes during surface immobilization required for atomic force microscopy. We use FRET distance measurement on the HIV-1 integrase complex with DNA tails labeled with Cy3 and Cy5 dyes near the ends as an example.

We isolate correctly assembled complex from unreacted substrate by native agarose gel electrophoresis. The proper band on the gel was identified and measured using a laser gel scanner with donor and acceptor excitation wavelengths in the donor, the acceptor, and the FRET channel. For fluorometer measurements, gel pieces containing the band of interest were cut out and placed in a cuvette with buffer or glycerol-buffer mix. Our objective was to estimate distances between different points on the DNA within the complex. The results on the HIV-1 complex structure will be published in a separate article. We do not discuss here any structural details of the complex.

The EAs of donor, acceptor, and FRET signals were measured for the distance uncertainty calculation due to DOF. The results of the EA measurements for two FRET pair configurations are summarized in Table 1. The range of the DOF, and the distance uncertainty, were calculated for two pairs of labeling positions. The first two rows of the table correspond to the FRET pair in the labeling position 1-1′, representing the cases of the unknown and known EA of the FRET signal. The last row corresponds to the FRET pair position 2-2′ with higher EA values of donor and acceptor and known FRET EA. If the FRET EA is known, the angle between donor and acceptor, ${\beta }_{\text{da}}$, was calculated using Eq. 20. For the position 1-1′ with known FRET EA, the admissible range for the polar angles, ${\theta }_{\text{d}}$ and ${\theta }_{\text{a}}$, from inequality 17 is drawn in Fig. 4; the dipole orientation and distance correction factors calculated using Eqs. 20–22 are graphed in Fig. 5 as functions of the polar angles within their admissible area. If the FRET EA is unknown, the ranges of the DOF and distance are calculated from Eq. 23. The ranges of the DOF and distance are graphed on Fig. 6 for the case r_d = r_a.

Table 1.

DOF range and distance uncertainties

Position	$r_{\text{d}}$	$r_{\text{a}}$	$r_{\text{FRET}}$	${\beta }_{\text{da}}$	${\kappa }^{\text{2}}$ range	R uncertainty
1–1′	0.275	0.292	—	—	0.11–3.21	−26 + 30%
1–1′	0.275	0.292	−0.026	58.6°	0.15–2.50	−22 + 25%
2–2′	0.340	0.316	0.230	25.1°	0.11–3.33	−26 + 31%

Figure 4.

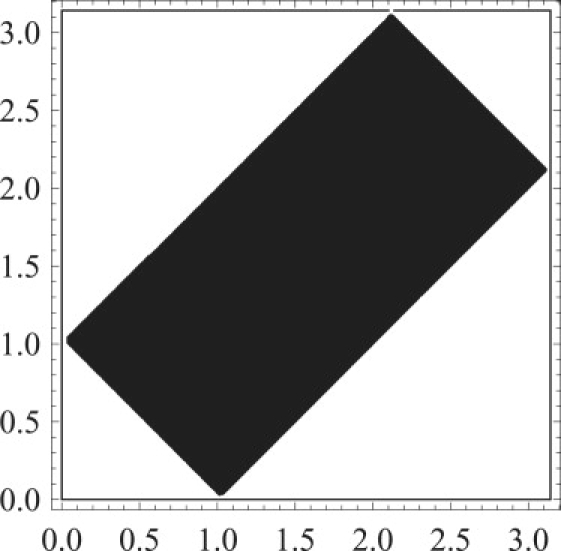
Admissible area on the polar angle plane $\left({\theta }_{\text{d}},{\theta }_{\text{a}}\right)$ (black rectangle; symmetric ${\theta }_{\text{d}}\leftrightarrow {\theta }_{\text{a}}$) has inequality 17 satisfied. To calculate this area, we use $r_{\text{d}}=0.275$, $r_{\text{a}}=0.292$, and $r_{\text{FRET}}=-0.026$. Because radiative dipole moments are projective vectors, it is enough to consider only a quarter of the symmetric admissible area with $0\le {\theta }_{\text{d}}\le \frac{\pi }{2}$ and $0\le {\theta }_{\text{a}}\le \frac{\pi }{2}$.

Figure 5.

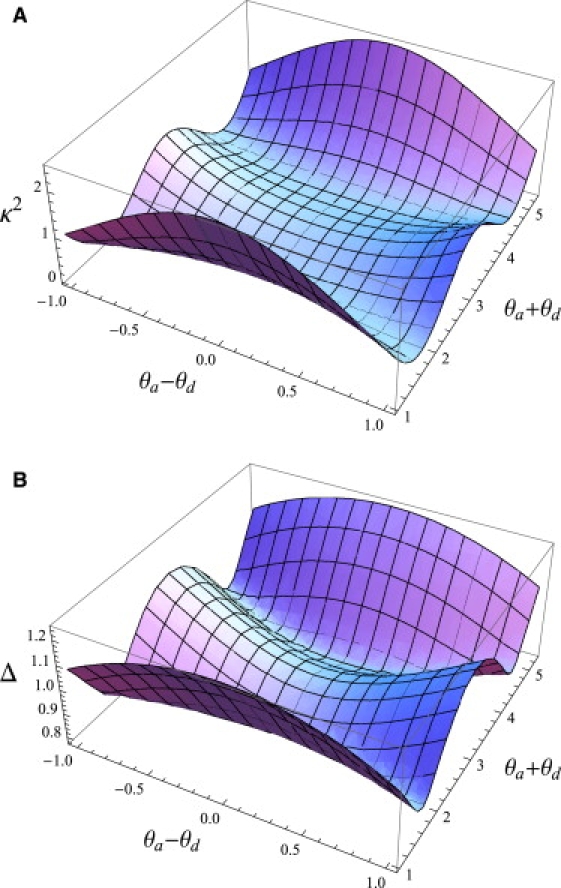
Graphs of the DOFs (A) and the distance correction factor, Δ (B) for $r_{\text{d}}=0.275$, $r_{\text{a}}=0.292,$ and $r_{\text{FRET}}=-0.026$ as a function of ${\theta }_{\text{a}}-{\theta }_{\text{d}}$ and ${\theta }_{\text{a}}+{\theta }_{\text{d}}$ over the admissible area from Fig. 4. The graphs are calculated using Eqs. 20–22.

Equation 4 describes the systematic error in the fluorescence intensity measured by the laser gel scanner due to the EA of the sample. The laser scanner may be lacking polarizers, but EA can be measured using a bulk fluorometer. The intensity correction for the Typhoon laser scanner was discussed above.

Conclusion

The EA of the sample can be calculated from parallel and perpendicular intensity components as $r=\left(I_{\Vert }-I_{\perp }\right)/\left(I_{\Vert }+2I_{\perp }\right)$. The parallel and perpendicular intensity components contribute with some weights to any intensity measurement (Eq. 1). We calculated the fractions of parallel illumination for the fluorometer with linear polarizers and cylindrically symmetric optics in Eq. 3. The b- and d-factors were introduced as the only characteristics of the source and detector with cylindrically symmetric collimating optics. Use of d- and b-factors greatly simplifies calculations compared with the more universal method of Axelrod (23). The discrepancy between intensity measurements without a polarizer and true unpolarized intensity averaged over the whole imaginary sphere with the sample in the center is described by Eq. 4. We introduced the g-factor, describing the light source polarization bias, similar to the previously defined detector G-factor for the arbitrary angle between light source and detector optical axes. In the second part of the article, we discuss effects of the sample EA on the accuracy of FRET distance measurements. We suggest calculating the distance based on the DOF average value $\frac{2}{3}$ first (even if the actual value of the DOF is different). If the DOF is different from $\frac{2}{3}$, the possible range of the distance correction factor, $\Delta \equiv \sqrt[6]{{\kappa }^2/\frac{2}{3}}$, can be calculated from EA data using Eqs. 20–22 or 23. The geometric constraint (Eq. 17) can be used to restrict the admissible area of the two remaining unknown angles in Eq. 21, if the FRET EA is known.

Fluorescently labeled HIV-1 integrase complex was used as an example of FRET distance measurement. Application of this technique to other macromolecules might require that our methods be customized, but the EAs of the donor, the acceptor, and the FRET signal are critical for the evaluation of FRET distance measurements, because the typical fluorophore EA range of 0.15–0.25 corresponds to $-15+20\%$ or even $-20+25\%$ uncertainty in the distance calculated from FRET efficiency. Our article, as well as that of Dale et al. (2), published previously, considers only cylindrically symmetric distributions of the rotating bonds that attach fluorophores to the macromolecule, as well as cylindrically symmetric optics of the illumination source and detector. The assumption about dipole orientation distribution is not valid in general, but it seems to be the only practical way to estimate the range of DOF and distance uncertainty. The rotation of the whole macromolecule complex during the excitation lifetime leads to an extra depolarization factor, which contributes to all measured EAs, but does not contribute to the DOF. As a result, Eqs. 21 and 23 might underestimate the distance error and the DOF range. The assumption about cylindrical symmetry of the optics is usually valid, but it must be verified for each setup. Calculation of the d- and b- factors might require beam profile measurements.

We suggest several different ways to deal with the uncertainty in FRET distance measurements due to DOF distribution. The choice of small, freely rotating fluorophores attached by flexible joints or of fluorophores with multiple dipole structure (21) might reduce EA. The EA value of 0.05 for both fluorophores provides a distance error of ∼$\pm 10\%$. Calculation of the integrase complex structure using exact values of DOFs (see example of DOF estimates in Iqbal et al. (6)) is impractical, but the structure can be calculated first with ${\kappa }^2=\frac{2}{3}$. Next, one could calculate the angles between dipoles, and recalculate corrected distances according to the values of the DOFs. The whole structure can be recalculated with corrected distances, which leads to recalculation of all angles again. After several iteration cycles, the algorithm might converge, so the distance and angle correction will become smaller after each iteration. If the dipole angles cannot be calculated from the structure, one can randomize DOFs within admissible ranges for all measured distances independently, calculate the structure, and compare the result with the structure calculated based on a value of $\frac{2}{3}$ for all DOFs. One should repeat randomization and structure calculation several times. Consistency among iterative calculations adds to the confidence level of the structure prediction.

The DOF does not depend on the distance between dipoles if the dipole angular diffusion relaxation time is shorter than the excitation lifetime. The DOF for the dipoles with rotation relaxation time longer than the fluorescent lifetime but shorter than the time between absorption of two photons by the same molecule (low light intensity) will be distance-dependent (Fig. 7). The FRET efficiency for slow-rotating fluorophores will be smaller than the FRET efficiency for fast-rotating fluorophores separated by the same distance (Fig. 8), because orientations with higher DOF values are depleting faster but not getting refilled by rotational diffusion. Because EA is correlated with the dipole orientation, depletion of the states with higher DOF values produces polarization of the FRET signal (Fig. 9). Another source of FRET distance measurement uncertainty might lie in the distance diffusion between fluorophores due to flexible bonds (Fig. 10). High illumination intensity in combination with extremely high viscosity (dry trehalose samples) might produce even higher dependence of the DOF on the distance between molecules if the time between photons absorbed by the same fluorophores is less than the diffusion relaxation time.

Figure 7.

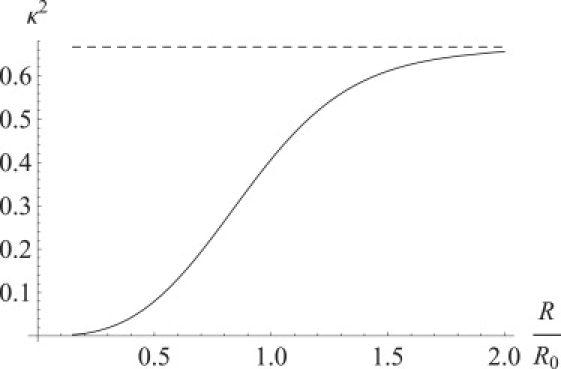
Dependence of the DOF on the distance between fluorophores if the fluorophores are rotating without constraints. The DOF for the fast-rotating fluorophores (dashed line) is equal to $\frac{2}{3}$. The effective ensemble average DOF for the slow-rotating fluorophores (solid line, calculated from the FRET efficiency curve (Fig. 8)) is smaller because of depletion of the states with higher DOF values. The distance between the fluorophores in Figs. 7–10 is measured in units of $R_0\left(\frac{2}{3}\right)$ (the Förster radius for the fluorophores with ${\kappa }^2=\frac{2}{3}$).

Figure 8.

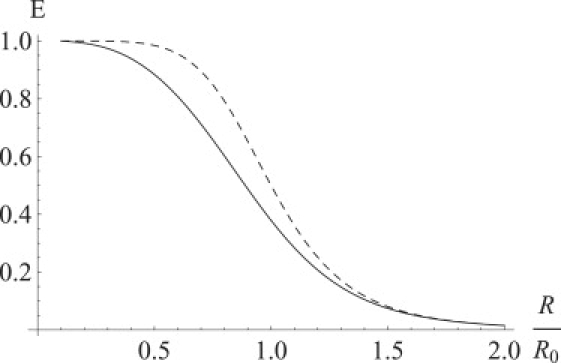
Dependence of FRET efficiency on the distance between fluorophores for the fast-rotating fluorophores $E=1/\left(1+R^6/R_0^6\left(\frac{2}{3}\right)\right)$ (dashed line) and the slow-rotating fluorophores (solid line). The FRET efficiencies for the slow-rotating fluorophores were calculated for different distances by numeric averaging of the FRET efficiency over an ensemble of randomly oriented, but motionless, FRET pairs.

Figure 9.

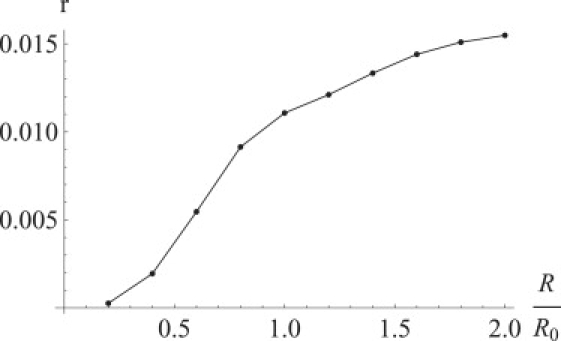
EA of the FRET signal from the slow-rotating fluorophore pair as a function of the distance between fluorophores. The EA for each distance was calculated by numeric averaging of $\frac{2}{5}{P}_2\left(\cos {\beta }_{\text{da}}\right)$ from Eq. 18 over anisotropic angular distribution with the extra weight equal to the FRET efficiency, and normalized by the average FRET efficiency, calculated as described in the legend for Fig. 8. The numeric result is not very precise due to the high dimension of integration. The EA increases with the distance to the finite limit ∼0.016.

Figure 10.

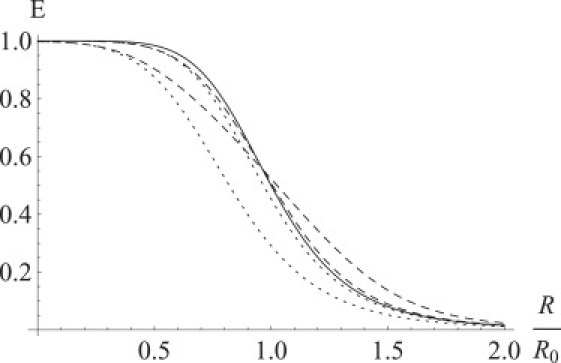
Dependence of the average FRET efficiency on the average distance between fluorophores for the different ranges of the distance diffusion for the molecules with fast rotational diffusion and fixed distance (solid line), fast rotational diffusion and fast distance diffusion (dashed lines), and fast rotational diffusion and slow distance diffusion (dotted lines). The FRET efficiency was numerically calculated for the uniform distance distributions over $\pm 0.2R_0\left(\frac{2}{3}\right)$ and $\pm 0.5R_0\left(\frac{2}{3}\right)$ by averaging FRET efficiency over distance distribution for the slow distance diffusion case and by averaging the kinetic rate and calculating FRET efficiency from it for fast distance diffusion. The smaller width of the distance distribution corresponds to the smaller deviation from the case with fast rotational diffusion and fixed distance.

Supporting Material

Mathematical equations and figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01030-3.