How Subdiffusion Changes the Kinetics of Binding to a Surface

Abstract

Under molecular crowding conditions, biopolymers have been reported to subdiffuse, $\langle {\mathbf{r}}^2\left(t\right)\rangle \simeq t^{\alpha }$, with 0 < α < 1. Here we study the exchange dynamics of such a subdiffusing particle with a reactive boundary using a continuous time random walk approach. We derive the generalized boundary condition and consider the unbinding from the boundary. An ensuing weak ergodicity breaking has profound consequences for material exchange between the boundary and bulk. We discuss the effects in biological contexts such as gene regulation or membrane-bulk exchange processes. We also suggest various methods to experimentally probe the subdiffusive behavior.

Introduction

Random motion of molecules is essential to life. It is a fundamental ingredient of, for example, oxygen and carbon dioxide transport during respiration or the spreading of chemicals and salts inside living cells (1). Such Brownian motion is characterized by the linear time dependence of the mean-squared displacement

$$\langle r^2\left(t\right)\rangle =2dKt$$ (1)

in d spatial dimensions. Here K denotes the diffusion constant of dimensions [K] = cm²/s. Normal diffusion is typically a good description of all diffusing concentrations in dilute homogeneous media. Under more complex conditions, such as the state of molecular crowding that occurs inside cells, small molecules diffuse normally whereas larger biopolymers display some deviations.

In contrast to Eq. 1, anomalous diffusion is defined by the nonlinear time dependence

$$\langle r^2\left(t\right)\rangle =\frac{2d{K}_{\alpha }{t}^{\alpha }}{\Gamma \left(1+\alpha \right)}$$ (2)

of the mean-squared displacement (2–4). The anomalous diffusion exponent α may be larger than 1 (enhanced diffusion or superdiffusion) or between 0 and 1 (subdiffusion). Here the generalized diffusion constant is of dimensions [K_α] = cm²/s^α. Roughly speaking, the dependence from Eq. 2 can be considered as diffusion with a time-dependent diffusivity $\tilde{K}\left(t\right)\propto t^{\alpha -1}$, which means that $\langle r^2\left(t\right)\rangle \propto \tilde{K}\left(t\right)t$. Thus, for subdiffusion, the diffusive spreading decreases with time.

We describe subdiffusion in terms of the continuous time random walk (CTRW) model (2). Accordingly, the motion of a particle is viewed as a random walk with variable jump lengths and variable waiting times spent between successive jumps. Subdiffusion in the CTRW model emerges from a jump length distribution λ(x) with finite variance 〈δx²〉 and a waiting time distribution of the form

$$\mathit{\psi }\left(t\right)\simeq \frac{{\tau }^{\alpha }}{t^{1+\alpha }},\text{with}0<\alpha <1\text{.}$$ (3)

We use the symbol ≃ to denote an asymptotic behavior neglecting constants. This means that individual jumps in this model have a well-defined length $\sqrt{\langle \delta x^2\rangle }$ whereas the sojourn time between successive jumps is so widely distributed that its mean ${\int }_0^{\mathrm{\infty }}t\mathit{\psi }\left(t\right)dt$ diverges. Such a behavior is well known from a wide range of systems (3,4). To name but a few, we refer to charge carrier transport in amorphous semiconductors (5), tracer spreading in subsurface aquifers (6), or subrecoil laser cooling (7).

In biological contexts, subdiffusive behavior has been shown to pertain at relevant timescales (4): The translocation of biopolymers through nanopores exhibits subdiffusion (10–13). In addition, the passive diffusion of larger objects in the cellular cytoplasm may be subdiffusive (8,9). In reconstituted actin networks, tracer beads subdiffuse with a long-tailed waiting time distribution of the kind shown in Eq. 3, where, by variation of the bead size, the anomalous diffusion exponent α was between 0 (complete localization for bead sizes larger than the typical mesh size) and 1 (normal diffusion when the bead is much smaller than the mesh size) (14). Subdiffusion is also found for the motion of lipid granules in living cells with α ≈ 0.75…0.85 (15–17). Similarly, fluorescently labeled mRNA molecules in Escherichia coli cells (α ≈ 0.7) (18), and adeno-associated viruses in HeLa cells (α ≈ 0.5…0.9) (19) have shown subdiffusion. Additional examples of subdiffusion include membrane protein motion (α ≈ 0.5…0.8) (20) and dextrane polymers of various lengths in living cells (α ≈ 0.5…1) (21,22). We note that there exist numerous examples in which single molecule trajectories are analyzed with models of normal diffusion. However, forcing such data to fit normal diffusion leads to a strong scatter of the diffusivities assigned to windows along the time series of the single trajectory (see (23), for instance). Such broad scatter may be related to the finding that the actual motion of the particle is subdiffusive while the time series analysis of a single trajectory suggests normal diffusion. This effect is related to the weak ergodicity breaking of subdiffusion with a waiting time distribution (Eq. 3) (24–25).

One aspect of subdiffusion that has not received much attention is how it might affect the interaction of a particle with a reactive boundary. The answer to this question is of fundamental importance to interface science and technology in which diffusing species can be subject to processes like sorption. However, it will also crucially affect exchange processes inside cells, where we encounter an abundance of two-dimensional boundaries in the form of intracellular membranes and the cell wall as well as one-dimensional interfaces such as the DNA or cytoskeletal elements. Proteins and other biomolecules that subdiffuse will transiently bind to these boundaries and we need to develop extensions of Brownian models if we want to properly include the effects of subdiffusion.

In what follows, we derive a generalization of the reactive boundary condition for a subdiffusive particle. We then further derive the probability densities for the unbinding times from the boundary to the bulk and for the rebinding times after escaping to the bulk. To that end, we consider two different scenarios comprising exponential and anomalous (nonexponential) unbinding from the surface. In the latter case, we uncover a weak ergodicity breaking according to which a particle either stays bound or does not return from the bulk for extremely long times due to the aforementioned scale-free nature of the waiting time distribution (Eq. 3). After establishing the model for the boundary interactions, we discuss its relevance to actual experiments. Moreover, we highlight some consequences for the exchange dynamics in cells with respect to the regulation of gene expression in particular.

A Random Walk into a Reactive Boundary

We first describe a one-dimensional model consisting of a particle that subdiffuses in a direction perpendicular to a reactive surface. The derivation of our main result here, a non-Markovian boundary condition for the particle propagator, is given in the Supporting Material. The approach is similar to one used for a different problem in Sokolov et al. (26). We apply our boundary condition to a cylindrical geometry, which was chosen because it is illustrative of many biological models (such as facilitated diffusion in gene regulation and interactions with cytoskeletal elements). The material in this section extends our earlier work presented in Lomholt et al. (27).

The reactive boundary condition

We consider a one-dimensional lattice with a boundary, as shown in Fig. 1. Most of the lattice consists of bulk sites (sites 1, 2, …) which are not influenced by boundary effects. A particle on the lattice occupies a bulk site for a time distributed according to the waiting time density ψ(t) from Eq. 3. Unlike at a bulk site, a particle at the exchange site (site 0) can bind to the boundary with rate κ. The probability that a particle is unbound if it is at the exchange site up to and including time t is e^−κt. As a particle is immobile while it is bound, the waiting time density for a particle at the exchange site is given by the product form

$${\mathit{\psi }}_{\kappa }\left(t\right)\equiv \mathit{\psi }\left(t\right)e^{-\kappa t}\text{.}$$ (4)

The release of a bound particle is included in our model as an unspecified flux j_release(t) per time.

Figure 1.

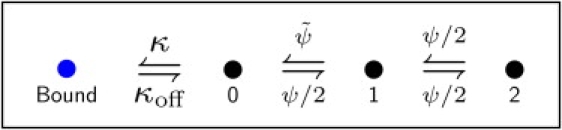
Illustration of the discrete random walk model for surface exchange. From the exchange site 0 next to the boundary, the particle can either bind to the boundary or jump to the bulk (sites 1, 2, …).

In the Supporting Material, a system of master equations is established for the probability density of the particle position. From these master equations, a fractional diffusion equation is derived in the continuum limit where the lattice spacing a goes to zero. Letting A(x, t) be the probability density of finding the particle at position x (corresponding to lattice site i = x/a), the derived fractional diffusion equation reads

$$\frac{\partial A\left(x,t\right)}{\partial t}=K_{\alpha }{}_{0}D_t^{1-\alpha }\frac{{\partial }^{2}A\left(x,t\right)}{\partial x^2}$$ (5)

for x > 0, where K_α = a²/[2τ^α] is the anomalous diffusion coefficient and

$${}_{0}D_t^{1-\alpha }A\left(x,t\right)=\frac{1}{\Gamma \left(\alpha \right)}\frac{\partial }{\partial t}\underset{0}{\overset{t}{\int }}\frac{A\left(x,\stackrel{\prime }{t}\right)}{{\left(t-\stackrel{\prime }{t}\right)}^{1-\alpha }}d\stackrel{\prime }{t}$$ (6)

is the fractional Riemann-Liouville operator (3,4). From the same system of master equations, a reactive boundary condition at x = 0 is derived in the Supporting Material. In the continuum limit, the result is

$$K_{\alpha }{}_{0}D_t^{-\alpha }{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}=-{\mathcal{A}}_0\left(0\right)+k{}_{0}D_t^{-\alpha }A\left(0,t\right)-\underset{0}{\overset{t}{\int }}{j}_{\text{release}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}\text{,}$$ (7)

where the value of ${\mathcal{A}}_0\left(0\right)$ is 1 if the particle is initially at the exchange site and 0 otherwise (see below), and the reaction rate constant k is in the continuum limit

$$\mathit{k}\sim a{\kappa }^{\alpha }\text{.}$$ (8)

Note that the term $-\delta \left(t\right){\mathcal{A}}_0\left(0\right)$ in Eq. 7, corresponding to the probability ${\mathcal{A}}_0\left(0\right)$ that the particle is initially at the exchange site, could equally well have been included in the release current j_release(t) as the particle being released from the boundary at time t = 0.

Some comments about the reactive boundary condition are in order. Note first that each side of Eq. 7 represents the cumulative probability that the particle binds to the boundary within time t. The left-hand side is just the flux through the boundary integrated until t. On the right-hand side, the presence of ${\mathcal{A}}_0\left(0\right)$ means that the cumulative probability has a negative initial value if the particle starts on the boundary. The second term on the right-hand side of Eq. 7 is the integral of the reaction rate j_react(t) for binding at the boundary

$$j_{\text{react}}\left(t\right)=k{}_{0}D_t^{1-\alpha }A\left(0,t\right)\text{.}$$ (9)

The third term is the cumulative release flux from the boundary.

To clarify the meaning of the initial condition ${\mathcal{A}}_0\left(0\right)$ (see the remarks in (29,30)), let us now look at ${\mathcal{A}}_0\left(0\right)$ a little more closely. By differentiating Eq. 7 with respect to time, we can obtain the instantaneous flux through the boundary. The a priori question is whether the initial conditions should be incorporated as a δ-function in the differentiated equation. We will therefore write Eq. 7 after differentiation as

$$K_{\alpha }{}_{0}D_t^{1-\alpha }{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}=B\delta \left(t\right)+k{}_{0}D_t^{1-\alpha }A\left(0,t\right)-j_{\text{release}}\left(t\right)\text{,}$$ (10)

where the constant B remains to be determined. We will determine it by securing that Eq. 10 will lead to the correct expression when Laplace-transformed. Using that for 0 < α < 1, the Laplace-transform of the fractional derivative is ($f\left(u\right)\equiv \mathcal{L}\left\{f\left(t\right)\right\}=\underset{0}{\overset{\mathrm{\infty }}{\int }}f\left(t\right)e^{-ut}dt$ (3))

$$\mathcal{L}\left\{{}_{0}D_t^{1-\alpha }f\left(t\right)\right\}=u^{1-\alpha }f\left(u\right)-\underset{\stackrel{\prime }{t}\to 0}{\lim }{D}_{\stackrel{\prime }{t}}^{-\alpha }f\left(\stackrel{\prime }{t}\right),$$ (11)

we find in Laplace space

$$K_{\alpha }\left[u^{1-\alpha }{\frac{\partial A\left(x,u\right)}{\partial x}|}_{x=0}-\underset{t\to 0}{\lim }{D}_t^{1-\alpha }{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}\right]=B+k\left[u^{1-\alpha }A\left(0,u\right)-\underset{t\to 0}{\lim }{}_{0}D_t^{-\alpha }A\left(0,t\right)\right]-j_{\text{release}}\left(u\right)\text{.}$$ (12)

When comparing with the Laplace-transform of Eq. 7,

$$K_{\alpha }{u}^{-\alpha }{\frac{\partial A\left(x,u\right)}{\partial x}|}_{x=0}=-\frac{{\mathcal{A}}_0\left(0\right)}{u}+k{u}^{-\alpha }A\left(0,u\right)-\frac{j_{\text{release}}\left(u\right)}{u},$$ (13)

we see that we require

$$K_{\alpha }\underset{t\to 0}{\lim }{}_{0}D_t^{-\alpha }{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}-k\underset{t\to 0}{\lim }{}_{0}D_t^{-\alpha }A\left(0,t\right)=-B-{\mathcal{A}}_0\left(0\right)\text{.}$$ (14)

On the other hand, we get directly by taking the limit t → 0 of Eq. 7,

$$K_{\alpha }\underset{t\to 0}{\lim }{}_{0}D_t^{-\alpha }{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}-k\underset{t\to 0}{\lim }{}_{0}D_t^{-\alpha }A\left(0,t\right)=-{\mathcal{A}}_0\left(0\right)-\underset{t\to 0}{\lim }{{\int }_0^{t}j}_{\text{release}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t},$$ (15)

and, therefore, we must require

$$B=\underset{t\to 0}{\lim }{{\int }_0^{t}j}_{\text{release}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}\text{.}$$ (16)

Thus, due to the definition of the Riemann-Liouville fractional derivative, all information on the initial presence and release of a particle at the boundary needs to be absent from the differentiated version of the boundary condition. Instead, one must specify an additional equation if α < 1, namely Eq. 15, to make the set of equations contain all information necessary for the problem to be well posed.

If α = 1, there is no fractional derivative in the differentiated version of the boundary condition. The initial value A₀ (0) then has to be present directly to get the correct boundary condition in Laplace space. In this case, we have

$$K_1{\frac{\partial A\left(x,t\right)}{\partial x}|}_{x=0}=-{\mathcal{A}}_0\left(0\right)\delta \left(t\right)+kA\left(0,t\right)-j_{\text{release}}\left(t\right),$$ (17)

and no additional equation is necessary to include information about the initial conditions.

We note that without any initial presence at and release from the boundary, which is for vanishing ${\mathcal{A}}_0\left(0\right)$ and initial j_release(t), the boundary condition obtained here agrees with the result obtained in Seki et al. (28).

Cylindrical geometry

We now proceed to apply the above formalism to a biologically relevant geometry, namely, a cylindrical geometry that plays a crucial role in any binding process of particles to a linear topology such as the binding to DNA of transcription factors, the binding of molecular motors to cytoskeletal filaments, or the binding of molecules or vesicles to elongated bacilli or their arrays. We represent each of these structures as a finite inner cylinder of radius R₁ and we assume that the motion of the diffusing particle is limited by an outer cylinder of radius R₂ with reflecting boundaries. This allows us to compare our results with the general modeling of facilitated diffusion in the Berg-von Hippel model of gene regulation, where the complex geometry of the DNA configuration is mapped onto a straight cylinder whose radius corresponds to some measure for the distance between neighboring DNA segments (31,32). Other direct examples may be the radius of a nerve cell's dendrite in which motor proteins transport cellular cargo along parallel filaments, DNA trapped in nanochannels, or bacilli in a microfluidic array.

We assume that the cylinder has a length L and that the cylinder is symmetric with respect to the z axis. We also require rotational and translational symmetry around and along this axis. For a particle subdiffusing in the space R₁ < r < R₂ with probability density P(r, t), the reactive boundary condition (Eq. 7) generalizes to

$$2\pi R_1{K}_{\alpha }{}_{0}D_t^{-\alpha }{\frac{\partial P\left(r,t\right)}{\partial r}|}_{r=R_1}=-\frac{P_0}{L}+k_{\text{on}}{}_{0}D_t^{-\alpha }{P\left(r,t\right)|}_{r=R_1},$$ (18)

where k_on = 2πR₁k contains the circumference of the inner cylinder due to the assumption of rotational symmetry. Here we have the initial condition P₀ = 1 if the particle begins at r = R₁, whereas P₀ = 0 otherwise. We neglected j_release since we are only interested in the time for the first binding event on the DNA. The reaction rate with the cylinder per length along the z axis is

$$j_{\text{react}}\left(t\right)=k_{\text{on}}{}_{0}D_t^{1-\alpha }{P\left(r,t\right)|}_{r=R_1},$$ (19)

and the fractional diffusion equation (Eq. 5) turns into its radial equivalent

$$\frac{\partial P\left(r,t\right)}{\partial t}=K_{\alpha }{}_{0}D_t^{1-\alpha }\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial P\left(r,t\right)}{\partial r}\right)\text{.}$$ (20)

To obtain the explicit solution of Eq. 20 under the reactive boundary condition at R₁ and reflecting conditions at R₂, we first Laplace-transform these equations. Denoting by P (r, t)|_t=0 the initial probability density at time t = 0, we obtain

$$2\pi R_1{K}_{\alpha }{u}^{1-\alpha }{\frac{\partial P\left(r,u\right)}{\partial r}|}_{r=R_1}=-\frac{P_0}{L}+k_{\text{on}}{u}^{1-\alpha }{P\left(r,u\right)|}_{r=R_1}$$ (21)

and

$$uP\left(r,u\right)-P\left(r,t=0\right)=K_{\alpha }{u}^{1-\alpha }\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial P\left(r,u\right)}{\partial r}\right)\text{.}$$ (22)

The second boundary condition is

$${\frac{\partial P\left(r,t\right)}{\partial r}|}_{r=R_2}={\frac{\partial P\left(r,u\right)}{\partial r}|}_{r=R_2}=0,$$ (23)

which is equivalent to the condition of vanishing flux into the cylindrical boundary at r = R₂ (33). We can also derive Eq. 23 from our reactive boundary condition if we set P₀ = 0 and k_on = 0 in Eq. 18.

Take $q_{\alpha }\equiv \sqrt{u^{\alpha }/K_{\alpha }}$. If the particle is initially at r = R₁, then P₀ = 1 and P(r, 0) = 0. The solution of Eq. 22 subject to the boundary conditions of Eqs. 21 and 23 is

$$P\left(r,u\right)=\frac{{\left(2\pi L\right)}^{-1}\varphi \left(r,u\right)u^{-1+\alpha }}{I_1\left(R_2{q}_{\alpha }\right)\left[k{K}_0\left(R_1{q}_{\alpha }\right)+K_{\alpha }{q}_{\alpha }{K}_1\left(R_1{q}_{\alpha }\right)\right]+\left[k{I}_0\left(R_1{q}_{\alpha }\right)-K_{\alpha }{q}_{\alpha }{I}_1\left(R_1{q}_{\alpha }\right)\right]K_1\left(R_2{q}_{\alpha }\right)}$$ (24)

with

$$\varphi \left(r,u\right)=\frac{1}{R_1}\left[I_1\left(R_2{q}_{\alpha }\right)K_0\left(r{q}_{\alpha }\right)+I_0\left(r{q}_{\alpha }\right)K_1\left(R_2{q}_{\alpha }\right)\right]\text{.}$$ (25)

I_n(x) and K_n(x) are the modified Bessel functions of the first and second kind, respectively. Now let the particle be initially localized at r = r′ (R₁ < r′ < R₂). We have P₀ = 0 and P(r, t = 0) = δ(r − r′)/(2πr′L). In this case, P(r, u) is equal to the right-hand side of Eq. 24 with the factor of ϕ(r, u) replaced by

$$\chi \left(r,r^{\prime },u\right)=\frac{1}{K_{\alpha }}\left[I_1\left(R_2{q}_{\alpha }\right)K_0\left(r{q}_{\alpha }\right)+I_0\left(r{q}_{\alpha }\right)K_1\left(R_2{q}_{\alpha }\right)\right]\times \{I_0\left(r^{\prime }{q}_{\alpha }\right)\left[k{K}_0\left(R_1{q}_{\alpha }\right)+K_{\alpha }{q}_{\alpha }{K}_1\left(R_1{q}_{\alpha }\right)\right]-\left[k{I}_0\left(R_1{q}_{\alpha }\right)-K_{\alpha }{q}_{\alpha }{I}_1\left(R_1{q}_{\alpha }\right)\right]K_0\left(r^{\prime }{q}_{\alpha }\right)\}$$ (26)

for r > r′. When r < r′, one has to add an additional term

$$\Delta \left(r,r^{\prime },u\right)=\frac{u^{\alpha -1}}{2\pi K_{\alpha }}\left[-I_0\left(r^{\prime }{q}_{\alpha }\right)K_0\left(r{q}_{\alpha }\right)+K_0\left(r^{\prime }{q}_{\alpha }\right)I_0\left(r{q}_{\alpha }\right)\right]$$ (27)

to the expression of P(r, u) for r > r′. Note that χ(r, r′, u) becomes ϕ(r, u) and Δ(r, r′, u) becomes zero in the limit r′ → R₁. Thus, both the distribution P(r, t) and the boundary reaction rate j_react(t) of Eq. 19 become identical in the limit r′ → R₁ to their corresponding quantities obtained when the particle is instead released directly from the boundary at t = 0 (P₀ = 1), which is as we expect.

Fig. 2 shows P(r, t) for subdiffusion and Brownian motion. Each line is a numerical Laplace inversion of Eq. 24 at some t. Here the derivative of P(r, t) with respect to r is negative at r = R₁ in the case of subdiffusion. This differs from Brownian motion, in which it is positive. Such an effect is due to the sensitivity of the reactive boundary condition to the initial condition. An application of ₀D_t^α to Eq. 18 gives the explicit relation

$$2\pi R_1{K}_{\alpha }{\frac{\partial P\left(r,t\right)}{\partial r}|}_{r=R_1}=-\frac{P_0/L}{\Gamma \left(1-\alpha \right)t^{\alpha }}+k_{\text{on}}{P\left(r,t\right)|}_{r=R_1}\text{.}$$ (28)

Hence a necessary and sufficient condition for ${\partial P\left(r,t\right)/\partial r|}_{r=R_1}>0$ is

$$t>{\left(\frac{P_0/L}{k_{\text{on}}\Gamma \left(1-\alpha \right)P\left(r,t\right){|}_{r=R_1}}\right)}^{1/\alpha }\text{.}$$ (29)

Note that for α = 1, the right-hand side vanishes and the slope is positive at all times, in agreement with Brownian motion.

Figure 2.

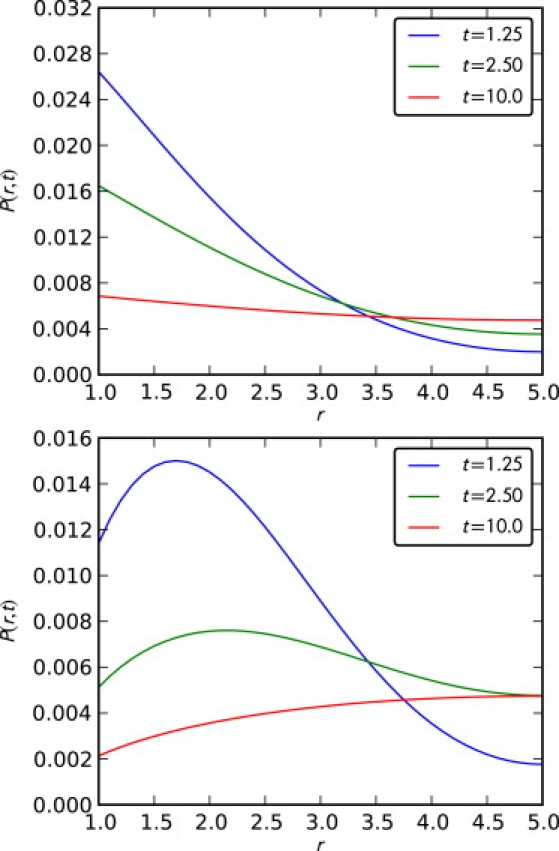
Probability density P(r, t) with α = 0.75 (top) and α = 1 (bottom). Here R₁ = 1 and R₂ = 5. Other parameters such as K_α, k, and L were set equal to one.

Rebinding

The probability density for the time, after unbinding at t = 0, when the particle rebinds to the reactive boundary is ℘_reb(t) = j_react(t)L. Hence ${\wp }_{\text{reb}}\left(u\right)=k_{\text{on}}{u}^{1-\alpha }{P\left(r,u\right)|}_{r=R_1}L$, because $j_{\text{react}}\left(u\right)=k_{\text{on}}{u}^{1-\alpha }{P\left(r,u\right)|}_{r=R_1}$. Using the limiting forms for small arguments of the modified Bessel functions (34), we obtain for our finite domain

$${\wp }_{\text{reb}}\left(u\right)\sim 1-S{u}^{\alpha }/k_{\text{on}}$$ (30)

at small u, where S = π(R₂² − R₁²) is the cylindrical cross section. This gives the long time behavior of the rebinding time density

$${\wp }_{\text{reb}}\left(t\right)\sim \alpha S/\left[k_{\text{on}}\Gamma \left(1-\alpha \right)t^{1+\alpha }\right]\text{.}$$ (31)

This result could equally be inferred from the knowledge that, for Brownian motion, the first-passage time density in a finite domain decays exponentially. By standard subordination arguments (4), the power-law behavior t^−1−α emerges. An analogous expansion at large u leads to

$${\wp }_{\text{reb}}\left(u\right)\simeq k/\left(\sqrt{K_{\alpha }}{u}^{\alpha /2}\right),$$ (32)

corresponding to the short time behavior

$${\wp }_{\text{reb}}\left(t\right)\simeq k/\left[\Gamma \left(\alpha /2\right)\sqrt{K_{\alpha }}{t}^{1-\alpha /2}\right]$$ (33)

of the rebinding time density. This latter case is but the subordination of the first-passage time density for an infinite domain when a particle is released in immediate vicinity of a planar surface (see Fig. 3).

Figure 3.

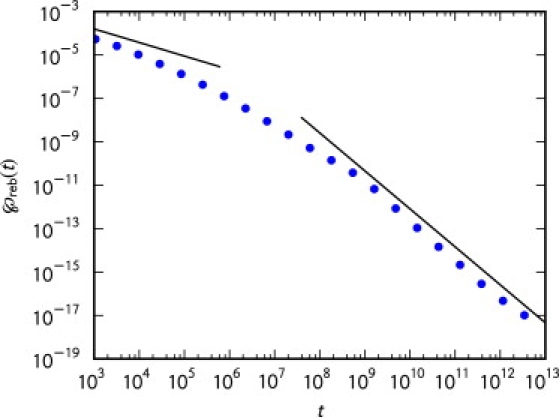
Rebinding time density ℘_reb(t) with α = 0.75 and τ = 1. The points were generated from simulations on a discrete one-dimensional lattice with n = 10³ sites. We evolved 2.5 × 10⁷ trajectories for a total time of 10¹³. Other parameters were τ = 1, κ = 0.001, and κ_off = 0.000001. The lines correspond to the asymptotic expansions in Eqs. 31 and 33, where, in Eq. 31, S/k_on is replaced with its one-dimensional analog na/k = n/κ^α , with $k/\sqrt{K_{\alpha }}={\kappa }^{\alpha }\sqrt{2{\tau }^{\alpha }}$.

Bulk Exchange

Anomalous unbinding

Consider now a subdiffusive particle that is initially bound at the boundary. We allow the particle to unbind with rate κ_off. The full escape of the particle to the bulk consists of unbinding from the boundary to site 0, and then jumping from site 0 to site 1. If the particle rebinds to the boundary before it jumps to site 1, then the process starts again. Thus, the unbinding time density ℘_unb(t) depends on the probability that the particle is unbound and the probability density for jumping to site 1.

Let P_bound(t) be the probability that the particle is bound at time t, given that it was bound at t = 0 and that it has not been allowed to jump. This satisfies the coupled system

$$\frac{d{\text{P}}_{\text{bound}}\left(t\right)}{dt}=-{\kappa }_{\text{off}}{\text{P}}_{\text{bound}}\left(t\right)+\kappa {\text{P}}_{\text{unbound}}\left(t\right),$$ (34a)

$$\frac{d{\text{P}}_{\text{unbound}}\left(t\right)}{dt}={\kappa }_{\text{off}}{\text{P}}_{\text{bound}}\left(t\right)-\kappa {\text{P}}_{\text{unbound}}\left(t\right)\text{.}$$ (34b)

Here P_unbound(t) = 1 − P_bound(t) is the probability that the particle is unbound at t. The solutions of the expressions in Eq. 34 with the initial condition P_bound(0) = 1 are

$$P_{\text{bound}}\left(t\right)=\frac{\kappa }{\kappa +{\kappa }_{\text{off}}}+\frac{{\kappa }_{\text{off}}}{\kappa +{\kappa }_{\text{off}}}{e}^{-\left(\kappa +{\kappa }_{\text{off}}\right)t},$$ (35a)

$$P_{\text{unbound}}\left(t\right)=\frac{{\kappa }_{\text{off}}}{\kappa +{\kappa }_{\text{off}}}-\frac{{\kappa }_{\text{off}}}{\kappa +{\kappa }_{\text{off}}}{e}^{-\left(\kappa +{\kappa }_{\text{off}}\right)t}\text{.}$$ (35b)

We assume that the dynamics of jumps from site 0 to site 1 are identical to those of jumps from site 1 to site 0. This means the particle jumps from site 0 to site 1 with probability 1/2 after time t elapses, with ψ(t) being the probability density of t. The remaining probability corresponds to a jump toward the boundary, in which case the particle returns to site 0 and waits for another opportunity to jump. So the probability density for the time when the particle jumps from site 0 to site 1 is the infinite series of convolutions

$$\tilde{\mathit{\psi }}\left(t\right)=\frac{\mathit{\psi }\left(t\right)}{2}+{\int }_0^{\text{t}}\frac{\mathit{\psi }\left(t-\stackrel{\prime }{t}\right)}{2}\frac{\mathit{\psi }\left(\stackrel{\prime }{t}\right)}{2}d\stackrel{\prime }{t}+{\int }_0^t\frac{\mathit{\psi }\left(t-\stackrel{\prime }{t}\right)}{2}{\int }_0^{\stackrel{\prime }{t}}\frac{\mathit{\psi }\left(\stackrel{\prime }{t}-t^{″}\right)}{2}\frac{\mathit{\psi }\left(t^{″}\right)}{2}d{t}^{″}d\stackrel{\prime }{t}+\dots ,$$ (36)

where successive terms represent increasing numbers of jumps toward the boundary. In the Laplace domain, $\tilde{\mathit{\psi }}\left(u\right)$ is the geometric series

$$\tilde{\mathit{\psi }}\left(u\right)=\frac{\mathit{\psi }\left(u\right)}{2}+\frac{\mathit{\psi }{\left(u\right)}^2}{4}+\frac{\mathit{\psi }{\left(u\right)}^3}{8}+\cdots =\frac{\mathit{\psi }\left(u\right)/2}{1-\mathit{\psi }\left(u\right)/2}\sim 1-2{\left(u\tau \right)}^{\alpha }\text{.}$$ (37)

Define $R\left(t\right)=\tilde{\mathit{\psi }}\left(t\right){\text{P}}_{\text{unbound}}\left(t\right)=\tilde{\mathit{\psi }}\left(t\right)\left[1-{\text{P}}_{\text{bound}}\left(t\right)\right]$ and $\Pi \left(t\right)=\tilde{\mathit{\psi }}\left(t\right){\text{P}}_{\text{bound}}\left(t\right)$. We can write ℘_unb(t) as

$${\wp }_{\text{unb}}\left(t\right)=R\left(t\right)+{\int }_0^{t}R\left(t-\stackrel{\prime }{t}\right)\Pi \left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}+{\int }_0^{t}R\left(t-\stackrel{\prime }{t}\right){\int }_0^{\stackrel{\prime }{t}}\Pi \left(\stackrel{\prime }{t}-t^{″}\right)\Pi \left(t^{″}\right)d{t}^{″}d\stackrel{\prime }{t}+\cdots ,$$ (38)

so

$${\wp }_{\text{unb}}\left(u\right)=\tilde{\mathit{\psi }}\left(u\right)-\Pi \left(u\right)+\left[\tilde{\mathit{\psi }}\left(u\right)-\Pi \left(u\right)\right]\Pi \left(u\right)+\left[\tilde{\mathit{\psi }}\left(u\right)-\Pi \left(u\right)\right]\Pi {\left(u\right)}^2+\cdots =\frac{\tilde{\mathit{\psi }}\left(u\right)-\Pi \left(u\right)}{1-\Pi \left(u\right)}\text{.}$$ (39)

Note that Π(u) has the exact form

$$\Pi \left(u\right)=\frac{\kappa }{\kappa +{\kappa }_{\text{off}}}\tilde{\mathit{\psi }}\left(u\right)+\frac{{\kappa }_{\text{off}}}{\kappa +{\kappa }_{\text{off}}}\tilde{\mathit{\psi }}\left(u+\kappa +{\kappa }_{\text{off}}\right)\text{.}$$ (40)

Collecting the results, we obtain at small u

$${\wp }_{\text{unb}}\left(u\right)\simeq 1-\frac{\kappa +{\kappa }_{\text{off}}}{{\kappa }_{\text{off}}{\left(\kappa +{\kappa }_{\text{off}}\right)}^{\alpha }}{u}^{\alpha }\equiv 1-u^{\alpha }/k_{\text{off}},$$ (41)

where k_off is fixed in the continuum limit leading to a scaling ${\kappa }_{\text{off}}\simeq a^{1-1/\alpha }$ that is weak compared with $\kappa \simeq a^{-1/\alpha }$ and thus k_off ∼ κ_off/κ^1−α. The effect of the crowded environment of the bulk on the unbinding ends up being a translation of the exponential distribution of the unbinding times to a power-law

$${\wp }_{\text{unb}}\left(t\right)\text{∼}\alpha /\left[\Gamma \left(1-\alpha \right)k_{\text{off}}{t}^{1+\alpha }\right]\text{.}$$ (42)

Taking the continuum limit as before (without assuming small u), we obtain the complete distribution

$${\wp }_{\text{unb}}\left(u\right)=\frac{1}{1+u^{\alpha }/k_{\text{off}}},$$ (43)

which means that the probability of the particle being bound after a time t decays according to a Mittag-Leffler pattern:

$$1-{\int }_0^t{\wp }_{\text{unb}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}=E_{\alpha }\left(-k_{\text{off}}{t}^{\alpha }\right)\text{.}$$ (44)

At small t, this leads to another power-law,

$${\wp }_{\text{unb}}\left(t\right)\sim \frac{k_{\text{off}}}{\Gamma \left(\alpha \right)t^{1-\alpha }}$$ (45)

(see Fig. 4).

Figure 4.

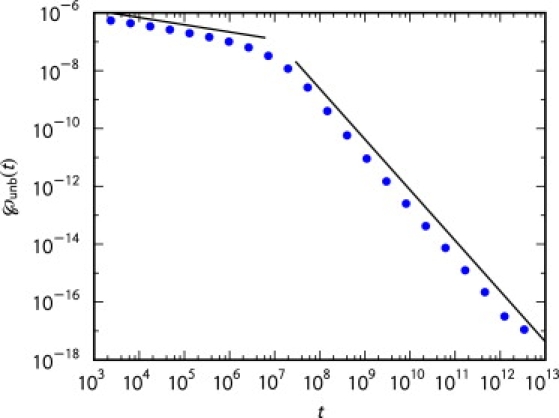
Unbinding time density ℘_unb(t) with α = 0.75 and τ = 1. The points were generated from simulations on a discrete lattice. We evolved 2.5 × 10⁷ trajectories for a total time of 10¹³. Other parameters were κ = 0.001 and κ_off = 0.000001. The lines correspond to the asymptotic expansions in Eqs. 42 and 45.

Above we assumed that at time t = 0 an event had just occurred where the environment had allowed for jumping between sites 0 and 1. While this is not strictly true, since the particle binds only after a time related to 1/κ after it jumped to site 0 from site 1, the error resulting from this assumption vanishes in the continuum limit. This happens because the unbinding time 1/κ_off becomes infinitely larger than the other two timescales of the problem, 1/κ and τ.

We note here the completely non-Markovian nature of the exchange site in the case of subdiffusion. When the particle jumps to site 0 from site 1, the probability that it returns to site 1 without binding is

$${\int }_0^{\mathrm{\infty }}\tilde{\mathit{\psi }}\left(t\right)e^{-\kappa \text{t}}dt=\tilde{\mathit{\psi }}\left(u=\kappa \right),$$ (46)

which approaches unity in the continuum limit since the timescale associated with jumping between lattice sites vanishes faster than the reaction time, κτ → 0. Similarly, when the particle enters the exchange site from the bound state, then the probability that the particle returns to the bound state approaches unity once the continuum limit is taken. This follows since the distribution of the effective unbinding times ℘_unb(t) converges whereas the unbinding rate κ_off diverges to infinity when α < 1.

Weak ergodicity breaking

In the above scenario, we therefore find that both unbinding to the bulk and rebinding from the bulk to the reactive boundary are associated with waiting time densities of the long-tailed form $\wp \simeq t^{-1-\alpha }$. This implies the divergence of the mean waiting times $\langle t\rangle \sim \underset{0}{\overset{\mathrm{\infty }}{\int }}t\wp \left(t\right)dt=\mathrm{\infty }$. The lack of a characteristic timescale separating microscopic and macroscopic events gives rise to aging (35) and weak ergodicity breaking (36). The latter, whose consequences we explore here, is the result of a few single events dominating time-averages. Consequently these time-averages become stochastic quantities and therefore different from the corresponding ensemble averages. Note that the term “weak ergodicity breaking” is meant to distinguish this phenomenon from systems in which part of the phase space can never be reached (strong ergodicity breaking).

Define the time-averaged probability that the particle is bound as

$${\overline{p}}_{\text{bound}}=\underset{\text{t}\to \mathrm{\infty }}{\lim }{t}_{\text{bound}}/t\text{.}$$ (47)

This has the probability density (37)

$$\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)={\delta }_{\alpha }\left(\beta =k_{\text{on}}/\left(S{k}_{\text{off}}\right),{\overline{p}}_{\text{bound}}\right)$$ (48)

with the Lamperti δ-function (38)

$${\mathit{\delta }}_{\alpha }\left(\mathit{\beta },\mathit{\rho }\right)=\frac{{\pi }^{-1}\sin \left(\pi \alpha \right)\mathit{\beta }{\mathit{\rho }}^{\alpha -1}{\left(1-\mathit{\rho }\right)}^{\alpha -1}}{{\mathit{\beta }}^2{\left(1-\mathit{\rho }\right)}^{2\alpha }+{\mathit{\rho }}^{2\alpha }+2\mathit{\beta }{\left(1-\mathit{\rho }\right)}^{\alpha }{\mathit{\rho }}^{\alpha }\cos \left(\pi \alpha \right)}\text{.}$$ (49)

Note that $\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)$ is normalized and reached in the long time limit. It is independent of t and in that sense, stationarity is obtained. However, while in the Brownian limit α = 1, ergodicity and a sharply peaked behavior are recovered: for $\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)=\delta \left({\overline{p}}_{\text{bound}}-k_{\text{on}}/S{k}_{\text{off}}\right)$. The distinct behavior of the Lamperti δ-function is shown in Figs. 5 and 6.

Figure 5.

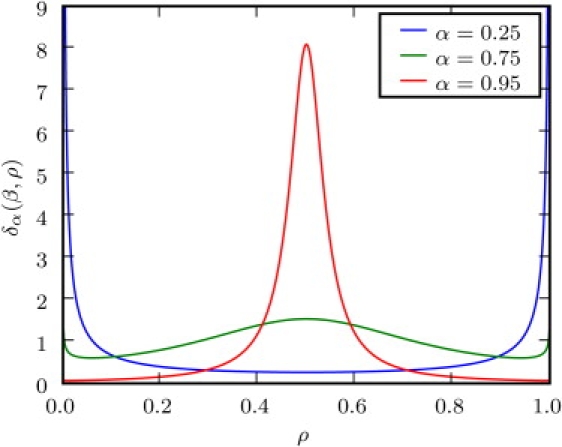
Lamperti δ-function δ_α(β, ρ) with β = 1. In the limit α → 1, a sharp delta peak is recovered.

Figure 6.

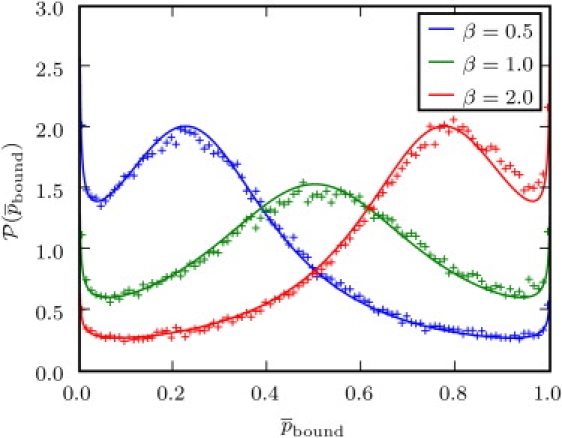
Probability distribution $\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)$ with α = 0.75 and τ = 1. The points were generated from simulations on a discrete lattice. Other parameters were chosen to give the specific values of β.

The distribution $\mathcal{P}\left({\overline{\mathcal{P}}}_{\text{bound}}\right)$ peaks when ${\overline{p}}_{\text{bound}}$ is 0 or 1, with a smaller maximum in between these peaks. Thus, a particle is typically either bound or unbound in a single trajectory, independently of the duration of the trajectory. This nonergodic behavior is imposed on the system by the probability $\underset{t}{\overset{\mathrm{\infty }}{\int }}\mathit{\psi }\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}\simeq t^{-\alpha }$ of never moving, which decays very slowly. For an ensemble of particles, k_on/k_off defines the nonspecific binding constant K_ns, which is equal to the ratio N_bound/(SN_unbound) of bound and unbound particles normalized by the cross section (39). Then $\langle {\overline{p}}_{\text{bound}}\rangle ={\left(1+S{k}_{\text{off}}/k_{\text{on}}\right)}^{-1}$ is the ensemble average for a particle to be bound. The behavior of $\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)$ over many trajectories corresponds to the form $\mathcal{P}\left({\overline{p}}_{\text{bound}}\right)=\delta \left({\overline{p}}_{\text{bound}}-k_{\text{on}}/\left[k_{\text{on}}+S{k}_{\text{off}}\right]\right)$ (37). Observe that the smaller the cross section S gets, the more likely it is that a particle is bound, which is as it should be.

Exponential unbinding

What if the subdiffusion of the particle is not due to crowded surroundings blocking the motion of the particle? For instance, the particle might instead slow its own motion by adsorption to immobile parts of the environment. In this case, the time t in the waiting time distribution ψ(t) for jumps is the time since the start of the latest adsorption event. The broadness of ψ(t) could be brought about by large variations of adsorption strengths, similar to the random trap model (58), or by a particle of polymeric nature entangling with the environment. A consequence of this is that the probability of jumping to site 1 after unbinding to site 0 is now

$$\underset{0}{\overset{\mathrm{\infty }}{\int }}\tilde{\mathit{\psi }}\left(t\right)e^{-\kappa t}dt=\tilde{\mathit{\psi }}\left(u=\kappa \right)\sim 1$$ (50)

in the continuum limit. Thus the particle escapes from the boundary whenever it unbinds, so that the effective unbinding time simply has the probability density ${\wp }_{\text{unb}}\left(t\right)={\kappa }_{\text{off}}{e}^{{\kappa }_{\text{off}}t}$. The mean unbinding time is now finite, while the mean rebinding time remains infinite. This means that at long times the particle is most likely to be found in the bulk. We here quantify this process of the particle getting trapped in the bulk.

Let ψ_cycle(t) be the probability density for the time of one unbinding and rebinding cycle. This is the convolution

$${\mathit{\psi }}_{\text{cycle}}\left(t\right)=\underset{0}{\overset{t}{\int }}{\wp }_{\text{unb}}\left(t-\stackrel{\prime }{t}\right){\wp }_{\text{reb}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t},$$ (51)

so, for small u,

$${\mathit{\psi }}_{\text{cycle}}\left(u\right)={\wp }_{\text{unb}}\left(u\right){\wp }_{\text{reb}}\left(u\right)\sim \left(1-u/k_{\text{off}}\right)\left(1-u^{\alpha }S/k_{\text{on}}\right)\sim 1-u^{\alpha }S/k_{\text{on}},$$ (52)

to leading order in small u. Therefore the distribution of cycle times has the same tail as the probability density for the rebinding, ${\mathit{\psi }}_{\text{cycle}}\left(t\right)\simeq S/\left(k_{\text{on}}{t}^{1+\alpha }\right)$.

An immediate way to obtain results for the unbinding-rebinding process is to view it as a one-sided Lévy flight with jump length distribution ψ_cycle(t) and jump rate κ_off. In this picture, the first-passage time for jumping a distance t corresponds to the time t_bound that the particle is bound during the time t. Results obtained previously for one-sided Lévy flights (40,41) tell us for instance that the first moment of the first passage time is

$$\langle t_{\text{bound}}\rangle =\frac{t^{\alpha }}{{\kappa }_{\text{off}}\left(S/k_{\text{on}}\right)\Gamma \left(1+\alpha \right)}\text{.}$$ (53)

The probability p_bound(t) that the particle is bound at t can be found as the derivative of 〈t_bound〉. To see this, we define an indicator variable I_bound(t), which is 1 if the particle is bound at t and 0 otherwise. Then $t_{\text{bound}}={\int }_0^t{I}_{\text{bound}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}$ and

$$p_{\text{bound}}\left(t\right)=\langle I_{\text{bound}}\left(t\right)\rangle =\langle \frac{d}{dt}{\int }_0^t{I}_{\text{bound}}\left(\stackrel{\prime }{t}\right)d\stackrel{\prime }{t}\rangle =\frac{d}{dt}\langle t_{\text{bound}}\rangle =\frac{\alpha }{{\kappa }_{\text{off}}\left(S/k_{\text{on}}\right)\Gamma \left(1+\alpha \right)t^{1-\alpha }}\text{.}$$ (54)

The fight between the boundary and the bulk is uneven: the particle is more and more likely to be found in the bulk as time passes.

Another question that can be answered immediately in this formalism is: at a given late time $t\gg {\kappa }_{\text{off}}^{-1}$, what is the distribution of waiting times τ for the next binding to the boundary? In the one-sided Lévy flight picture where the cycle times correspond to jump lengths, this waiting time is the leapover at the first passage. From the literature (40,41), we therefore get that the waiting time density for the next binding is

$${\mathit{\psi }}_{\text{binding}}\left(\tau \right)=\frac{\sin \left(\pi \alpha \right)}{\pi }\frac{t^{\alpha }}{{\tau }^{\alpha }\left(t+\tau \right)}\text{.}$$ (55)

The tail of this distribution ψ_binding(τ) ∼ [ sin(πα)/π]t^α/τ^1+α becomes heavier and heavier at large t, and thus the waiting times for binding become longer and longer. Note also that the distribution is independent of the rate constants, and therefore solely determined by the anomalous exponent α for the bulk dynamics.

Equivalence of the two scenarios at finite experimental resolution

In a discrete lattice model, the difference between exponential and anomalous unbinding dynamics changes the occupation time of the exchange site. In the continuum picture, this means that the unbinding time is broadly distributed for the case of anomalous unbinding, contrasting the exponential unbinding with finite characteristic unbinding time in the opposite case. However, in a typical experiment it may be impossible to distinguish whether the particle is actually at the exchange site or just close to the surface. Given an experimental resolution Δ in the direction perpendicular to the surface, we would therefore consider a particle bound if it is in the hollow cylinder with radius in the interval (R₁, R₁ + Δ). If Δ is sufficiently large such that many waiting events occur before leaving the Δ-zone, then by our usual subordination argument we see that the residence time PDF to remain in this cylinder volume would contain a tail that scales as

$${\wp }_{\Delta }\left(t\right)\simeq t^{-1-\alpha },$$ (56)

the same way as the returning time PDF ${\wp }_{\Delta }\left(t\right)$ from the bulk to the Δ-zone, such that we return to the scenario of weak ergodicity breaking. In this type of experiment the likelihood that a particle remains in the volume (R₁, R₁ + Δ), or does not return to this volume for very long times could be high, and in that sense both anomalous and exponential unbinding cases become equivalent.

To gauge this effect, one should determine the magnitude Δ of the resolution. It could be, for instance, the width of the focal spot of a confocal microscopy setup. Or it could correspond to the Förster radius of a fluorophore attached to the particle interacting with dyes on the surface.

Measuring Weak Ergodicity Breaking

There are various ways one could, in principle, measure the occurrence of the weak ergodicity breaking, three of which are discussed here (compare Fig. 7).

Figure 7.

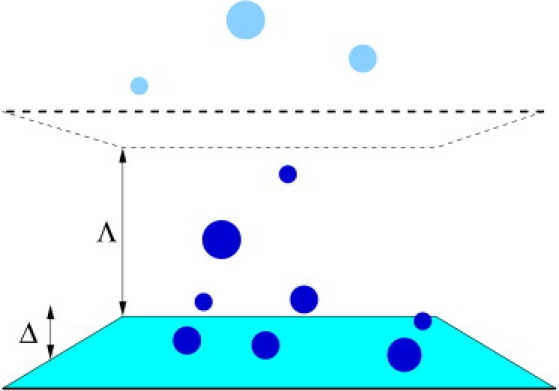
Measuring weak ergodicity breaking. Particles initially bound to a surface will eventually unbind and start to diffuse in the bulk. One can i), measure their immediate unbinding from the surface; ii), observe their leaving a focal zone of width Δ; or iii), observe their first passage across a plane at a distance Λ from the surface.

First-passage measurement

One possibility is to measure the first passage of particles, as already suggested in Condamin et al. (42). Namely, one releases a particle a certain distance Λ away from a plane and measures the density ℘_fp of passage across this plane. While for regular diffusion this density would behave like ${\wp }_{\text{fp}}\simeq t^{-3/2}$, for longer times for CTRW subdiffusion one would observe the scaling ${\wp }_{\text{fp}}\simeq t^{-1-\alpha /2}$ (4,10,43). This result is valid for an infinite domain, but will hold for a sufficiently large container. In a finite domain, the classical exponential behavior ${\wp }_{\text{fp}}\simeq \exp \left(-t/{\tau }_{\text{fp}}\right)$ would again change to ${\wp }_{\text{fp}}\simeq t^{-1-\alpha }$. Finally, one could also measure the particle under the influence of an external force field. If this force F is constant and directed toward the point of first passage, the result for normal diffusion is ${\wp }_{\text{fp}}\simeq t^{-3/2}\exp \left(-{\left[\mathrm{\Lambda }-Ft\right]}^2/\left[4Kt\right]\right)$. For CTRW subdiffusion, this behavior would change asymptotically to ${\wp }_{\text{fp}}\simeq t^{-1-\alpha }$ (10).

Experimentally one could realize the first-passage scenario by releasing a particle from an optical trap and measure its passage across a plane by single particle tracking. Or one could use particles carrying a charge, initially forcing them against a surface by an electrical field. After switching off the electrical field, the particles are released and one can measure their first passage across a plane. To avoid too early bleaching, one could illuminate only one part of the volume and regard the first passage into the illuminated region by recording the moment when a particle starts to fluoresce.

Leaving a focus zone

A similar effect would be to measure when the particles leave a focus zone. For instance, one could attach particles to a surface either by chemical/adhesive/ionic bonds or by forcing them against the surface by an external field and observe them with a confocal microscope. Once the particles leave the focus of width Δ, they disappear from the confocal image. When Δ is sufficiently large, the escape from the focal zone corresponds to a first-passage problem in a finite interval, and the regular Brownian behavior ${\wp }_{\text{fp}}\simeq \exp \left(-t/{\tau }_{\text{fp}}\right)$ would change to the power-law form ${\wp }_{\text{fp}}\simeq t^{-1-\alpha }$ for CTRW subdiffusion.

A similar experiment could be done with fluorescent dyes. As long as the particle is close enough to the surface, a resonant transfer between surface labels and the dye on the particle would maintain fluorescence. Once the particle is separated from the surface by a distance more than Δ, fluorescence would cease.

Unbinding time measurement

The above two first-passage type assays consider the motion perpendicular to some surface. Conversely, one might use the lateral motion of the particles to directly measure their unbinding. While a particle is still bound to the surface, its lateral motion will be small. Once unbound, this lateral motion will increase significantly and could be used to observe the actual unbinding time. For typical chemical bonds in an environment allowing Brownian motion of the particle, we would expect the classical exponential unbinding behavior to be

$${\wp }_{\text{unbind}}\simeq \frac{1}{{\tau }_{\text{unbind}}}\exp \left(-\frac{t}{{\tau }_{\text{unbind}}}\right)\text{.}$$ (57)

Once the vicinal environment causes subdiffusion as in the model developed here, the density of unbinding times would turn to the power-law form

$${\wp }_{\text{unbind}}\simeq t^{-1-\alpha },$$ (58)

as derived above.

Alternatively, one could prepare many samples with particles attached to the surface, remove the bulk liquid after some time, and dry the surface. Counting the remaining particles after different times could reconstruct the unbinding time distribution. Or one could introduce a fluorescent dye connected with a charge of the same sign as charges of the surface (for instance, mica is negatively charged). Once unbound from the surface, the charges would repel each other, and the dye fluorescence, initially masked by the larger particle of interest, by rotational diffusion would become visible to an optical device.

Other observable signatures

Apart from the mean-squared displacement or the first-passage and unbinding scenarios sketched above, single-molecule trajectories encode additional information. Thus, one may be able to collect sufficient statistics to reconstruct the underlying waiting-time distribution itself, as demonstrated for beads in actin networks producing the form from Eq. 3 (14). Such an observation would naturally be the most direct proof for CTRW-type subdiffusion.

In current records for tracked particles in cells this has not been achieved to date, to our knowledge. However, for the data recorded in vivo for both the motion of granule particles in yeast cells (16) and for the traces described by fluorescently labeled mRNA molecules in E. coli cells (18) one observes a quite distinct scatter of the amplitudes in the log-log plots of the mean-squared displacement. This corresponds to a scatter of the generalized diffusion constant. Why should this be? Due to the fact that CTRW subdiffusion is associated with a diverging characteristic timescale of the distribution of waiting times a single particle may get arrested in space over times whose span is of the order of magnitude of the entire measurement time, and therefore rare events can influence the statistics even in the long time limit. The scale-free form (Eq. 3) of the waiting-time distribution indeed causes a weak ergodicity breaking (36,37) that in turn is responsible for the scatter in the data. This effect has recently obtained some attention (24,25). The scattering width could actually be quantified analytically for both free diffusion and under the impact of a constant external force field (25). Thus, the scatter of the observable that may at first appear as an undesired effect of subdiffusion may actually turn out to be a useful measure in analyzing the behavior of the system.

Finally one may also extract information from the trajectory itself. Namely, the existence of long immobilization periods versus fast transitions may indicate subdiffusion of the type presented here (compare the trajectories in (14)).

Relevance for Surface-Bulk Exchange

We derived the generalized reactive boundary condition for the interaction of a subdiffusive particle with a boundary characterized by a reaction rate κ. It was shown that the distributions of unbinding and rebinding times become long-tailed in the presence of waiting times with a diverging characteristic waiting time. In general, the power-law behavior of waiting times of the form from Eq. 3 will be cut off at times larger than some t_max, and the diffusion eventually turn over to Brownian motion. For crowding conditions, this scale t_max will depend on the size of the particle as well as its shape (for instance, globular versus coil-like). At present, the magnitude of this scale t_max is not known, although it appears from a number of experiments that the power-law behavior is persistent enough to significantly alter the diffusion properties of larger biopolymers, and even larger particles in living cells.

We now address the question how the weak ergodicity breaking of the particle interaction with a reactive boundary derived above influences the exchange between the surface and the vicinal bulk. We distinguish two biologically relevant cases, namely, a linear and a planar surface. In that course, we assume that the subdiffusion of the particles of interest is in the class of the CTRW subdiffusion as described in our formalism. Such subdiffusion, with power-law waiting-time distributions, was shown to exist in reconstituted actin networks (14). For larger biomolecules such as messenger RNA and transcription factors, the strong scatter in the experiments reported in Golding and Cox (18) in E. coli cells, suggests the presence of CTRW-like subdiffusion as well. Finally, also the strong scatter in Platani et al. (23) indicates similar effects. Whether this is indeed so has to remain open, until results from experiments of the type described above become available. We discuss possible consequences for the surface exchange of binding proteins in the following.

Exchange with a linear surface

Transcription factors (TFs) are DNA-binding proteins that regulate the transcription of a specific gene. These may occur in very small numbers (a few to some hundred per cell corresponding to concentrations down to nM (44)), and the stability of many genetic circuits usually requires that a TF is always bound at some operator site on the DNA (45–47). Although the random motion of TFs in the dilute conditions of most in vitro experiments is Brownian, molecular crowding (48–52) causes subdiffusion of the TFs (21,22). As a consequence of the nonergodic behavior demonstrated here, an appreciable portion of TFs will typically stay close to their binding site with a characteristic timescale that diverges. This greatly reduces the probability that a TF will unbind from the DNA and escape to the volume. However, a TF that does escape has an infinite mean time for returning to the DNA.

There also exists a large class of TFs, such as the Lac and bacteriophage λ-repressors in E. coli (47), whose specific binding sites are located immediately adjacent to their coding region. It is likely that biochemical production occurs very close to the coding region (colocalization) (53–56), and therefore from the specific binding site. The weak ergodicity breaking would then help keep those TFs within a small volume around their complete biochemical cycle, very likely leading to a significant increase in the stability of the regulation of that particular gene. Subdiffusion caused by molecular crowding could therefore be very beneficial for living cells, allowing them to maintain the concentrations of even vital TFs at nanomolar levels. This may significantly impact our understanding of gene regulation in vivo and identify the need to perform experiments much closer to crowding conditions in order to obtain meaningful data for the in vivo situation.

Exchange with a planar surface

Consider a vesicle at the cell wall created by endocytosis. To make its way into the cell, it needs to detach from the cell wall. Due to the crowding and the presence of the cytoskeleton in the cell, this process may be inhibited by a long-tailed waiting-time distribution Such vesicles, that is, would typically need a very long time to actually move away from the surface. This observation may have relevance to processes involved with drug delivery for which the vesicle would be supposed to act as a vehicle toward other cell compartments. In this case, it would therefore be vital to engineer the system such that active transport by motors assists the motion of the vesicle. Conversely, in other cases it may be profitable for the cell if vesicles stay close to the surface longer, where they may be less dangerous for cellular entities until they may be attacked by cellular defense mechanisms.

Conclusions

Ever since Arthur Kornberg's “Ten Commandments” commentary (57), biochemists have been aware of the essential role of molecular crowding in the performance of enzymes. More recently, experiments indicate that transport processes of larger molecules in the living cell are also affected by crowding.

Subdiffusion may represent a vital part in biological processes on the cellular and subcellular level. At present, it has not been quantitatively established on what timescales subdiffusion persists and how the associated anomalous diffusion exponents depend on the size of the diffusing particle and the exact environmental conditions of molecular crowding. In this work we suggest a number of methods to establish the presence of subdiffusion in crowded environments and test whether indeed it belongs to the class of CTRW processes. The latter point should be true for vesicles or granules whose size is of the order of or larger than the cytoskeleton mesh. For biopolymers of the typical size of transcription factors (some 5 nm in diameter), this remains to be proven experimentally. A strong scatter of the (anomalous) diffusivity in single particle traces will speak in favor of the presence of weak ergodicity breaking and therefore CTRW subdiffusion with a diverging characteristic waiting time (or, more precisely, with a cutoff time t_max that is long enough to be relevant for the process under consideration).

Subdiffusion in the bulk changes the material exchange dynamics between surfaces and the bulk and also renders bulk diffusion itself less efficient. In turn, it will keep a considerable portion of the subdiffusing particles close to the reactive boundary. Given the emerging knowledge of coregulative elements and the astonishing precision of genetic control units at nanomolar transcription factor concentrations, the pronouncedly more local picture of gene regulation, which may eventually grow from our better understanding of the nature of intracellular diffusion, may be a result of an evolutionary development toward a high economy of transcription factors and other elements of cellular control.

Supporting Material

Additional equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00983-7.